Simplified Relations for the Martian Night-Time OH* Suitable for the Interpretation of Observations
Abstract
1. Introduction
2. Analytical Formulae Derivation
2.1. Peak Concentration of the Excited Hydroxyl Layer and Its Altitude
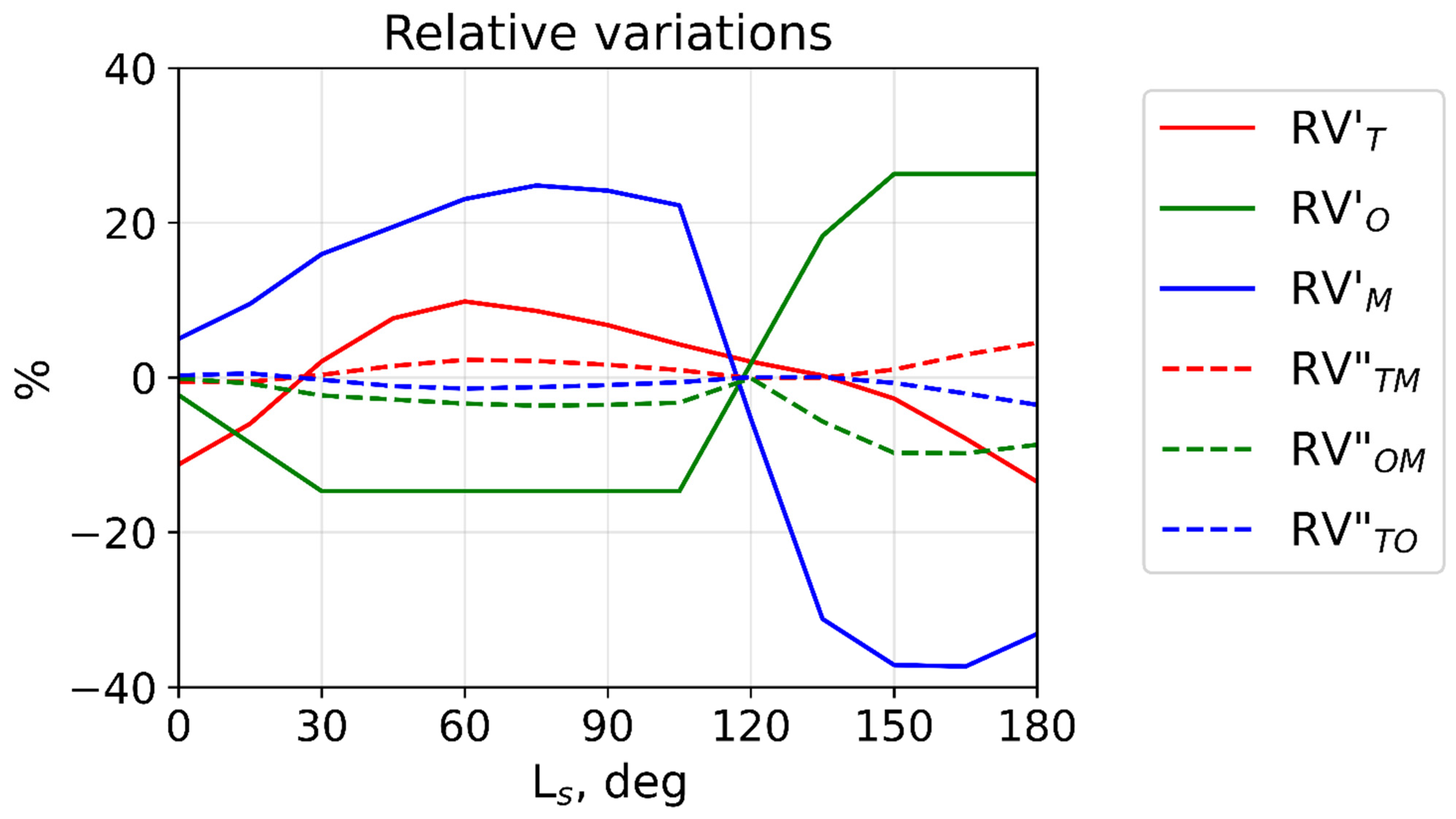
2.2. Variations of the Excited Hydroxyl Layer
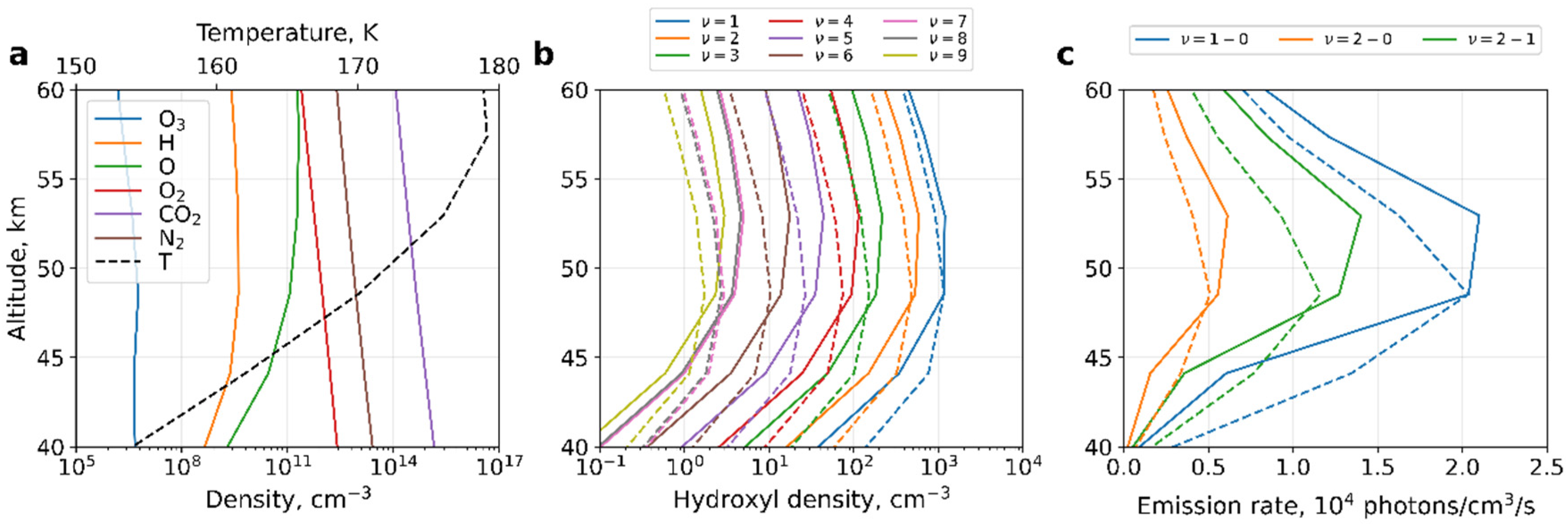
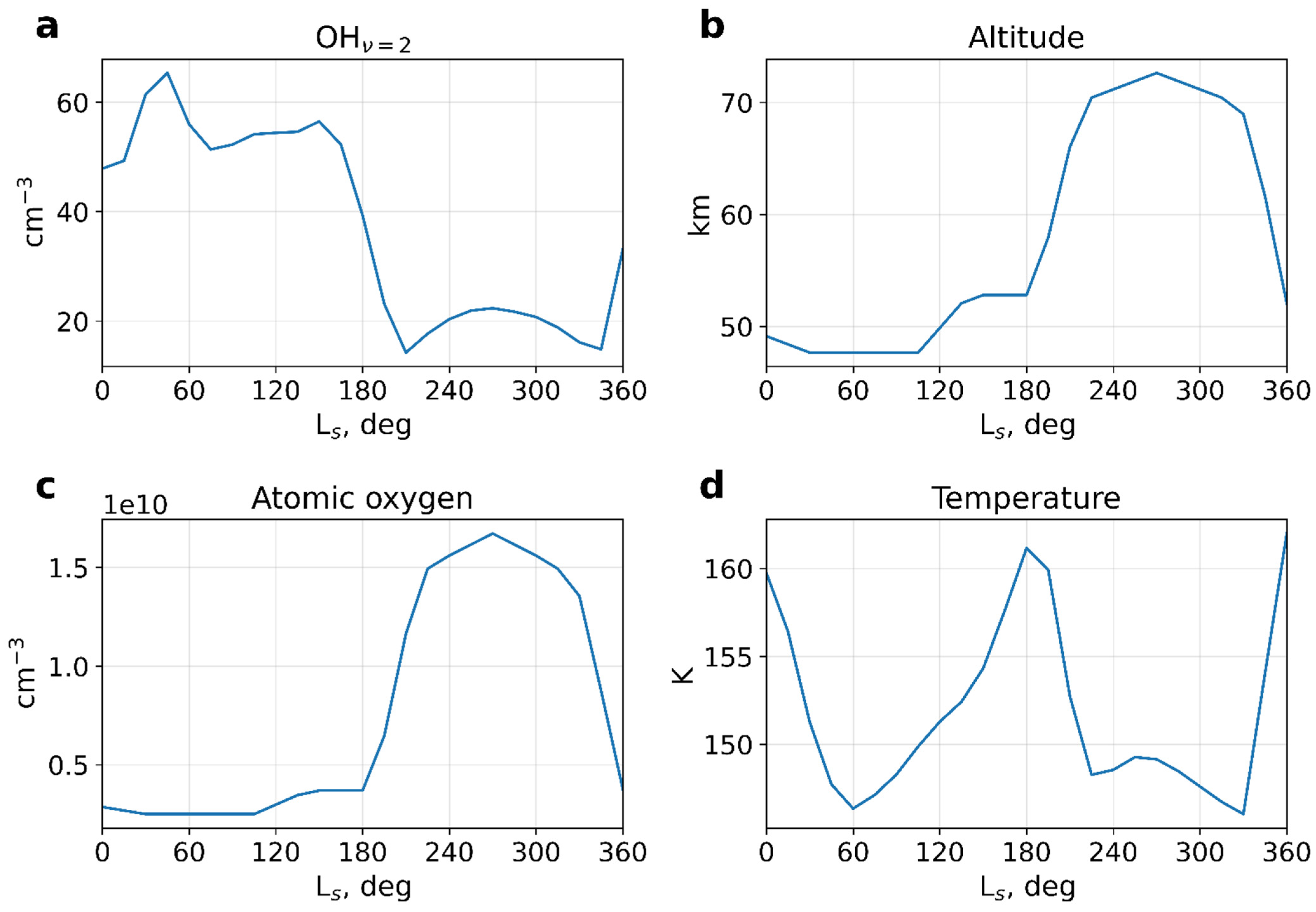
3. Calculations and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lopez-Gonzalez, M.J.; Rodríguez, E.; Shepherd, G.G.; Sargoytchev, S.; Shepherd, M.G.; Aushev, V.M.; Brown, S.; García-Comas, M.; Wiens, R.H. Tidal variations of O2 Atmospheric and OH(6-2) airglow and temperature at mid-latitudes from SATI observations. Ann. Geophys. 2005, 23, 3579–3590. [Google Scholar] [CrossRef]
- Xu, J.; Smith, A.K.; Jiang, G.; Gao, H.; Wei, Y.; Mlynczak, M.G.; Russell, J.M., III. Strong longitudinal variations in the OH nightglow. Geophys. Res. Lett. 2010, 37, L21801. [Google Scholar] [CrossRef]
- Buriti, R.A.; Takahashi, H.; Lima, L.M.; Medeiros, A.F. Equatorial planetary waves in the mesosphere observed by airglow periodic oscillations. Adv. Space Res. 2005, 35, 2031–2036. [Google Scholar] [CrossRef]
- Lopez-Gonzalez, M.J.; Rodríguez, E.; García-Comas, M.; Costa, V.; Shepherd, M.G.; Shepherd, G.G.; Aushev, V.M.; Sargoytchev, S. Climatology of planetary wave type oscillations with periods of 2–20 days derived from O2 atmospheric and OH(6-2) airglow observations at mid-latitude with SATI. Ann. Geophys. 2009, 27, 3645–3662. [Google Scholar] [CrossRef]
- Taylor, M.J.; Espy, P.J.; Baker, D.J.; Sica, R.J.; Neal, P.C.; Pendleton, W.R., Jr. Simultaneous intensity, temperature and imaging measurements of short period wave structure in the OH nightglow emission. Planet. Space Sci. 1991, 39, 1171–1188. [Google Scholar] [CrossRef]
- Shepherd, G.G.; Thuillier, G.; Cho, Y.-M.; Duboin, M.-L.; Evans, W.F.J.; Gault, W.A.; Hersom, C.; Kendall, D.J.W.; Lathuillère, C.; Lowe, R.P.; et al. The Wind Imaging Interferometer (WINDII) on the Upper Atmosphere Research Satellite: A 20 year perspective. Rev. Geophys. 2012, 50, RG2007. [Google Scholar] [CrossRef]
- Wachter, P.; Schmidt, C.; Wüst, S.; Bittner, M. Spatial gravity wave characteristics obtained from multiple OH(3-1) airglow temperature time series. J. Atmos. Sol. Terr. Phys. 2015, 135, 192–201. [Google Scholar] [CrossRef]
- Gao, H.; Xu, J.; Wu, Q. Seasonal and QBO variations in the OH nightglow emission observed by TIMED/SABER. J. Geophys. Res. 2010, 115, A06313. [Google Scholar] [CrossRef]
- Shepherd, M.G.; Cho, Y.-M.; Shepherd, G.G.; Ward, W.; Drummond, J.R. Mesospheric temperature and atomic oxygen response during the January 2009 major stratospheric warming. J. Geophys. Res. 2010, 115, A07318. [Google Scholar] [CrossRef]
- Shepherd, M.G.; Meek, C.E.; Hocking, W.K.; Hall, C.M.; Partamies, N.; Sigernes, F.; Manson, A.H.; Ward, W.E. Multi-instrument study of the mesosphere-lower thermosphere dynamics at 80°N during the major SSW in January 2019. J. Atmos. Sol. Terr. Phys. 2020, 210, 105427. [Google Scholar] [CrossRef]
- Bittner, M.; Offermann, D.; Graef, H.-H.; Donner, M.; Hamilton, K. An 18 year time series of OH rotational temperatures and middle atmosphere decadal variations. J. Atmos. Sol. Terr. Phys. 2002, 64, 1147–1166. [Google Scholar] [CrossRef]
- Espy, P.J.; Stegman, J.; Forkman, P.; Murtagh, D. Seasonal variation in the correlation of airglow temperature and emission rate. Geophys. Res. Lett. 2007, 34, L17802. [Google Scholar] [CrossRef]
- Pertsev, N.; Perminov, V. Response of the mesopause airglow to solar activity inferred from measurements at Zvenigorod, Russia. Ann. Geophys. 2008, 26, 1049–1056. [Google Scholar] [CrossRef]
- Dalin, P.; Perminov, V.; Pertsev, N.; Romejko, V. Updated long-term trends in mesopause temperature, airglow emissions, and noctilucent clouds. J. Geophys. Res. 2020, 125, e2019JD030814. [Google Scholar] [CrossRef]
- Perminov, V.I.; Pertsev, N.N.; Dalin, P.A.; Zheleznov, Y.A.; Sukhodoev, V.A.; Orekhov, M.D. Seasonal and Long-Term Changes in the Intensity of O2(b1Σ) and OH(X2Π) Airglow in the Mesopause Region. Geomagn. Aeron. 2021, 61, 589–599. [Google Scholar] [CrossRef]
- Russell, J.P.; Ward, W.E.; Lowe, R.P.; Roble, R.G.; Shepherd, G.G.; Solheim, B. Atomic oxygen profiles (80 to 115 km) derived from Wind Imaging Interferometer/Upper Atmospheric Research Satellite measurements of the hydroxyl and greenline airglow: Local time–latitude dependence. J. Geophys. Res. 2005, 110, D15305. [Google Scholar] [CrossRef]
- Mlynczak, M.G.; Hunt, L.A.; Mast, J.C.; Marshall, B.T.; Russell, J.M., III; Smith, A.K.; Siskind, D.E.; Yee, J.-H.; Mertens, C.J.; Martin-Torres, F.J.; et al. Atomic oxygen in the mesosphere and lower thermosphere derived from SABER: Algorithm theoretical basis and measurement uncertainty. J. Geophys. Res. 2013, 118, 5724–5735. [Google Scholar] [CrossRef]
- Mlynczak, M.G.; Hunt, L.A.; Marshall, B.T.; Mertens, C.J.; Marsh, D.R.; Smith, A.K.; Russell, J.M.; Siskind, D.E.; Gordley, L.L. Atomic hydrogen in the mesopause region derived from SABER: Algorithm theoretical basis, measurement uncertainty, and results. J. Geophys. Res. 2014, 119, 3516–3526. [Google Scholar] [CrossRef]
- Piccioni, G.; Drossart, P.; Zasova, L.; Migliorini, A.; Gérard, J.-C.; Mills, F.P.; Shakun, A.; García Muñoz, A.; Ignatiev, N.; Grassi, D.; et al. First detection of hydroxyl in the atmosphere of Venus. Astron. Astrophys. 2008, 483, L29–L33. [Google Scholar] [CrossRef]
- Gérard, J.-C.; Soret, L.; Saglam, A.; Piccioni, G.; Drossart, P. The distributions of the OH Meinel and O2(a1∆ − X3Σ) nightglow emissions in the Venus mesosphere based on VIRTIS observations. Adv. Space Res. 2010, 45, 1268–1275. [Google Scholar] [CrossRef]
- Soret, L.; Gérard, J.-C.; Piccioni, G.; Drossart, P. Venus OH nightglow distribution based on VIRTIS limb observations from Venus Express. Geophys. Res. Lett. 2010, 37, L06805. [Google Scholar] [CrossRef]
- Migliorini, A.; Piccioni, G.; Cardesín Moinelo, A.; Drossart, P. Hydroxyl airglow on Venus in comparison with Earth. Planet. Space Sci. 2011, 59, 974–980. [Google Scholar] [CrossRef]
- Migliorini, A.; Piccioni, G.; Capaccioni, F.; Filacchione, G.; Tosi, F.; Gérard, J.C. Comparative analysis of airglow emissions in terres-trial planets, observed with VIRTIS-M instruments on board Rosetta and Venus Express. Icarus 2013, 226, 1115–1127. [Google Scholar] [CrossRef]
- Clancy, R.T.; Sandor, B.J.; García-Muñoz, A.; Lefèvre, F.; Smith, M.D.; Wolff, M.J.; Montmessin, F.; Murchie, S.L.; Nair, H. First detection of Mars atmospheric hydroxyl: CRISM Near-IR measurement versus LMD GCM simulation of OH Meinel band emission in the Mars polar winter atmosphere. Icarus 2013, 226, 272–281. [Google Scholar] [CrossRef]
- Burkholder, J.B.; Sander, S.P.; Abbatt, J.; Barker, J.R.; Cappa, C.; Crounse, J.D.; Dibble, T.S.; Huie, R.E.; Kolb, C.E.; Kurylo, M.J.; et al. Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies; Evaluation No. 19; JPL Publication 19-5; Jet Propulsion Laboratory: Pasadena, CA, USA, 2020. Available online: http://jpldataeval.jpl.nasa.gov (accessed on 12 October 2021).
- Adler-Golden, S. Kinetic parameters for OH nightglow modeling consistent with recent laboratory measurements. J. Geophys. Res. 1997, 102, 19969–19976. [Google Scholar] [CrossRef]
- Caridade, P.J.S.B.; Horta, J.-Z.J.; Varandas, A.J.C. Implications of the O + OH reaction in hydroxyl nightglow modeling. Atmos. Chem. Phys. 2013, 13, 1–13. [Google Scholar] [CrossRef]
- Makhlouf, U.B.; Picard, R.H.; Winick, J.R. Photochemical-dynamical modeling of the measured response of airglow to gravity waves. 1. Basic model for OH airglow. J. Geophys. Res. 1995, 100, 11289–11311. [Google Scholar] [CrossRef]
- Krasnopolsky, V.A. Nighttime photochemical model and night airglow on Venus. Planet. Space Sci. 2013, 85, 78–88. [Google Scholar] [CrossRef]
- Xu, J.; Gao, H.; Smith, A.K.; Zhu, Y. Using TIMED/SABER nightglow observations to investigate hydroxyl emission mechanisms in the mesopause region. J. Geophys. Res. 2012, 117, D02301. [Google Scholar] [CrossRef]
- García-Muñoz, A.; McConnell, J.C.; McDade, I.C.; Melo, S.M.L. Airglow on Mars: Some model expectations for the OH Meinel bands and the O2 IR atmospheric band. Icarus 2005, 176, 75–95. [Google Scholar] [CrossRef]
- Llewellyn, E.J.; Long, B.H.; Solheim, B.H. The quenching of OH* in the atmosphere. Planet. Space Sci. 1978, 26, 525–531. [Google Scholar] [CrossRef]
- McDade, I.C.; Llewellyn, E.J. Kinetic parameters related to sources and sinks of vibrationally excited OH in the nightglow. J. Geophys. Res. 1987, 92, 7643–7650. [Google Scholar] [CrossRef]
- Meriwether, J.W., Jr. A review of the photochemistry of selected nightglow emissions from the mesopause. J. Geophys. Res. 1989, 94, 14629–14646. [Google Scholar] [CrossRef]
- Krasnopolsky, V.A.; Lefèvre, F. Chemistry of the atmospheres of Mars, Venus, and Titan. In Comparative Climatology of Terrestrial Planets, 1st ed.; Mackwell, S.J., Simon-Miller, A.A., Eds.; University of Arizona: Tucson, AZ, USA, 2013; pp. 231–275. [Google Scholar] [CrossRef]
- Nair, H.; Allen, M.; Anbar, A.D.; Yung, Y.L.; Clancy, R.T. A Photochemical Model of the Martian Atmosphere. Icarus 1994, 111, 124–150. [Google Scholar] [CrossRef] [PubMed]
- Dodd, J.A.; Lipson, S.J.; Blumberg, W.A.M. Formation and vibrational relaxation of OH(X2Πi, v) by O2 and CO2. J. Chem. Phys. 1991, 95, 5752–5762. [Google Scholar] [CrossRef]
- Chalamala, B.R.; Copeland, R.A. Collision dynamics of OH(X2Π, v = 9). J. Chem. Phys. 1993, 99, 5807–5811. [Google Scholar] [CrossRef]
- Soret, L.; Gérard, J.-C.; Piccioni, G.; Drossart, P. The OH Venus nightglow spectrum: Intensity and vibrational composition from VIRTIS Venus Express observations. Planet. Space Sci. 2012, 73, 387–396. [Google Scholar] [CrossRef][Green Version]
- Krasnopolsky, V.A. Photochemistry of the martian atmosphere: Seasonal, latitudinal, and diurnal variations. Icarus 2006, 185, 153–170. [Google Scholar] [CrossRef]
- Krasnopolsky, V.A. Solar activity variations of thermospheric temperatures on Mars and a problem of CO in the lower atmosphere. Icarus 2010, 207, 638–647. [Google Scholar] [CrossRef]
- Lindner, B.L. Ozone on Mars: The effects of clouds and airborne dust. Planet. Space Sci. 1988, 36, 125–144. [Google Scholar] [CrossRef]
- Lefèvre, F.; Lebonnois, S.; Montmessin, F.; Forget, F. Three-dimensional modeling of ozone on Mars. J. Geophys. Res. 2004, 109, E07004. [Google Scholar] [CrossRef]
- Forget, F.; Hourdin, F.; Fournier, R.; Hourdin, C.; Talagrand, O.; Collins, M.; Lewis, S.R.; Read, P.L.; Huot, J.-P. Improved general circulation models of the Martian atmosphere from the surface to above 80 km. J. Geophys. Res. 1999, 104, 24155–24176. [Google Scholar] [CrossRef]
- Millour, E.; Forget, F.; Spiga, A.; Vals, M.; Zakharov, V.; Montabone, L.; Lefèvre, F.; Montmessin, F.; Chaufray, J.-Y.; López-Valverde, M.A.; et al. The Mars Climate Database (Version 5.3). In Proceedings of the Scientific Workshop: From Mars Express to ExoMars, ESAC, Madrid, Spain, 27–28 February 2018; Available online: https://ui.adsabs.harvard.edu/link_gateway/2018fmee.confE..68M/PUB_PDF (accessed on 12 October 2021).
- Lefèvre, F.; Bertaux, J.-L.; Clancy, R.T.; Encrenaz, T.; Fast, K.; Forget, F.; Lebonnois, S.; Montmessin, F.; Perrier, S. Heterogeneous chemistry in the atmosphere of Mars. Nature 2008, 454, 971–975. [Google Scholar] [CrossRef] [PubMed]
- Navarro, T.; Madeleine, J.-B.; Forget, F.; Spiga, A.; Millour, E.; Montmessin, F.; Määttänen, A. Global climate modeling of the Martian water cycle with improved microphysics and radiatively active water ice clouds. J. Geophys. Res. 2014, 119, 1479–1495. [Google Scholar] [CrossRef]
- Forget, F.; Hourdin, F.; Talagrand, O. CO2 Snowfall on Mars: Simulation with a General Circulation Model. Icarus 1998, 131, 302–316. [Google Scholar] [CrossRef]
- Forget, F.; Millour, E.; Montabone, L.; Lefevre, F. Non condensable gas enrichment and depletion in the Martian polar regions. In Proceedings of the 3rd Workshop Mars Atmosphere: Modeling and Observations, Williamsburg, VA, USA, 10–13 November 2008. [Google Scholar]
- Shaposhnikov, D.S.; Medvedev, A.S.; Rodin, A.V.; Hartogh, P. Seasonal water “pump” in theatmosphere of mars: Vertical transport to the thermosphere. Geophys. Res. Lett. 2019, 46, 4161–4169. [Google Scholar] [CrossRef]
- Swenson, G.R.; Gardner, C.S. Analytical models for the resposes of the mesospheric OH* and Na layers to atmospheric gravity waves. J. Geophys. Res. 1998, 103, 6271–6294. [Google Scholar] [CrossRef]
- Liu, G.; Shepherd, G.G.; Roble, R.G. Seasonal variations of the nighttime O(1S) and OH airglow emission rates at mid-to-high latitudes in the context of the large-scale circulation. J. Geophys. Res. 2008, 113, A06302. [Google Scholar] [CrossRef]
- Marsh, D.R.; Smith, A.K.; Mlynczak, M.G.; Russell, J.M., III. SABER observations of the OH Meinel airglow variability near the mesopause. J. Geophys. Res. 2006, 111, A10S05. [Google Scholar] [CrossRef]
- Liu, G.; Shepherd, G.G. An empirical model for the altitude of the OH nightglow emission. Geophys. Res. Lett. 2006, 33, L09805. [Google Scholar] [CrossRef]
- Mulligan, F.G.; Dyrland, M.E.; Sigernes, F.; Deehr, C.S. Inferring hydroxyl layer peak heights from ground-based measurements of OH(6–2) band integrated emission rate at Longyearbyen (78°N, 16°E). Ann. Geophys. 2009, 27, 4197–4205. [Google Scholar] [CrossRef][Green Version]
- McElroy, M.B.; Donahue, T.M. Stability of the Martian Atmosphere. Science 1972, 177, 986–988. [Google Scholar] [CrossRef] [PubMed]
- Parkinson, T.D.; Hunten, D.M. Spectroscopy and aeronomy of O2 on Mars. J. Atmos. Sci. 1972, 29, 1380–1390. [Google Scholar] [CrossRef]
- Olsen, K.S.; Lefèvre, F.; Montmessin, F.; Fedorova, A.A.; Trokhimovskiy, A.; Baggio, L.; Korablev, O.; Alday, J.; Wilson, C.F.; Forget, F.; et al. The vertical structure of CO in the Martian atmosphere from the ExoMars Trace Gas Orbiter. Nat. Geosci. 2021, 14, 67–71. [Google Scholar] [CrossRef]
- Conway, S. Methods for Deriving Temperature Profiles of Mars from OH Meinel Airglow Observations. Ph.D. Thesis, York University, Toronto, ON, Canada, March 2012. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grygalashvyly, M.; Shaposhnikov, D.S.; Medvedev, A.S.; Sonnemann, G.R.; Hartogh, P. Simplified Relations for the Martian Night-Time OH* Suitable for the Interpretation of Observations. Remote Sens. 2022, 14, 3866. https://doi.org/10.3390/rs14163866
Grygalashvyly M, Shaposhnikov DS, Medvedev AS, Sonnemann GR, Hartogh P. Simplified Relations for the Martian Night-Time OH* Suitable for the Interpretation of Observations. Remote Sensing. 2022; 14(16):3866. https://doi.org/10.3390/rs14163866
Chicago/Turabian StyleGrygalashvyly, Mykhaylo, Dmitry S. Shaposhnikov, Alexander S. Medvedev, Gerd Reinhold Sonnemann, and Paul Hartogh. 2022. "Simplified Relations for the Martian Night-Time OH* Suitable for the Interpretation of Observations" Remote Sensing 14, no. 16: 3866. https://doi.org/10.3390/rs14163866
APA StyleGrygalashvyly, M., Shaposhnikov, D. S., Medvedev, A. S., Sonnemann, G. R., & Hartogh, P. (2022). Simplified Relations for the Martian Night-Time OH* Suitable for the Interpretation of Observations. Remote Sensing, 14(16), 3866. https://doi.org/10.3390/rs14163866








