Energy-Barycenter Based Waveform Centroid Algorithm for Pulse Lidar Ranging System
Abstract
:1. Introduction
2. Lidar System Models
2.1. Transmitted Pulse Model in the Lidar System
2.2. Echo Pulse Model in the Lidar System
3. The Waveform Centroid Algorithm Analysis
3.1. Conventional Waveform Centroid Algorithm (CWCA)
3.2. Intensity-Weighted Waveform Centroid Discrimination Algorithm (IWCD)
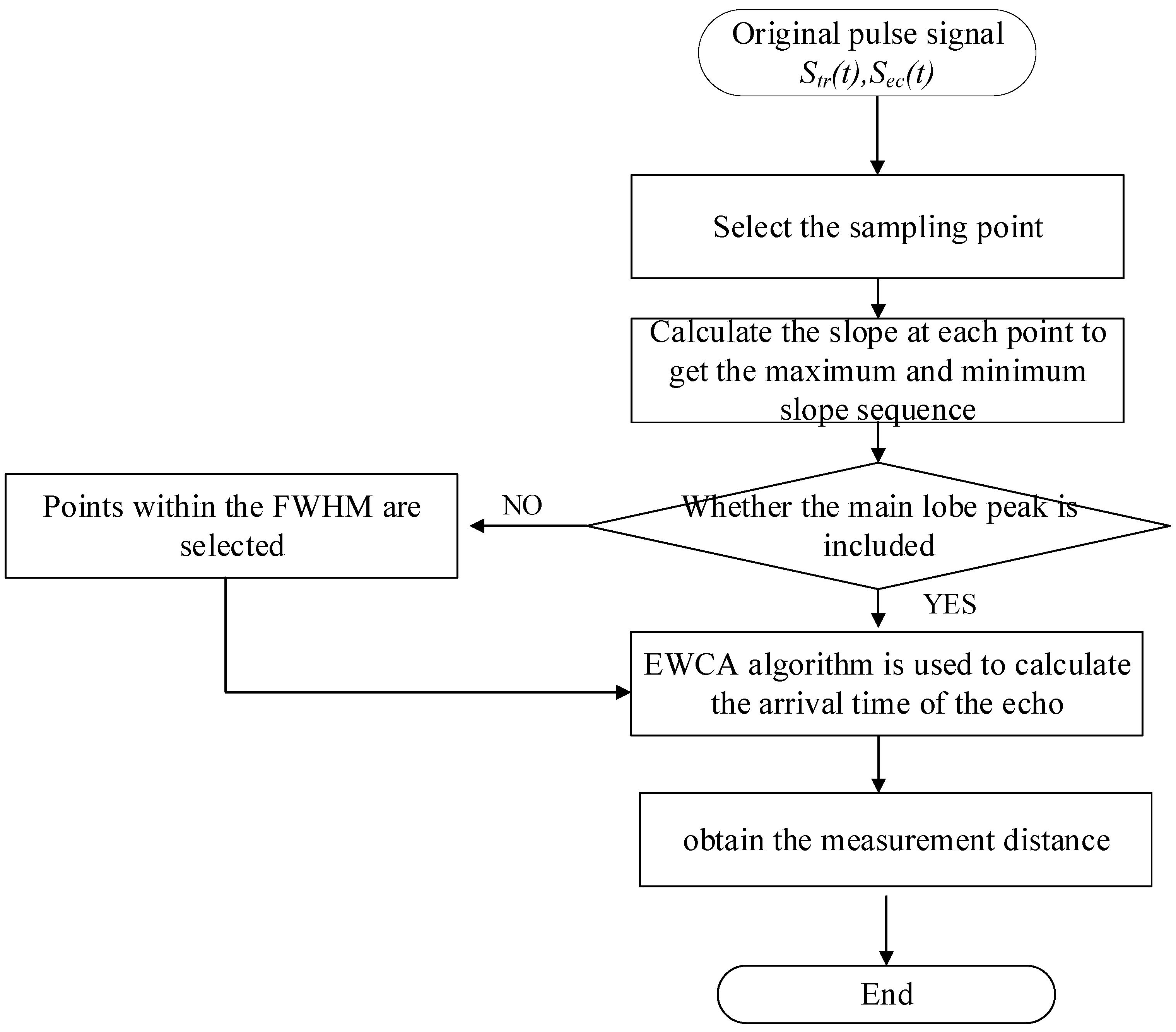
3.3. Energy-Barycenter Based Waveform Centroid Algorithm (EWCA)
- Select the sampling points. Calculate the slope of each point and record the maximum and minimum slopes of the sampling points at the corresponding time. The sampling sequence from the time corresponding to the maximum slope, to the time corresponding to the minimum slope is selected;
- Determine whether the main lobe peak is included. Judge whether the peak point is included in the sampling sequence. If included, proceed to step 4. Otherwise, proceed to step 3;
- Select a new sampling sequence. When the slope sequence does not meet the condition of including the peak value, the point between the full width at half maximum (FWHM) is selected as the sampling point sequence;
- The energy-barycenter based waveform centroid algorithm is used to calculate the arrival time of the echo. Calculate the arrival time of the echo through EWCA, and then the time interval between transmitted pulses is calculated to obtain the measured distance.
| Algorithm 1. Pseudocode for EWCA |
| The reference and the echo Lidar signals were input |
| The slope sequences and of Lidar signal were calculated, respectively Input the reference signal and the echo signal , respectively, and calculate their slope sequences respectively |
| Calculate the beginning and end of the slope sequence = the maximum value of = the minimum value of = the maximum value of = the minimum value of |
| If (the minimum to maximum slope interval contains the maximum values of ) for each point in the slope sequence The centroid time and centroid amplitude of EWCA reference and echo signals were calculated by Equation (9) end for else for each point in the FWHM sequence The centroid time and centroid amplitude of EWCA reference and echo signals were calculated by Equation (9) end for end if |
| return, |
4. Simulation Analysis
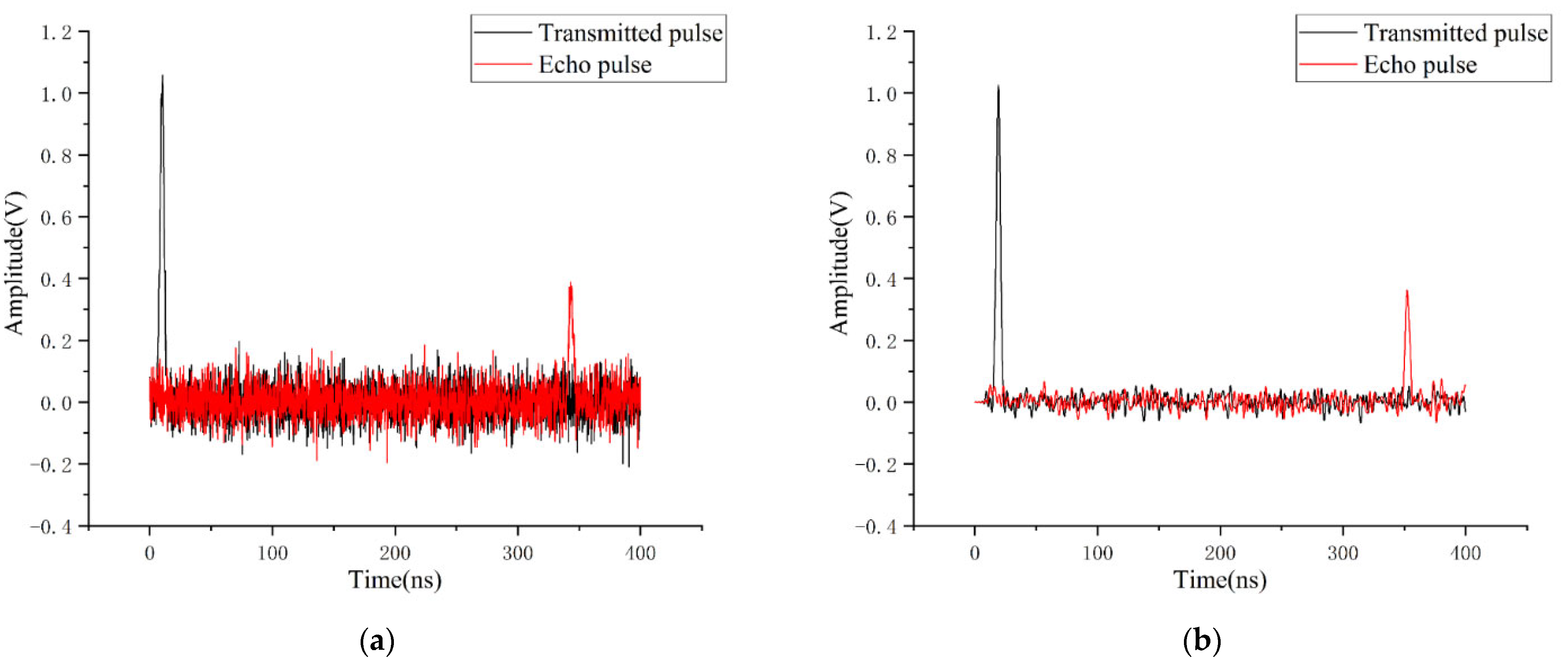
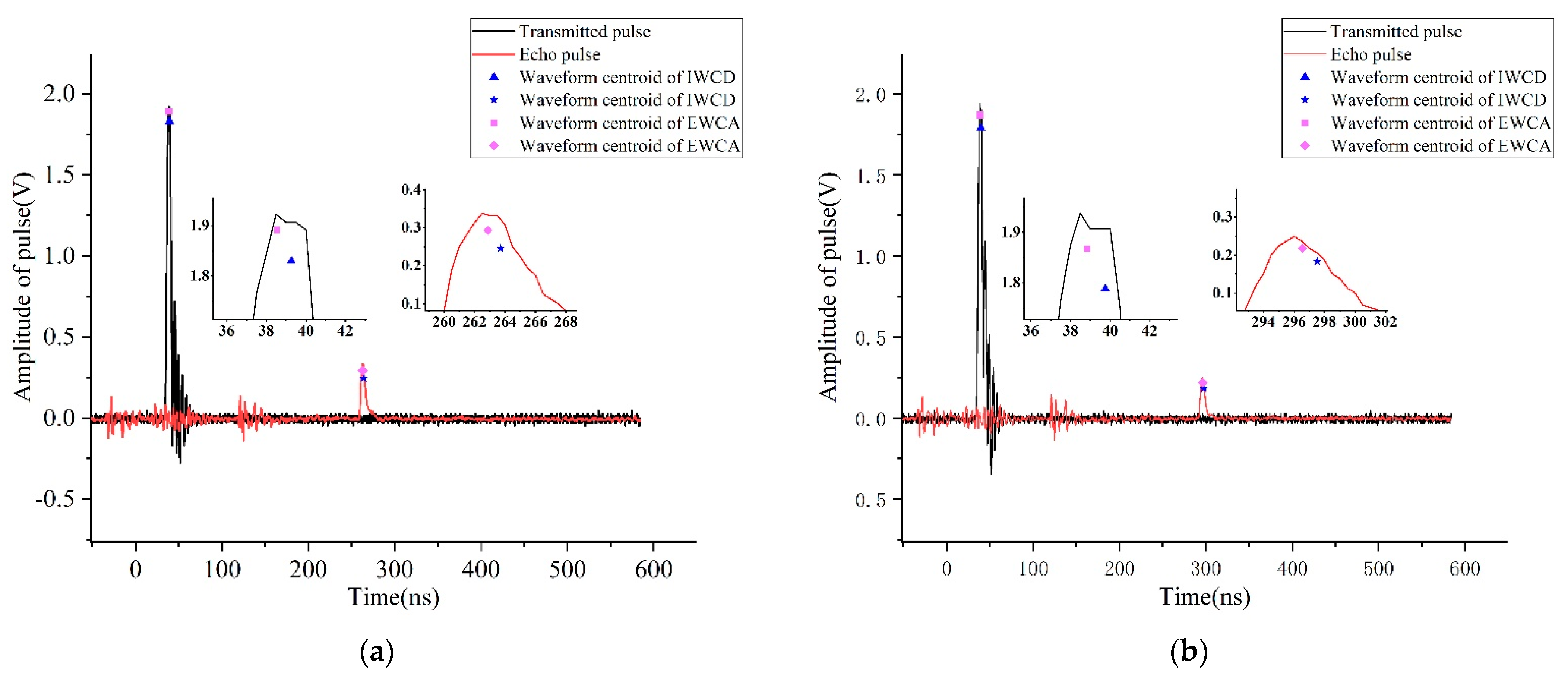
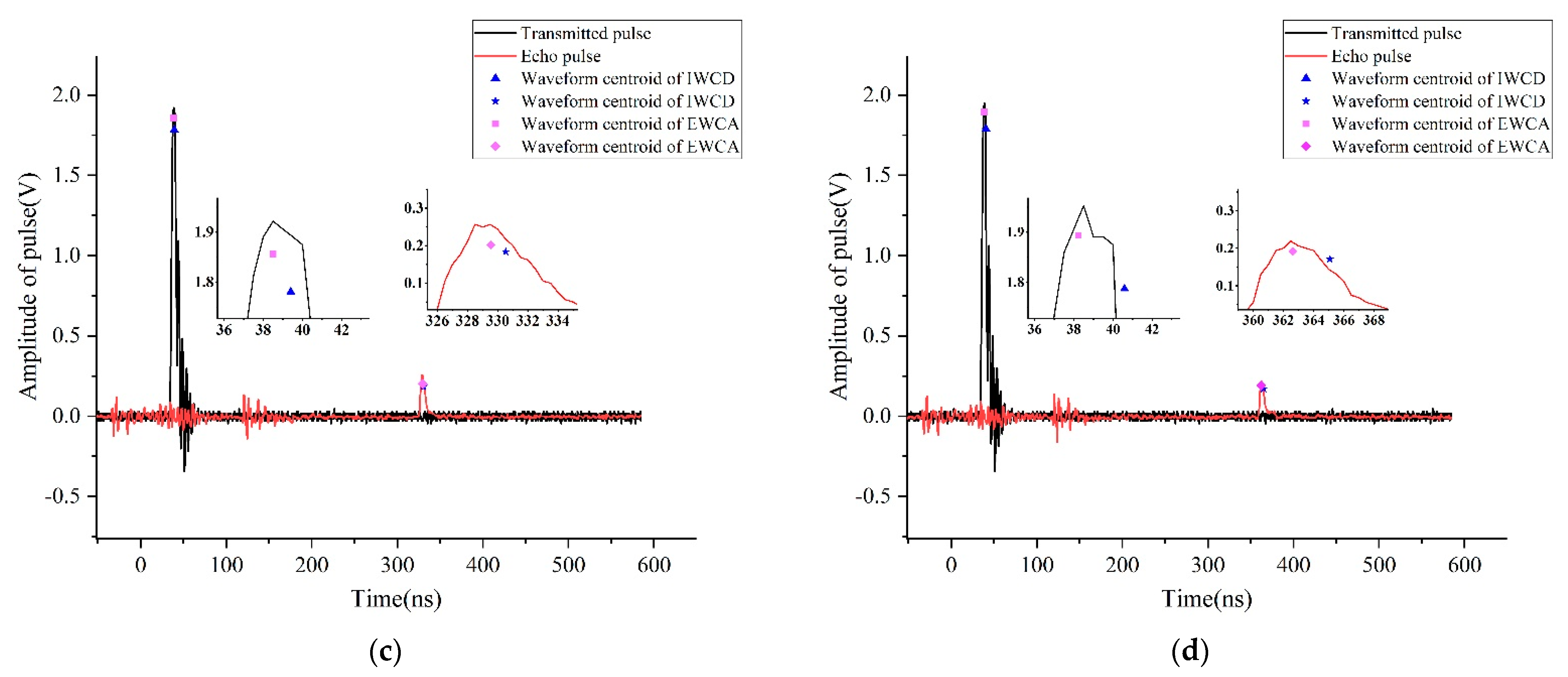
5. Experiments and Evaluation
5.1. Experimental System Description
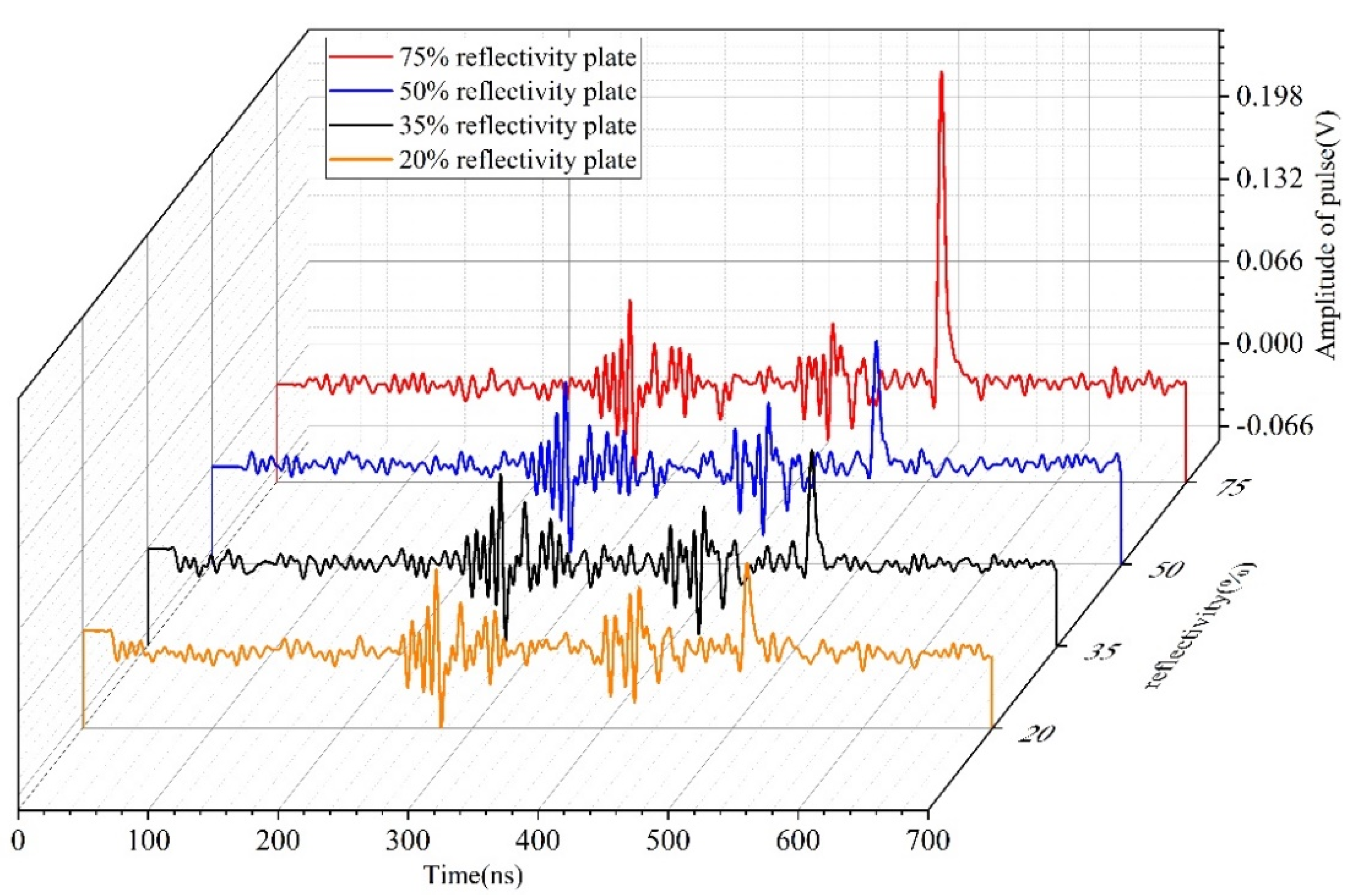
5.2. Experimental Results and Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hongji, H.; Yuchun, Y.; Guan, G.; Hikmet, S. Deep Reinforcement Learning for UAV Navigation Through Massive MIMO Technique. IEEE Trans. Veh. Technol. 2020, 69, 1117–1121. [Google Scholar]
- Mohammadikaji, M.; Bergamann, S.; Irgenfried, S.; Beyerer, J.; Dachsbacher, C.; Worn, H. A framework for uncertainty propagation in 3d shape measurement using laser triangulation. In Proceedings of the 2016 IEEE International Instrumentation and Measurement Technology Conference Proceedings, Taipei, Taiwan, 23–26 May 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Gallay, M.; Hochmuth, Z.; Kanuk, J.; Hofierka, J. Geomorphometric analysis of cave ceiling channels mapped with 3-D terrestrial laser scanning. Hydrol. Earth Syst. Sci. 2016, 20, 1827–1849. [Google Scholar] [CrossRef]
- Krivic, S.; Piater, J. Pushing corridors for delivering unknown objects with a mobile robot. Auton. Robot. 2019, 43, 1435–1452. [Google Scholar] [CrossRef]
- Kurtti, S.; Jansson, J.P.; Kostamovaara, J. A CMOS Receiver—TDC Chip Set for Accurate Pulsed TOF Laser Ranging. IEEE Trans. Instrum. Meas. 2020, 69, 2208–2217. [Google Scholar] [CrossRef]
- Chao, Z.; Lindner, S.; Antolovic, I.M.; Wolf, M.; Charbon, E. A CMOS SPAD Imager with Collision Detection and 128 Dynamically Reallocating TDCs for Single-Photon Counting and 3D Time-of-Flight Imaging. Sensors 2018, 18, 11. [Google Scholar]
- Kurtti, S.; Nissinen, J.; Kostamovaara, J. A wide dynamic range CMOS laser radar receiver with a time-domain walk error compensation scheme. IEEE Trans. Circuit. Syst. I-Regul. Pap. 2017, 64, 550–561. [Google Scholar] [CrossRef]
- Jie, C.; Qun, H.; Yang, C.; Yuxin, P.; Kaiyu, Z.; Jiaxing, M.; Peng, W. Differential time domain method improves performance of pulsed laser ranging and three-dimensional imaging. Appl. Optics. 2016, 55, 360–367. [Google Scholar]
- Xiaolu, L.; Bingwei, Y.; Xinhao, X.; Duan, L.; Lijun, X. Influence of waveform characteristics on LiDAR ranging accuracy and precision. Sensors 2018, 18, 1156. [Google Scholar] [CrossRef] [PubMed]
- Shiyu, Y.; Guohui, Y.; Qingyan, L.; Bin, Z.; Yu, W.; Yu, Z.; Chunhui, W. Distance-Intensity Image Strategy for Pulsed LiDAR Based on the Double-Scale Intensity-Weighted Centroid Algorithm. Remote Sens. 2021, 13, 432. [Google Scholar] [CrossRef]
- Wu, Q.; Qiang, S.; Wang, Y. Continuous wavelet transform and iterative decrement algorithm for the Lidar full-waveform echo decomposition. Appl. Opt. 2019, 58, 9360. [Google Scholar]
- Milutin, M.; Sebastian, S.; Johan, H.; Camillo, R.; Eva, L.; Markus, H.; Norbert, P.; Hakan, O. Influence of footprint size and geolocation error on the precision of forest biomass estimates from space-borne waveform LiDAR. Remote Sens. Environ. 2017, 200, 74–88. [Google Scholar]
- Salas, E.A.L. Waveform LiDAR concepts and applications for potential vegetation phenology monitoring and modeling: A comprehensive review. Geo-Spat. Inf. Sci. 2020, 24, 179–200. [Google Scholar] [CrossRef]
- Shiyu, Y.; Guohui, Y.; Qingyan, L.; Chunhui, W. Waveform centroid discrimination of pulsed Lidar by combining EMD and intensity weighted method under low SNR conditions. Infrared Phys. Technol. 2020, 109, 103385. [Google Scholar]
- Muss, J.D.; Aguilar-Amuchastegui, N.; Mladenoff, D.J.; Henebry, G.M. Analysis of waveform lidar data using shape-based metrics. IEEE Geosci. Remote Sens. Lett. 2012, 10, 106–110. [Google Scholar] [CrossRef]
- Fieber, K.D.; Davenport, I.J.; Ferryman, J.M.; Gurney, R.J.; Walker, J.P.; Hacker, J.M. Analysis of full-waveform LiDAR pulse properties for vegetation discrimination and characterisation. ISPRS-J. Photogramm. Remote Sens. 2013, 82, 63–82. [Google Scholar] [CrossRef]
- Yunxi, L.; Tianxiang, C.; Qingyan, L.; Bin, Z.; Yuru, B.; Chunhui, W. Waveform centroid discrimination of return pulse weighting method in LIDAR system. Optik 2019, 180, 840–846. [Google Scholar]
- Abdallah, H.; Baghdadi, N.; Bailly, J.S.; Pastol, Y.; Fabre, F. Wa-LiD: A new LiDAR simulator for waters. IEEE Geosci. Remote Sens. Lett. 2012, 9, 744–748. [Google Scholar] [CrossRef]




| SNR (dB) | Average Time Error (ns) | Standard Deviation (ns) | Variance (ns) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| CWCA | IWCD | EWCA | CWCA | IWCD | EWCA | CWCA | IWCD | EWCA | |
| 5 | 45.6039 | 0.1663 | 0.1235 | 17.6129 | 0.1617 | 0.0848 | 62.2137 | 0.0262 | 0.0072 |
| 6 | 35.2123 | 0.1678 | 0.0965 | 15.1467 | 0.1351 | 0.0704 | 57.5210 | 0.0183 | 0.0050 |
| 7 | 29.4283 | 0.1593 | 0.0781 | 11.0965 | 0.1429 | 0.0576 | 53.1320 | 0.0204 | 0.0033 |
| 8 | 24.1494 | 0.1592 | 0.0663 | 8.4397 | 0.1552 | 0.0498 | 45.2288 | 0.0241 | 0.0025 |
| 9 | 18.9067 | 0.1560 | 0.0594 | 7.0873 | 0.1041 | 0.0448 | 40.2299 | 0.0108 | 0.0020 |
| 10 | 15.2086 | 0.1566 | 0.0569 | 5.9159 | 0.1369 | 0.0425 | 34.9983 | 0.0187 | 0.0018 |
| 11 | 17.2132 | 0.1552 | 0.0538 | 5.2481 | 0.1093 | 0.0418 | 27.5424 | 0.0119 | 0.0018 |
| 12 | 10.9086 | 0.1555 | 0.0576 | 4.5167 | 0.1094 | 0.0436 | 20.4010 | 0.0120 | 0.0019 |
| 13 | 10.8383 | 0.1566 | 0.0552 | 4.0168 | 0.1519 | 0.0444 | 16.1348 | 0.0231 | 0.0020 |
| 14 | 8.9395 | 0.1560 | 0.0483 | 3.5012 | 0.1241 | 0.0446 | 12.2585 | 0.0154 | 0.0020 |
| 15 | 6.7230 | 0.1555 | 0.0455 | 2.8880 | 0.1322 | 0.0477 | 8.3407 | 0.0150 | 0.0023 |
| Parameter | Value |
|---|---|
| Laser wavelength | 1064 nm |
| Pulse width | 4 ns |
| Model of APD | PDB430C |
| APD response frequency band | 250 MHz |
| Size of APD photosensitive surface | 3 mm |
| Receiving system optical aperture | 50 mm |
| ADC sampling rate | 5 GSa/s |
| ADC bandwidth | 1 GHz |
| Distance (m) | Average Time Error (ns) | Average Distance Error (mm) | ||
|---|---|---|---|---|
| IWCD | EWCA | IWCD | EWCA | |
| 25 | 0.167 | 0.076 | 25 | 11 |
| 30 | 0.182 | 0.088 | 27 | 13 |
| 35 | 0.196 | 0.102 | 29 | 15 |
| 40 | 0.220 | 0.114 | 33 | 17 |
| Reflectivity (%) | MATE (ns) | DSR (%) | ||||
|---|---|---|---|---|---|---|
| CWCD | IWCD | EWCA | CWCD | IWCD | EWCA | |
| 20 | 1.6775 | 1.6603 | 0.7788 | 5.4 | 5.4 | 81.4 |
| 35 | 1.0199 | 1.0165 | 0.6826 | 46.3 | 46.7 | 94.7 |
| 50 | 0.6538 | 0.6607 | 0.5356 | 87.3 | 88.4 | 99.4 |
| 75 | 0.5065 | 0.5043 | 0.4445 | 100 | 100 | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, B.; Wang, L.; Guo, D.; Wang, C. Energy-Barycenter Based Waveform Centroid Algorithm for Pulse Lidar Ranging System. Remote Sens. 2022, 14, 3938. https://doi.org/10.3390/rs14163938
Qi B, Wang L, Guo D, Wang C. Energy-Barycenter Based Waveform Centroid Algorithm for Pulse Lidar Ranging System. Remote Sensing. 2022; 14(16):3938. https://doi.org/10.3390/rs14163938
Chicago/Turabian StyleQi, Baoling, Lijun Wang, Dongbin Guo, and Chunhui Wang. 2022. "Energy-Barycenter Based Waveform Centroid Algorithm for Pulse Lidar Ranging System" Remote Sensing 14, no. 16: 3938. https://doi.org/10.3390/rs14163938
APA StyleQi, B., Wang, L., Guo, D., & Wang, C. (2022). Energy-Barycenter Based Waveform Centroid Algorithm for Pulse Lidar Ranging System. Remote Sensing, 14(16), 3938. https://doi.org/10.3390/rs14163938





