1. Introduction
The ability to map and monitor the spatial distribution of crop types is critical for applying precision agriculture, preserving crop diversity, and increasing food production [
1,
2,
3]. Remote sensing provides an important and efficient way to obtain crop distribution maps over time and space [
4]. Time series of satellite images have been widely used for crop identification as they can better capture the growth characteristics of individual crops than a single image [
5,
6]. One of the key challenges of using time series images is the extraction of discriminative features to represent the growing stages and phenological characteristics for crop identification.
Crop classification often uses vegetation indexes (VIs) and phenological metrics obtained from time series images. Numerous VIs have been developed using the form of simple ratios or normalized difference ratios of the red and near infrared (NIR) spectral bands, such as the Enhanced Vegetation Index (EVI), Normalized Difference Vegetation Index (NDVI), and Difference Vegetation Index (DVI) [
7,
8]. VIs relate to the dynamics and physiological properties of vegetation across time and space [
9]. Thus, a great number of studies have directly utilized time series of VIs for crop classification with distinctive seasonal characteristics such as soybean and rice [
10,
11,
12,
13].
Phenological metrics are usually extracted from time series of VIs or band reflectance. Because phenological changes such as germination and leaf development depend on crop type, phenological features play an important role in crop delineation [
14]. Statistical or threshold-based methods have been employed to calculate phenological patterns such as time of peak VI, maximum VI, phenological stages, and onset of green-up [
15]. Bargiel [
14] developed a new method to identify phenological sequence patterns by using time series Sentinel-1 data for crop classification. Zhong et al. [
16] employed Landsat data to derive vegetation phenology based on the crop calendar, such as the amplitude of EVI variation within the growth cycle, change rate parameters of growth curves, and start and end dates of growth curves, for corn and soybean classification.
Although several methods have been developed for extracting features for crop classification, this step is still challenging in practice because the methods depend heavily on domain knowledge and human experiences, which cause the following issues:
Manual feature extraction is tedious and time-consuming. Features are usually extracted by trial and error, and the classification results tend to be subjective [
6]. Features tend to vary for the same crop classification in the same study area for different studies.
Most of the existing methods can only extract low-level features from the original image, such as spectral features, VIs, and phenological features. Low-level features might ignore useful time series information while including redundant information for crop classification. Complex factors, such as intra-class variability, inter-class similarity, light-scattering mechanisms, and atmospheric conditions, are difficult to be accounted for with only domain knowledge and human experience.
Manual feature extraction approaches depend on the inter-regional and inter-annual variations of the crop calendar. Phenological characteristics of the same crops in different regions may differ because of various climate and geographic factors. Therefore, manually extracted features may be merely adequate for the specific study area and temporal pattern.
Feature learning techniques provide an alternative way to automatically generate/learn effective features from original data to achieve high classification performance without domain knowledge [
17]. Deep learning methods, such as Convolutional Neural Networks (CNNs), can automatically discover data representations in an end-to-end regime to solve a particular problem [
18]. However, designing an effective deep learning architecture often requires a series of trials and errors or domain knowledge, and the deep models are a black box with poor interpretability [
19]. In addition, the performance of deep learning methods typically relies on a large number of high-quality training samples, which are usually limited and unavailable in crop classification.
Evolutionary computation is a family of nature-inspired and population-based algorithms, which have powerful search and learning ability by evolving a population of candidate solutions (individuals) towards optimal solutions to solve a problem [
20]. As an evolutionary algorithm, Genetic Programming (GP) is a popular and fast-developing approach to automatic programming [
21,
22]. In GP, a solution is typically a computer program that can be represented by different forms, including a flexible tree-based representation. The flexibility of the solution representation and the powerful search ability enable GP to be an effective method in feature learning for many problems related to computer vision and pattern recognition. Bi et al. [
17] proposed a GP-based method to learn different types and numbers of global and local image features for face recognition. Ain et al. [
23] developed a multi-tree representation of GP to learn features for melanoma detection from skin images. A novel multi-objective GP technology was used in image segmentation to learn high-level features and improve the separation of objects from target images [
24]. GP provides improved interpretability of the evolved solutions and does not rely on predefined solution structures or a huge number of training samples.
Recently, GP has been gradually introduced into remote sensing and achieved promising results. Puente et al. [
25] applied GP to automatically produce a new vegetation index to estimate soil erosion from satellite images. Cabral et al. [
26] employed GP for classifying burned areas and indicated that the performance of GP is better than Maximum Likelihood and Regression Trees. Batista et al. [
27] used the M3GP algorithm to create hyper features for land cover classification, and the accuracy is higher than adding NDVI and NDWI. Applying GP to times series of satellite images for crop classification is still challenging as GP needs to be adapted to exploit their temporal, spatial, and spectral information. In general, GP constructs one feature from a set of input features and performs binary classification using the constructed feature. However, crop classification usually includes multiple crop types, and one feature may not be effective for this task. Therefore, it is necessary to investigate a new GP approach for constructing multiple features for multi-class crop classification.
To address the above limitation, the goal of this study is to develop a GP approach with a new representation to automatically learn multiple high-level features for multi-class crop classification. To achieve this goal, we develop a new GP representation to learn multiple features from the input time series data using a single tree. The new representation enables GP to automatically extend the width and depth of the GP trees to obtain fixed or flexible features without relying on domain knowledge. This proposed GP approach is wrapped with different classification algorithms, i.e., K-Nearest Neighbor (KNN), Naive Bayes (NB), Decision Tree (DT), and Support Vector Machine (SVM), for crop classification in Heilongjiang Province, China. The performance of the proposed GP approach is compared with the classification with the traditional VIs features and the classifier of Multilayer Perceptron (MLP) to analyze the effectiveness. The main contributions of this paper are summarized as follows.
- (1)
The new approach for feature learning based on GP represents, to the best of our knowledge, the first time that GP is used to learn multiple features for crop classification.
- (2)
The new GP representation with COMB functions learns multiple high-level features based on a single tree for the classification of crops. The new GP representation automatically selects the discriminable low-level features from the raw images and then constructs a fixed or flexible number of high-level features based on the low-level ones.
2. Background on GP
GP aims to automatically evolve computer programs (models or solutions) to solve a problem/task without requiring extensive domain knowledge [
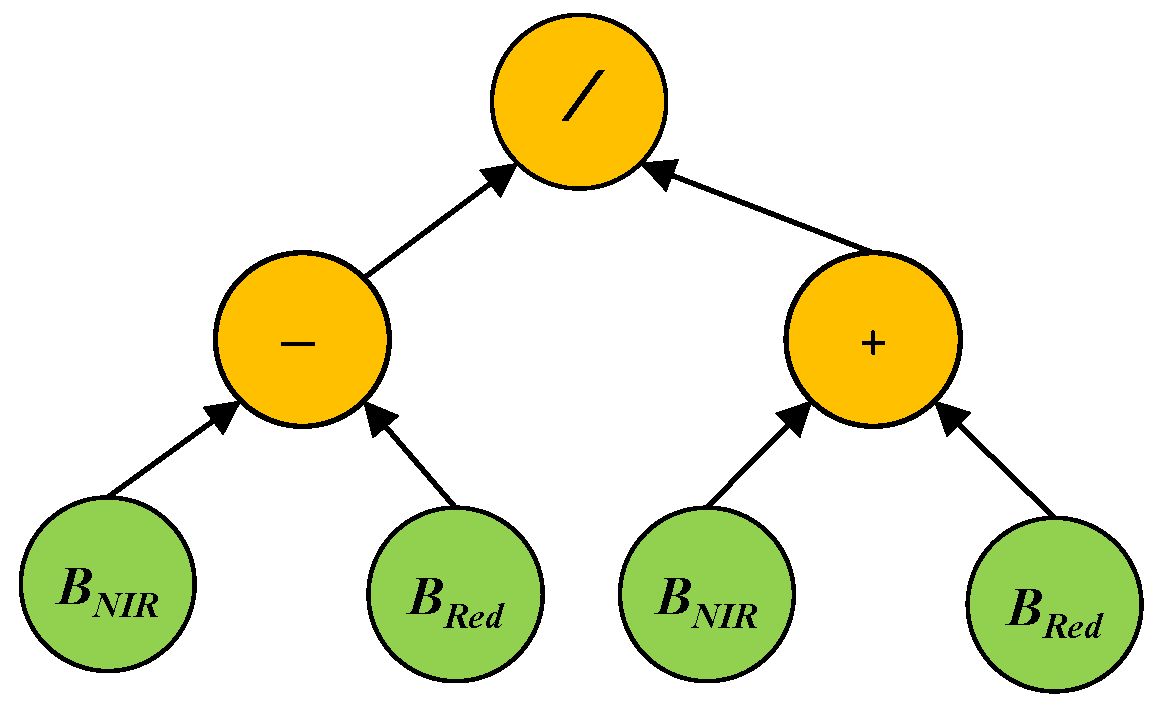
22]. Following the principles of Darwinian evolution and natural selection, GP can automatically evolve a population of programs to search for the best solution via several generations/iterations to solve specific problems. The programs/solutions of GP can be represented by different forms, such as trees, grammar, and linear. Among all these representations, tree-based GP is the most popular and widely used one. The trees are constructed by using functions or operators, such as +, −, ×, and protected /, to form the internal/root nodes, and using terminals, such as constants or variables/features, to form the leaf nodes. The functions are selected from a predefined function set, which often contains arithmetic and logic operators that can be used to solve this problem. The terminals are selected from a predefined terminal set, which often contains random constants and all the possible input variables/features of the problem. We take NDVI as an example to show the structure of a GP tree (
Figure 1). In this example GP tree, the functions are /, +, and −, and the terminals are the NIR and Red bands. The GP tree can be formulated as
, which is a feature constructed by using the NIR and Red bands.
The general process of GP starts by randomly initializing a population of trees (also called solutions, individuals, and programs) using a tree generation method [
22]. Each tree is assigned a fitness value through fitness evaluation using a fitness function. The fitness value indicates how well the tree fits into the problem. GP searches for the best solution from the population via several generations, where the overall process is known as the evolutionary process. During the evolutionary process, better trees with higher fitness values have a large chance to survive and generate offspring for the next generation. These trees are selected by a selection method, and the offspring are generated from the selected trees (known as parents) using genetic operators. The commonly used genetic operators are crossover, mutation, and elitism of the subtree. A new population is generated using these operators for the next generation. The overall evolutionary process proceeds until it satisfies a termination criterion, and the best tree is returned. On a feature learning task, the best tree indicates the best feature set.
3. GP-Based Feature Learning for Crop Classification
The overview of the whole GP approach for feature learning in crop classification is shown in
Figure 2. We developed a new GP representation with a set of
COMB functions, i.e.,
COMB1 as the root node to generate a fixed number of features, and
COMB2 and
COMB3 as the internal/root nodes to generate a dynamic number of features. The feature learning process of GP starts by randomly generating an initial population of trees based on the new representation, functions, and terminal sets. A new fitness function is designed to evaluate the goodness of each tree in the population with the training samples. At each generation, a new population is generated using the selection method and three common genetic operators, i.e., elitism, crossover, and mutation, to replace the current population. Then, the new population is evaluated using the fitness function, and evaluation processes are repeated until the maximum number of generations. Then the best GP tree is returned and applied to generate informative features for crop classification. The important parts of GP approach for high-level feature learning include the new GP representation, function and terminal sets, fitness function, and genetic operators, which are described in detail below.
3.1. The New Tree Representation of GP
Two representations of GP with COMB functions are developed to automatically learn/generate a predefined number or a dynamic number of features from the input data. The tree representation is based on strongly typed GP, where type constraints must be met when building new trees in the population initialization process and the genetic operations, i.e., crossover and mutation. The followings present how the GP trees are built using these different COMB functions in two ways.
In the first tree representation, the function
COMB1 is used as a root node to produce features with a fixed size. In other words, the root node of a GP tree has a predefined number of child nodes to produce features. An example tree with
COMB1 that produces five different features is shown in
Figure 3. This example program has five branches split from the root node
COMB1. Each branch is a normal GP tree that can produce one feature using arithmetic operators. For example, the first feature
F1 is
, which indicates that the learned feature is a combination of the three bands. The five features are learned using different operators and the original bands.
The tree representation with function
COMB1 is further extended by increasing the width of the tree to construct more high-level features with a fixed number (
Figure 4). In this representation, we can define a number of learned features, and then the representation is extended to include more branches as each branch can produce a feature. For example, if
m features are expected to be learned for crop classification, the GP representation can be changed to have
m branches by designing a new root node
COMB1. As shown in
Figure 4b, the
COMB1 function has
m branches that produce
m features. This new design of the
COMB1 node allows GP to generate a predefined number of features for crop classification.
In the second tree representation, the
COMB2 and
COMB3 functions are developed as internal and root nodes to allow GP to learn a dynamic/flexible number of features by increasing the depth of the tree. The
COMB2 and
COMB3 functions accept two or three nodes as child nodes and can combine features from their child nodes. When the
COMB2 or
COMB3 function only appears at the root node, a GP tree can produce two or three features, respectively (as shown in
Figure 5a). When the
COMB2 and
COMB3 functions appear at both internal and root nodes, a GP tree can concatenate the features from the internal nodes and has a deeper size to produce a large flexible number of features (as shown in
Figure 5b). Compared with the first representation (
Figure 4), the second representation does not need to predefine the number of features by automatically learning a dynamic number of features. The internal nodes and root nodes of
COMB2 and
COMB3 in GP trees determine the number of the features.
3.2. Function Set and Terminal Set
The function set includes the
COMB functions (
COMB1,
COMB2, and
COMB3), four arithmetic operators (
,
,
, protected /), and a logic operator (
IF) (
Table 1). Except for the
COMB functions, the other functions are commonly used for feature learning in the GP community. The
COMB functions were specifically developed to allow the proposed approach to generate additional high-level features using a single tree. The four arithmetic functions each take two arguments as inputs and return one floating-point number. The division operation (/) is protected by returning one if the divisor is zero. The logic function
IF returns one number by taking three arguments as inputs.
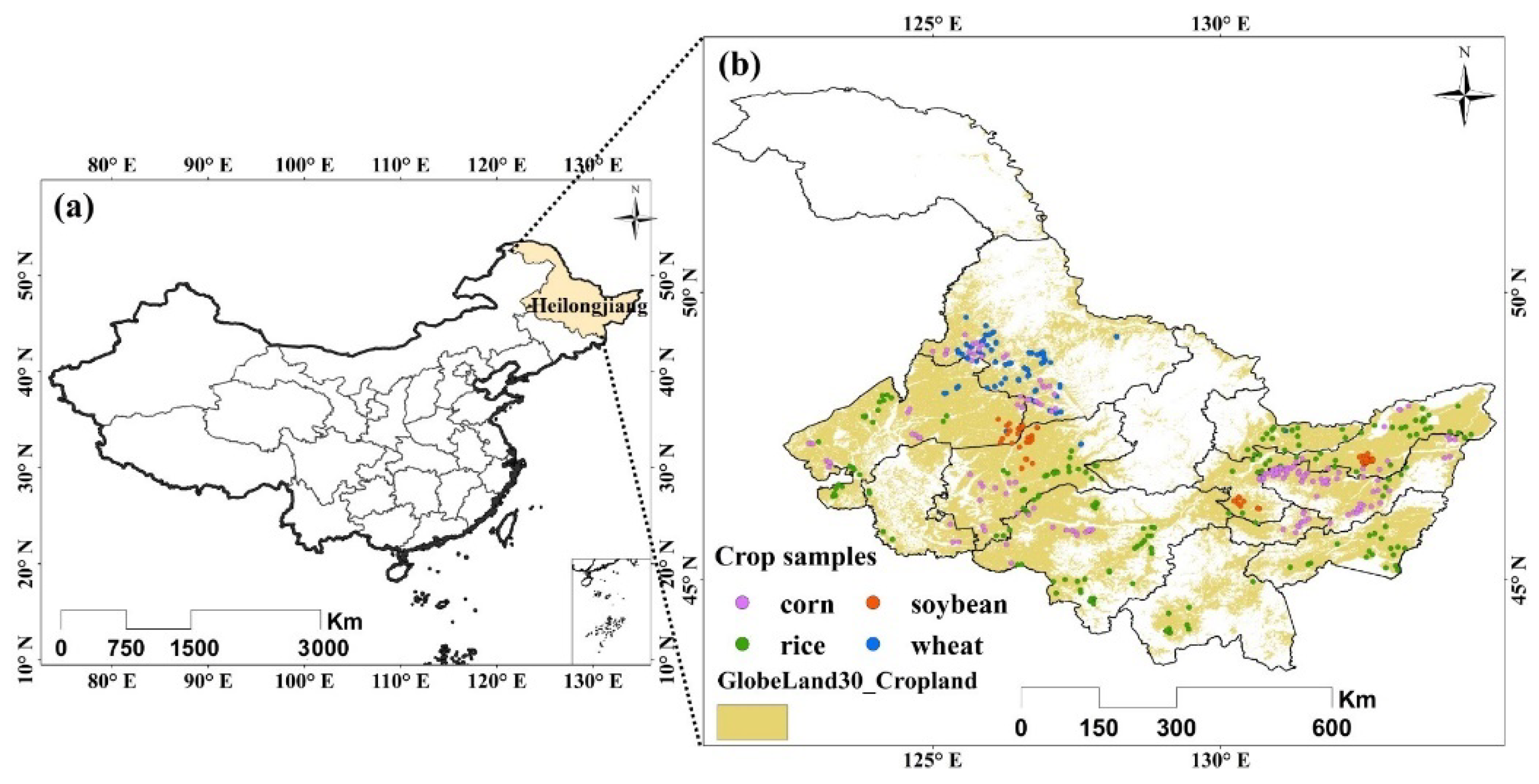
The terminal set includes original band values and random constants. The original bands are from the time series images for crop classification. Specifically, there are 217 band values for a pixel/example/instance as inputs of GP trees, where more details of them will be presented in
Section 4.2. The random constants are random floating-point numbers sampled within the range [0.0, 1.0].
3.3. Fitness Function
During the evolution of GP, the effectiveness of the features learned by GP is evaluated by using a fitness function. The fitness function is the classification accuracy obtained by an external classification algorithm (such as KNN, NB, DT, or SVM) with five-fold cross-validation using all samples in the training set.
In the fitness evaluation process, all samples with band values in the training set are transformed into features using a GP tree, and then the transformed training set is split into five folds. Four folds (evaluation training set) are used to train the classifier and the other one fold (evaluation test set) is used to evaluate the classifier and calculate the accuracy. This process repeats five times until each fold is used as the evaluation test set exactly once. The detailed process is shown in
Figure 6. The test accuracy of each fold
is defined in Equation (1), and the mean accuracy is calculated in Equation (2) as the fitness function.
where
,
,
, and
are the numbers of true positives, true negatives, false negatives, and false negatives of the corresponding (
nth) fold, respectively. The
acc and
Fitness are in the range of [0, 1].
3.4. Genetic Operators
At each generation of GP, selection and genetic operators, including
elitism,
subtree crossover, and
subtree mutation, are employed to create a new population to construct more promising features. The
elitism operator copies several best trees with good fitness values from the current population to the new population. We apply
tournament selection as the selection method to select trees with better fitness from the current population for crossover and mutation. The
subtree crossover operator creates two new trees (offspring) by randomly selecting a branch of two trees (parents) and swapping the selected branches (
Figure 7a). The
subtree mutation operator creates a new tree (offspring) by randomly selecting one branch from a tree (parent) and replacing it with a new randomly generated branch (
Figure 7b). In the GP approach with the
COMB1 function, the genetic operators, i.e., crossover and mutation operators, do not change the root node since all GP methods use the same root node. In the GP approach with the
COMB2 and
COMB3 functions, the genetic operators work on the nodes with the same input and output types, i.e., meeting the constraints of the input and output types of nodes. The genetic operators not only maintain the goodness of the current population but can also search for promising spaces to produce the best features.
6. Discussion
Automatic feature extraction is still challenging for crop classification because the manual methods are tedious, time-consuming, and subjective. GP is a very powerful and flexible method to automatically evolve mathematical models from a set of terminals and operators without extensive domain knowledge. We introduced a new GP method to automatically learn high-level, effective features based on time series images. We developed new representations for GP by using a set of
COMB functions to automatically produce fixed and flexible numbers of high-level features from the time series data. The
COMB1 function was developed to produce a predefined number of features by extending the width of the GP tree, while the
COMB2 and
COMB3 functions were proposed to produce a flexible number of features by extending the GP tree depth. The proposed GP method can automatically select valuable bands with typical spectral and temporal characteristics from the original data and simultaneously construct high-level features from the selected features using predefined operators or functions (
Figure 10).
The features learned by GP significantly improved the classification accuracy for two reasons. The first one is that GP creates new features from the original features, and automatically transforms the original representation space into a new one that better represents the spatial and temporal characteristics of crops. The process of feature learning combines features selected from the original features and then creates new high-level features for classification. The second reason is that GP employs the fitness function wrapped with a classifier to assess the effectiveness of the learned features in the evolutionary process.
GP is more robust and stable with various classifiers and different numbers of features compared with VIs. The average accuracy differences of the four classifiers are small using features learned by GP, while they are large when using VIs. The feature number of GP has little effect on the classification performance since classification accuracy is high even with only five GP-based features. By contrast, VIs usually require a large number of features to reach the highest classification accuracy. Additionally, GP can achieve excellent accuracy even with a small training subset. The overall accuracy of MLP increases with more training samples, while GP is more stable with various training sets. The number of training samples has less influence on the classification accuracy of GP than that of MLP.
The features learned by GP are easier to understand and interpret because of their origin and formation compared with other feature learning methods such as deep learning. In the experiments, GP first identified the original bands with typical spectral and temporal characteristics for feature learning. Bands with high usage frequencies for GP were NIR and SWIR bands, which are also widely used to construct vegetation indices (such as EVI and NDVI). Meanwhile, most bands were selected during DOYs 145-177 and 217-249, which are DOYs in the middle of the crop growing seasons and represent optimal window periods for crop identification in Heilongjiang Province. Based on the selected bands, GP constructed new high-level features by the tree representation using a series of functions and operators (
Table 1). Deep learning models (such as CNNs and other neural networks) can achieve high classification accuracy in several cases but are considered black boxes because they learn arcane features with poor interpretability. By comparison, GP has good interpretability and can explain how and why the features are obtained.
GP is one of the most versatile artificial intelligence methods but is still largely underused in remote sensing. Our study demonstrated the outstanding performance of GP for feature-learning based on MODIS time series images, suggesting that it is worthwhile to explore its potential applications in remote sensing. The GP for feature learning with dynamic/flexible number is more promising because predefining the number of features is not necessary. However, this method may not always achieve the best accuracy, because the search space of GP is much larger than with learning a fixed number of features, and the model suffers from local optima. How to automatically decide the optimal number of constructed features with high classification accuracy is still an open issue and needs further research. In practice, GP can also be used for classifier construction with its flexible representation and distinctive features [
33]. GP will be investigated in future work to explore additional applications using higher spatial and temporal images, such as tree-based GP for image classification, feature transfer learning, and change detection.
7. Conclusions
We developed a novel GP approach to learn high-level features for crop classification using time series images to address the inefficiencies of manual feature extraction in this study. We proposed a new GP representation with a single tree to flexibly learn multiple high-level features. GP with this representation produces high-level features by increasing the widths or depths of the trees based on a set of COMB functions. We employed four classifiers (KNN, NB, DT, and SVM) for crop classification by using the features learned by GP, and the accuracies were significantly improved. Compared with the traditional VIs features, GP demonstrated better performance and robustness for various classifiers and feature numbers. Additionally, we found that the number of training samples influenced GP less compared with MLP and that GP could produce excellent accuracy even with a small training subset.
This was the first time that GP was utilized to learn multiple features for crop classification by using time series images. The new GP approach automatically selected discriminable low-level features from the original band images and learned additional high-level features without domain knowledge. This study showed the advantages of GP in feature learning, i.e., flexible representation and high interpretability. These promising results demonstrated the potential of GP in remote sensing, which will be further explored by applying it to more applications with higher resolution data in the future. In addition, it is possible to investigate different experiment designs such as using the validation set to further improve the performance of the GP approach on real-world applications.