Coordinated Attitude Control of Spacecraft Formation Flying via Fixed-Time Estimators under a Directed Graph
Abstract
:1. Introduction
2. Preliminaries and Problem Formulation
2.1. Dynamics of Spacecraft Attitude
2.2. Graph Theory
2.3. The Concept of Fixed-Time Convergence and Some Lemmas
2.4. Problem Formulation
3. Design of the Control Law
3.1. Distributed Fixed-Time Estimator Design
3.2. Distributed Fixed-Time Control Law Design
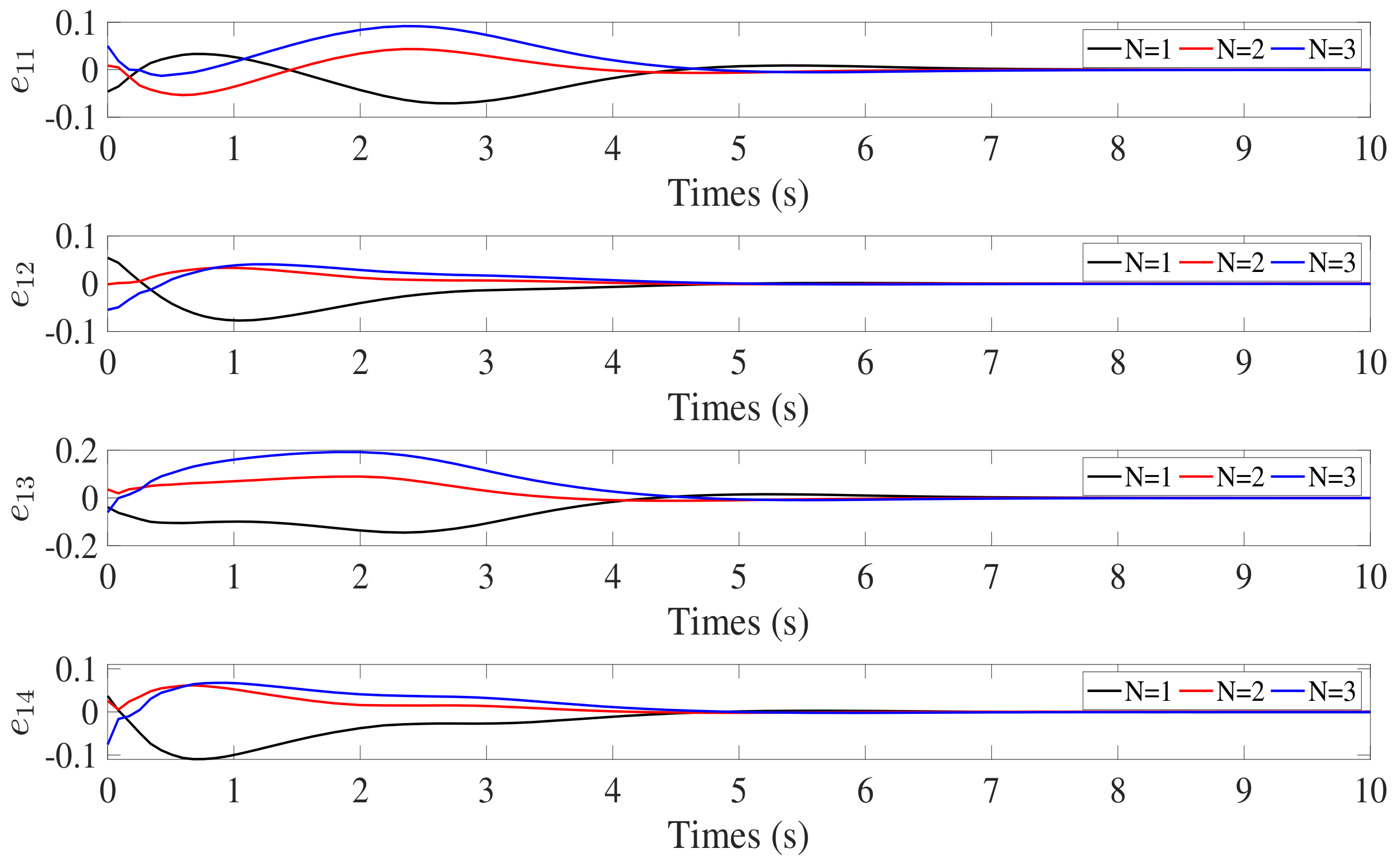
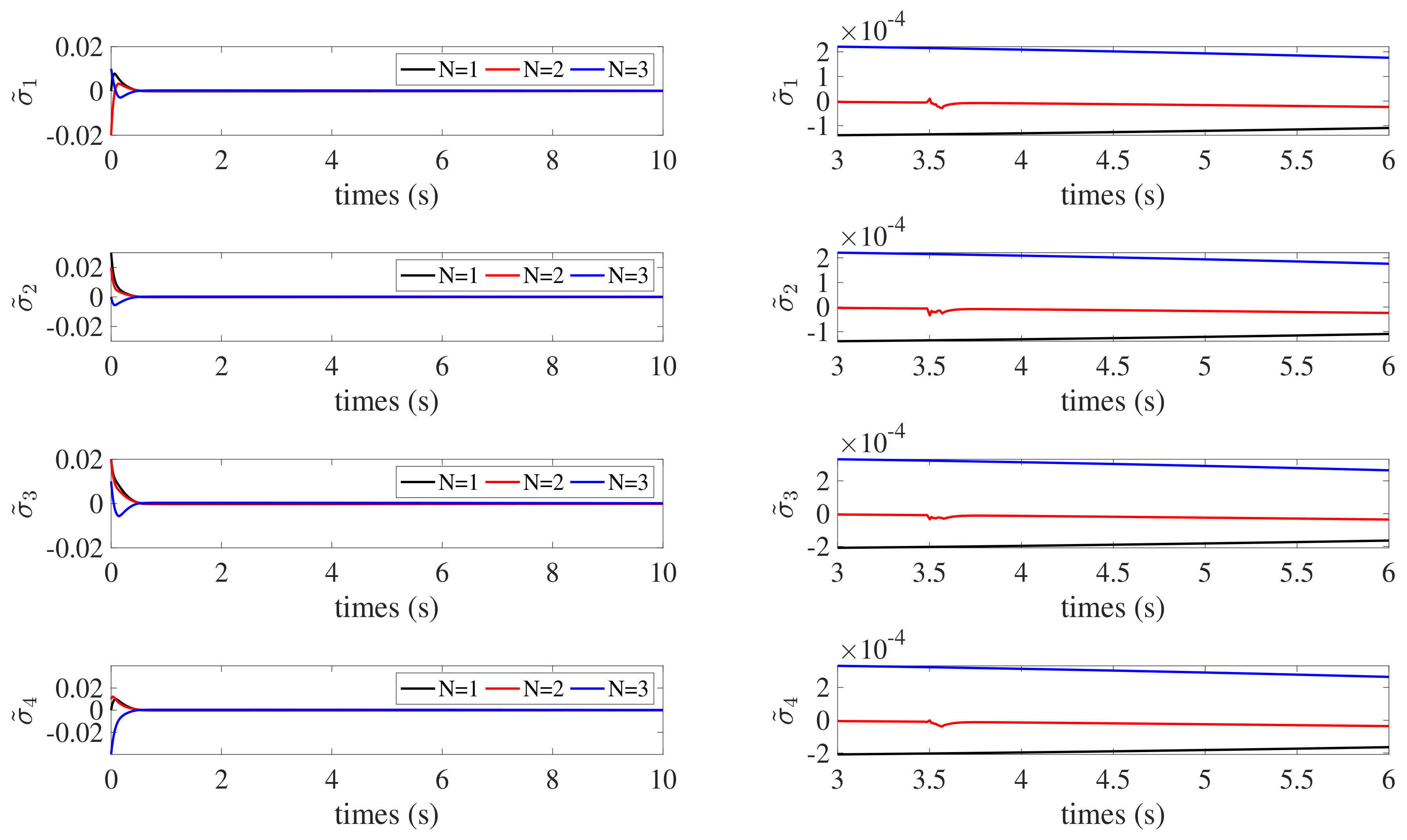
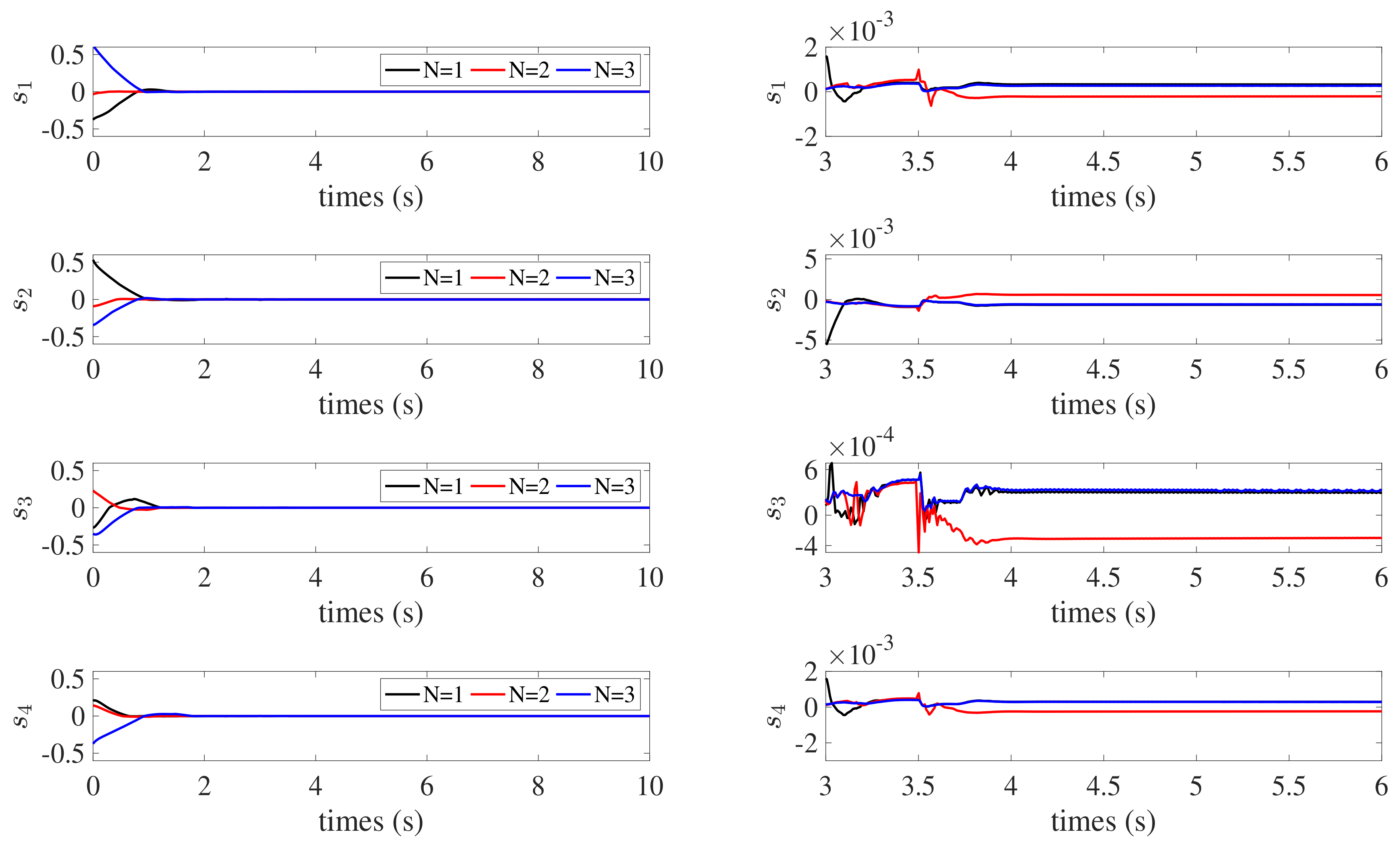
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Du, H.B.; Li, S.H.; Qian, C.J. Finite-Time attitude tracking control of spacecraft with application to attitude synchronization. IEEE Trans. Autom. Control. 2011, 56, 2711–2717. [Google Scholar] [CrossRef]
- Wu, B.; Wang, D.; Poh, E.K. Decentralized sliding-mode control for attitude synchronization in spacecraft formation. Int. Robust Nonlinear Control. 2013, 23, 1183–1197. [Google Scholar] [CrossRef]
- Cai, H.; Huang, J. The leader-following attitude control of multiple rigid spacecraft systems. Automatica 2014, 50, 1109–1115. [Google Scholar] [CrossRef]
- Zhang, C.X.; Ahn, C.K.; Wu, J.; He, W. Online-Learning Control with Weakened Saturation Response to Attitude Tracking: A Variable Learning Intensity Approach. Aerosp. Sci. Technol. 2021, 117, 106981. [Google Scholar] [CrossRef]
- Cao, Y.; Ren, W. Distributed coordinated tracking with reduced interaction via a variable structure approach. IEEE Trans. Autom. Control. 2012, 57, 33–48. [Google Scholar]
- Zhang, Y.; Yang, Y.; Zhao, Y. Distributed finite-time tracking control for nonlinear multi-agent systems subject to external disturbances. Int. J. Control. 2013, 86, 29–40. [Google Scholar] [CrossRef]
- Wang, X.; Li, S.; Shi, P. Distributed finite-time containment control for double-integrator multiagent systems. IEEE Trans. Cybern. 2014, 44, 1518–1528. [Google Scholar] [CrossRef] [PubMed]
- Tian, B.; Yin, L.; Wang, H. Finite-time reentry attitude control based on adaptive multivariable disturbance compensation. IEEE Trans. Ind. Electron. 2015, 62, 5889–5898. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of Linear Control Systems. IEEE Trans. Autom. Control. 2012, 57, 2106–2110. [Google Scholar] [CrossRef]
- Sui, W.S.; Duan, G.R.; Hou, M.Z. Distributed fixed-time attitude synchronization control for sultiple rigid spacecraft. Int. J. Control. Autom. Syst. 2019, 17, 6. [Google Scholar] [CrossRef]
- Zou, A.; Li, W. Fixed-Time output-feedback consensus tracking control for second-order multiagent systems. Int. J. Robust Nonlinear Control. 2019, 29, 2. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, Z.; Huang, Z. Distributed fault detection for nonlinear multi-agent systems under fixed-time observer. J. Frankl. Inst. 2019, 256, 13. [Google Scholar] [CrossRef]
- Mei, J.; Ren, W.; Ma, G.F. Distributed containment control for Lagrangian networks with parametric uncertainties under a directed graph. Automatica 2012, 48, 653–659. [Google Scholar] [CrossRef]
- Wang, W.; Li, C.; Sun, Y. Distributed coordinated attitude tracking control for spacecraft formation with communication delays. ISA Trans. 2018, 85, 97–106. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.J. Distributed Fixed-Time Coordinated Attitude Tracking Control with a Dynamic Leader for Spacecraft Formation Flying System. Math. Probl. Eng. 2022, 2022, 3425073. [Google Scholar] [CrossRef]
- Chen, T.; Shan, J.; Wen, H. Distributed Adaptive Attitude Control for Networked Underactuated Flexible Spacecraft. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 215–225. [Google Scholar] [CrossRef]
- Zhai, D.H.; Xia, Y.Q. Adaptive control of semi-autonomous teleoperation system with asymmetric time-varying delays and input uncertainties. IEEE Trans. Cybern. 2017, 47, 3621–3633. [Google Scholar] [CrossRef] [PubMed]
- Godsil, C.; Royle, G. Algebraic Graph Theory; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Ren, W.; Cao, Y. Distributed Coordination of Multi-Agent Networks; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Qu, Z. Cooperative Control of Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Roger, H.; Charles, J. Topics in Matrix Analysis; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Zuo, Z.Y.; Lin, T. A new class of finite-time nonlinear consensus protocols for multiagent systems. Int. J. Control. 2014, 87, 363–370. [Google Scholar] [CrossRef]
- Peng, K.; Yang, Y. Leader-following consensus problem with a varying-velocity leader and time-varying delays. Phys. A Stat. Mech. Its Appl. 2009, 388, 193–208. [Google Scholar] [CrossRef]
- Zhu, Z.H.; Guo, Y. Adaptive coordinated attitude control for spacecraft formation with saturating actuators and unknown inertia. J. Frankl. Inst. 2019, 356, 1021–1037. [Google Scholar] [CrossRef]





| Spacecraft | Inertia | Initial | Initial |
|---|---|---|---|
| Matrix | Attitude | Derivative | |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Wang, Y. Coordinated Attitude Control of Spacecraft Formation Flying via Fixed-Time Estimators under a Directed Graph. Remote Sens. 2022, 14, 4162. https://doi.org/10.3390/rs14174162
Zhou Z, Wang Y. Coordinated Attitude Control of Spacecraft Formation Flying via Fixed-Time Estimators under a Directed Graph. Remote Sensing. 2022; 14(17):4162. https://doi.org/10.3390/rs14174162
Chicago/Turabian StyleZhou, Zhanjie, and Yan Wang. 2022. "Coordinated Attitude Control of Spacecraft Formation Flying via Fixed-Time Estimators under a Directed Graph" Remote Sensing 14, no. 17: 4162. https://doi.org/10.3390/rs14174162
APA StyleZhou, Z., & Wang, Y. (2022). Coordinated Attitude Control of Spacecraft Formation Flying via Fixed-Time Estimators under a Directed Graph. Remote Sensing, 14(17), 4162. https://doi.org/10.3390/rs14174162






