A Polarization Stacking Method for Optimizing Time-Series Interferometric Phases of Distributed Scatterers
Abstract
:1. Introduction
2. Method
2.1. TS(Pol)InSAR Data Generation
2.2. TS(Pol)InSAR Coherency Matrix Statistic and Equivalent Number of Looks (ENL) Estimation
2.3. Phase Linking (PL) Theory
2.4. Cramer–Rao Lower Bound (CRLB) for Estimating ESM Interferometric Phases and Research Motivation
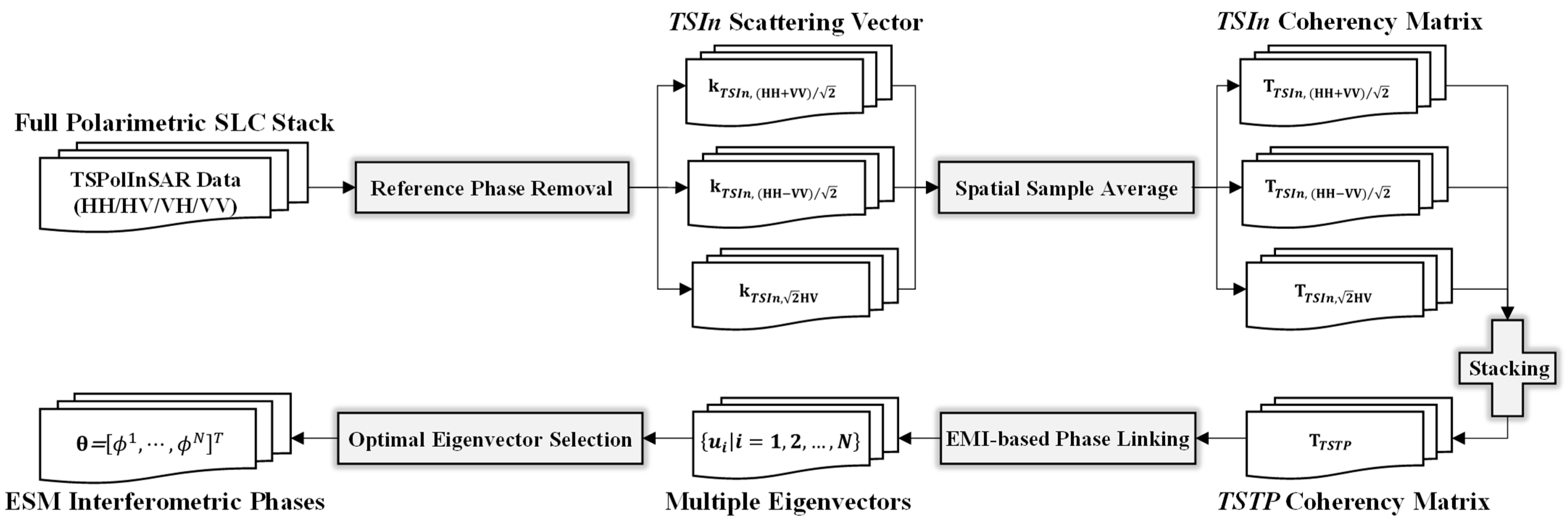
2.5. Proposed TSTP Coherency Matrix Construction and Theoretical Interpretation
- The TSIn scattering vector of each Pauli basis polarimetric channel is generated from the time-series full polarimetric SLC stack according to Equation (4), whose reference phase components are removed by the external DEM and the orbital information.
- The TSIn coherency matrix of each Pauli basis polarimetric channel is generated from the corresponding TSIn scattering vector according to Equation (4), and a spatial sample average estimation is performed on each TSIn coherency matrix.
- The TSTP coherency matrix is constructed by the polarization stacking operation in Equation (17) and normalized to obtain the corresponding TSCoh matrix.
- As an efficient MLE of PL, the EMI method [20] is selected to obtain multiple eigenvectors from the normalized TSTP coherency matrix according to Equation (13).
- Finally, the ESM interferometric phases can be extracted from the phases of the optimal eigenvector corresponding to the minimum eigenvector under the premise that a certain image is the master one.
3. Result
3.1. Simulated Experimental Data Simulation and Parameter Setting
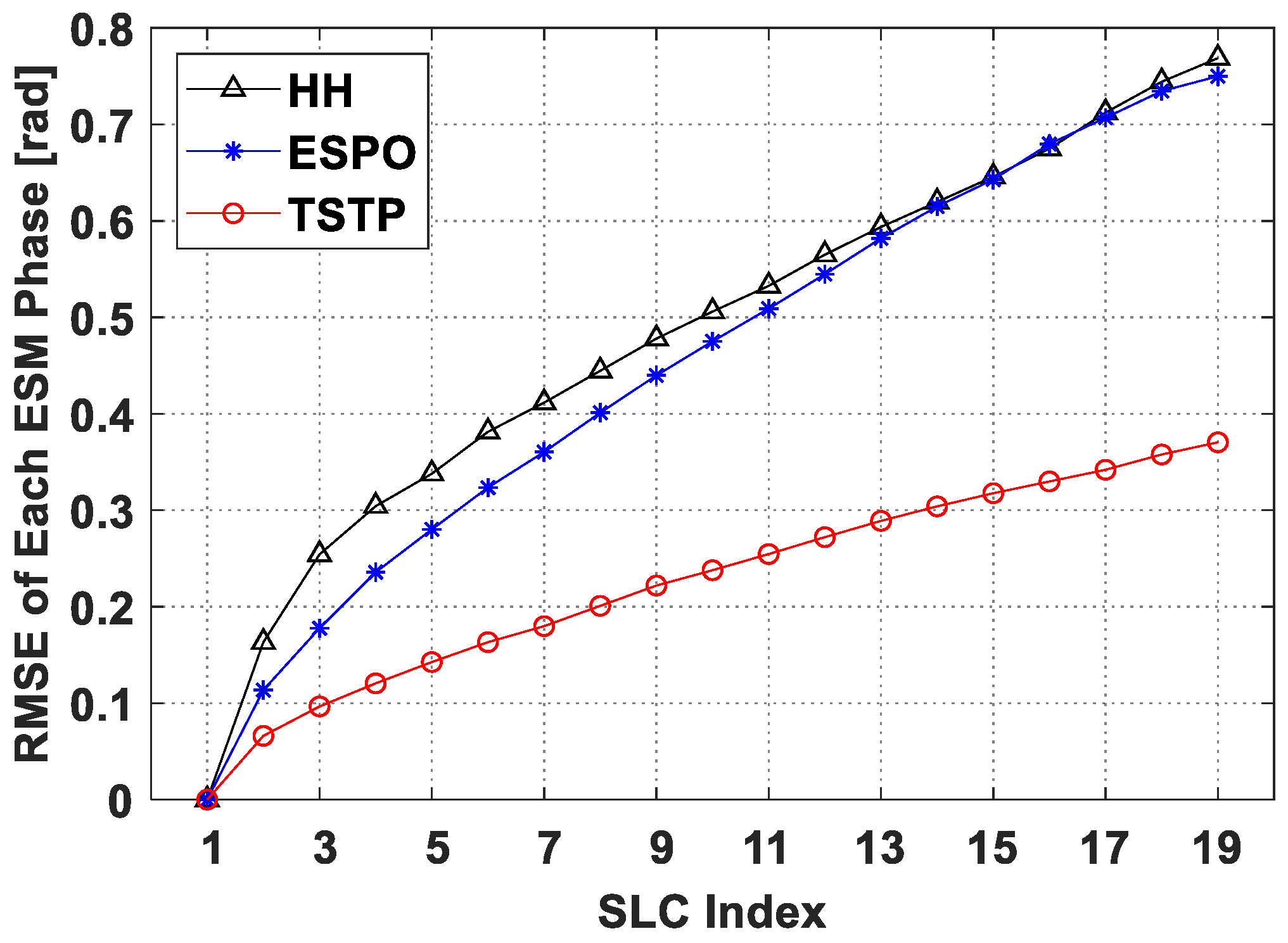
3.2. Simulated Experimental Result
3.3. Real Experimental Data Description and Parameter Setting
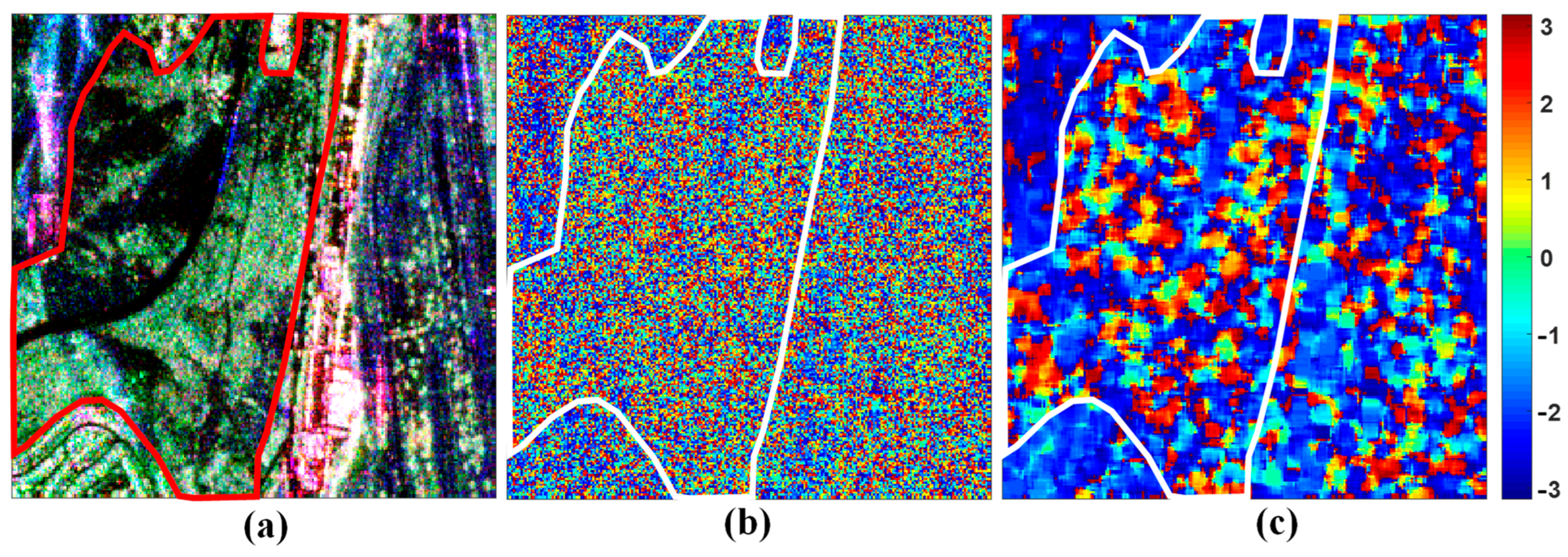
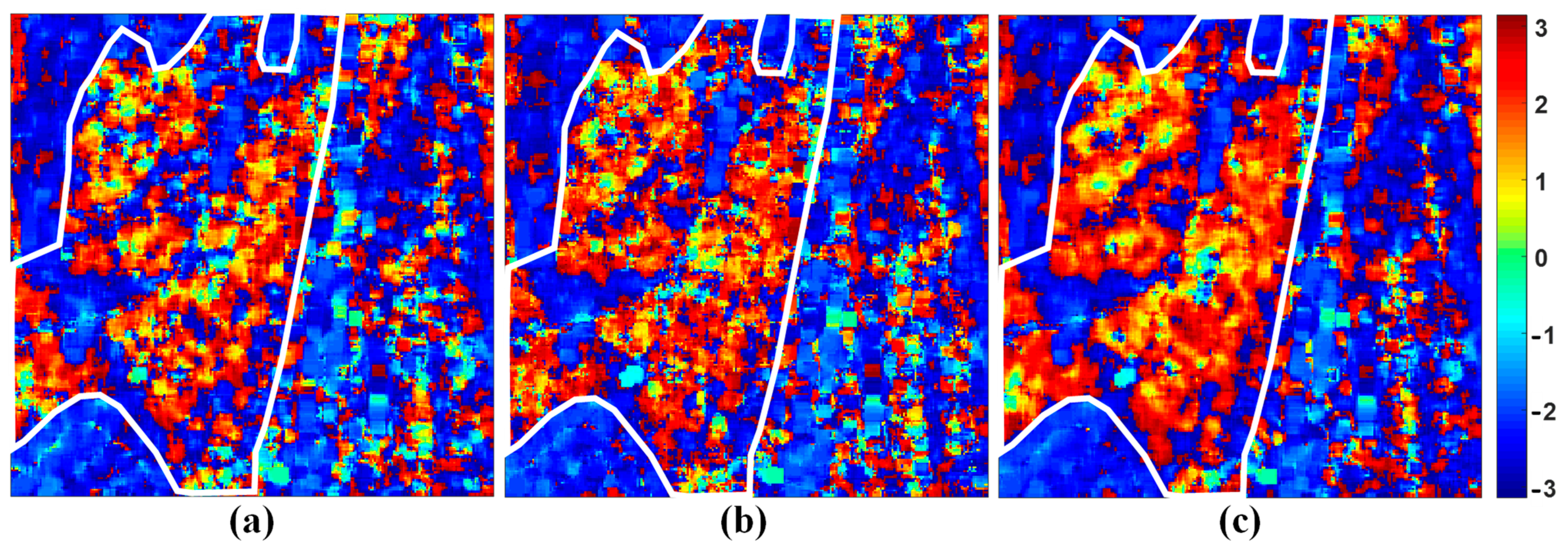
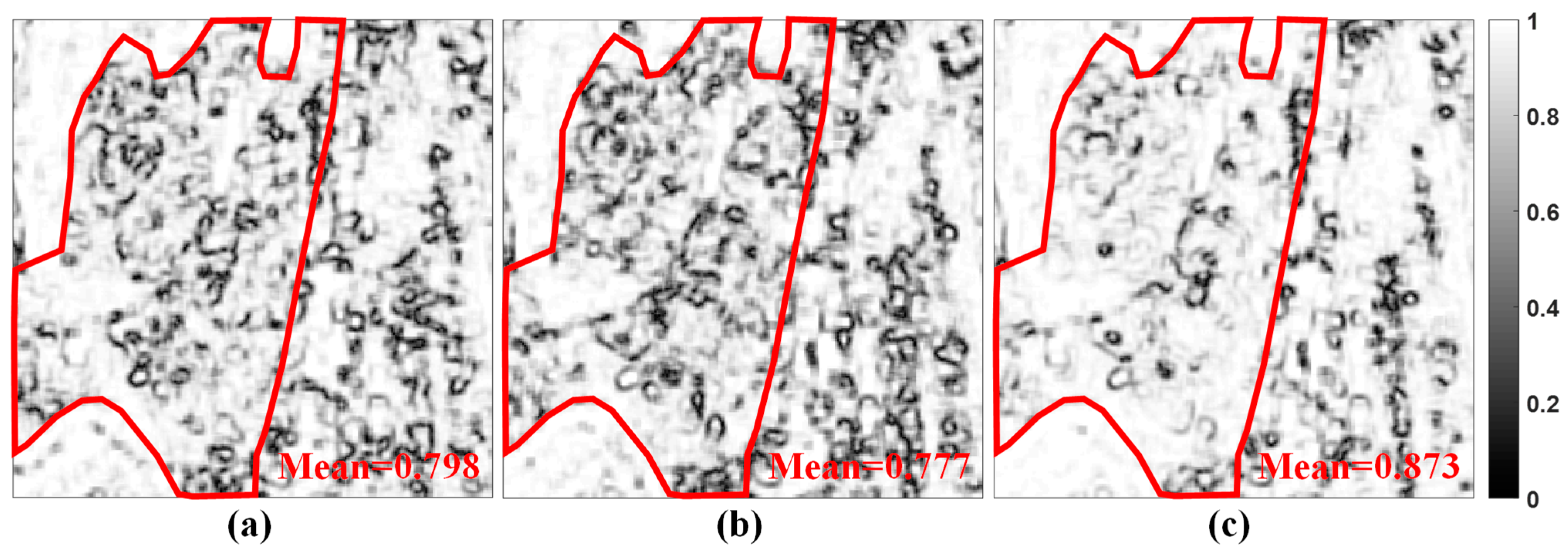
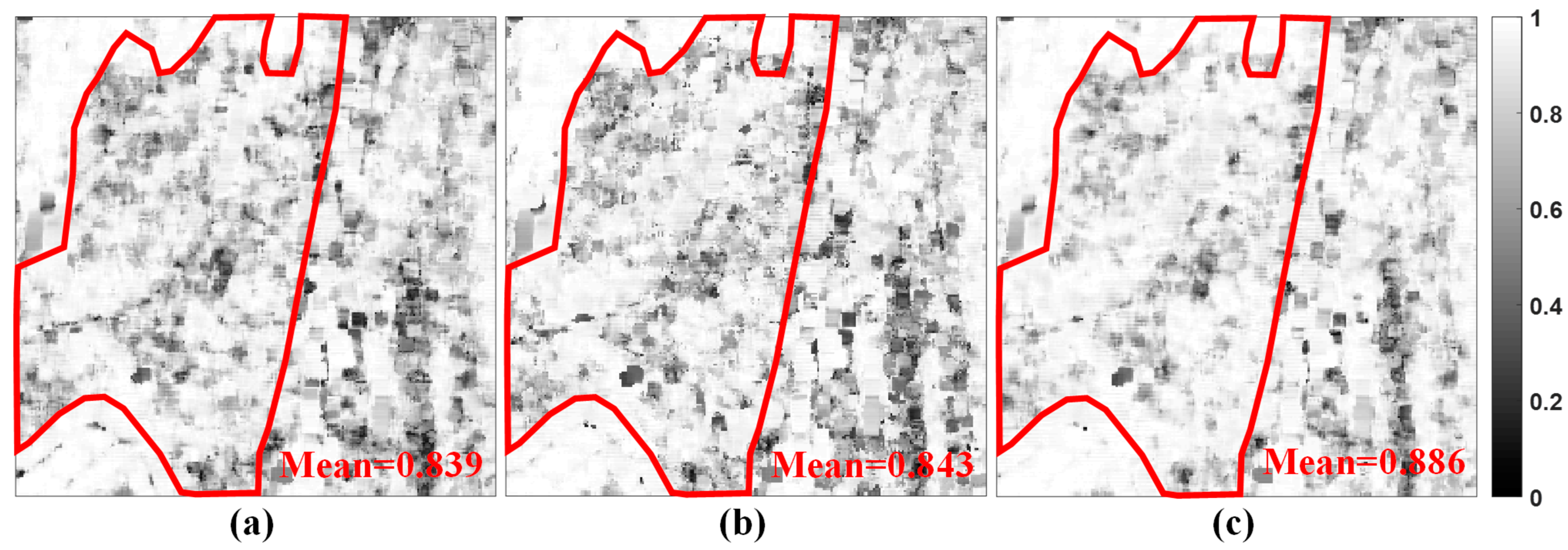
3.4. Real Experimental Result
4. Discussion
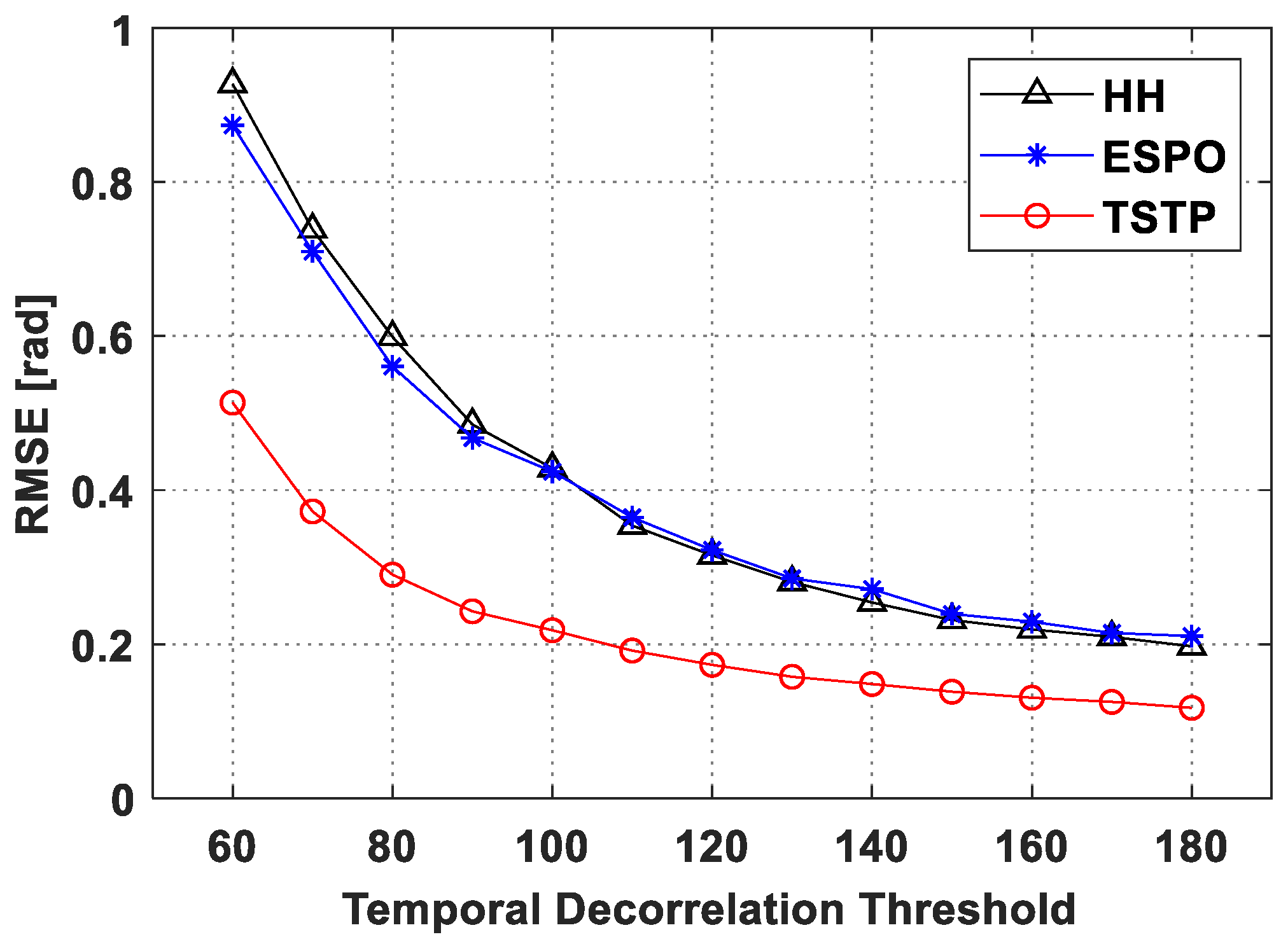
4.1. Simulated Experimental Discussion under Different Multilooking Size and Decorrelation Degrees
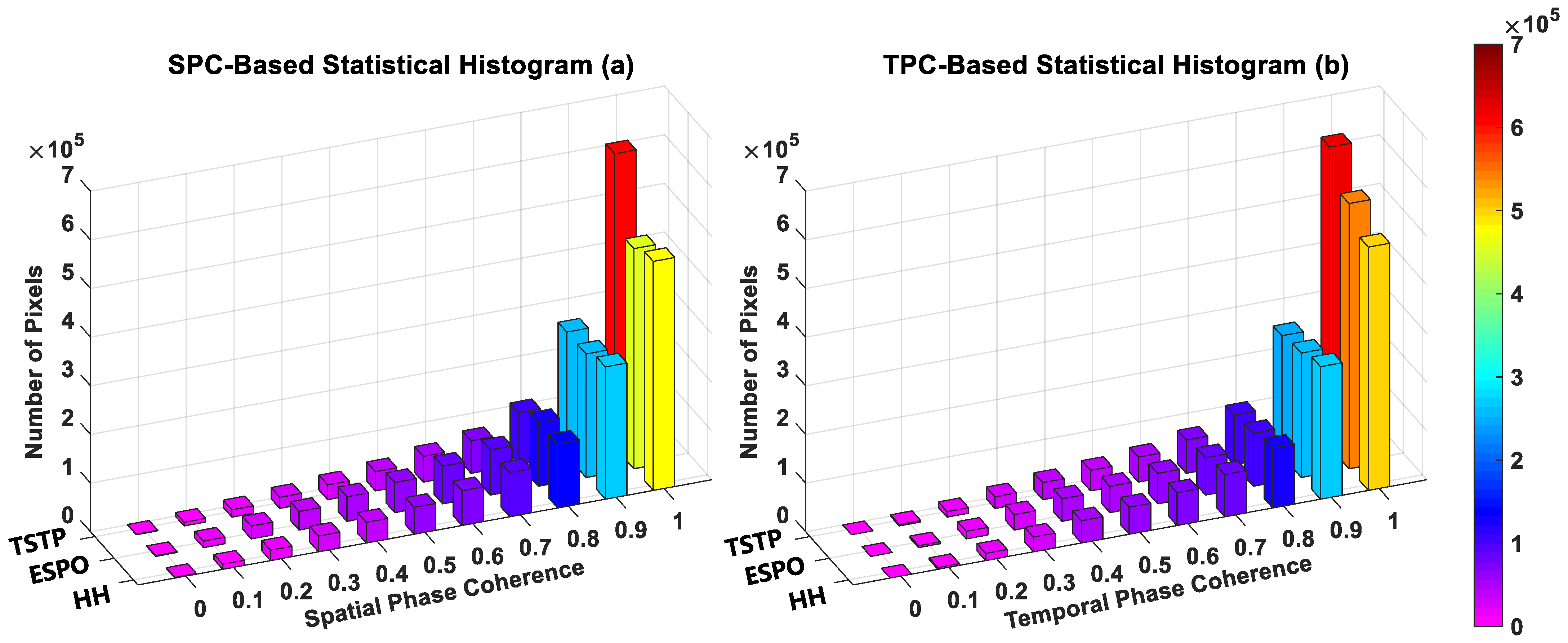
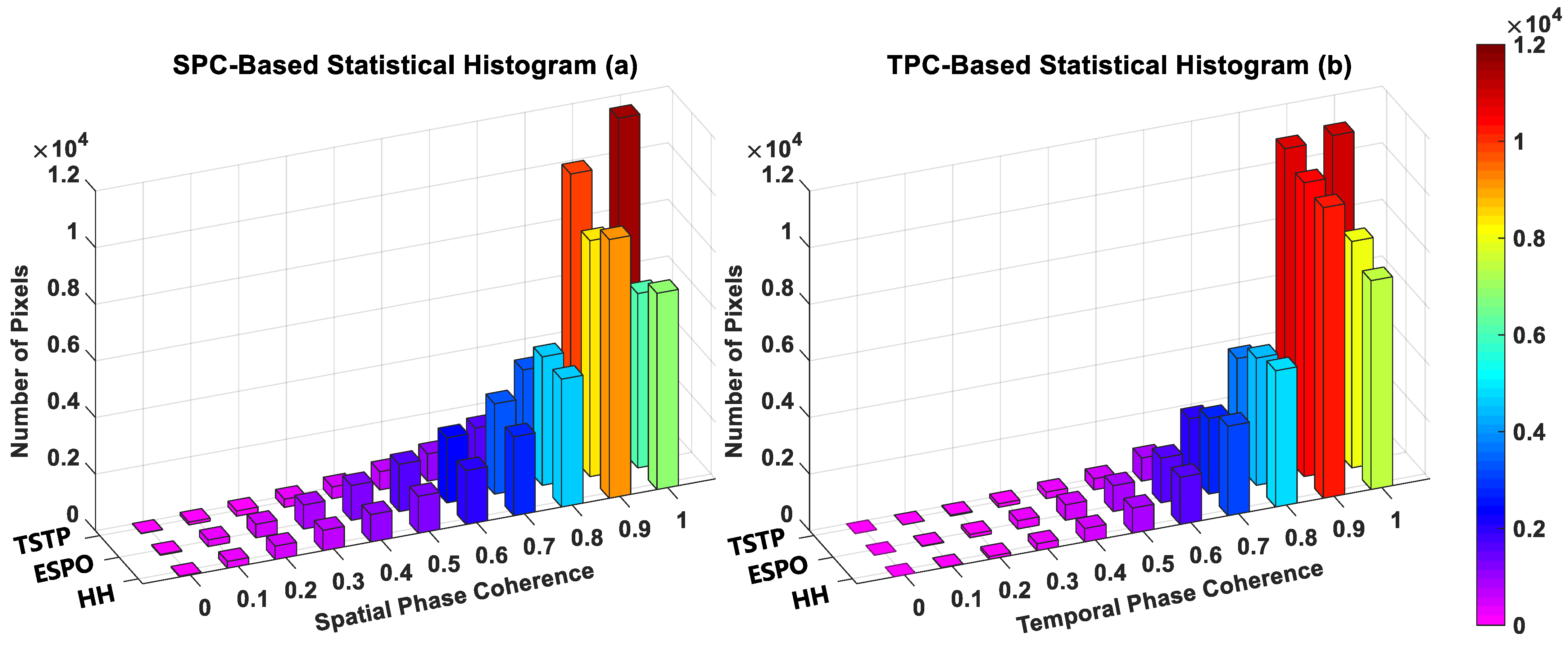
4.2. Real Experimental Discussion of The Full Scene
4.3. Real Experimental Discussion of The Selected ROI
4.4. Computational Efficiency Comparison between Two Polarimetric Optimization Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zebker, H.A.; Villasenor, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Springer Science & Business Media: Berlin, Germany, 2001; ISBN 0792369459. [Google Scholar]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Werner, C.; Wegmuller, U.; Strozzi, T.; Wiesmann, A. Interferometric point target analysis for deformation mapping. In Proceedings of the IGARSS 2003. 2003 IEEE International Geoscience and Remote Sensing Symposium. Proceedings, Toulouse, France, 21–25 July 2003; pp. 4362–4364. [Google Scholar]
- Costantini, M.; Falco, S.; Malvarosa, F.; Minati, F. A new method for identification and analysis of persistent scatterers in series of SAR images. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; pp. II-449–II–452. [Google Scholar]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31, L23611. [Google Scholar] [CrossRef]
- Hooper, A.; Segall, P.; Zebker, H. Persistent scatterer interferometric synthetic aperture radar for crustal deformation analysis, with application to Volcan Alcedo, Galapagos. J. Geophys. Res. Earth 2007, 112, B07407. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Lanari, R.; Mora, O.; Manunta, M.; Mallorqui, J.J.; Berardino, P.; Sansosti, E. A small-baseline approach for investigating deformations on full-resolution differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1377–1386. [Google Scholar] [CrossRef]
- Xiao, R.; Jiang, M.; Li, Z.; He, X. New insights into the 2020 Sardoba dam failure in Uzbekistan from Earth observation. Int. J. Appl. Earth Obs. Geoinf. 2022, 107, 102705. [Google Scholar] [CrossRef]
- Blanco-Sanchez, P.; Mallorqui, J.J.; Duque, S.; Monells, D. The Coherent Pixels Technique (CPT): An advanced DInSAR technique for nonlinear deformation monitoring. Pure Appl. Geophys. 2008, 165, 1167–1193. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A New Algorithm for Processing Interferometric Data-Stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Zhang, L.; Ding, X.; Lu, Z. Modeling PSInSAR time series without phase unwrapping. IEEE Trans. Geosci. Remote Sens. 2011, 49, 547–556. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, Z.; Ding, X.; Jung, H.; Feng, G.; Lee, C.-W. Mapping ground surface deformation using temporarily coherent point SAR interferometry: Application to Los Angeles Basin. Remote Sens. Environ. 2012, 117, 429–439. [Google Scholar] [CrossRef]
- Guarnieri, A.M.; Tebaldini, S. On the exploitation of target statistics for SAR interferometry applications. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3436–3443. [Google Scholar] [CrossRef]
- Jiang, M.; Ding, X.; Hanssen, R.F.; Malhotra, R.; Chang, L. Fast statistically homogeneous pixel selection for covariance matrix estimation for multitemporal InSAR. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1213–1224. [Google Scholar] [CrossRef]
- Dong, J.; Liao, M.; Zhang, L.; Gong, J. A unified approach of multitemporal sar data filtering through adaptive estimation of complex covariance matrix. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5320–5333. [Google Scholar] [CrossRef]
- Fornaro, G.; Verde, S.; Reale, D.; Pauciullo, A. CAESAR: An approach based on covariance matrix decomposition to improve multibaseline-multitemporal interferometric SAR processing. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2050–2065. [Google Scholar] [CrossRef]
- Ansari, H.; De Zan, F.; Bamler, R. Efficient Phase Estimation for Interferogram Stacks. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4109–4125. [Google Scholar] [CrossRef]
- Jiang, M.; Guarnieri, A.M. Distributed Scatterer Interferometry with the Refinement of Spatiotemporal Coherence. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3977–3987. [Google Scholar] [CrossRef]
- Ansari, H.; Zan, F.D.; Bamler, R. Sequential Estimator: Toward Efficient InSAR Time Series Analysis. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5637–5652. [Google Scholar] [CrossRef]
- Neumann, M.; Ferro-Famil, L.; Reigber, A. Multibaseline polarimetric SAR interferometry coherence optimization. IEEE Geosci. Remote Sens. Lett. 2008, 5, 93–97. [Google Scholar] [CrossRef] [Green Version]
- Navarro-Sanchez, V.D.; Lopez-Sanchez, J.M.; Vicente-Guijalba, F. A contribution of polarimetry to satellite differential SAR interferometry: Increasing the number of pixel candidates. IEEE Geosci. Remote Sens. Lett. 2010, 7, 276–280. [Google Scholar] [CrossRef]
- Navarro-Sanchez, V.D.; Lopez-Sanchez, J.M. Improvement of persistent-scatterer interferometry performance by means of a polarimetric optimization. IEEE Geosci. Remote Sens. Lett. 2012, 9, 609–613. [Google Scholar] [CrossRef]
- Iglesias, R.; Monells, D.; Fabregas, X.; Mallorqui, J.J.; López-Martínez, C. Phase Quality Optimization in Polarimetric Differential SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2875–2888. [Google Scholar] [CrossRef]
- Zhao, F.; Mallorqui, J.J. Coherency matrix decomposition-based polarimetric persistent scatterer interferometry. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7819–7831. [Google Scholar] [CrossRef]
- Wu, B.; Tong, L.; Chen, Y.; He, L. New Methods in Multibaseline Polarimetric SAR Interferometry Coherence Optimization. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2016–2020. [Google Scholar] [CrossRef]
- Sadeghi, Z.; Zoej, M.J.V.; Hooper, A.; Lopez-Sanchez, J.M. A new polarimetric persistent scatterer interferometry method using temporal coherence optimization. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6547–6555. [Google Scholar] [CrossRef]
- Shen, P.; Wang, C.; Hu, J.; Fu, H.; Zhu, J. Interferometric Phase Optimization Based on PolInSAR Total Power Coherency Matrix Construction and Joint Polarization-Space Nonlocal Estimation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5201014. [Google Scholar] [CrossRef]
- Shen, P.; Wang, C.; Lu, L.; Luo, X.; Hu, J.; Fu, H.; Zhu, J. A Novel Polarimetric PSI Method Using Trace Moment-Based Statistical Properties and Total Power Interferogram Construction. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4402815. [Google Scholar] [CrossRef]
- Guarnieri, A.M.; Tebaldini, S. Hybrid Cramér-Rao bounds for crustal displacement field estimators in SAR interferometry. IEEE Signal Process. Lett. 2007, 14, 1012–1015. [Google Scholar] [CrossRef]
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Lee, J.S.; Hoppel, K.W.; Mango, S.A.; Miller, A.R. Intensity and phase statistics of multilook polarimetric and interferometric SAR imagery. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1017–1028. [Google Scholar] [CrossRef]
- Oliver, C.; Quegan, S. Understanding Synthetic Aperture Radar Images, 2nd ed.; SciTech Publishing: Raleigh, NC, USA, 2004. [Google Scholar]
- Anfinsen, S.N.; Doulgeris, A.P.; Eltoft, T. Estimation of the equivalent number of looks in polarimetric synthetic aperture radar imagery. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3795–3809. [Google Scholar] [CrossRef]
- Shen, P.; Wang, C.; Fu, H.; Zhu, J.; Hu, J. Estimation of Equivalent Number of Looks in Time-Series Pol(In)SAR Data. Remote Sens. 2020, 12, 2715. [Google Scholar] [CrossRef]
- Gao, H.; Wang, C.; Xiang, D.; Ye, J.; Wang, G. TSPol-ASLIC: Adaptive Superpixel Generation with Local Iterative Clustering for Time-Series Quad- and Dual-Polarization SAR Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5217015. [Google Scholar] [CrossRef]
- Maiwald, D.; Kraus, D. Calculation of moments of complex Wishart and complex inverse Wishart distributed matrices. IEE Proc. Radar Sonar Navig. 2000, 147, 162–168. [Google Scholar] [CrossRef]
- Marino, A. Trace Coherence: A New Operator for Polarimetric and Interferometric SAR images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2326–2339. [Google Scholar] [CrossRef]
- Tao, X.; Jian, Y.; Weijie, Z. Interferometric Phase Improvement Based on Polarimetric Data Fusion. Sensors 2008, 8, 7172–7190. [Google Scholar] [CrossRef]
- Kwok, R.; Lee, J.S.; Grunes, M.R. Classification of Multi-Look Polarimetric SAR Imagery Based on Complex Wishart Distribution. Int. J. Remote Sens. 1994, 15, 2299–2312. [Google Scholar] [CrossRef]




| Sensor | Polarization | Number of Images | Frequency | Range Spacing | Azimuth Spacing | Incident Angle |
|---|---|---|---|---|---|---|
| ALOS PALSAR-2 | Full | 12 | 1.24 GHz | 2.86 m | 3.05 m | 33.24° |
| Acquisition Time | Perpendicular Baseline (m) | Temporal Baseline (Day) |
|---|---|---|
| 20150324 | 29.5 | −756 |
| 20160209 | 30.2 | −434 |
| 20160223 | −260.4 | −420 |
| 20160809 | −33.0 | −252 |
| 20161004 | 26.6 | −196 |
| 20161101 | 28.1 | −168 |
| 20170124 | −51.8 | −84 |
| 20170404 | 225.7 | −14 |
| 20170418 | 0 | 0 |
| 20170822 | −64.7 | 126 |
| 20180821 | 6.0 | 490 |
| 20190625 | −112.4 | 798 |
| Method | ALOS PALSAR-2 (1200 × 1000 pixels) |
|---|---|
| ESPO | 1,408,181.04 s |
| TSTP | 2.28 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, P.; Wang, C.; Hu, J. A Polarization Stacking Method for Optimizing Time-Series Interferometric Phases of Distributed Scatterers. Remote Sens. 2022, 14, 4168. https://doi.org/10.3390/rs14174168
Shen P, Wang C, Hu J. A Polarization Stacking Method for Optimizing Time-Series Interferometric Phases of Distributed Scatterers. Remote Sensing. 2022; 14(17):4168. https://doi.org/10.3390/rs14174168
Chicago/Turabian StyleShen, Peng, Changcheng Wang, and Jun Hu. 2022. "A Polarization Stacking Method for Optimizing Time-Series Interferometric Phases of Distributed Scatterers" Remote Sensing 14, no. 17: 4168. https://doi.org/10.3390/rs14174168
APA StyleShen, P., Wang, C., & Hu, J. (2022). A Polarization Stacking Method for Optimizing Time-Series Interferometric Phases of Distributed Scatterers. Remote Sensing, 14(17), 4168. https://doi.org/10.3390/rs14174168






