Validating Ionospheric Scintillation Indices Extracted from 30s-Sampling-Interval GNSS Geodetic Receivers with Long-Term Ground and In-Situ Observations in High-Latitude Regions
Abstract
:1. Introduction
2. Methods to Estimating the Scintillation Indices
2.1. Phase Scintillation Index () from 50 Hz ISMR Observations
2.2. Rate of Change of Density Index (RODI) Estimated from the Electric Field Instrument of Swarm Satellites
2.3. Rate of TEC Index (ROTI) Estimated from 30s-Sampling-Interval GNSS Observations
2.4. The Index Based on Continuous Wavelet Transform
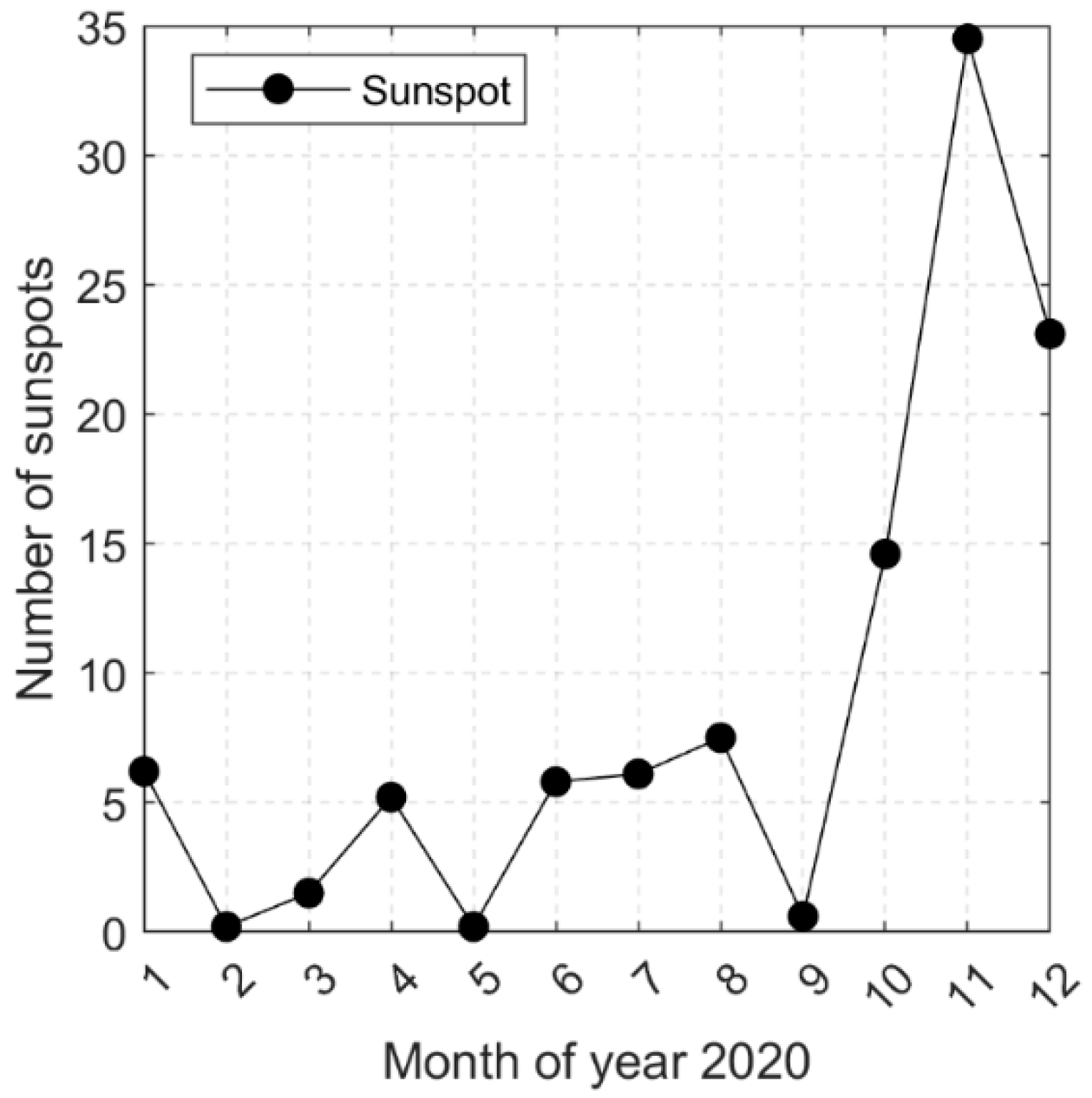
3. Introduction to the Adopted Data
4. Performance of the 30s-Sampling-Interval Scintillation Indices in Monitoring Scintillations
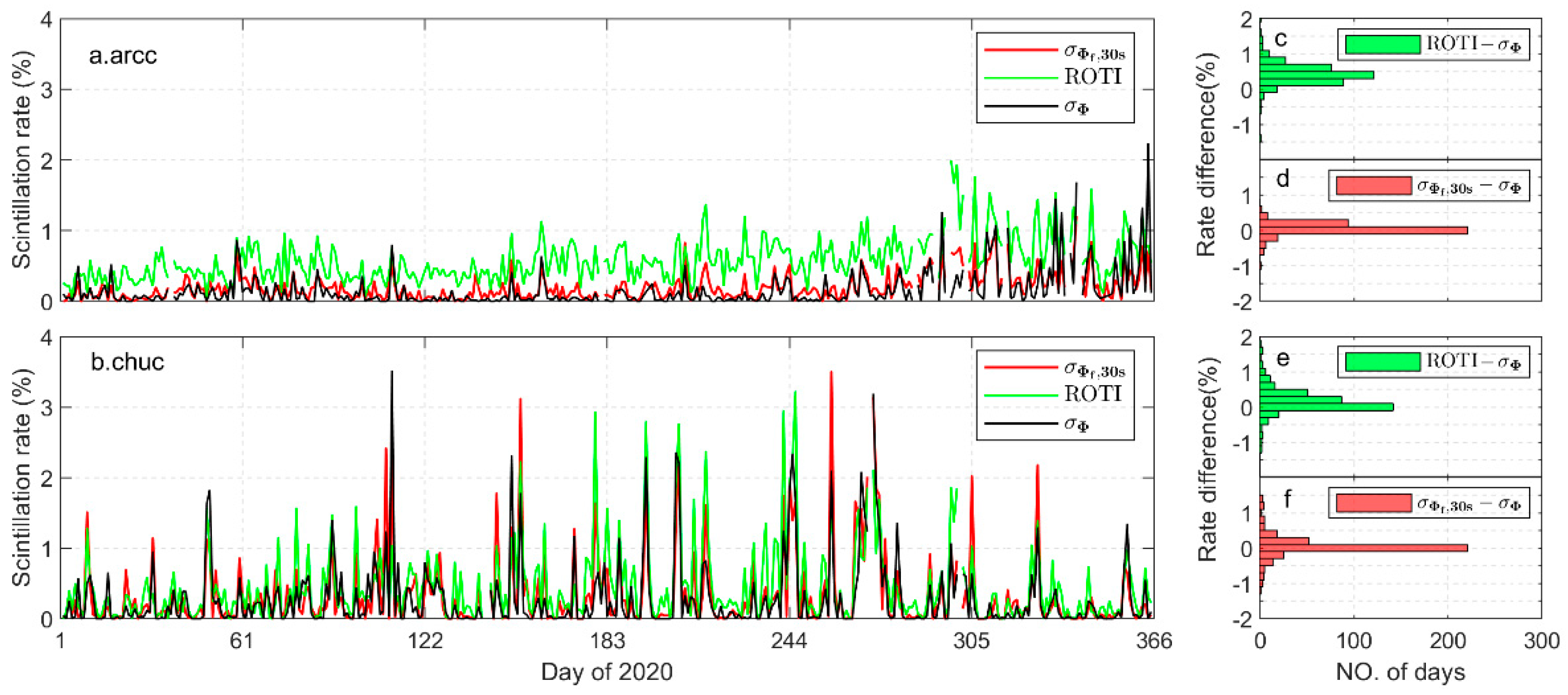
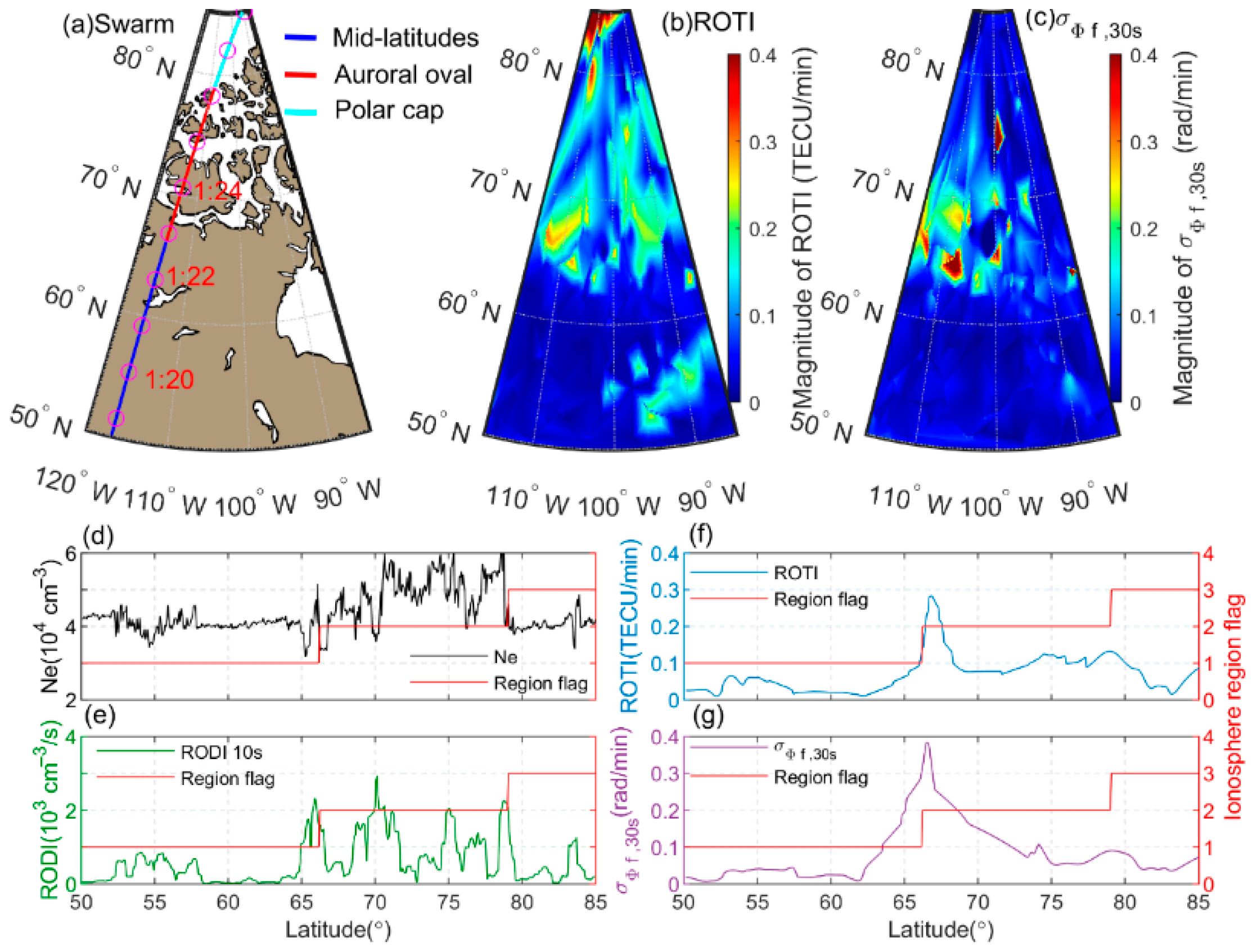
4.1. Analysis on the Accuracy of the 30s-Sampling-Interval Scintillation Indices in the Time Aspect
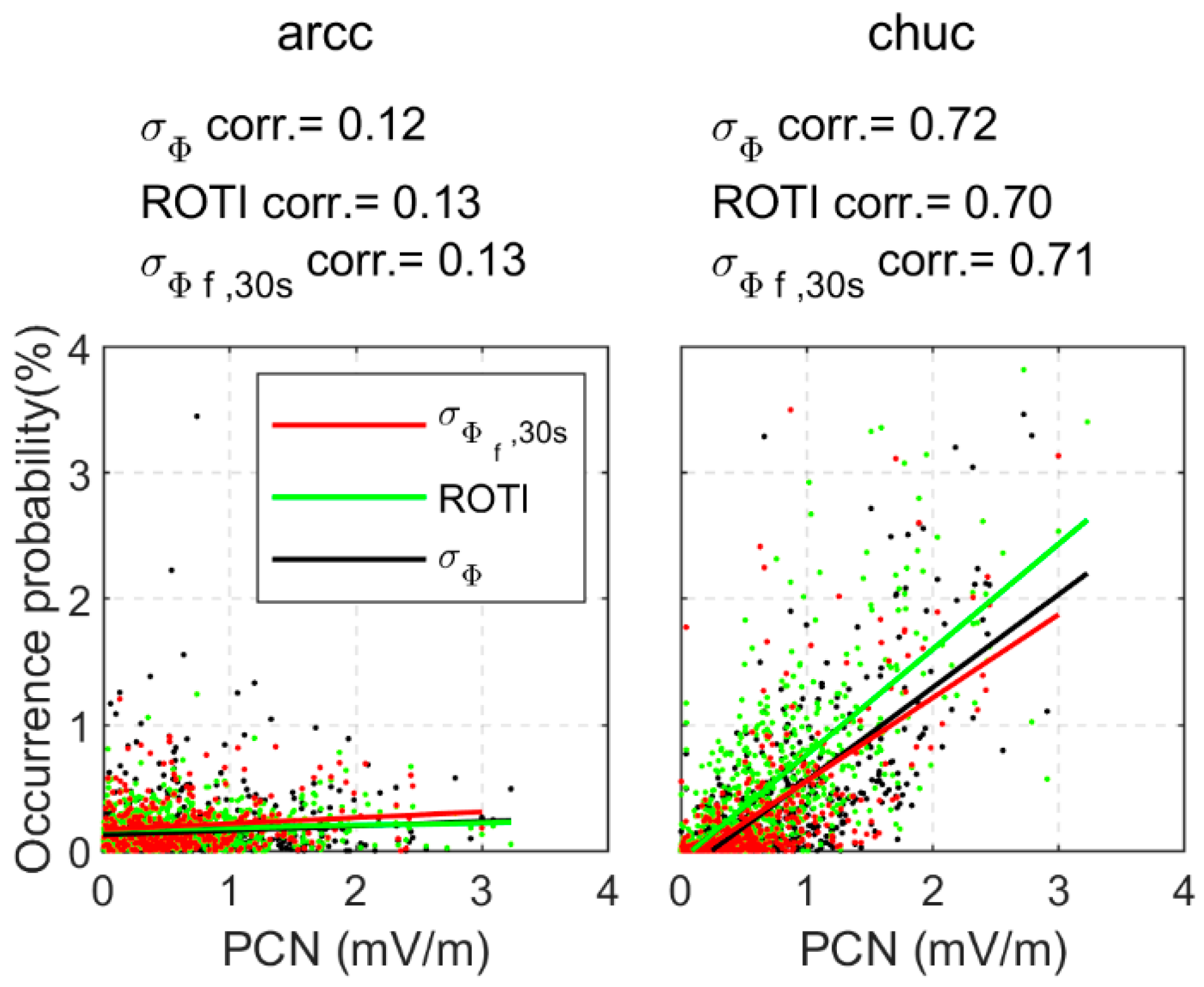
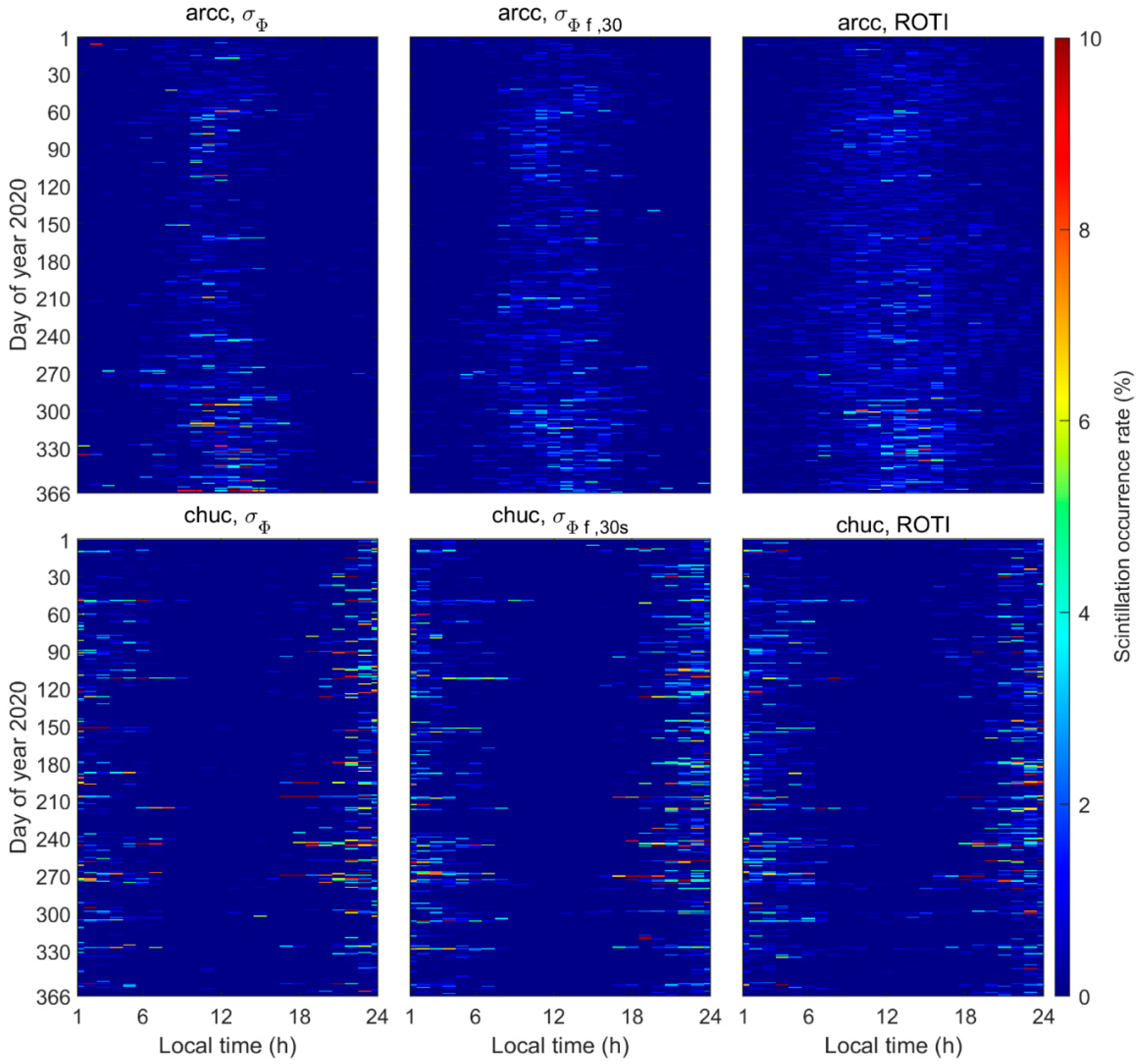
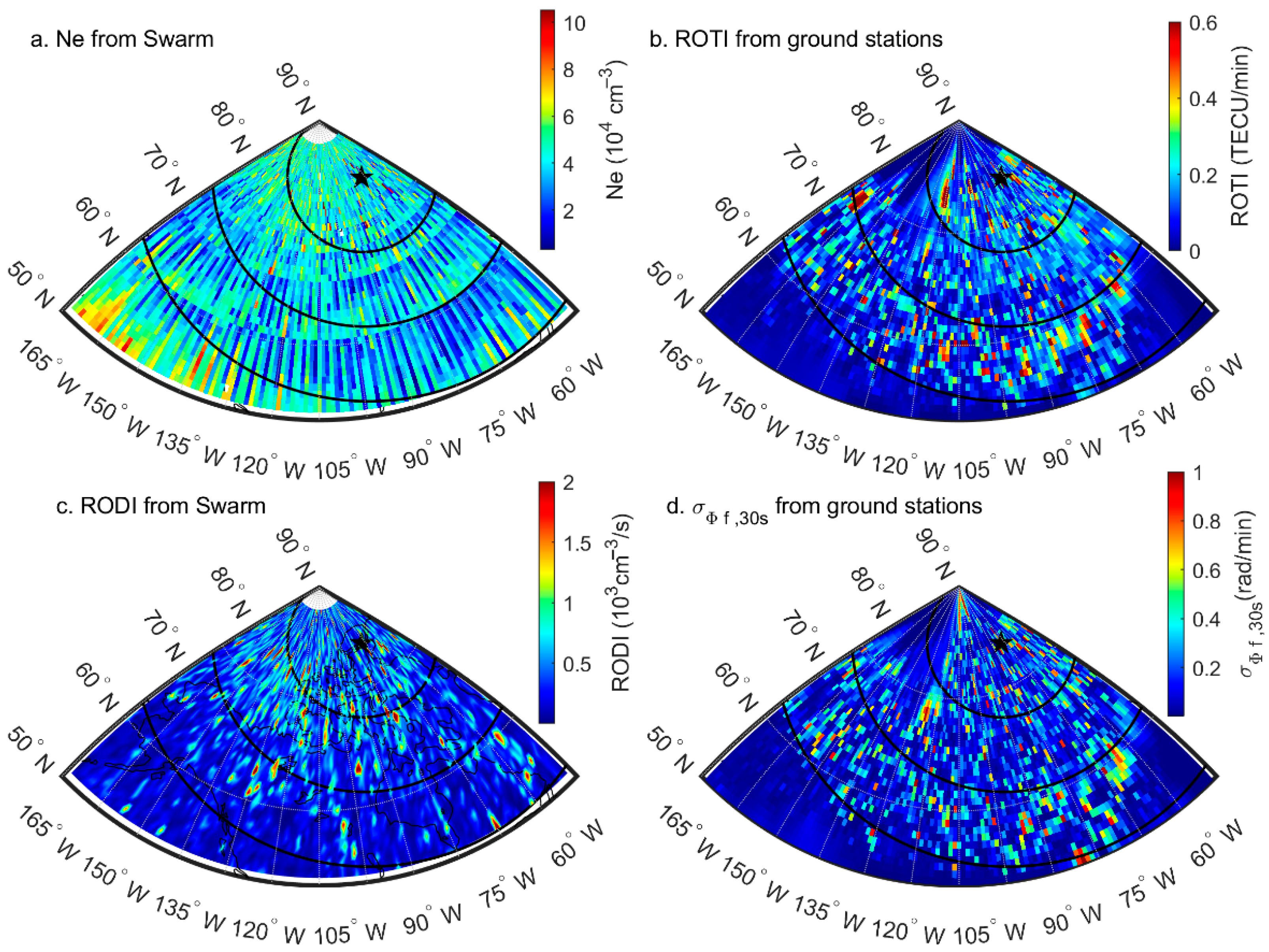
4.2. Analysis on the Accuracy of the 30s-Sampling-Interval Scintillation Indices in the Space Aspect
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aarons, J. Global morphology of ionospheric scintillations. Proc. IEEE 1982, 70, 360–378. [Google Scholar] [CrossRef]
- Béniguel, Y.; Cherniak, I.; Garcia-Rigo, A.; Hamel, P.; Hernández-Pajares, M.; Kameni, R.; Kashcheyev, A.; Krankowski, A.; Monnerat, M.; Nava, B. MONITOR Ionospheric Network: Two case studies on scintillation and electron content variability. Ann. Geophys. 2017, 35, 377–391. [Google Scholar] [CrossRef]
- Vani, B.C.; Shimabukuro, M.H.; Galera Monico, J.F. Visual exploration and analysis of ionospheric scintillation monitoring data: The ISMR Query Tool. Comput. Geosci. 2017, 104, 125–134. [Google Scholar] [CrossRef]
- Jayachandran, P.; Langley, R.; MacDougall, J.; Mushini, S.; Pokhotelov, D.; Hamza, A.; Mann, I.; Milling, D.; Kale, Z.; Chadwick, R. Canadian high arctic ionospheric network (CHAIN). Radio Sci. 2009, 44, 1–10. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, Q.; Hu, C.; Yu, Z.; Wu, W. Modeling and assessment of five-frequency BDS precise point positioning. Satell. Navig. 2022, 3, 8. [Google Scholar] [CrossRef]
- Juan, J.M.; Aragon-Angel, A.; Sanz, J.; González-Casado, G.; Rovira-Garcia, A. A method for scintillation characterization using geodetic receivers operating at 1 Hz. J. Geod. 2017, 91, 1383–1397. [Google Scholar] [CrossRef]
- Juan, J.M.; Sanz, J.; Rovira-Garcia, A.; González-Casado, G.; Ibáñez, D.; Perez, R.O. AATR an ionospheric activity indicator specifically based on GNSS measurements. J. Space Weather Space Clim. 2018, 8, A14. [Google Scholar] [CrossRef]
- Nguyen, V.K.; Rovira-Garcia, A.; Juan, J.M.; Sanz, J.; González-Casado, G.; La, T.V.; Ta, T.H. Measuring phase scintillation at different frequencies with conventional GNSS receivers operating at 1 Hz. J. Geod. 2019, 93, 1985–2001. [Google Scholar] [CrossRef]
- Ahmed, A.; Tiwari, R.; Strangeways, H.; Dlay, S.; Johnsen, M. Wavelet-based analogous phase scintillation index for high latitudes. Space Weather 2015, 13, 503–520. [Google Scholar] [CrossRef]
- Zhao, D.; Li, W.; Li, C.; Tang, X.; ZHANG, K. Extracting an ionospheric phase scintillation index based on 1 Hz GNSS observations and its verification in the Arctic region. Acta Geod. Cartogr. Sin. 2021, 50, 368–383. [Google Scholar] [CrossRef]
- Olwendo, J.O.; Cilliers, P.; Weimin, Z.; Ming, O.; Yu, X. Validation of ROTI for ionospheric amplitude scintillation measurements in a low-latitude region over Africa. Radio Sci. 2018, 53, 876–887. [Google Scholar] [CrossRef]
- Zhao, D.; Li, W.; Li, C.; Hancock, C.M.; Roberts, G.W.; Wang, Q. Analysis on the ionospheric scintillation monitoring performance of ROTI extracted from GNSS observations in high-latitude regions. Adv. Space Res. 2022, 69, 142–158. [Google Scholar] [CrossRef]
- Kivanç, Ö.; Heelis, R.A. Structures in ionospheric number density and velocity associated with polar cap ionization patches. J. Geophys. Res. Space Phys. 1997, 102, 307–318. [Google Scholar] [CrossRef]
- Coley, W.R.; Heelis, R.A. Seasonal and universal time distribution of patches in the northern and southern polar caps. J. Geophys. Res. Space Phys. 1998, 103, 29229–29237. [Google Scholar] [CrossRef]
- Chartier, A.T.; Mitchell, C.N.; Miller, E.S. Annual Occurrence Rates of Ionospheric Polar Cap Patches Observed Using Swarm. J. Geophys. Res. Space Phys. 2018, 123, 2327–2335. [Google Scholar] [CrossRef]
- Goodwin, L.V.; Iserhienrhien, B.; Miles, D.M.; Patra, S.; Van der Meeren, C.; Buchert, S.C.; Burchill, J.K.; Clausen, L.B.N.; Knudsen, D.J.; McWilliams, K.A.; et al. Swarm in situ observations of F region polar cap patches created by cusp precipitation. Geophys. Res. Lett. 2015, 42, 996–1003. [Google Scholar] [CrossRef]
- Spicher, A.; Cameron, T.; Grono, E.M.; Yakymenko, K.N.; Buchert, S.C.; Clausen, L.B.N.; Knudsen, D.J.; McWilliams, K.A.; Moen, J.I. Observation of polar cap patches and calculation of gradient drift instability growth times: A Swarm case study. Geophys. Res. Lett. 2015, 42, 201–206. [Google Scholar] [CrossRef]
- Park, J.; Lühr, H.; Kervalishvili, G.; Rauberg, J.; Stolle, C.; Kwak, Y.-S.; Lee, W.K. Morphology of high-latitude plasma density perturbations as deduced from the total electron content measurements onboard the Swarm constellation. J. Geophys. Res. Space Phys. 2017, 122, 1338–1359. [Google Scholar] [CrossRef]
- Jin, Y.; Spicher, A.; Xiong, C.; Clausen, L.B.N.; Kervalishvili, G.; Stolle, C.; Miloch, W.J. Ionospheric Plasma Irregularities Characterized by the Swarm Satellites: Statistics at High Latitudes. J. Geophys. Res. Space Phys. 2019, 124, 1262–1282. [Google Scholar] [CrossRef]
- Pi, X.; Mannucci, A.J.; Lindqwister, U.J.; Ho, C.M. Monitoring of global ionospheric irregularities using the Worldwide GPS Network. Geophys. Res. Lett. 1997, 24, 2283–2286. [Google Scholar] [CrossRef]
- Zhao, D.; Li, W.; Li, C.; Tang, X.; Wang, Q.; Hancock, C.M.; Roberts, G.W.; Zhang, K. Ionospheric Phase Scintillation Index Estimation Based on 1 Hz Geodetic GNSS Receiver Measurements by Using Continuous Wavelet Transform. Space Weather 2022, 20, e2021SW003015. [Google Scholar] [CrossRef]
- Priyadarshi, S.; Zhang, Q.; Ma, Y.; Xing, Z.; Hu, Z.; Li, G. The Behaviors of Ionospheric Scintillations Around Different Types of Nightside Auroral Boundaries Seen at the Chinese Yellow River Station, Svalbard. Front. Astron. Space Sci. 2018, 5, 26. [Google Scholar] [CrossRef]
- Zhao, D.; Li, W.; Wang, Q.; Liu, X.; Li, C.; Hancock, C.M.; Roberts, G.W.; Zhang, K. Statistical study on the characterization of phase and amplitude scintillation events in the high-latitude region during 2014–2020 based on ISMR. Adv. Space Res. 2022, 69, 3435–3459. [Google Scholar] [CrossRef]
- Forte, B.; Radicella, S.M. Problems in data treatment for ionospheric scintillation measurements. Radio Sci. 2002, 37, 1–5. [Google Scholar] [CrossRef]
- Forte, B. Optimum detrending of raw GPS data for scintillation measurements at auroral latitudes. J. Atmos. Sol. Terr. Phys. 2005, 67, 1100–1109. [Google Scholar] [CrossRef]
- Spicher, A.; Clausen, L.B.N.; Miloch, W.J.; Lofstad, V.; Jin, Y.; Moen, J.I. Interhemispheric study of polar cap patch occurrence based on Swarm in situ data. J. Geophys. Res. Space Phys. 2017, 122, 3837–3851. [Google Scholar] [CrossRef]
- Zhao, D.; Hancock, C.M.; Roberts, G.W.; Jin, S. Cycle Slip Detection during High Ionospheric Activities Based on Combined Triple-Frequency GNSS Signals. Remote Sens. 2019, 11, 250. [Google Scholar] [CrossRef]
- Zhao, D.; Roberts, G.W.; Hancock, C.M.; Lau, L.; Bai, R. A triple-frequency cycle slip detection and correction method based on modified HMW combinations applied on GPS and BDS. GPS Solut. 2019, 23, 22. [Google Scholar] [CrossRef]
- Wu, J.-T.; Wu, S.C.; Hajj, G.A.; Bertiger, W.I.; Lichten, S.M. Effects of antenna orientation on GPS carrier phase. In Astrodynamics 1991, Proceedings of the AAS/AIAA Astrodynamics Conference, Durango, CO, 19–22 August 1991; Univelt, Inc.: San Diego, CA, USA, 1992; pp. 1647–1660. [Google Scholar]
- Beard, R.; Senior, K. Clock. In Springer Handbook of Global Navigation Satellite Systems; Springer: Cham, Switzerland, 2017; pp. 121–164. [Google Scholar]
- Lagler, K.; Schindelegger, M.; Böhm, J.; Krásná, H.; Nilsson, T. GPT2: Empirical slant delay model for radio space geodetic techniques. Geophys. Res. Lett. 2013, 40, 1069–1073. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, Y.; Yuan, Y. PPP-RTK based on undifferenced and uncombined observations: Theoretical and practical aspects. J. Geod. 2019, 93, 1011–1024. [Google Scholar] [CrossRef]
- Zhang, B.; Hou, P.; Zha, J.; Liu, T. Integer-estimable FDMA model as an enabler of GLONASS PPP-RTK. J. Geod. 2021, 95, 91. [Google Scholar] [CrossRef]
- Olhede, S.C.; Walden, A.T. Generalized Morse wavelets. IEEE Trans. Signal Process. 2002, 50, 2661–2670. [Google Scholar] [CrossRef]
- Liu, L.; Su, X.; Wang, G. On Inversion of Continuous Wavelet Transform. Open J. Stat. 2015, 5, 714–720. [Google Scholar] [CrossRef]
- Sharma, G. Manifestation of earthquake preparation zone in the ionosphere before 2021 Sonitpur, Assam earthquake revealed by GPS-TEC data. Geod. Geodyn. 2022, 13, 230–237. [Google Scholar] [CrossRef]
- Khazanov, G.V. Space Weather Fundamentals, 1st ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Eshkuvatov, H.E.; Ahmedov, B.J.; Tillayev, Y.A.; Tariq, M.A.; Shah, M.A.; Liu, L. Ionospheric precursors of strong earthquakes observed using six GNSS stations data during continuous five years (2011–2015). Geod. Geodyn. 2022. [Google Scholar] [CrossRef]
- Maltseva, O.; Nikitenko, T. The effect of space weather on the ionosphere at the 110° meridian during CAWSES-II period. Geod. Geodyn. 2021, 12, 93–101. [Google Scholar] [CrossRef]
- Matzka, J.; Stolle, C.; Yamazaki, Y.; Bronkalla, O.; Morschhauser, A. The geomagnetic Kp index and derived indices of geomagnetic activity. Space Weather 2021, 19, e2020SW002641. [Google Scholar] [CrossRef]
- Meeus, J. Astronomical Algorithms, 2nd ed.; Willmann-Bell, Inc.: Cambridge, MA, USA, 1998. [Google Scholar]
- Xiong, C.; Lühr, H. An empirical model of the auroral oval derived from CHAMP field-aligned current signatures—Part 2. Ann. Geophys. 2014, 32, 623–631. [Google Scholar] [CrossRef]
- Jin, Y.; Moen, J.I.; Miloch, W.J.; Clausen, L.B.; Oksavik, K. Statistical study of the GNSS phase scintillation associated with two types of auroral blobs. J. Geophys. Res. Space Phys. 2016, 121, 4679–4697. [Google Scholar] [CrossRef]
- Deng, X.; Tang, Z. Moving Surface Spline Interpolation Based on Green’s Function. Math. Geosci. 2011, 43, 663–680. [Google Scholar] [CrossRef]
- Alken, P.; Thébault, E.; Beggan, C.D.; Amit, H.; Aubert, J.; Baerenzung, J.; Bondar, T.N.; Brown, W.J.; Califf, S.; Chambodut, A.; et al. International Geomagnetic Reference Field: The thirteenth generation. Earth Planets Space 2021, 73, 49. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, D.; Wang, Q.; Li, W.; Shi, S.; Quan, Y.; Hancock, C.M.; Roberts, G.W.; Zhang, K.; Chen, Y.; Liu, X.; et al. Validating Ionospheric Scintillation Indices Extracted from 30s-Sampling-Interval GNSS Geodetic Receivers with Long-Term Ground and In-Situ Observations in High-Latitude Regions. Remote Sens. 2022, 14, 4255. https://doi.org/10.3390/rs14174255
Zhao D, Wang Q, Li W, Shi S, Quan Y, Hancock CM, Roberts GW, Zhang K, Chen Y, Liu X, et al. Validating Ionospheric Scintillation Indices Extracted from 30s-Sampling-Interval GNSS Geodetic Receivers with Long-Term Ground and In-Situ Observations in High-Latitude Regions. Remote Sensing. 2022; 14(17):4255. https://doi.org/10.3390/rs14174255
Chicago/Turabian StyleZhao, Dongsheng, Qianxin Wang, Wang Li, Shuangshuang Shi, Yiming Quan, Craig M. Hancock, Gethin Wyn Roberts, Kefei Zhang, Yu Chen, Xin Liu, and et al. 2022. "Validating Ionospheric Scintillation Indices Extracted from 30s-Sampling-Interval GNSS Geodetic Receivers with Long-Term Ground and In-Situ Observations in High-Latitude Regions" Remote Sensing 14, no. 17: 4255. https://doi.org/10.3390/rs14174255
APA StyleZhao, D., Wang, Q., Li, W., Shi, S., Quan, Y., Hancock, C. M., Roberts, G. W., Zhang, K., Chen, Y., Liu, X., Hao, Z., Cui, S., Zhang, X., & Wang, X. (2022). Validating Ionospheric Scintillation Indices Extracted from 30s-Sampling-Interval GNSS Geodetic Receivers with Long-Term Ground and In-Situ Observations in High-Latitude Regions. Remote Sensing, 14(17), 4255. https://doi.org/10.3390/rs14174255










