Global Empirical Models for Tropopause Height Determination
Abstract
:1. Introduction
2. Datasets and Methods
2.1. Weather Model Data
2.2. Dynamical Tropopause
2.3. Thermal Tropopause
2.4. Dynamical and Thermal Tropopause Blend
2.5. Tropopause Variability
2.6. Numerical Models
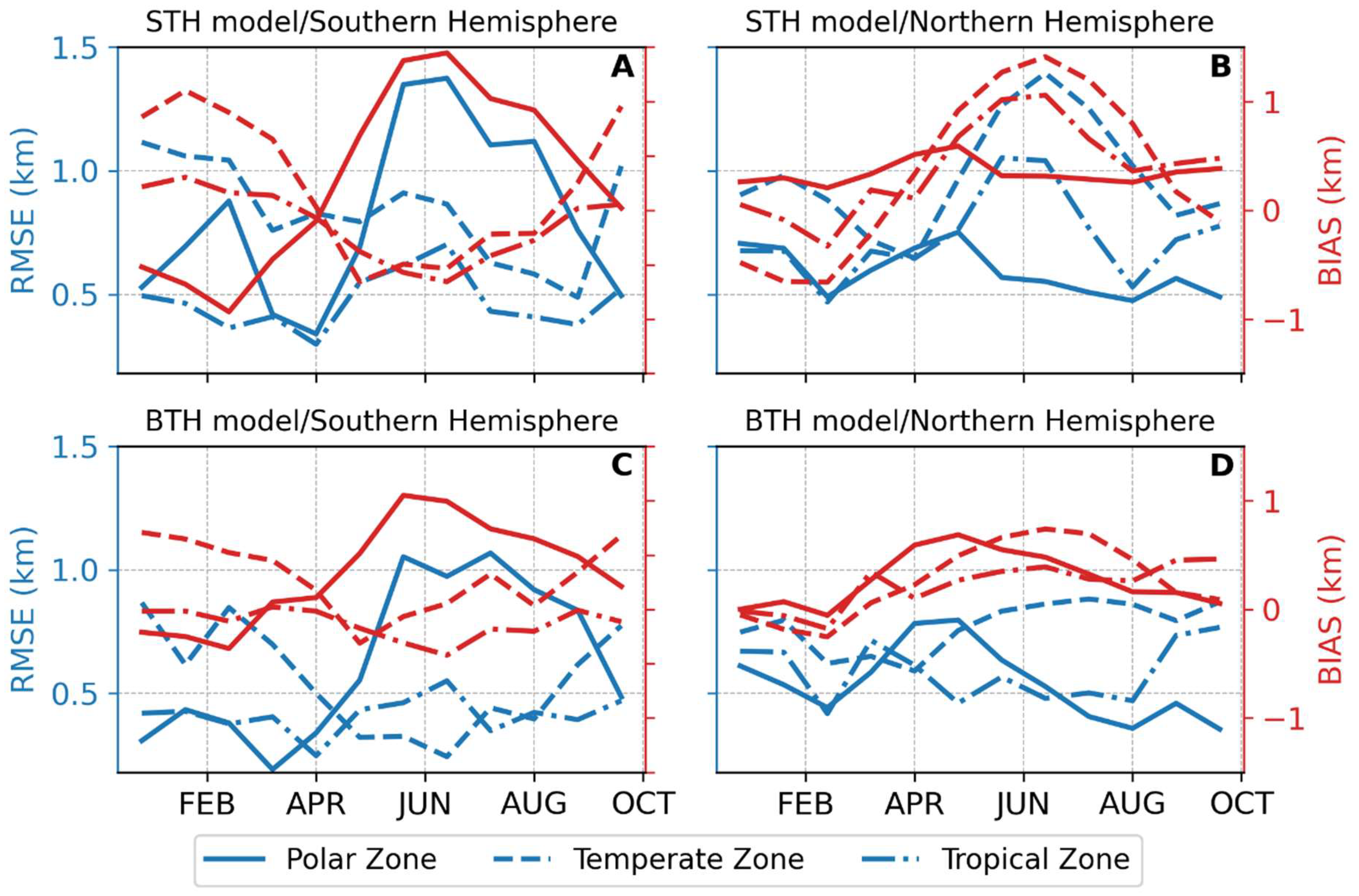
3. Result and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wallace, J.; Hobbs, P. Atmospheric Science: An Introductory Survey, 2nd ed.; International Geophysics Series; Academic Press: Cambridge, MA, USA, 2006; ISBN 9780080499536. [Google Scholar]
- Hoinka, K.P.; Claude, H.; Köhler, U. On the Correlation between Tropopause Pressure and Ozone above Central Europe. Geophys. Res. Lett. 1996, 23, 1753–1756. [Google Scholar] [CrossRef]
- Steinbrecht, W.; Claude, H.; Köhler, U.; Hoinka, K.P. Correlations between Tropopause Height and Total Ozone: Implications for Long-Term Changes. J. Geophys. Res. Atmos. 1998, 103, 19183–19192. [Google Scholar] [CrossRef]
- Santer, B.D.; Wigley, T.M.L.; Simmons, A.J.; Kållberg, P.W.; Kelly, G.A.; Uppala, S.M.; Ammann, C.; Boyle, J.S.; Brüggemann, W.; Doutriaux, C.; et al. Identification of Anthropogenic Climate Change Using a Second-Generation Reanalysis. J. Geophys. Res. Atmos. 2004, 109, 21104. [Google Scholar] [CrossRef]
- Yang, K.; Liu, X. Ozone Profile Climatology for Remote Sensing Retrieval Algorithms. Atmos. Meas. Tech. 2019, 12, 4745–4778. [Google Scholar] [CrossRef]
- Zahn, A.; Brenninkmeijer, C.A.M.; van Velthoven, P.F.J. Passenger Aircraft Project CARIBIC 1997–2002, Part I: The Extratropical Chemical Tropopause. Atmos. Chem. Phys. Discuss. 2004, 4, 1091–1117. [Google Scholar]
- Bethan, S.; Vaughan, G.; Reid, S.J. A Comparison of Ozone and Thermal Tropopause Heights and the Impact of Tropopause Definition on Quantifying the Ozone Content of the Troposphere. Q. J. R. Meteorol. Soc. 1996, 122, 929–944. [Google Scholar] [CrossRef]
- Thouret, V.; Marenco, A.; Logan, J.A.; Nédélec, P.; Grouhel, C. Comparisons of Ozone Measurements from the MOZAIC Airborne Program and the Ozone Sounding Network at Eight Locations. J. Geophys. Res. Atmos. 1998, 103, 25695–25720. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, P.; Xu, X. Variations of the Tropopause over Different Latitude Bands Observed Using COSMIC Radio Occultation Bending Angles. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2339–2349. [Google Scholar] [CrossRef]
- Rieckh, T.; Scherllin-Pirscher, B.; Ladstädter, F.; Foelsche, U. Characteristics of Tropopause Parameters as Observed with GPS Radio Occultation. Atmos. Meas. Tech. 2014, 7, 3947–3958. [Google Scholar] [CrossRef]
- Vespe, F.; Pacione, R.; Rosciano, E. A Novel Tool for the Determination of Tropopause Heights by Using GNSS Radio Occultation Data. Atmos. Clim. Sci. 2017, 7, 301–313. [Google Scholar] [CrossRef]
- WMO. World Meteorological Organization (WMO): Geneva, Switzerland, 1957.
- Reichler, T.; Dameris, M.; Sausen, R. Determining the Tropopause Height from Gridded Data. Geophys. Res. Lett. 2003, 30, 2042. [Google Scholar] [CrossRef] [Green Version]
- Wilcox, L.J.; Hoskins, B.J.; Shine, K.P. A Global Blended Tropopause Based on ERA Data. Part I: Climatology. Q. J. R. Meteorol. Soc. 2012, 138, 561–575. [Google Scholar] [CrossRef]
- Highwood, E.J.; Hoskins, B.J. The Tropical Tropopause. Q. J. R. Meteorol. Soc. 1998, 124, 1579–1604. [Google Scholar] [CrossRef]
- Wirth, V. Thermal versus Dynamical Tropopause in Upper-Tropospheric Balanced Flow Anomalies. Q. J. R. Meteorol. Soc. 2000, 126, 299–317. [Google Scholar] [CrossRef]
- Zängl, G.; Hoinka, K.P. The Tropopause in the Polar Regions. J. Clim. 2001, 14, 3117–3139. [Google Scholar] [CrossRef]
- Seidel, D.J.; Ross, R.J.; Angell, J.K.; Reid, G.C. Climatological Characteristics of the Tropical Tropopause as Revealed by Radiosondes. J. Geophys. Res. Atmos. 2001, 106, 7857–7878. [Google Scholar] [CrossRef]
- Seidel, D.J.; Randel, W.J. Variability and Trends in the Global Tropopause Estimated from Radiosonde Data. J. Geophys. Res. Atmos. 2006, 111, D21101. [Google Scholar] [CrossRef]
- Thuburn, J.; Craig, G.C. GCM Tests of Theories for the Height of the Tropopause. J. Atmos. Sci. 1997, 54, 869–882. [Google Scholar] [CrossRef]
- Reed, R.J. A Study of a Characteristic Tpye of Upper-Level Frontogenesis. J. Meteorol. 1955, 12, 226–237. [Google Scholar] [CrossRef]
- Danielsen, E.F. Stratospheric-Tropospheric Exchange Based on Radioactivity, Ozone and Potential Vorticity. J. Atmos. Sci. 1968, 25, 502–518. [Google Scholar] [CrossRef]
- Shapiro, M.A. Further Evidence of the Mesoscale and Turbulent Structure of Upper Level Jet Stream–Frontal Zone Systems. Mon. Weather Rev. 1978, 106, 1100–1111. [Google Scholar] [CrossRef]
- Shapiro, M.A. Turbulent Mixing within Tropopause Folds as a Mechanism for the Exchange of Chemical Constituents between the Stratosphere and Troposphere. J. Atmos. Sci. 1980, 37, 994–1004. [Google Scholar] [CrossRef]
- Berthet, G.; Esler, J.G.; Haynes, P.H. A Lagrangian Perspective of the Tropopause and the Ventilation of the Lowermost Stratosphere. J. Geophys. Res. Atmos. 2007, 112, D18102. [Google Scholar] [CrossRef]
- Kunz, A.; Konopka, P.; Müller, R.; Pan, L.L. Dynamical Tropopause Based on Isentropic Potential Vorticity Gradients. J. Geophys. Res. Atmos. 2011, 116, 1110. [Google Scholar] [CrossRef]
- WMO. Atmospheric Ozone 1985: Global Ozone Research and Monitoring Report; World Meteorological Organization (WMO): Geneva, Switzerland, 1986. [Google Scholar]
- Hoerling, M.P.; Schaack, T.K.; Lenzen, A.J. Global Objective Tropopause Analysis. Mon. Weather Rev. 1991, 119, 1816–1831. [Google Scholar] [CrossRef]
- Ivanova, A.R. The Tropopause: Variety of Definitions and Modern Approaches to Identification. Russ. Meteorol. Hydrol. 2013, 38, 808–817. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Lanyi, G. Tropospheric delay effects in radio interferometry. TDA Prog. Rep. 1984, 42–78. [Google Scholar]
- Davis, J.L.; Herring, T.A.; Shapiro, I.I.; Rogers, A.E.E.; Elgered, G. Geodesy by Radio Interferometry: Effects of Atmospheric Modeling Errors on Estimates of Baseline Length. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
- Randel, W.J.; Jensen, E.J. Physical Processes in the Tropical Tropopause Layer and Their Roles in a Changing Climate. Nat. Geosci. 2013, 6, 169–176. [Google Scholar] [CrossRef]
- Randel, W.J.; Wu, F. Variability of Zonal Mean Tropical Temperatures Derived from a Decade of GPS Radio Occultation Data. J. Atmos. Sci. 2015, 72, 1261–1275. [Google Scholar] [CrossRef]
- Wang, W.; Matthes, K.; Omrani, N.E.; Latif, M. Decadal Variability of Tropical Tropopause Temperature and Its Relationship to the Pacific Decadal Oscillation. Sci. Rep. 2016, 6, 29537. [Google Scholar] [CrossRef] [Green Version]
- Johnston, B.R.; Xie, F.; Liu, C. The Effects of Deep Convection on Regional Temperature Structure in the Tropical Upper Troposphere and Lower Stratosphere. J. Geophys. Res. Atmos. 2018, 123, 1585–1603. [Google Scholar] [CrossRef]
- Maddox, E.M.; Mullendore, G.L. Determination of Best Tropopause Definition for Convective Transport Studies. J. Atmos. Sci. 2018, 75, 3433–3446. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Horányi, A.; Sabater, J.M.; Nicolas, J.; Radu, R.; Schepers, D.; Simmons, A.; Soci, C.; et al. Global Reanalysis: Goodbye ERA-Interim, Hello ERA5. ECMWF Newsl. 2019, 17–24. [Google Scholar] [CrossRef]
- Santer, B.D.; Sausen, R.; Wigley, T.M.L.; Boyle, J.S.; AchutaRao, K.; Doutriaux, C.; Hansen, J.E.; Meehl, G.A.; Roeckner, E.; Ruedy, R.; et al. Behavior of Tropopause Height and Atmospheric Temperature in Models, Reanalyses, and Observations: Decadal Changes. J. Geophys. Res. Atmos. 2003, 108, ACL 1-1–ACL 1-22. [Google Scholar] [CrossRef]
- Martin, J. Mid-Latitude Atmospheric Dynamics: A First Course; Wiley: Hoboken, NJ, USA, 2006; ISBN 9780470864647. [Google Scholar]
- Buja, L.E. CCM Processor Users’ Guide (UNICOS Version); No. NCAR/TN-384+IA; University Corporation for Atmospheric Research: Boulder, CO, USA, 1993. [Google Scholar]
- Hinze, W.J.; Von Frese, R.R.B.; Saad, A.H. Gravity and Magnetic Exploration: Principles, Practices, and Applications; Cambridge University Press: Cambridge, UK, 2010; ISBN 9780511843129. [Google Scholar]
- Hoinka, K.P. Statistics of the Global Tropopause Pressure. Mon. Weather Rev. 1998, 126, 3303–3325. [Google Scholar] [CrossRef]
- Hoinka, K.P. Temperature, Humidity, and Wind at the Global Tropopause. Mon. Weather Rev. 1999, 127, 2248–2265. [Google Scholar] [CrossRef]
- Santer, B.D.; Wehner, M.F.; Wigley, T.M.L.; Sausen, R.; Meehl, G.A.; Taylor, K.E.; Ammann, C.; Arblaster, J.; Washington, W.M.; Boyle, J.S.; et al. Contributions of Anthropogenic and Natural Forcing to Recent Tropopause Height Changes. Science 2003, 301, 479–483. [Google Scholar] [CrossRef]
- Ackerman, S.A.; Knox, J.A. Meteorology: Understanding the Atmosphere, 4th ed.; Jones & Bartlett Learning: Burlington, MA, USA, 2013. [Google Scholar]
- Mendes, V.B. Modeling the Neutral-Atmospheric Propagation Delay in Radiometric Space Techniques; Technical Report; UNB Geodesy and Geomatics Engineering: Fredericton, NB, Canada, 1999; Volume 353. [Google Scholar]
- Snedecor, G.W.; William, G. Cochran Statistical Methods, 8th ed.; Iowa State University Press: Ames, IA, USA, 1989; ISBN 978-0-8138-1561-9. [Google Scholar]
- Highwood, E.J.; Hoskins, B.J.; Berrisford, P. Properties of the Arctic Tropopause. Q. J. R. Meteorol. Soc. 2000, 126, 1515–1532. [Google Scholar] [CrossRef]
- Lorenz, D.J.; DeWeaver, E.T. Tropopause Height and Zonal Wind Response to Global Warming in the IPCC Scenario Integrations. J. Geophys. Res. Atmos. 2007, 112, 10119. [Google Scholar] [CrossRef]
- Niell, A.E. Global Mapping Functions for the Atmosphere Delay at Radio Wavelengths. J. Geophys. Res. B Solid Earth 1996, 101, 3227–3246. [Google Scholar] [CrossRef]
- Mendes, V.B.; Prates, G.; Pavlis, E.C.; Pavlis, D.E.; Langley, R.B. Improved Mapping Functions for Atmospheric Refraction Correction in SLR. Geophys. Res. Lett. 2002, 29, 53-1–53-4. [Google Scholar] [CrossRef]
- Seber, G.A.F.; Wild, C.J. Nonlinear Regression; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 2003; ISBN 978-0-471-47135-6. [Google Scholar]
- Durre, I.; Vose, R.S.; Wuertz, D.B. Overview of the Integrated Global Radiosonde Archive. J. Clim. 2006, 19, 53–68. [Google Scholar] [CrossRef]
- Shaw, T.A. On the Role of Planetary-Scale Waves in the Abrupt Seasonal Transition of the Northern Hemisphere General Circulation. J. Atmos. Sci. 2014, 71, 1724–1746. [Google Scholar] [CrossRef] [Green Version]
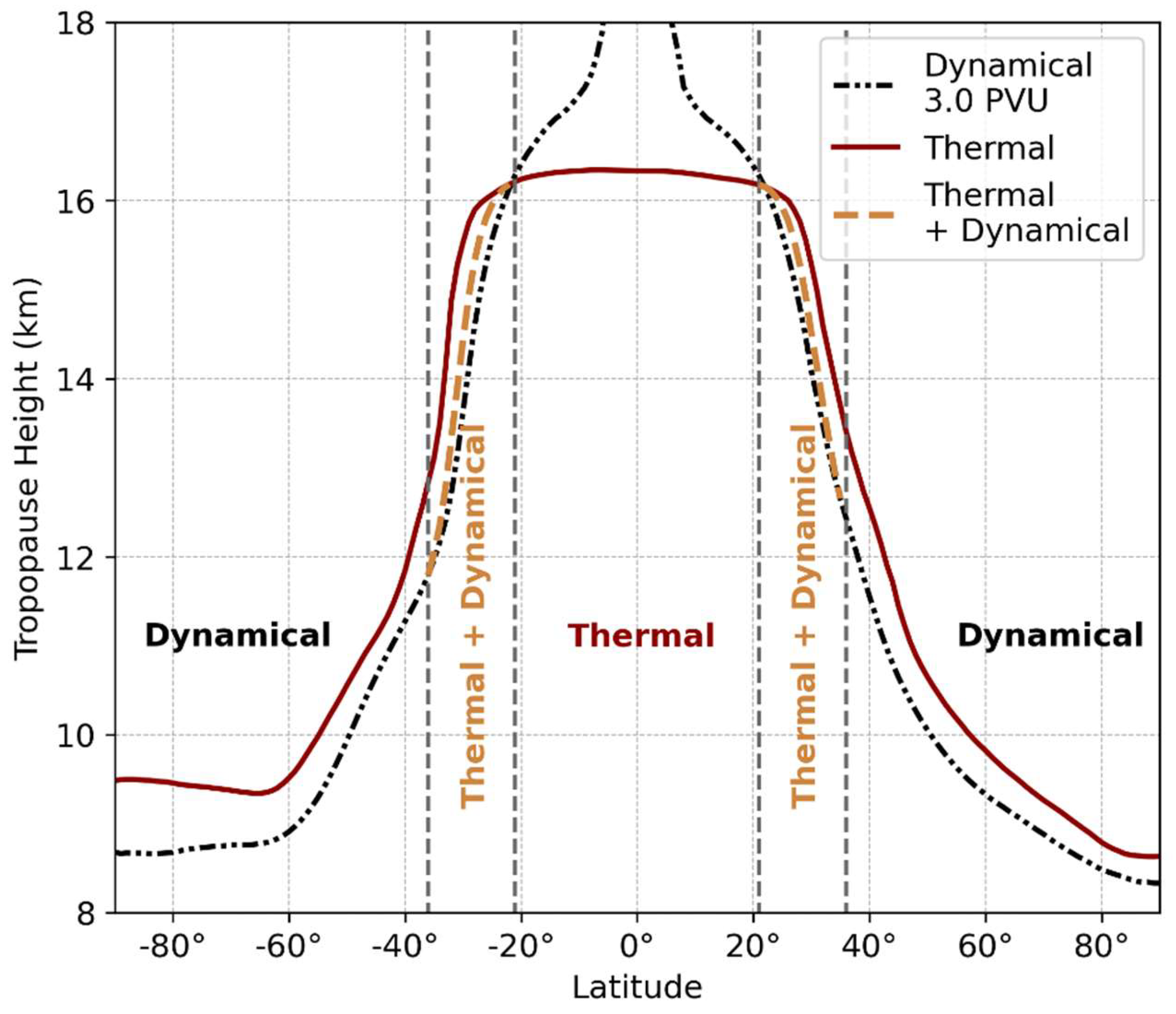

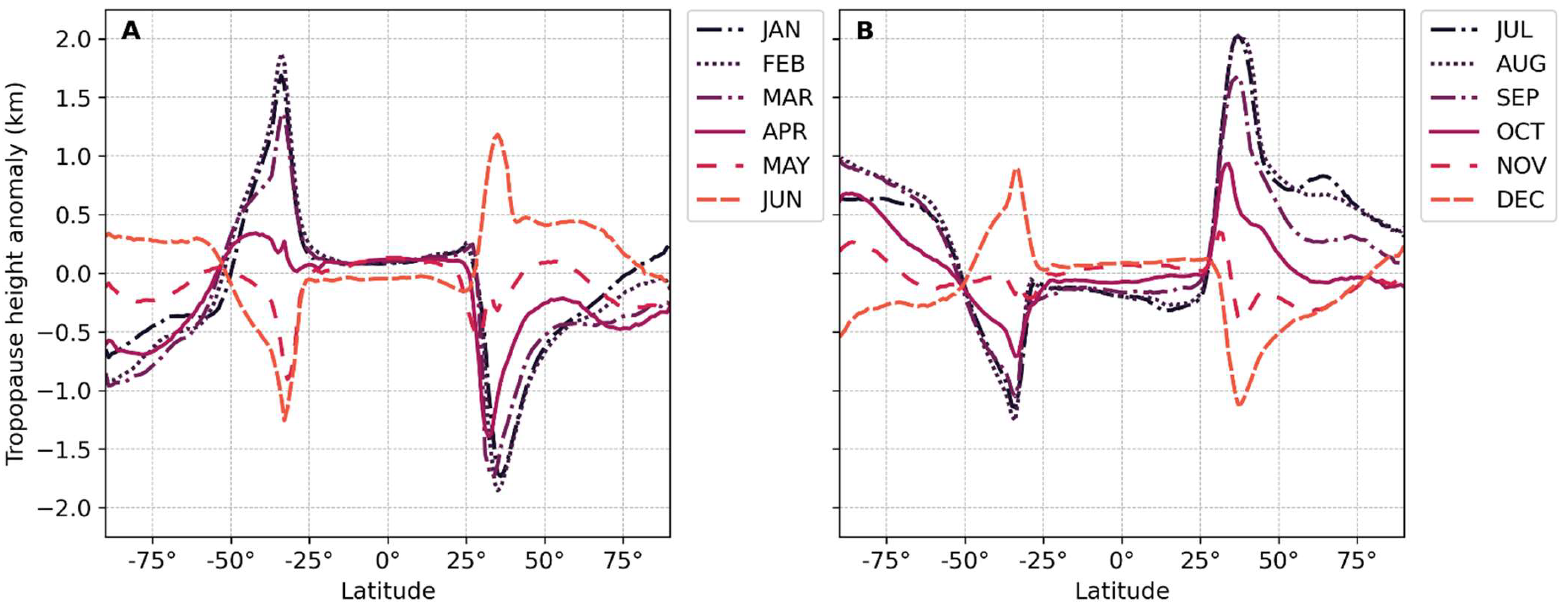
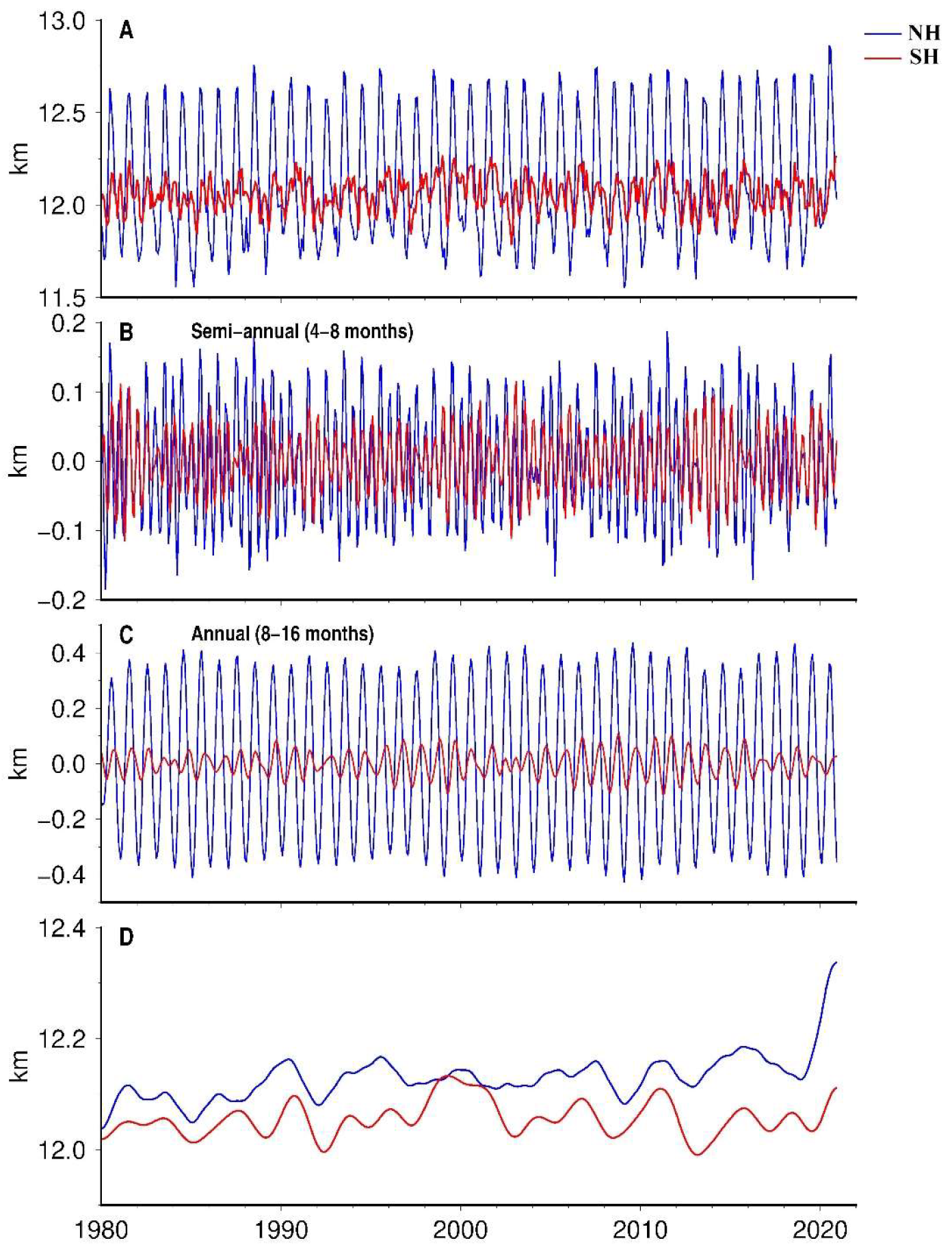
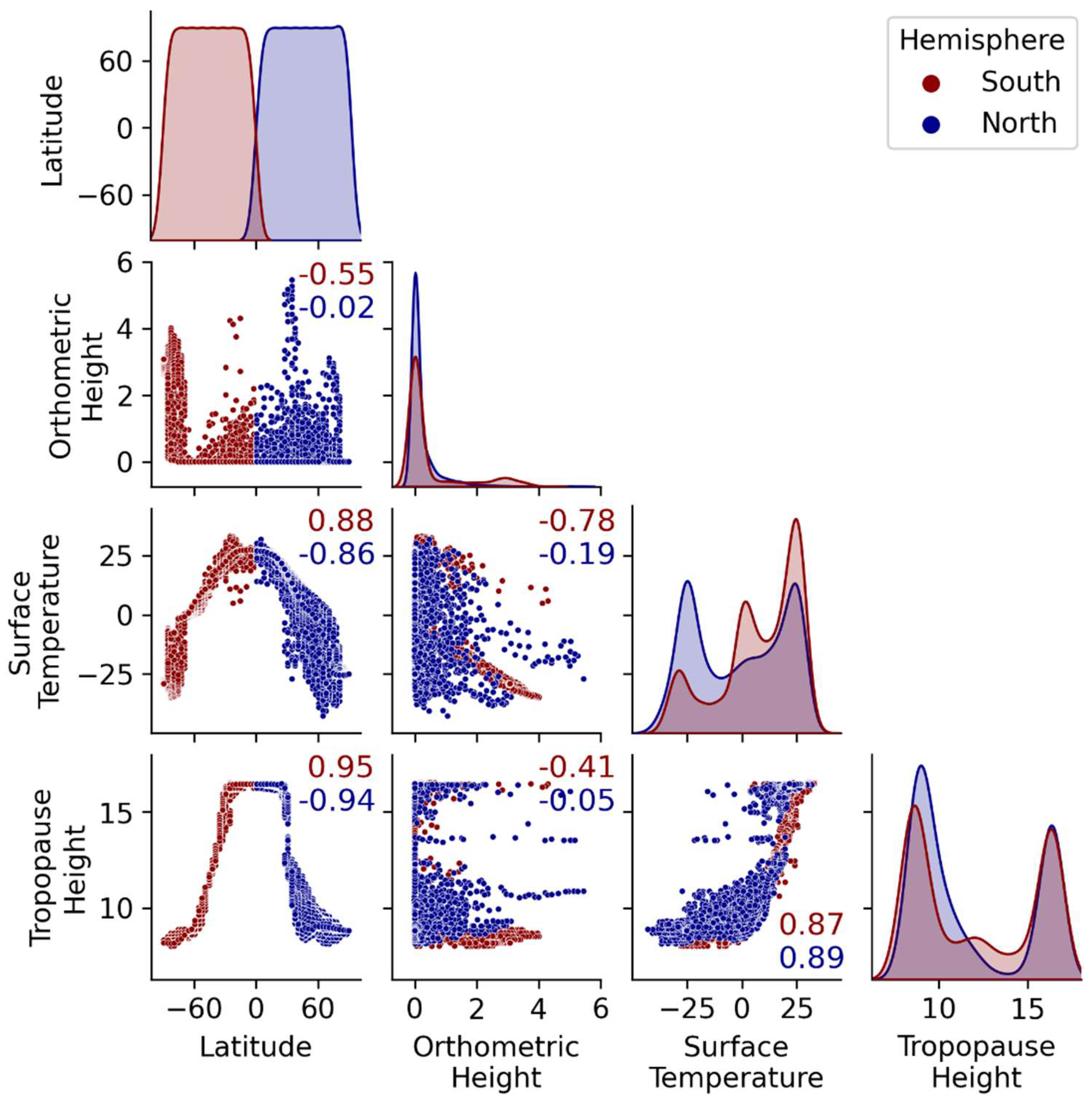


| Type | PVU Value/Latitude | ||||
|---|---|---|---|---|---|
| 1.6 | 2.0 | 2.5 | 3.0 | 3.5 | |
| Dynamical | 90°–25° | 90°–29° | 90°–33° | 90°–36° | 90°–39° |
| Dynamical + Thermal | 25°–10° | 29°–14° | 33°–18° | 36°–21° | 39°–24° |
| Thermal | 10°–0° | 14°–0° | 18°–0° | 21°–0° | 24°–0° |
| PVU VALUE | ||||||
|---|---|---|---|---|---|---|
| 1.6 | 7.209 (±0.040) | 9.119 (±0.040) | −18.95 (±0.24) | 1.81 (±0.23) | 0.107 (±0.015) | −0.18593 (±0.00075) |
| 2.0 | 7.775 (±0.037) | 8.552 (±0.037) | −21.36 (±0.21) | 1.36 (±0.24) | 0.088 (±0.016) | −0.16402 (±0.00064) |
| 2.5 | 8.180 (±0.036) | 8.146 (±0.036) | −23.48 (±0.21) | 1.15 (±0.25) | 0.079 (±0.018) | −0.14909 (±0.00063) |
| 3.0 | 8.505 (±0.036) | 7.818 (±0.036) | −25.32 (±0.22) | 1.11 (±0.25) | 0.082 (±0.019) | −0.13704 (±0.00071) |
| 3.5 | 8.779 (±0.039) | 7.542 (±0.039) | −26.73 (±0.24) | 1.15 (±0.25) | 0.087 (±0.021) | −0.1255 (±0.0010) |
| PVU VALUE | ||||||
|---|---|---|---|---|---|---|
| 1.6 | 7.145 (±0.066) | 9.185 (±0.067) | 20.12 (±0.43) | −2.81 (±0.33) | 0.151 (±0.022) | −0.186 (±0.018) |
| 2.0 | 7.650 (±0.060) | 8.677 (±0.062) | 22.43 (±0.38) | −2.32 (±0.32) | 0.133 (±0.022) | −0.164 (±0.017) |
| 2.5 | 7.993 (±0.056) | 8.333 (±0.058) | 24.17 (±0.33) | −1.81 (±0.32) | 0.108 (±0.021) | −0.149 (±0.016) |
| 3.0 | 8.265 (±0.055) | 8.058 (±0.057) | 25.56 (±0.31) | −1.55 (±0.32) | 0.095 (±0.022) | −0.137 (±0.016) |
| 3.5 | 8.499 (±0.057) | 7.823 (±0.058) | 26.73 (±0.33) | −1.58 (±0.34) | 0.098 (±0.023) | −0.126 (±0.016) |
| Model | Hemisphere | PVU Value | ||||
|---|---|---|---|---|---|---|
| 1.6 | 2.0 | 2.5 | 3.0 | 3.5 | ||
| STH | S | 434.4 (5.8) | 429.9 (4.0) | 437.2 (4.1) | 451.2 (5.7) | 478.5 (7.9) |
| N | 494.9 (5.8) | 478.3 (7.4) | 465.7 (9.4) | 466.6 (11.7) | 475.1 (13.2) | |
| BTH | S | 101.5 (36.0) | 170.9 (−87.2) | 195.5 (−100.8) | 148.4 (−54.8) | 122.1 (36.6) |
| N | 182.2 (128.4) | 115.2 (5.5) | 126.4 (−12.0) | 119.2 (33.5) | 162.1 (116.2) | |
| RMSE | MEAN | STD | 1st Quartile | Median | 3rd Quartile | |
|---|---|---|---|---|---|---|
| BTH | 0.67 | −0.24 | 0.84 | −0.78 | −0.25 | 0.23 |
| STH | 0.88 | −0.26 | 1.03 | −0.99 | −0.32 | 0.35 |
| M1 | 1.82 | −0.46 | 1.75 | −1.35 | −0.31 | 0.70 |
| M2 | 2.05 | −1.06 | 1.76 | −2.72 | −0.93 | 0.12 |
| M3 | 1.67 | −0.47 | 1.61 | −1.52 | −0.56 | 0.55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mateus, P.; Mendes, V.B.; Pires, C.A.L. Global Empirical Models for Tropopause Height Determination. Remote Sens. 2022, 14, 4303. https://doi.org/10.3390/rs14174303
Mateus P, Mendes VB, Pires CAL. Global Empirical Models for Tropopause Height Determination. Remote Sensing. 2022; 14(17):4303. https://doi.org/10.3390/rs14174303
Chicago/Turabian StyleMateus, Pedro, Virgílio B. Mendes, and Carlos A.L. Pires. 2022. "Global Empirical Models for Tropopause Height Determination" Remote Sensing 14, no. 17: 4303. https://doi.org/10.3390/rs14174303






