Optomechanical Accelerometers for Geodesy
Abstract
:1. Introduction
2. Methods
2.1. Optomechanical Accelerometers
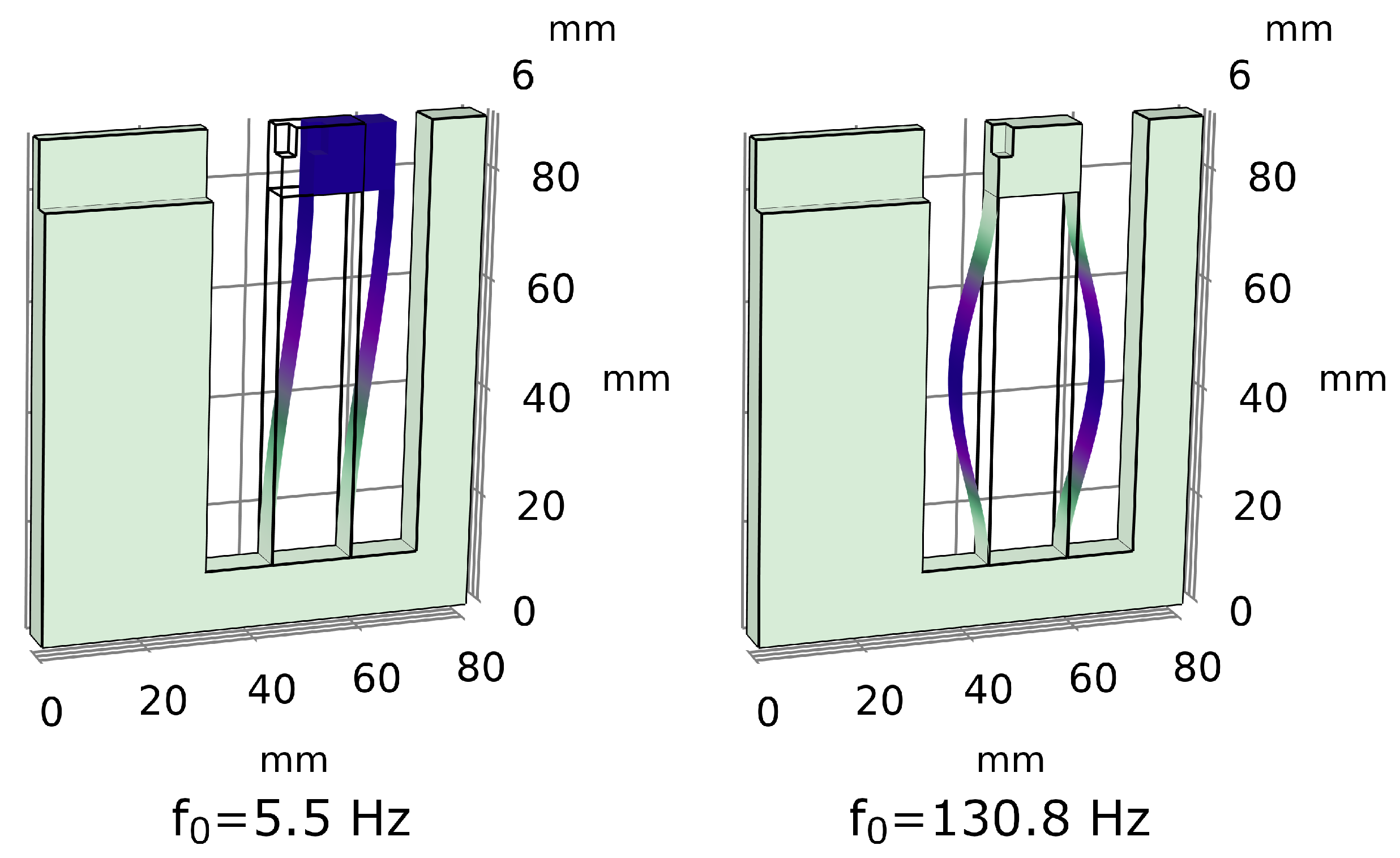
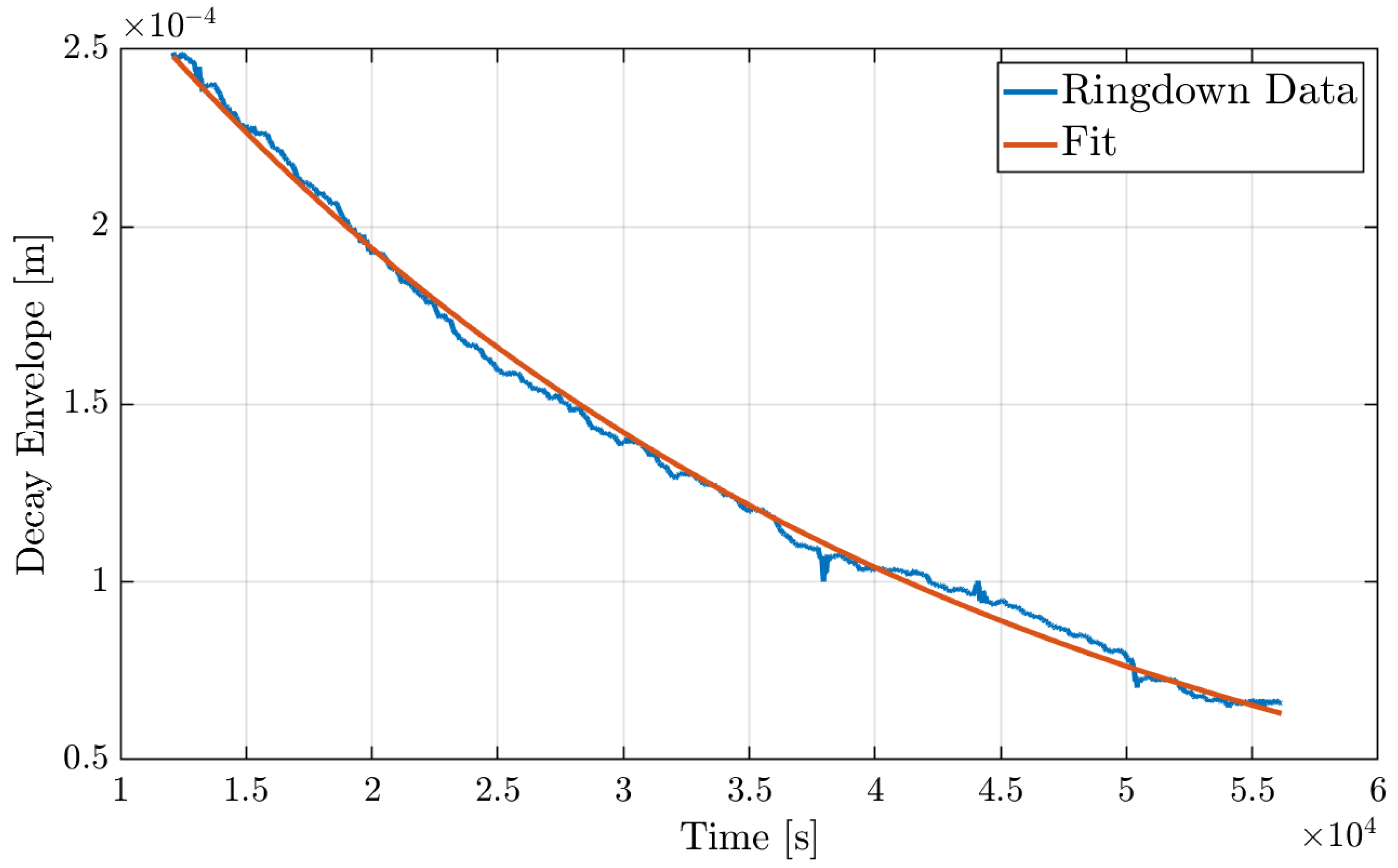
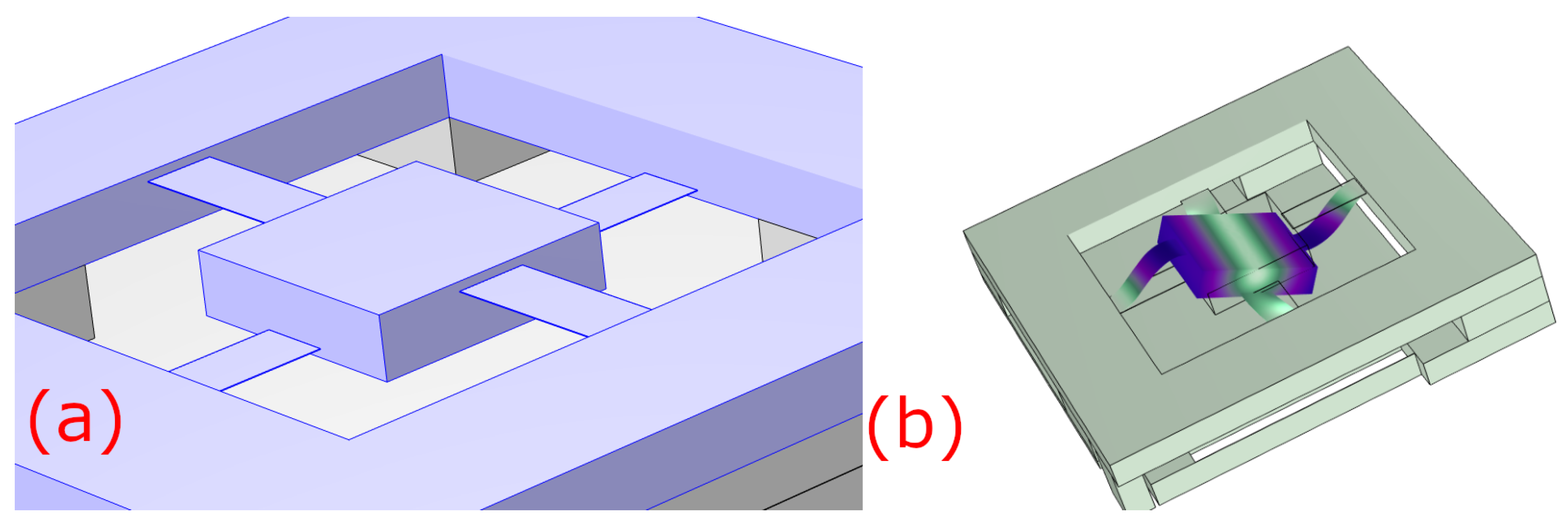
2.1.1. Resonator—Design and Characterization
2.1.2. Laser Interferometer—Design and Characterization
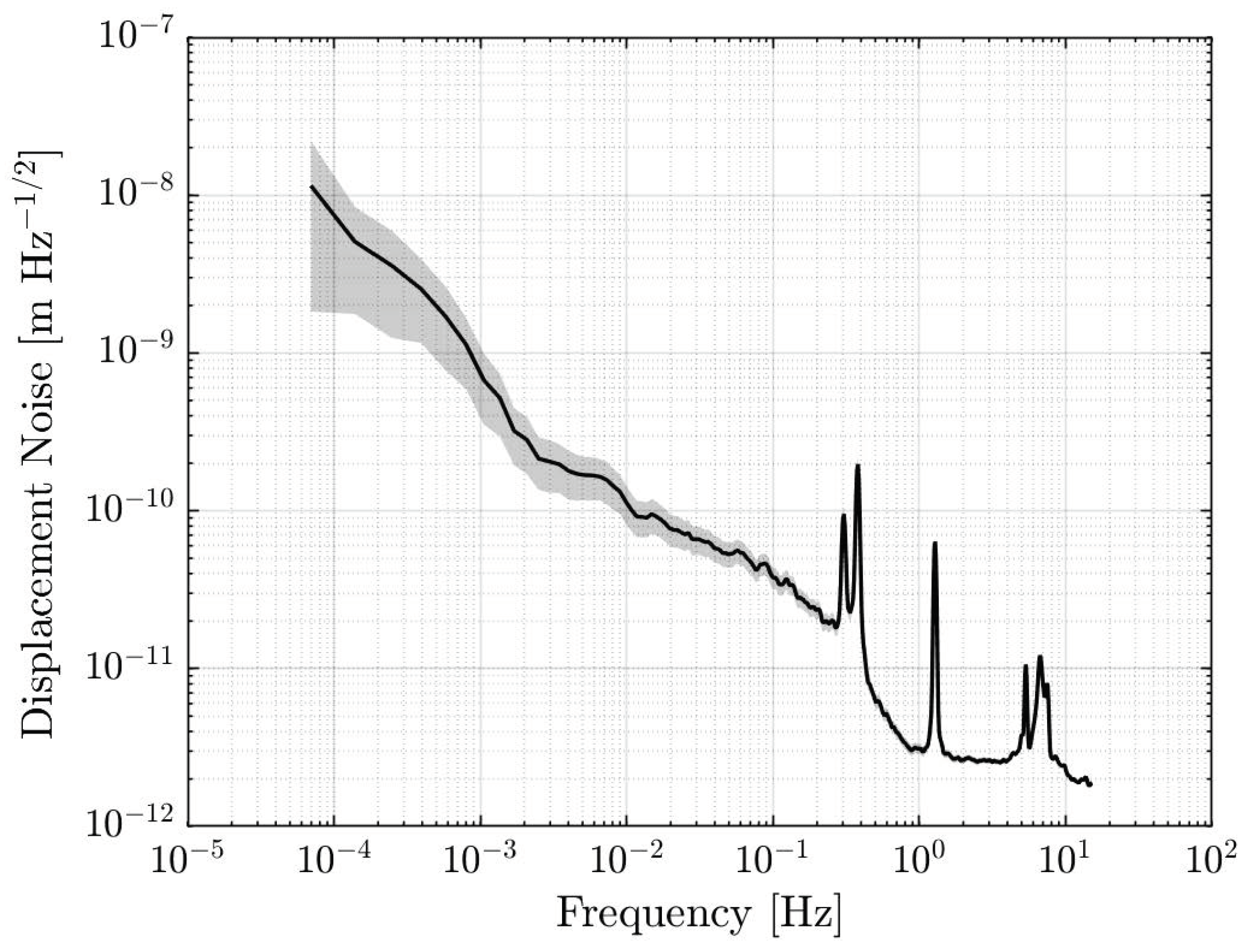
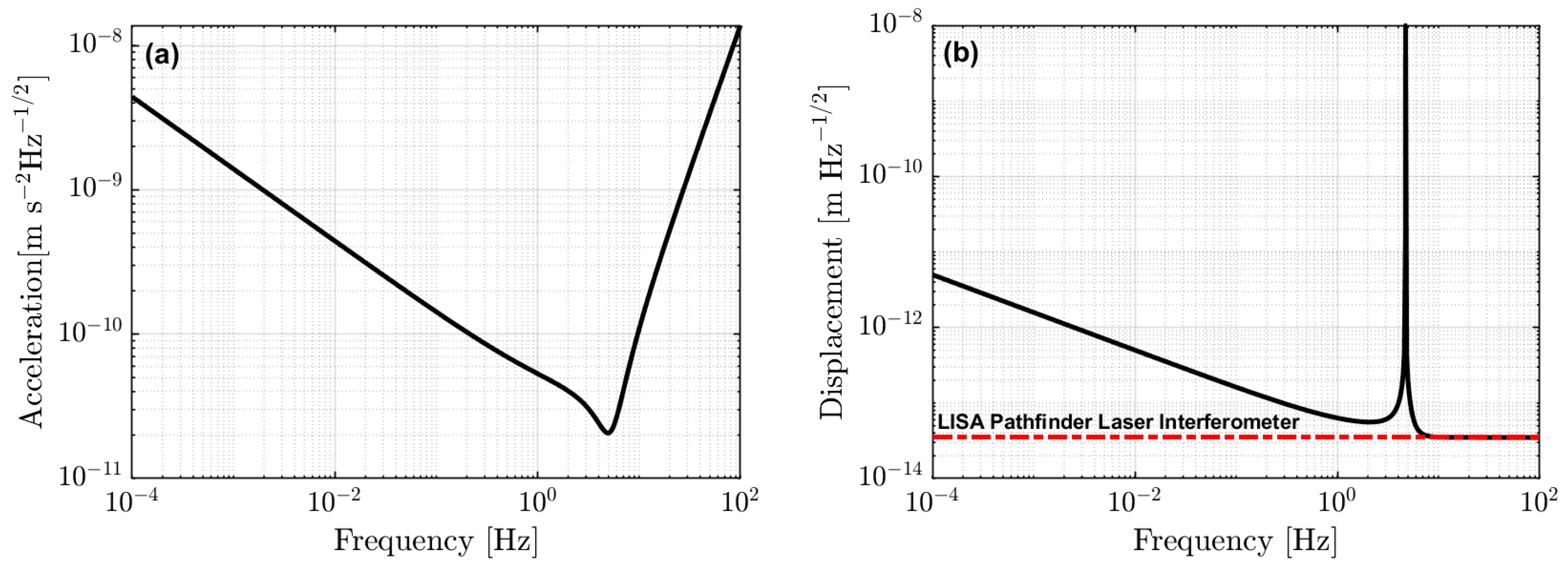
2.2. Accelerometer Noise Floor
3. Results
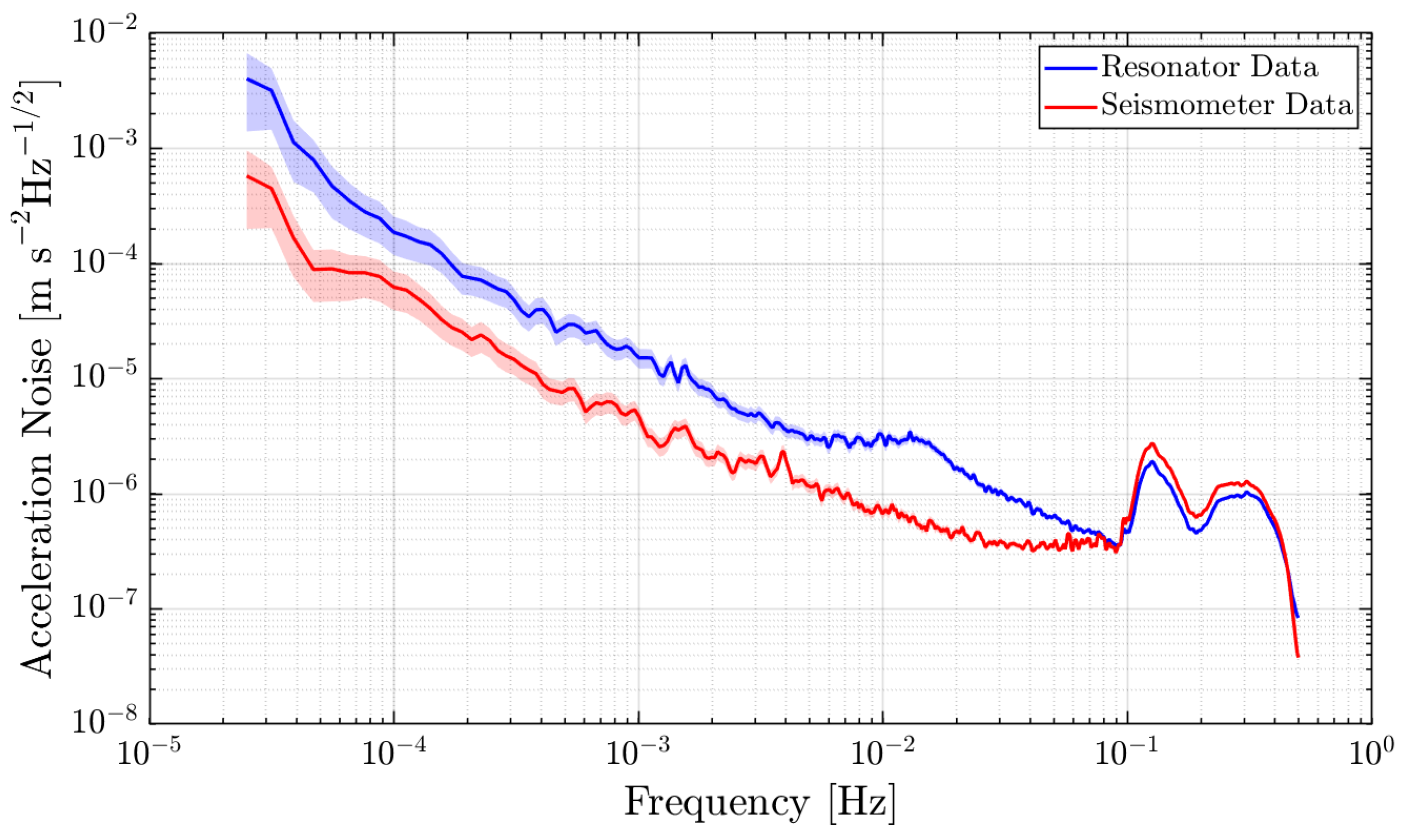
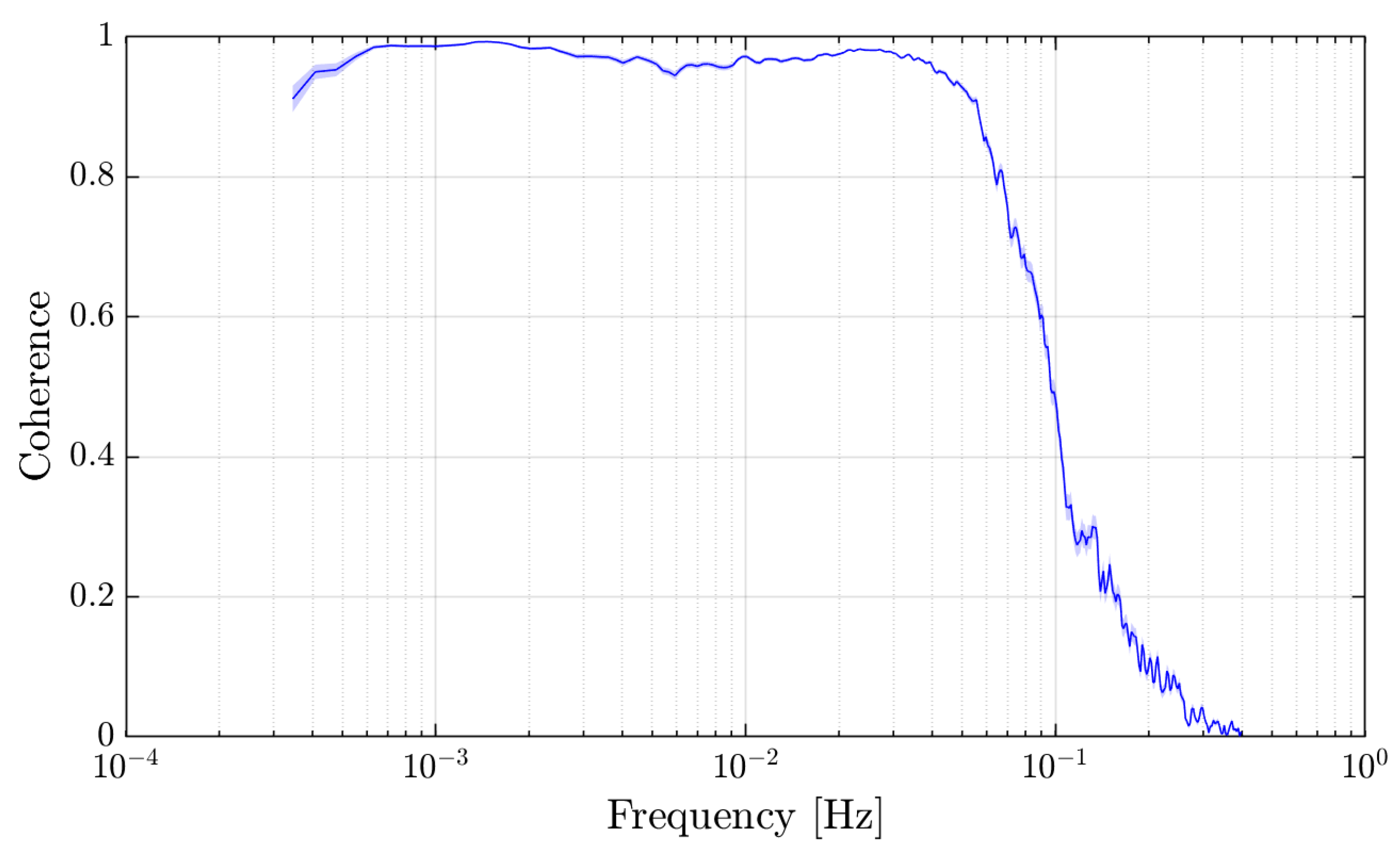
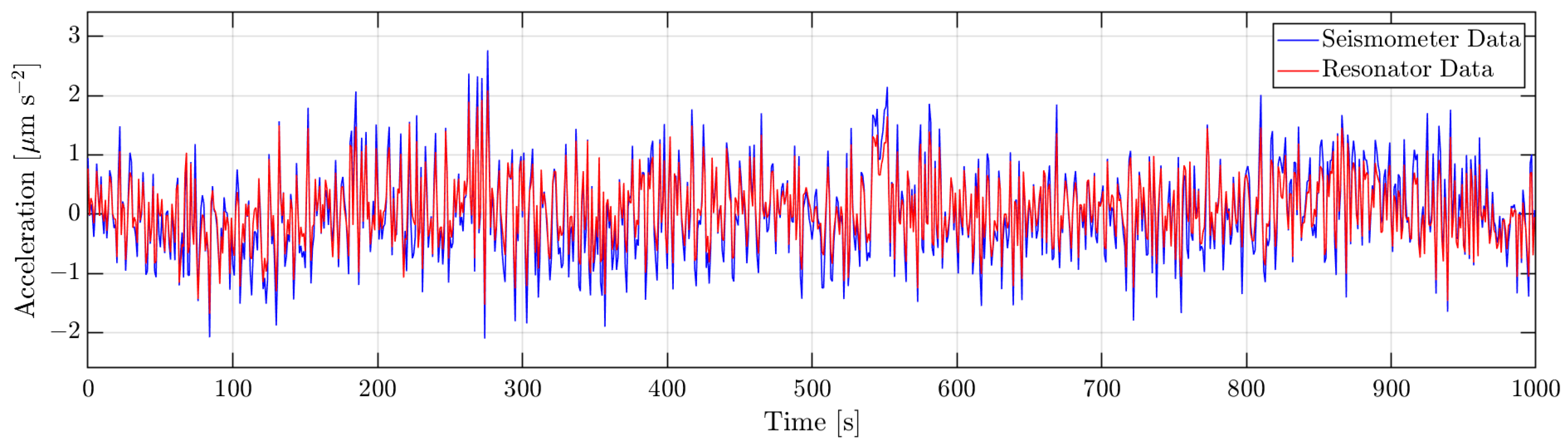
3.1. Measuring Seismic Noise
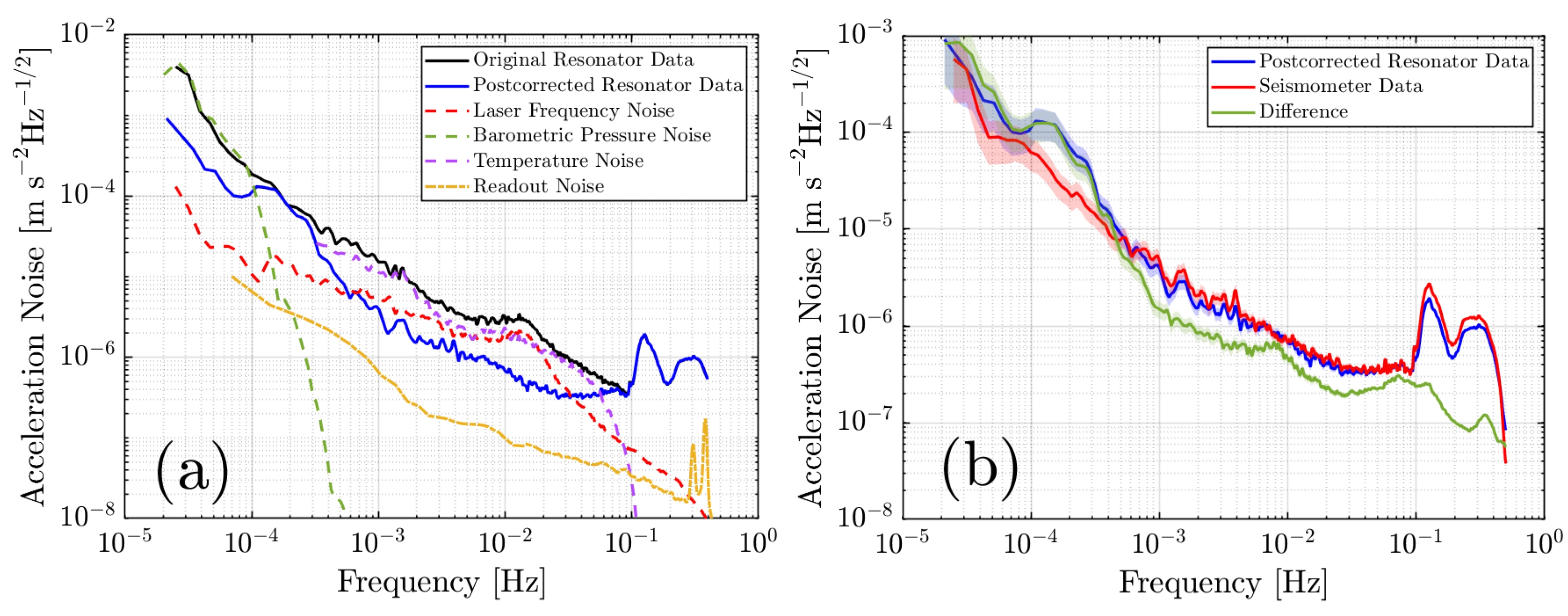
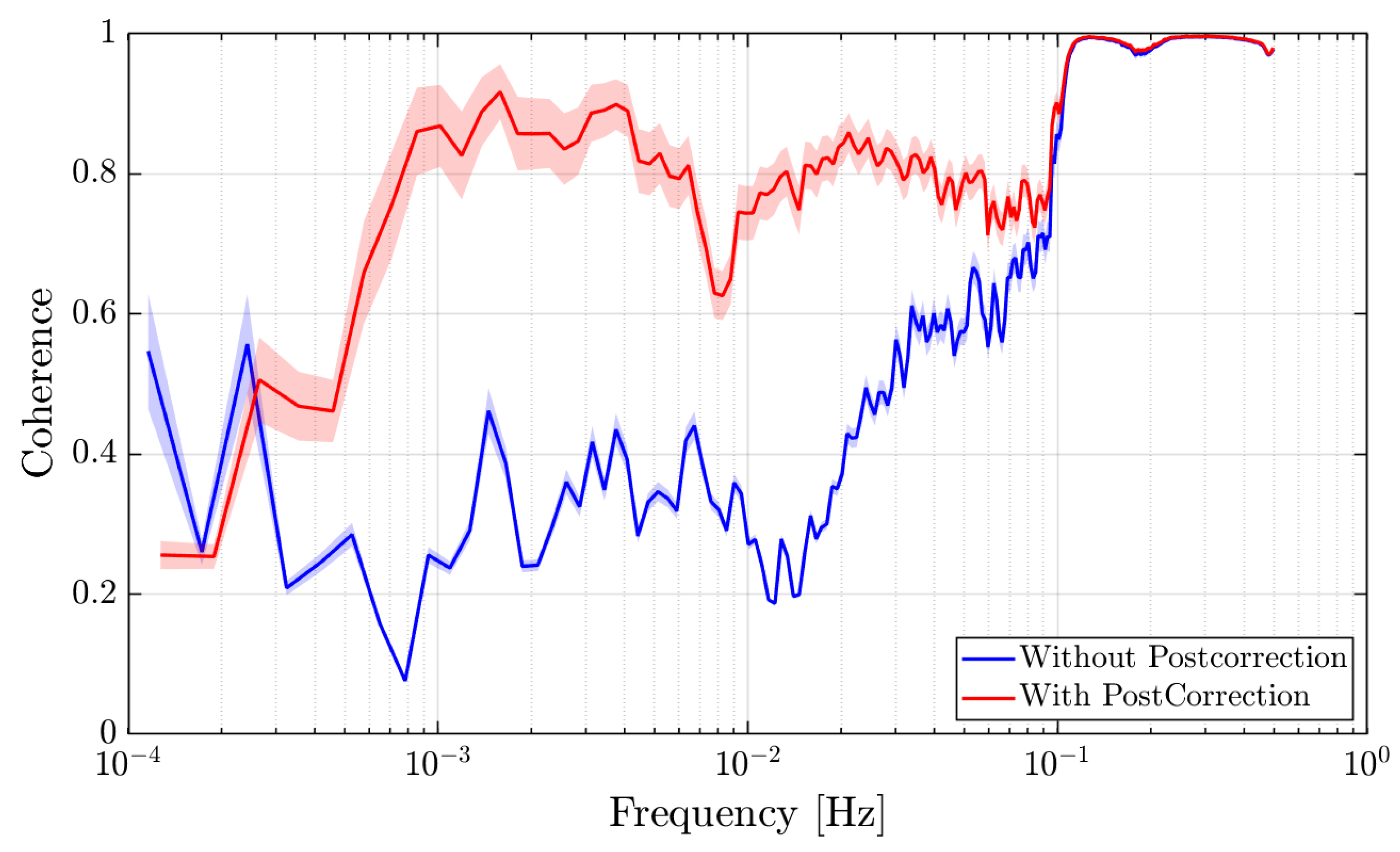
3.2. Data Post-Correction
3.2.1. Time-Domain Linear Regression
3.2.2. Transfer Function
4. Discussion
4.1. Comparative Technology Assessment
4.2. Planned Developments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31, 19920. [Google Scholar] [CrossRef]
- Kornfeld, R.P.; Arnold, B.W.; Gross, M.A.; Dahya, N.T.; Klipstein, W.M.; Gath, P.F.; Bettadpur, S. GRACE-FO: The gravity recovery and climate experiment follow-on mission. J. Spacecr. Rocket. 2019, 56, 931–951. [Google Scholar] [CrossRef]
- Flury, J.; Bettadpur, S.; Tapley, B.D. Precise accelerometry onboard the GRACE gravity field satellite mission. Adv. Space Res. 2008, 42, 1414–1423. [Google Scholar] [CrossRef]
- Bandikova, T.; McCullough, C.; Kruizinga, G.L.; Save, H.; Christophe, B. GRACE accelerometer data transplant. Adv. Space Res. 2019, 64, 623–644. [Google Scholar] [CrossRef]
- Weber, W.J.; Bortoluzzi, D.; Bosetti, P.; Consolini, G.; Dolesi, R.; Vitale, S. Application of LISA Gravitational Reference Sensor Hardware to Future Intersatellite Geodesy Missions. Remote Sens. 2022, 14, 3092. [Google Scholar] [CrossRef]
- Alvarez, A.D.; Bevilacqua, R.; Hollis, H.; Mueller, G.; Knudston, A.; Patel, U.; Sanjuan, J.; Wass, P.; Conklin, J.W. A simplified gravitational reference sensor for satellite geodesy. arXiv 2021, arXiv:2107.08545. [Google Scholar]
- Yu, N.; Kohel, J.; Kellogg, J.; Maleki, L. Development of an atom-interferometer gravity gradiometer for gravity measurement from space. Appl. Phys. B 2006, 84, 647–652. [Google Scholar] [CrossRef]
- Zhu, Z.; Liao, H.; Tu, H.; Duan, X.; Zhao, Y. Spaceborne Atom-Interferometry Gravity Gradiometry Design towards Future Satellite Gradiometric Missions. Aerospace 2022, 9, 253. [Google Scholar] [CrossRef]
- Trimeche, A.; Battelier, B.; Becker, D.; Bertoldi, A.; Bouyer, P.; Braxmaier, C.; Charron, E.; Corgier, R.; Cornelius, M.; Douch, K.; et al. Concept study and preliminary design of a cold atom interferometer for space gravity gradiometry. Class. Quantum Gravity 2019, 36, 215004. [Google Scholar] [CrossRef]
- Santoli, F.; Fiorenza, E.; Lefevre, C.; Lucchesi, D.M.; Lucente, M.; Magnafico, C.; Morbidini, A.; Peron, R.; Iafolla, V. ISA, a high sensitivity accelerometer in the interplanetary space. Space Sci. Rev. 2020, 216, 145. [Google Scholar] [CrossRef]
- Panning, M.P.; Pike, W.T.; Lognonné, P.; Banerdt, W.B.; Murdoch, N.; Banfield, D.; Charalambous, C.; Kedar, S.; Lorenz, R.D.; Marusiak, A.G.; et al. On-deck seismology: Lessons from InSight for future planetary seismology. J. Geophys. Res. Planets 2020, 125, e2019JE006353. [Google Scholar] [CrossRef] [Green Version]
- Fernández, J.; Pepe, A.; Poland, M.P.; Sigmundsson, F. Volcano Geodesy: Recent developments and future challenges. J. Volcanol. Geotherm. Res. 2017, 344, 1–12. [Google Scholar] [CrossRef]
- Melcher, J.; Stirling, J.; Cervantes, F.G.; Pratt, J.R.; Shaw, G.A. A self-calibrating optomechanical force sensor with femtonewton resolution. Appl. Phys. Lett. 2014, 105, 233109. [Google Scholar] [CrossRef]
- Colombano, M.F.; Arregui, G.; Bonell, F.; Capuj, N.E.; Chavez-Angel, E.; Pitanti, A.; Valenzuela, S.O.; Sotomayor-Torres, C.M.; Navarro-Urrios, D.; Costache, M.V. Ferromagnetic Resonance Assisted Optomechanical Magnetometer. Phys. Rev. Lett. 2020, 125, 147201. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Pagliano, F.; van Veldhoven, R.; Pogoretskiy, V.; Jiao, Y.; Fiore, A. Integrated nano-optomechanical displacement sensor with ultrawide optical bandwidth. Nat. Commun. 2020, 11, 2407. [Google Scholar] [CrossRef] [PubMed]
- Guzmán Cervantes, F.; Kumanchik, L.; Pratt, J.; Taylor, J.M. High sensitivity optomechanical reference accelerometer over 10 kHz. Appl. Phys. Lett. 2014, 104, 221111. [Google Scholar] [CrossRef]
- Hines, A.; Richardson, L.; Wisniewski, H.; Guzman, F. Optomechanical inertial sensors. Appl. Opt. 2020, 59, G167–G174. [Google Scholar] [CrossRef]
- Zhang, Y.; Hines, A.S.; Valdes, G.; Guzman, F. Investigation and Mitigation of Noise Contributions in a Compact Heterodyne Interferometer. Sensors 2021, 21, 5788. [Google Scholar] [CrossRef]
- Saulson, P.R. Thermal noise in mechanical experiments. Phys. Rev. D 1990, 42, 2437–2445. [Google Scholar] [CrossRef]
- Cumming, A.; Heptonstall, A.; Kumar, R.; Cunningham, W.; Torrie, C.; Barton, M.; Strain, K.A.; Hough, J.; Rowan, S. Finite element modelling of the mechanical loss of silica suspension fibres for advanced gravitational wave detectors. Class. Quantum Gravity 2009, 26, 215012. [Google Scholar] [CrossRef]
- Cumming, A.V.; Bell, A.S.; Barsotti, L.; Barton, M.A.; Cagnoli, G.; Cook, D.; Cunningham, L.; Evans, M.; Hammond, G.D.; Harry, G.M.; et al. Design and development of the advanced LIGO monolithic fused silica suspension. Class. Quantum Gravity 2012, 29, 035003. [Google Scholar] [CrossRef]
- Penn, S.D.; Ageev, A.; Busby, D.; Harry, G.M.; Gretarsson, A.M.; Numata, K.; Willems, P. Frequency and surface dependence of the mechanical loss in fused silica. Phys. Lett. A 2006, 352, 3–6. [Google Scholar] [CrossRef]
- Gretarsson, A.M.; Harry, G.M.; Penn, S.D.; Saulson, P.R.; Startin, W.J.; Rowan, S.; Cagnoli, G.; Hough, J. Pendulum mode thermal noise in advanced interferometers: A comparison of fused silica fibers and ribbons in the presence of surface loss. Phys. Lett. A 2000, 270, 108–114. [Google Scholar] [CrossRef]
- Numata, K.; Otsuka, S.; Ando, M.; Tsubono, K. Intrinsic losses in various kinds of fused silica. Class. Quantum Gravity 2002, 19, 1697–1702. [Google Scholar] [CrossRef]
- Startin, W.J.; Beilby, M.A.; Saulson, P.R. Mechanical quality factors of fused silica resonators. Rev. Sci. Instrum. 1998, 69, 3681–3689. [Google Scholar] [CrossRef]
- Ahamed, M.J.; Senkal, D.; Shkel, A.M. Effect of annealing on mechanical quality factor of fused quartz hemispherical resonator. In Proceedings of the 2014 International Symposium on Inertial Sensors and Systems (ISISS), Laguna Beach, CA, USA, 25–26 February 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Nagourney, T.; Cho, J.Y.; Shiari, B.; Darvishian, A.; Najafi, K. 259 Second ring-down time and 4.45 million quality factor in 5.5 kHz fused silica birdbath shell resonator. In Proceedings of the 2017 19th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Kaohsiung, Taiwan, 18–22 June 2017; pp. 790–793. [Google Scholar] [CrossRef]
- Singh, S.; Nagourney, T.; Cho, J.Y.; Darvishian, A.; Najafi, K.; Shiari, B. Design and fabrication of high-Q birdbath resonator for MEMS gyroscopes. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 15–19. [Google Scholar] [CrossRef]
- Schroeter, A.; Nawrodt, R.; Schnabel, R.; Reid, S.; Martin, I.; Rowan, S.; Schwarz, C.; Koettig, T.; Neubert, R.; Thürk, M.; et al. On the mechanical quality factors of cryogenic test masses from fused silica and crystalline quartz. arXiv 2007, arXiv:0709.4359. [Google Scholar]
- Armano, M.; Audley, H.; Auger, G.; Baird, J.T.; Bassan, M.; Binetruy, P.; Born, M.; Bortoluzzi, D.; Brandt, N.; Caleno, M.; et al. Sub-Femto-g Free Fall for Space-Based Gravitational Wave Observatories: LISA Pathfinder Results. Phys. Rev. Lett. 2016, 116, 231101. [Google Scholar] [CrossRef]
- Nanometrics Inc. Trillium Horizon 120. Available online: https://www.nanometrics.ca/products/seismometers/trillium-horizon-120 (accessed on 1 July 2022).
- Texas A&M University Department of Atmospheric Sciences Mesonet Site. Available online: https://atmo.tamu.edu/facilities-resources/mesonet-site/index.html (accessed on 1 July 2022).
- Thompson, R.; Folkner, W.; De Vine, G.; Klipstein, W.; McKenzie, K.; Spero, R.; Yu, N.; Stephens, M.; Leitch, J.; Pierce, R.; et al. A flight-like optical reference cavity for GRACE follow-on laser frequency stabilization. In Proceedings of the 2011 Joint Conference of the IEEE International Frequency Control and the European Frequency and Time Forum (FCS) Proceedings, San Francisco, CA, USA, 2–5 May 2011; pp. 1–3. [Google Scholar]
- Nofrarias, M.; Gibert, F.; Karnesis, N.; Garcia, A.; Hewitson, M.; Heinzel, G.; Danzmann, K. Subtraction of temperature induced phase noise in the LISA frequency band. Phys. Rev. D 2013, 87, 102003. [Google Scholar] [CrossRef]
- Bendat, J.S. Statistical errors in measurement of coherence functions and input/output quantities. J. Sound Vib. 1978, 59, 405–421. [Google Scholar] [CrossRef]
- LTPDA: A MATLAB Toolbox for Accountable and Reproducible Data Analysis. Available online: https://www.elisascience.org/ltpda/ (accessed on 1 July 2022).
- Middlemiss, R.; LIGO Scientific Collaboration, Cambridge, MA, USA. Private communication, 2019.
- Wiese, D.N.; Nerem, R.S.; Han, S.C. Expected improvements in determining continental hydrology, ice mass variations, ocean bottom pressure signals, and earthquakes using two pairs of dedicated satellites for temporal gravity recovery. J. Geophys. Res. Solid Earth 2011, 116. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hines, A.; Nelson, A.; Zhang, Y.; Valdes, G.; Sanjuan, J.; Stoddart, J.; Guzmán, F. Optomechanical Accelerometers for Geodesy. Remote Sens. 2022, 14, 4389. https://doi.org/10.3390/rs14174389
Hines A, Nelson A, Zhang Y, Valdes G, Sanjuan J, Stoddart J, Guzmán F. Optomechanical Accelerometers for Geodesy. Remote Sensing. 2022; 14(17):4389. https://doi.org/10.3390/rs14174389
Chicago/Turabian StyleHines, Adam, Andrea Nelson, Yanqi Zhang, Guillermo Valdes, Jose Sanjuan, Jeremiah Stoddart, and Felipe Guzmán. 2022. "Optomechanical Accelerometers for Geodesy" Remote Sensing 14, no. 17: 4389. https://doi.org/10.3390/rs14174389
APA StyleHines, A., Nelson, A., Zhang, Y., Valdes, G., Sanjuan, J., Stoddart, J., & Guzmán, F. (2022). Optomechanical Accelerometers for Geodesy. Remote Sensing, 14(17), 4389. https://doi.org/10.3390/rs14174389





