Introducing ARTMO’s Machine-Learning Classification Algorithms Toolbox: Application to Plant-Type Detection in a Semi-Steppe Iranian Landscape
Abstract
:1. Introduction
2. Materials and Methods
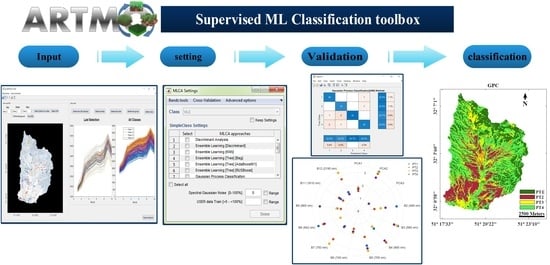
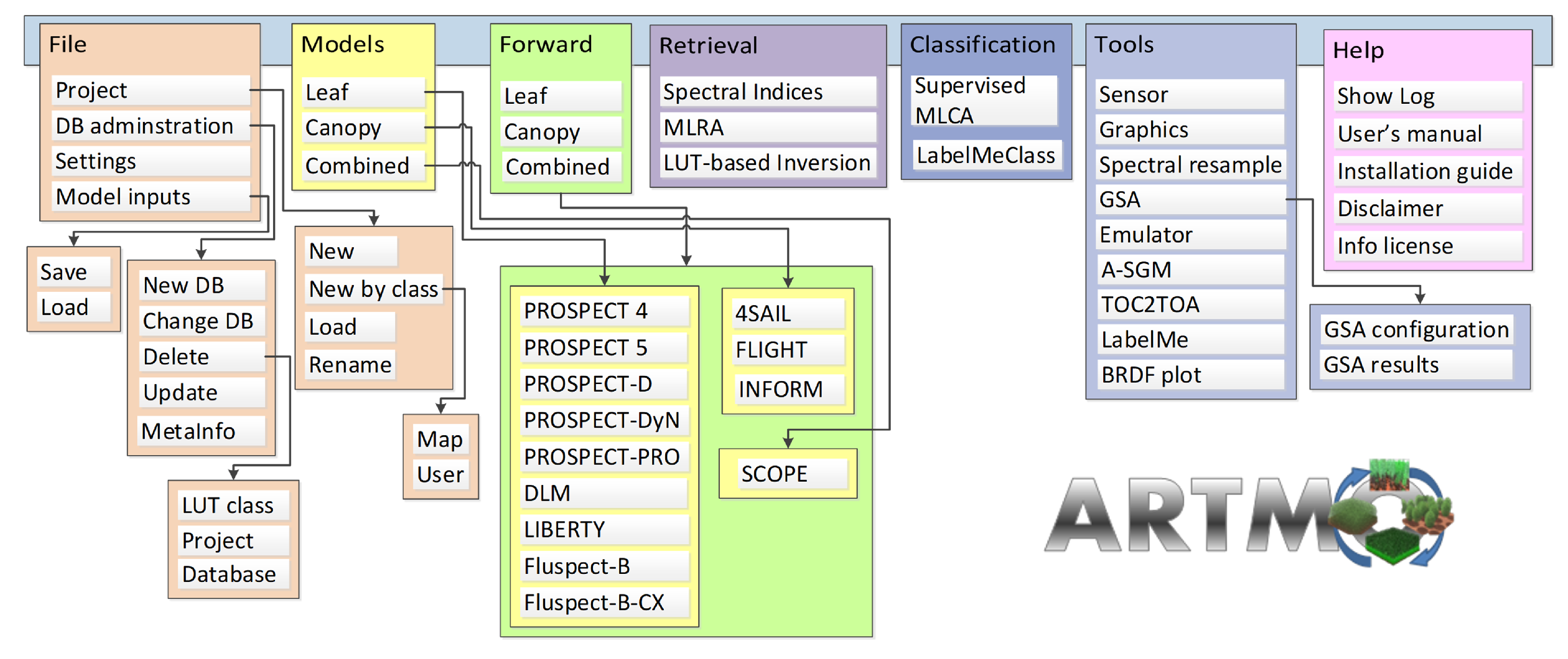
2.1. ARTMO Toolbox
2.2. ARTMO’s Machine-Learning Classification Algorithms (MLCA) Toolbox: Classifiers
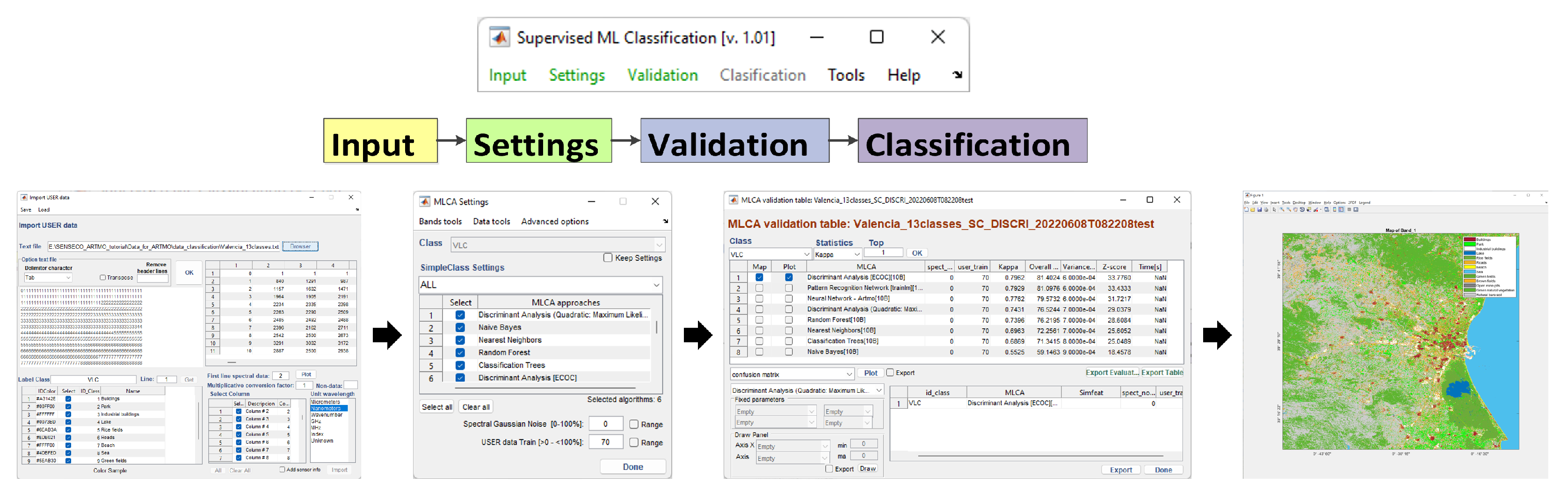
2.3. MLCA Toolbox: Workflow
2.3.1. Data Splitting and Cross-Validation Options
2.3.2. Dimensionality Reduction, Noise, and Advanced Options
2.3.3. Accuracy Metrics and Mapping
2.4. Extracting Labeled Spectra from Images: LabelMeClass
- 1.
- Load coordinates based on a .txt file consisting of GPS coordinates. The file should consist of class labels and associated coordinates. The tool then checks if the coordinates match within the loaded imagery. It will then extract the associated spectra and visualize the spectra with different colors per class.
- 2.
- Manual generation of labeled data. Based on the visualization of the image, pixels can be selected and then assigned to a class. In this way, labeled spectra per class are selected.
2.5. Demonstration Study: Satellite Data and Feature Selection
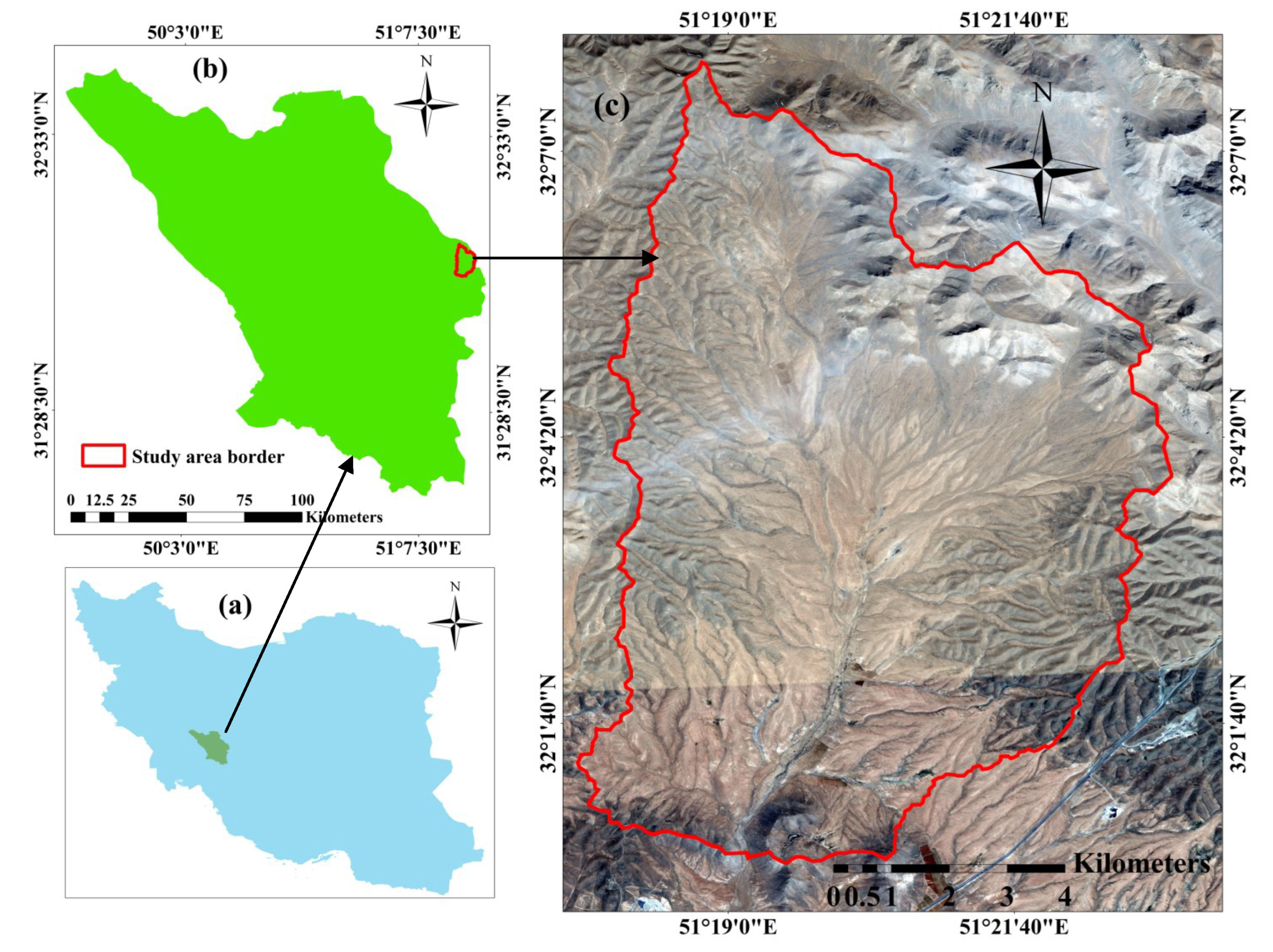
2.6. Study Area and Ground Data
3. Results
4. Discussion
4.1. Selection of the Best Machine-Learning Classification Algorithm
4.2. Perspectives of Gaussian Process Classifier (GPC) in Remote Sensing
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, X.; Liu, L.; Wang, Y.; Hu, Y.; Zhang, B. A SPECLib-based operational classification approach: A preliminary test on China land cover mapping at 30 m. Int. J. Appl. Earth Obs. Geoinf. 2018, 71, 83–94. [Google Scholar] [CrossRef]
- Yang, C.; Rottensteiner, F.; Heipke, C. Classification of land cover and land use based on convolutional neural networks. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 4, 251–258. [Google Scholar] [CrossRef]
- Jensen, J.R. Introductory Digital Image Processing: A Remote Sensing Perspective; Technical Report; University of South Carolina: Columbus, SC, USA, 1986. [Google Scholar]
- Comber, A.J. The separation of land cover from land use using data primitives. J. Land Use Sci. 2008, 3, 215–229. [Google Scholar] [CrossRef]
- Albert, L.; Rottensteiner, F.; Heipke, C. A higher order conditional random field model for simultaneous classification of land cover and land use. ISPRS J. Photogramm. Remote Sens. 2017, 130, 63–80. [Google Scholar] [CrossRef]
- Pflugmacher, D.; Rabe, A.; Peters, M.; Hostert, P. Mapping pan-European land cover using Landsat spectral-temporal metrics and the European LUCAS survey. Remote Sens. Environ. 2019, 221, 583–595. [Google Scholar] [CrossRef]
- Feizabadi, M.F.; Tahmasebi, P.; Broujeni, E.A.; Ebrahimi, A.; Omidipour, R. Functional diversity, functional composition and functional β diversity drive aboveground biomass across different bioclimatic rangelands. Basic Appl. Ecol. 2021, 52, 68–81. [Google Scholar] [CrossRef]
- Macintyre, P.; Van Niekerk, A.; Mucina, L. Efficacy of multi-season Sentinel-2 imagery for compositional vegetation classification. Int. J. Appl. Earth Obs. Geoinf. 2020, 85, 101980. [Google Scholar] [CrossRef]
- Quijas, S.; Boit, A.; Thonicke, K.; Murray-Tortarolo, G.; Mwampamba, T.; Skutsch, M.; Simoes, M.; Ascarrunz, N.; Peña-Claros, M.; Jones, L.; et al. Modelling carbon stock and carbon sequestration ecosystem services for policy design: A comprehensive approach using a dynamic vegetation model. Ecosyst. People 2019, 15, 42–60. [Google Scholar] [CrossRef]
- Rodwell, J.S.; Evans, D.; Schaminée, J.H. Phytosociological relationships in European Union policy-related habitat classifications. Rend. Lincei. Sci. Fis. Nat. 2018, 29, 237–249. [Google Scholar] [CrossRef]
- Spiegal, S.; Bartolome, J.W.; White, M.D. Applying ecological site concepts to adaptive conservation management on an iconic Californian landscape. Rangelands 2016, 38, 365–370. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Q.; Wei, Y.; Meng, X.; Shen, H.; Zhang, L. A multiscale and multidepth convolutional neural network for remote sensing imagery pan-sharpening. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 978–989. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E.; Rogan, J.; Kellndorfer, J. Assessment of spectral, polarimetric, temporal, and spatial dimensions for urban and peri-urban land cover classification using Landsat and SAR data. Remote Sens. Environ. 2012, 117, 72–82. [Google Scholar] [CrossRef]
- Topaloğlu, R.H.; Sertel, E.; Musaoğlu, N. Assessment of classification accuracies of sentinel-2 and landsat-8 data for land cover/use mapping. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 1055–1059. [Google Scholar] [CrossRef]
- Wang, M.; Liu, Z.; Baig, M.H.A.; Wang, Y.; Li, Y.; Chen, Y. Mapping sugarcane in complex landscapes by integrating multi-temporal Sentinel-2 images and machine learning algorithms. Land Use Policy 2019, 88, 104190. [Google Scholar] [CrossRef]
- Xie, Q.; Dash, J.; Huete, A.; Jiang, A.; Yin, G.; Ding, Y.; Peng, D.; Hall, C.C.; Brown, L.; Shi, Y.; et al. Retrieval of crop biophysical parameters from Sentinel-2 remote sensing imagery. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 187–195. [Google Scholar] [CrossRef]
- Blanco, P.D.; del Valle, H.F.; Bouza, P.J.; Metternicht, G.I.; Hardtke, L.A. Ecological site classification of semiarid rangelands: Synergistic use of Landsat and Hyperion imagery. Int. J. Appl. Earth Obs. Geoinf. 2014, 29, 11–21. [Google Scholar] [CrossRef]
- Hurskainen, P.; Adhikari, H.; Siljander, M.; Pellikka, P.; Hemp, A. Auxiliary datasets improve accuracy of object-based land use/land cover classification in heterogeneous savanna landscapes. Remote Sens. Environ. 2019, 233, 111354. [Google Scholar] [CrossRef]
- Aghababaei, M.; Ebrahimi, A.; Naghipour, A.A.; Asadi, E.; Verrelst, J. Classification of Plant Ecological Units in Heterogeneous Semi-Steppe Rangelands: Performance Assessment of Four Classification Algorithms. Remote Sens. 2021, 13, 3433. [Google Scholar] [CrossRef]
- Claverie, M.; Masek, J.G.; Ju, J.; Dungan, J.L. Harmonized Landsat-8 Sentinel-2 (HLS) Product User’s Guide; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 2017. [Google Scholar]
- Yan, L.; Roy, D.P.; Zhang, H.; Li, J.; Huang, H. An automated approach for sub-pixel registration of Landsat-8 Operational Land Imager (OLI) and Sentinel-2 Multi Spectral Instrument (MSI) imagery. Remote Sens. 2016, 8, 520. [Google Scholar] [CrossRef]
- Rapinel, S.; Mony, C.; Lecoq, L.; Clement, B.; Thomas, A.; Hubert-Moy, L. Evaluation of Sentinel-2 time-series for mapping floodplain grassland plant communities. Remote Sens. Environ. 2019, 223, 115–129. [Google Scholar] [CrossRef]
- Li, W.; Dong, R.; Fu, H.; Wang, J.; Yu, L.; Gong, P. Integrating Google Earth imagery with Landsat data to improve 30-m resolution land cover mapping. Remote Sens. Environ. 2020, 237, 111563. [Google Scholar] [CrossRef]
- Stumpf, F.; Schneider, M.K.; Keller, A.; Mayr, A.; Rentschler, T.; Meuli, R.G.; Schaepman, M.; Liebisch, F. Spatial monitoring of grassland management using multi-temporal satellite imagery. Ecol. Indic. 2020, 113, 106201. [Google Scholar] [CrossRef]
- Griffiths, P.; Nendel, C.; Pickert, J.; Hostert, P. Towards national-scale characterization of grassland use intensity from integrated Sentinel-2 and Landsat time series. Remote Sens. Environ. 2020, 238, 111124. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Morgan, J.L.; Gergel, S.E.; Ankerson, C.; Tomscha, S.A.; Sutherland, I.J. Historical aerial photography for landscape analysis. In Learning Landscape Ecology; Springer: Berlin/Heidelberg, Germany, 2017; pp. 21–40. [Google Scholar]
- De Torres, F.N.; Richter, R.; Vohland, M. A multisensoral approach for high-resolution land cover and pasture degradation mapping in the humid tropics: A case study of the fragmented landscape of Rio de Janeiro. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 189–201. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009; p. 533. [Google Scholar]
- Ludwig, M.; Morgenthal, T.; Detsch, F.; Higginbottom, T.P.; Valdes, M.L.; Nauß, T.; Meyer, H. Machine learning and multi-sensor based modelling of woody vegetation in the Molopo Area, South Africa. Remote Sens. Environ. 2019, 222, 195–203. [Google Scholar] [CrossRef]
- Zhou, B.; Okin, G.S.; Zhang, J. Leveraging Google Earth Engine (GEE) and machine learning algorithms to incorporate in situ measurement from different times for rangelands monitoring. Remote Sens. Environ. 2020, 236, 111521. [Google Scholar] [CrossRef]
- Lu, D.; Weng, Q. A survey of image classification methods and techniques for improving classification performance. Int. J. Remote Sens. 2007, 28, 823–870. [Google Scholar] [CrossRef]
- Abedi, R. Comparison of Parametric and Non-Parametric Techniques to Accurate Classification of Forest Attributes on Satellite Image Data. J. Environ. Sci. Stud. 2020, 5, 3229–3235. [Google Scholar]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Schölkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; The MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Verrelst, J.; Rivera, J.; Alonso, L.; Moreno, J. ARTMO: An Automated Radiative Transfer Models Operator toolbox for automated retrieval of biophysical parameters through model inversion. In Proceedings of the EARSeL 7th SIG-Imaging Spectroscopy Workshop, Edinburgh, UK, 11–13 April 2011. [Google Scholar]
- Rivera, J.P.; Verrelst, J.; Gómez-Dans, J.; Muñoz-Marí, J.; Moreno, J.; Camps-Valls, G. An emulator toolbox to approximate radiative transfer models with statistical learning. Remote Sens. 2015, 7, 9347–9370. [Google Scholar] [CrossRef]
- Verrelst, J.; Malenovskỳ, Z.; Van der Tol, C.; Camps-Valls, G.; Gastellu-Etchegorry, J.P.; Lewis, P.; North, P.; Moreno, J. Quantifying vegetation biophysical variables from imaging spectroscopy data: A review on retrieval methods. Surv. Geophys. 2019, 40, 589–629. [Google Scholar] [CrossRef]
- Verrelst, J.; Berger, K.; Rivera-Caicedo, J.P. Intelligent Sampling for Vegetation Nitrogen Mapping Based on Hybrid Machine Learning Algorithms. IEEE Geosci. Remote Sens. Lett. 2020, 18, 2038–2042. [Google Scholar] [CrossRef]
- Verrelst, J.; Romijn, E.; Kooistra, L. Mapping Vegetation Density in a Heterogeneous River Floodplain Ecosystem Using Pointable CHRIS/PROBA Data. Remote Sens. 2012, 4, 2866–2889. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Talukdar, S.; Singha, P.; Mahato, S.; Shahfahad; Pal, S.; Liou, Y.A.; Rahman, A. Land-use land-cover classification by machine learning classifiers for satellite observations-A review. Remote Sens. 2020, 12, 1135. [Google Scholar] [CrossRef]
- Hubert-Moy, L.; Cotonnec, A.; Le Du, L.; Chardin, A.; Perez, P. A Comparison of Parametric Classification Procedures of Remotely Sensed Data Applied on Different Landscape Units. Remote Sens. Environ. 2001, 75, 174–187. [Google Scholar] [CrossRef]
- Phiri, D.; Morgenroth, J. Developments in Landsat land cover classification methods: A review. Remote Sens. 2017, 9, 967. [Google Scholar] [CrossRef]
- Fisher, R.A. The use of multiple measurements in taxonomic problems. Ann. Eugen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
- Schütze, H.; Manning, C.D.; Raghavan, P. Introduction to Information Retrieval; Cambridge University Press: Cambridge, UK, 2008; Volume 39. [Google Scholar]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Adugna, T.; Xu, W.; Fan, J. Comparison of Random Forest and Support Vector Machine Classifiers for Regional Land Cover Mapping Using Coarse Resolution FY-3C Images. Remote Sens. 2022, 14, 574. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; Wadsworth and Brooks: Monterey, CA, USA, 1984. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks—A Comprehensive Foundation, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 1999. [Google Scholar]
- Kudo, M.; Toyama, J.; Shimbo, M. Multidimensional curve classification using passing-through regions. Pattern Recognit. Lett. 1999, 20, 1103–1111. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Fürnkranz, J. Round robin classification. J. Mach. Learn. Res. 2002, 2, 721–747. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; The MIT Press: New York, NY, USA, 2006. [Google Scholar]
- Hughes, G. On The Mean Accuracy Of Statistical Pattern Recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
- Liu, H.; Motoda, H. Feature Extraction, Construction and Selection: A Data Mining Perspective; Springer Science & Business Media: New York, NY, USA, 1998; Volume 453. [Google Scholar]
- Arenas-Garcia, J.; Petersen, K.; Camps-Valls, G.; Hansen, L. Kernel multivariate analysis framework for supervised subspace learning: A tutorial on linear and kernel multivariate methods. IEEE Signal Process. Mag. 2013, 30, 16–29. [Google Scholar] [CrossRef]
- Damodaran, B.B.; Nidamanuri, R.R. Assessment of the impact of dimensionality reduction methods on information classes and classifiers for hyperspectral image classification by multiple classifier system. Adv. Space Res. 2014, 53, 1720–1734. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis; Springer-Verlag: New York, NY, USA, 1986. [Google Scholar]
- De Grave, C.; Verrelst, J.; Morcillo-Pallarés, P.; Pipia, L.; Rivera-Caicedo, J.P.; Amin, E.; Belda, S.; Moreno, J. Quantifying vegetation biophysical variables from the Sentinel-3/FLEX tandem mission: Evaluation of the synergy of OLCI and FLORIS data sources. Remote Sens. Environ. 2020, 251, 112101. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera-Caicedo, J.P.; Reyes-Muñoz, P.; Morata, M.; Amin, E.; Tagliabue, G.; Panigada, C.; Hank, T.; Berger, K. Mapping landscape canopy nitrogen content from space using PRISMA data. ISPRS J. Photogramm. Remote Sens. 2021, 178, 382–395. [Google Scholar] [CrossRef]
- Pascual-Venteo, A.B.; Portalés, E.; Berger, K.; Tagliabue, G.; Garcia, J.L.; Pérez-Suay, A.; Rivera-Caicedo, J.P.; Verrelst, J. Prototyping Crop Traits Retrieval Models for CHIME: Dimensionality Reduction Strategies Applied to PRISMA Data. Remote Sens. 2022, 14, 2448. [Google Scholar] [CrossRef] [PubMed]
- Wold, H. Partial least squares. Encycl. Stat. Sci. 1985, 6, 581–591. [Google Scholar]
- Rivera-Caicedo, J.P.; Verrelst, J.; Muñoz-Marí, J.; Camps-Valls, G.; Moreno, J. Hyperspectral dimensionality reduction for biophysical variable statistical retrieval. ISPRS J. Photogramm. Remote Sens. 2017, 132, 88–101. [Google Scholar] [CrossRef]
- Foody, G.M. Explaining the unsuitability of the kappa coefficient in the assessment and comparison of the accuracy of thematic maps obtained by image classification. Remote Sens. Environ. 2020, 239, 111630. [Google Scholar] [CrossRef]
- Tharwat, A. Classification assessment methods. Appl. Comput. Inform. 2020, 17, 168–192. [Google Scholar] [CrossRef]
- Hill, M.J. Vegetation index suites as indicators of vegetation state in grassland and savanna: An analysis with simulated SENTINEL 2 data for a North American transect. Remote Sens. Environ. 2013, 137, 94–111. [Google Scholar] [CrossRef]
- Vasilakos, C.; Kavroudakis, D.; Georganta, A. Machine learning classification ensemble of multitemporal Sentinel-2 images: The case of a mixed mediterranean ecosystem. Remote Sens. 2020, 12, 2005. [Google Scholar] [CrossRef]
- Muthoka, J.M.; Salakpi, E.E.; Ouko, E.; Yi, Z.F.; Antonarakis, A.S.; Rowhani, P. Mapping Opuntia stricta in the arid and semi-arid environment of kenya using sentinel-2 imagery and ensemble machine learning classifiers. Remote Sens. 2021, 13, 1494. [Google Scholar] [CrossRef]
- Gašparović, M.; Jogun, T. The effect of fusing Sentinel-2 bands on land-cover classification. Int. J. Remote Sens. 2018, 39, 822–841. [Google Scholar] [CrossRef]
- Aghababaei, M.; Ebrahimi, A.; Naghipour, A.A.; Asadi, E.; Verrelst, J. Vegetation Types Mapping Using Multi-Temporal Landsat Images in the Google Earth Engine Platform. Remote Sens. 2021, 13, 4683. [Google Scholar] [CrossRef]
- Bernardo, J.; Berger, J.; Dawid, A.; Smith, A. Regression and classification using Gaussian process priors. Bayesian Stat. 1998, 6, 475. [Google Scholar]
- Ayala Izurieta, J.E.; Jara Santillán, C.A.; Márquez, C.O.; García, V.J.; Rivera-Caicedo, J.P.; Van Wittenberghe, S.; Delegido, J.; Verrelst, J. Improving the remote estimation of soil organic carbon in complex ecosystems with Sentinel-2 and GIS using Gaussian processes regression. Plant Soil 2022, 1–25. [Google Scholar] [CrossRef]
- Blickensdörfer, L.; Schwieder, M.; Pflugmacher, D.; Nendel, C.; Erasmi, S.; Hostert, P. Mapping of crop types and crop sequences with combined time series of Sentinel-1, Sentinel-2 and Landsat 8 data for Germany. Remote Sens. Environ. 2022, 269, 112831. [Google Scholar] [CrossRef]
- Heckel, K.; Urban, M.; Schratz, P.; Mahecha, M.D.; Schmullius, C. Predicting forest cover in distinct ecosystems: The potential of multi-source Sentinel-1 and-2 data fusion. Remote Sens. 2020, 12, 302. [Google Scholar] [CrossRef]
- Mirmazloumi, S.M.; Kakooei, M.; Mohseni, F.; Ghorbanian, A.; Amani, M.; Crosetto, M.; Monserrat, O. ELULC-10, a 10 m European Land Use and Land Cover Map Using Sentinel and Landsat Data in Google Earth Engine. Remote Sens. 2022, 14, 3041. [Google Scholar] [CrossRef]
- Verrelst, J.; Muñoz, J.; Alonso, L.; Delegido, J.; Rivera, J.; Camps-Valls, G.; Moreno, J. Machine learning regression algorithms for biophysical parameter retrieval: Opportunities for Sentinel-2 and -3. Remote Sens. Environ. 2012, 118, 127–139. [Google Scholar] [CrossRef]
- Delegido, J.; Verrelst, J.; Alonso, L.; Moreno, J. Evaluation of sentinel-2 red-edge bands for empirical estimation of green LAI and chlorophyll content. Sensors 2011, 11, 7063–7081. [Google Scholar] [CrossRef] [Green Version]
- Phiri, D.; Simwanda, M.; Salekin, S.; Nyirenda, V.R.; Murayama, Y.; Ranagalage, M. Sentinel-2 Data for Land Cover/Use Mapping: A Review. Remote Sens. 2020, 12, 2291. [Google Scholar] [CrossRef]
- Mas, J.F.; Flores, J.J. The application of artificial neural networks to the analysis of remotely sensed data. Int. J. Remote Sens. 2008, 29, 617–663. [Google Scholar] [CrossRef]
- Na, X.; Zhang, S.; Li, X.; Yu, H.; Liu, C. Improved land cover mapping using random forests combined with landsat thematic mapper imagery and ancillary geographic data. Photogramm. Eng. Remote Sens. 2010, 76, 833–840. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Shao, Y.; Lunetta, R.S. Comparison of support vector machine, neural network, and CART algorithms for the land-cover classification using limited training data points. ISPRS J. Photogramm. Remote Sens. 2012, 70, 78–87. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, J.; Xun, L.; Wang, J.; Wu, Z.; Henchiri, M.; Zhang, S.; Zhang, S.; Bai, Y.; Yang, S.; et al. Evaluating the Effectiveness of Machine Learning and Deep Learning Models Combined Time-Series Satellite Data for Multiple Crop Types Classification over a Large-Scale Region. Remote Sens. 2022, 14, 2341. [Google Scholar] [CrossRef]
- Tamborrino, C.; Interdonato, R.; Teisseire, M. Sentinel-2 Satellite Image Time-Series Land Cover Classification with Bernstein Copula Approach. Remote Sens. 2022, 14, 3080. [Google Scholar] [CrossRef]
- Rogan, J.; Franklin, J.; Stow, D.; Miller, J.; Woodcock, C.; Roberts, D. Mapping land-cover modifications over large areas: A comparison of machine learning algorithms. Remote Sens. Environ. 2008, 112, 2272–2283. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Chica-Rivas, M. Evaluation of different machine learning methods for land cover mapping of a Mediterranean area using multi-seasonal Landsat images and Digital Terrain Models. Int. J. Digit. Earth 2014, 7, 492–509. [Google Scholar] [CrossRef]
- Rivera Caicedo, J.; Verrelst, J.; Muñoz-Marí, J.; Moreno, J.; Camps-Valls, G. Toward a semiautomatic machine learning retrieval of biophysical parameters. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1249–1259. [Google Scholar] [CrossRef]
- Valderrama-Landeros, L.; Flores-Verdugo, F.; Rodríguez-Sobreyra, R.; Kovacs, J.M.; Flores-de Santiago, F. Extrapolating canopy phenology information using Sentinel-2 data and the Google Earth Engine platform to identify the optimal dates for remotely sensed image acquisition of semiarid mangroves. J. Environ. Manag. 2021, 279, 111617. [Google Scholar] [CrossRef] [PubMed]
- Asam, S.; Gessner, U.; Almengor González, R.; Wenzl, M.; Kriese, J.; Kuenzer, C. Mapping Crop Types of Germany by Combining Temporal Statistical Metrics of Sentinel-1 and Sentinel-2 Time Series with LPIS Data. Remote Sens. 2022, 14, 2981. [Google Scholar] [CrossRef]
- Shang, X.; Chisholm, L.A. Classification of Australian Native Forest Species Using Hyperspectral Remote Sensing and Machine-Learning Classification Algorithms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2481–2489. [Google Scholar] [CrossRef]
- Bazi, Y.; Melgani, F. Gaussian process approach to remote sensing image classification. IEEE Trans. Geosci. Remote Sen. 2009, 48, 186–197. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.; Moreno, J.; Camps-Valls, G. Gaussian processes uncertainty estimates in experimental Sentinel-2 LAI and leaf chlorophyll content retrieval. ISPRS J. Photogramm. Remote Sens. 2013, 86, 157–167. [Google Scholar] [CrossRef]
- Sun, S.; Zhong, P.; Xiao, H.; Wang, R. Active learning with Gaussian process classifier for hyperspectral image classification. IEEE Trans. Geosci. Remote Sen. 2014, 53, 1746–1760. [Google Scholar] [CrossRef]
- Morales-Alvarez, P.; Pérez-Suay, A.; Molina, R.; Camps-Valls, G. Remote sensing image classification with large-scale Gaussian processes. IEEE Trans. Geosci. Remote Sen. 2017, 56, 1103–1114. [Google Scholar] [CrossRef] [Green Version]

| Classifier | Description | Ref. |
|---|---|---|
| Discriminant Analysis (DA) | DA is a linear model for classification and dimensionality reduction, most commonly used for feature extraction in pattern classification problems. First, in 1936, Fisher formulated linear discriminant for two classes, and in 1948, C.R Rao generalized it for multiple classes. LDA projects data from a D dimensional feature space down to a D’ (D > D’) dimensional space in a way to maximize the variability between the classes and reduce the variability within the classes. The quadratic DA is also known as maximum likelihood classification within popular remote sensing software packages. | [45] |
| Naive Bayes (NB) | The NB is a classification algorithm based on the concept of the Bayes theorem with the “naive” assumption of conditional independence between every pair of features given the value of the class variable. | [46] |
| Classifier | Description | Ref. |
|---|---|---|
| Nearest neighbor (NN) | The principle behind NN methods is to find a predefined number of training samples closest in distance to the new point, and predict the label from these. The basic NN classification uses uniform weights; that is, the value assigned to a query point is computed from a simple majority vote of the nearest neighbors. | [47] |
| Decision trees (DT) | Classification trees (CF) fit binary decision tree for multiclass classification. See also: https://es.mathworks.com/help/stats/fitctree.html (accessed on 2 July 2022). Random forests (RF) bags an ensemble of decision trees. Bagging stands for bootstrap aggregation. Every tree in the ensemble is grown on an independently drawn bootstrap replica of input data. See also: https://es.mathworks.com/help/stats/treebagger-class.html (accessed on 2 July 2022). For RF, by default, 100 trees are set as recommended according to [48]. | [49,50] |
| Neural networks (NN) | ANNs in their basic form are essentially fully connected layered structures of artificial neurons (AN). An AN is basically a pointwise nonlinear function (e.g., a sigmoid or Gaussian function) applied to the output of a linear regression. ANs with different neural layers are interconnected with weighted links. The most common ANN structure is a feed-forward ANN, where information flows in a unidirectional forward mode. From the input nodes, data pass hidden nodes (if any) toward the output nodes. The following algorithms have been implemented:
| [51,52] |
| Ensemble learners (EL) | EL combines a set of trained weak learner models and data on which these learners were trained. EL can predict ensemble response for new data by aggregating predictions from its weak learners. The following EL are provided: (1) discriminant EL, (2) k-nearest neighbor (KNN) EL, (3) tree EL (bagging), (4) tree EL (AdaBoost), (5) tree EL (RUSBoost). Bagging and boosting techniques are typically applied to decision trees. Bag generally constructs deep trees. This construction is both time-consuming and memory-intensive. This also leads to relatively slow predictions. Boost algorithms generally use very shallow trees. This construction uses relatively little time or memory. However, for effective predictions, boosted trees might need more ensemble members than bagged trees. See also: https://es.mathworks.com/help/stats/framework-for-ensemble-learning.html (accessed on 2 July 2022) | [50,53] |
| error-correcting output codes (ECOC) | The ECOC method is a technique that allows a multi-class classification problem to be reframed as multiple binary classification problems, allowing the use of native binary classification models to be used directly. Unlike one-vs-rest and one-vs-one methods that offer a similar solution by dividing a multi-class classification problem into a fixed number of binary classification problems, the error-correcting output codes technique allows each class to be encoded as an arbitrary number of binary classification problems. When an overdetermined representation is used, it allows the extra models to act as “error-correction” predictions that can result in better predictive performance. The following ECOC are provided: (1) discriminant analysis, (2) kernel classification, (3) KNN, (4) linear classification, (5) naive Bayes classification, (6) decision tree, (7) support vector machine. See also https://machinelearningmastery.com/error-correcting-output-codes-ecoc-for-machine-learning/ (accessed on 2 July 2022). | [54] |
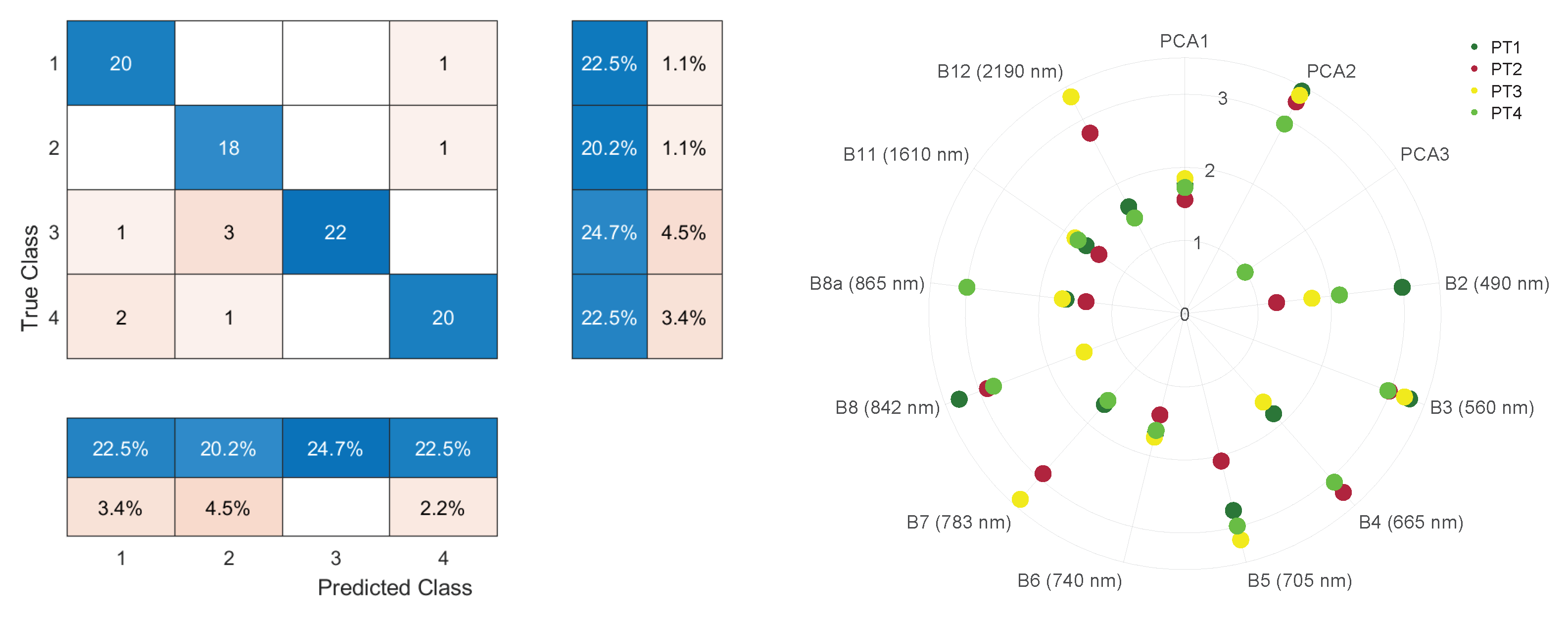
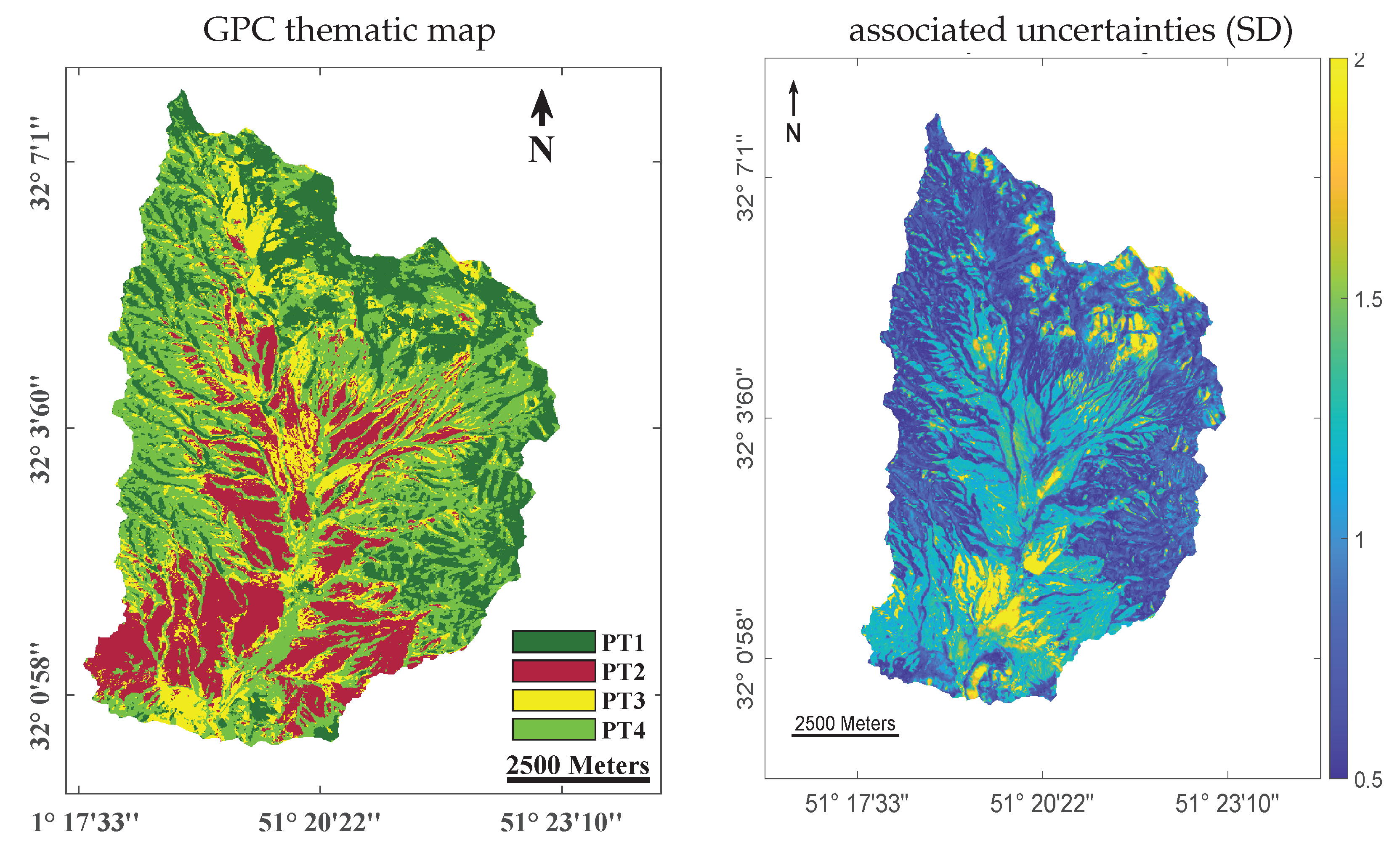
| Gaussian process (GP) | The GP is a stochastic process where each random variable follows a multivariate normal distribution. The goal is to learn mapping from the input data to their corresponding classification label, which can then be used on new, unseen data pixels. When the GP is developed with kernel methods, it allows mapping the original data into a possibly infinite dimensional space in which the input–output relation can be better estimated as it considers more complex and flexible functions than the linear models. As the GP is based on a probabilistic framework, it allows to provide uncertainty estimation per sample. This measurement becomes useful for taking decisions and allows to be more or less confident with the inferred classification label. Moreover, the GP can use more sophisticated kernel functions than the standard linear kernel or the radial basis function (RBF) kernel , which can be optimally tuned through the likelihood maximization. In the classification case, the output values are discrete (); this causes the likelihood function to be non-Gaussian, and then, some approximations should be performed [55]. We choose the Laplace approximation which performs well and is robust. One notable kernel function is the automatic relevance determination (ARD) kernel , where is a diagonal matrix whose diagonal tries are constituted by parameters to weight each input dimension. This kernel covariance function requires one parameter per input feature; it can be optimized under that framework and it allows to provide a band ranking based on their optimal values. Source code is in: https://github.com/IPL-UV/simpleClass (accessed on 2 July 2022). | [55] |
| MLCA | PT1 | PT2 | PT3 | PT4 | |
|---|---|---|---|---|---|
| Gaussian processes classifier | Precision (PA %) | 86.9 | 81.8 | 100 | 90.9 |
| Sensitivity (UA %) | 95.2 | 94.7 | 84.6 | 86.9 | |
| Specificity (%) | 95.5 | 94.2 | 100 | 96.9 | |
| F1-Score (%) | 90.9 | 87.8 | 91.6 | 88.8 | |
| OA = 90.0% | |||||
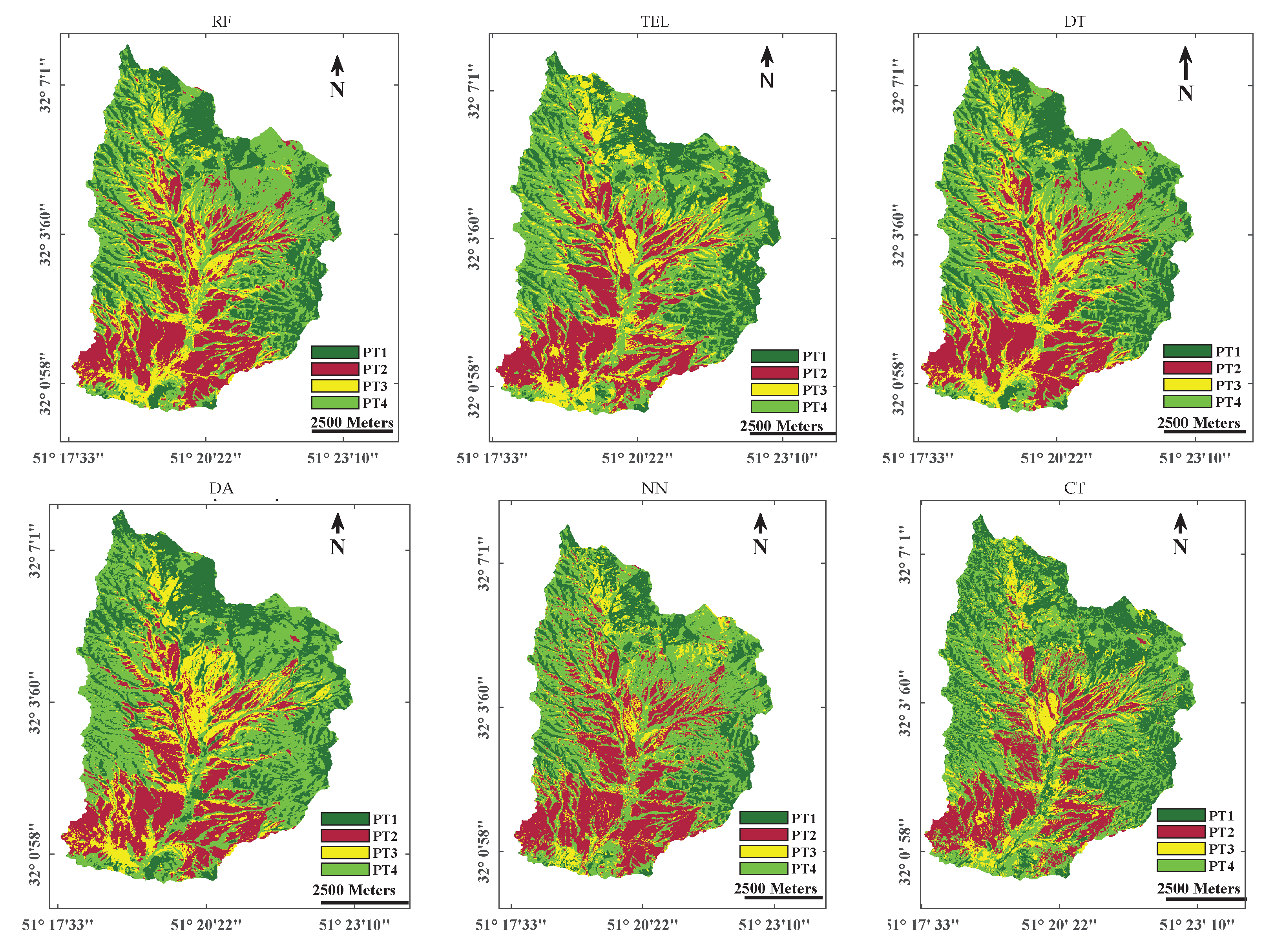
| Random forest | Precision (PA %) | 86.9 | 86.3 | 86.3 | 86.3 |
| Sensitivity (UA %) | 90.9 | 86.3 | 86.3 | 82.6 | |
| Specificity (%) | 95.5 | 95.5 | 95.5 | 95.4 | |
| F1-Score (%) | 86.3 | 86.3 | 86.3 | 84.4 | |
| OA = 86.5% | |||||
| Tree EL (bag) | Precision (PA %) | 91.3 | 86.3 | 86.3 | 68.0 |
| Sensitivity (UA %) | 80.7 | 82.6 | 382.6 | 88.2 | |
| Specificity (%) | 96.8 | 95.4 | 95.4 | 90.2 | |
| F1-Score (%) | 85.7 | 84.4 | 84.4 | 76.9 | |
| OA = 83.1% | |||||
| Decision tree (ECOC) | Precision (PA %) | 91.3 | 75.7 | 81.8 | 81.8 |
| Sensitivity (UA %) | 87.5 | 84.2 | 72.0 | 85.7 | |
| Specificity (%) | 96.9 | 91.4 | 93.7 | 94.0 | |
| F1-Score (%) | 89.3 | 78.0 | 76.6 | 83.7 | |
| OA = 82.0% | |||||
| Discriminant analysis (ECOC) | Precision (PA %) | 86.9 | 86.3 | 81.8 | 63.6 |
| Sensitivity (UA %) | 83.3 | 79.1 | 85.7 | 70.0 | |
| Specificity (%) | 95.3 | 95.3 | 94.0 | 88.4 | |
| F1-Score (%) | 85.1 | 82.6 | 83.7 | 66.6 | |
| OA = 79.7% | |||||
| Neural network (Adam) | Precision (PA %) | 95.6 | 81.8 | 72.7 | 68.1 |
| Sensitivity (UA %) | 81.4 | 81.0 | 84.2 | 71.4 | |
| Specificity (%) | 98.3 | 94.0 | 91.4 | 89.7 | |
| F1-Score (%) | 88.0 | 81.0 | 78.0 | 69.7 | |
| OA = 79.0% | |||||
| Classification trees | Precision (PA %) | 91.3 | 72.7 | 81.8 | 68.1 |
| Sensitivity (UA %) | 87.5 | 80.0 | 72.0 | 75.0 | |
| Specificity (%) | 96.9 | 91.3 | 93.7 | 89.8 | |
| F1-Score (%) | 89.3 | 76.1 | 76.6 | 71.4 | |
| OA = 78.6% | |||||
| Discriminant analysis (quadratic) | Precision (PA %) | 86.9 | 72.7 | 81.8 | 72.2 |
| Sensitivity (UA %) | 86.9 | 80.0 | 69.2 | 80.0 | |
| Specificity (%) | 95.4 | 91.3 | 93.6 | 91.3 | |
| F1-Score (%) | 86.9 | 76.2 | 75.0 | 76.1 | |
| OA = 78.6% | |||||
| k-nearest neighbors (ECOC) | Precision (PA %) | 82.6 | 63.6 | 81.8 | 77.2 |
| Sensitivity (UA %) | 90.4 | 73.6 | 69.2 | 73.9 | |
| Specificity (%) | 94.1 | 88.5 | 93.6 | 92.4 | |
| F1-Score (%) | 86.3 | 68.3 | 75.0 | 75.5 | |
| OA = 76.4% | |||||
| Neural network (trainbr) | Precision (PA %) | 82.6 | 68.1 | 89.3 | 59.0 |
| Sensitivity (UA %) | 76.0 | 78.9 | 79.1 | 61.9 | |
| Specificity (%) | 93.7 | 90.0 | 95.3 | 86.7 | |
| F1-Score (%) | 79.1 | 73.1 | 82.6 | 60.4 | |
| OA = 74.1% | |||||
| Support vector machines (ECOC) | Precision (PA %) | 86.9 | 68.1 | 77.2 | 63.6 |
| Sensitivity (UA %) | 80.0 | 71.4 | 68.0 | 77.7 | |
| Specificity (%) | 95.3 | 89.7 | 92.1 | 88.7 | |
| F1-Score (%) | 83.3 | 69.7 | 72.3 | 70.0 | |
| OA = 74.1% | |||||
| Linear classification (ECOC) | Precision (PA %) | 86.9 | 68.1 | 77.2 | 36.3 |
| Sensitivity (UA %) | 80.0 | 71.4 | 68.0 | 77.7 | |
| Specificity (%) | 95.3 | 89.7 | 92.1 | 88.7 | |
| F1-Score (%) | 83.3 | 69.7 | 72.3 | 70.0 | |
| OA = 74.0% | |||||
| Neural network (trainscg) | Precision (PA %) | 82.6 | 72.7 | 72.7 | 63.6 |
| Sensitivity (UA %) | 86.3 | 69.5 | 66.6 | 70.0 | |
| Specificity (%) | 94.0 | 90.9 | 90.7 | 88.4 | |
| F1-Score (%) | 84.4 | 71.1 | 69.5 | 66.6 | |
| OA = 73.0% | |||||
| Naive Bayes | Precision (PA %) | 78.2 | 90.9 | 45.4 | 72.7 |
| Sensitivity (UA %) | 81.8 | 76.9 | 90.9 | 53.3 | |
| Specificity (%) | 92.5 | 96.8 | 84.6 | 89.8 | |
| F1-Score (%) | 80.0 | 83.3 | 60.6 | 61.5 | |
| OA = 72.0% | |||||
| Neural network (trainlm) | Precision (PA %) | 82.6 | 63.6 | 77.2 | 63.6 |
| Sensitivity (UA %) | 82.6 | 77.7 | 60.7 | 70.0 | |
| Specificity (%) | 93.9 | 88.8 | 91.8 | 88.4 | |
| F1-Score (%) | 82.6 | 70.0 | 68.0 | 66.6 | |
| OA = 72.0% | |||||
| Tree EL (AdaBoost) | Precision (PA %) | 86.9 | 95.4 | 45.4 | 54.5 |
| Sensitivity (UA %) | 83.3 | 61.7 | 62.5 | 80.0 | |
| Specificity (%) | 95.3 | 98.1 | 83.5 | 86.4 | |
| F1-Score (%) | 85.0 | 75.0 | 52.6 | 64.8 | |
| OA = 70.7% | |||||
| Discriminant EL | Precision (PA %) | 86.9 | 90.9 | 36.3 | 63.6 |
| Sensitivity (UA %) | 76.9 | 71.4 | 88.8 | 53.8 | |
| Specificity (%) | 95.2 | 96.7 | 82.5 | 87.3 | |
| F1-Score (%) | 81.6 | 80.0 | 51.6 | 58.3 | |
| OA = 69.6% | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aghababaei, M.; Ebrahimi, A.; Naghipour, A.A.; Asadi, E.; Pérez-Suay, A.; Morata, M.; Garcia, J.L.; Rivera Caicedo, J.P.; Verrelst, J. Introducing ARTMO’s Machine-Learning Classification Algorithms Toolbox: Application to Plant-Type Detection in a Semi-Steppe Iranian Landscape. Remote Sens. 2022, 14, 4452. https://doi.org/10.3390/rs14184452
Aghababaei M, Ebrahimi A, Naghipour AA, Asadi E, Pérez-Suay A, Morata M, Garcia JL, Rivera Caicedo JP, Verrelst J. Introducing ARTMO’s Machine-Learning Classification Algorithms Toolbox: Application to Plant-Type Detection in a Semi-Steppe Iranian Landscape. Remote Sensing. 2022; 14(18):4452. https://doi.org/10.3390/rs14184452
Chicago/Turabian StyleAghababaei, Masoumeh, Ataollah Ebrahimi, Ali Asghar Naghipour, Esmaeil Asadi, Adrián Pérez-Suay, Miguel Morata, Jose Luis Garcia, Juan Pablo Rivera Caicedo, and Jochem Verrelst. 2022. "Introducing ARTMO’s Machine-Learning Classification Algorithms Toolbox: Application to Plant-Type Detection in a Semi-Steppe Iranian Landscape" Remote Sensing 14, no. 18: 4452. https://doi.org/10.3390/rs14184452
APA StyleAghababaei, M., Ebrahimi, A., Naghipour, A. A., Asadi, E., Pérez-Suay, A., Morata, M., Garcia, J. L., Rivera Caicedo, J. P., & Verrelst, J. (2022). Introducing ARTMO’s Machine-Learning Classification Algorithms Toolbox: Application to Plant-Type Detection in a Semi-Steppe Iranian Landscape. Remote Sensing, 14(18), 4452. https://doi.org/10.3390/rs14184452