Correction of Terrain Effects on Forest Canopy Height Estimation Using ICESat-2 and High Spatial Resolution Images
Abstract
:1. Introduction
2. Materials and Methods
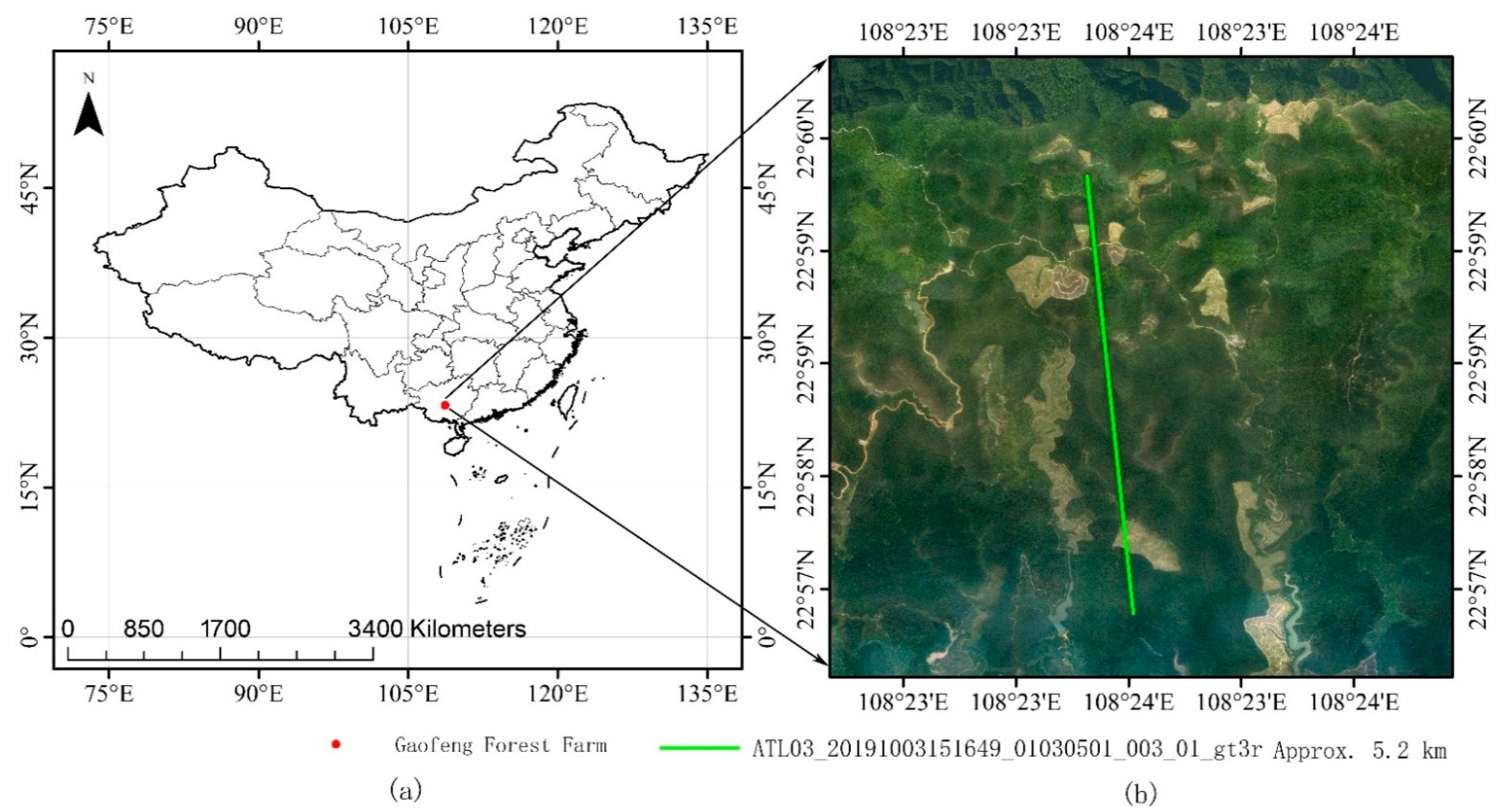
2.1. Study Area
2.2. Research Data
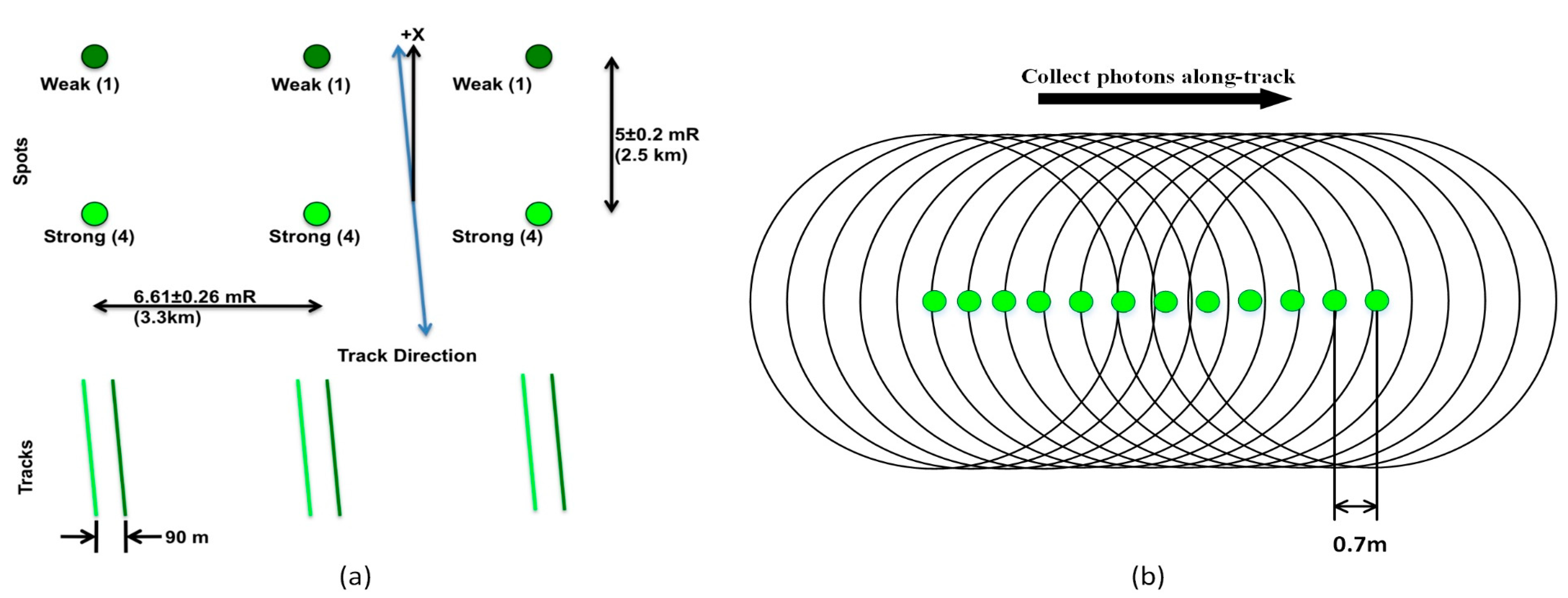
2.2.1. ICESat–2 Data
2.2.2. ALOS PALSAR DEM Data
2.2.3. CAF–LiCHy LiDAR Data
2.2.4. Ancillary Image Data
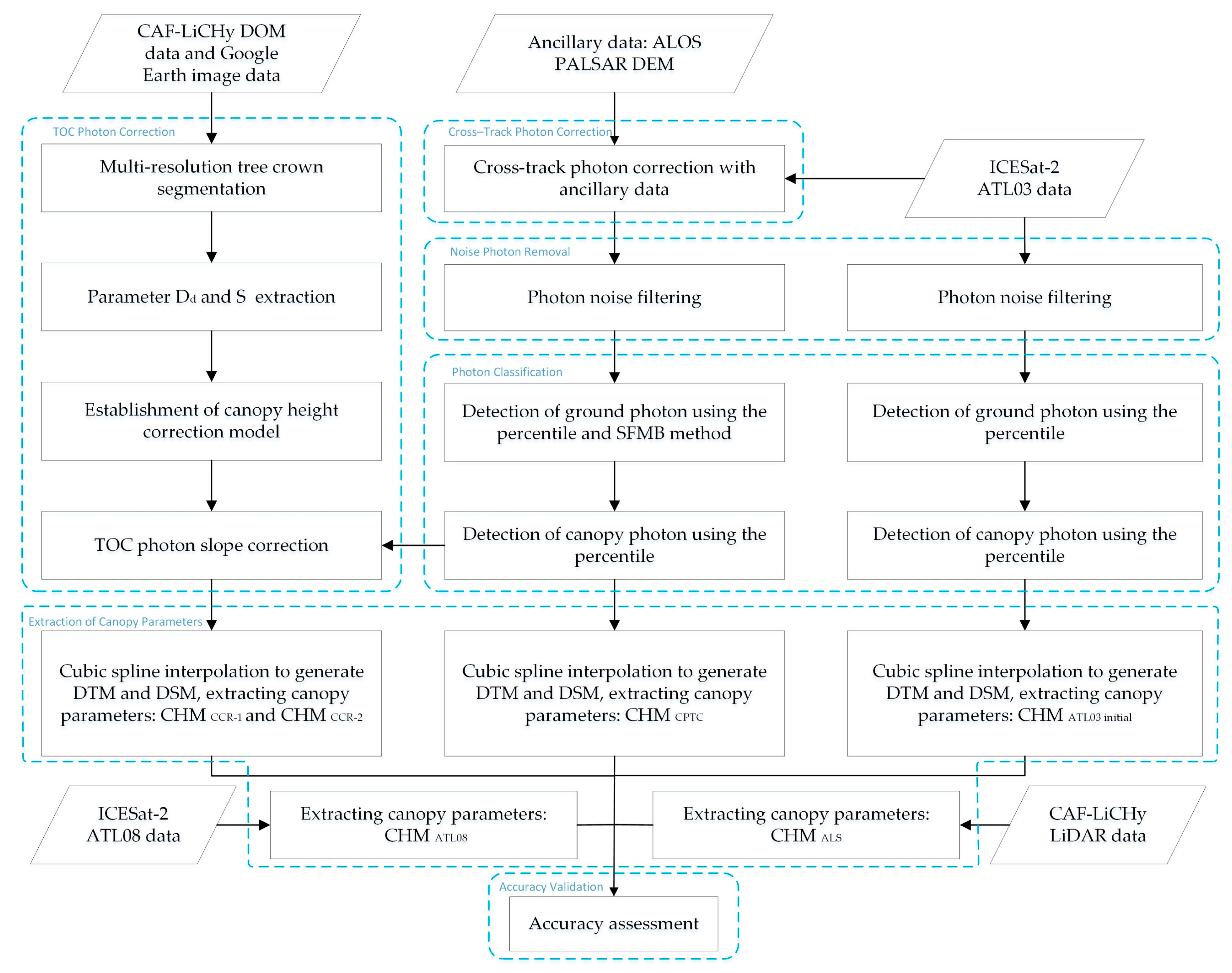
2.3. Methodologies
2.3.1. Cross-Track Photon Correction
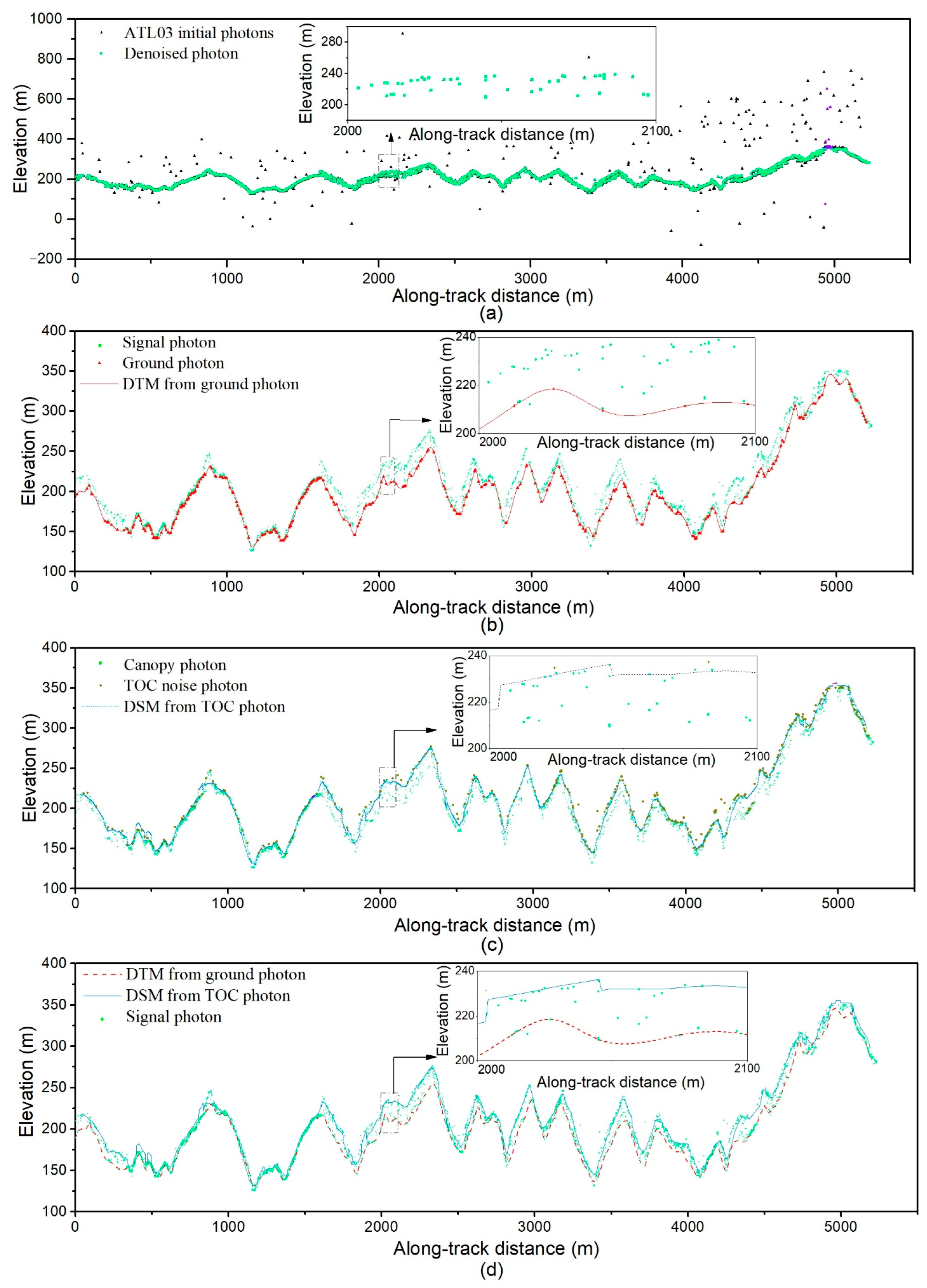
2.3.2. Noise Photon Removal
2.3.3. Photon Classification
2.3.4. TOC Photon Correction
Effect of Slope
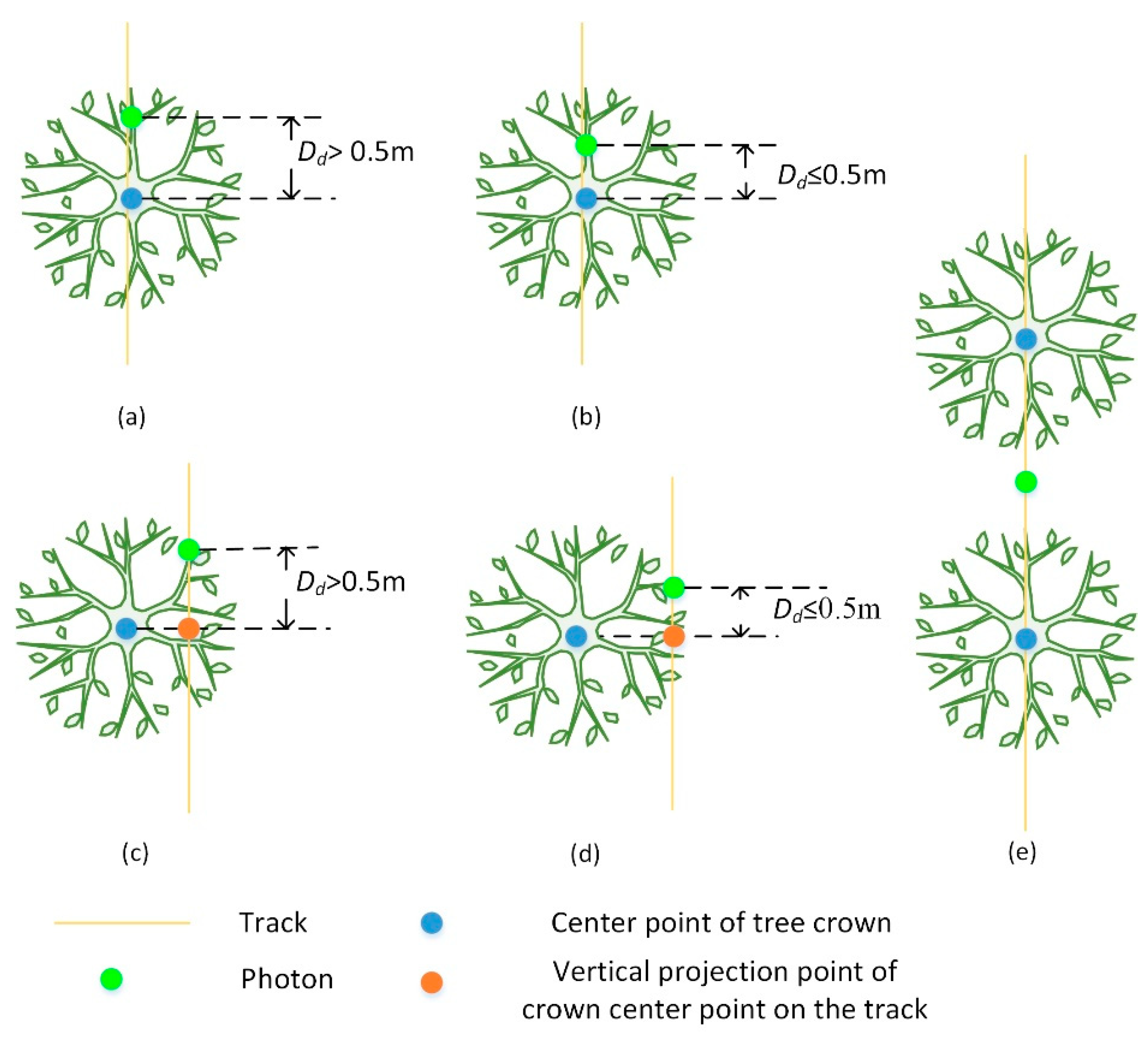
Crown Segmentation
TOC Photon Correction
2.3.5. Extraction of Canopy Parameters
2.3.6. Accuracy Validation
3. Results
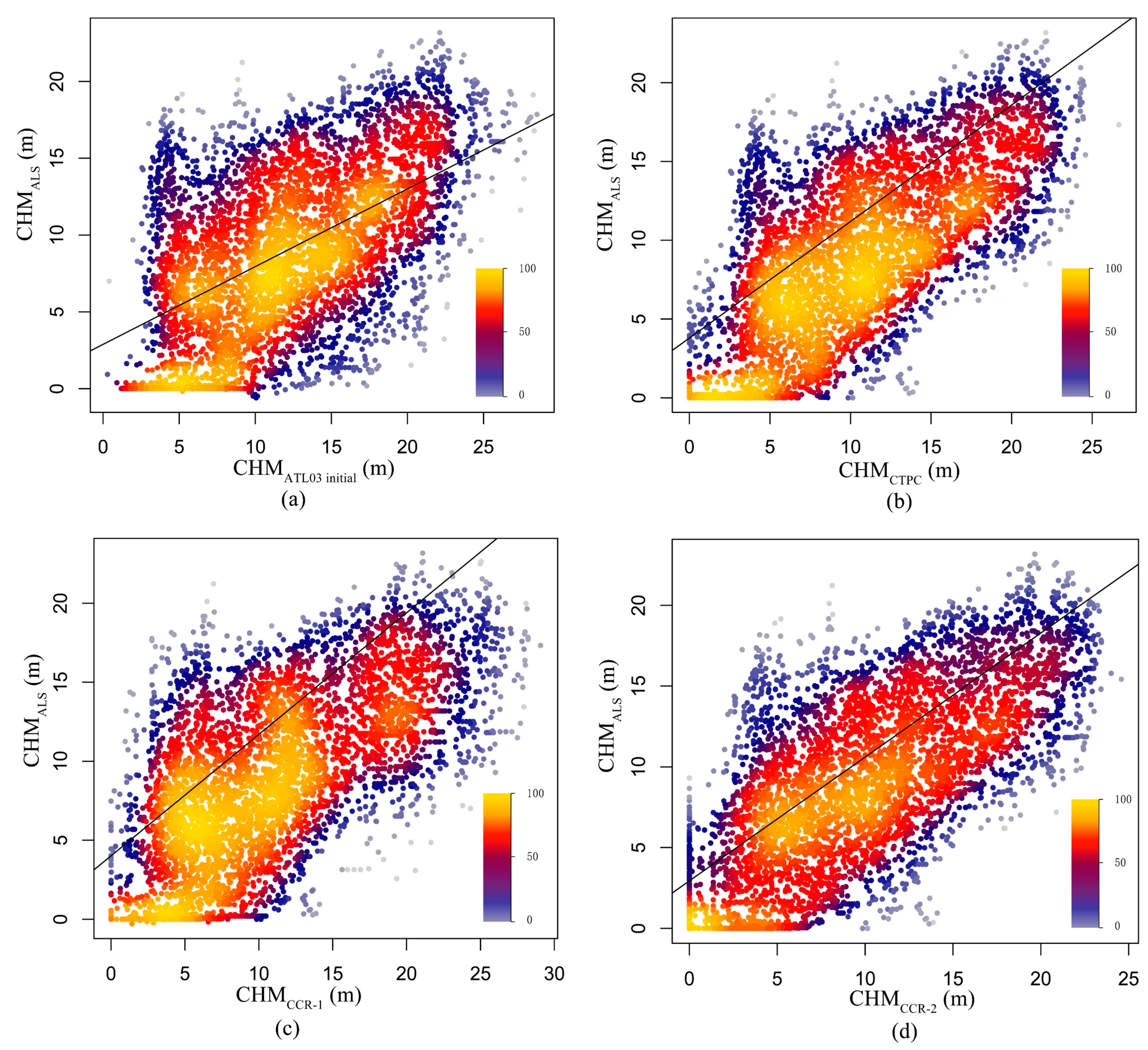
3.1. Canopy Height before and after Correction
3.2. Accuracy of Canopy Height Estimation for Different Segment Sizes and Relative Heights
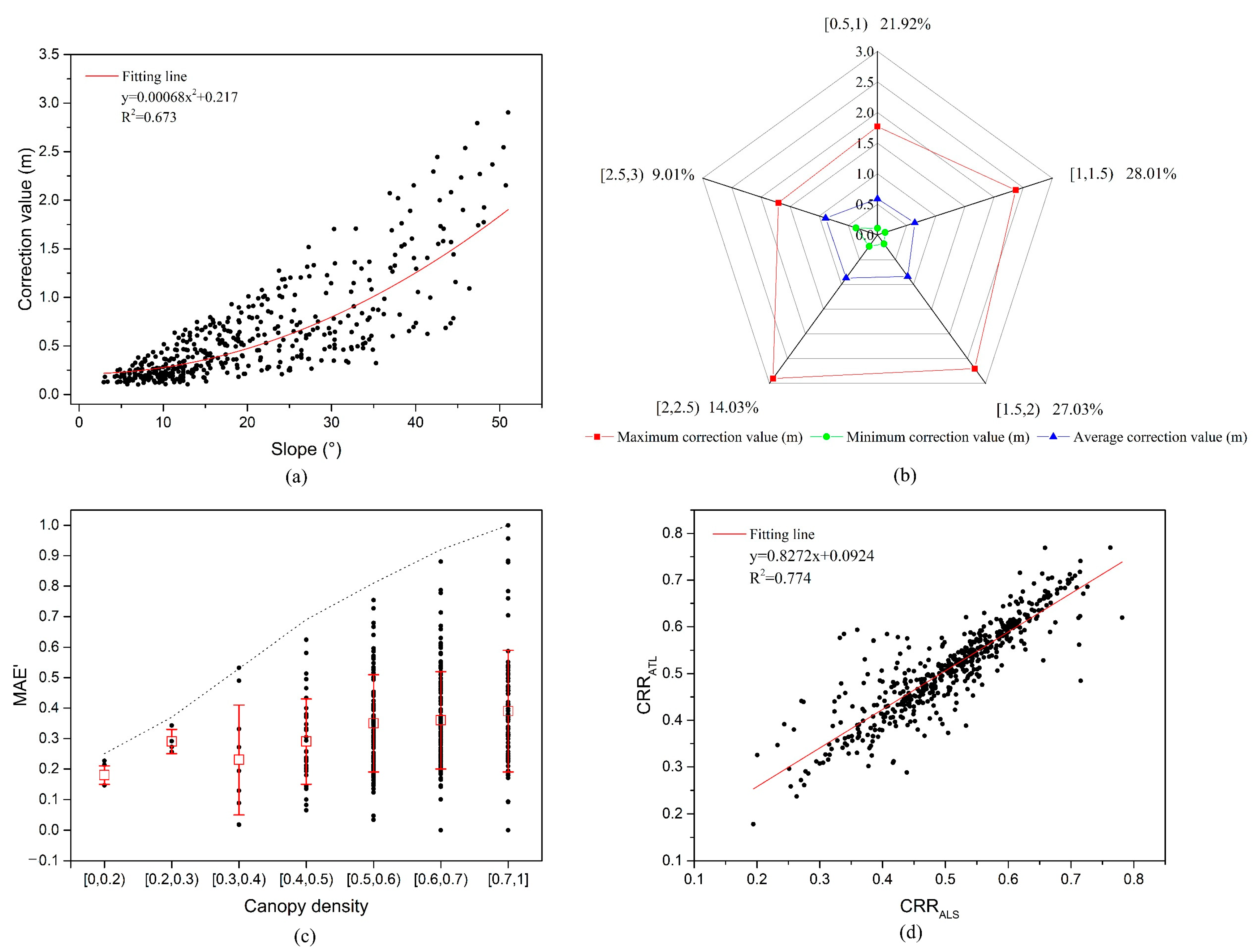
3.3. Effect of Slope on Canopy Correction
4. Discussion
4.1. Comparison of ICESat–2 Canopy Height Inversion Accuracy
4.2. Influencing Factors of ICESat–2 CHM Inversion
4.3. Future Directions and Implications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Streutker, D.R.; Glenn, N.F. LiDAR measurement of sagebrush steppe vegetation heights. Remote Sens. Environ. 2006, 102, 135–145. [Google Scholar] [CrossRef]
- Nie, S.; Wang, C.; Zeng, H.; Xi, X.; Xia, S. A revised terrain correction method for forest canopy height estimation using ICESat/GLAS data. ISPRS J. Photogramm. 2015, 108, 183–190. [Google Scholar] [CrossRef]
- Fayad, I.; Baghdadi, N.; Bailly, J.S.; Barbier, N.; Gond, V.; Herault, B.; Hajj, M.E.; Fabre, F.; Perrin, J. Regional Scale Rain–Forest Height Mapping Using Regression–Kriging of Spaceborne and Airborne LiDAR Data: Application on French Guiana. Remote Sens. 2016, 8, 240. [Google Scholar] [CrossRef]
- Schimel, D.; Pavlick, R.; Fisher, J.B.; Asner, G.P.; Saatchi, S.; Townsend, P.; Miller, C.; Frankenberg, C.; Hibbard, K.; Cox, P. Observing terrestrial ecosystems and the carbon cycle from space. Glob. Chang. Biol. 2015, 21, 1762–1776. [Google Scholar] [CrossRef]
- Tao, S.; Guo, Q.; Li, C.; Wang, Z.; Fang, J. Global patterns and determinants of forest canopy height. Ecology 2016, 97, 3265–3270. [Google Scholar] [CrossRef]
- Malambo, L.; Popescu, S.C. Assessing the agreement of ICESat–2 terrain and canopy height with airborne lidar over US ecozones. Remote Sens. Environ. 2021, 266, 112711. [Google Scholar] [CrossRef]
- Wulder, M.A.; Bater, C.W.; Coops, N.C.; Hilker, T.; White, J.C. The role of LiDAR in sustainable forest management. For. Chron. 2008, 84, 807–826. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Naesset, E.; Orka, H.O.; Coops, N.C.; Hilker, T.; Bater, C.W.; Gobakken, T. LiDAR sampling for large–area forest characterization: A review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote sensing Technologies for Enhancing Forest Inventories: A review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef]
- Scott, C.P.; Phan, M.; Crosby, C.J.; Nandigam, V.; Arrowsmith, R. On–demand 3D topographic differencing hosted by open topography. In Proceedings of the AGU Fall Meeting Abstracts 2019 (AGUFM 2019), San Francisco, CA, USA, 9–13 December 2019. [Google Scholar]
- Thatcher, C.A.; Lukas, V.; Stoker, J.M. The 3D Elevation Program and Energy for the Nation; US Geological Survey: Reston, VA, USA, 2020.
- Narine, L.L.; Popescu, S.C.; Malambo, L. Using ICESat–2 to estimate and map forest aboveground biomass: A first example. Remote Sens. 2020, 12, 1824. [Google Scholar] [CrossRef]
- Neumann, T.A.; Martino, A.J.; Markus, T.; Bae, S.; Bock, M.R.; Brenner, A.C.; Brunt, K.M.; Cavanaugh, J.; Fernandes, S.T.; Hancock, D.W.; et al. The Ice, Cloud, and Land Elevation Satellite–2 mission: A global geolocated photon product derived from the Advanced Topographic Laser Altimeter System. Remote Sens. Environ. 2019, 233, 111325. [Google Scholar] [CrossRef] [PubMed]
- Degnan, J.J. Scanning, multibeam, single photon lidars for rapid, large scale, high resolution, topographic and bathymetric mapping. Remote Sens. 2016, 8, 958. [Google Scholar] [CrossRef]
- Magruder, L.A.; Brunt, K.M.; Alonzo, M. Early ICESat–2 on–orbit Geolocation Validation Using Ground–Based Corner Cube Retro–Reflectors. Remote Sens. 2020, 12, 3653. [Google Scholar] [CrossRef]
- Harding, D.J.; Dabney, P.W.; Valett, S. Polarimetric, two–color, photon–counting laser altimeter measurements of forest canopy structure. In International Symposium on Lidar and Radar Mapping 2011: Technologies and Applications; International Society for Optics and Photonics: San Diego, CA, USA, 2011; p. 828629. [Google Scholar]
- Zhu, X.; Nie, S.; Wang, C.; Xi, X.B.; Li, D.; Li, G.Y.; Wang, P.; Cao, D.; Yang, X.B. Estimating Terrain Slope from ICESat–2 Data in Forest Environments. Remote Sens. 2020, 12, 3300. [Google Scholar] [CrossRef]
- Lin, X.; Xu, M.; Cao, C.; Dang, Y.; Huang, Z. Estimates of forest canopy height using a combination of ICESat–2/atlas data and stereo–photogrammetry. Remote Sens. 2020, 12, 3649. [Google Scholar] [CrossRef]
- Gwenzi, D.; Lefsky, M.A.; Suchdeo, V.P.; David, J.H. Prospects of the ICESat–2 laser altimetry mission for savanna ecosystem structural studies based on airborne simulation data. ISPRS J. Photogramm. 2016, 118, 68–82. [Google Scholar] [CrossRef]
- Popescu, S.C.; Zhou, T.; Nelson, R.; Neuenschwander, A.; Sheridan, R.; Narine, L.; Walsh, K.M. Photon counting LiDAR: An adaptive ground and canopy height retrieval algorithm for ICESat–2 data. Remote Sens. Environ. 2018, 208, 154–170. [Google Scholar] [CrossRef]
- Narine, L.L.; Popescu, S.; Neuenschwander, A.; Zhou, T.; Srinivasan, S.; Harbeck, K. Estimating aboveground biomass and forest canopy cover with simulated ICESat–2 data. Remote Sens. Environ. 2019, 224, 1–11. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Guenther, E.; White, J.C.; Duncanson, L.; Montesano, P. Validation of ICESat–2 terrain and canopy heights in boreal forests. Remote Sens. Environ. 2020, 251, 112110. [Google Scholar] [CrossRef]
- Liu, A.; Cheng, X.; Chen, Z. Performance evaluation of GEDI and ICESat–2 laser altimeter data for terrain and canopy height retrievals. Remote Sens. Environ. 2021, 264, 112571. [Google Scholar] [CrossRef]
- Neuenschwander, A.L.; Magruder, L.A. Canopy and Terrain Height Retrievals with ICESat–2: A First Look. Remote Sens. 2019, 11, 1721. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Li, S.; Zhou, H. Error analysis of estimated canopy height based on photon counting laser altimetry. Infrared Laser Eng. 2021, 40, 223–229. [Google Scholar]
- Moussavi, M.S.; Abdalati, W.; Scambos, T.; Neuenschwander, A. Applicability of an automatic surface detection approach to micro–pulse photon–counting lidar altimetry data: Implications for canopy height retrieval from future ICESat–2 data. Int. J. Remote Sens. 2014, 35, 5263–5279. [Google Scholar] [CrossRef]
- Kwok, R.; Markus, T.; Morison, J.; Palm, S.P.; Neumann, T.A.; Brunt, K.M.; Cook, W.B.; Hancock, D.W.; Cunningham, G.F. Profiling Sea Ice with a Multiple Altimeter Beam Experimental Lidar (MABEL). J. Atmos. Ocean Technol. 2014, 31, 1151–1168. [Google Scholar] [CrossRef]
- Nie, S.; Wang, C.; Xi, X.; Luo, S.Z.; Li, G.Y.; Tian, J.Y.; Wang, H.G. Estimating the vegetation canopy height using micro–pulse photon–counting LiDAR data. Opt. Express 2018, 26, 520–540. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Pitts, K. The ATL08 land and vegetation product for the ICESat–2 Mission. Remote Sens. Environ. 2019, 221, 247–259. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, X.; Nie, S.; Xi, X.; Li, D.; Zheng, W.; Chen, S. Ground elevation accuracy verification of ICESat–2 data: A case study in Alaska, USA. Opt. Express 2019, 27, 38168–38179. [Google Scholar] [CrossRef]
- Takahashi, T.; Yamamoto, K.; Senda, Y.; Tsuzuku, M. Estimating individual tree heights of sugi (Cryptomeria japonica D. Don) plantations in mountainous areas using small–footprint airborne LiDAR. J. For. Res. 2005, 10, 135–142. [Google Scholar] [CrossRef]
- Hodgson, M.E.; Bresnahan, E. Accuracy of airborne LiDAR–derived elevation: Empirical assessment and error budget. Photogramm. Eng. Remote Sens. 2004, 70, 331–339. [Google Scholar] [CrossRef]
- Zhu, X.; Nie, S.; Wang, C.; Xi, X.H.; Hu, Z.Y. A Ground Elevation and Vegetation Height Retrieval Algorithm Using Micro–Pulse Photon–Counting Lidar Data. Remote Sens. 2018, 10, 1962. [Google Scholar] [CrossRef]
- Wang, L.X.; Zhou, H.; Li, Z.L.; Liu, G.G.; Wang, H.; Wang, Y.P. Simulation of terrestrial target response function for satellite laser altimeter. Infrared Laser Eng. 2015, 34, 3424–3430. [Google Scholar]
- Zhang, Z.Y.; Wang, H.; Zhang, W.H.; Huang, K.; Zhou, H.; Ma, Y.; Li, S. Semi–analytical model of the waveform of plantation target for a satellite laser altimater. Acta Geod. Cartogr. Sin. 2018, 47, 142–152. [Google Scholar]
- Ni, X.; Xu, M.; Cao, C.; Chen, W.; Yang, B.; Xie, B. Forest height estimation and change monitoring based on artificial neural network using Geoscience Laser Altimeter System and Landsat data. J. Appl. Remote Sens. 2019, 14, 022207. [Google Scholar] [CrossRef]
- Martino, A.; Bock, M.R.; Jones, R.L.; Neumann, T.A.; Hancock, D.W.; Dabney, P.W.; Webb, C.E. The Ice, Cloud and Land Elevation Satellite–2 Project: Algorithm Theoretical Basis Document (ATBD)for ATL02 (Level 1B) Data Product, NASA Tech. Document, ICESat–2–SIPS–SPEC–0150. Available online: https://ICESat–2.gsfc.nasa.gov/sites/default/files/page_files/ICESat2_ATL02_ATBD_r003.pdf (accessed on 23 November 2020).
- Li, S.; Zhang, Z.; Ma, Y.; Zeng, H.M.; Zhao, P.F.; Zhang, W.H. Ranging performance models based on negative–binomial (NB) distribution for photon–counting lidars. Opt. Express 2019, 27, 861–877. [Google Scholar] [CrossRef] [PubMed]
- Magruder, L.A.; Brunt, K.M. Performance Analysis of Airborne Photon–Counting Lidar Data in Preparation for the ICESat–2 Mission. IEEE Trans. Geosci. Remote 2018, 56, 2911–2918. [Google Scholar] [CrossRef]
- Tadono, T.; Ishida, H.; Oda, F.; Naito, S.; Minakawa, K.; Iwamoto, H. Precise global DEM generation by ALOS PRISM. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 71–76. [Google Scholar] [CrossRef]
- Shebl, A.; Csámer, A. Reappraisal of DEMs, Radar and optical datasets in lineaments extraction with emphasis on the spatial context. Remote Sens. Appl. Soc. Environ. 2021, 24, 100617. [Google Scholar] [CrossRef]
- Lu, D.S.; Chen, Q.; Wang, G.X.; Liu, L.J.; Li, G.Y.; Moran, E. A survey of remote sensing–based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2014, 9, 63–105. [Google Scholar] [CrossRef]
- Ma, L.X.; Zheng, G.; Eitel, J.U.H.; Magney, T.S.; Moskal, L.M. Retrieving forest canopy extinction coefficient from terrestrial and airborne LiDAR. Agric. For. Meteorol. 2017, 236, 1–21. [Google Scholar] [CrossRef]
- Falkowski, M.J.; Wulder, M.A.; White, J.C.; Gillis, M.D. Supporting large–area, sample–based forest inventories with very high spatial resolution satellite imagery. Prog. Phys. Geog. 2009, 33, 403–423. [Google Scholar] [CrossRef]
- Pang, Y.; Li, Z.Y.; Ju, H.B.; Lu, H.; Jia, W.; Si, L.; Guo, Y.; Liu, Q.W.; Li, S.M.; Liu, L.X.; et al. LiCHy: The CAF’s LiDAR, CCD and Hyperspectral Integrated Airborne Observation System. Remote Sens. 2016, 8, 398. [Google Scholar] [CrossRef]
- Nie, S.; Wang, C.; Dong, P.; Xi, X.; Luo, S.; Qin, H. A revised progressive TIN densification for filtering airborne LiDAR data. Measurement 2017, 104, 70–77. [Google Scholar] [CrossRef]
- Li, B.; Fan, G.P.; Zhao, T.Z.; Deng, Z.; Yu, Y.H. Retrieval of DTM under Complex Forest Stand Based on Spaceborne LiDAR Fusion Photon Correction. Remote Sens. 2022, 14, 218. [Google Scholar] [CrossRef]
- Tian, X.; Shan, J. Comprehensive Evaluation of the ICESat–2 ATL08 Terrain Product. IEEE Trans. Geosci. Remote 2021, 99, 1–15. [Google Scholar] [CrossRef]
- Fu, H.; Zhu, J.; Wang, C.; Wang, H.; Zhao, R. Underlying topography estimation over forest areas using high–resolution p–band single–baseline polinsar data. Remote Sens. 2017, 9, 363. [Google Scholar] [CrossRef]
- Herzfeld, U.C.; McDonald, B.W.; Wallin, B.F.; Neumann, T.A.; Markus, T.; Brenner, A.; Fileld, C. Algorithm for detection of ground and canopy cover in micropulse photon–counting Lidar altimeter data in preparation for the ICESat–2 mission. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2109–2125. [Google Scholar] [CrossRef]
- Duan, Z.G.; Zhao, D.; Zeng, Y.; Zhao, Y.J.; Wu, B.F.; Zhu, J.J. Assessing and Correcting Topographic Effects on Forest Canopy Height Retrieval Using Airborne LiDAR Data. Sensors 2015, 15, 12133–12155. [Google Scholar] [CrossRef]
- Neuenschwander, A.N.; Magruder, L.M. The Potential Impact of Vertical Sampling Uncertainty on ICESat–2/ATLAS Terrain and Canopy Height Retrievals for Multiple Ecosystems. Remote Sens. 2016, 8, 1039. [Google Scholar] [CrossRef]
- Duncanson, L.; Neuenschwander, A.; Hancock, S.; Thomas, N.; Fatoyinbo, T.; Simard, M.; Silva, C.A.; Armston, J.; Scott, B. Biomass estimation from simulated GEDI, ICESat–2 and NISAR across environmental gradients in sonoma county, california. Remote Sens. Environ. 2020, 242, 111779. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, Q.; Jing, C. Multi–resolution segmentation parameters optimization and evaluation for VHR remote sensing image based on mean NSQI and discrepancy measure. J. Spat. Sci. 2019, 66, 1–26. [Google Scholar]
- Roth, K.L.; Roberts, D.A.; Dennison, P.E.; Peterson, S.H.; Alonzo, M. The impact of spatial resolution on the classification of plant species and functional types within imaging spectrometer data. Remote Sens. Environ. 2015, 171, 45–57. [Google Scholar] [CrossRef]
- Skurikhin, A.N.; Garrity, S.R.; McDowell, N.G.; Dongming, M. Automated tree crown detection and size estimation using multi–scale analysis of high–resolution satellite imagery. Remote Sens. Lett. 2013, 4, 465–474. [Google Scholar] [CrossRef]
- Dong, X.Y.; Li, J.G.; Chen, H.Y.; Zhao, L.; Zhang, L.M.; Xing, S.H. Extraction of individual tree information based on remote sensing images from an Unmanned Aerial Vehicle. J. Remote Sens. 2019, 23, 1269–1280. [Google Scholar]
- Parker, G.G.; Russ, M.E. The canopy surface and stand development: Assessing forest canopy structure and complexity with near–surface altimetry. For. Ecol. Manag. 2004, 189, 307–315. [Google Scholar] [CrossRef]
- Chirici, G.; McRoberts, R.E.; Fattorini, L.; Mura, M.; Marchetti, M. Comparing echo–based and canopy height model–based metrics for enhancing estimation of forest aboveground biomass in a model–assisted framework. Remote Sens. Environ. 2016, 174, 1–9. [Google Scholar] [CrossRef]
- Gatziolis, D.; Fried, J.S.; Monleon, V.S. Challenges to estimating tree height via LiDAR in closed–canopy forests: A parable from western Oregon. For. Sci. 2010, 56, 139–155. [Google Scholar]
- Sun, T.; Qi, J.; Huang, H. Discovering forest height changes based on spaceborne lidar data of ICESat–1 in 2005 and ICESat–2 in 2019: A case study in the Beijing–Tianjin–Hebei region of China. For. Ecosyst. 2020, 7, 53. [Google Scholar] [CrossRef]
- Sexton, J.O.; Song, X.P.; Feng, M.; Noojipady, P.; Anand, A.; Huang, C.; Kim, D.H.; Collins, K.M.; Channan, S.; DiMiceli, C. Global, 30–m resolution continuous fields of tree cover: Landsat–based rescaling of MODIS vegetation continuous fields with lidar–based estimates of error. Int. J. Digit. Earth 2013, 6, 427–448. [Google Scholar] [CrossRef]
- Bolton, D.K.; Coops, N.C.; Wulder, M.A. Investigating the agreement between global canopy height maps and airborne Lidar derived height estimates over Canada. Can. J. Remote Sens. 2014, 39, 139–151. [Google Scholar] [CrossRef]
- Zhu, X.X.; Wang, C.; Nie, S.; Pan, F.F.; Xi, X.H.; Hu, Z.Y. Mapping forest height using photon–counting LiDAR data and Landsat 8 OLI data: A case study in Virginia and North Carolina, USA–ScienceDirect. Ecol. Indic. 2020, 114, 106287. [Google Scholar] [CrossRef]
- Dong, X.Y.; Zhang, Z.C.; Yu, R.Y.; Tian, Q.J.; Zhu, X.C. Extraction of Information about Individual Trees from High–Spatial–Resolution UAV–Acquired Images of an Orchard. Remote Sens. 2020, 12, 133. [Google Scholar] [CrossRef]
- Martin, Q.; Joanne, C.W.; Nicholas, C.C. Comparing airborne and spaceborne photon–counting LiDAR canopy structural estimates across different boreal forest types. Remote Sens. Environ. 2021, 262, 112510. [Google Scholar]
- Montesano, P.M.; Rosette, J.; Sun, G.; North, P.; Nelson, R.F.; Dubayah, R.O.; Ranson, K.J.; Kharuk, V. The uncertainty of biomass estimates from modeled ICESat–2 returns across a boreal forest gradient. Remote Sens. Environ. 2015, 158, 95–109. [Google Scholar] [CrossRef]
- Martin, B.; Compton, J.T.; Ankit, K.; Kjeld, R.; Christin, A.; Jennifer, S.; Jerome, C.; Laura, V.R.; Pierre, H.; Abdoul, A.D.; et al. An unexpectedly large count of trees in the West African Sahara and Sahel. Nature 2020, 587, 78–82. [Google Scholar]
- Nie, S.; Wang, C.; Xi, X.H.; Luo, S.Z.; Zhu, X.X.; Li, G.Y.; Liu, H.; Tian, J.Y.; Zhang, S. Assessing the Impacts of Various Factors on Treetop Detection Using LiDAR–Derived Canopy Height Models. IEEE Trans. Geosci. Remote 2019, 57, 10099–10115. [Google Scholar] [CrossRef]




| LiDAR: Riegl LMS–Q680i | |||
|---|---|---|---|
| Wavelength | 1550 nm | Laser beam divergence | 0.5 mrad |
| Laser pulse length | 3 ns | Cross-track FOV | ±30° |
| Maximum laser pulse repetition rate | 400 khz | Waveform sampling interval | 1 ns |
| Vertical resolution | 0.15 m | Point density @1000 m altitude | 3.6 pts/m2 |
| CCD: DigiCAM–60 | |||
| Frame size | 8956 × 6708 | Pixel size | 6 µm |
| Imaging sensor size | 40.30 mm × 53.78 mm | Focal length | 50 mm |
| FOV | 56.2° | Spatial resolution | 0.2 m |
| Offset Distance/(m) | Slope | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5° | 10° | 15° | 20° | 25° | 30° | 35° | 40° | 45° | 50° | |
| 1 | 0.09 | 0.18 | 0.27 | 0.36 | 0.47 | 0.58 | 0.70 | 0.84 | 1.00 | 1.19 |
| 2 | 0.17 | 0.35 | 0.54 | 0.73 | 0.93 | 1.15 | 1.40 | 1.68 | 2.00 | 2.38 |
| 3 | 0.26 | 0.53 | 0.80 | 1.09 | 1.40 | 1.73 | 2.10 | 2.52 | 3.00 | 3.58 |
| CHMATL08 | CHMATL03 initial | CHMCTPC | CHMCCR–1 | CHMCCR–2 | |
|---|---|---|---|---|---|
| R2 | 0.19 | 0.34 | 0.47 | 0.61 | 0.65 |
| Bias/(m) | 22.91 | 1.17 | 1.39 | 1.55 | −0.75 |
| MAE/(m) | 22.96 | 6.02 | 3.87 | 3.26 | 2.98 |
| RMSE/(m) | 27.68 | 7.31 | 4.68 | 4.08 | 3.78 |
| Datasets | Accuracy Indices | Segment Size/(m) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | ||
| CHMATL03 initial | R2 | 0.35 | 0.36 | 0.38 | 0.39 | 0.40 | 0.40 | 0.40 | 0.40 | 0.42 | 0.41 |
| Bias/(m) | 1.16 | 1.20 | 1.19 | 1.27 | 1.25 | 1.17 | 1.26 | 1.19 | 1.19 | 1.16 | |
| MAE/(m) | 5.94 | 5.79 | 5.61 | 5.43 | 5.33 | 5.13 | 5.03 | 5.07 | 4.88 | 4.76 | |
| RMSE/(m) | 7.17 | 6.96 | 6.70 | 6.57 | 6.35 | 6.08 | 6.03 | 5.89 | 5.85 | 5.79 | |
| CHMCTPC | R2 | 0.58 | 0.62 | 0.64 | 0.64 | 0.65 | 0.66 | 0.67 | 0.68 | 0.69 | 0.68 |
| Bias/(m) | 1.39 | 1.39 | 1.39 | 1.39 | 1.40 | 1.39 | 1.40 | 1.40 | 1.40 | 1.40 | |
| MAE/(m) | 3.29 | 3.10 | 3.00 | 2.91 | 2.90 | 2.78 | 2.75 | 2.67 | 2.60 | 2.63 | |
| RMSE/(m) | 4.03 | 3.79 | 3.64 | 3.58 | 3.50 | 3.40 | 3.36 | 3.26 | 3.19 | 3.18 | |
| CHMCCR–2 | R2 | 0.66 | 0.69 | 0.70 | 0.71 | 0.72 | 0.73 | 0.73 | 0.73 | 0.74 | 0.74 |
| Bias/(m) | −0.74 | −0.74 | −0.74 | −0.74 | −0.72 | −0.74 | −0.73 | −0.72 | −0.72 | −0.72 | |
| MAE/(m) | 2.78 | 2.66 | 2.56 | 2.43 | 2.43 | 2.31 | 2.31 | 2.20 | 2.12 | 2.10 | |
| RMSE/(m) | 3.53 | 3.33 | 3.21 | 3.10 | 3.03 | 2.94 | 2.91 | 2.82 | 2.77 | 2.72 | |
| Datasets | Accuracy Indices | RH70 | RH75 | RH80 | RH85 | RH90 | RH95 | RH98 | RH100 |
|---|---|---|---|---|---|---|---|---|---|
| CHMATL08 | Bias/(m) | 13.10 | 14.73 | 16.37 | 18.00 | 19.64 | 21.27 | 22.26 | 22.91 |
| MAE/(m) | 13.60 | 15.12 | 16.64 | 18.19 | 19.76 | 21.36 | 22.31 | 22.96 | |
| RMSE/(m) | 16.90 | 18.68 | 20.47 | 22.26 | 24.06 | 25.87 | 26.95 | 27.68 | |
| CHMATL03 initial | Bias/(m) | −2.43 | −1.83 | −1.23 | −0.63 | −0.03 | 0.57 | 0.93. | 1.17 |
| MAE/(m) | 4.94 | 4.92 | 4.97 | 5.10 | 5.32 | 5.61 | 5.81 | 6.02 | |
| RMSE/(m) | 6.08 | 6.07 | 6.14 | 6.30 | 6.53 | 6.82 | 7.03 | 7.31 | |
| CHMCTPC | Bias/(m) | −1.79 | −1.26 | −0.73 | −0.20 | 0.33 | 0.86 | 1.18 | 1.39 |
| MAE/(m) | 3.40 | 3.31 | 3.29 | 3.34 | 3.46 | 3.64 | 3.77 | 3.87 | |
| RMSE/(m) | 4.41 | 4.25 | 4.19 | 4.21 | 4.31 | 4.50 | 4.64 | 4.68 | |
| CHMCCR–2 | Bias/(m) | −3.75 | −3.25 | −2.75 | −2.25 | −1.75 | −1.25 | −0.95 | −0.75 |
| MAE/(m) | 4.21 | 3.83 | 3.50 | 3.22 | 3.03 | 2.95 | 2.95 | 2.98 | |
| RMSE/(m) | 5.00 | 4.63 | 4.31 | 4.06 | 3.88 | 3.79 | 3.77 | 3.78 |
| Datasets | Accuracy Indices | Slope Classes | |||||
|---|---|---|---|---|---|---|---|
| Ⅰ (0° ≤ Slope < 5°) | Ⅱ (5° ≤ Slope < 15°) | Ⅲ (15° ≤ Slope < 25°) | Ⅳ (25° ≤ Slope < 35°) | Ⅴ (35° ≤ Slope < 45°) | Ⅵ (Slope ≥ 45°) | ||
| CHM ATL03 initial | R2 | 0.43 | 0.36 | 0.28 | 0.24 | 0.19 | 0.15 |
| Bias/(m) | 6.98 | 6.12 | 6.00 | 4.54 | 4.00 | 3.09 | |
| MAE(m) | 9.22 | 8.41 | 9.28 | 8.93 | 9.94 | 8.67 | |
| RMSE(m) | 10.39 | 11.50 | 12.90 | 13.10 | 12.62 | 11.95 | |
| CHMCTPC | R2 | 0.67 | 0.55 | 0.52 | 0.50 | 0.44 | 0.39 |
| Bias/(m) | 2.05 | 1.79 | 1.84 | 1.27 | 1.06 | 1.18 | |
| MAE(m) | 2.97 | 3.53 | 3.79 | 3.79 | 3.97 | 4.24 | |
| RMSE(m) | 3.67 | 4.29 | 4.56 | 4.70 | 4.90 | 5.17 | |
| CHMCCR–2 | R2 | 0.81 | 0.69 | 0.64 | 0.64 | 0.60 | 0.55 |
| Bias/(m) | 0.74 | −0.45 | −0.47 | −0.79 | −0.95 | −1.04 | |
| MAE(m) | 2.76 | 2.77 | 2.82 | 2.99 | 3.00 | 3.48 | |
| RMSE(m) | 3.37 | 3.43 | 3.57 | 3.76 | 3.81 | 4.41 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Zhao, T.; Su, X.; Fan, G.; Zhang, W.; Deng, Z.; Yu, Y. Correction of Terrain Effects on Forest Canopy Height Estimation Using ICESat-2 and High Spatial Resolution Images. Remote Sens. 2022, 14, 4453. https://doi.org/10.3390/rs14184453
Li B, Zhao T, Su X, Fan G, Zhang W, Deng Z, Yu Y. Correction of Terrain Effects on Forest Canopy Height Estimation Using ICESat-2 and High Spatial Resolution Images. Remote Sensing. 2022; 14(18):4453. https://doi.org/10.3390/rs14184453
Chicago/Turabian StyleLi, Bin, Tianzhong Zhao, Xiaohui Su, Guangpeng Fan, Wenjie Zhang, Zhuo Deng, and Yonghui Yu. 2022. "Correction of Terrain Effects on Forest Canopy Height Estimation Using ICESat-2 and High Spatial Resolution Images" Remote Sensing 14, no. 18: 4453. https://doi.org/10.3390/rs14184453
APA StyleLi, B., Zhao, T., Su, X., Fan, G., Zhang, W., Deng, Z., & Yu, Y. (2022). Correction of Terrain Effects on Forest Canopy Height Estimation Using ICESat-2 and High Spatial Resolution Images. Remote Sensing, 14(18), 4453. https://doi.org/10.3390/rs14184453







