A Two-Step Block Adjustment Method for DSM Accuracy Improvement with Elevation Control of ICESat-2 Data
Abstract
:1. Introduction
2. Methodology
2.1. DSM Tie-Point Extraction
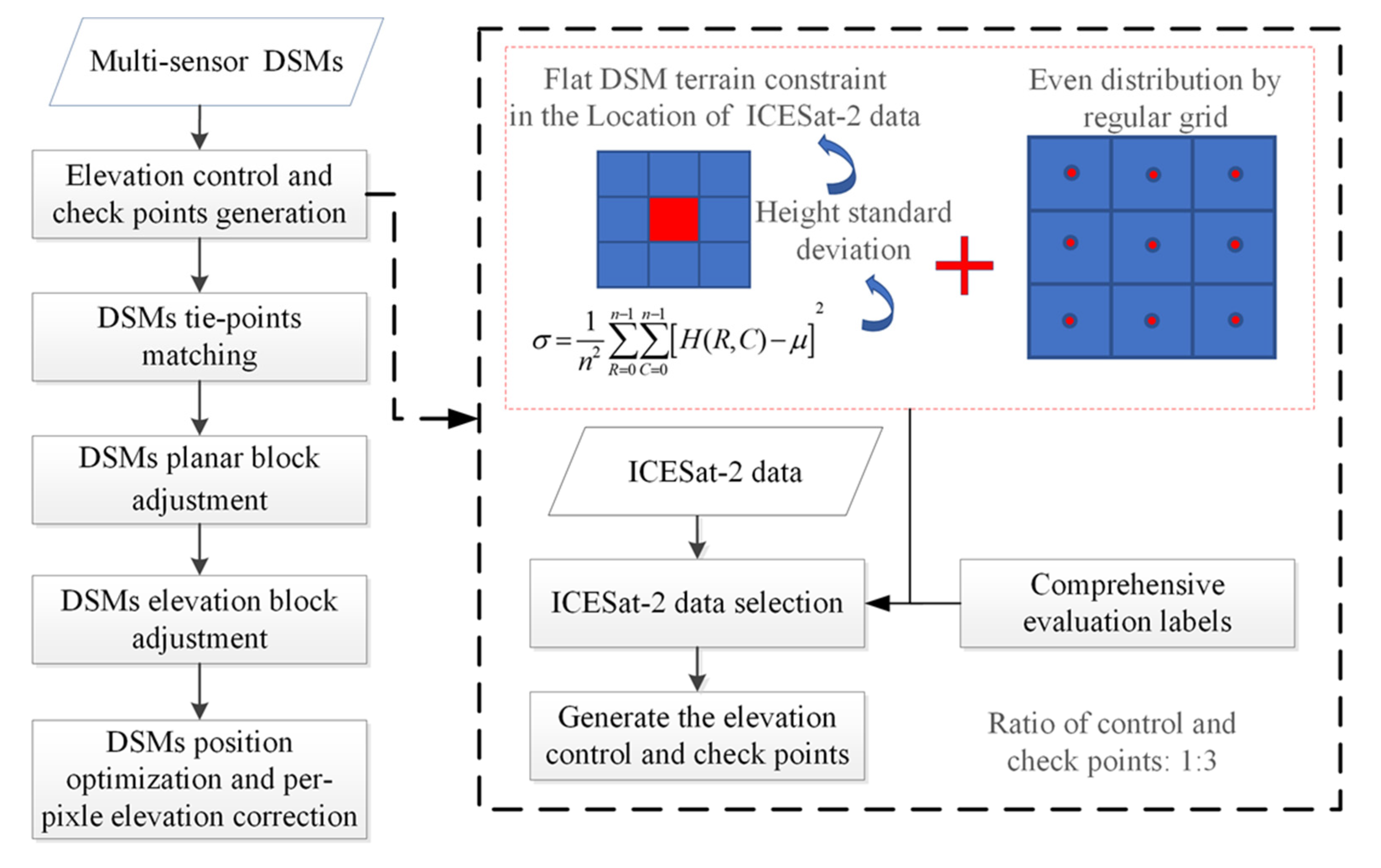
2.2. Elevation Control/Check Points Selection from ICESat-2 Laser Altimetry Data
2.3. Two-Step DSM Block Adjustment
2.4. Accuracy Assessment
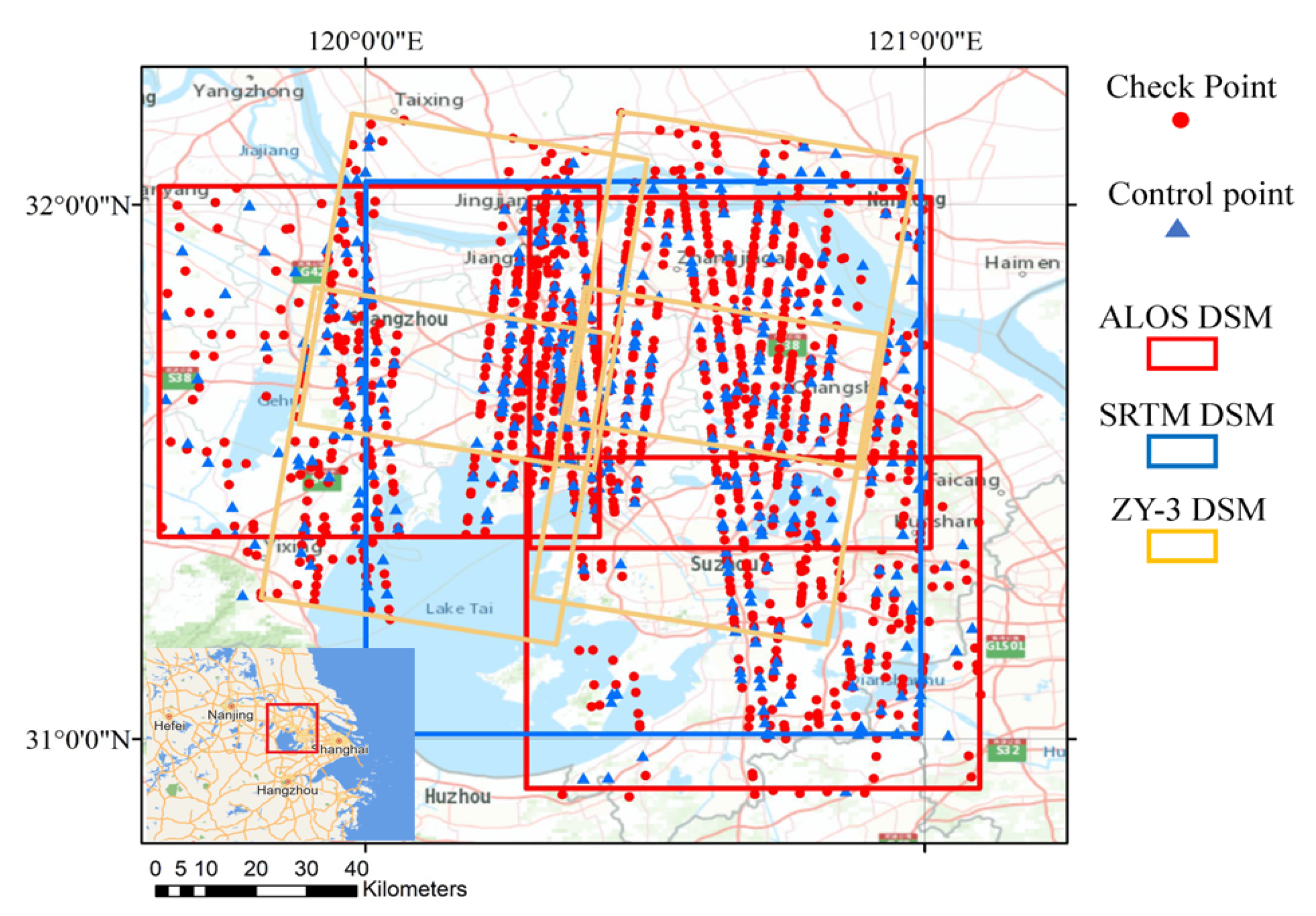
3. Study Area and Experimental Data
4. Experimental Results
4.1. Elevation Control and Check Point Selection and Elevation Correction Model Detection
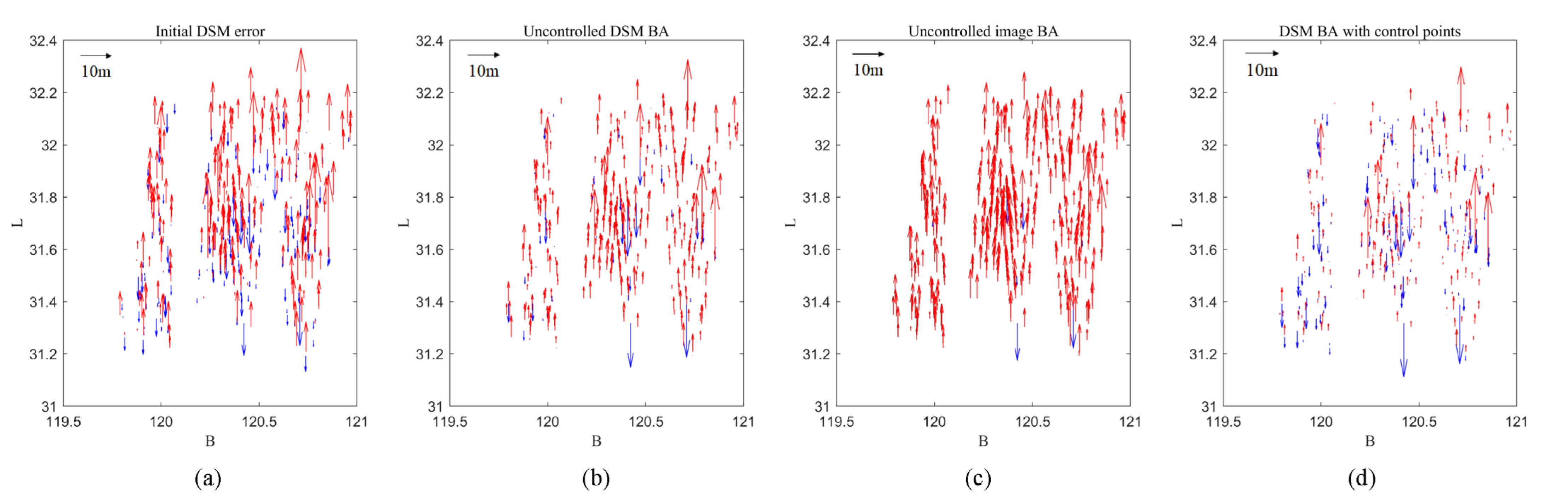
4.2. Comparison of GCP-Free Block Adjustment Conducted on Image and Object Space
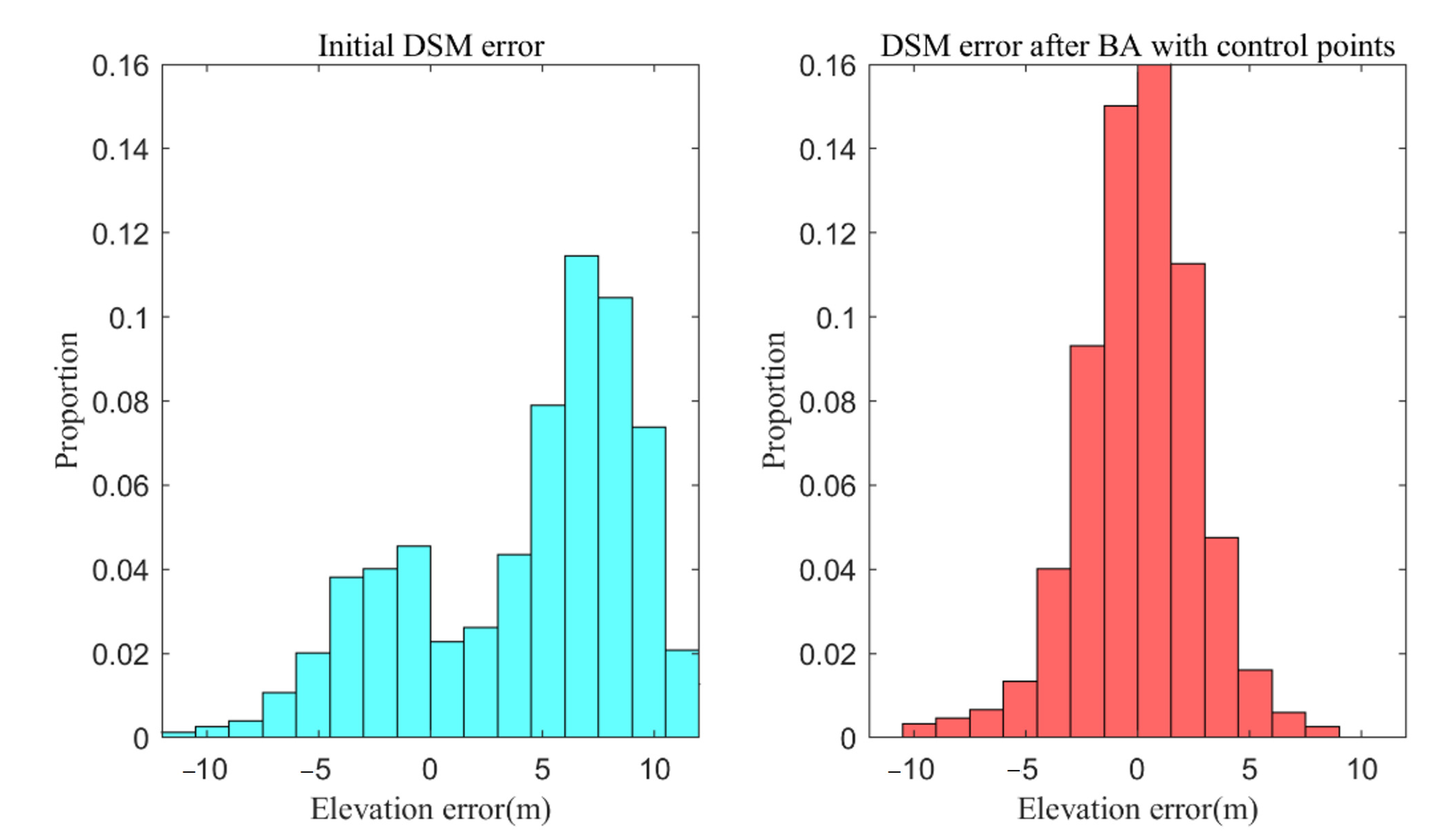
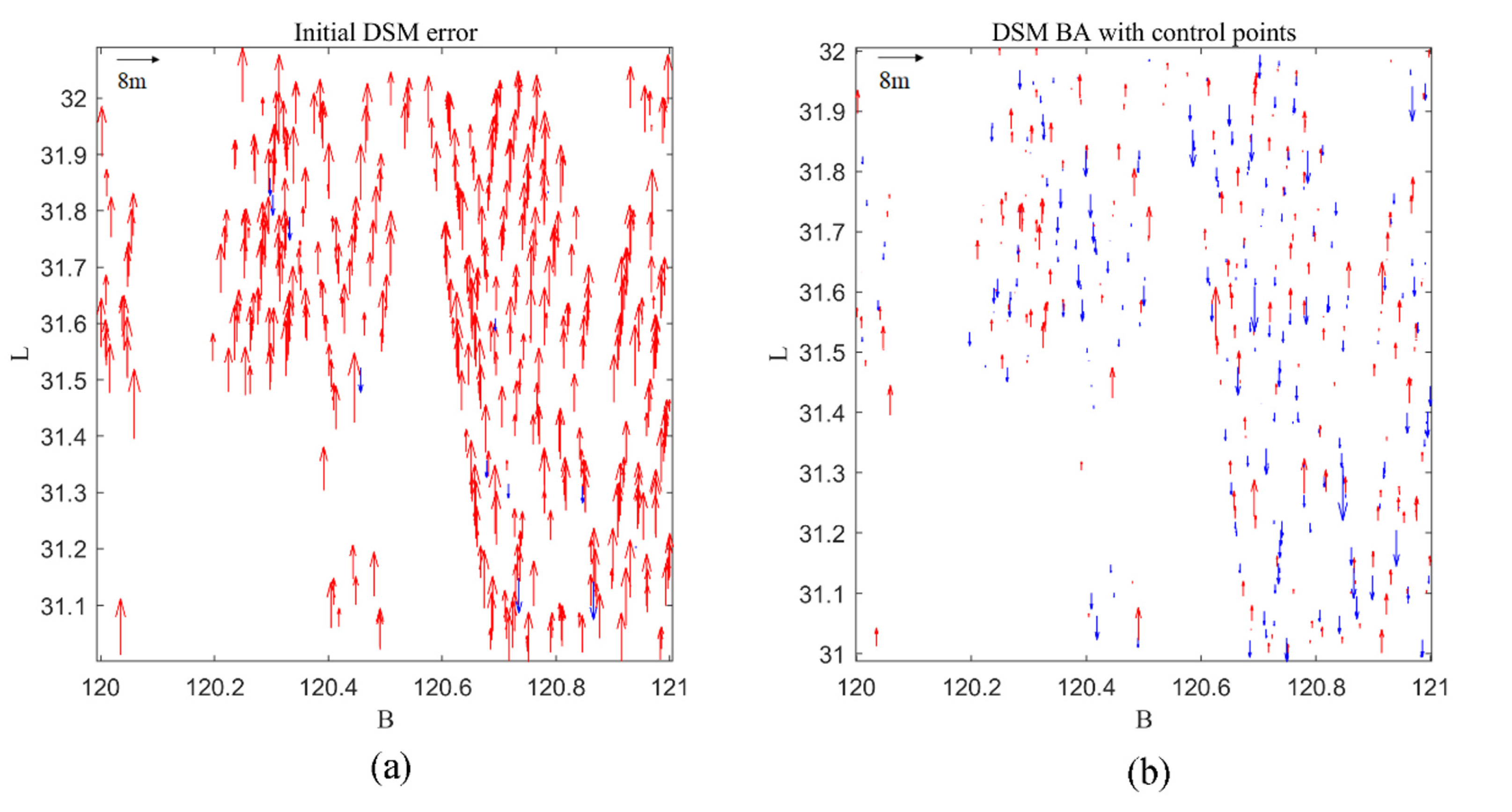
4.3. Block Adjustment Results Conducted on DSMs with Elevation Control
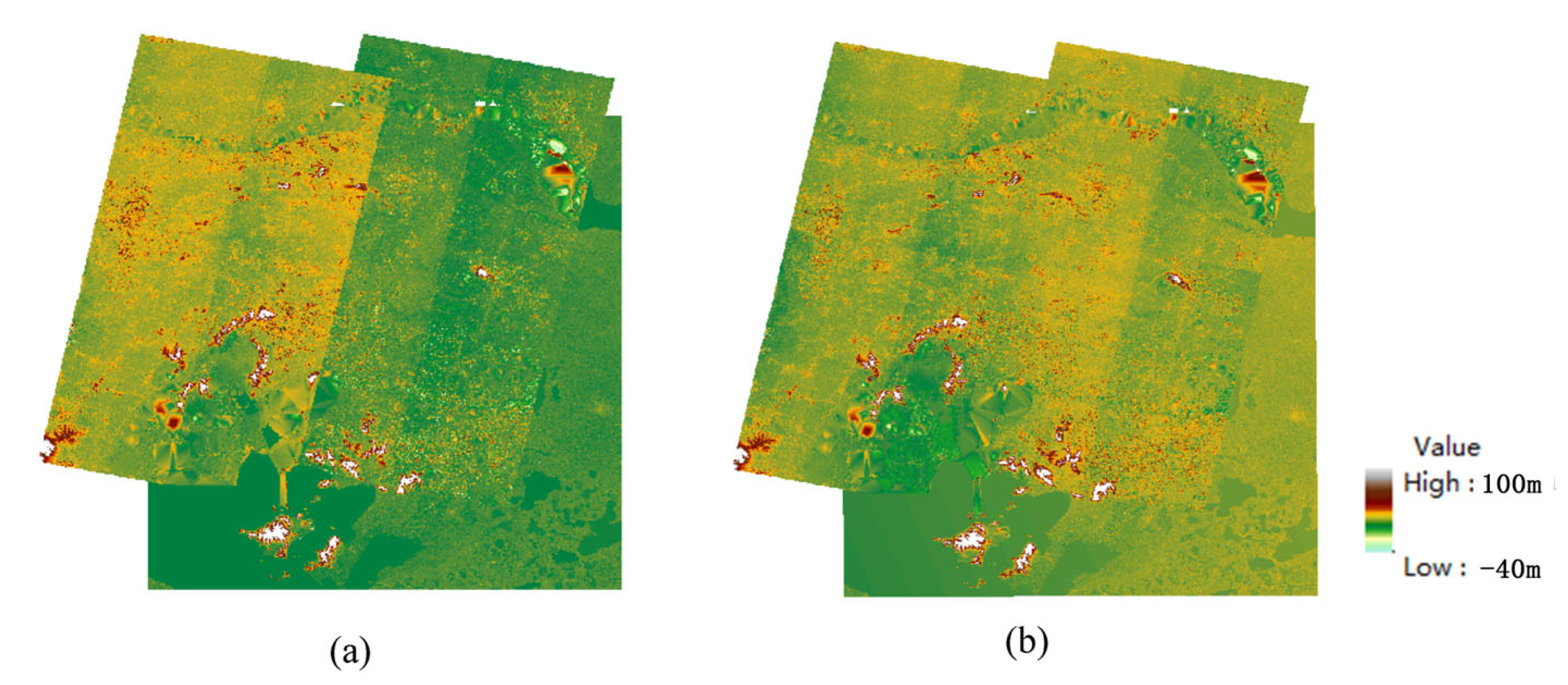
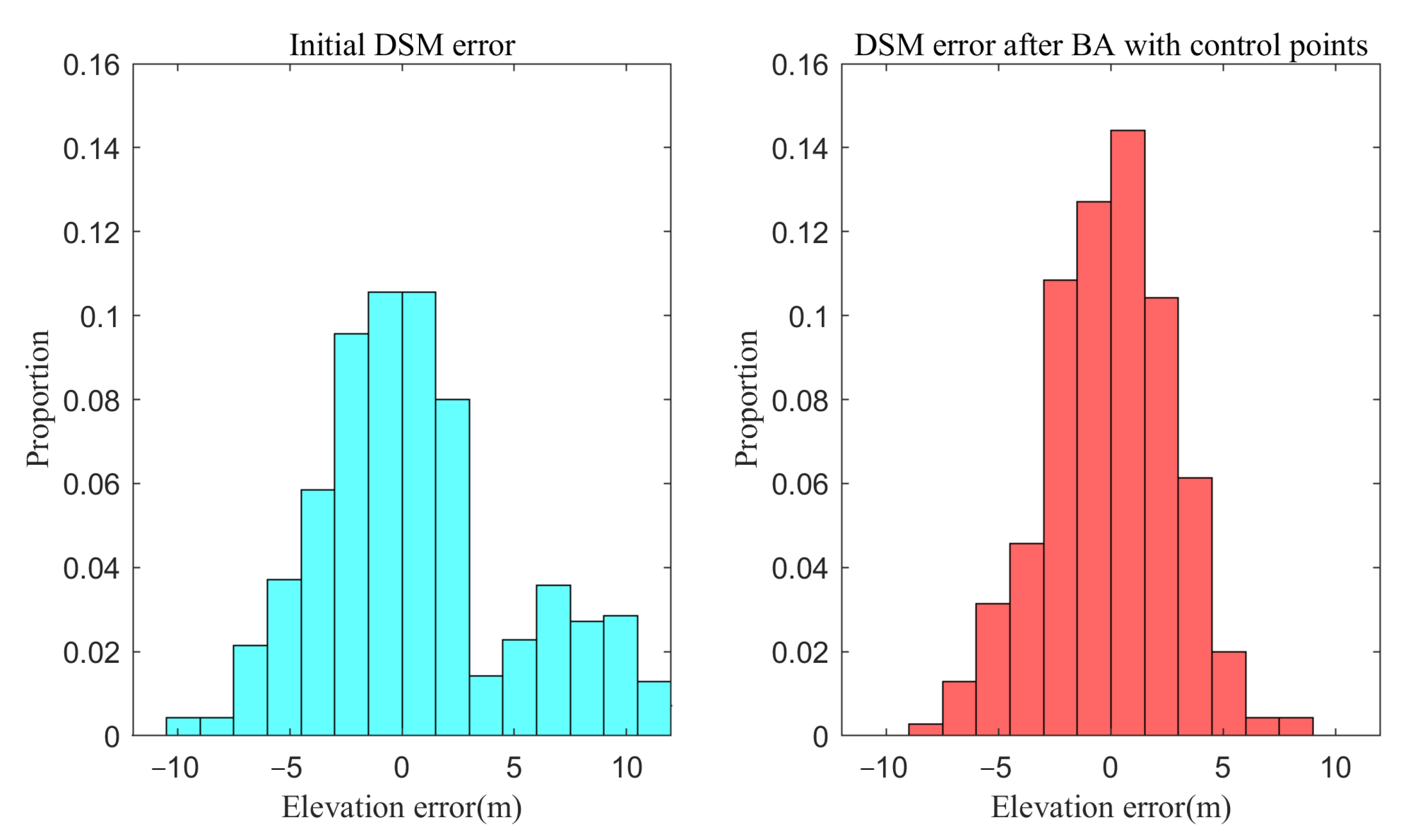
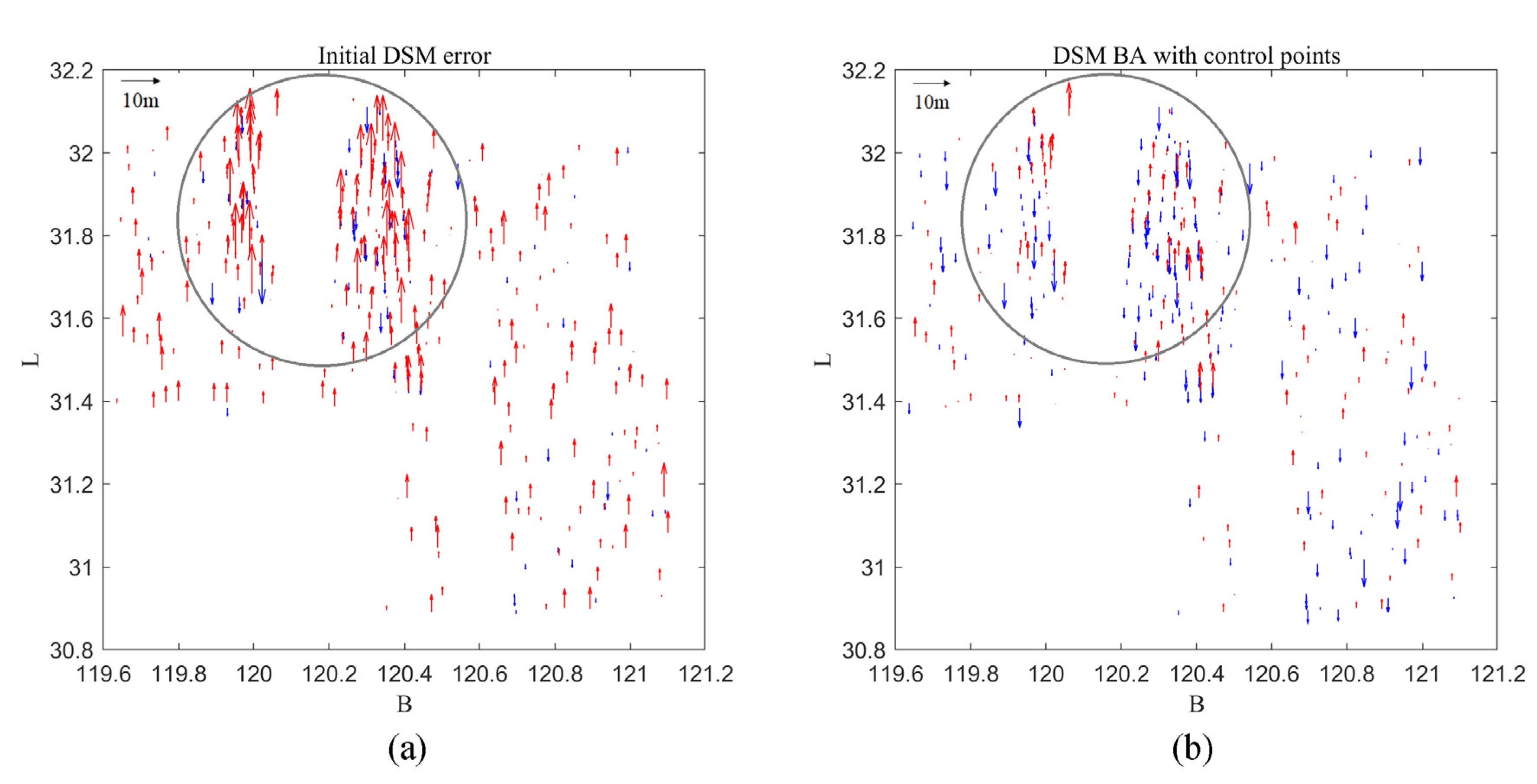
4.4. Block Adjustment Results are Conducted on Multisource DSM with Elevation Control
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Okolie, C.J.; Smit, J.L. A systematic review and meta-analysis of Digital elevation model (DEM) fusion: Pre-processing, methods and applications. ISPRS J. Photogramm. Remote Sens. 2022, 188, 1–29. [Google Scholar] [CrossRef]
- Luethje, F.; Tiede, D.; Eisank, C. Terrain Extraction in Built-Up Areas from Satellite Stereo-Imagery-Derived Surface Models: A Stratified Object-Based Approach. ISPRS Int. J. Geo Inf. 2017, 6, 9. [Google Scholar] [CrossRef]
- Fisher, P.F.; Tate, N.J. Causes and consequences of error in digital elevation models. Prog. Phys. Geogr. Earth Environ. 2016, 30, 467–489. [Google Scholar] [CrossRef]
- Jinaya Gong, Z.L.; Qing, Z.; Haigang, S.; Yi, Z. Effects of Various Factors on the Accuracy of DEMs: An Intensive Experimental Investigation. Photogramm. Eng. Remote Sens. 2000, 66, 1113–1117. [Google Scholar]
- Grodecki, J.; Dial, G. Block Adjustment of High-Resolution Satellite Images Described by Rational Polynomials. Photogramm. Eng. Remote Sens. 2003, 69, 59–68. [Google Scholar] [CrossRef]
- Fraser, C.S.; Hanley, H.B. Bias Compensation in Rational Functions for Ikonos Satellite Imagery. Photogramm. Eng. Remote Sens. 2003, 69, 53–57. [Google Scholar] [CrossRef]
- Tong, X.; Liu, S.; Weng, Q. Bias-corrected rational polynomial coefficients for high accuracy geo-positioning of QuickBird stereo imagery. ISPRS J. Photogramm. Remote Sens. 2010, 65, 218–226. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, G.; Zhu, X.; Pan, H.; Jiang, Y.; Zhou, P.; Wang, X. Triple linear-array image geometry model of ZiYuan-3 surveying satellite and its validation. Int. J. Image Data Fusion 2013, 4, 33–51. [Google Scholar] [CrossRef]
- Li, G.; Tang, X.; Gao, X.; Wang, H.; Wang, Y. ZY-3 Block adjustment supported by glas laser altimetry data. Photogramm. Rec. 2016, 31, 88–107. [Google Scholar] [CrossRef]
- Zhang, Y.; Wan, Y.; Huang, X.; Ling, X. DEM-Assisted RFM Block Adjustment of Pushbroom Nadir Viewing HRS Imagery. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1025–1034. [Google Scholar] [CrossRef]
- Zhou, P.; Tang, X.; Wang, Z.; Cao, N.; Wang, X. SRTM-assisted block adjustment for stereo pushbroom imagery. Photogramm. Rec. 2018, 33, 49–65. [Google Scholar] [CrossRef]
- Arefi, H.; Reinartz, P. Accuracy Enhancement of ASTER Global Digital Elevation Models Using ICESat Data. Remote Sens. 2011, 3, 1323–1343. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, L.; Wang, Y.; Liao, M. Fusion of high-resolution DEMs derived from COSMO-SkyMed and TerraSAR-X InSAR datasets. J. Geod. 2014, 88, 587–599. [Google Scholar] [CrossRef]
- Yue, L.; Shen, H.; Zhang, L.; Zheng, X.; Zhang, F.; Yuan, Q. High-quality seamless DEM generation blending SRTM-1, ASTER GDEM v2 and ICESat/GLAS observations. ISPRS J. Photogramm. Remote Sens. 2017, 123, 20–34. [Google Scholar] [CrossRef]
- Hong, Z.; Sun, P.; Zhou, R.; Tong, X.; Feng, Y.; Liu, S. Fast mosaicking method of InSAR-generated multi stripe digital elevation model. J. Infrared Millineter. 2022, 41, 493–500. [Google Scholar]
- Gruber, A.; Wessel, B.; Huber, M.; Roth, A. Operational TanDEM-X DEM calibration and first validation results. ISPRS J. Photogramm. Remote Sens. 2012, 73, 39–49. [Google Scholar] [CrossRef]
- Birgit Wessela, A.G.; Gonzálezb, J.H.; Bachmannb, M.; Wendleder, A. Tandem-x block adjustment of interferometric height models. In Proceedings of the IGARSS’08, Wessling, Germany, 2008; pp. 111–114. [Google Scholar]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The Ice, Cloud, and land Elevation Satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Neuenschwander, A.L.; Magruder, L.A. Canopy and Terrain Height Retrievals with ICESat-2: A First Look. Remote Sens. 2019, 11, 1721. [Google Scholar] [CrossRef]
- Li, B.; Xie, H.; Liu, S.; Tong, X.; Tang, H.; Wang, X. A Method of Extracting High-Accuracy Elevation Control Points from ICESat-2 Altimetry Data. Photogramm. Eng. Remote Sens. 2021, 87, 821–830. [Google Scholar] [CrossRef]
- Carabajal, C.C.; Boy, J.P. Icesat-2 Altimetry as Geodetic Control. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLIII-B3-2020, 1299–1306. [Google Scholar] [CrossRef]
- Moudrý, V.; Gdulová, K.; Gábor, L.; Šárovcová, E.; Barták, V.; Leroy, F.; Špatenková, O.; Rocchini, D.; Prošek, J. Effects of environmental conditions on ICESat-2 terrain and canopy heights retrievals in Central European mountains. Remote Sens. Environ. 2022, 279, 113112. [Google Scholar] [CrossRef]
- Cao, N.; Zhou, P.; Wang, X.; Tang, X.; Li, G. Refined processing of laser altimeter data-aided satellite geometry model. J. Remote Sens. 2018, 22, 599–610. [Google Scholar] [CrossRef]
- Zhang, G.; Jiang, B.; Wang, T.; Ye, Y.; Li, X. Combined Block Adjustment for Optical Satellite Stereo Imagery Assisted by Spaceborne SAR and Laser Altimetry Data. Remote Sens. 2021, 13, 3062. [Google Scholar] [CrossRef]
- Mouratidis, A.; Ampatzidis, D. European Digital Elevation Model Validation against Extensive Global Navigation Satellite Systems Data and Comparison with SRTM DEM and ASTER GDEM in Central Macedonia (Greece). ISPRS Int. J. Geo Inf. 2019, 8, 108. [Google Scholar] [CrossRef]
- Shimada, M.; Tadono, T.; Matsuoka, M. Calibration and validation plans for ALOS/PRISM. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; pp. 384–386. [Google Scholar]
- Tian, X.; Shan, J. Comprehensive Evaluation of the ICESat-2 ATL08 Terrain Product. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8195–8209. [Google Scholar] [CrossRef]



| Attribute Label | Description | Threshold Value |
|---|---|---|
| h_te_std | The standard deviation of the photon heights above the WGS84 Ellipsoid, classified as terrain within the segment. | h_te_std < 2 m |
| terrain_slope | The along-track slope of terrain, within each segment; computed by a linear fit of terrain classified photons. | terrain_slope × 100 < 2 |
| h_dif_ref | Difference between h_te_median and ref_DEM | h_dif_ref ≤ 30 m |
| cloud_flag_atm | Cloud confidence flag from ATL09 that indicates the number of cloud or aerosol layers identified in each 25 Hz atmospheric profile. If the flag is greater than 0, aerosols or clouds could be present. Valid range is 0–10. | cloud_flag_atm ≤ 1 |
| h_te_skew | The skewness of the photon heights | h_te_skew ≤ 1 |
| n_te_photons | The number of the photons classified as terrain within the segment. | (n_te_photons/n_seg_ph) × 100% > 70% |
| n_seg_ph | Number of photons within each land segment. |
| Mean Elevation Error | Elevation RMSE | Relative Elevation Error | Relative Planar Error | ||
|---|---|---|---|---|---|
| Before BA | 3.18 | 7.62 | 8.89 | 13.45 | |
| Uncontrolled image BA | 7.64 | 7.00 | 1.96 | 3.26 | |
| Uncontrolled DSM BA | 3.71 | 5.85 | 1.02 | 3.11 | |
| Elevation-controlled DSM BA | First-order | 1.02 | 3.54 | 1.24 | 3.11 |
| Second-order | 0.55 | 2.60 | 1.09 | 3.11 | |
| Input DSMs for BA | Mean Elevation Error | Elevation RMSE | Relative Elevation Error | Relative Planar Error | |
|---|---|---|---|---|---|
| ZY-3 and SRTM | Before BA | 4.43 | 6.80 | 9.27 | 37.64 |
| After BA | 0.87 | 2.61 | 1.48 | 5.65 | |
| ZY-3 and ALOS | Before BA | 2.06 | 4.81 | 10.58 | 28.56 |
| After BA | 0.76 | 2.81 | 1.25 | 4.26 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Xie, B.; Liu, S.; Tong, X.; Ding, R.; Xie, H.; Hong, Z. A Two-Step Block Adjustment Method for DSM Accuracy Improvement with Elevation Control of ICESat-2 Data. Remote Sens. 2022, 14, 4455. https://doi.org/10.3390/rs14184455
Zhang X, Xie B, Liu S, Tong X, Ding R, Xie H, Hong Z. A Two-Step Block Adjustment Method for DSM Accuracy Improvement with Elevation Control of ICESat-2 Data. Remote Sensing. 2022; 14(18):4455. https://doi.org/10.3390/rs14184455
Chicago/Turabian StyleZhang, Xin, Baorong Xie, Shijie Liu, Xiaohua Tong, Rongli Ding, Huan Xie, and Zhonghua Hong. 2022. "A Two-Step Block Adjustment Method for DSM Accuracy Improvement with Elevation Control of ICESat-2 Data" Remote Sensing 14, no. 18: 4455. https://doi.org/10.3390/rs14184455
APA StyleZhang, X., Xie, B., Liu, S., Tong, X., Ding, R., Xie, H., & Hong, Z. (2022). A Two-Step Block Adjustment Method for DSM Accuracy Improvement with Elevation Control of ICESat-2 Data. Remote Sensing, 14(18), 4455. https://doi.org/10.3390/rs14184455








