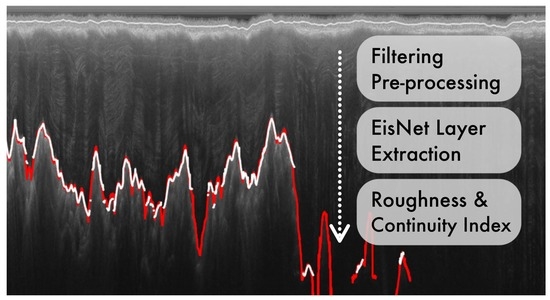
Quantifying Basal Roughness and Internal Layer Continuity Index of Ice Sheets by an Integrated Means with Radar Data and Deep Learning

Abstract

Understanding englacial and subglacial structures is a fundamental method of inferring ice sheets’ historical evolution and surface mass balance. The internal layer continuity index and the basal roughness are key parameters and indicators for the speculation of the relationship between the ice sheet’s internal structure or bottom and ice flow. Several methods have been proposed in the past two decades to quantitatively calculate the continuity index of ice layer geometry and the roughness of the ice–bedrock interface based on radar echo signals. These methods are mainly based on the average of the absolute value of the vertical gradient of the echo signal amplitude and the standard deviation of the horizontal fluctuation of the bedrock interface. However, these methods are limited by the amount and quality of unprocessed radar datasets and have not been widely used, which also hinders further research, such as the analysis of the englacial reflectivity, the subglacial conditions, and the history of the ice sheets. In this paper, based on geophysical processing methods for radar image denoising and deep learning for ice layer and bedrock interface extraction, we propose a new method for calculating the layer continuity index and basal roughness. Using this method, we demonstrate the ice-penetrating radar data processing and compare the imaging and calculation of the radar profiles from Dome A to Zhongshan Station, East Antarctica. We removed the noise from the processed radar data, extracted ice layer continuity features, and used other techniques to verify the calculation. The potential application of this method in the future is illustrated by several examples. We believe that this method can become an effective approach for future Antarctic geophysical and glaciological research and for obtaining more information about the history and dynamics of ice sheets from their radar-extracted internal structure.

1. Introduction

The contribution of the continental ice sheet is the largest uncertainty source in estimating future sea-level rise. Because the potential instabilities of ice sheet dynamics cause profound indeterminacy, high greenhouse gas emissions can cause massive ice loss of the Antarctic ice sheet (AIS) [1,2]. The evaluation of ice sheet modeling and the prediction of the future sea-level rise are the frontiers of ice sheet dynamics research [3,4,5,6,7]. The main uncertainty of ice sheet evolution is the incomplete knowledge of basal conditions and englacial processes of the AIS [8,9]. Currently, ice sheet simulations are still limited by the incomplete knowledge of boundary conditions, such as the subglacial topography, geothermal flux, englacial layer structure, and parameterization of the ice flow and ice shelf calving process [10,11]. Ice-penetrating radar (IPR) imaging of the internal and bottom layers of ice sheets is an effective method to derive the digital elevation model of the subglacial topography and obtain the internal isochronous layers of the past ice surface [12]; therefore, IPR can provide an extra constraint for modeling predictions [13,14].

Since the 1960s, IPR has been widely applied in the observation of englacial layers and subglacial topography in ice sheets. Vast data from radar surveys have been collected, such as the SPRI/NSF/TUD radar-sounding data from the Scott Polar Research Institute (SPRI) at the University of Cambridge, the National Science Foundation (NSF), and the Technical University of Denmark (TUD) [15]; airborne radar data from Princess Elizabeth Land, East Antarctica, Polar Research Institute of China (PRIC) [16]; NASA’s Operation IceBridge [17]; the British Antarctic Survey’s Aerogeophysical Data [18]. Several studies indicate the potential application of IPR data to quantify the ice sheet subglacial topography and internal layer reflectors.

Basal roughness can be obtained from the radar-derived subglacial topography of ice sheets [19,20], or by utilizing the electromagnetic scattering properties of bed echo waveforms [21,22]. In [19,23,24], a Fourier transform method was used to calculate the roughness parameter ξ, which reflects the vertical irregularity of the subglacial topography, and the parameter η, which reflects the horizontal variation in the subglacial topography. Shepard and others (2001) used the root-mean-square (RMS) of the bed elevation to estimate the basal roughness [25]. This approach allows shorter length scales than the fast Fourier transform (FFT), which not only facilitates subsequent anisotropic analysis of cross-sections but also provides finer-scale roughness information. In general, the spatial distribution of roughness quantified by FFT and RMS height methods is essentially similar [26]. In [21], the Hurst exponent was calculated by using the self-affine fractal properties of the subglacial topography at different scales to analyze the radar scattering extent and thus evaluate the relationship between subglacial roughness and the basal thermal state of the AIS. Lang and others (2021) proposed a multi-scale self-adaptive two-parameter algorithm for quantifying the basal roughness, similar to the wavelet transform [27]. Bingham and Siegert (2009) provided a conceptual framework for studying the causes and controls of smooth or rough beds in the case of hard and soft beds [28].

Basal roughness is widely used in glaciology. Studies have shown that topographic roughness can be used as an indicator of subglacial conditions during present and past ice flow activities, and as a control over current ice sheet dynamics [26,29,30,31]. Quantitative basal roughness can be applied to assess the ice velocity of the Antarctic and Greenland ice sheets [26,32,33,34]. In [35], it was found that the basal roughness of ice sheets is associated with contemporary or past ice velocities and geological conditions. A fast flow may be associated with rougher beds, where areas with a slow flow are smoother. Most studies to date have quantified large-scale topographic roughness information (approximately 1000 m in scale); however, the direct relation to basal friction remains unclear [26]. Recently, Franke and others (2021) suggested a spectral approach combining RMS measurements of bed elevation to quantify basal roughness for characterizing landscapes and geomorphological histories preserved in the Jutulstraumen Basin of the AIS [30].

The internal layer continuity index (ILCI) is a parameter for the quantitative assessment of radar-derived englacial reflectors [20,36]. Generally, radar data can be presented in two forms, namely, A-scope, which records a single pulse signal, and Z-scope, which consists of multiple adjacent traces [37]. Several methods have been developed to manually or automatically draw hierarchical englacial continuity, such as manually picking internal layers [32], iterative peak tracking and pattern matching using ice models [38], automatic radio echo sounding processing (ARESP) algorithms [39], and englacial-dip estimation algorithms of continuous wavelet transform peak detection [40,41]. However, most of these methods are based on peak-tracking analysis, which can transfer the unclear ice layer to the adjacent ice layer when connecting the poor-quality areas of the radar images and cannot realize automatic quantitative analysis. ILCI can be used to assess the degree of continuity of reflectors by calculating the mean of the absolute values of the vertical power gradient of A-scope profiles [36]. Studies have shown that ILCI is very sensitive to the number and intensity of internal reflectors. In general, low values indicate discontinuity, and high values correspond to high continuity, which shows that ILCI has a good correlation with the historical change of ice flows [20,36,42]. In addition, the ILCI method can eliminate the potential subjectivity of layer continuity evaluation and greatly improve efficiency in processing large amounts of radar data. The ILCI method is currently widely used in the assessment of internal layer continuity for airborne and ground-based radar data in Antarctica [20,42,43,44,45]; therefore, ILCI is more efficient and reliable where internal layers can be tracked and has the potential to be applied on a larger scale of ice sheets.

However, the roughness calculation methods above rarely require multiple preprocessing, and most of the englacial layers are manually extracted with high time consumption and low efficiency. Recently, EisNet and later work [46,47] suggested a radar data processing method fused with conventional geophysical processing and a deep learning network, which can effectively reduce noise and implement rapid automatic extraction of the bedrock interface and internal ice layers. In this communication, we first discuss the application of the geophysical–deep learning fusion method to an airborne radar image to denoise and extract the bedrock interface and ice layers. Second, we calculate the subglacial basal roughness and ILCI based on the airborne radar data along the traverse from Zhongshan Station to Dome A in Princess Elizabeth Land, East Antarctica, and compare the result with the ground-based radar data [20] to validate the workflow’s performance and capacity on large-scale airborne radar data. Section 2 introduces the methods, including the deep-learning-based EisNet, and the calculation of basal roughness and ILCI; Section 3 is about the radar data and research region; Section 4 presents and discusses the result of the deep learning method and roughness/ILCI calculation; finally, Section 5 draws conclusions.

2. Method

2.1. Geophysics Preprocessing

IPR is the most widely used geophysical detection method due to its advantages, such as high efficiency, high resolution, strong penetration ability, and low maintenance requirements. IPR has been applied in measuring the ice thickness, subglacial topography, and internal layers of the Greenland and Antarctic ice sheets, and other alpine glaciers. The IPR system emits electromagnetic waves by a transmitter, and a receiver records the echo signals reflected from interfaces with different dielectric properties when the signals propagate in the air, ice, and snow [32,39]; therefore, radar images can be used to determine the ice surface, bedrock interface, and ice thickness of the ice sheet. Moreover, the radar-extracted englacial structure is often applied in ice sheet modeling for inversion of the ice deformation process, past accumulation rate, and age stratigraphy and is further used to understand the changes in paleoclimate and past ice dynamics [14]. Before these application studies, extractions of the ice surface, bedrock interface, and internal layers are essential. Therefore, this paper mainly introduces the application of deep learning in radar image geometric feature extraction.

2.2. EisNet Model

EisNet is designed to extract the stratigraphy of ice sheets, including ice layers and bedrock interfaces [47]. As a deep-learning-based method, EisNet is composed of three subnetworks. The EisNet part in Figure 1 demonstrates EisNet’s structures: a convolutional discriminator (Conv. Disc.) first classifies the input radar image slices, and two convolutional encoder–decoders (CED-II/IR) then process the classified slices to obtain the extractions. Each subnetwork is implemented by a multi-layer neural network and is trained by synthetic radar image datasets [47]. EisNet is trained and applied as follows: (1) Training dataset synthesis based on the visual features of layer targets, noises, and interference in observational radar images generates sufficient synthetic radar image datasets. The distinct layer targets those that are thicker and brighter than two experiential thresholds are reserved as extraction labels for the training. Slices from observation radar data are also collected to enhance the performance of a subnetwork in EisNet. (2) Subnetworks are trained on corresponding training datasets. Transfer training of the convolutional discriminator in observational radar slices is suggested to further enhance the performance in field application. The model files of each subnetwork are saved when training ends. (3) After loading the trained subnetwork model files, EisNet can extract the internal isochrones from radar images (as shown in Figure 1). The large-scale radar images are first cropped and sampled to slices with the same shapes as 512 × 512. The convolutional discriminator then classifies the image slices into different types. Following this, two extractors: CED-II and CED-IR, extract layer features from the image slices based on the corresponding type classification. Finally, after the extractions on all the slices finish, the extracted layer features from each slice are merged and resampled to the same size as the input image. The final product of EisNet extraction is two pixel-to-pixel distributions of both the bedrock interface and ice layers. After training, EisNet is first quantitatively analyzed with fresh synthetic data by Dice, MIoU, and PSNR [47] and then applied to large-scale observational radar images.

2.3. Basal Roughness

We used a spectral method based on FFT to quantify the roughness of the basal topography. The two parameters (ξ and η) calculated were used to quantify the vertical and horizontal irregularities of the topography [19]. In this study, we followed the basal roughness calculation of Luo and others (2020) [20]. The average along-track sampling interval of radar data was 20.07 m. A fixed spatial resampling interval of 20 m was used in the linear interpolation. During resampling, the missing data points with an interval of more than 200 m were considered as being ‘broken’ and were not analyzed by FFT. Here, FFT was carried out over a moving window of 2^N sampling points, where N = 5 (L = 640 m), which is the suggested minimum value [24]. The specific calculation process of the two-parameter roughness is as follows:

First, the linear detrending elevation profile was obtained by subtracting the average value of the subglacial topography elevation within the moving window length:

$$Z_0(x)=Z(x)-<Z(x)>$$

(1)

where x is the horizontal window (−L/2, L/2); $Z\left(x\right)$ is the subglacial topography elevation; <$Z\left(x\right)$> is the mean subglacial topography elevation of a profile with length L.

A slope profile, $Z_{sl}\left(x\right)$, can be obtained from the detrended elevation profile by $Z_{sl}\left(x\right)$ = ∂Z₀(x)/∂x. Then, the total roughness parameter (the first roughness parameter ξ) and slope roughness parameter (${\xi }_{sl}$) can be defined by integrating the power spectral density function (S(k) and S_sl(k)):

$$\xi ={{\displaystyle \int }}_{k1}^{k2}S\left(k\right)dk={{\displaystyle \int }}_{k1}^{k2}\frac{1}{l}{|{\tilde{Z}}_0\left(k\right)|}^{2}dk$$

(2)

$${\xi }_{sl}={{\displaystyle \int }}_{k1}^{k2}{S}_{sl}\left(k\right)dk={{\displaystyle \int }}_{k1}^{k2}\frac{1}{l}{|{\tilde{Z}}_{sl}\left(k\right)|}^{2}dk$$

(3)

where ${\tilde{Z}}_0\left(k\right)$ and ${\tilde{Z}}_{sl}\left(k\right)$ are, respectively, the Fourier transforms of $Z_0\left(x\right)$ and $Z_{sl}\left(x\right)$.

The frequency roughness parameter (the second roughness parameter, η) is defined by dividing the total roughness by the slope roughness:

$$\eta =\frac{\xi }{{\xi }_{sl}}$$

(4)

Finally, in order to compare with previous studies, we calculated half the mean square of roughness parameters, $\sqrt{2\xi }$ and $\sqrt{2\eta }$, to quantitatively describe the basal roughness characteristics [20]. The total roughness parameter, ξ, reflects the main vertical amplitude information and the vertical irregularity of the subglacial topography. A value of ξ close to 0 reflects a smaller amplitude and smoother bed. The frequency roughness parameter, η, reflects the advantage of a specific wavelength on the horizontal change. A high η means that the subglacial topography is dominated by relatively longer wavelengths; a low η indicates that relatively shorter wavelengths dominate [48].

2.4. Internal Layer Continuity Index

The information about the locations and ice dynamics of current and past ice flows can be recorded by internal layers [36,43]. Karlsson et al. (2012) proposed the method of ILCI, which is often widely used to quantify the continuity of the internal reflector from huge amounts of radar datasets [36]. The ILCI method is based on the observation that the relative power of the reflected signal from the internal ice layers and bedrock interface in each A-scope is higher than the relative power without clear layering. That is to say, when the ice formation contains numerous clear internal layers, the A-scope signal exhibits high-amplitude fluctuations. On the contrary, when the ice formation contains less clear internal layers or is absent, low-frequency and low-amplitude oscillating signals are generated. The quantitative results of a low ILCI can help us quickly understand the historical ice flow information [36,39,43,45], and internal layering with good continuity can be used for ice core drilling site selection or provide new strategies for repeated investigation [18,42]. We calculated the ILCI by the absolute value of the gradient of the A-scopes. That is,

$$\mathsf{\Psi }=\frac{1}{2\Delta \mathrm{r}N}{{\displaystyle \sum }}_{i{=}_{L_1}}^{L_2}|P_{i+1}-P_{i-1}|$$

(5)

where Ψ represents the calculated continuity index parameter; P_i is the reflected relative power (dB) at the time sample point, i; ∆r is the depth (m) and equal to 1; and N = [L₁:L₂] is the number of sampling points in the time sub-interval, which is usually set equal to the middle 3/5 of the ice column for analysis [34,36,47,49]. We followed the calculation of Luo et al. (2020) and assessed overall layer continuity along the traverse by smoothing the windows of 100 traces (about 2 km) and 500 traces (about 10 km) [20].

3. Test Ice Sheet Profile and Radar Data

The radar data applied in the test were from the traverse from Zhongshan Station to Dome A observed during the airborne geophysical survey in the 32nd CHINARE, 2015/2016. The airborne radar profile is the same as the inland traverse by CHINARE in East Antarctica, which is also a transect of the International Trans-Antarctic Scientific Expedition (ITASE) project. It is about 1200 km long and can be used for comparison and verification of the previous profile from ground-based radar detection. In the previous ground-based radar study by Luo et al. (2020), long intermittent measurements resulted in discontinuity section data due to the limited speed of the snow vehicle. As shown in Figure 2a, the line segments in different colors are the sections collected by the ground-based deep IPR during CHINARE 29, 2012/2013, and the black line is the complete line path obtained by the airborne radar. The inland investigation transect starts from Zhongshan Station along the coast and passes through the west of Princess Elizabeth Land (PEL), the east of the upper reach of the Lambert Glacier Basin (LGB), the Gamburtsev Subglacial Mountains (GSM), and the Dome A area [20].

The airborne ice radar system used in the airborne geophysical surveys is functionally similar to the High Capability Airborne Radar System (HiCARS), which was developed by the University of Texas Institute for Geophysics (UTIG). It is also a phase-coherent radar system transmitting a 1 µs-wide chirp pulse with a 60 MHz center frequency (see Tang et al. (2022) for more details on the system parameters [46]). We conducted processing based on the ‘pik1′ data, which are a field data product [46]. In order to improve the signal-to-noise ratio (SNR) of the pik1 data, we carried out DC filtering, Karhunen–Loeve (KL) filtering (eliminating background speckle noise), frequency–wavenumber domain (F–K) filtering (removing inclined stripe noise), and mean filtering (eliminating angular reflection and enhancing the horizontal signal) of the A-A’ profile in Figure 2a. An example of the processed radar image is shown in Figure 2b. Figure 2c is a cross profile of the ground-based radar that was not continuously detected compared with the airborne radar profile.

4. Results and Discussion

4.1. Radar Detection

Comparisons between the airborne radar segment (Figure 2a) and the ground-based radar segment (Figure 2b) suggest that the airborne radar complements the incomplete feature not detected by the ground-based radar (the green line in Figure 2b) and also supplements the blind detection area of the ground-based radar near 500 m in the shallow layer. However, as the blue arrow in Figure 2b,c indicates, the main factor is the difference in the track stacking processing of different radar data that makes the ground-based radar records more clearly reflected from the inclined internal ice layer above the steep terrain. The yellow asterisk marks the same manually picked deep layer in two different radar data. Below this layer, the ground-based radar can observe more deep layers than the airborne radar, which demonstrates the ground-based radar system’s higher deep detection capability.

4.2. Bedrock Interface and Internal Ice Layer Extraction

Figure 3 shows the ice surface and bedrock interface extraction from the manual method (blue curve) and automatic EisNet method. Due to the pixelized resolution limitation in radar images, few experience interventions can be submitted to EisNet extraction. Therefore, the extracted layers show horizontal discontinuity and high-frequency joggle in the pixel-scale results. To optimize the result and obtain continuous layer extraction, we appended the post-processing of EisNet as interpolation and smoothness. We used the trace number threshold to detect discontinuity. In the EisNet-extracted layers, a discontinuous range smaller than the threshold is determined to be the temporary discontinuity, which will be interpolated and smoothed. Meanwhile, a discontinuous range larger than the threshold will be retained in the final result. We applied linear interpolation to complement the temporary discontinuity and Gaussian smoothing to reduce the high-frequency pixelized joggle. The final results after interpolation and smoothing are shown as black curves in Figure 3a. Figure 3b,c are the pixel-scale images corresponding to the green boxes b and c, respectively, in Figure 3a. The yellow curves indicate the post-processed EisNet extractions, which are consistent with the manual extractions. The standard deviation between the post-processed EisNet and manual extraction was 3.16 m, which is smaller than the sample interval and shows the reliability of EisNet and post-processing. As the red curve shows in Figure 3c, the raw EisNet extraction of the bedrock interface was highly sensitive to the high reflection signal but lacked extraction to the steep interfaces with a low reflection signal. The blue and black curves in Figure 3a indicate EisNet’s low sensitivity to the bedrock in the deep valley compared with the manual method. The depth of the valley was even shallower after interpolation. Figure 3d is the difference histogram of the bedrock elevation from the manual and EisNet extractions. It shows a Gaussian-like distribution, in which the maximum elevation difference is about 630 m, and the standard variance is 61.1 m.

In addition to the extraction of the ice surface, we also used EisNet to extract the internal isochronous layer inside the ice sheet. Figure 4 shows the internal layer extractions obtained by the EisNet workflow. In Figure 4a,b, the inclined stripe texture caused by interference at the 1500 trace position is incorrectly extracted, but the effect can be effectively reduced using the FK filtering method (Figure 4c,d). Comparisons between the subfigures suggest that the filtering methods in radar data preprocessing can primarily exclude the specified texture in the radar image but also bring unexpected data loss. EisNet can extract the internal layers with obvious features with high continuity. However, due to irregular changes in the brightness and thickness of the internal ice layer in different radar images, there are also discontinuities and multiple candidate targets in EisNet’s internal layer extractions. In this complex instance, it is still a challenge to determine the same layer and further connect the disturbed layer.

4.3. Basal Roughness and Continuity Index

To further compare the bedrock interface extraction by different methods in the same dataset, we also applied the final results of the interpolation and smoothing of the bedrock interface extracted by EisNet to calculate the basal roughness, which was later compared with the results from the manual method. Figure 5 shows the normalized result of the basal roughness after the 500 (~10 km) traces’ Gaussian smoothing processing (red line for manual method; yellow line for EisNet and post-processing). From the comparisons, we can conclude the following: (1) Two distribution trends of the total roughness (ξ) are consistent around 30–380 km, 420–740 km, 1040–1100 km, and 1200 km; however, in the region around 10–30 km, 380–420 km, and 1160 km, the total roughness shows a large difference and an opposite distribution trend. (2) Because the bedrock interface is poorly extracted by EisNet near the deep mountain valley, the slope at the steep terrain is reduced by the interpolation/smoothing process, which results in the total slope roughness (ξ_sl) being lower than the result from the manual method. Therefore, the frequency roughness (η) distribution from the EisNet extraction shows a significant difference from the manual method, with a larger value. This indicates that the subglacial topography extracted by EisNet after interpolation and smoothing is dominated by long wavelengths.

Figure 6 shows the ILCI calculated from the middle 3/5 ice column of the airborne radar profile. To highlight the regional characteristics, the results were averaged by 100 traces (~2 km) and 500 traces (~10 km). Figure 7 is the variation in the ILCI with depth calculated from the airborne radar profile. As shown in Figure 6, the low ILCI values indicate low internal layer continuity in the 0–80, 340, 390, 410–440, 550, 770–970, and 1050–1120 km regions; the high ILCI values in the 260–320, 370, 400, 480–530, 600–700, 1020–1070, and 1140–1240 km regions show high continuity of the internal layer. The ice continuities of 0–20% at the top and 80–100% at the bottom of the ice column are ignored in the analysis of the ILCI distribution with depth. As shown in Figure 7b–d, the ILCI in the middle depth (40–60%) at 0–50 km is higher than that in the upper and lower depths; the ILCI at 50–970 km decreases with the increase in depth; the ILCI at 970–1130 km increases with the increase in depth; internal layers show high continuity in the 1130–1240 km region.

4.4. Discussion

The application of the airborne IPR survey profile from Zhongshan Station to Dome A can supplement the data flaw of the ground-based radar profile [20] and reveal the potential application of large-scale airborne radar data. The airborne flight route overlaps with the vehicle-borne route between 0 and 1080 km, where 2333 intersections are affirmed with a distance smaller than 28 m. In intersections, the corresponding difference between the manually picked elevation from the ground-based radar data and the EisNet-detected bedrock interfaces is in the range of 0–600 m, in which the standard variances of the bed elevation difference are 82.4 m and 95.2 m, respectively. The influence factors of the bed elevation difference at the intersection include the GPS location accuracy, manual picking misfit, and radar system resolution. Compared with the results of the ILCI and basal roughness from Luo et al., 2020 [20], we can conclude the following: (1) In the area of 0~1080 km, where the detection route is approximate, the total basal roughness obtained from the airborne radar (red line in Figure 5a) is consistent with the results of the ground-based radar (purple line in Figure 5a). The frequency roughness distribution trends between them are consistent, but the ground-based frequency roughness is higher than that of the airborne data at 150~220 km and 370~420 km, and lower than that of the airborne data at 260~320 km and 970~1080 km. The difference in frequency roughness indicates the difference in the variation frequency of the horizontal fluctuation of the subglacial topography detected by the two radar data in the same region. (2) In 1080~1240 km areas with different detection routes, although the distribution of the subglacial topography is different, both of the data have high total roughness and frequency roughness, which also indicates that the GSM in the Dome A region are supposed to be mountain landscapes under the typical continental environment [20]. (3) Because of the different radar systems used in airborne and ground-based detection, there are large differences in both the acquisition parameters and data processing detection. To reduce the influence introduced by differences in systems and data processing when calculating the ILCI, we did not directly compare the ILCI results specifically. Overall, even though there is also a large difference between the continuity and discontinuity of the ILCI between the two detections in the local region, they can still reveal the high continuity of internal layers near Taishan Station (500 km) and Dome A and the low continuity in the upstream of the Lambert Glacier.

The EisNet automatic extractions of the internal ice layer and bedrock interface from the IPR data suggest the capability of synthetic radar images in neural network training and provide alternative data with a similar number of labels to the conventional manually picked labels [47]. EisNet can obtain performance after training to extract both types of layer targets with high sensitivity and efficiency. Meanwhile, the noise and interference in radar images can be effectively reduced. The basal roughness from Zhongshan Station to Dome A calculated by the EisNet-extracted layer features shows high consistency with Luo et al. (2020) [20]. However, there is still optimization space for EisNet’s internal layer extraction in fast-ice flow regions due to the complex fractures, distortion, and interferences. EisNet is a relatively capable method in the automatic and rapid extraction of internal ice layers and subglacial topography, which will bring significant advancements in the extraction of ice layers from more than 170,000 km airborne radar lines obtained by the Polar Research Institute of China.

5. Conclusions

In this research, we proposed a fusion method based on the ice radar data process and deep learning method to extract the internal/bottom geometric features of the AIS and calculate the basal roughness and ILCI. We used the airborne radar images from Dome A to Zhongshan Station to validate the workflow of the application. The result indicates that this method can effectively extract the internal layers and bedrock interface from radar images of the ice sheet. Based on the extracted layers and interface, we further quantitatively calculated and verified the basal roughness and ILCI results from a previous study intermittently measured by ground IPR [20] and thus demonstrated the method’s reliability. The deep learning method showed high capability when extracting layers from the high-continuity radar images, but it remains to be improved when fractures or high interference exist in radar images. The automatically extracted layer features have a potentially important impact on the basal roughness and ILCI calculated in large-scale radar data. This fact directly relates the detection in the AIS to the glacial parameters and makes a unique contribution to effectively quantitating ice sheet dynamics. In addition, this method integrates the conventional radar data preprocessing denoising and deep learning geometric feature extraction and has an obvious advantage in efficiency over the manual or semi-automatic extraction of layer features from radar images.