Estimating Regional PM2.5 Concentrations in China Using a Global-Local Regression Model Considering Global Spatial Autocorrelation and Local Spatial Heterogeneity
Abstract
:1. Introduction
2. Materials and Methods
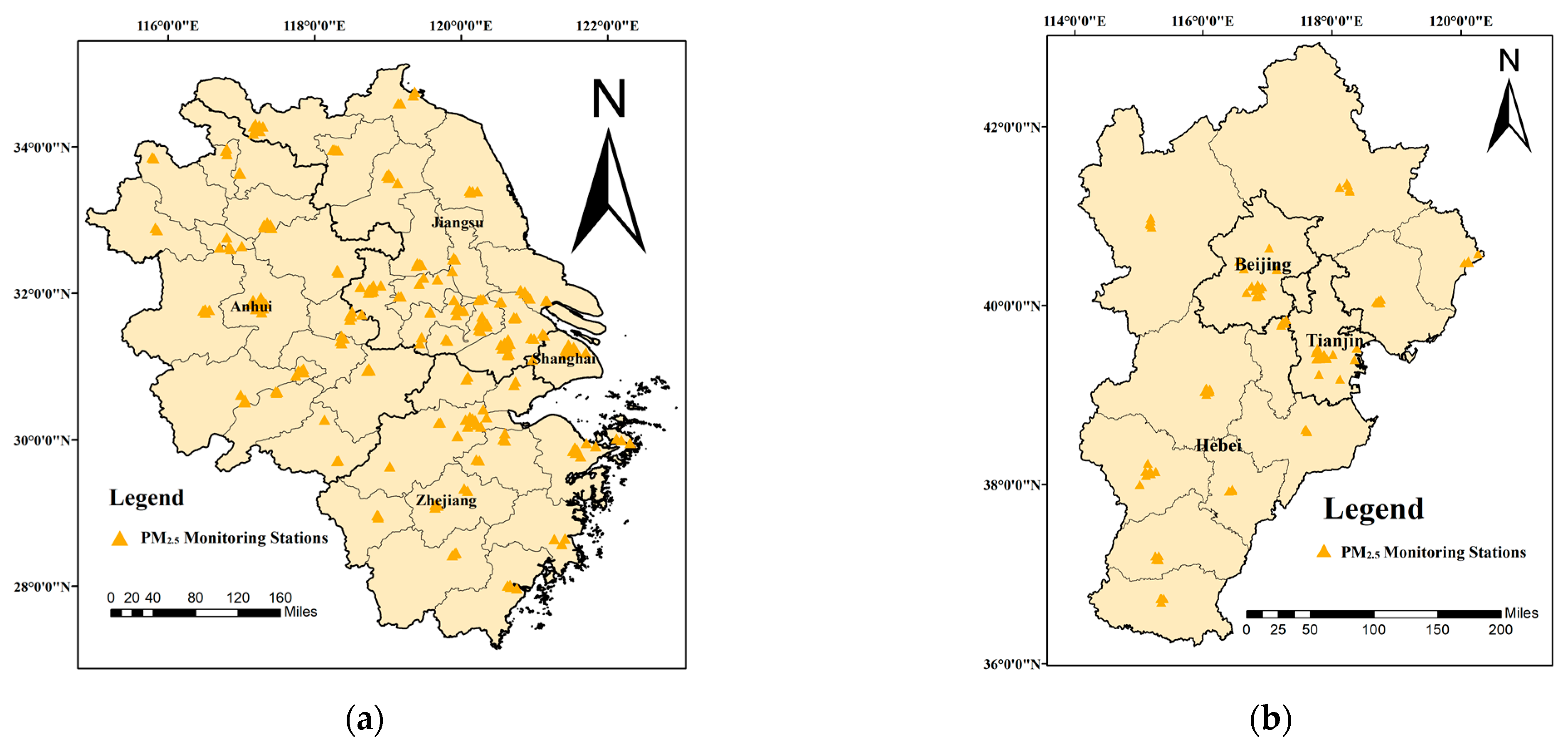
2.1. Study Areas
2.2. Data Integration
2.3. Global-Local Regression Modeling Method
2.3.1. The Extraction of Global Spatial Factors
2.3.2. The Construction of the GLR Model
2.3.3. Model Assessment, Comparison, and Validation
3. Results
3.1. Descriptive Statistics for PM2.5 and Its Variables
3.2. Model Results and Validation
3.2.1. The Assessment and Comparison of Models
3.2.2. The MCs for Residuals
3.2.3. Cross-Validation
3.3. PM2.5 Distribution Maps and Spatiotemporal Characteristics
3.3.1. Continuous PM2.5 Distribution Maps
3.3.2. Spatiotemporal Distribution Based on the PM2.5 Distribution Maps
4. Discussion
4.1. Method Improvement and Accuracy Enhancement
4.2. Comparison of PM2.5 in the YRD and BTH Regions
4.3. Limitations and Future Works
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bonyadi, Z.; Ehrampoush, M.H.; Ghaneian, M.T.; Mokhtari, M.; Sadeghi, A. Cardiovascular, respiratory, and total mortality attributed to PM2.5 in Mashhad, Iran. Environ. Monit. Assess. 2016, 188, 570. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Guo, Y.; Liu, Y.; Wang, J.; Wang, Q.; Sun, Z.; He, M.Z.; Shi, X. Estimating mortality burden attributable to short-term PM2.5 exposure: A national observational study in China. Environ. Int. 2019, 125, 245–251. [Google Scholar] [CrossRef]
- Xiao, Q.; Liang, F.; Ning, M.; Zhang, Q.; Bi, J.; He, K.; Lei, Y.; Liu, Y. The long-term trend of PM2.5-related mortality in China: The effects of source data selection. Chemosphere 2021, 263, 127894. [Google Scholar] [CrossRef] [PubMed]
- Brauer, M.; Freedman, G.; Frostad, J.; Van Donkelaar, A.; Martin, R.V.; Dentener, F.; Dingenen, R.V.; Estep, K.; Amini, H.; Apte, J.S.; et al. Ambient Air Pollution Exposure Estimation for the Global Burden of Disease 2013. Environ. Sci. Technol. 2016, 50, 79–88. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.; Mengersen, K.; Kimlin, M.; Zhou, M.; Tong, S.; Fang, L.; Wang, B.; Hu, W. Lung cancer and particulate pollution: A critical review of spatial and temporal analysis evidence. Environ. Res. 2018, 164, 585–596. [Google Scholar] [CrossRef] [PubMed]
- Cao, Q.; Rui, G.; Liang, Y. Study on PM2.5 pollution and the mortality due to lung cancer in China based on geographic weighted regression model. BMC Public Health 2018, 18, 925. [Google Scholar] [CrossRef]
- Pun, V.C.; Kazemiparkouhi, F.; Manjourides, J.; Suh, H.H. Long-Term PM2.5 Exposure and Respiratory, Cancer, and Cardiovascular Mortality in Older US Adults. Am. J. Epidemiol. 2017, 186, 961–969. [Google Scholar] [CrossRef]
- Hyslop, N.P. Impaired visibility: The air pollution people see. Atmos. Environ. 2009, 43, 182–195. [Google Scholar] [CrossRef]
- Guo, J.P.; Zhang, X.Y.; Che, H.Z.; Gong, S.L.; An, X.; Cao, C.X.; Guang, J.; Zhang, H.; Wang, Y.Q.; Zhang, X.C.; et al. Correlation between PM concentrations and aerosol optical depth in eastern China. Atmos. Environ. 2009, 43, 5876–5886. [Google Scholar] [CrossRef]
- Lin, C.; Li, Y.; Yuan, Z.; Lau, A.K.H.; Li, C.; Fung, J.C.H. Using satellite remote sensing data to estimate the high-resolution distribution of ground-level PM2.5. Remote Sens. Environ. 2015, 156, 117–128. [Google Scholar] [CrossRef]
- He, Q.; Huang, B. Satellite-based mapping of daily high-resolution ground PM2.5 in China via space-time regression modeling. Remote Sens. Environ. 2018, 206, 72–83. [Google Scholar] [CrossRef]
- Lee, S.; Serre, M.L.; Van Donkelaar, A.; Martin, R.V.; Burnett, R.T.; Jerrett, M. Comparison of Geostatistical Interpolation and Remote Sensing Techniques for Estimating Long-Term Exposure to Ambient PM2.5 Concentrations across the Continental United States. Environ. Health Perspect. 2012, 120, 1727–1732. [Google Scholar] [CrossRef] [PubMed]
- Pan, Q.; Wen, X.; Lu, Z.; Li, L.; Jing, W. Dynamic speed control of unmanned aerial vehicles for data collection under internet of things. Sensors 2018, 18, 3951. [Google Scholar] [CrossRef] [PubMed]
- Bai, K.; Li, K.; Chang, N.B.; Gao, W. Advancing the prediction accuracy of satellite-based PM2.5 concentration mapping: A perspective of data mining through in situ PM2.5 measurements. Environ. Pollut. 2019, 254, 113047. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Li, Y.; Zhou, Y.; Shi, C.; Guo, Y.; Liu, Y. The comparison of AOD-based and non-AOD prediction models for daily PM2.5 estimation in Guangdong province, China with poor AOD coverage. Environ. Res. 2021, 195, 110735. [Google Scholar] [CrossRef]
- Carmona, J.M.; Gupta, P.; Lozano-García, D.F.; Vanoye, A.Y.; Hernández-Paniagua, I.Y.; Mendoza, A. Evaluation of modis aerosol optical depth and surface data using an ensemble modeling approach to assess PM2.5 temporal and spatial distributions. Remote Sens. 2021, 13, 3102. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z. Remote sensing of atmospheric fine particulate matter (PM2.5) mass concentration near the ground from satellite observation. Remote Sens. Environ. 2015, 160, 252–262. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, L.; Tao, J.; Zhang, Y.; Su, L. Satellite-based estimation of regional particulate matter (PM) in Beijing using vertical-and-RH correcting method. Remote Sens. Environ. 2010, 114, 50–63. [Google Scholar] [CrossRef]
- Bai, Y.; Wu, L.; Qin, K.; Zhang, Y.; Shen, Y.; Zhou, Y. A geographically and temporally weighted regression model for ground-level PM2.5 estimation from satellite-derived 500 m resolution AOD. Remote Sens. 2016, 8, 262. [Google Scholar] [CrossRef]
- Reyes, J.M.; Serre, M.L. An LUR/BME framework to estimate PM2.5 explained by on road mobile and stationary sources. Environ. Sci. Technol. 2014, 48, 1736–1744. [Google Scholar] [CrossRef]
- Zheng, C.; Zhao, C.; Zhu, Y.; Wang, Y.; Shi, X.; Wu, X.; Chen, T.; Wu, F.; Qiu, Y. Analysis of influential factors for the relationship between PM2.5 and AOD in Beijing. Atmos. Chem. Phys. 2017, 17, 13473–13489. [Google Scholar] [CrossRef]
- Chen, X.; Li, H.; Zhang, S.; Chen, Y.; Fan, Q. High Spatial Resolution PM2.5 Retrieval Using MODIS and Ground Observation Station Data Based on Ensemble Random Forest. IEEE Access 2019, 7, 44416–44430. [Google Scholar] [CrossRef]
- Shen, H.; Li, T.; Yuan, Q.; Zhang, L. Estimating Regional Ground-Level PM 2.5 Directly From Satellite Top-Of-Atmosphere Reflectance Using Deep Belief Networks. J. Geophys. Res. Atmos. 2018, 123, 13, 875–913, 886. [Google Scholar] [CrossRef]
- Zhang, J.J.Y.; Sun, L.; Rainham, D.; Dummer, T.J.B.; Wheeler, A.J.; Anastasopolos, A.; Gibson, M.; Johnson, M. Predicting intraurban airborne PM1.0-trace elements in a port city: Land use regression by ordinary least squares and a machine learning algorithm. Sci. Total Environ. 2022, 806, 150149. [Google Scholar] [CrossRef] [PubMed]
- Wong, P.Y.; Lee, H.Y.; Zeng, Y.T.; Chern, Y.R.; Chen, N.T.; Candice Lung, S.C.; Su, H.J.; Wu, C. Da Using a land use regression model with machine learning to estimate ground level PM2.5. Environ. Pollut. 2021, 277, 116846. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Huang, W.; Li, Z.; Xue, W.; Peng, Y.; Sun, L.; Cribb, M. Estimating 1-km-resolution PM2.5 concentrations across China using the space-time random forest approach. Remote Sens. Environ. 2019, 231, 111221. [Google Scholar] [CrossRef]
- Son, Y.; Osornio-Vargas, Á.R.; O’Neill, M.S.; Hystad, P.; Texcalac-Sangrador, J.L.; Ohman-Strickland, P.; Meng, Q.; Schwander, S. Land use regression models to assess air pollution exposure in Mexico City using finer spatial and temporal input parameters. Sci. Total Environ. 2018, 639, 40–48. [Google Scholar] [CrossRef]
- Chu, Y.; Liu, Y.; Li, X.; Liu, Z.; Lu, H.; Lu, Y.; Mao, Z.; Chen, X.; Li, N.; Ren, M.; et al. A review on predicting ground PM2.5 concentration using satellite aerosol optical depth. Atmosphere 2016, 7, 129. [Google Scholar] [CrossRef]
- Zhou, C.; Chen, J.; Wang, S. Examining the effects of socioeconomic development on fine particulate matter (PM2.5) in China’s cities using spatial regression and the geographical detector technique. Sci. Total Environ. 2018, 619–620, 436–445. [Google Scholar] [CrossRef]
- Hao, Y.; Liu, Y.M. The influential factors of urban PM2.5 concentrations in China: A spatial econometric analysis. J. Clean. Prod. 2016, 112, 1443–1453. [Google Scholar] [CrossRef]
- Cheng, L.; Zhang, T.; Chen, L.; Li, L.; Wang, S.; Hu, S.; Yuan, L.; Wang, J.; Wen, M. Investigating the impacts of urbanization on PM2.5 pollution in the yangtze river delta of china: A spatial panel data approach. Atmosphere 2020, 11, 1058. [Google Scholar] [CrossRef]
- Griffith, D.A. Spatial autocorrelation and eigenfunctions of the geographic weights matrix accompanying geo-referenced data. Can. Geogr.-Geogr. Can. 1996, 40, 351–367. [Google Scholar] [CrossRef]
- Zhang, J.; Li, B.; Chen, Y.; Chen, M.; Fang, T.; Liu, Y. Eigenvector spatial filtering regression modeling of ground PM2.5 concentrations using remotely sensed data. Int. J. Environ. Res. Public Health 2018, 15, 1228. [Google Scholar] [CrossRef]
- Lin, G.; Fu, J.; Jiang, D.; Hu, W.; Dong, D.; Huang, Y.; Zhao, M. Spatio-temporal variation of PM2.5 concentrations and their relationship with geographic and socioeconomic factors in China. Int. J. Environ. Res. Public Health 2013, 11, 173–186. [Google Scholar] [CrossRef]
- Ma, Z.; Hu, X.; Huang, L.; Bi, J.; Liu, Y. Estimating ground-level PM2.5 in china using satellite remote sensing. Environ. Sci. Technol. 2014, 48, 7436–7444. [Google Scholar] [CrossRef] [PubMed]
- Jiang, M.; Sun, W.; Yang, G.; Zhang, D. Modelling seasonal GWR of daily PM2.5 with proper auxiliary variables for the Yangtze River Delta. Remote Sens. 2017, 9, 346. [Google Scholar] [CrossRef]
- Christakos, G.; Serre, M.L. BME analysis of spatiotemporal particulate matter distributions in North Carolina. Atmos. Environ. 2000, 34, 3393–3406. [Google Scholar] [CrossRef]
- Wang, W.; Sun, Y. Penalized local polynomial regression for spatial data. Biometrics 2019, 75, 1179–1190. [Google Scholar] [CrossRef] [PubMed]
- Brunsdon, C.; Fotheringham, A.S.; Charlton Martin, E. Geographically weighted regression: A method for exploring spatial nonstationarity. Encycl. Geogr. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Wu, T.; Zhou, L.; Jiang, G.; Meadows, M.E.; Zhang, J.; Pu, L.; Wu, C.; Xie, X. Modelling spatial heterogeneity in the effects of natural and socioeconomic factors, and their interactions, on atmospheric PM2.5 concentrations in china from 2000–2015. Remote Sens. 2021, 13, 2152. [Google Scholar] [CrossRef]
- Mirzaei, M.; Amanollahi, J.; Tzanis, C.G. Evaluation of linear, nonlinear, and hybrid models for predicting PM2.5 based on a GTWR model and MODIS AOD data. Air Qual. Atmos. Health 2019, 12, 1215–1224. [Google Scholar] [CrossRef]
- Guo, Y.; Tang, Q.; Gong, D.Y.; Zhang, Z. Estimating ground-level PM2.5 concentrations in Beijing using a satellite-based geographically and temporally weighted regression model. Remote Sens. Environ. 2017, 198, 140–149. [Google Scholar] [CrossRef]
- Wu, S.; Du, Z.; Wang, Y.; Lin, T.; Zhang, F.; Liu, R. Modeling spatially anisotropic nonstationary processes in coastal environments based on a directional geographically neural network weighted regression. Sci. Total Environ. 2020, 709, 136097. [Google Scholar] [CrossRef] [PubMed]
- Zhai, L.; Li, S.; Zou, B.; Sang, H.; Fang, X.; Xu, S. An improved geographically weighted regression model for PM2.5 concentration estimation in large areas. Atmos. Environ. 2018, 181, 145–154. [Google Scholar] [CrossRef]
- Hu, J.; Wang, Y.; Ying, Q.; Zhang, H. Spatial and temporal variability of PM2.5 and PM10 over the North China Plain and the Yangtze River Delta, China. Atmos. Environ. 2014, 95, 598–609. [Google Scholar] [CrossRef]
- Fang, C.; Wang, Z.; Xu, G. Spatial-temporal characteristics of PM2.5 in China: A city-level perspective analysis. J. Geogr. Sci. 2016, 26, 1519–1532. [Google Scholar] [CrossRef]
- Li, T.; Shen, H.; Yuan, Q.; Zhang, L. A Locally Weighted Neural Network Constrained by Global Training for Remote Sensing Estimation of PM. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Liu, J.; Chen, W. First satellite-based regional hourly NO2 estimations using a space-time ensemble learning model: A case study for Beijing-Tianjin-Hebei Region, China. Sci. Total Environ. 2022, 820, 153289. [Google Scholar] [CrossRef]
- Tan, H.; Chen, Y.; Wilson, J.P.; Zhang, J.; Cao, J.; Chu, T. An eigenvector spatial filtering based spatially varying coefficient model for PM2.5 concentration estimation: A case study in Yangtze River Delta region of China. Atmos. Environ. 2020, 223, 117205. [Google Scholar] [CrossRef]
- Getis, A.; Aldstadt, J. Constructing the spatial weights matrix using a local statistic. Adv. Spat. Sci. 2004, 61, 147–163. [Google Scholar] [CrossRef]
- Aldstadt, J.; Getis, A. Using AMOEBA to create a spatial weights matrix and identify spatial clusters. Geogr. Anal. 2006, 38, 327–343. [Google Scholar] [CrossRef]
- Griffith, D.A.; Paelinck, J.H.P. Non-standard Spatial Statistics and Spatial Econometrics. In Advances in Geographic Information Science; 2011; Volume 1, pp. 1–256. ISBN 9783642160424. [Google Scholar]
- Chun, Y.; Griffith, D.A. A quality assessment of eigenvector spatial filtering based parameter estimates for the normal probability model. Spat. Stat. 2014, 10, 1–11. [Google Scholar] [CrossRef]
- Chun, Y.; Griffith, D.A.; Lee, M.; Sinha, P. Eigenvector selection with stepwise regression techniques to construct eigenvector spatial filters. J. Geogr. Syst. 2016, 18, 67–85. [Google Scholar] [CrossRef]
- Fan, J.; Gijbels, I. Variable Bandwidth and Local Linear Regression Smoothers. Ann. Stat. 1992, 20, 2008–2036. [Google Scholar] [CrossRef]
- Imbens, G.; Kalyanaraman, K. Optimal bandwidth choice for the regression discontinuity estimator. Rev. Econ. Stud. 2012, 79, 933–959. [Google Scholar] [CrossRef]
- Tan, H.; Chen, Y.; Wilson, J.P.; Zhou, A.; Chu, T. Self-adaptive bandwidth eigenvector spatial filtering model for estimating PM2.5 concentrations in the Yangtze River Delta region of China. Environ. Sci. Pollut. Res. 2021, 28, 67800–67813. [Google Scholar] [CrossRef]
- Wang, J.; Ogawa, S. Effects of meteorological conditions on PM2.5 concentrations in Nagasaki, Japan. Int. J. Environ. Res. Public Health 2015, 12, 9089–9101. [Google Scholar] [CrossRef]
- Hu, H.; Hu, Z.; Zhong, K.; Xu, J.; Zhang, F.; Zhao, Y.; Wu, P. Satellite-based high-resolution mapping of ground-level PM 2.5 concentrations over East China using a spatiotemporal regression kriging model. Sci. Total Environ. 2019, 672, 479–490. [Google Scholar] [CrossRef]
- Yang, Q.; Yuan, Q.; Li, T.; Shen, H.; Zhang, L. The relationships between PM2.5 and meteorological factors in China: Seasonal and regional variations. Int. J. Environ. Res. Public Health 2017, 14, 1510. [Google Scholar] [CrossRef]
- Liang, Y.; Fang, L.; Pan, H.; Zhang, K.; Kan, H.; Brook, J.R.; Sun, Q. PM2.5 in Beijing-temporal pattern and its association with influenza. Environ. Health A Glob. Access Sci. Source 2014, 13, 102. [Google Scholar] [CrossRef] [Green Version]
- Lin, G.; Fu, J.; Jiang, D.; Wang, J.; Wang, Q.; Dong, D. Spatial variation of the relationship between PM2.5 concentrations and meteorological parameters in China. Biomed Res. Int. 2015, 2015, 684618. [Google Scholar] [CrossRef] [PubMed]
- Fang, X.; Zou, B.; Liu, X.; Sternberg, T.; Zhai, L. Satellite-based ground PM2.5 estimation using timely structure adaptive modeling. Remote Sens. Environ. 2016, 186, 152–163. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, B.; Huang, B.; Ma, Z.; Biswas, A.; Jiang, Y.; Shi, Z. Predicting annual PM2.5 in mainland China from 2014 to 2020 using multi temporal satellite product: An improved deep learning approach with spatial generalization ability. ISPRS J. Photogramm. Remote Sens. 2022, 187, 141–158. [Google Scholar] [CrossRef]
- Pak, U.; Ma, J.; Ryu, U.; Ryom, K.; Juhyok, U.; Pak, K.; Pak, C. Deep learning-based PM2.5 prediction considering the spatiotemporal correlations: A case study of Beijing, China. Sci. Total Environ. 2020, 699, 133561. [Google Scholar] [CrossRef]





| Factors | Source | Spatial Resolution | Temporal Resolution | |
|---|---|---|---|---|
| AOD | MCD19A2 https://ladsweb.modaps.eosdis.nasa.gov/search/ (accessed on 10 March 2022) | 1 km (BTH) 3 km (YRD) | Daily | |
| DEM | Shuttle Radar Topography Mission (SRTM) DEM http://srtm.csi.cgiar.org1 (accessed on 9 March 2022) | 90 m | / | |
| Meteorological Data | TS | European Centre for Medium-Range Weather Forecasts (ECMWF) ERA5 (https://cds.climate.copernicus.eu) (accessed on 9 March 2022) | 0.25° latitude × 0.25° longitude | Hourly |
| PBLH | ||||
| PS | ||||
| RH | ||||
| NDVI | MOD13A3 https://ladsweb.modaps.eosdis.nasa.gov/search/ (accessed on 10 March 2022) | 1 km | Monthly | |
| Factors | YRD | BTH | ||||||
|---|---|---|---|---|---|---|---|---|
| Max | Min | Mean | Std. Dev | Max | Min | Mean | Std. Dev | |
| PM2.5 (μg/m3) | 134.80 | 7.00 | 49.78 | 22.11 | 264.96 | 17.99 | 76.04 | 42.34 |
| AOD (/) | 2.25 | 0.06 | 0.62 | 0.30 | 1.77 | 0.06 | 0.50 | 0.26 |
| NDVI (/) | 0.88 | 0.16 | 0.39 | 0.13 | 0.85 | 0.08 | 0.27 | 0.14 |
| TS (K) | 327.72 | 271.13 | 292.41 | 13.55 | 301.01 | 253.80 | 283.42 | 11.99 |
| RH (/) | 0.89 | 0.48 | 0.70 | 0.08 | 0.84 | 0.29 | 0. 53 | 14.08 |
| PS (hPa) | 1029.50 | 955.83 | 1010.78 | 13.04 | 1029.88 | 850.92 | 968.99 | 65.88 |
| PBLH (m) | 896.68 | 135.24 | 399.65 | 143.39 | 1135.44 | 174.19 | 529.17 | 187.07 |
| DEM (m) | 256.00 | 1.00 | 24.57 | 31.33 | 816.00 | 0.00 | 108.46 | 191.56 |
| ROAD (km/km2) | 3.56 | 0.217 | 1.30 | 0.729 | 5.63 | 0.45 | 1.75 | 1.37 |
| FACT (count/km2) | 0.69 | 0.00 | 0.21 | 0.14 | 0.54 | 0.03 | 0.26 | 0.13 |
| Time | ESF | GWR | GLR | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Adj.R2 | AIC | RMSE | Adj.R2 | AIC | RMSE | Adj.R2 | AIC | RMSE | ||
| YRD | Monthly average | 0.574 | 1447.911 | 7.101 | 0.578 | 1404.906 | 5.854 | 0.620 | 1378.899 | 5.401 |
| Winter | 0.686 | 1495.584 | 7.463 | 0.698 | 1466.581 | 7.155 | 0.703 | 1463.351 | 7.086 | |
| Spring | 0.449 | 1431.397 | 6.356 | 0.548 | 1354.051 | 5.08 | 0.564 | 1345.9 | 4.975 | |
| Summer | 0.382 | 1299.773 | 4.637 | 0.445 | 1240.45 | 3.912 | 0.534 | 1189.853 | 3.309 | |
| Autumn | 0.652 | 1262.926 | 4.777 | 0.709 | 1189.827 | 3.947 | 0.734 | 1173.29 | 3.796 | |
| Annual | 0.687 | 1193.754 | 4.334 | 0.733 | 1174.324 | 3.798 | 0.748 | 1114.99 | 3.427 | |
| BTH | Monthly average | 0.799 | 528.971 | 7.733 | 0.797 | 504.516 | 6.907 | 0.853 | 467.312 | 4.885 |
| Winter | 0.897 | 584.789 | 10.309 | 0.902 | 564.62 | 9.585 | 0.938 | 520.819 | 6.533 | |
| Spring | 0.77 | 513.331 | 5.973 | 0.758 | 496.641 | 5.685 | 0.809 | 475.005 | 4.748 | |
| Summer | 0.711 | 482.871 | 5.231 | 0.745 | 450.135 | 4.389 | 0.786 | 431.469 | 3.705 | |
| Autumn | 0.925 | 501.961 | 5.871 | 0.912 | 492.028 | 6.029 | 0.96 | 416.32 | 3.174 | |
| Annual | 0.926 | 486.544 | 5.362 | 0.943 | 451.56 | 4.437 | 0.959 | 410.66 | 3.138 | |
| Time | MC | Time | MC | ||
|---|---|---|---|---|---|
| YRD | BTH | YRD | BTH | ||
| 15_Dec | 0.283 ** | −0.371 ** | 16_Sep | 0.132 ** | −0.217 * |
| 16_Jan | / | / | 16_Oct | 0.122 ** | / |
| 16_Feb | / | −0.298 ** | 16_Nov | / | / |
| 16_Mar | / | / | Winter | 0.238 ** | −0.239 * |
| 16_Apr | / | / | Spring | / | / |
| 16_May | 0.268 ** | / | Summer | / | / |
| 16_Jun | / | / | Autumn | / | / |
| 16_Jul | / | −0.244 * | Annual | / | −0.218 * |
| 16_Aug | / | / | |||
| Time | YRD | BTH | ||||
|---|---|---|---|---|---|---|
| ESF | GWR | GLR | ESF | GWR | GLR | |
| Monthly average | 7.650 | 7.286 | 7.024 | 10.526 | 11.001 | 9.499 |
| Winter | 7.789 | 7.665 | 6.932 | 8.037 | 8.984 | 8.261 |
| Spring | 6.680 | 6.419 | 6.073 | 7.229 | 6.868 | 6.848 |
| Summer | 4.840 | 4.669 | 4.790 | 5.968 | 5.719 | 5.662 |
| Autumn | 5.188 | 4.861 | 4.731 | 11.584 | 12.201 | 10.955 |
| Annual | 4.701 | 4.865 | 4.599 | 5.711 | 5.485 | 5.302 |
| Time | YRD | BTH | ||
|---|---|---|---|---|
| Max | Mean | Max | Mean | |
| Winter | 96.27 | 66.86 | 153.36 | 94.91 |
| Spring | 74.03 | 45.68 | 76.96 | 61.21 |
| Summer | 48.83 | 26.77 | 83.55 | 48.94 |
| Autumn | 60.82 | 36.08 | 110.34 | 75.68 |
| Annual | 62.08 | 44.85 | 114.74 | 80.21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, H.; Chen, Y.; Tan, H.; Zhou, A.; Chen, G.; Chen, Y. Estimating Regional PM2.5 Concentrations in China Using a Global-Local Regression Model Considering Global Spatial Autocorrelation and Local Spatial Heterogeneity. Remote Sens. 2022, 14, 4545. https://doi.org/10.3390/rs14184545
Su H, Chen Y, Tan H, Zhou A, Chen G, Chen Y. Estimating Regional PM2.5 Concentrations in China Using a Global-Local Regression Model Considering Global Spatial Autocorrelation and Local Spatial Heterogeneity. Remote Sensing. 2022; 14(18):4545. https://doi.org/10.3390/rs14184545
Chicago/Turabian StyleSu, Heng, Yumin Chen, Huangyuan Tan, Annan Zhou, Guodong Chen, and Yuejun Chen. 2022. "Estimating Regional PM2.5 Concentrations in China Using a Global-Local Regression Model Considering Global Spatial Autocorrelation and Local Spatial Heterogeneity" Remote Sensing 14, no. 18: 4545. https://doi.org/10.3390/rs14184545
APA StyleSu, H., Chen, Y., Tan, H., Zhou, A., Chen, G., & Chen, Y. (2022). Estimating Regional PM2.5 Concentrations in China Using a Global-Local Regression Model Considering Global Spatial Autocorrelation and Local Spatial Heterogeneity. Remote Sensing, 14(18), 4545. https://doi.org/10.3390/rs14184545





