Numerical Imaging of the Seabed and Acoustic Flares with Topography and Velocity Variance
Abstract
:1. Introduction
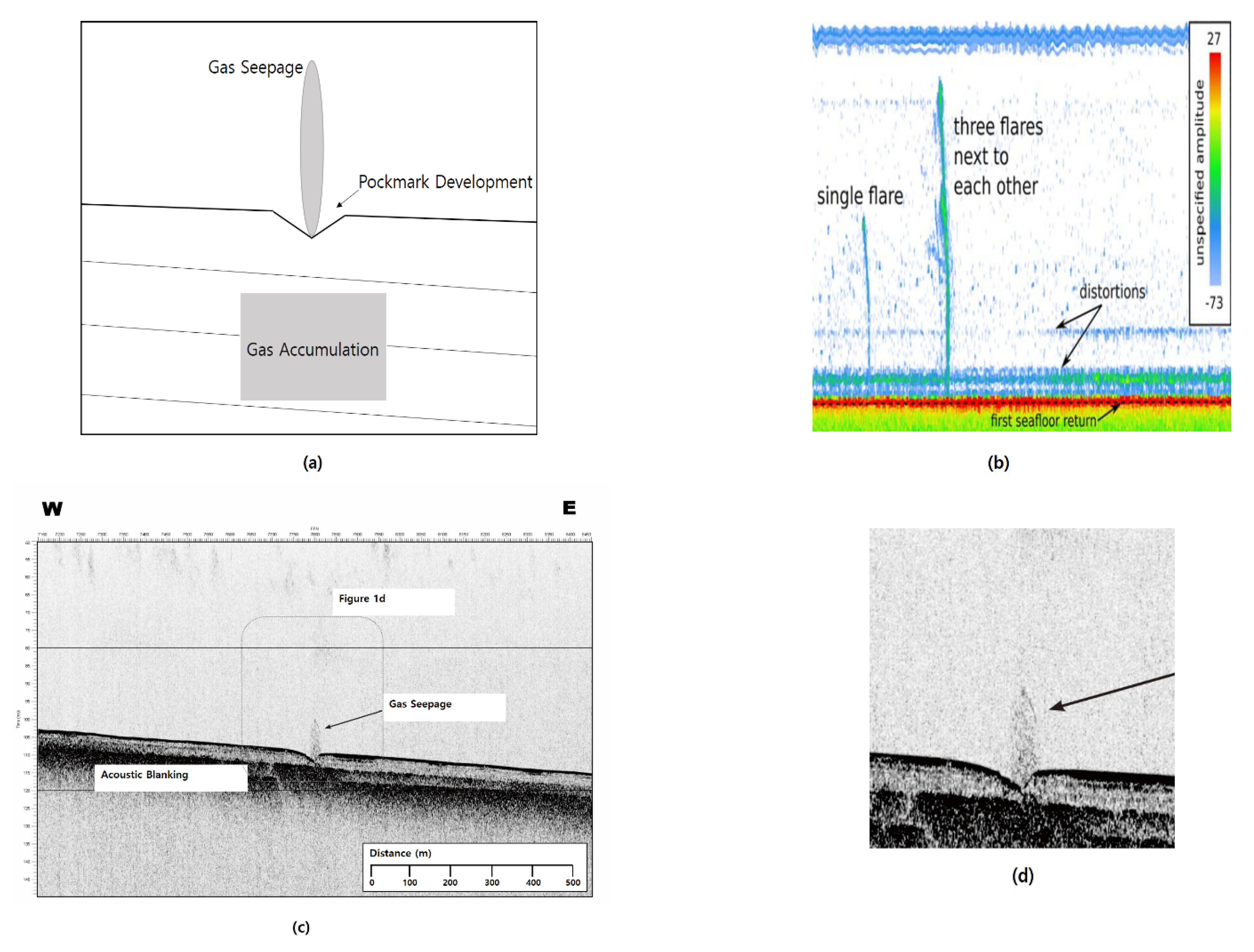
2. Aspects of Acoustic Flares
3. Numerical Modeling Results
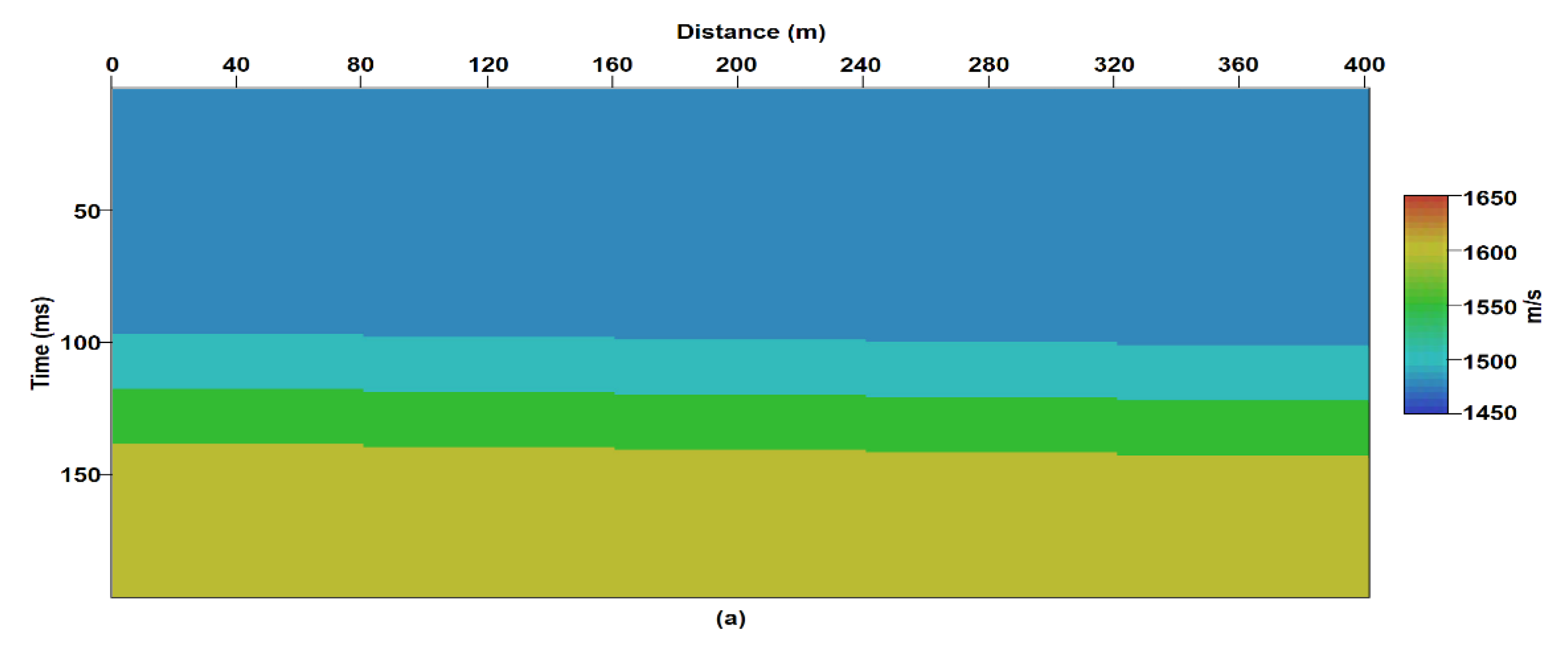
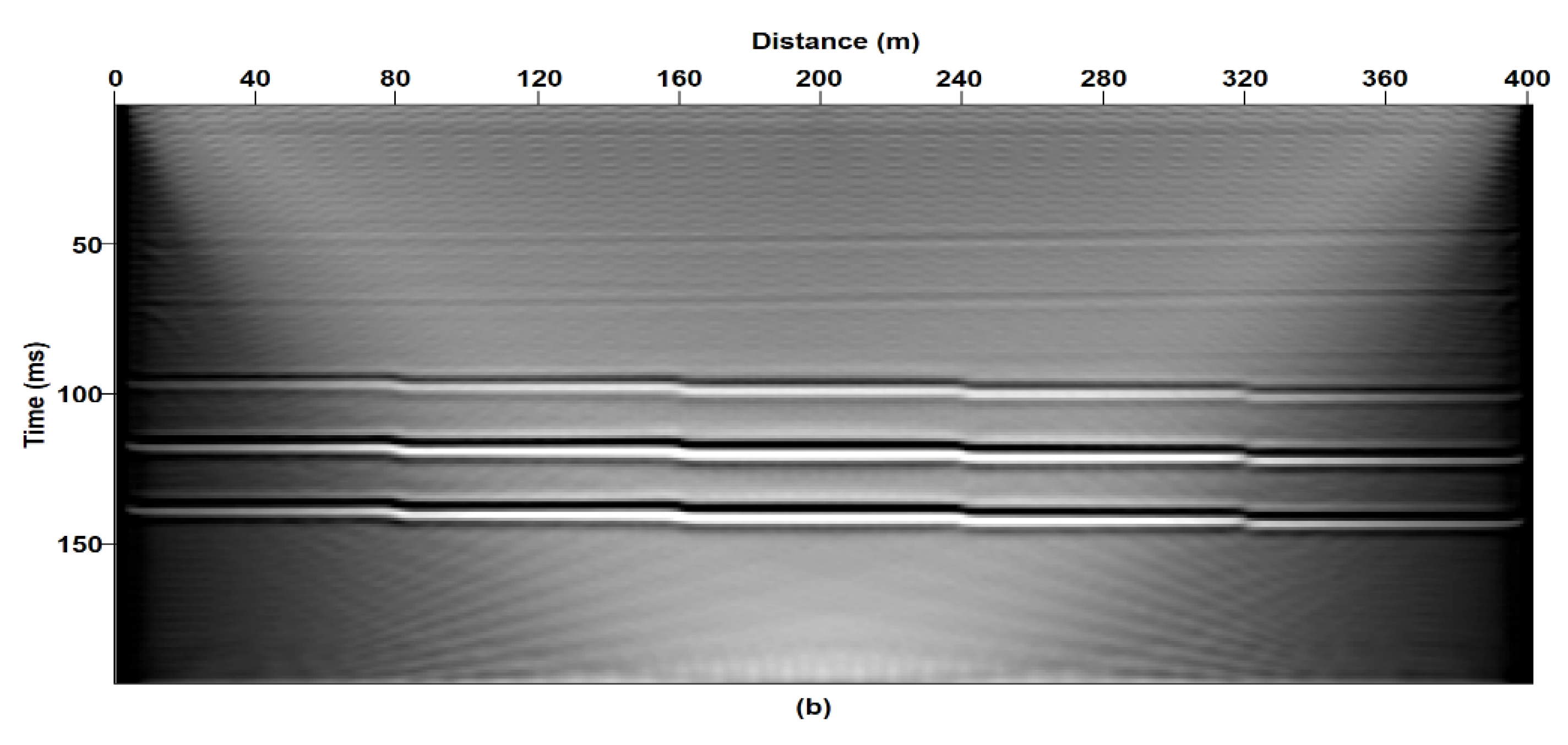
3.1. Reverse Time Migration (RTM)
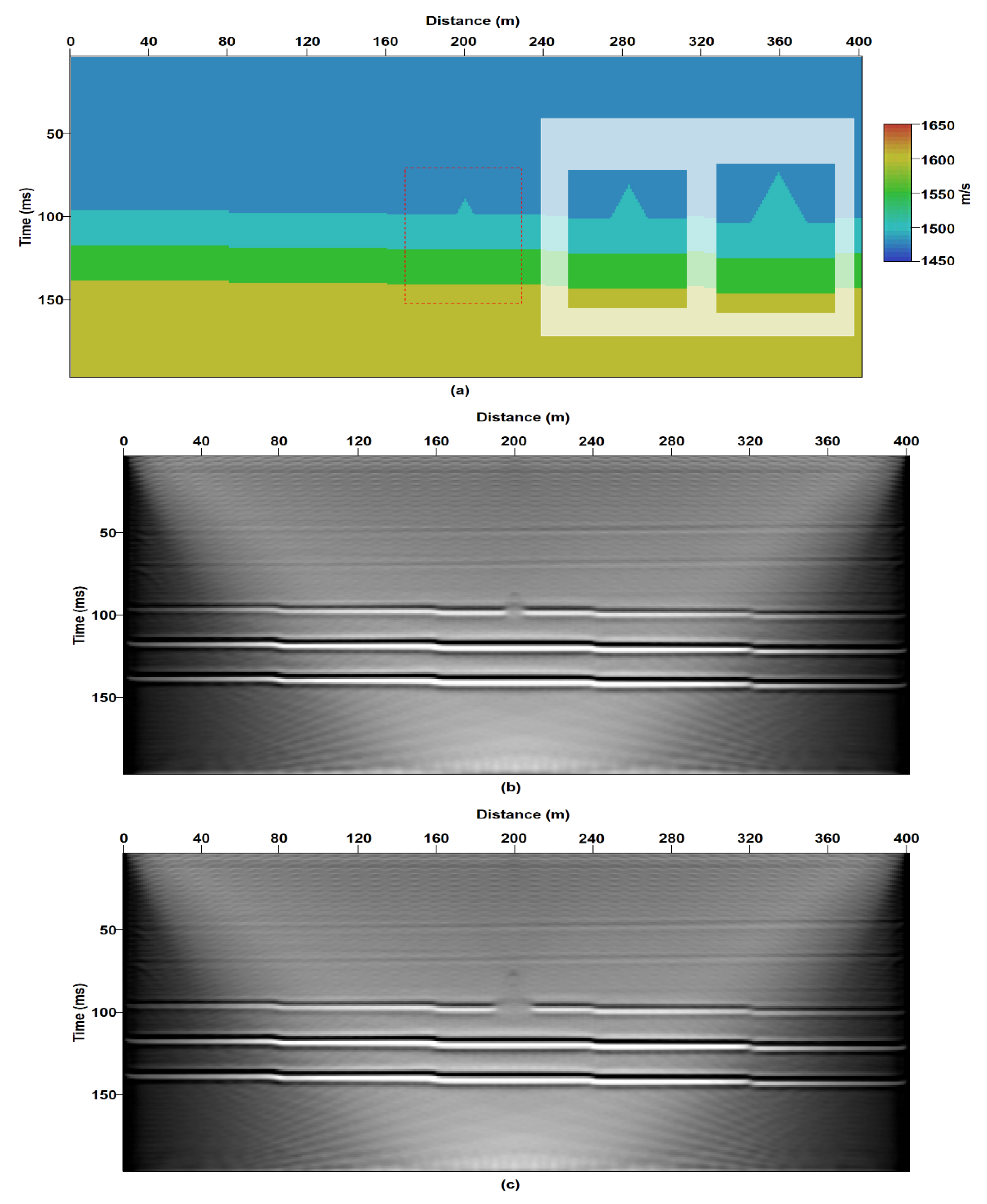
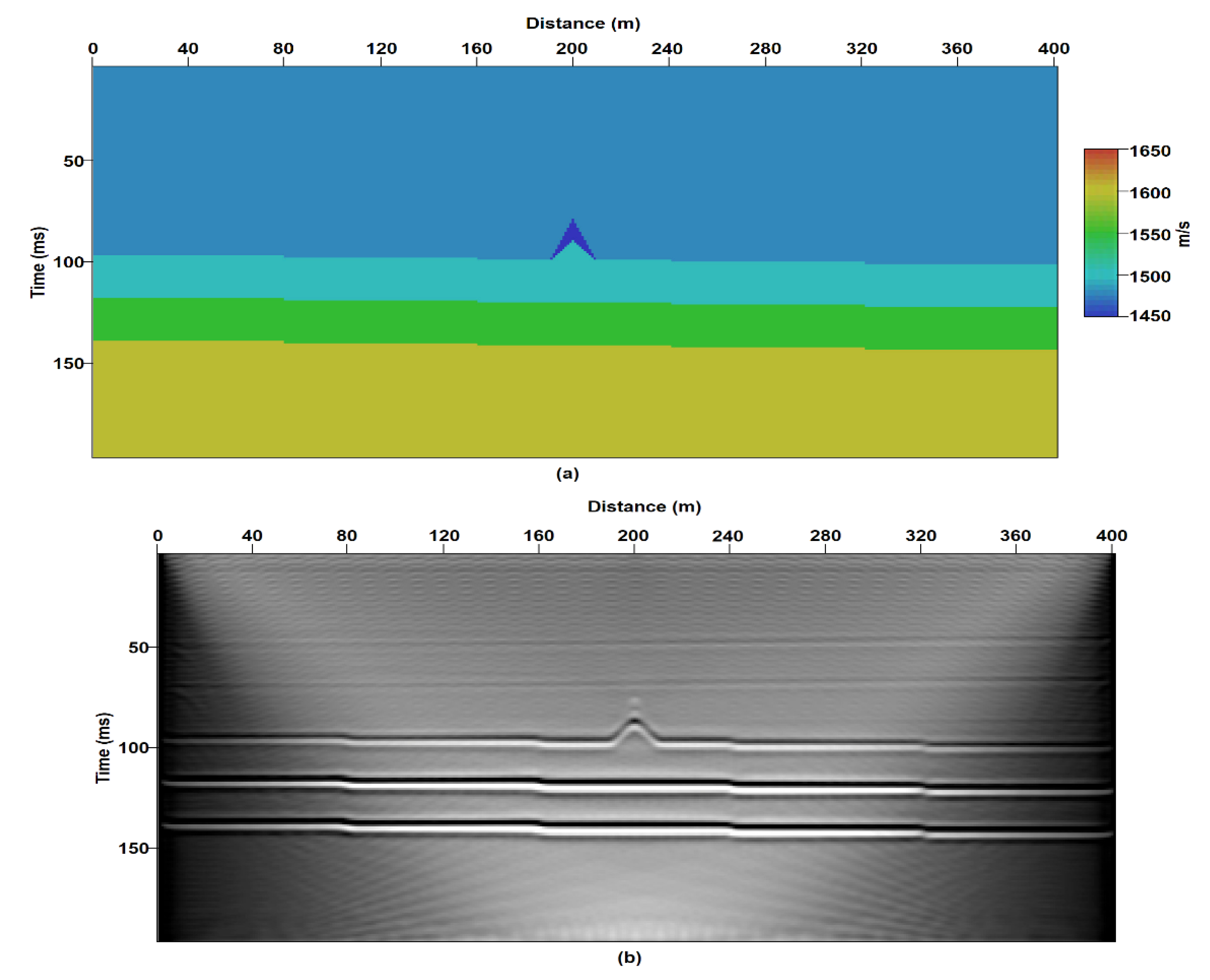
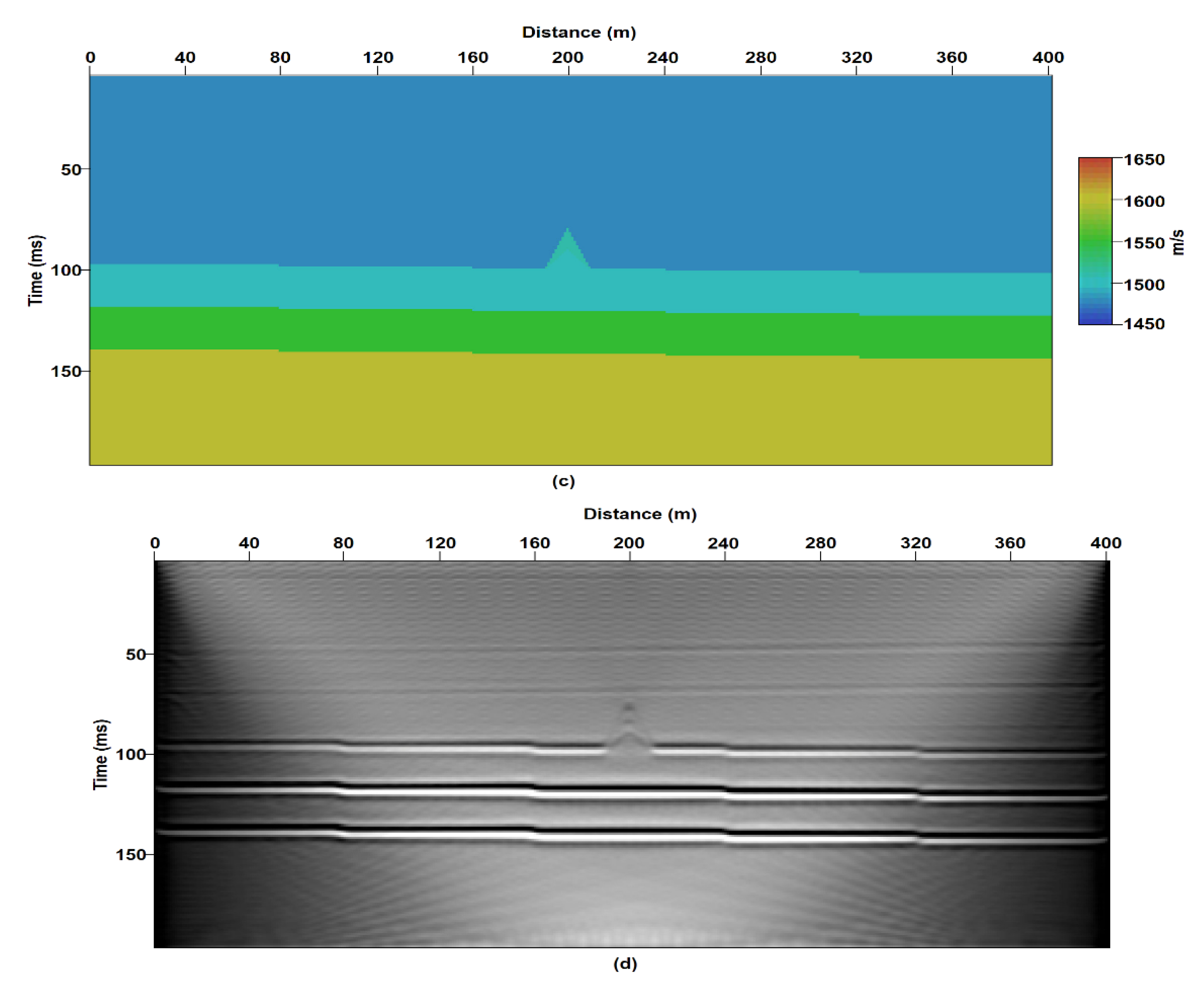
3.2. Topographic Variant Model
3.3. Acoustic Variant Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pryor, D.E. Theory and test of bathymetric side scan sonar. In Proceedings of the Oceans’88 ‘A Partnership of Marine Interests’, Baltimore, MD, USA, 31 October–2 November 1988. [Google Scholar]
- Biju-Duval, B.; Le Quellec, P.; Mascle, A.; Renard, V.; Valery, P. Multibeam bathymetric survey and high resolution seismic investigation on the Barbados ridge complex (Eastern Caribbean): A key to the knowledge and interpretation of an accretionary wedge. Tectonophysics 1982, 86, 275–304. [Google Scholar] [CrossRef]
- Guenther, G.C.; Cunningham, A.G.; LaRocque, P.E.; Reid, D.J. Meeting the Accuracy Challenge in Airborne Lidar Bathymetry. In Proceedings of the 20th EARSeL Symposium: Workshop on Lidar Remote Sensing of Land and Sea, Dresden, Germany, 16–17 June 2000; National Oceanic Atmospheric Administration: Washington, DC, USA, 2000. [Google Scholar]
- Roberts, A.C.B. Shallow water bathymetry using integrated airborne multi-spectral remote sensing. Int. J. Remote Sens. 1999, 20, 497–510. [Google Scholar] [CrossRef]
- Smith, W.H.; Sandwell, D.T. Bathymetry prediction from dense satellite altimetry and sparse shipboard bathymetry. J. Geophys. Res. 1994, 9, 21803–21824. [Google Scholar] [CrossRef]
- Casal, G.; Hedley, J.D.; Monteys, X.; Harris, P.; Cahalane, C.; McCarthy, T. Satellite-derived bathymetry in optically complex waters using a model inversion approach and Sentinel-2 data. Estuar. Coast. Shelf Sci. 2020, 241, 106814. [Google Scholar] [CrossRef]
- Agrafiotis, P.; Skarlatos, D.; Georgopoulos, A.; Karantzalos, K. Shallow water bathymetry mapping from UAV imagery based on machine learning. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W10, 9–16. [Google Scholar] [CrossRef]
- Mandlberger, G.; Hauer, C.; Wieser, M.; Pfeifer, N. Topo-Bathymetric LiDAR for monitoring river morphodynamics and Instreamhabitats-A case study at the Pielach river. Remote Sens. 2015, 7, 6160–6195. [Google Scholar] [CrossRef]
- Mandlberger, G. A review of airborne laser bathymetry for mapping of inland and coastal waters. Hydraul. Nach. 2020, 116, 6–15. [Google Scholar]
- Salomatin, A.S.; Yusupov, V.I. Seabed and seawater column investigations by acoustic remote sensing. In Proceedings of the XIX Session of the Russian Acoustical Society, Nizhny Novgorod, Russia, 24–28 September 2007. [Google Scholar]
- Canet, C.; Prol-Ledesma, R.M.; Dando, P.R.; Vazquez-Figueroa, V.; Shumilin, E.; Birosta, E.; Sanchez, A.; Robinson, C.J.; Camprubi, A.; Tauler, E. Discovery of massive seafloor gas seepage along the Wagner Fault, northern Gulf of Califonia. Sediment. Geol. 2010, 228, 292–303. [Google Scholar] [CrossRef]
- Klauke, I.; Weinrebe, W.; Petersen, C.J.; Bowden, D. Temporal variability of gas seeps offshore New Zealand: Multi-frequency geoacoustic imaging of the Wairarapa area, Hikurangi margin. Mar. Geol. 2010, 272, 49–58. [Google Scholar] [CrossRef]
- Dondurur, D.; Cifci, G.; Drahor, M.G.; Coskun, S. Acoustic evidence of shallow gas accumulations and active pockmarks in the Izmir Gulf, Aegean sea. Mar. Petrol. Geol. 2011, 28, 1505–1516. [Google Scholar] [CrossRef]
- Jin, Y.K.; Kim, Y.; Baranov, B.; Shoji, H.; Obzhirov, A. Distribution and expression of gas seeps in a gas hydrate province of the northeastern Sakhalin continental slope, Sea of Okhotsk. Mar. Petrol. Geol. 2011, 28, 1844–1855. [Google Scholar] [CrossRef]
- Rajan, A.; Mienert, J.; Bunz, S. Acoustic evidence for a gas migration and release system in Arctic glaciated continental margins offshore NW-Svalbard. Mar. Petrol. Geol. 2012, 32, 36–49. [Google Scholar] [CrossRef]
- Dewangan, P.; Sriram, G.; Kumar, A.; Mazumdar, A.; Peketi, A.; Mahale, V.; Reddy, S.S.C.; Babu, A. Widespread occurrence of methane seeps in deep-water regions of Krishna-Godavari basin, Bay of Bengal. Mar. Petrol. Geol. 2021, 124, 104783. [Google Scholar] [CrossRef]
- Von Deimling, J.S.; Greinert, J.; Chapman, N.R.; Rabbel, W.; Linke, P. Acoustic imaging of natural gas seepage in the North Sea: Sensing bubbles controlled by variable currents. Limnol. Oceanogr. Methods 2010, 8, 155–171. [Google Scholar] [CrossRef]
- Greinert, J. Monitoring temporal variability of bubble release at seeps: The hydroacoustic swath system GasQuant. J. Geoph. Res. 2008, 113, C07048. [Google Scholar] [CrossRef]
- Kannberg, P.K.; Trehu, A.M.; Pierce, S.D.; Paull, C.K.; Caress, D.W. Temporal variation of methane flares in the ocean above Hydrate Ridge, Oregon. Earth Plan. Sci. Lett. 2013, 368, 33–42. [Google Scholar] [CrossRef]
- Gentz, T.; Damm, E.; Von Deimling, J.S.; Mau, S.; McGInnis, D.F.; Schluter, M. A water column study of methane around gas flares located at the West Spitsbergen continental margin. Cont. Shelf. Res. 2014, 72, 107–118. [Google Scholar] [CrossRef]
- Urban, P.; Koser, K.; Greinert, J. Processing of multibeam water column image data for automated bubble/seep detection and repeated mapping. Limnol. Oceanogr. Methods 2017, 15, 1–21. [Google Scholar] [CrossRef]
- Longo, M.; Lazzaro, G.; Caruso, C.G.; Radulescu, V.; Radulescu, R.; Scappuzzo, S.S.S.; Birot, D.; Italiano, F. Black sea methane flares from the seafloor: Tracking outgrassing by using passive acoustics. Front. Earth Sci. 2021, 9, 678834. [Google Scholar] [CrossRef]
- Bednar, J.B. A brief history of seismic migration. Geophysics 2005, 70, 3MJ–20MJ. [Google Scholar] [CrossRef]
- McMechan, G.A. Determination of source parameters by wavefield extrapolation. Geophys. J. Int. 1982, 71, 613–628. [Google Scholar] [CrossRef] [Green Version]
- Loewenthal, D.; Hu, L. Two methods for computing the imaging condition for common-shot prestack migration. Geophysics 1991, 56, 378–381. [Google Scholar] [CrossRef]
- Yoon, K.; Marfurt, K.J.; Starr, W. Challenges in reverse-time migration. In Proceedings of the SEG Technical Program Expanded Abstracts, Denver, CO, USA, 10–15 October 2004. [Google Scholar]
- Zhou, H.; Hu, H.; Zou, Z.; Wo, Y.; Youn, O. Reverse time migration: A prospect of seismic imaging methodology. Earth-Sci. Rev. 2018, 179, 207–227. [Google Scholar] [CrossRef]
- Etgen, J.; Gray, S.H.; Zhang, Y. An overview of depth imaging in exploration geophysics. Geophysics 2009, 74, WCA5–WCA17. [Google Scholar] [CrossRef]
- Huang, Y.; Lin, D.; Bai, B.; Roby, S.; Ricardez, C. Challenges in presalt depth imaging of the deepwater Santos Basin, Brazil. Lead. Edge 2010, 29, 820–825. [Google Scholar] [CrossRef]
- Salomatin, A.S.; Yusupov, V.I. Acoustic investigation of gas “flares” in the Sea of Okhotsk. Oceanology 2011, 51, 857–865. [Google Scholar] [CrossRef]
- Greinert, J.; Artemov, Y.; Egorov, V.; Batist, M.D.; McGinnis, D. 1300-m-high rising bubbles from mud volcanos at 2080m in the Black Sea: Hydroacoustic characteristics and temporal variability. Earth Plan. Sci. Lett. 2006, 244, 33–42. [Google Scholar] [CrossRef]
- Granin, N.G.; Makarov, M.M.; Kucher, K.M.; Gnatovsky, R.Y. Gas seeps in Lake Biakal-detection, distribution, and implications for water column mixing. Geo-Mar. Lett. 2010, 30, 399–409. [Google Scholar] [CrossRef]
- Chen, S.; Hsu, S.; Tsai, C.; Ku, C.; Yeh, Y.; Wang, Y. Gas seepage, pockmarks and mud volcanoes in the near shore of SW Taiwan. Mar. Geophys. Res. 2010, 31, 133–147. [Google Scholar] [CrossRef]
- Kosloff, D.D.; Baysal, E. Migration with the full acoustic wave equation. Geophysics 1983, 48, 677–687. [Google Scholar] [CrossRef]
- Teng, Y.; Dai, T. Finite-element prestack reverse-time migration for elastic waves. Geophysics 1989, 54, 1204–1208. [Google Scholar] [CrossRef]
- Baysal, E.; Kosloff, D.D.; Sherwood, J.W.C. Reverse time migration. Geophysics 1983, 48, 1514–1524. [Google Scholar] [CrossRef]
- Gutowski, M.; Bull, J.; Henstock, T.; Dix, J.; Hogarth, P.; Leighton, T.; White, P. Chirp sub-bottom profiler source signature design and field testing. Mar. Geophys. Res. 2002, 23, 481–492. [Google Scholar] [CrossRef]
- Caldwell, J.; Dragoset, W. A brief review of seismic air-gun arrays. Lead. Edge 2000, 19, 898–902. [Google Scholar] [CrossRef]
- Hayashi, K.; Burns, D.R.; Toksoz, M.N. Discontinuous-Grid Finite-Difference seismic modeling including surface topography. Bull. Seismol. Soc. Am. 2001, 91, 1750–1764. [Google Scholar] [CrossRef]
- Ryberg, T.; Weber, M. Receiver function arrays: A reflection seismic approach. Geophys. J. Int. 2000, 141, 1–11. [Google Scholar] [CrossRef]
- Karplus, H.B. Velocity of sound in a liquid containing gas bubbles. J. Acoust. Soc. Am. 1957, 29, 1261–1262. [Google Scholar] [CrossRef]
- Nakoryakov, V.E.; Dontsov, V.E.; Pokusaev, B.G. Pressure wave in a liquid suspension with solid particles and gas bubbles. Int. J. Multiph. Flow 1996, 22, 417–429. [Google Scholar] [CrossRef]
- Stolojanu, V.; Prakash, A. Hydrodynamic measurements in a slurry bubble column using ultrasonic techniques. Chem. Eng. Sci. 1997, 52, 4225–4230. [Google Scholar] [CrossRef]
- Roy, S.; Senger, K.; Hovland, M.; Romer, M.; Braathen, A. Geological controls on shallow gas distribution and seafloor seepage in an Arctic fjord of Spitsbergen, Norway. Mar. Petrol. Geol. 2019, 107, 237–254. [Google Scholar] [CrossRef]
- Duarte, H.; Pinheiro, L.M.; Teixeira, F.C.; Monteiro, J.H. High-resolution seismic imaging of gas accumulations and seepage in the sediments of the Ria de Aveiro barrier lagoon (Portugal). Geo-Mar. Lett. 2007, 27, 115–126. [Google Scholar] [CrossRef]
- Kamath, A.; Bihs, H.; Arntsen, O.A. Numerical investigations of the hydrodynamics of an oscillating water column device. Ocean Eng. 2015, 102, 40–50. [Google Scholar] [CrossRef]
- Casadio, S.; Arino, O.; Serpe, D. Gas flaring monitoring from space using the ATSR instrument series. Remote Sens. Environ. 2012, 116, 239–249. [Google Scholar] [CrossRef]
- Smith, A.J.; Mienert, J.; Bunz, S.; Greinert, J. Thermogenic methane injection via bubble transport into the upper Arctic Ocean from the hydrate-charged Vestnesa Ridge, Svalbard. Geochem. Geophys. Geosyst. 2014, 15, 1945–1959. [Google Scholar] [CrossRef]
- Li, Z.; Tang, B.; Ji, S. Subsalt illumination analysis using RTM 3D dip gathers. In Proceedings of the SEG Annual Meeting, Las Vegas, NV, USA, 4–9 November 2012. [Google Scholar]
- Singh, B.; Malinnowski, M.; Gorszczyk, A.; Malehmir, A.; Buske, S.; Sito, L.; Marsden, P. 3D high-resolution seismic imaging of the iron-oxide deposits in Ludvika (Sweden) using full-waveform inversion and reverse-time migration. Solid Earth Disc. 2021, 1, 1065–1085. [Google Scholar] [CrossRef]
- Davis, T. The state of EOR with CO2 and associated seismic monitoring. Lead. Edge 2010, 29, 31–33. [Google Scholar] [CrossRef]
- Furre, A.; Eiken, O.; Alnes, H.; Vevatne, J.N.; Kiaer, A.F. 20 years of monitoring CO2-injection at Sleipner. Energy Proced. 2017, 114, 3916–3926. [Google Scholar] [CrossRef]
- Cohen, J.K.; Stockwell, J.W. CWP/SU: Seismic Un*x Release No. 42: An Open Source Software Package for Seismic Research and Processing; Center for Wave Phenomena, Colorado School of Mines: Golden, CO, USA, 2010. [Google Scholar]



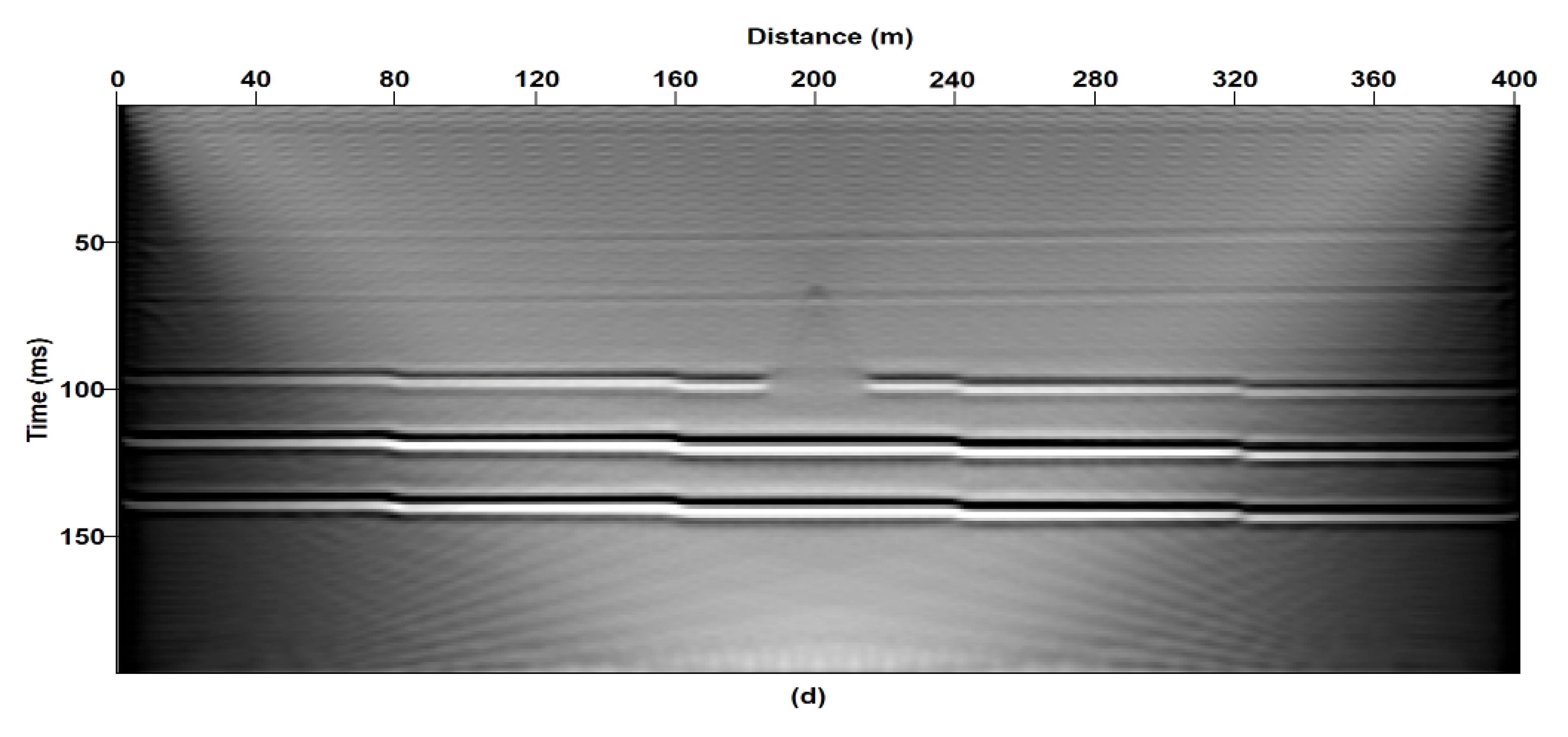
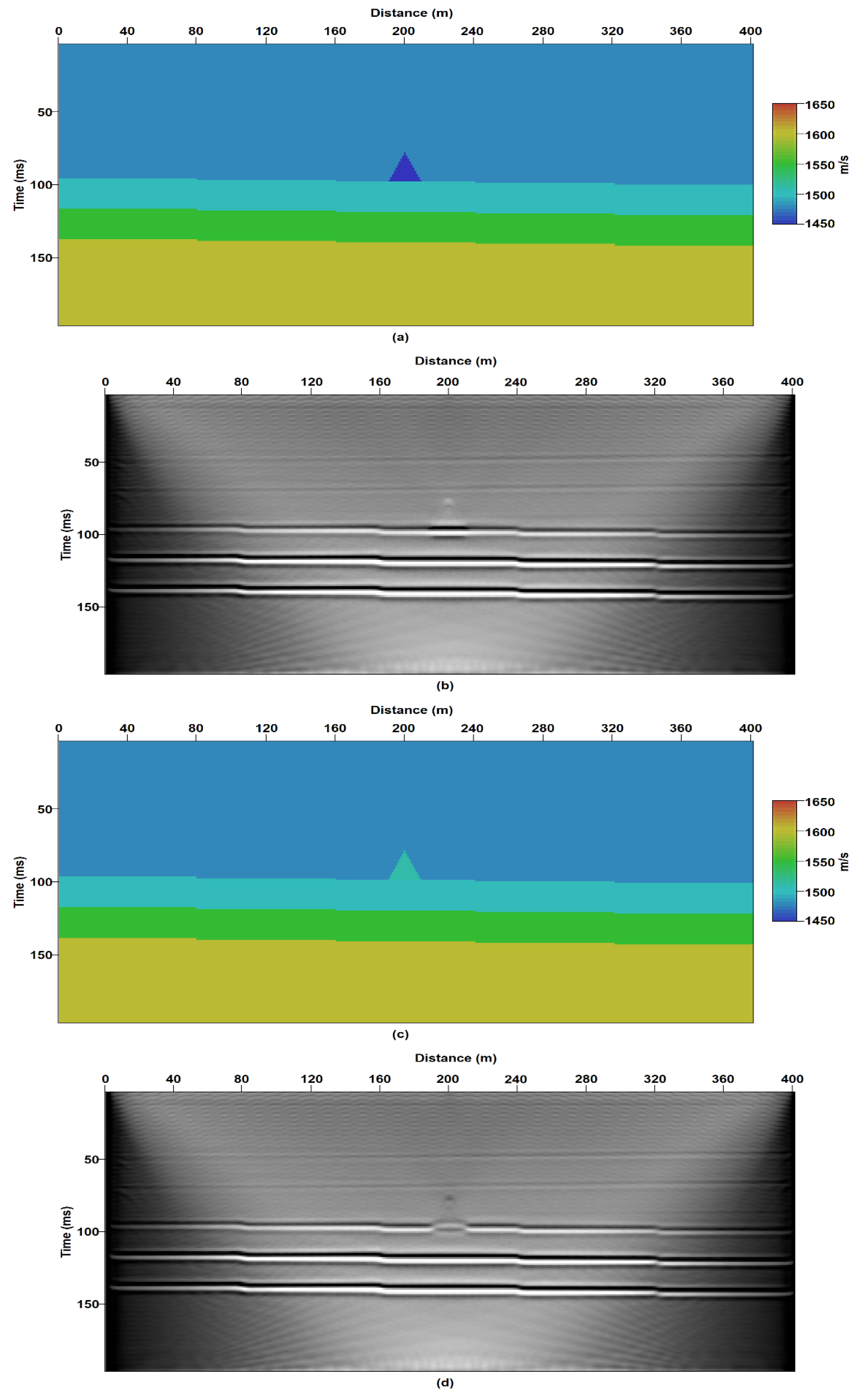
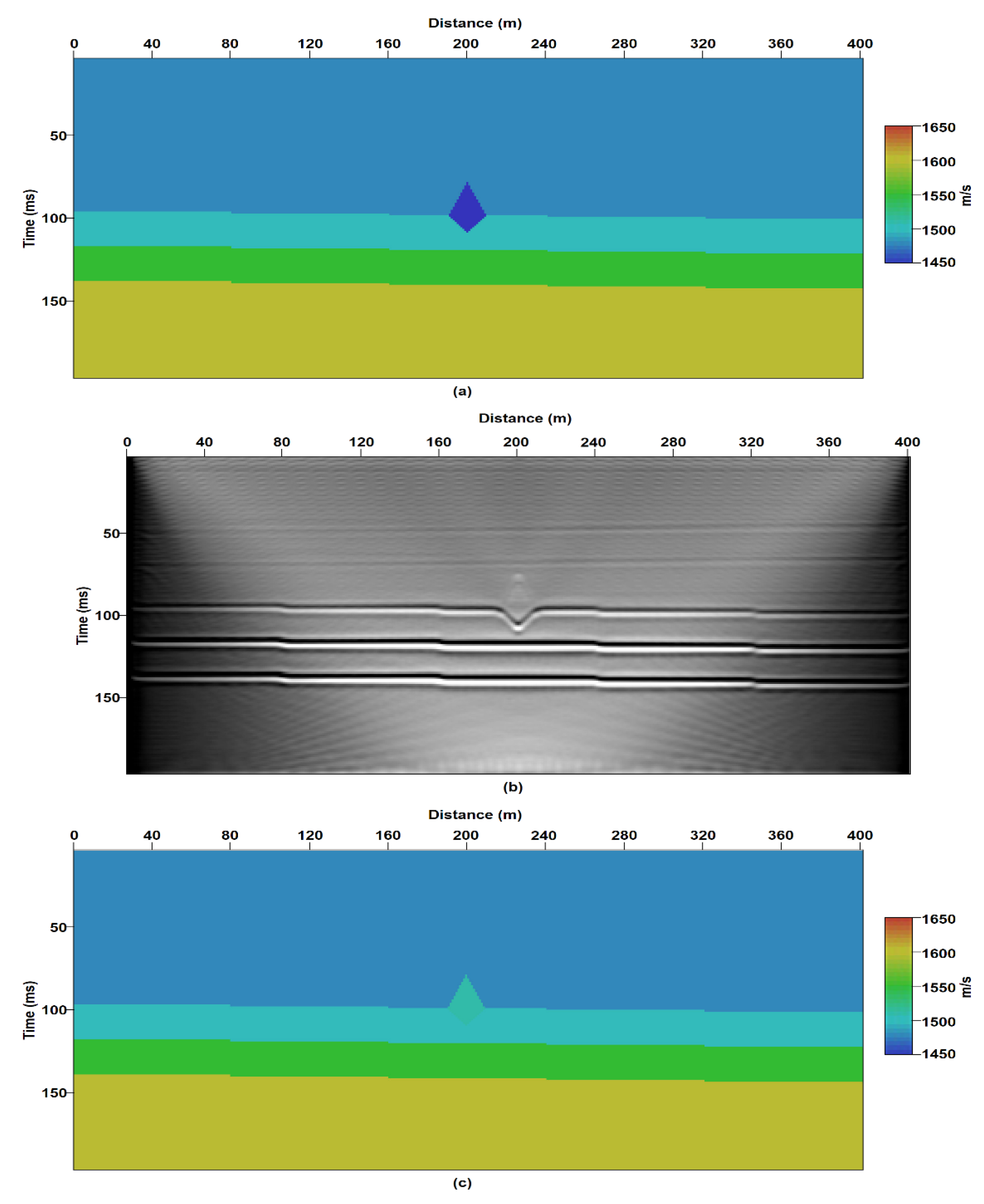
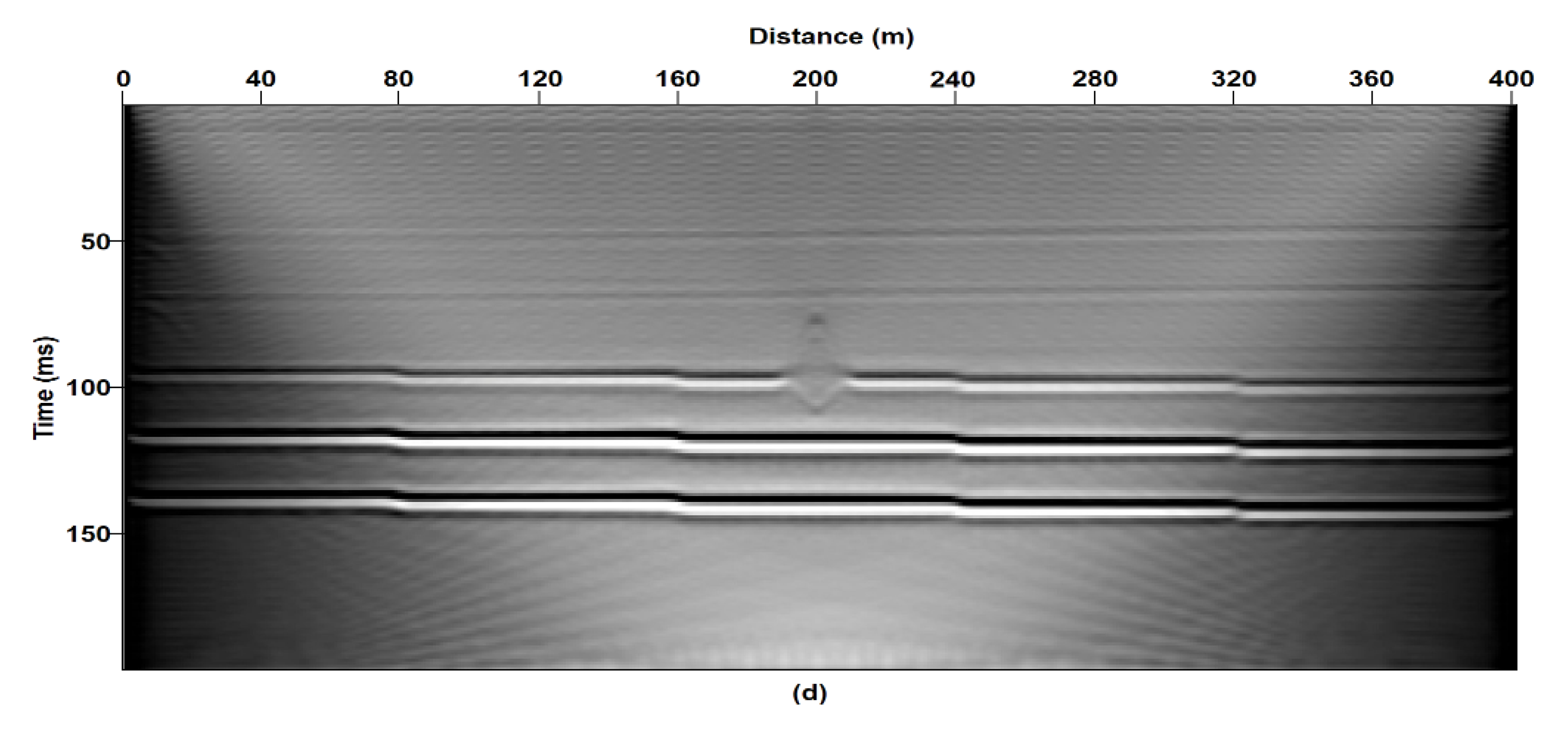

| Model Name | Variables | Objective |
|---|---|---|
| Flat | Acoustic velocities of seawater and three sediment layers | Validation |
| Pockmark | Size (10/20/30 m) | Depression effect |
| Mound | Size (10/20/30 m) | Protrusion effect |
| Model Name | Velocity Change | Objective |
|---|---|---|
| Velocity variant at flat | Negative (−30 m/s) and positive (+30 m/s) | Perturbation of seawater above seabed |
| Velocity variant at pockmark | Negative (−30 m/s) and positive (+30 m/s) | Perturbation with pockmark |
| Velocity variant at mound | Negative (−30 m/s) and positive (+30 m/s) | Perturbation with mound |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheong, S.; Yelisetti, S.; Chun, J.-H. Numerical Imaging of the Seabed and Acoustic Flares with Topography and Velocity Variance. Remote Sens. 2022, 14, 4652. https://doi.org/10.3390/rs14184652
Cheong S, Yelisetti S, Chun J-H. Numerical Imaging of the Seabed and Acoustic Flares with Topography and Velocity Variance. Remote Sensing. 2022; 14(18):4652. https://doi.org/10.3390/rs14184652
Chicago/Turabian StyleCheong, Snons, Subbarao Yelisetti, and Jong-Hwa Chun. 2022. "Numerical Imaging of the Seabed and Acoustic Flares with Topography and Velocity Variance" Remote Sensing 14, no. 18: 4652. https://doi.org/10.3390/rs14184652
APA StyleCheong, S., Yelisetti, S., & Chun, J.-H. (2022). Numerical Imaging of the Seabed and Acoustic Flares with Topography and Velocity Variance. Remote Sensing, 14(18), 4652. https://doi.org/10.3390/rs14184652








