Analysis of GNSS-Derived Tropospheric Zenith Non-Hydrostatic Delay Anomaly during Sandstorms in Northern China on 15th March 2021
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methodology
2.2.1. PWV Inversion Based on GNSS Data
2.2.2. Singular Spectrum Analysis
3. Results and Discussion
3.1. Relationship between ZNHD/PWV and PM2.5/PM10
3.2. Monitoring Sandstorms Based on the ZNHD Residual
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yao, L.; Lu, N.; Yue, X.; Du, J.; Yang, C. Comparison of hourly PM2.5 observations between urban and suburban areas in Beijing, China. Int. J. Environ. Res. Public Health 2015, 12, 12264–12276. [Google Scholar] [CrossRef] [PubMed]
- Kiser, D.; Metcalf, W.; Elhanan, G.; Schnieder, B.; Schlauch, K.; Joros, A.; Petersen, C.; Grzymski, J. Particulate matter and emergency visits for asthma: A time-series study of their association in the presence and absence of wildfire smoke in Reno, Nevada, 2013–2018. Environ. Health 2020, 19, 92. [Google Scholar] [CrossRef] [PubMed]
- Kuempel, E.; Attfield, M.; Vallyathan, V.; Lapp, N.; Hale, J.; Smith, R.; Castranova, V. Pulmonary inflammation and crystalline silica in respirable coal mine dust: Dose response. J. Biosci. 2003, 28, 61. [Google Scholar] [CrossRef] [PubMed]
- Lei, Y.; Chan, C.; Wang, P.; Lee, C.; Cheng, T. Effects of Asian dust event particles on inflammation markers in peripheral blood and bronchoalveolar lavage in pulmonary hypertensive rats. Environ. Res. 2004, 95, 71–76. [Google Scholar] [CrossRef]
- Wang, P.; Vuran, M.; Al-Rodhaan, M.; Al-Dhelaan, A.; Akyildiz, I. Topology analysis of wireless sensor networks for sandstorm monitoring. In Proceedings of the IEEE International Conference on Communications (ICC), Kyoto, Japan, 5–9 June 2011. [Google Scholar]
- Pun, V.; Tian, L.; Ho, K. Particulate matter from re-suspended mineral dust and emergency cause-specific respiratory hospitalizations in Hong Kong. Atmos. Environ. 2017, 165, 191–197. [Google Scholar] [CrossRef]
- The New York Times. The Worst Dust Storm in a Decade Shrouds Beijing and Northern China. Available online: https://www.nytimes.com/2021/03/15/world/asia/china-sandstorm.html (accessed on 15 March 2021).
- NPR. Desert Dust Sweeps into Beijing, Causing China’s Worst Sandstorm in 10 Years. Available online: https://www.npr.org/2021/03/15/977397941/desert-dust-sweeps-into-beijing-causing-chinas-worst-sandstorm-in-10-years (accessed on 15 March 2021).
- Reuters. Beijing Choked in Dust Storm Stirred by Heavy Northwest Winds. 14 March 2021. Available online: https://www.reuters.com/article/us-china-weather-sandstorm/beijing-choked-in-duststorm-amid-heavy-northwest-winds-idUSKBN2B703O?il=0 (accessed on 15 March 2021).
- South China Morning Post. Six Dead, Dozens Missing as Beijing, Northern China and Mongolia Hit by Worst Sandstorm in a Decade. Available online: https://www.scmp.com/news/china/article/3125433/worst-sandstorm-decade-hits-beijing-huge-parts-northern-china (accessed on 15 March 2021).
- NASA Earth Observatory. Early Season Dust Storm Hits Beijing. Available online: https://earthobservatory.nasa.gov/images/148052/early-season-dust-storm-hits-beijing (accessed on 15 March 2021).
- World Meteorological Organization. Severe Sand and Dust Storm Hits Asia. Available online: https://public.wmo.int/en/media/news/severe-sand-and-dust-storm-hits-asia (accessed on 16 March 2021).
- Qu, J.; Hao, X.; Kafatos, M.; Wang, L. Asian dust storm monitoring combining terra and aqua MODIS SRB measurements. IEEE Geosci. Remote Sens. Lett. 2006, 3, 484–486. [Google Scholar] [CrossRef]
- Hao, X. Saharan dust storm detection using moderate resolution imaging spectroradiometer thermal infrared bands. J. Appl. Remote Sens. 2007, 1, 13510. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, W.; Qu, J. Detection of Asian dust storm using MODIS measurements. Remote Sens. 2017, 9, 869. [Google Scholar] [CrossRef]
- Sun, K.; Su, Q.; Ming, Y. Dust storm remote sensing monitoring supported by MODIS land surface reflectance database. Remote Sens. 2019, 11, 1772. [Google Scholar] [CrossRef]
- Rayegania, B.; Baratib, S.; Goshtasba, H.; Gachpaza, S.; Ramezanic, J.; Sarkheild, H. Sand and dust storm sources identification: A remote sensing approach. Ecol. Indic. 2020, 112, 106099. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.; Rocken, C.; Anthes, R.; Ware, R. GPS meteorology: Remote sensing of atmospheric water vapor using the global positioning system. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Rohm, W. The precision of humidity in GNSS tomography. Atmos. Res. 2012, 107, 69–75. [Google Scholar] [CrossRef]
- Jiang, P.; Ye, S.; Liu, Y.; Zhang, J.; Xia, P. Near real-time water vapor tomography using ground-based GPS and meteorological data: Long-term experiment in Hong Kong. Ann. Geophys. 2014, 32, 911–923. [Google Scholar] [CrossRef]
- Benevides, P.; Catalao, J.; Miranda, P. On the inclusion of GPS precipitable water vapour in the nowcasting of rainfall. Nat. Hazards Earth Syst. Sci. 2015, 15, 2605–2616. [Google Scholar] [CrossRef]
- Yong, W.; Liu, Y.; Li, J.; Liu, L. The Effect of PM2. 5/PM10 variation based on precipitable water vapor and wind speed. J. Catastrophol. 2015, 30, 5–7. [Google Scholar]
- Ye, S.; Xia, P.; Cai, C. Optimization of GPS water vapor tomography technique with radiosonde and COSMIC historical data. Ann. Geophys. 2016, 34, 789–799. [Google Scholar] [CrossRef]
- Stoycheva, A.; Guerova, G. Study of fog in Bulgaria by using the GNSS tropospheric products and large scale dynamic analysis. J. Atmos. Sol. Terr. Phys. 2015, 133, 87–97. [Google Scholar] [CrossRef]
- Tang, X.; Hancock, C.; Xiang, Z.; Kong, Y.; Shi, L.; Jonathan Arthur Quaye-Ballard. Precipitable water vapour retrieval from GPS precise point positioning and NCEP CFSv2 dataset during typhoon events. Sensors 2018, 18, 3831. [Google Scholar] [CrossRef]
- Zhu, E.; Yang, L.; Jia, P.; Zhao, S.; Gao, Y. Correlation between GNSS Tropospheric Delay and Smog Haze; China Satellite Navigation System Management Office Academic Exchange Center: Beijing, China, 2018. [Google Scholar]
- Guo, J.; Hou, R.; Zhou, M.; Jin, X.; Li, C.; Liu, X.; Gao, H. Monitoring 2019 forest fires in southeastern Australia with GNSS technique. Remote Sens. 2021, 13, 386. [Google Scholar] [CrossRef]
- Guo, J.; Hou, R.; Zhou, M.; Jin, X.; Li, G. Detection of particulate matter changes caused by 2020 California wildfires based on GNSS and radiosonde station. Remote Sens. 2021, 13, 4557. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y.; Yao, W. GPS-based PWV for precipitation forecasting and its application to a typhoon event. J. Atmos. Sol. Terr. Phys. 2018, 167, 124–133. [Google Scholar] [CrossRef]
- Choy, S.; Wang, C.; Zhang, K.; Kuleshov, Y. GPS sensing of precipitable water vapour during the March 2010 Melbourne storm. Adv. Space Res. 2013, 52, 1688–1699. [Google Scholar] [CrossRef]
- Nykiel, G.; Figurski, M.; Baldysz, Z. Analysis of GNSS sensed precipitable water vapour and tropospheric gradients during the derecho event in Poland of 11 August 2017. J. Atmos. Sol. Terr. Phys. 2019, 193, 105082. [Google Scholar] [CrossRef]
- Yu, J.; Tan, K.; Zhang, C.; Zhao, B.; Wang, D.; Li, Q. Present-day crustal movement of the Chinese mainland based on Global Navigation Satellite System data from 1998 to 2018. Adv. Space Res. 2019, 63, 840–856. [Google Scholar] [CrossRef]
- Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites. Use Artif. Satell. Geod. 1972, 15, 247–251. [Google Scholar]
- Byun, S.H.; Bar-Sever, Y.E. A new type of troposphere zenith path delay product of the international GNSS service. J. Geod. 2009, 83, 367–373. [Google Scholar] [CrossRef]
- Wen, H.; Dang, Y.; Li, L. Short-Term PM2.5 concentration prediction by combining GNSS and meteorological factors. IEEE Access 2020, 8, 115202–115216. [Google Scholar] [CrossRef]
- Jin, S.G.; Luo, O.; Ren, C. Effects of physical correlations on long-distance GPS positioning and zenith tropospheric delay estimates. Adv. Space Res. 2010, 46, 190–195. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y.; Li, F.; Guo, J. Estimation and evaluation of the precipitable water vapor from GNSS PPP in Asia Region. In Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2017; pp. 85–95. [Google Scholar]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Randolph, H.W. GPS meteorology: Mapping zenith wet delays onto precipitable water. J. Appl. Meteorol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Vautard, R.; Yiou, P.; Ghil, M. Singular spectrum analysis: A toolkit for short, noisy chaotic signals. Phys. D 1992, 58, 95–126. [Google Scholar] [CrossRef]
- Chen, Q.; van Dam, T.; Sneeuw, N.; Collilieux, X.; Weigelt, M.; Rebischung, P. Singular spectrum analysis for modeling seasonal signals from GPS time series. J. Geodyn. 2013, 72, 25–35. [Google Scholar] [CrossRef]
- Kondrashov, D.; Berloff, P. Stochastic modeling of decadal variability in ocean gyres. Geophys. Res Lett. 2015, 42, 1543–1553. [Google Scholar] [CrossRef]
- Shen, Y.; Guo, J.; Liu, X.; Kong, Q.; Guo, L.; Li, W. Long-term prediction of polar motion using a combined SSA and ARMA model. J. Geod. 2018, 92, 333–343. [Google Scholar] [CrossRef]
- Zhou, M.S.; Guo, J.Y.; Liu, X.; Shen, Y.; Zhao, C.M. Crustal movement derived by GNSS technique considering common mode error with MSSA. Adv. Space Res. 2020, 66, 1819–1828. [Google Scholar] [CrossRef]
- Hassani, H. Singular spectrum analysis: Methodology and comparison. J. Data Sci. 2007, 5, 239–257. [Google Scholar] [CrossRef]
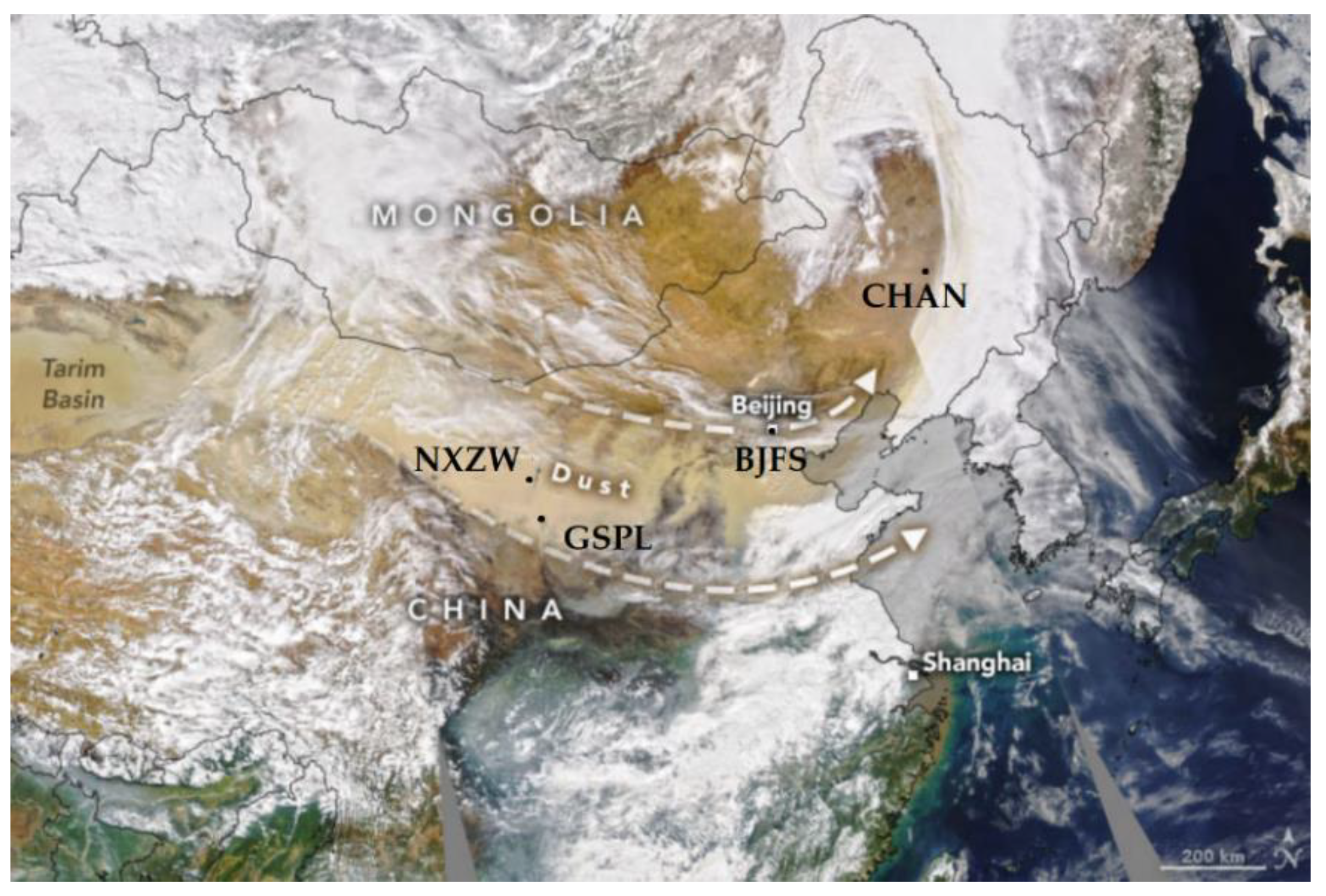
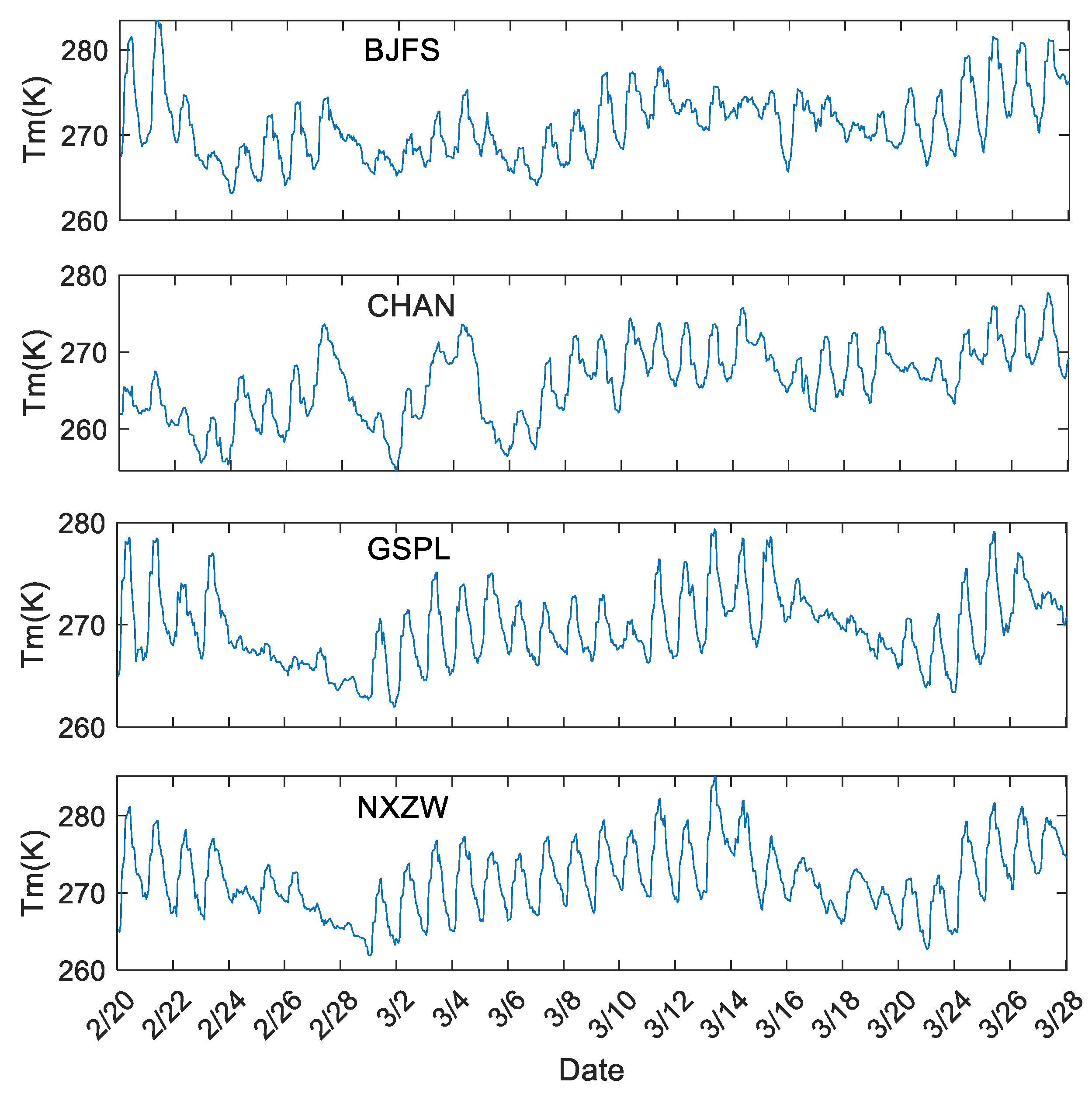
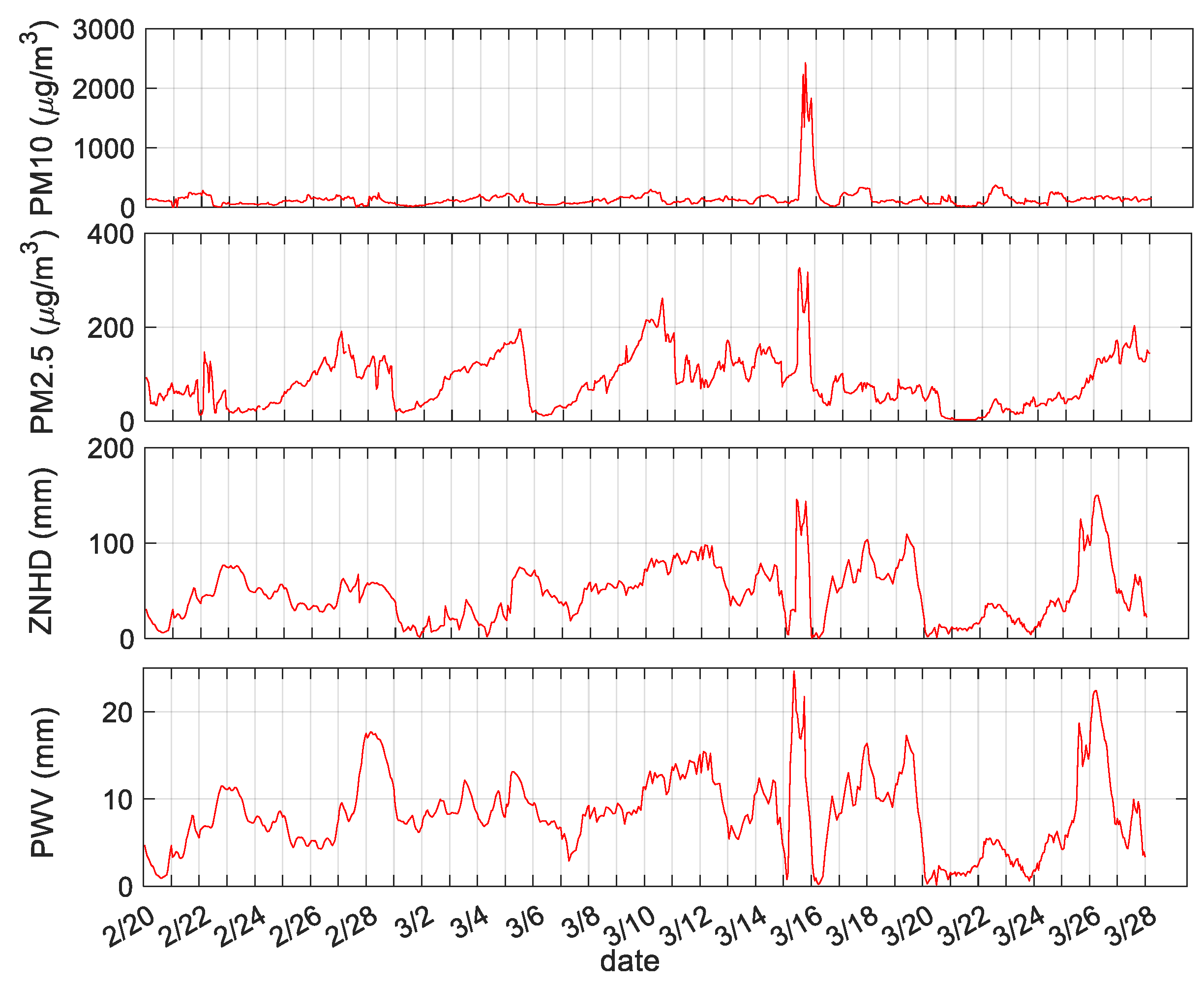
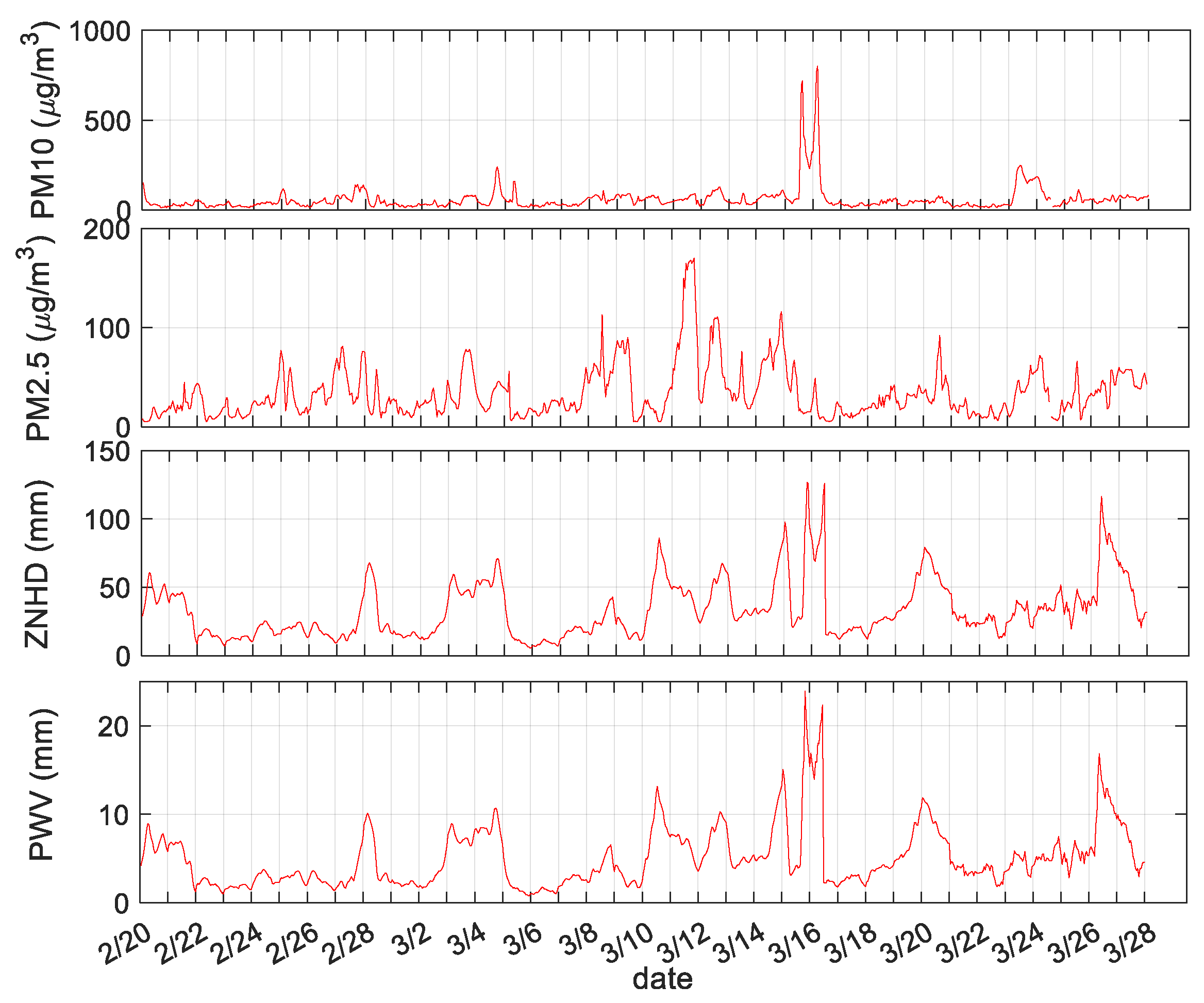


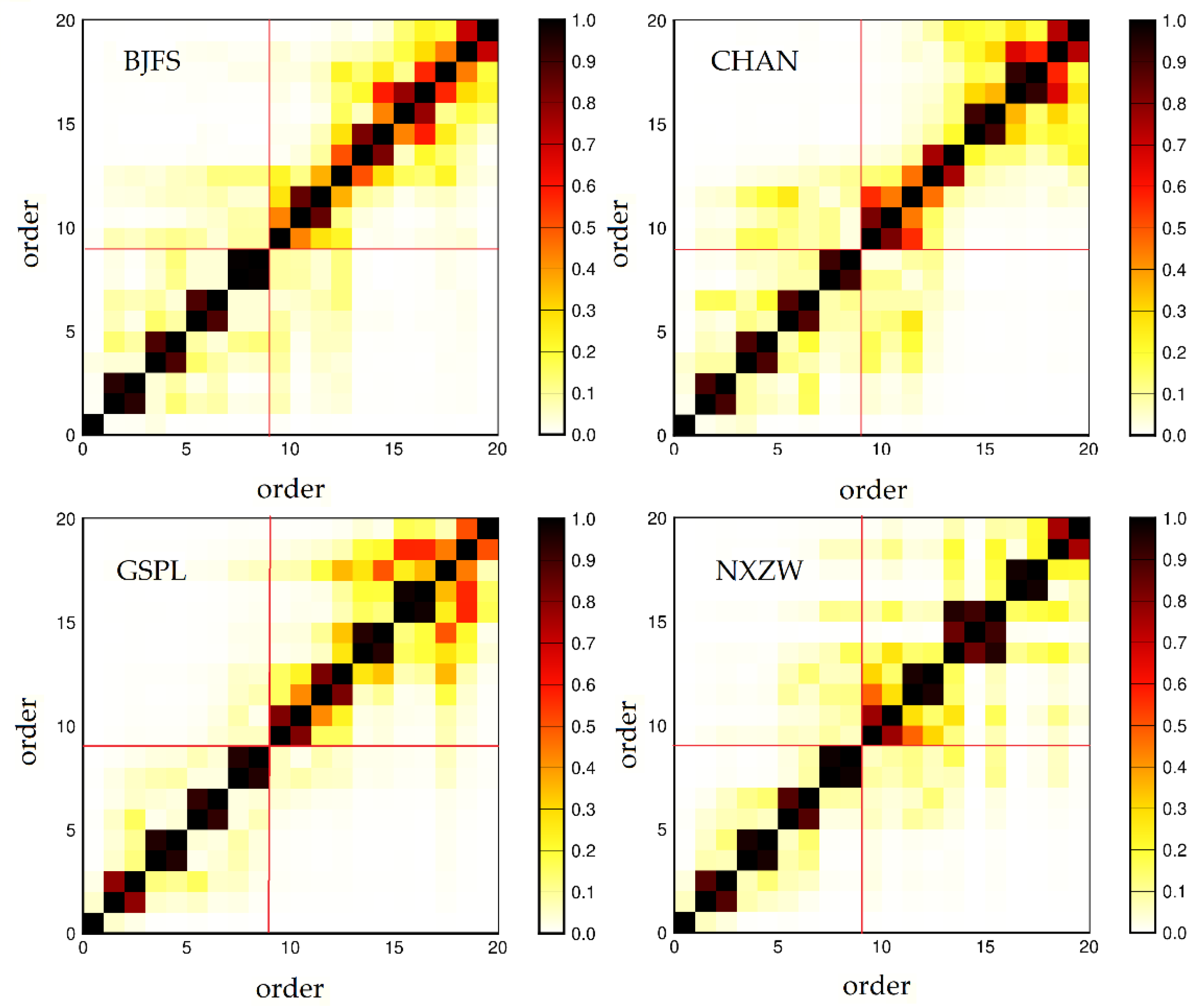

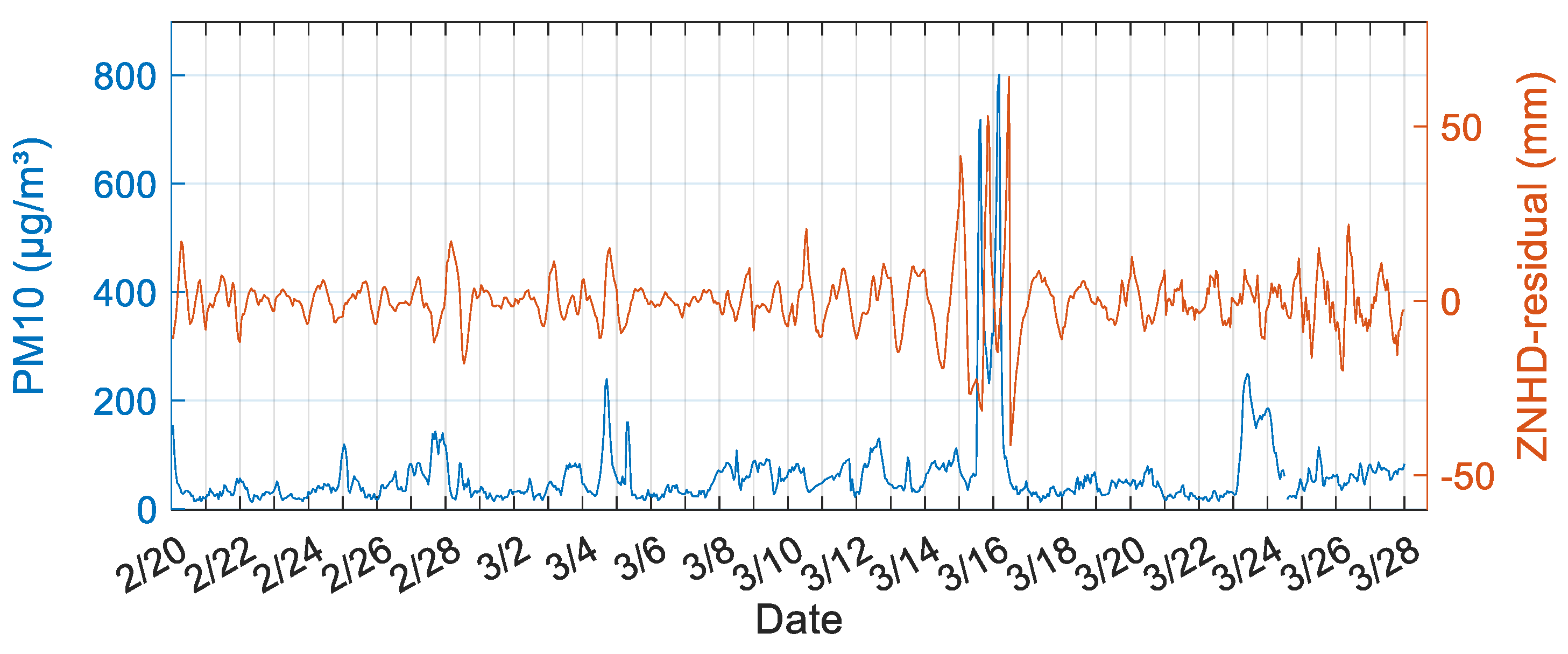
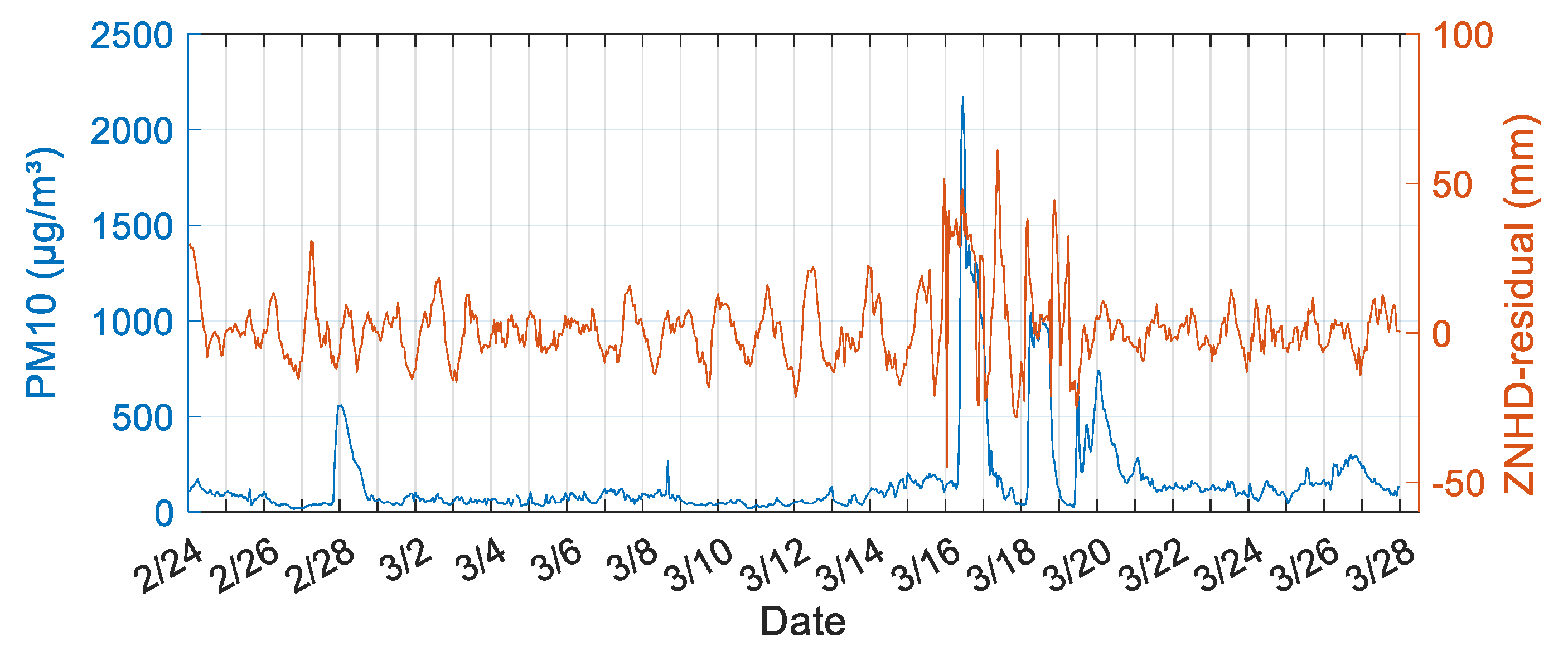
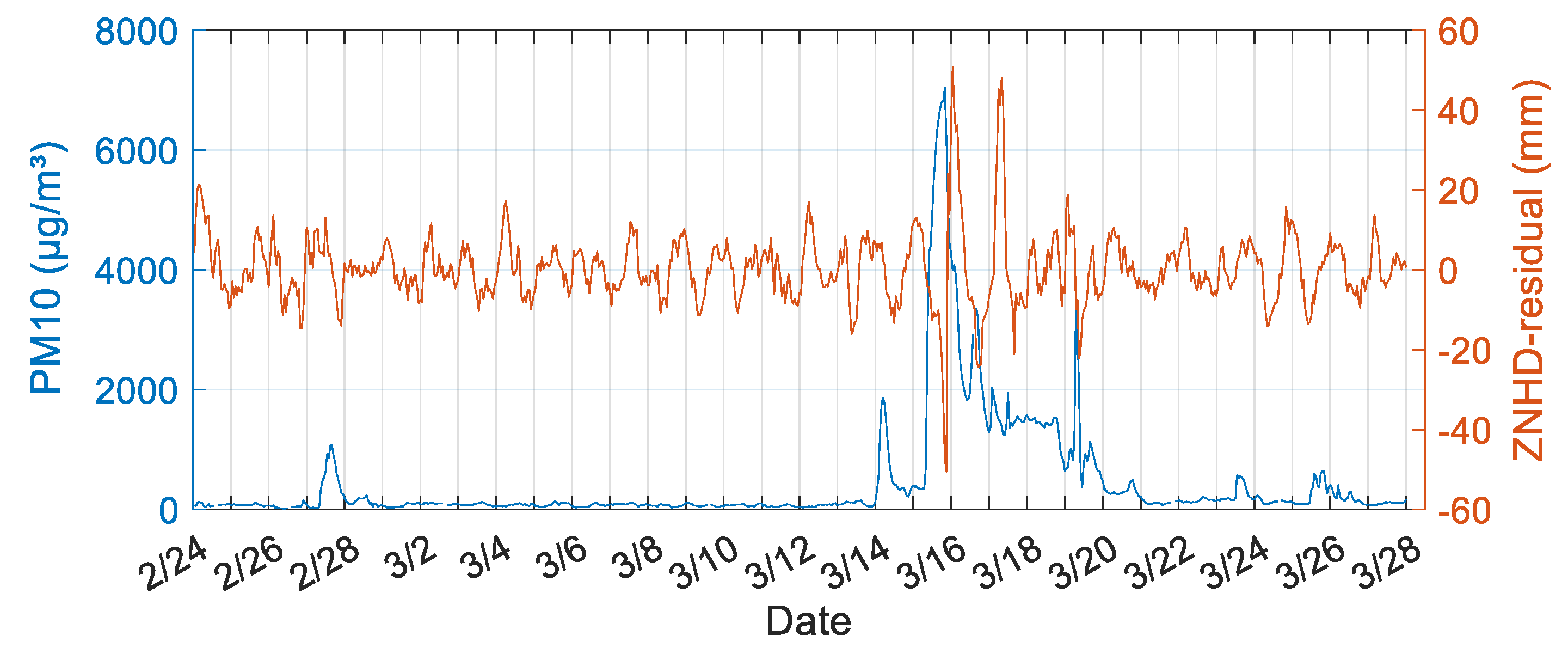
| Site | GSPL | NXZW | BJFS | CHAN |
|---|---|---|---|---|
| Maximum (Max) | 6.02 | 5.61 | 5.12 | 6.06 |
| Minimum (Min) | 4.03 | 3.72 | 3.62 | 3.61 |
| Mean | 4.81 | 4.41 | 4.28 | 4.32 |
| Standard deviation (Std) | 0.53 | 0.54 | 0.43 | 0.57 |
| Before Sandstorms | During Sandstorms | After Sandstorms | |
|---|---|---|---|
| BJFS | 0.08 | 0.75 | 0.27 |
| CHAN | 0.16 | 0.71 | 0.05 |
| GSPL | 0.23 | 0.54 | 0.18 |
| NXZW | 0.14 | 0.35 | 0.24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, M.; Guo, J.; Liu, X.; Hou, R.; Jin, X. Analysis of GNSS-Derived Tropospheric Zenith Non-Hydrostatic Delay Anomaly during Sandstorms in Northern China on 15th March 2021. Remote Sens. 2022, 14, 4678. https://doi.org/10.3390/rs14184678
Zhou M, Guo J, Liu X, Hou R, Jin X. Analysis of GNSS-Derived Tropospheric Zenith Non-Hydrostatic Delay Anomaly during Sandstorms in Northern China on 15th March 2021. Remote Sensing. 2022; 14(18):4678. https://doi.org/10.3390/rs14184678
Chicago/Turabian StyleZhou, Maosheng, Jinyun Guo, Xin Liu, Rui Hou, and Xin Jin. 2022. "Analysis of GNSS-Derived Tropospheric Zenith Non-Hydrostatic Delay Anomaly during Sandstorms in Northern China on 15th March 2021" Remote Sensing 14, no. 18: 4678. https://doi.org/10.3390/rs14184678
APA StyleZhou, M., Guo, J., Liu, X., Hou, R., & Jin, X. (2022). Analysis of GNSS-Derived Tropospheric Zenith Non-Hydrostatic Delay Anomaly during Sandstorms in Northern China on 15th March 2021. Remote Sensing, 14(18), 4678. https://doi.org/10.3390/rs14184678







