Gap-Filling and Missing Information Recovery for Time Series of MODIS Data Using Deep Learning-Based Methods
Abstract
:1. Introduction
2. Study Materials
3. Methodology
3.1. Data Quality Evaluation and Preprocessing
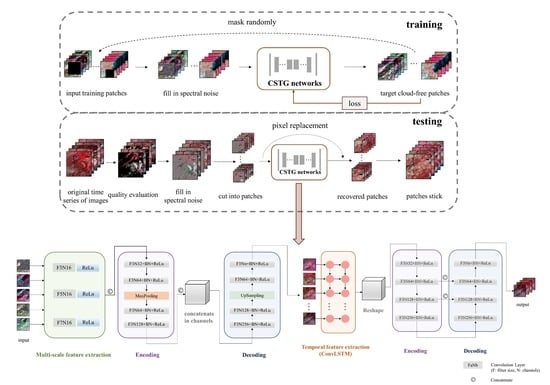
3.2. The Content Generation Network
3.3. The Sequence-Texture Generation Network
4. Experiment Design
4.1. Model Training and Setup
4.2. Model Comparisons
4.3. Evaluation Metrics
5. Results
5.1. Experiments Based on Artificial Datasets
5.2. Experiments Based on Observed Datasets
5.3. Ablation Study of Sequence-Texture Generation Network
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Di Vittorio, C.A.; Georgakakos, A.P. Land cover classification and wetland inundation mapping using modis. Remote Sens. Environ. 2018, 204, 1–17. [Google Scholar] [CrossRef]
- Vali, A.; Comai, S.; Matteucci, M. Deep learning for land use and land cover classification based on hyperspectral and multispectral earth observation data: A review. Remote Sens. 2020, 12, 2495. [Google Scholar] [CrossRef]
- Li, Z.; Xin, Q.; Sun, Y.; Cao, M. A deep learning-based framework for automated extraction of building footprint polygons from very high-resolution aerial imagery. Remote Sens. 2021, 13, 3630. [Google Scholar] [CrossRef]
- Xin, Q.C.; Dai, Y.J.; Liu, X.P. A simple time-stepping scheme to simulate leaf area index, phenology, and gross primary production across deciduous broadleaf forests in the eastern united states. Biogeosciences 2019, 16, 467–484. [Google Scholar] [CrossRef]
- Wu, W.; Sun, Y.; Xiao, K.; Xin, Q. Development of a global annual land surface phenology dataset for 1982–2018 from the avhrr data by implementing multiple phenology retrieving methods. Int. J. Appl. Earth Obs. 2021, 103, 102487. [Google Scholar] [CrossRef]
- Omori, K.; Sakai, T.; Miyamoto, J.; Itou, A.; Oo, A.N.; Hirano, A. Assessment of paddy fields’ damage caused by cyclone nargis using modis time-series images (2004–2013). Paddy Water Environ. 2021, 19, 271–281. [Google Scholar] [CrossRef]
- Yokoya, N.; Yamanoi, K.; He, W.; Baier, G.; Adriano, B.; Miura, H.; Oishi, S. Breaking limits of remote sensing by deep learning from simulated data for flood and debris-flow mapping. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4400115. [Google Scholar] [CrossRef]
- Chen, S.; Chen, X.; Chen, X.; Chen, J.; Cao, X.; Shen, M.; Yang, W.; Cui, X. A novel cloud removal method based on ihot and the cloud trajectories for landsat imagery. Remote Sens. 2018, 10, 1040. [Google Scholar] [CrossRef]
- Shen, H.; Li, H.; Qian, Y.; Zhang, L.; Yuan, Q. An effective thin cloud removal procedure for visible remote sensing images. ISPRS J. Photogramm. Remote Sens. 2014, 96, 224–235. [Google Scholar] [CrossRef]
- Richter, R. Atmospheric correction of satellite data with haze removal including a haze/clear transition region. Comput. Geosci. 1996, 22, 675–681. [Google Scholar] [CrossRef]
- Guillemot, C.; Le Meur, O. Image inpainting: Overview and recent advances. IEEE Signal Proc. Mag. 2014, 31, 127–144. [Google Scholar] [CrossRef]
- Sadiq, A.; Sulong, G.; Edwar, L. Recovering defective landsat 7 enhanced thematic mapper plus images via multiple linear regression model. IET Comput. Vis. 2016, 10, 788–797. [Google Scholar] [CrossRef]
- Pringle, M.J.; Schmidt, M.; Muir, J.S. Geostatistical interpolation of slc-off landsat etm plus images. ISPRS J. Photogramm. Remote Sens. 2009, 64, 654–664. [Google Scholar] [CrossRef]
- Zhang, C.R.; Li, W.D.; Civco, D. Application of geographically weighted regression to fill gaps in slc-off landsat etm plus satellite imagery. Int. J. Remote Sens. 2014, 35, 7650–7672. [Google Scholar] [CrossRef]
- Cheng, Q.; Shen, H.F.; Zhang, L.P.; Yuan, Q.Q.; Zeng, C. Cloud removal for remotely sensed images by similar pixel replacement guided with a spatio-temporal mrf model. ISPRS J. Photogramm. Remote Sens. 2014, 92, 54–68. [Google Scholar] [CrossRef]
- Yang, J.F.; Yin, W.T.; Zhang, Y.; Wang, Y.H. A fast algorithm for edge-preserving variational multichannel image restoration. SIAM J. Imaging Sci. 2009, 2, 569–592. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, L.; Li, Z.; Tong, X.; Atkinson, P.M. Spatial–spectral radial basis function-based interpolation for landsat etm+ slc-off image gap filling. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7901–7917. [Google Scholar] [CrossRef]
- Lin, C.H.; Tsai, P.H.; Lai, K.H.; Chen, J.Y. Cloud removal from multitemporal satellite images using information cloning. IEEE Trans. Geosci. Remote Sens. 2013, 51, 232–241. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, Y.; Lv, H.T.; Qian, J. Removal of thin clouds in landsat-8 oli data with independent component analysis. Remote Sens. 2015, 7, 11481–11500. [Google Scholar] [CrossRef]
- Makarau, A.; Richter, R.; Schlapfer, D.; Reinartz, P. Combined haze and cirrus removal for multispectral imagery. IEEE Geosci. Remote Sens. Lett. 2016, 13, 379–383. [Google Scholar] [CrossRef]
- Zhang, Y.; Guindon, B.; Cihlar, J. An image transform to characterize and compensate for spatial variations in thin cloud contamination of landsat images. Remote Sens. Environ. 2002, 82, 173–187. [Google Scholar] [CrossRef]
- Gladkova, I.; Grossberg, M.D.; Shahriar, F.; Bonev, G.; Romanov, P. Quantitative restoration for modis band 6 on aqua. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2409–2416. [Google Scholar] [CrossRef]
- Xin, Q.C.; Olofsson, P.; Zhu, Z.; Tan, B.; Woodcock, C.E. Toward near real-time monitoring of forest disturbance by fusion of modis and landsat data. Remote Sens. Environ. 2013, 135, 234–247. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, Q.Q.; Li, T.W.; Shen, H.F.; Zheng, L.; Zhang, L.P. Large-scale modis aod products recovery: Spatial-temporal hybrid fusion considering aerosol variation mitigation. ISPRS J. Photogramm. Remote Sens. 2019, 157, 1–12. [Google Scholar] [CrossRef]
- Roy, D.P.; Ju, J.; Lewis, P.; Schaaf, C.; Gao, F.; Hansen, M.; Lindquist, E. Multi-temporal modis-landsat data fusion for relative radiometric normalization, gap filling, and prediction of landsat data. Remote Sens. Environ. 2008, 112, 3112–3130. [Google Scholar] [CrossRef]
- Moreno-Martínez, Á.; Izquierdo-Verdiguier, E.; Maneta, M.P.; Camps-Valls, G.; Robinson, N.; Muñoz-Marí, J.; Sedano, F.; Clinton, N.; Running, S.W. Multispectral high resolution sensor fusion for smoothing and gap-filling in the cloud. Remote Sens. Environ. 2020, 247, 111901. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.; Huo, L.; Zhang, Z.; Tang, P. Multi-temporal landsat data automatic cloud removal using poisson blending. IEEE Access 2020, 8, 46151–46161. [Google Scholar] [CrossRef]
- Tseng, D.C.; Tseng, H.T.; Chien, C.L. Automatic cloud removal from multi-temporal spot images. Appl. Math. Comput. 2008, 205, 584–600. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, X.L.; Vogelmann, J.E.; Gao, F.; Jin, S.M. A simple and effective method for filling gaps in landsat etm plus slc-off images. Remote Sens. Environ. 2011, 115, 1053–1064. [Google Scholar] [CrossRef]
- Zeng, C.; Shen, H.F.; Zhang, L.P. Recovering missing pixels for landsat etm plus slc-off imagery using multi-temporal regression analysis and a regularization method. Remote Sens. Environ. 2013, 131, 182–194. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; MIT Press: Cambridge, MA, USA, 2014; Volume 2, pp. 2672–2680. [Google Scholar]
- Zhang, H.; Xu, T.; Li, H.; Zhang, S.; Wang, X.; Huang, X.; Metaxas, D. Stackgan: Text to photo-realistic image synthesis with stacked generative adversarial networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 5908–5916. [Google Scholar]
- Zhu, J.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2242–2251. [Google Scholar]
- Chen, Y.; Tang, L.L.; Yang, X.; Fan, R.S.; Bilal, M.; Li, Q.Q. Thick clouds removal from multitemporal zy-3 satellite images using deep learning. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2019, 13, 143–153. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, Q.Q.; Li, J.; Li, Z.W.; Shen, H.F.; Zhang, L.P. Thick cloud and cloud shadow removal in multitemporal imagery using progressively spatio-temporal patch group deep learning. ISPRS J. Photogramm. Remote Sens. 2020, 162, 148–160. [Google Scholar] [CrossRef]
- Li, W.; Li, Y.; Chan, J.C.W. Thick cloud removal with optical and sar imagery via convolutional-mapping-deconvolutional network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2865–2879. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, S.X.; Woodcock, C.E. Improvement and expansion of the fmask algorithm: Cloud, cloud shadow, and snow detection for landsats 4-7, 8, and sentinel 2 images. Remote Sens. Environ. 2015, 159, 269–277. [Google Scholar] [CrossRef]
- Li, Z.W.; Shen, H.F.; Cheng, Q.; Liu, Y.H.; You, S.C.; He, Z.Y. Deep learning based cloud detection for medium and high resolution remote sensing images of different sensors. ISPRS J. Photogramm. Remote Sens. 2019, 150, 197–212. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional Lstm Network: A Machine Learning Approach for Precipitation Nowcasting; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Si, C.; Chen, W.; Wang, W.; Wang, L.; Tan, T. An attention enhanced graph convolutional lstm network for skeleton-based action recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 1227–1236. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Zhang, Q.; Yuan, Q.; Chao, Z.; Li, X.; Wei, Y. Missing data reconstruction in remote sensing image with a unified spatial-temporal-spectral deep convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4274–4288. [Google Scholar] [CrossRef] [Green Version]













| Data Usage | Site Location | MODIS Tile ID | Product Type | Longitude and Latitude | Date Ranges |
|---|---|---|---|---|---|
| Training data | North America | H12V04 | MOD09A1 | 74.315°W–79.478°W, 39.927°N–41.615°N | 1 January 2016–31 December 2016 |
| Europe | H19V03 | MOD09A1 | 15.667°E–19.12°E 51.068°N–52.737°N | ||
| Asia | H27V05 | MOD09A1 | 107.888°E–112.234°E 32.985°N–34.674°N | ||
| H27V05 | MOD09A1 | 111.881°E–116.068°E 31.808°N–33.485°N | |||
| H27V06 | MOD13Q1 | 98.310°E–99.71°E 21.793°N–22.476°N | |||
| Validation data | North America | H12V04 | MOD09A1 | 80.721°W–85.922°W 41.004°N–42.686°N | 1 January 2017–31 December 2017 |
| Europe | H19V03 | MOD13Q1 | 25.503°E–27.437°E 54.832°N–55.658°N | ||
| Test data | North America | H12V04 | MOD09A1 | 71.618°W–75.790°W 41.251°N–42.615°N | 10 June 2017, 18 July 2017, 29 August 2017, 30 September 2017, 16 October 2017 |
| Europe | H19V03 | MOD09A1 | 18.404°E–20.379°E 51.252°N–52.915°N | 16 September 2020–14 October 2020 | |
| H20V03 | MOD09A1 | 34.639°E–36.013°E 50.002°N–51.665°N | 12 February 2019–12 March 2019, 29 August 2019 | ||
| Asia | H27V06 | MOD13Q1 | 99.366°E–99.986°E 22.801°N–22.632°N | 2 February 2020, 5 March 2020, 31 October 2020, 16 November 2020, 18 December 2020 | |
| H27V06 | MOD13Q1 | 103.088°E–106.084°E 20.002°N–29.167°N | 11 June 2019–9 July 2019 | ||
| H28V06 | MOD09A1 | 113.367°E–113.775°E 22.152°N–22.632°N | 18 February 2020, 21 March 2020, 22 April 2020, 15 October 2020, 24 November 2020 |
| Methods | Band 1 | Band 2 | Band 3 | Band 4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | MAE | SSIM | R2 | MAE | SSIM | R2 | MAE | SSIM | R2 | MAE | SSIM | |
| WLR | 0.925 | 0.011 | 0.948 | 0.933 | 0.024 | 0.950 | 0.925 | 0.006 | 0.938 | 0.915 | 0.008 | 0.943 |
| STS | 0.894 | 0.014 | 0.924 | 0.890 | 0.032 | 0.913 | 0.907 | 0.006 | 0.919 | 0.894 | 0.009 | 0.922 |
| Chen’s | 0.930 | 0.011 | 0.960 | 0.914 | 0.027 | 0.949 | 0.934 | 0.005 | 0.953 | 0.928 | 0.008 | 0.958 |
| Zhang’s | 0.915 | 0.012 | 0.946 | 0.928 | 0.025 | 0.949 | 0.919 | 0.006 | 0.938 | 0.908 | 0.008 | 0.941 |
| CSTG | 0.943 | 0.010 | 0.958 | 0.938 | 0.024 | 0.951 | 0.932 | 0.006 | 0.950 | 0.930 | 0.008 | 0.952 |
| Methods | B1 | B2 | B3 | B4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | MAE | SSIM | R2 | MAE | SSIM | R2 | MAE | SSIM | R2 | MAE | SSIM | |
| WLR | 0.861 | 0.009 | 0.871 | 0.681 | 0.025 | 0.740 | 0.855 | 0.005 | 0.917 | 0.889 | 0.006 | 0.912 |
| STS | 0.813 | 0.012 | 0.863 | 0.794 | 0.020 | 0.848 | 0.765 | 0.007 | 0.831 | 0.787 | 0.008 | 0.874 |
| Chen’s | 0.783 | 0.012 | 0.897 | 0.813 | 0.023 | 0.783 | 0.875 | 0.004 | 0.930 | 0.868 | 0.007 | 0.921 |
| Zhang’s | 0.849 | 0.010 | 0.886 | 0.821 | 0.018 | 0.821 | 0.856 | 0.005 | 0.923 | 0.886 | 0.006 | 0.920 |
| CSTG | 0.877 | 0.009 | 0.905 | 0.860 | 0.016 | 0.870 | 0.860 | 0.005 | 0.928 | 0.868 | 0.007 | 0.924 |
| Methods | Zhang’s | CSTG | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario A | Scenario B | Scenario A | Scenario B | |||||||||
| R2 | MAE | SSIM | R2 | MAE | SSIM | R2 | MAE | SSIM | R2 | MAE | SSIM | |
| Image 1 | 0.967 | 0.018 | 0.913 | 0.947 | 0.016 | 0.944 | 0.971 | 0.017 | 0.900 | 0.986 | 0.011 | 0.958 |
| Image 2 | 0.982 | 0.013 | 0.986 | 0.974 | 0.015 | 0.965 | 0.987 | 0.013 | 0.986 | 0.978 | 0.014 | 0.970 |
| Image 3 | 0.948 | 0.017 | 0.898 | 0.946 | 0.013 | 0.929 | 0.965 | 0.015 | 0.930 | 0.959 | 0.010 | 0.931 |
| Image 4 | 0.979 | 0.010 | 0.990 | 0.805 | 0.043 | 0.911 | 0.985 | 0.009 | 0.993 | 0.962 | 0.024 | 0.934 |
| Image 5 | 0.937 | 0.013 | 0.934 | 0.959 | 0.020 | 0.968 | 0.968 | 0.010 | 0.950 | 0.947 | 0.023 | 0.970 |
| Mean | 0.963 | 0.014 | 0.944 | 0.926 | 0.021 | 0.943 | 0.975 | 0.013 | 0.952 | 0.966 | 0.016 | 0.953 |
| Method | Image 1 R2/MAE/SSIM | Image 2 R2/MAE/SSIM | Image 3 R2/MAE/SSIM | Image 4 R2/MAE/SSIM | Image 5 R2/MAE/SSIM |
|---|---|---|---|---|---|
| Without sequence-texture generation | 0.957/0.016/0.951 | 0.979/0.014/0.968 | 0.870/0.027/0.929 | 0.896/0.033/0.914 | 0.900/0.028/0.967 |
| With sequence-texture generation | 0.986/0.011/0.958 | 0.978/0.014/0.970 | 0.959/0.010/0.931 | 0.962/0.024/0.934 | 0.947/0.023/0.970 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhou, X.; Ao, Z.; Xiao, K.; Yan, C.; Xin, Q. Gap-Filling and Missing Information Recovery for Time Series of MODIS Data Using Deep Learning-Based Methods. Remote Sens. 2022, 14, 4692. https://doi.org/10.3390/rs14194692
Wang Y, Zhou X, Ao Z, Xiao K, Yan C, Xin Q. Gap-Filling and Missing Information Recovery for Time Series of MODIS Data Using Deep Learning-Based Methods. Remote Sensing. 2022; 14(19):4692. https://doi.org/10.3390/rs14194692
Chicago/Turabian StyleWang, Yidan, Xuewen Zhou, Zurui Ao, Kun Xiao, Chenxi Yan, and Qinchuan Xin. 2022. "Gap-Filling and Missing Information Recovery for Time Series of MODIS Data Using Deep Learning-Based Methods" Remote Sensing 14, no. 19: 4692. https://doi.org/10.3390/rs14194692
APA StyleWang, Y., Zhou, X., Ao, Z., Xiao, K., Yan, C., & Xin, Q. (2022). Gap-Filling and Missing Information Recovery for Time Series of MODIS Data Using Deep Learning-Based Methods. Remote Sensing, 14(19), 4692. https://doi.org/10.3390/rs14194692