A Novel Freeze-Thaw State Detection Algorithm Based on L-Band Passive Microwave Remote Sensing
Abstract
:1. Introduction
2. Methodology
2.1. Study Area and Data
- (1)
- SMAP TB observations and the derived FT-state indicator [26] with 36 km × 36 km spatial resolution at 6 a.m. and 6 p.m. local time. The SMAP L3 product includes an FT state indicator besides H and V polarized TB observations at the L band (1.41 GHz). The data is available starting on 30 March 2015 [26]. The derived FT-state indicator (SMAP L3c FT product) is available globally from 85.044°S to 85.044°N, and we focus on the domain from 20°N to 85.044°N. We use the SMAP TBs for the new algorithm and the binary FT-state indicator for frozen (1) and thawed soil (0), including the transition direction for its evaluation. Moreover, SMAP also provides a 9-km spatial resolution FT product. As noted on https://nsidc.org/data/SPL3FTP_E/versions/3 (accessed on 1 April 2021), the 9-km product is derived from SMAP-enhanced Level-1C brightness temperatures (SPL1CTB_E). For SPL1CTB_E, Backus–Gilbert optimal interpolation techniques are used to extract enhanced information from SMAP antenna temperatures before they are converted to brightness temperatures. Since the Backus–Gilbert optimal interpolation techniques added more noise, we prefer 36 km × 36 km spatial resolution in this study [37]. Only H-polarization is used in this study because the DAV signals between H/V polarizations are small.
- (2)
- Hourly 2m-air (T2m), skin (Tskin), and soil temperatures from the ERA5-land reanalysis available on https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-land?tab=overview (accessed on 1 April 2021) [38]. ERA5-land provides a consistent representation of the evolution of land state variables over several decades at a higher resolution (0.1° × 0.1°) than ERA5 (0.25° × 0.25°). ERA5-land has been produced by replaying the land component of the ECMWF ERA5 climate reanalysis at an enhanced resolution. ERA5-land also provides soil profile information that is vital to the analysis of L-band TBs.
2.2. Methodology
2.2.1. The SMAP F/T Algorithm
2.2.2. The New FT Algorithm
2.3. Evaluation of the New FT-State Detection Algorithm
3. Results
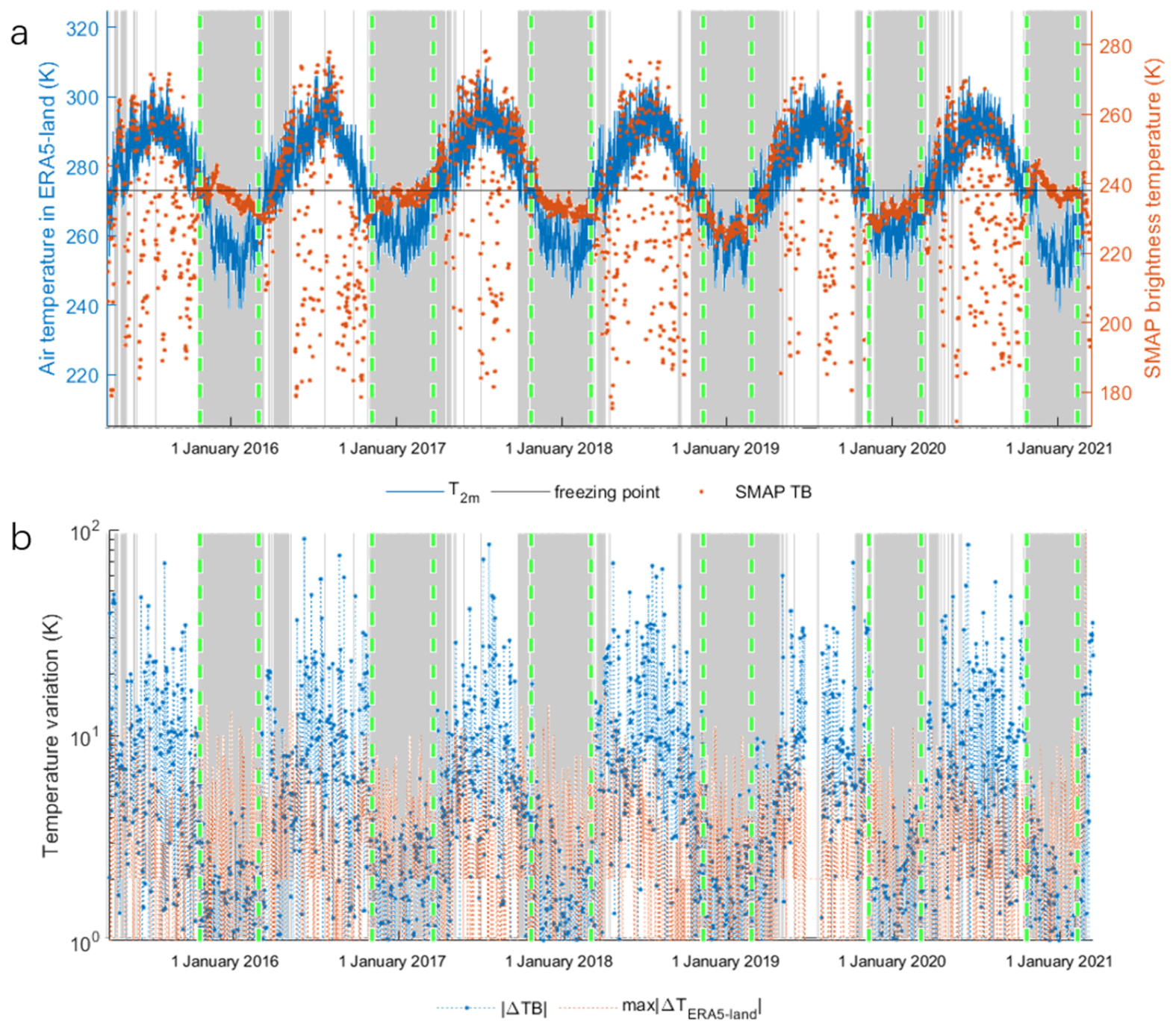
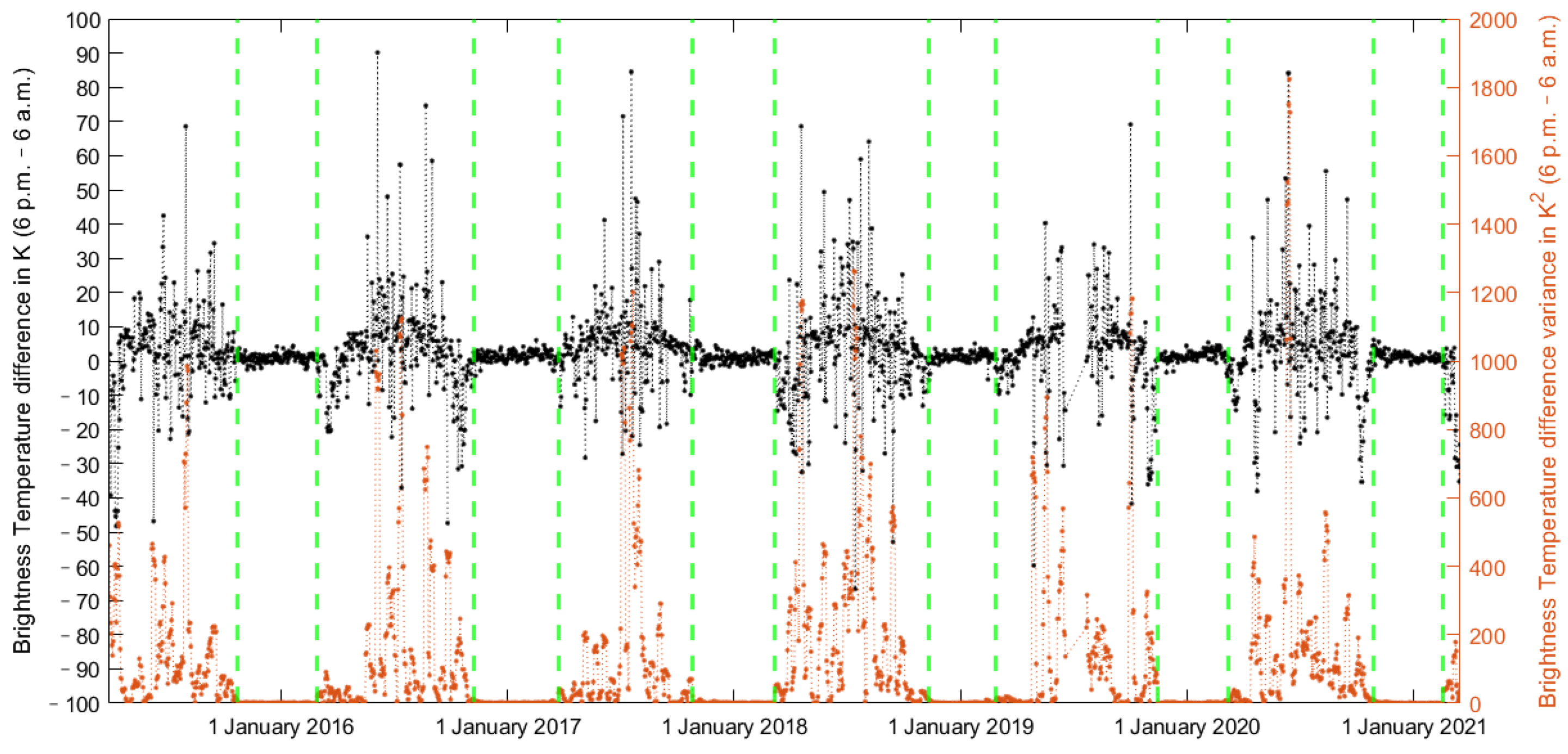
3.1. The Demonstration of the New Method at the Xilinhot Site
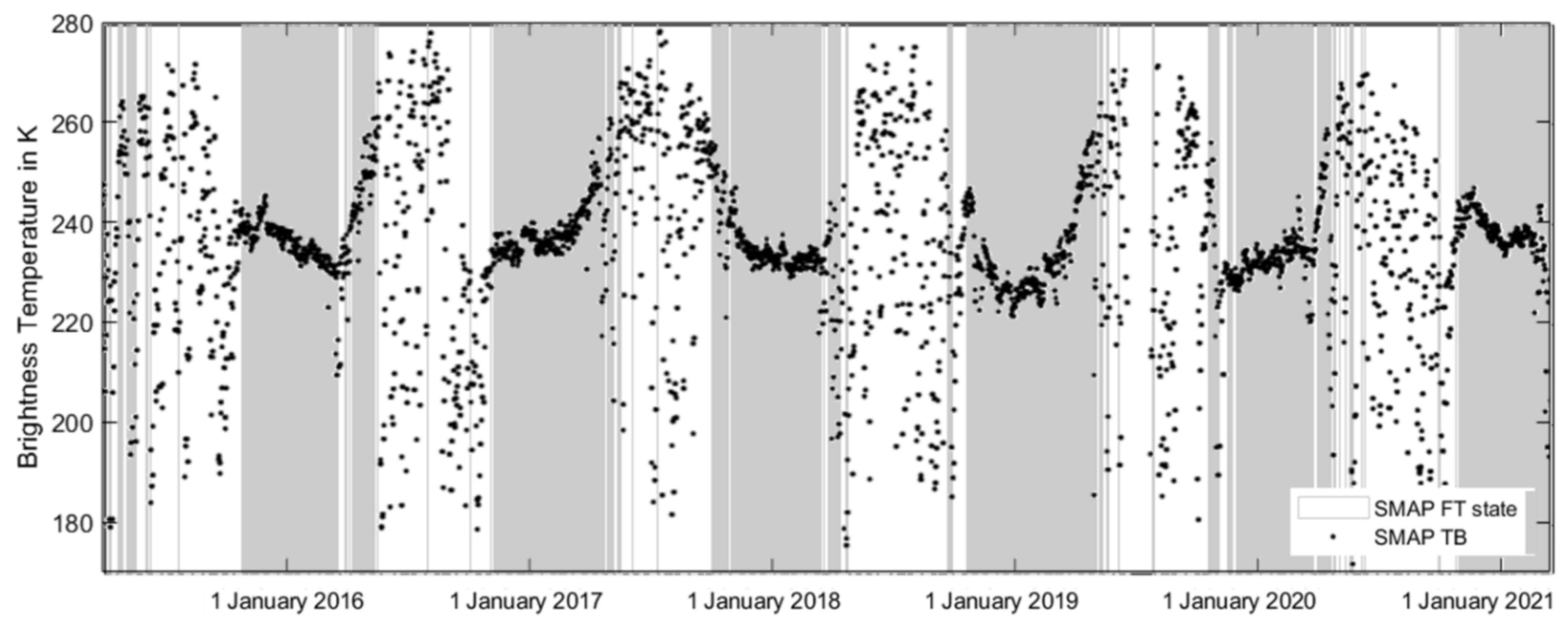
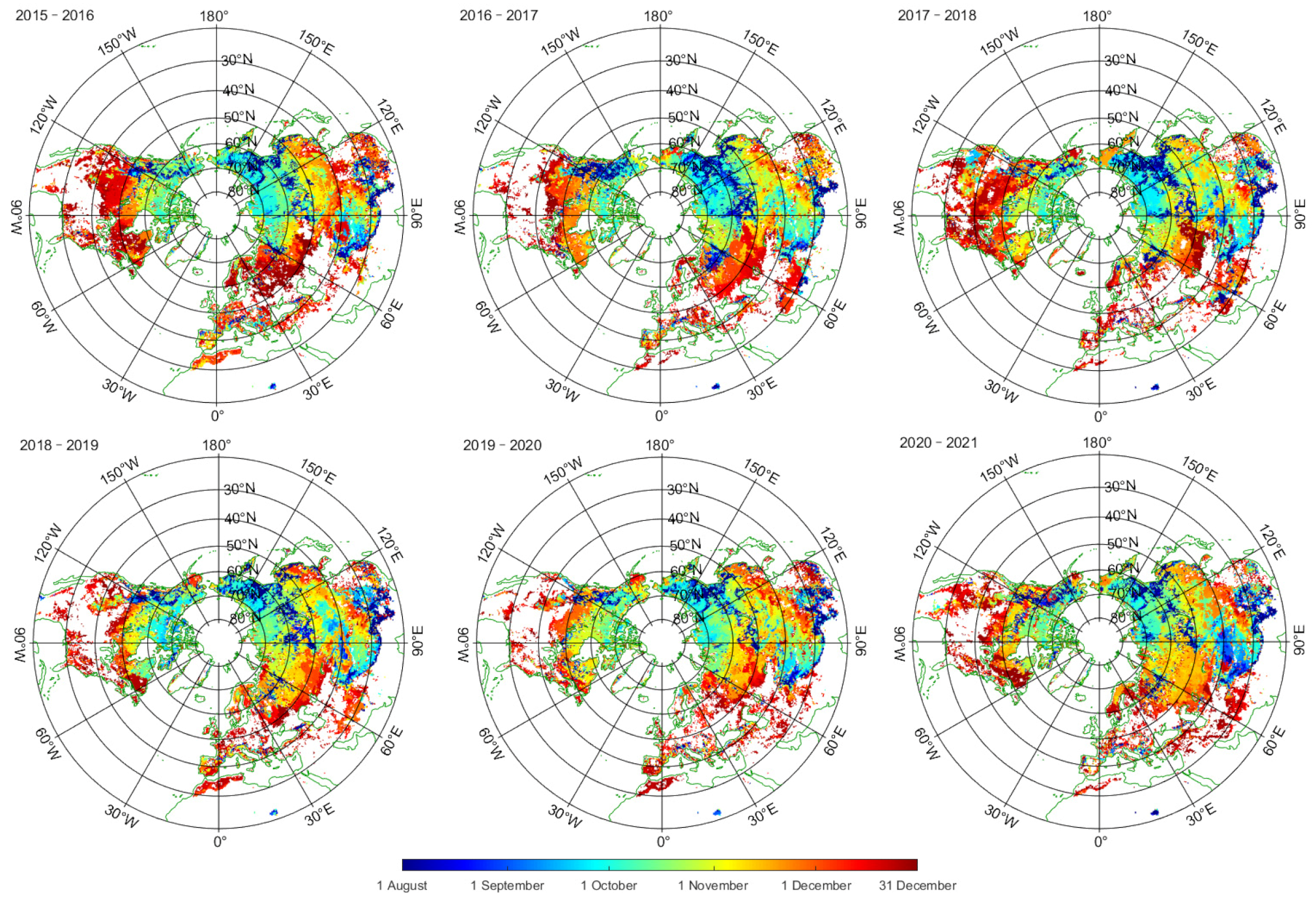
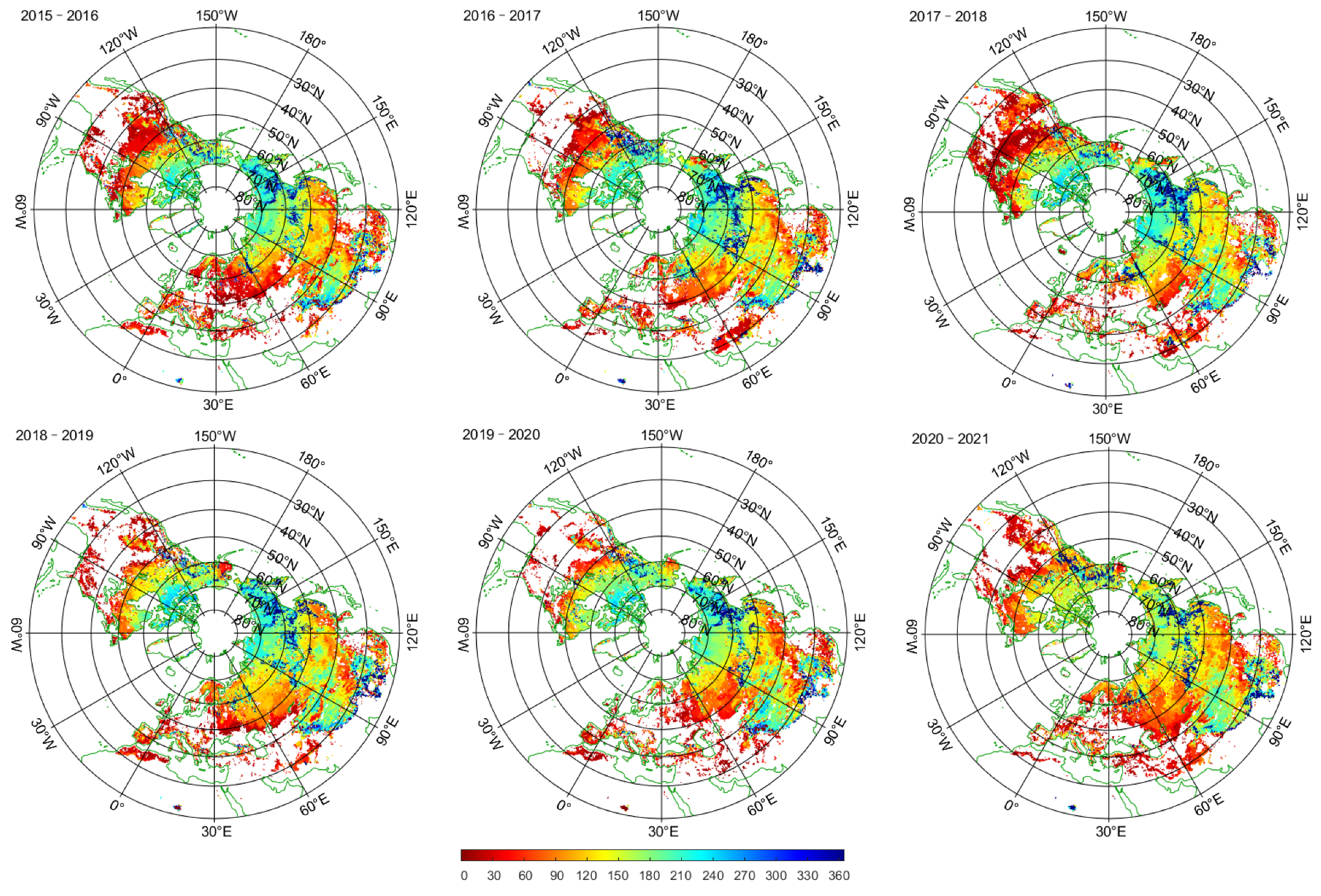
3.2. Result over the Northern Hemisphere
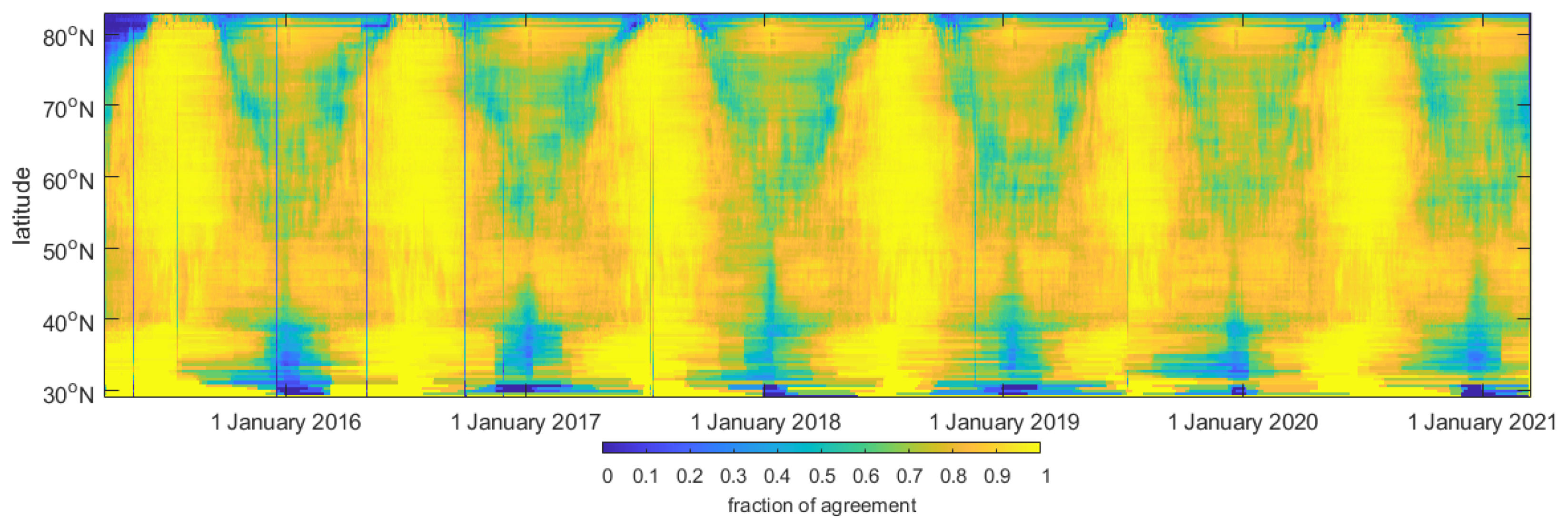
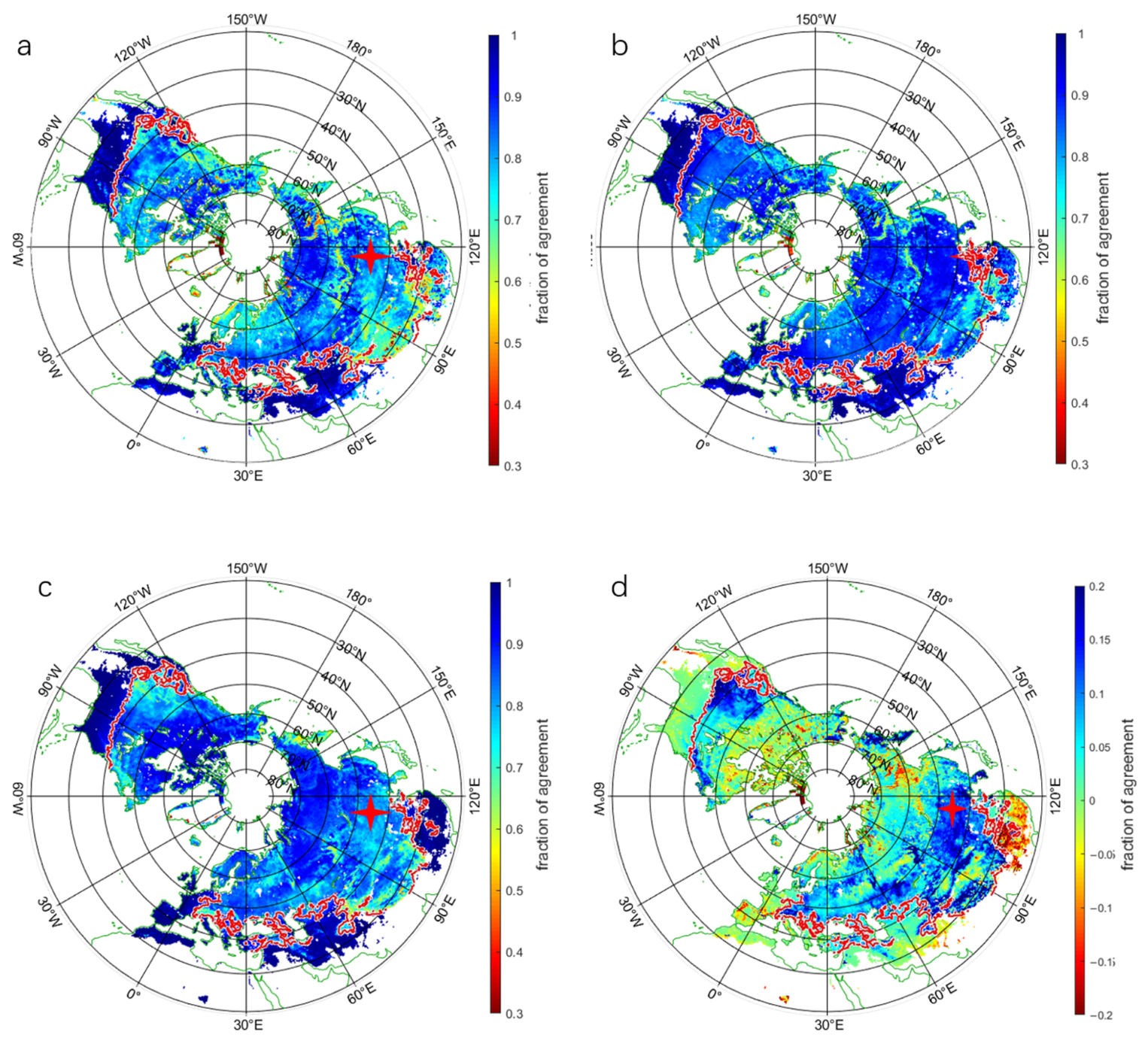
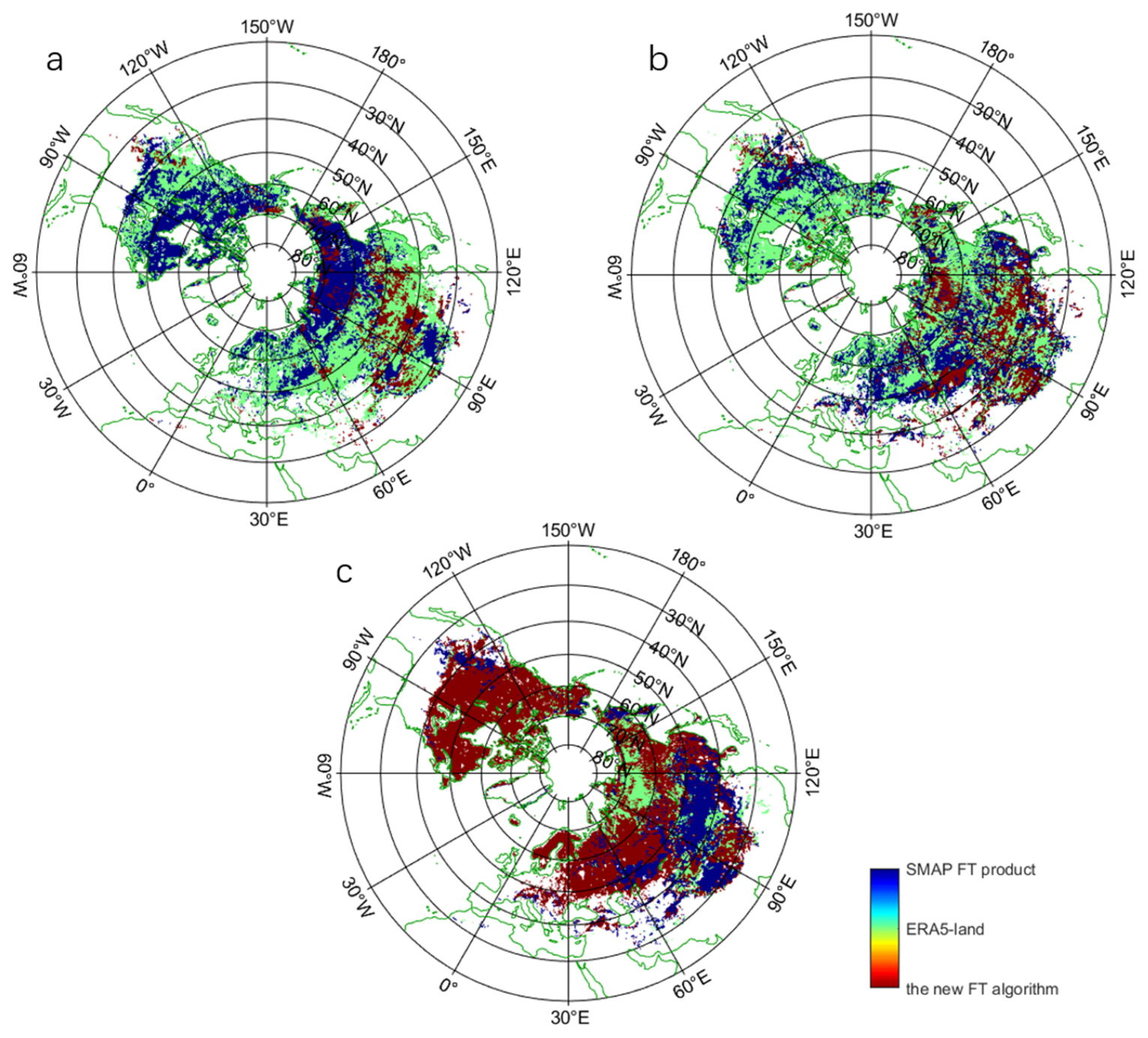
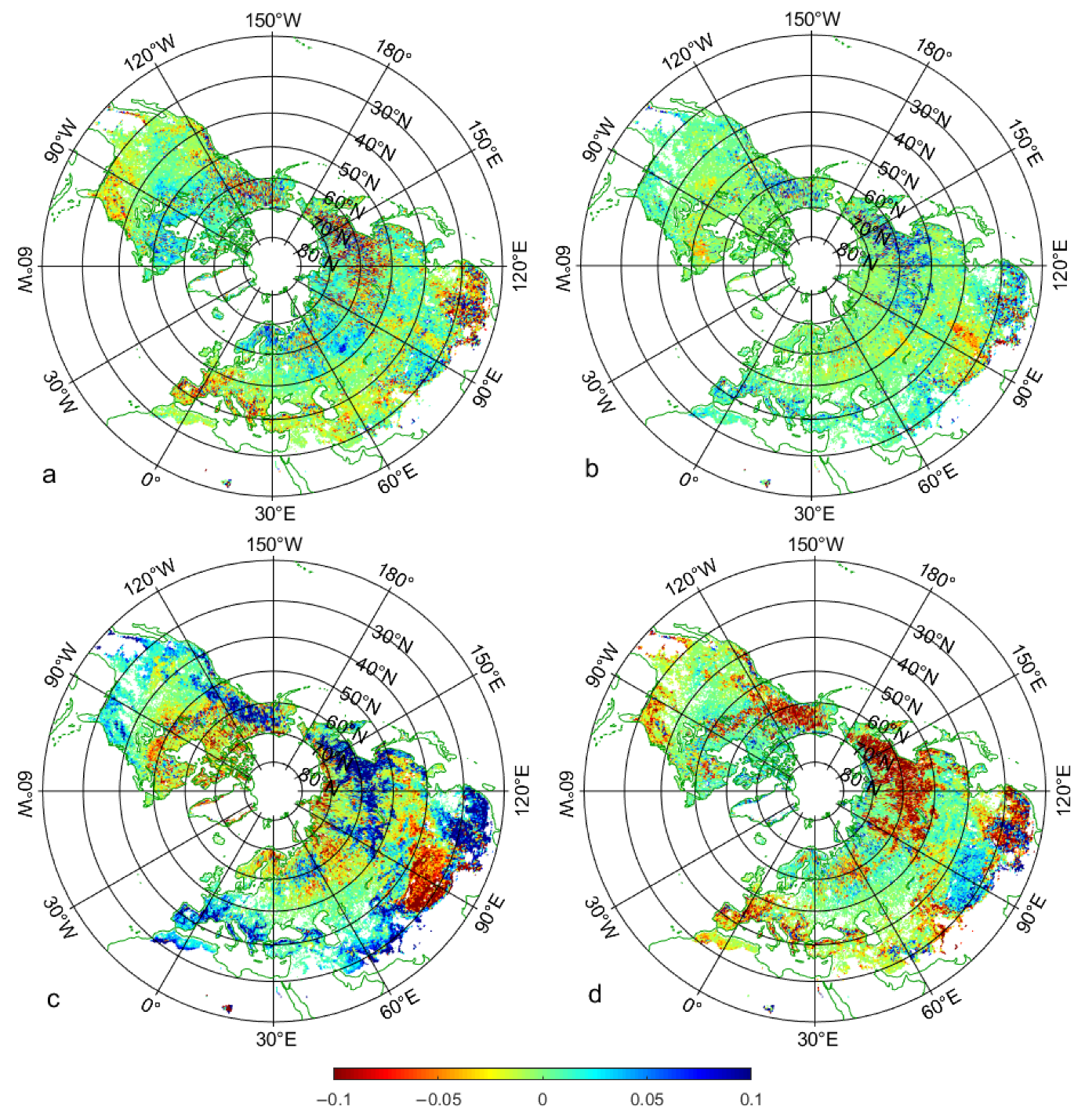
3.3. The Comparison with the SMAP FT Products
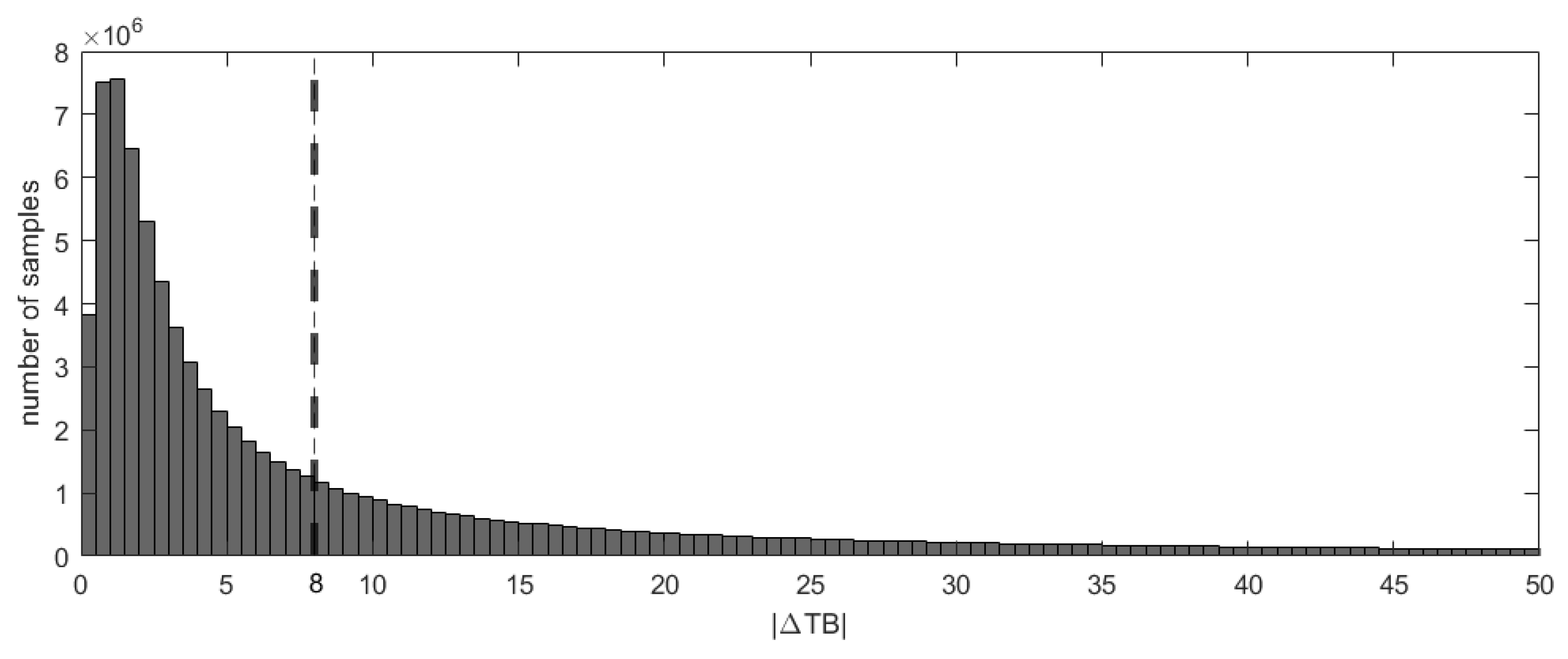
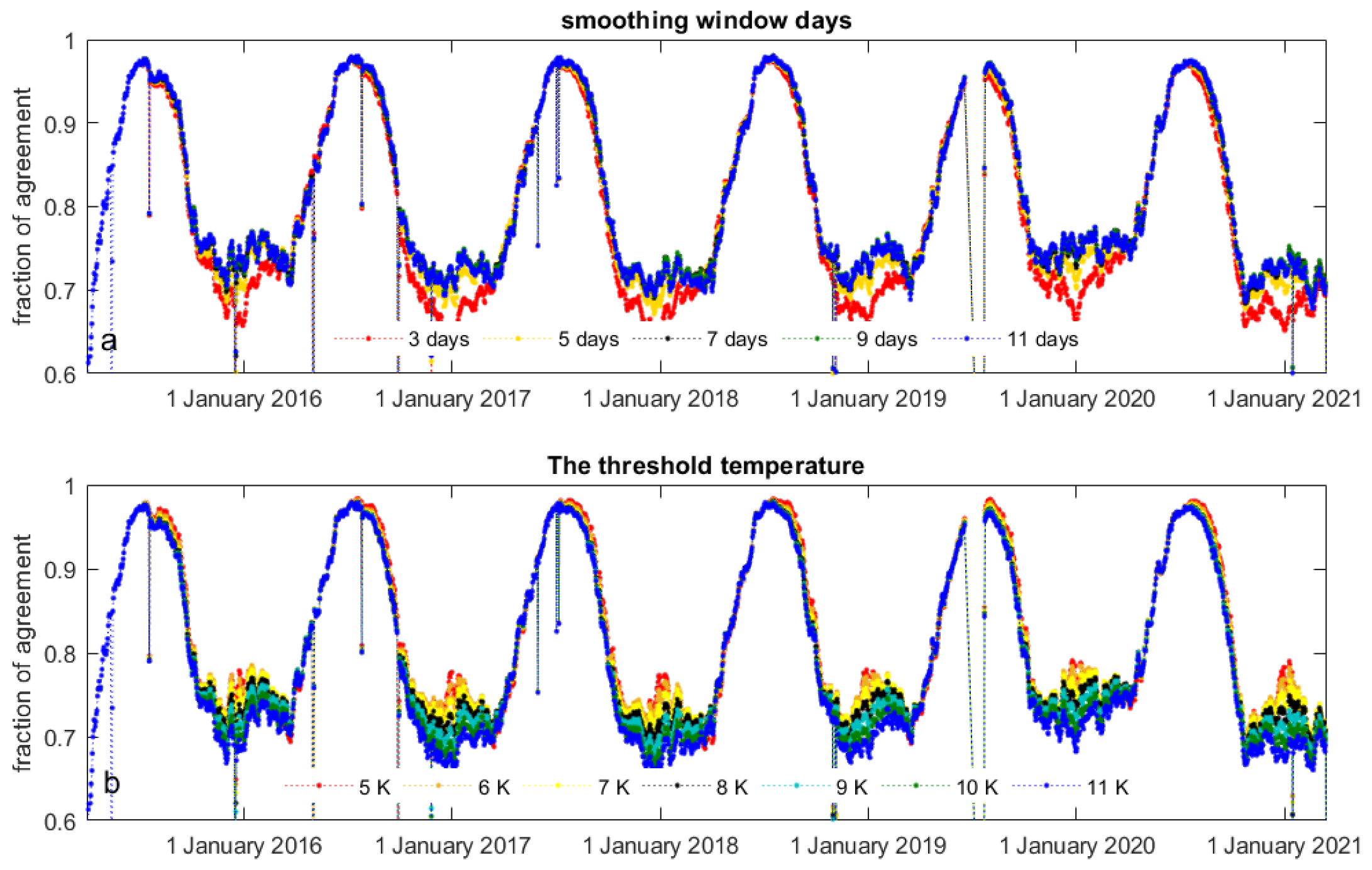
3.4. Sensitivity Test
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Walvoord, M.A.; Kurylyk, B.L. Hydrologic Impacts of Thawing Permafrost-A Review. Vadose Zone J. 2016, 15, 1–20. [Google Scholar] [CrossRef]
- Schuur, E.A.G.; McGuire, A.D.; Schädel, C.; Grosse, G.; Harden, J.W.; Hayes, D.J.; Hugelius, G.; Koven, C.D.; Kuhry, P.; Lawrence, D.M.; et al. Climate change and the permafrost carbon feedback. Nature 2015, 520, 171–179. [Google Scholar] [CrossRef]
- Zeng, Y.; Su, Z.; Barmpadimos, I.; Perrels, A.; Poli, P.; Boersma, K.F.; Frey, A.; Ma, X.; de Bruin, K.; Goosen, H.; et al. Towards a Traceable Climate Service: Assessment of Quality and Usability of Essential Climate Variables. Remote Sens. 2019, 11, 1186. [Google Scholar] [CrossRef]
- Yu, L.; Fatichi, S.; Zeng, Y.; Su, Z. The role of vadose zone physics in the ecohydrological response of a Tibetan meadow to freeze-thaw cycles. Cryosphere 2020, 14, 4653–4673. [Google Scholar] [CrossRef]
- Hu, G.; Zhao, L.; Wu, X.; Li, R.; Wu, T.; Xie, C.; Pang, Q.; Zou, D. Comparison of the thermal conductivity parameterizations for a freeze-thaw algorithm with a multi-layered soil in permafrost regions. CATENA 2017, 156, 244–251. [Google Scholar] [CrossRef]
- Gao, J.Q.; Xie, Z.H.; Wang, A.W.; Luo, Z.D. Numerical simulation based on two-directional freeze and thaw algorithm for thermal diffusion model. Appl. Math. Mech.-Engl. 2016, 37, 1467–1478. [Google Scholar] [CrossRef]
- Zhao, T.; Shi, J.; Hu, T.; Zhao, L.; Zou, D.; Wang, T.; Ji, D.; Li, R.; Wang, P. Estimation of high-resolution near-surface freeze/thaw state by the integration of microwave and thermal infrared remote sensing data on the Tibetan Plateau. Earth Space Sci. 2017, 4, 472–484. [Google Scholar] [CrossRef]
- Koven, C.D.; Ringeval, B.; Friedlingstein, P.; Ciais, P.; Cadule, P.; Khvorostyanov, D.; Krinner, G.; Tarnocai, C. Permafrost carbon-climate feedbacks accelerate global warming. Proc. Natl. Acad. Sci. USA 2011, 108, 14769–14774. [Google Scholar] [CrossRef]
- Koven, C.D.; Riley, W.J.; Stern, A. Analysis of Permafrost Thermal Dynamics and Response to Climate Change in the CMIP5 Earth System Models. J. Clim. 2013, 26, 1877–1900. [Google Scholar] [CrossRef]
- Zhao, P.; Xu, X.; Chen, F.; Guo, X.; Zheng, X.; Liu, L.; Hong, Y.; Li, Y.; La, Z.; Peng, H.; et al. The Third Atmospheric Scientific Experiment for Understanding the Earth-Atmosphere Coupled System over the Tibetan Plateau and Its Effects. Bull. Am. Meteorol. Soc. 2018, 99, 757–776. [Google Scholar] [CrossRef]
- Kimball, J.S.; White, M.A.; Running, S.W. BIOME-BGC simulations of stand hydrologic processes for BOREAS. J. Geophys. Res. -Atmos. 1997, 102, 29043–29051. [Google Scholar] [CrossRef]
- Li, F.Y.; Newton, P.C.D.; Lieffering, M. Testing simulations of intra- and inter-annual variation in the plant production response to elevated CO2 against measurements from an 11-year FACE experiment on grazed pasture. Glob. Chang. Biol. 2014, 20, 228–239. [Google Scholar] [CrossRef] [PubMed]
- Cramer, W.; Kicklighter, D.W.; Bondeau, A.; Iii, B.M.; Churkina, G.; Nemry, B.; Ruimy, A.; Schloss, A.L.; Participants Potsdam, N.P.P.M.I. Comparing global models of terrestrial net primary productivity (NPP): Overview and key results. Glob. Chang. Biol. 1999, 5, 1–15. [Google Scholar] [CrossRef]
- Matzner, E.; Borken, W. Do freeze-thaw events enhance C and N losses from soils of different ecosystems? A review. Eur. J. Soil Sci. 2008, 59, 274–284. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Lu, S.; Su, P.; Shang, L.; Li, Z. Biophysical regulation of carbon fluxes over an alpine meadow ecosystem in the eastern Tibetan Plateau. Int. J. Biometeorol. 2016, 60, 801–812. [Google Scholar] [CrossRef] [PubMed]
- Xie, Z.H.; Liu, S.; Zeng, Y.J.; Gao, J.Q.; Qin, P.H.; Jia, B.H.; Xie, J.B.; Liu, B.; Li, R.C.; Wang, Y.; et al. A High-Resolution Land Model With Groundwater Lateral Flow, Water Use, and Soil Freeze-Thaw Front Dynamics and its Application in an Endorheic Basin. J. Geophys. Res. -Atmos. 2018, 123, 7204–7222. [Google Scholar] [CrossRef]
- Swenson, S.C.; Lawrence, D.; Lee, H. Improved simulation of the terrestrial hydrological cycle in permafrost regions by the Community Land Model. J. Adv. Modeling Earth Syst. 2012, 4, M08002. [Google Scholar] [CrossRef]
- Yu, L.; Zeng, Y.; Su, Z. Understanding the mass, momentum, and energy transfer in the frozen soil with three levels of model complexities. Hydrol. Earth Syst. Sci. 2020, 24, 4813–4830. [Google Scholar] [CrossRef]
- Yu, L.Y.; Zeng, Y.J.; Wen, J.; Su, Z.B. Liquid-Vapor-Air Flow in the Frozen Soil. J. Geophys. Res. -Atmos. 2018, 123, 7393–7415. [Google Scholar] [CrossRef]
- Mwangi, S.; Zeng, Y.; Montzka, C.; Yu, L.; Su, Z. Assimilation of Cosmic-Ray Neutron Counts for the Estimation of Soil Ice Content on the Eastern Tibetan Plateau. J. Geophys. Res. -Atmos. 2020, 125, e2019JD031529. [Google Scholar] [CrossRef] [Green Version]
- Yashchenko, A.S.; Bobrov, P.P. Impact of the Soil Moisture Distribution in the Top Layer on the Accuracy Moisture Retrieval by Microwave Radiometer Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5239–5246. [Google Scholar] [CrossRef]
- Schwank, M.; Stahli, M.; Wydler, H.; Leuenberger, J.; Matzler, C.; Fluhler, H. Microwave L-band emission of freezing soil. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1252–1261. [Google Scholar] [CrossRef]
- Rautiainen, K.; Lemmetyinen, J.; Schwank, M.; Kontu, A.; Ménard, C.B.; Mätzler, C.; Drusch, M.; Wiesmann, A.; Ikonen, J.; Pulliainen, J. Detection of soil freezing from L-band passive microwave observations. Remote Sens. Environ. 2014, 147, 206–218. [Google Scholar] [CrossRef]
- Kim, Y.; Kimball, J.S.; Glassy, J.; McDonald, K.C. MEaSUREs Global Record of Daily Landscape Freeze/Thaw Status, Version 4 [dataset]. 2017. [Google Scholar] [CrossRef]
- Kim, Y.; Kimball, J.S.; McDonald, K.C.; Glassy, J. Developing a Global Data Record of Daily Landscape Freeze/Thaw Status Using Satellite Passive Microwave Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2011, 49, 949–960. [Google Scholar] [CrossRef]
- Xu, X.; Dunbar, R.; Derksen, C.; Colliander, A.; Kim, Y.; Kimball, J. SMAP L3 Radiometer Global and Northern Hemisphere Daily 36 km EASE-Grid Freeze/Thaw State, Version 3, Thaw State, Version, 3. 2020. Available online: https://nsidc.org/data/spl3ftp/versions/2 (accessed on 1 May 2020).
- Rautiainen, K.; Parkkinen, T.; Lemmetyinen, J.; Schwank, M.; Wiesmann, A.; Ikonen, J.; Derksen, C.; Davydov, S.; Davydova, A.; Boike, J.; et al. SMOS prototype algorithm for detecting autumn soil freezing. Remote Sens. Environ. 2016, 180, 346–360. [Google Scholar] [CrossRef]
- Lv, S.; Zeng, Y.; Su, Z.; Wen, J. A Closed-Form Expression of Soil Temperature Sensing Depth at L-Band. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4889–4897. [Google Scholar] [CrossRef]
- Zhao, T.; Shi, J.; Zhao, S.; Chen, K.; Wang, P.; Li, S.; Xiong, C.; Xiao, Q. Measurement and Modeling of Multi-Frequency Microwave Emission of Soil Freezing and Thawing Processes. In Proceedings of the 2018 Progress in Electromagnetics Research Symposium (PIERS-Toyama), Toyama, Japan, 1–4 August 2018; pp. 31–36. [Google Scholar] [CrossRef]
- Lv, S.; Zeng, Y.; Wen, J.; Zhao, H.; Su, Z. Estimation of Penetration Depth from Soil Effective Temperature in Microwave Radiometry. Remote Sens. 2018, 10, 519. [Google Scholar] [CrossRef]
- Kim, Y.; Kimball, J.S.; Glassy, J.; Du, J.Y. An extended global Earth system data record on daily landscape freeze-thaw status determined from satellite passive microwave remote sensing. Earth Syst. Sci. Data 2017, 9, 133–147. [Google Scholar] [CrossRef] [Green Version]
- Dunbar, S.; Xu, X.; Colliander, A.; Derksen, C.; Kimball, J.; Kim, Y. Algorithm Theoretical Basis Document (ATBD). SMAP Level 3 Radiometer Freeze/Thaw Data Products. JPL CIT JPL 2020, 500, 33. [Google Scholar]
- Sharifnezhad, Z.; Norouzi, H.; Prakash, S.; Blake, R.; Khanbilvardi, R. Diurnal Cycle of Passive Microwave Brightness Temperatures over Land at a Global Scale. Remote Sens. 2021, 13, 817. [Google Scholar] [CrossRef]
- Kopczynski, S.; Ramage, J.; Lawson, D.; Goetz, S.; Evenson, E.; Denner, J.; Larson, G. Passive microwave (SSM/I) satellite predictions of valley glacier hydrology, Matanuska Glacier, Alaska. Geophys. Res. Lett. 2008, 35, 2008GL034615. [Google Scholar] [CrossRef]
- Tedesco, M. Snowmelt detection over the Greenland ice sheet from SSM/I brightness temperature daily variations. Geophys. Res. Lett. 2007, 34, 2006GL028466. [Google Scholar] [CrossRef]
- Guo, D.; Wang, H. Simulated change in the near-surface soil freeze/thaw cycle on the Tibetan Plateau from 1981 to 2010. Chin. Sci. Bull. 2014, 59, 2439–2448. [Google Scholar] [CrossRef]
- Chaubell, J.; Yueh, S.; Entekhabi, D.; Peng, J. Resolution enhancement of SMAP radiometer data using the Backus Gilbert optimum interpolation technique. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 284–287. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data Discuss 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Baker, D.G.; Ruschy, D.L. Calculated and Measured Air and Soil Freeze-Thaw Frequencies. J. Appl. Meteorol. Climatol. 1995, 34, 2197–2205. [Google Scholar] [CrossRef]
- Fortin, G. Variability and frequency of the freeze thaw cycles in Quebec region, 1977-2006. Can. Geogr. -Geogr. Can. 2010, 54, 196–208. [Google Scholar] [CrossRef]
- Ho, E.; Gough, W.A. Freeze thaw cycles in Toronto, Canada in a changing climate. Theor. Appl. Climatol. 2006, 83, 203–210. [Google Scholar] [CrossRef]
- Zhao, T.; Shi, J.; Entekhabi, D.; Jackson, T.J.; Hu, L.; Peng, Z.; Yao, P.; Li, S.; Kang, C.S. Retrievals of soil moisture and vegetation optical depth using a multi-channel collaborative algorithm. Remote Sens. Environ. 2021, 257, 112321. [Google Scholar] [CrossRef]
- Yamano, H.; Chen, J.; Tamura, M. Hyperspectral identification of grassland vegetation in Xilinhot, Inner Mongolia, China. Int. J. Remote Sens. 2003, 24, 3171–3178. [Google Scholar] [CrossRef]
- Shi, C.X.; Xie, Z.H.; Qian, H.; Liang, M.L.; Yang, X.C. China land soil moisture EnKF data assimilation based on satellite remote sensing data. Sci. China-Earth Sci. 2011, 54, 1430–1440. [Google Scholar] [CrossRef]
- Wu, S.; Chen, J. Validation of AMSR-E soil moisture products in Xilinhot grassland. In Proceedings of the Remote Sensing for Agriculture, Ecosystems, and Hydrology XIV, Edinburgh, UK, 24–26 September 2012; p. 85311J. [Google Scholar]
- Chapin, F.S.; Sala, O.E.; Huber-Sannwald, E. Global Biodiversity in a Changing Environment: Scenarios for the 21st Century; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Derksen, C.; Xu, X.L.; Dunbar, R.S.; Colliander, A.; Kim, Y.; Kimball, J.S.; Black, T.A.; Euskirchen, E.; Langlois, A.; Loranty, M.M.; et al. Retrieving landscape freeze/thaw state from Soil Moisture Active Passive (SNAP) radar and radiometer measurements. Remote Sens. Environ. 2017, 194, 48–62. [Google Scholar] [CrossRef]
- Lv, S.; Zeng, Y.; Wen, J.; Zheng, D.; Su, Z. Determination of the Optimal Mounting Depth for Calculating Effective Soil Temperature at L-Band: Maqu Case. Remote Sens. 2016, 8, 476. [Google Scholar] [CrossRef]
- Blackmon, M.L. A Climatological Spectral Study of the 500 mb Geopotential Height of the Northern Hemisphere. J. Atmos. Sci. 1976, 33, 1607–1623. [Google Scholar] [CrossRef]
- Cao, B.; Gruber, S.; Zheng, D.; Li, X. The ERA5-Land soil temperature bias in permafrost regions. Cryosphere 2020, 14, 2581–2595. [Google Scholar] [CrossRef]
- McColl, K.A.; Roy, A.; Derksen, C.; Konings, A.; Alemohammad, S.H.; Entekhabi, D. Triple collocation for binary and categorical variables: Application to validating landscape freeze/thaw retrievals. Remote Sens. Environ. 2016, 176, 31–42. [Google Scholar] [CrossRef]
- Scott, K.A. Assessment of Categorical Triple Collocation for Sea Ice/Open Water Observations: Application to the Gulf of Saint Lawrence. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9659–9673. [Google Scholar] [CrossRef]
- Stoffelen, A. Toward the true near-surface wind speed: Error modeling and calibration using triple collocation. J. Geophys. Res. Ocean. 1998, 103, 7755–7766. [Google Scholar] [CrossRef]
- Li, H.; Chai, L.; Crow, W.; Dong, J.; Liu, S.; Zhao, S. The reliability of categorical triple collocation for evaluating soil freeze/thaw datasets. Remote Sens. Environ. 2022, 281, 113240. [Google Scholar] [CrossRef]
- Su, Z.; Wen, J.; Zeng, Y.; Zhao, H.; Lv, S.; Van Der Velde, R.; Zheng, D.; Wang, X.; Wang, Z.; Schwank, M.; et al. Multiyear in-situ L-band microwave radiometry of land surface processes on the Tibetan Plateau. Sci. Data 2020, 7, 317. [Google Scholar] [CrossRef]
- Wang, B.; Ho, L.; Zhang, Y.; Lu, M.-M. Definition of South China Sea monsoon onset and commencement of the East Asia summer monsoon. J. Clim. 2004, 17, 699–710. [Google Scholar] [CrossRef]
- Cai, M.; Ren, R.C. Meridional and downward propagation of atmospheric circulation anomalies. Part I: Northern Hemisphere cold season variability. J. Atmos Sci. 2007, 64, 1880–1901. [Google Scholar] [CrossRef]
- Harris, C.; Arenson, L.U.; Christiansen, H.H.; Etzemuller, B.; Frauenfelder, R.; Gruber, S.; Haeberli, W.; Hauck, C.; Holzle, M.; Humlum, O.; et al. Permafrost and climate in Europe: Monitoring and modelling thermal, geomorphological and geotechnical responses. Earth-Sci. Rev. 2009, 92, 117–171. [Google Scholar] [CrossRef]
- Huang, X.; Han, S.; Shi, C. Multiscale Assessments of Three Reanalysis Temperature Data Systems over China. Agriculture 2021, 11, 1292. [Google Scholar] [CrossRef]
- Kraatz, S.; Jacobs, J.M.; Schröder, R.; Cho, E.; Cosh, M.; Seyfried, M.; Prueger, J.; Livingston, S. Evaluation of SMAP Freeze/Thaw Retrieval Accuracy at Core Validation Sites in the Contiguous United States. Remote Sens. 2018, 10, 1483. [Google Scholar] [CrossRef]
- Zheng, D.; Li, X.; Zhao, T.; Wen, J.; van der Velde, R.; Schwank, M.; Wang, X.; Wang, Z.; Su, Z. Impact of Soil Permittivity and Temperature Profile on L-Band Microwave Emission of Frozen Soil. IEEE Trans. Geosci. Remote Sens. 2020, 59, 4080–4093. [Google Scholar] [CrossRef]
- Zheng, D.; Li, X.; Wang, X.; Wang, Z.; Wen, J.; van der Velde, R.; Schwank, M.; Su, Z. Sampling depth of L-band radiometer measurements of soil moisture and freeze-thaw dynamics on the Tibetan Plateau. Remote Sens. Environ. 2019, 226, 16–25. [Google Scholar] [CrossRef]
- Roy, A.; Toose, P.; Williamson, M.; Rowlandson, T.; Derksen, C.; Royer, A.; Berg, A.A.; Lemmetyinen, J.; Arnold, L. Response of L-Band brightness temperatures to freeze/thaw and snow dynamics in a prairie environment from ground-based radiometer measurements. Remote Sens. Environ. 2017, 191, 67–80. [Google Scholar] [CrossRef]
- Rowlandson, T.L.; Berg, A.A.; Roy, A.; Kim, E.; Lara, R.P.; Powers, J.; Lewis, K.; Houser, P.; McDonald, K.; Toose, P.; et al. Capturing agricultural soil freeze/thaw state through remote sensing and ground observations: A soil freeze/thaw validation campaign. Remote Sens. Environ. 2018, 211, 59–70. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, L.; Cui, H.; Wang, G.; Yang, J.; Liu, X.; Su, X. Evaluation and analysis of SMAP, AMSR2 and MEaSUREs freeze/thaw products in China. Remote Sens. Environ. 2020, 242, 111734. [Google Scholar] [CrossRef]


| Summer | 2015 | 2016 | 2017 | 2018 | 2019 |
|---|---|---|---|---|---|
| 0.1085 | 0.1118 | 0.1078 | 0.1095 | 0.1074 | |
| winter | 2015–2016 | 2015–2016 | 2015–2016 | 2015–2016 | 2015–2016 |
| 0.0251 | 0.0277 | 0.0302 | 0.0274 | 0.0295 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, S.; Wen, J.; Simmer, C.; Zeng, Y.; Guo, Y.; Su, Z. A Novel Freeze-Thaw State Detection Algorithm Based on L-Band Passive Microwave Remote Sensing. Remote Sens. 2022, 14, 4747. https://doi.org/10.3390/rs14194747
Lv S, Wen J, Simmer C, Zeng Y, Guo Y, Su Z. A Novel Freeze-Thaw State Detection Algorithm Based on L-Band Passive Microwave Remote Sensing. Remote Sensing. 2022; 14(19):4747. https://doi.org/10.3390/rs14194747
Chicago/Turabian StyleLv, Shaoning, Jun Wen, Clemens Simmer, Yijian Zeng, Yuanyuan Guo, and Zhongbo Su. 2022. "A Novel Freeze-Thaw State Detection Algorithm Based on L-Band Passive Microwave Remote Sensing" Remote Sensing 14, no. 19: 4747. https://doi.org/10.3390/rs14194747
APA StyleLv, S., Wen, J., Simmer, C., Zeng, Y., Guo, Y., & Su, Z. (2022). A Novel Freeze-Thaw State Detection Algorithm Based on L-Band Passive Microwave Remote Sensing. Remote Sensing, 14(19), 4747. https://doi.org/10.3390/rs14194747









