Path Planning of Spacecraft Cluster Orbit Reconstruction Based on ALPIO
Abstract
:1. Introduction
2. Relative Motion Model of Spacecraft
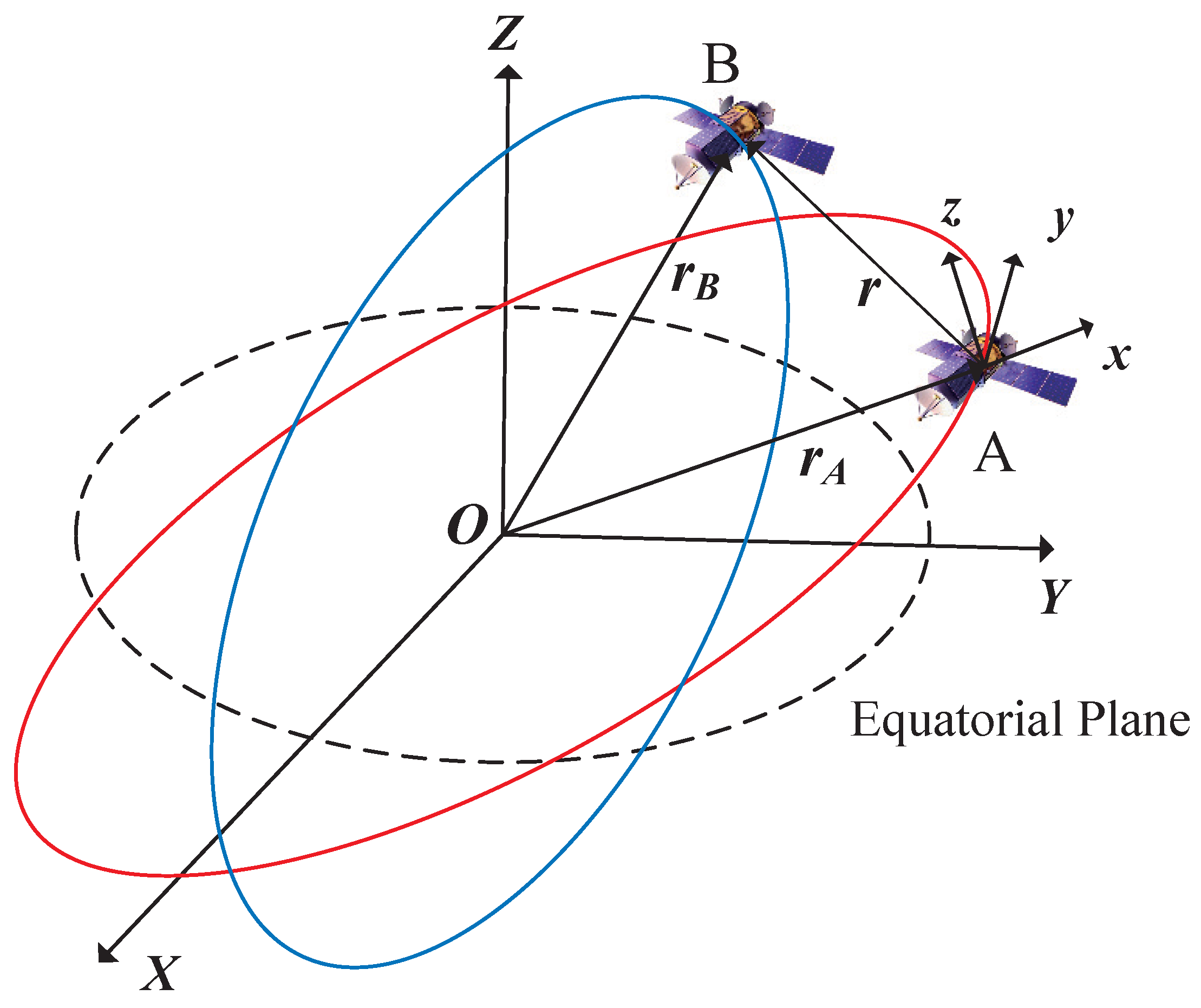
2.1. Coordinate System of Relative Motion
2.2. Relative Motion Equation
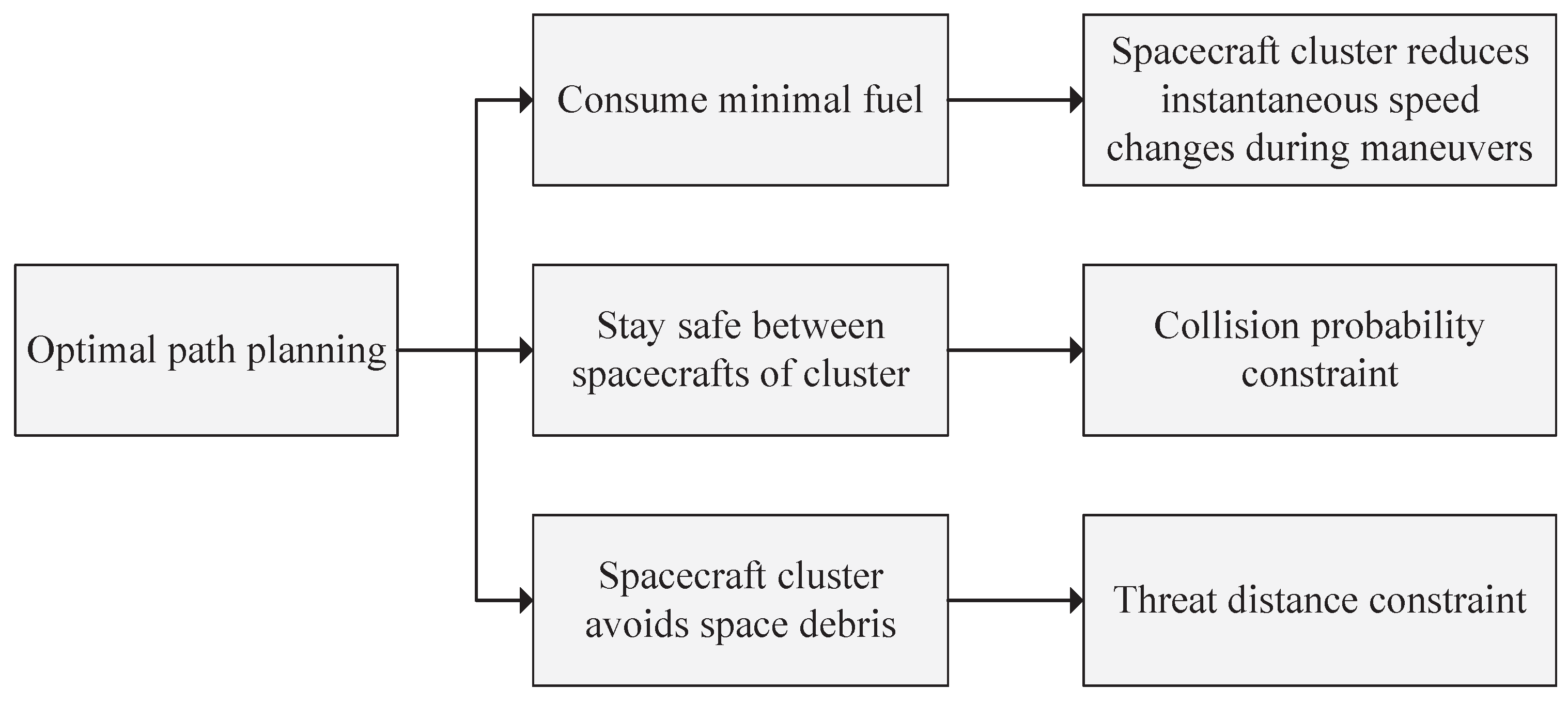
3. Path Planning Fitness Function Design
3.1. Performance Index Based on Fuel Consumption
3.2. Constraints
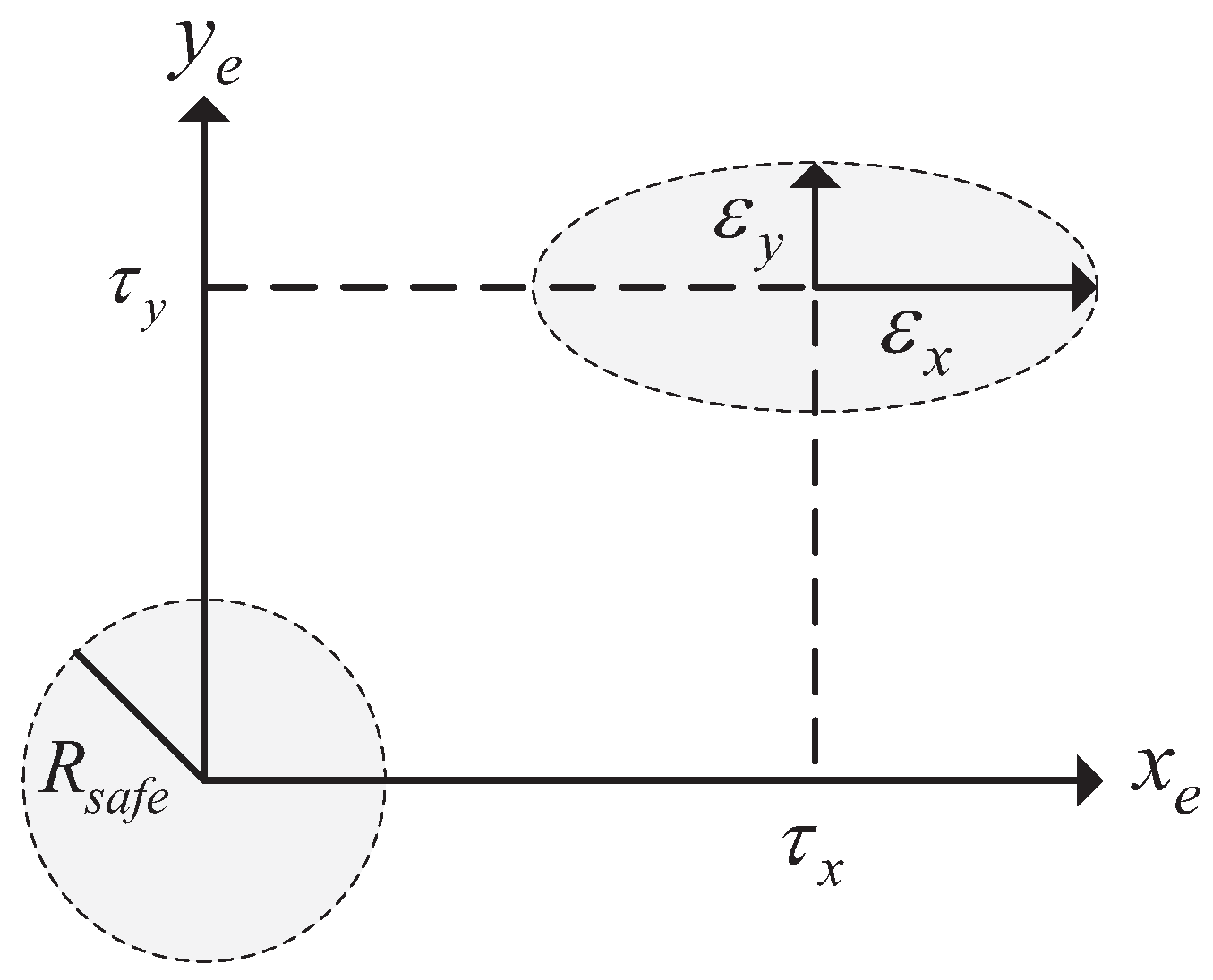
3.2.1. Keeping a Safe Distance between Two Spacecraft Inside the Cluster
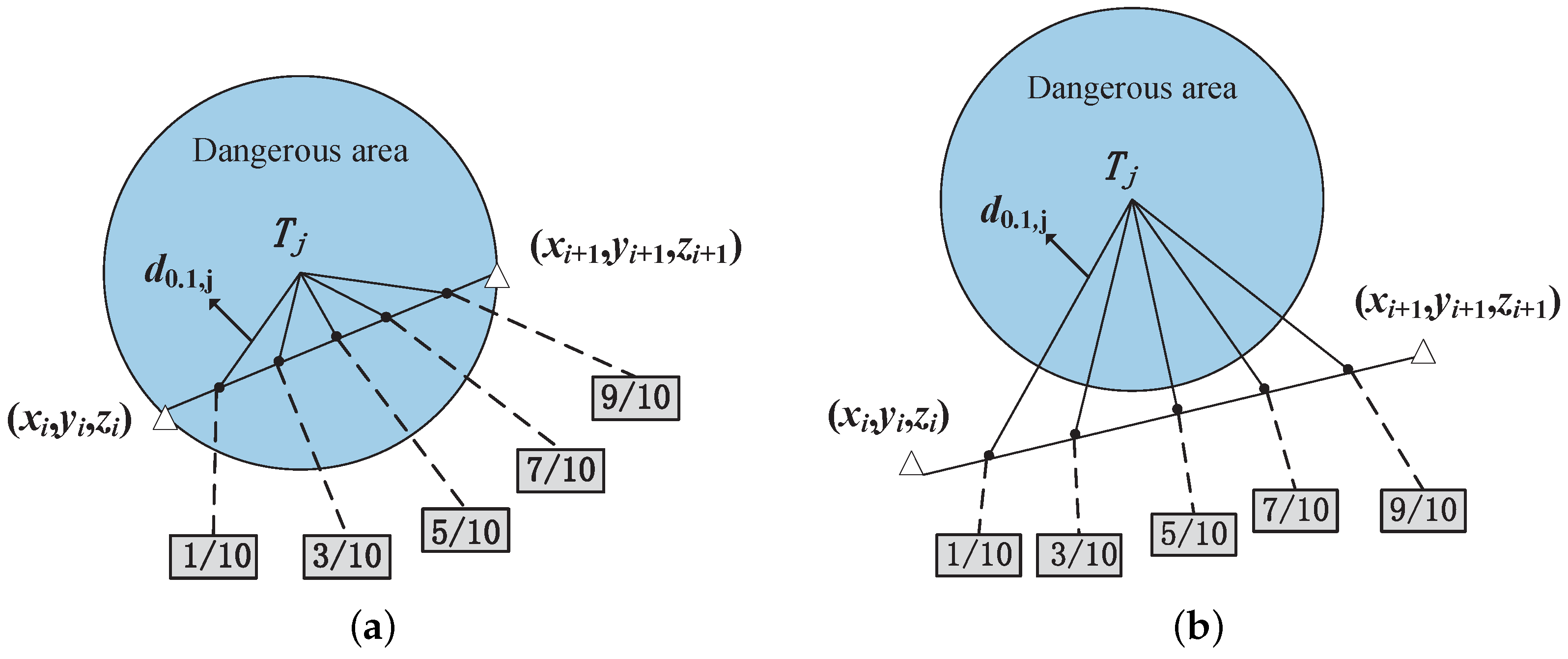
3.2.2. Spacecraft Maintain a Safe Distance Constraint from Other Space Targets
4. ALPIO for Path Planning
4.1. ALPIO Algorithm Structure
4.2. Initialization Based on Tent Map Chaotic and Elite Backward Learning
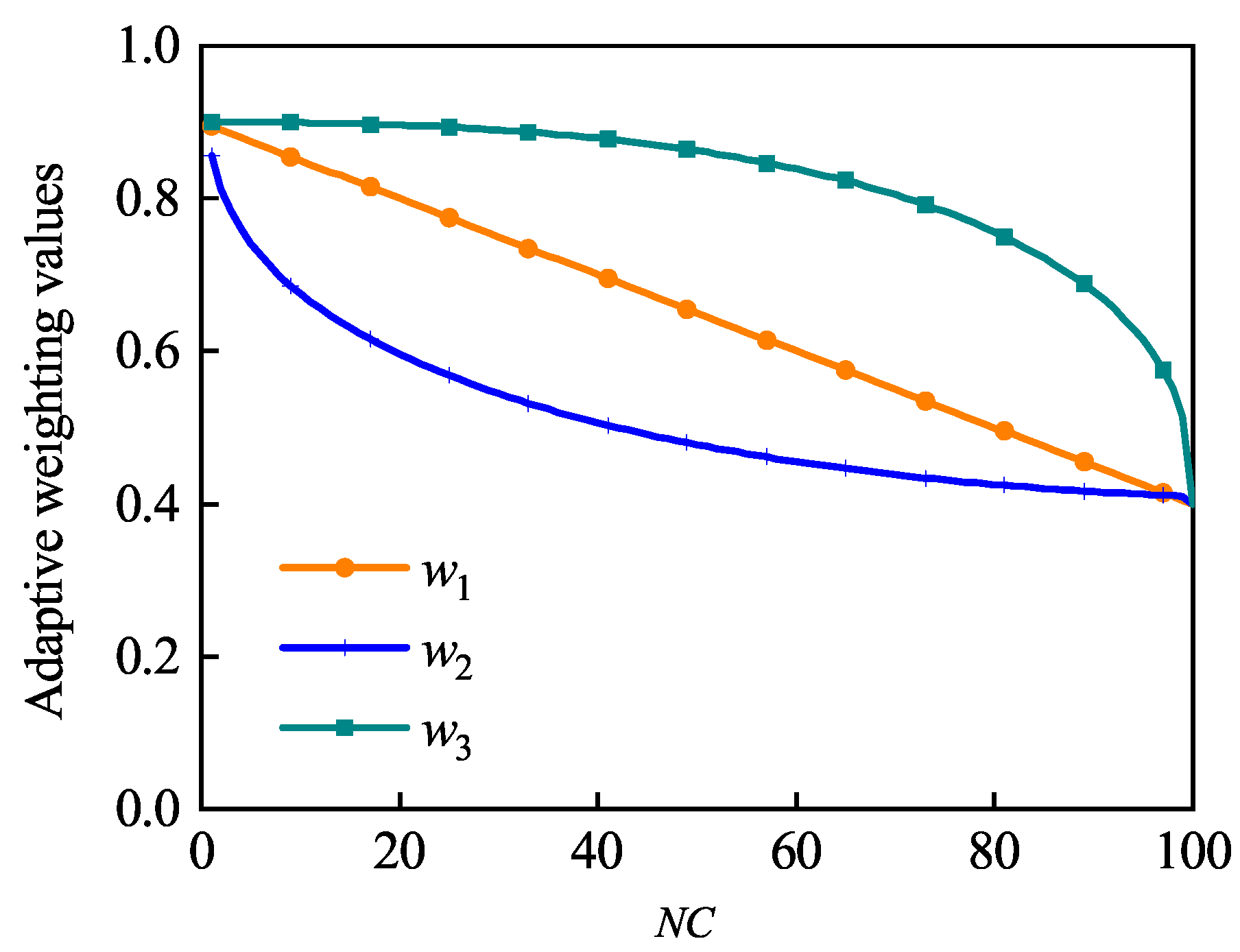
4.3. Nonlinear Adaptive Strategy to Improve Convergence Accuracy
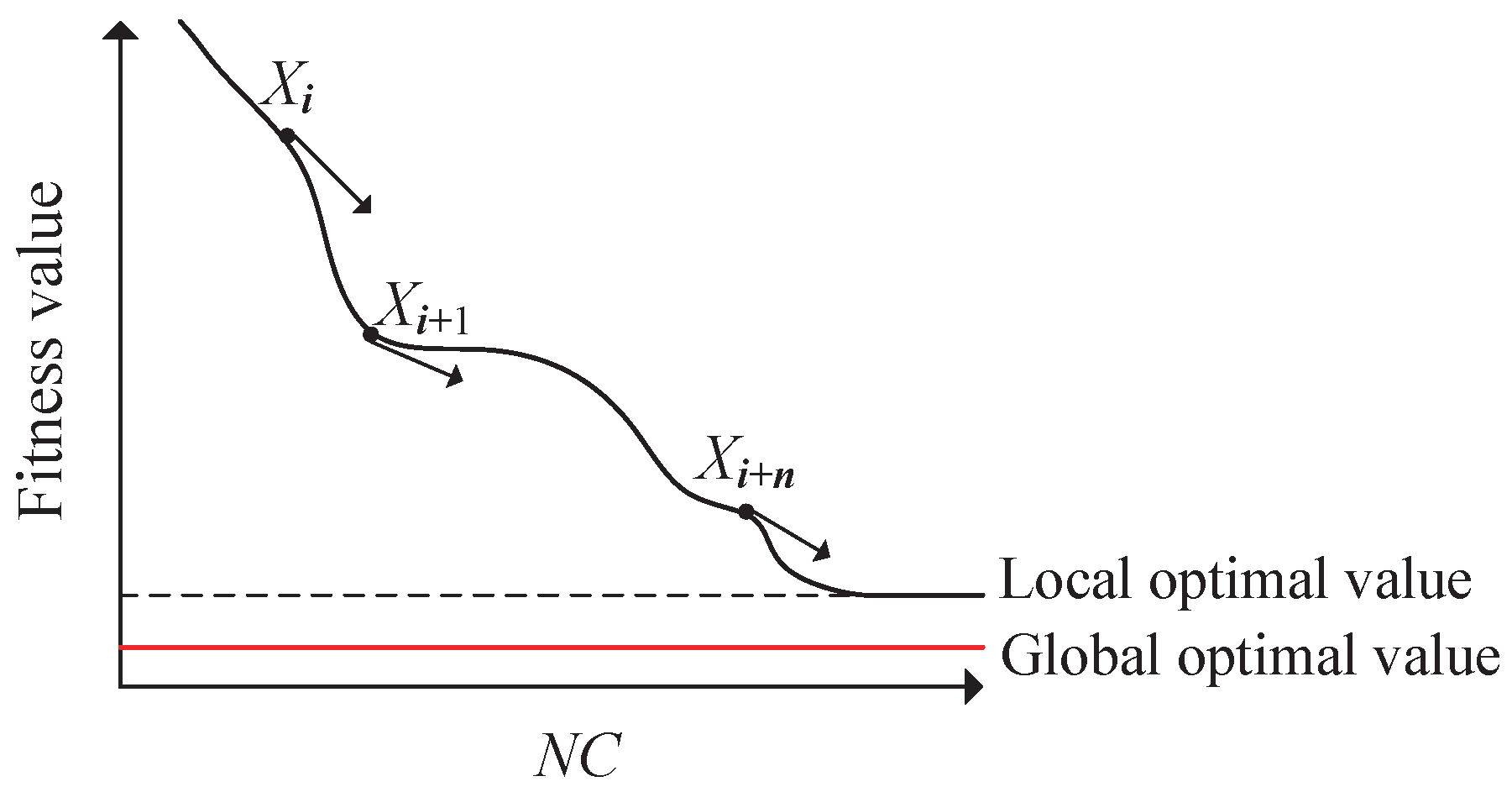
4.4. Cauchy Mutation Strategy for Avoiding Local Optima
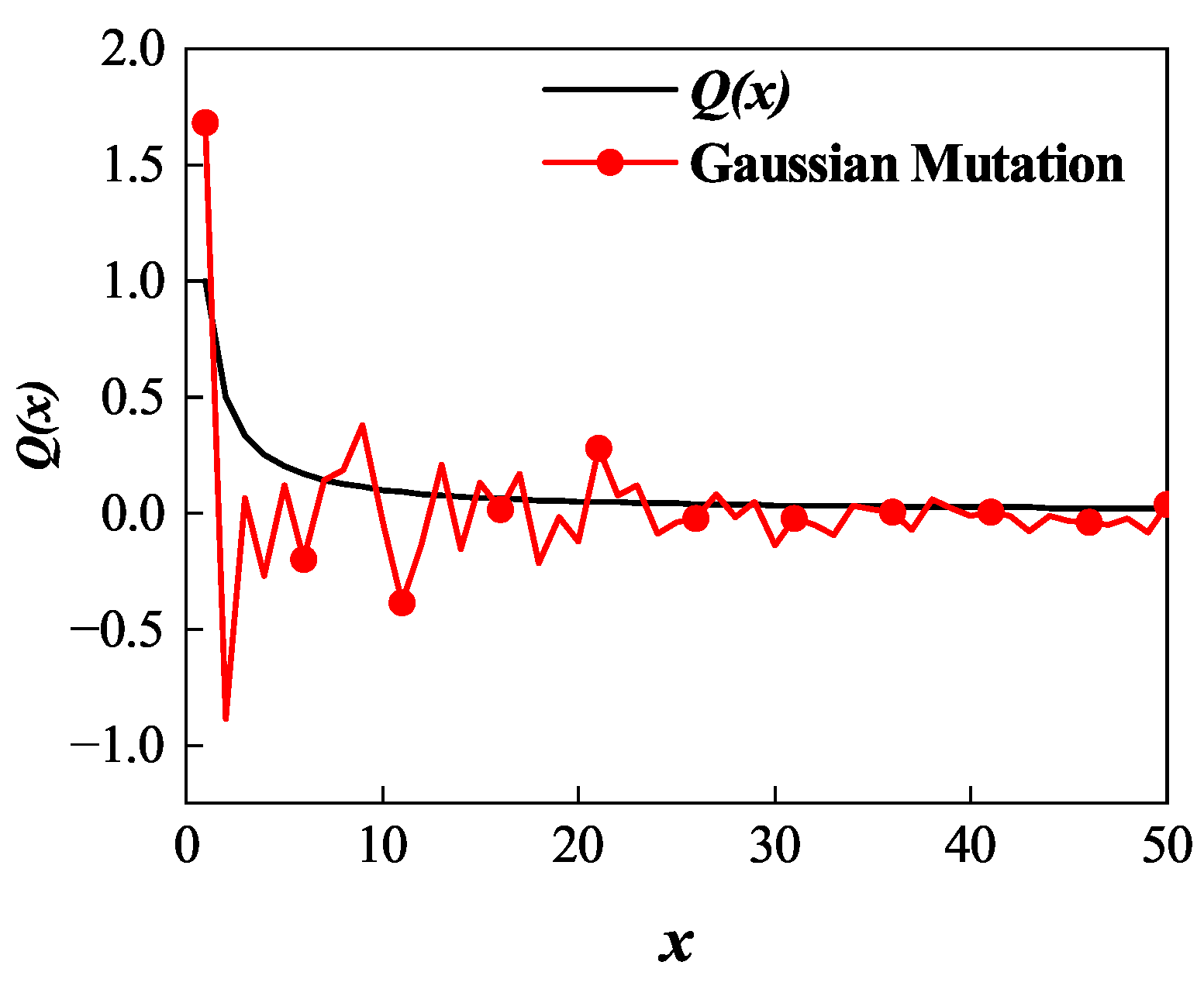
4.5. Gaussian Mutation Strategy to Prevent Population Evolution from Stagnation
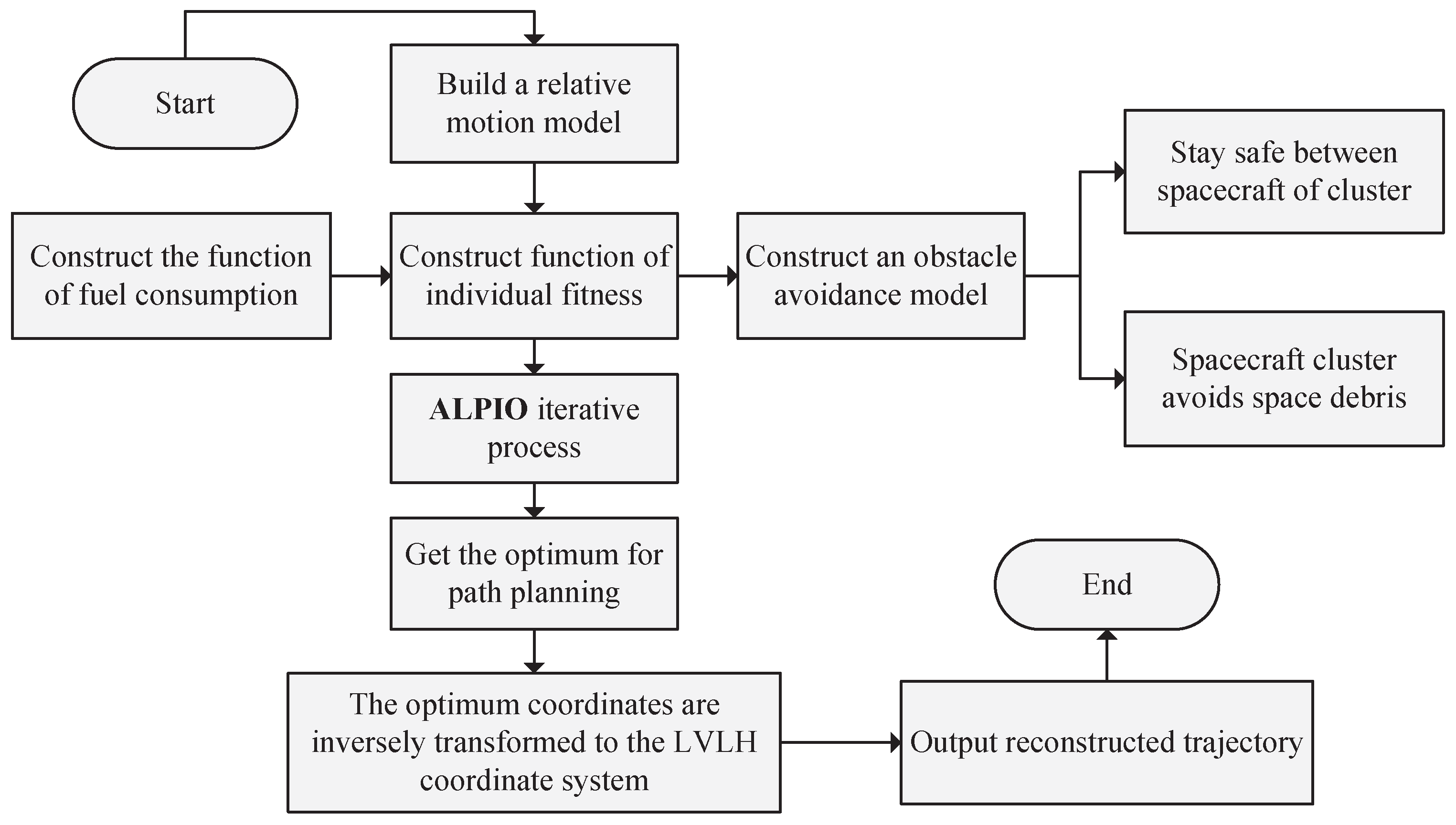
4.6. Scheme of Path Planning of Orbit Reconstruction
5. Simulation Experiment and Result Analysis
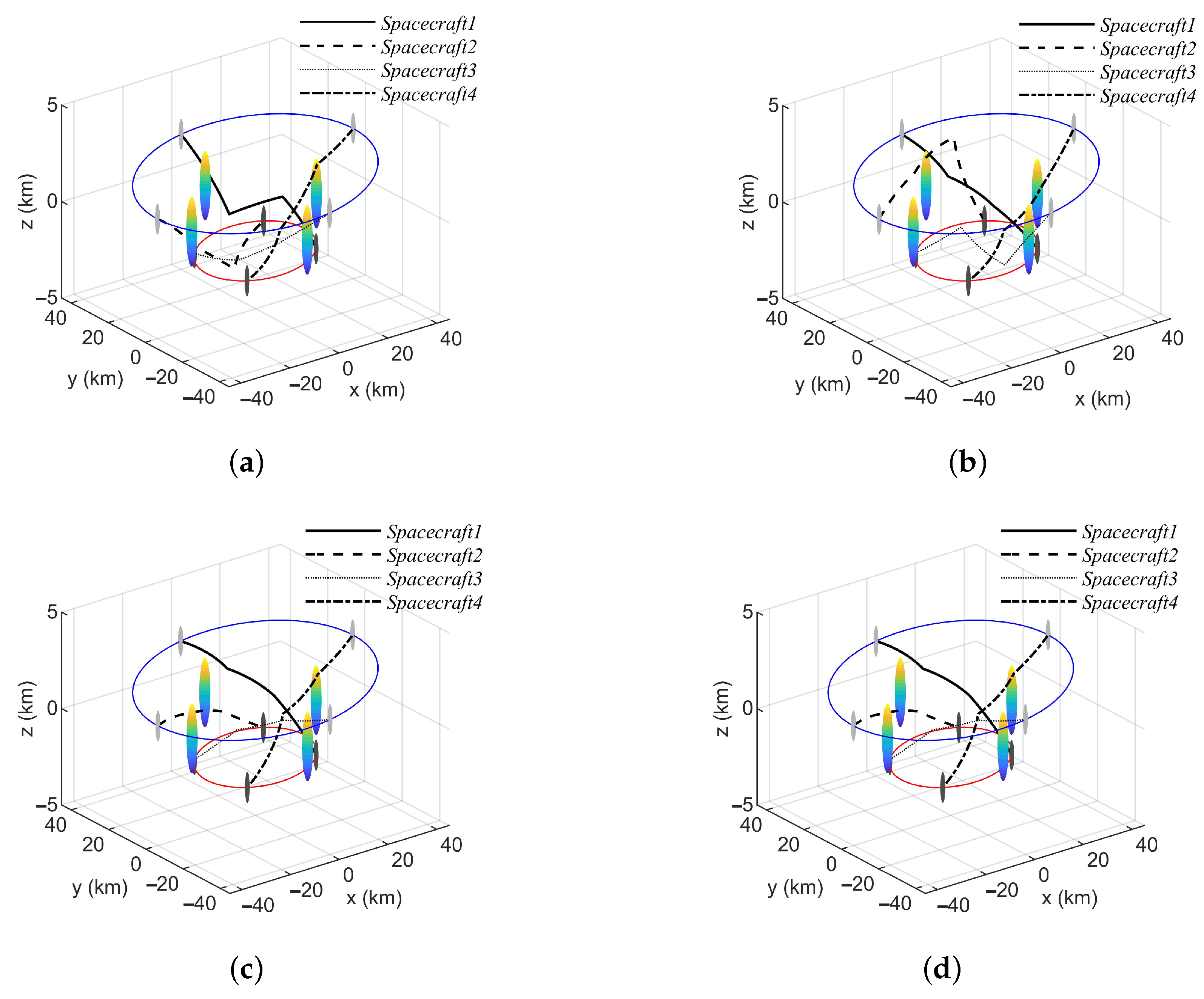
5.1. Track Reconstruction Path Planning
5.2. Simulation of Different Algorithms for Path Planning
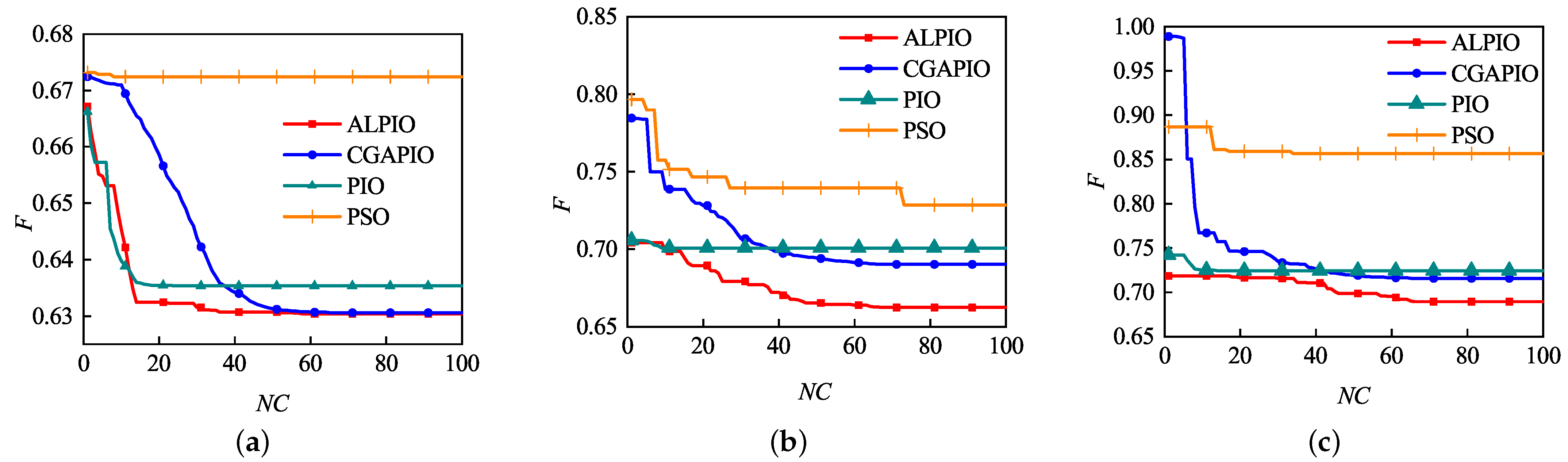
5.3. Comparison of Fuel Consumption with Different Algorithms
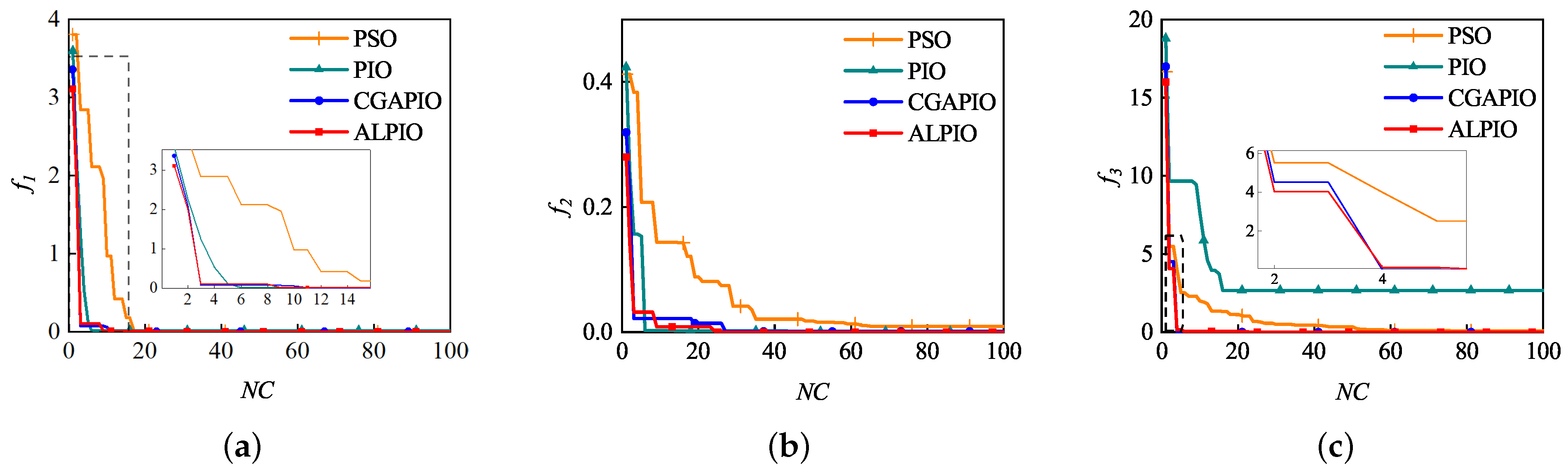
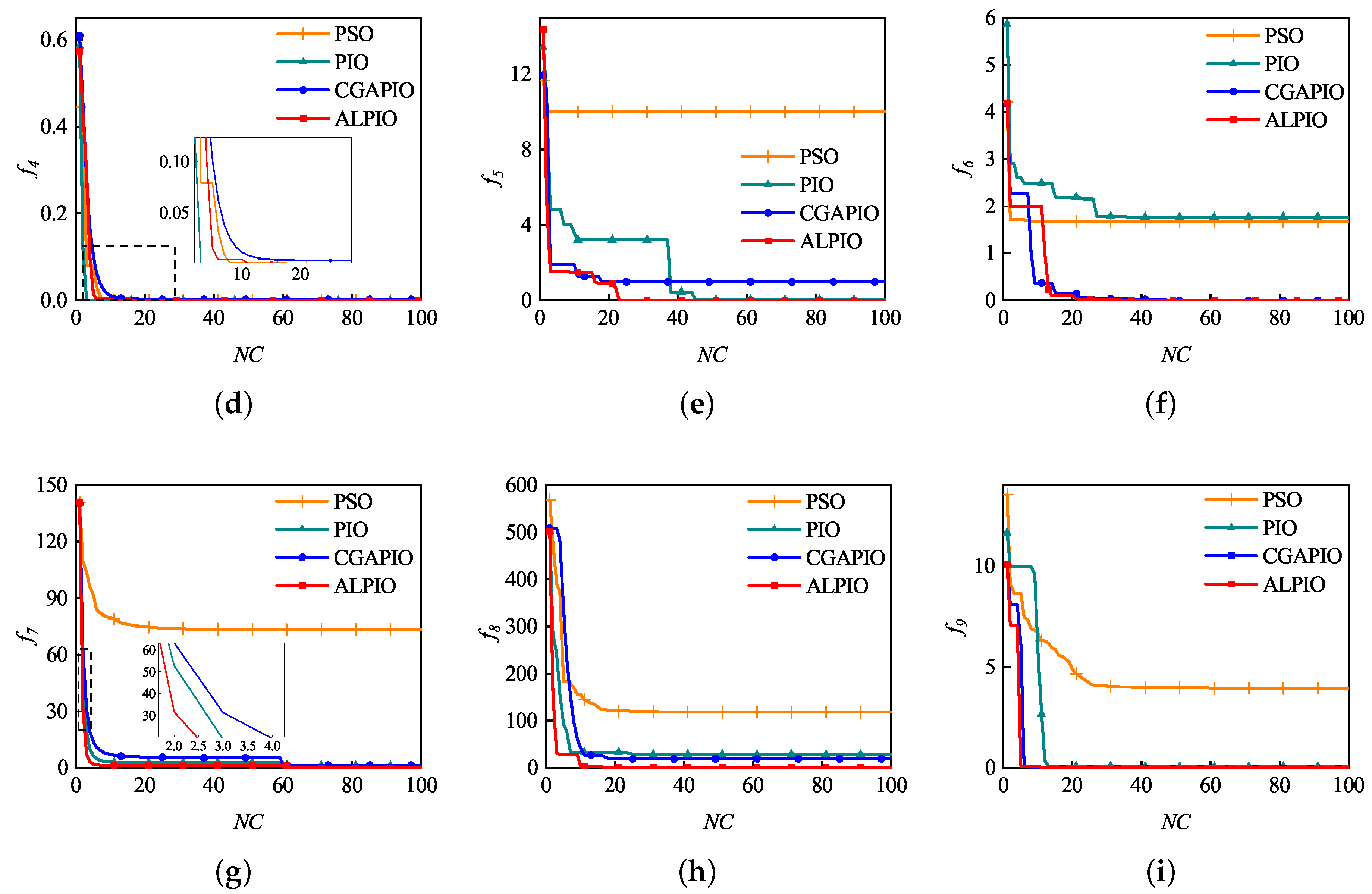
5.4. Comparison of Fitness Value Changes of Different Algorithms
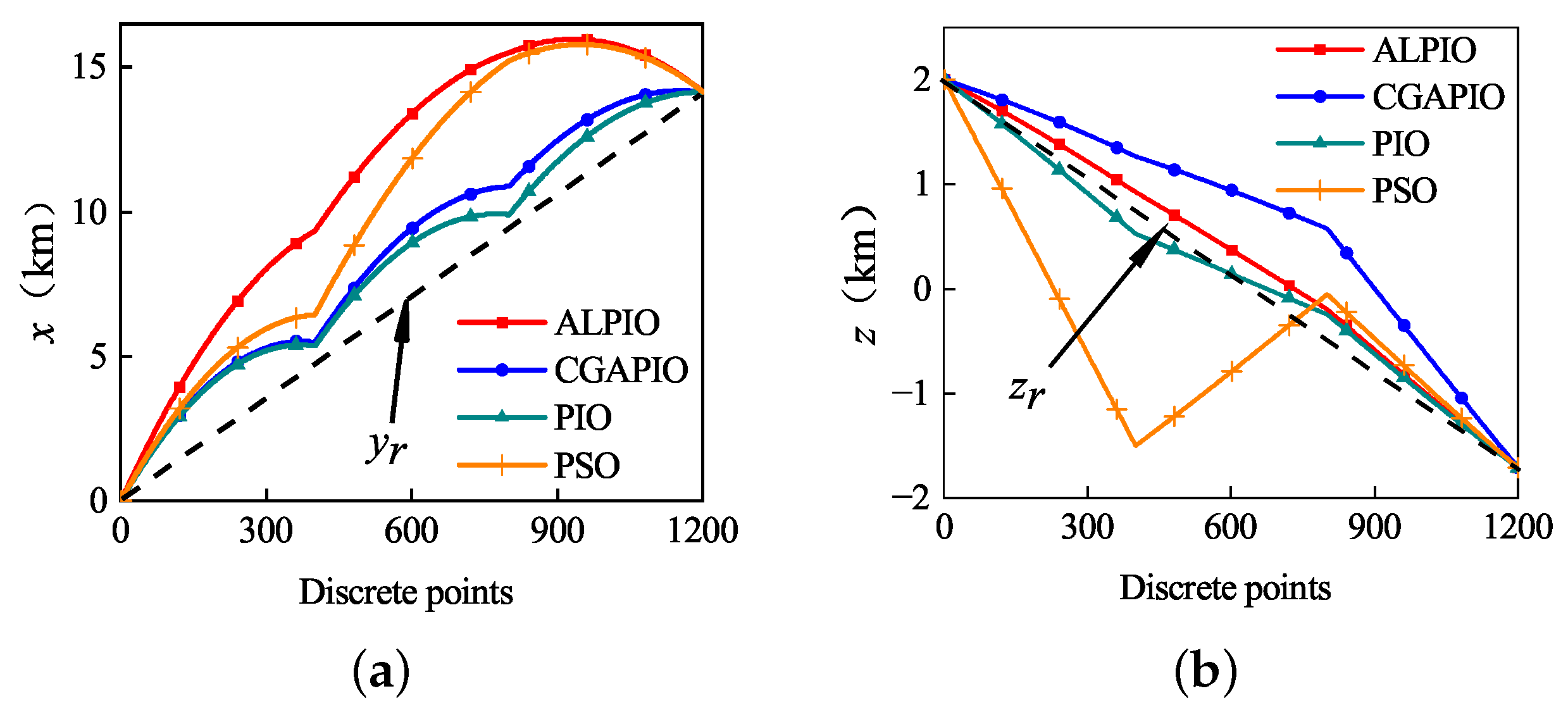
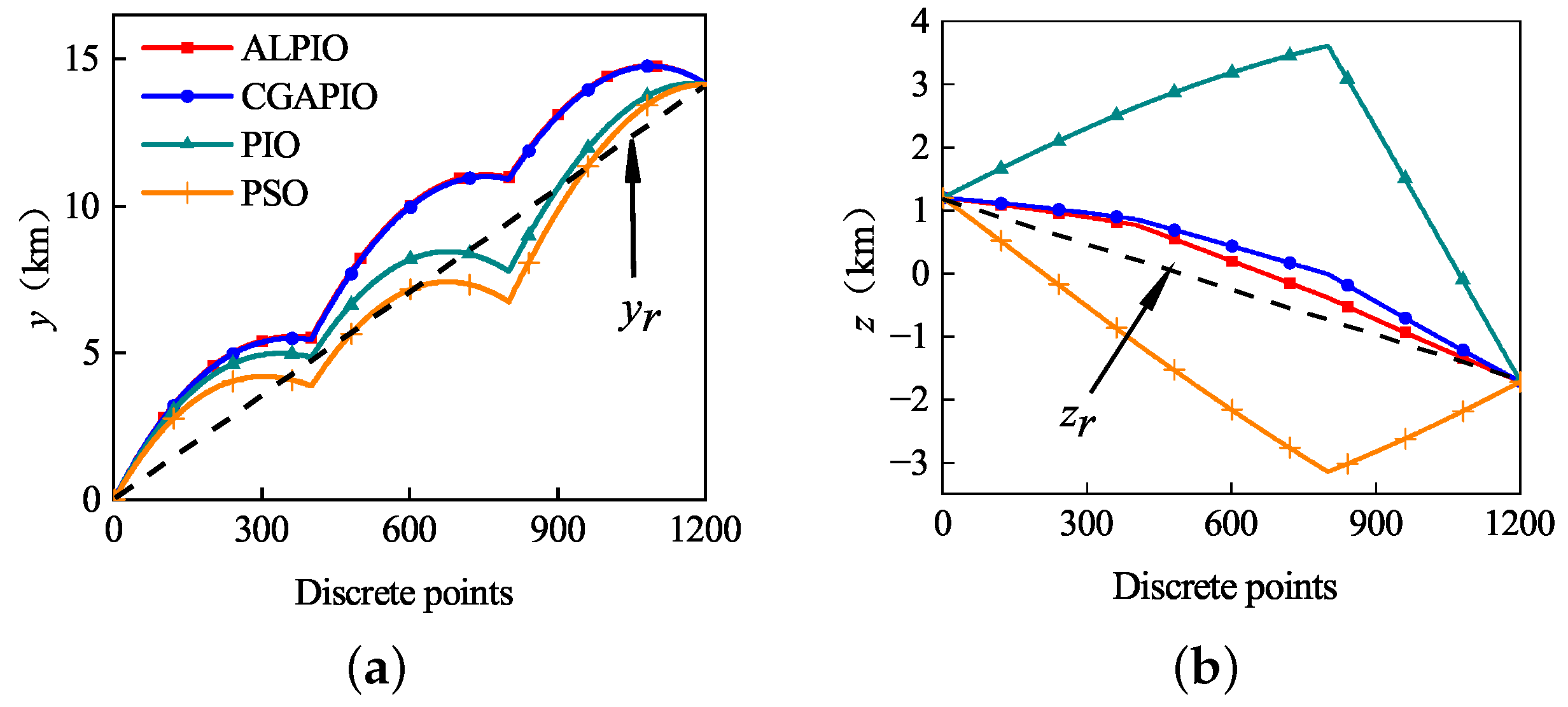
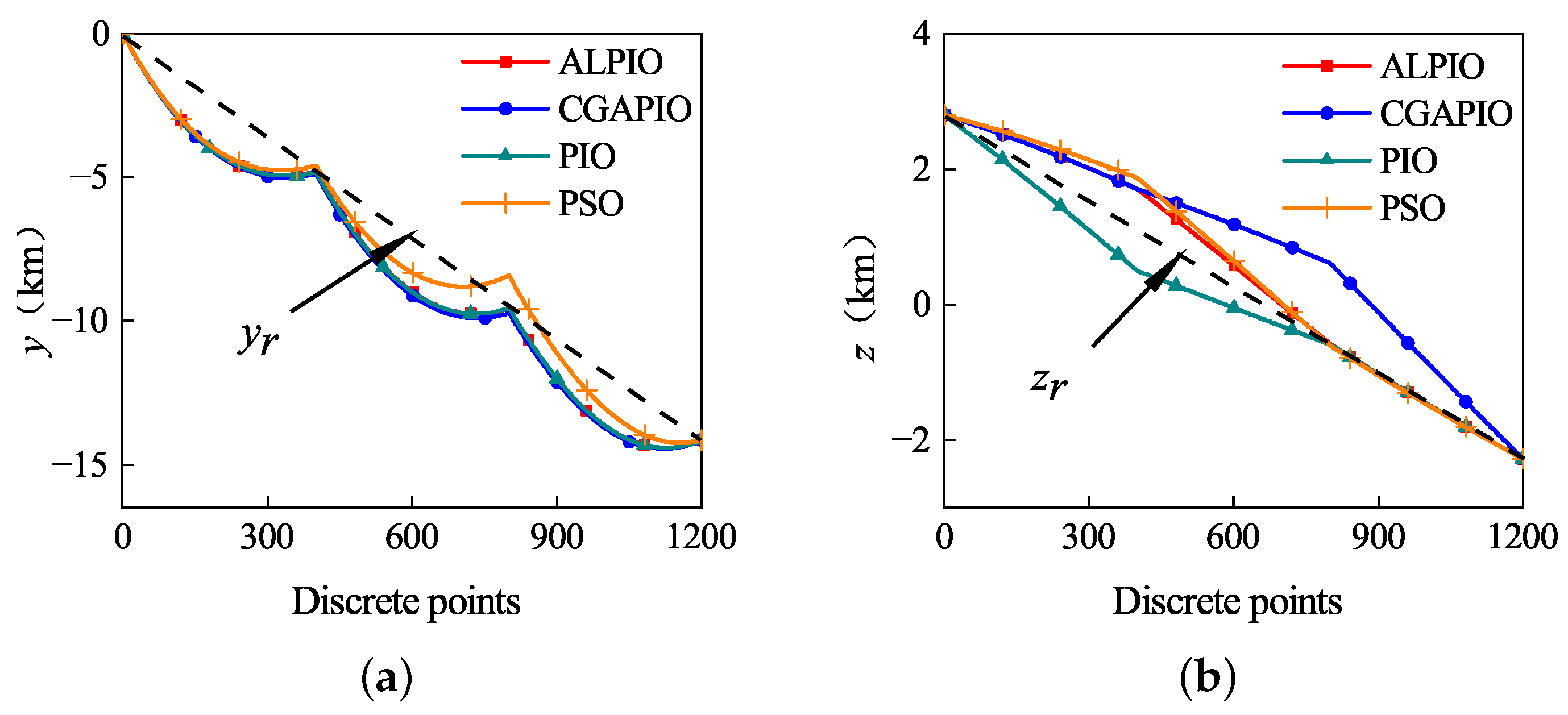
5.5. Comparison of the Smoothness of the Path Planning Trajectory with Different Algorithms
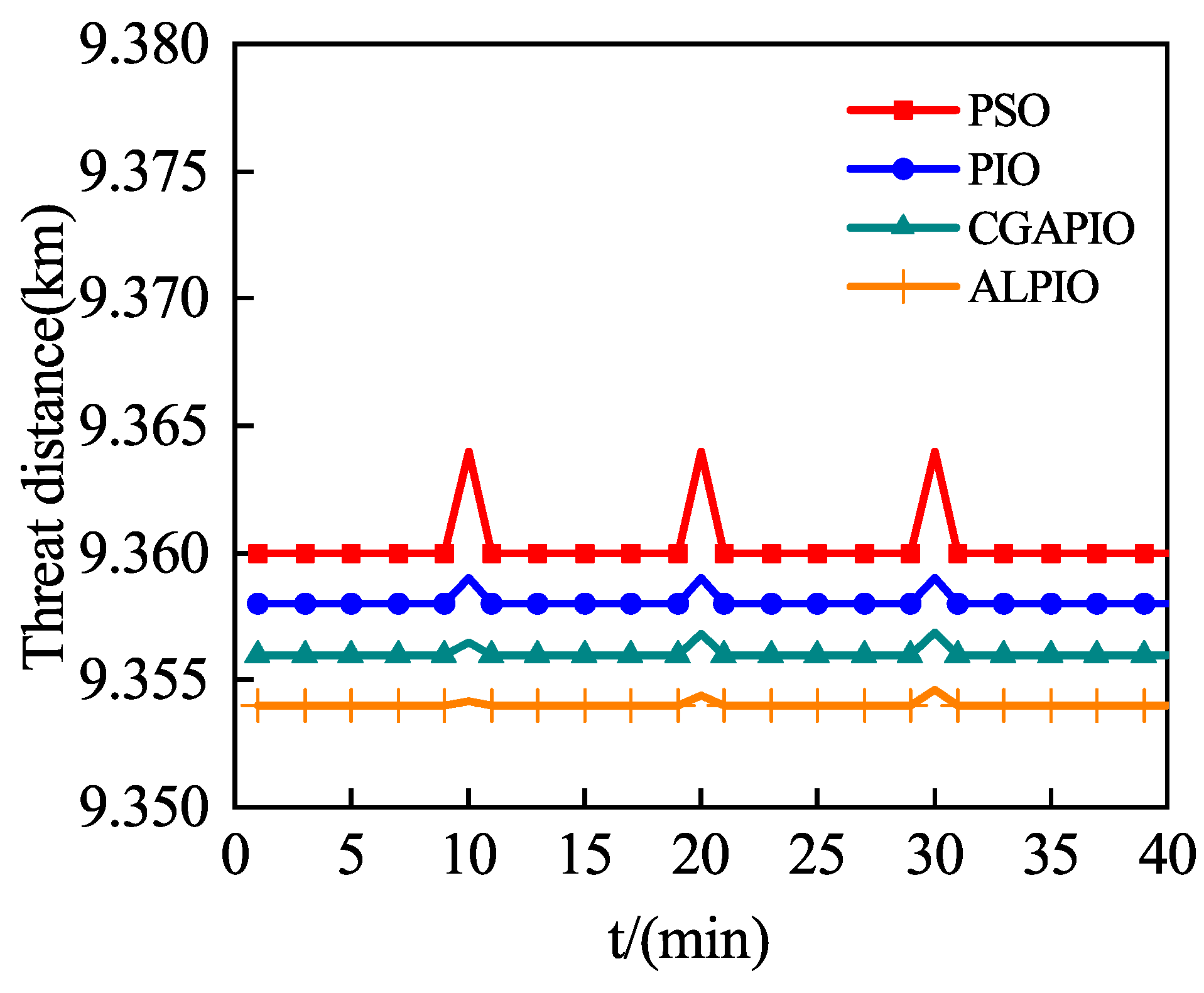
5.6. Comparison of Obstacle Avoidance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hanson, J.; Chartres, J.; Sanchez, H.; Oyadomari, K. The EDSN intersatellite communications architecture. In Proceedings of the Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 14–17 August 2014. [Google Scholar]
- Clark, P.; Rilee, M.; Curtis, S.; Truszkowski, W.; Marr, G.; Cheung, C.; Rudisill, M. BEES for ANTS: Space mission applications for the autonomous nanotechnology swarm. In Proceedings of the AIAA 1st Intelligent Systems Technical Conference, Chicago, IL, USA, 20–22 September 2004; p. 6303. [Google Scholar]
- Akioka, M.; Nagatsuma, T.; Miyake, W.; Ohtaka, K.; Marubashi, K. The L5 mission for space weather forecasting. Adv. Space Res. 2005, 35, 65–69. [Google Scholar] [CrossRef]
- Němec, F.; Kotková, M. Evaluating the Accuracy of Magnetospheric Magnetic Field Models Using Cluster Spacecraft Magnetic Field Measurements. Universe 2021, 7, 282. [Google Scholar] [CrossRef]
- Chu, J.; Guo, J.; Gill, E. A survey of autonomous cooperation of modules’ cluster operations for fractionated spacecraft. Int. J. Space Sci. Eng. 2013, 1, 3–19. [Google Scholar] [CrossRef]
- Xu, M.; Liang, Y.; Tan, T.; Wei, L. Cluster flight control for fractionated spacecraft on an elliptic orbit. Celest. Mech. Dyn. Astron. 2016, 125, 383–412. [Google Scholar] [CrossRef]
- Wang, W.; Wu, D.; Lei, H.; Baoyin, H. Fuel-Optimal Spacecraft Cluster Flight Around an Ellipsoidal Asteroid. J. Guid. Control Dyn. 2021, 44, 1875–1882. [Google Scholar] [CrossRef]
- Fowler, K.; Teixeira-Dias, F. Hybrid Shielding for Hypervelocity Impact of Orbital Debris on Unmanned Spacecraft. Appl. Sci. 2022, 12, 7071. [Google Scholar] [CrossRef]
- Zhu, Z.; Qian, Y.; Zhang, W. Research on UAV Searching Path Planning Based on Improved Ant Colony Optimization Algorithm. In Proceedings of the 2021 IEEE 3rd International Conference on Civil Aviation Safety and Information Technology (ICCASIT), Changsha, China, 20–22 October 2021; pp. 1319–1323. [Google Scholar]
- Rokbani, N.; Neji, B.; Slim, M.; Mirjalili, S.; Ghandour, R. A Multi-Objective Modified PSO for Inverse Kinematics of a 5-DOF Robotic Arm. Appl. Sci. 2022, 12, 7091. [Google Scholar] [CrossRef]
- Duan, H.; Qiao, P. Pigeon-inspired optimization: A new swarm intelligence optimizer for air robot path planning. Int. J. Intell. Comput. Cybern. 2014, 7, 24–37. [Google Scholar] [CrossRef]
- Yuan, G.; Xia, J.; Duan, H. A continuous modeling method via improved pigeon-inspired optimization for wake vortices in UAVs close formation flight. Aerosp. Sci. Technol. 2022, 120, 107259. [Google Scholar] [CrossRef]
- Hua, B.; Huang, Y.; Wu, Y.; Chen, Z.; Nicholas, D. Spacecraft formation reconfiguration trajectory planning with avoidance constraints using adaptive pigeon-inspired optimization. Sci. China Inf. Sci. 2019, 62, 70209. [Google Scholar] [CrossRef]
- Xian, N.; Chen, Z. A quantum-behaved pigeon-inspired optimization approach to explicit nonlinear model predictive controller for quadrotor. Int. J. Intell. Comput. Cybern. 2018, 11, 47–63. [Google Scholar] [CrossRef]
- Pei, J.; Su, Y.; Zhang, D. Fuzzy energy management strategy for parallel HEV based on pigeon-inspired optimization algorithm. Sci. China Technol. Sci. 2017, 60, 425–433. [Google Scholar] [CrossRef]
- Lyu, Y.; Zhang, Y.; Chen, H. An Improved Pigeon-Inspired Optimization for Multi-focus Noisy Image Fusion. J. Bionic Eng. 2021, 18, 1452–1462. [Google Scholar] [CrossRef]
- Yuan, Y.; Duan, H. Active disturbance rejection attitude control of unmanned quadrotor via paired coevolution pigeon-inspired optimization. Aircr. Eng. Aerosp. Technol. 2021, 94, 302–314. [Google Scholar] [CrossRef]
- Mirjalili, S. Evolutionary algorithms and neural networks. In Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2019; Volume 780. [Google Scholar]
- Wang, J.; Song, X.; Le, Y.; Wu, W.; Zhou, B.; Ning, X. Design of self-shielded uniform magnetic field coil via modified pigeon-inspired optimization in miniature atomic sensors. IEEE Sens. J. 2020, 21, 315–324. [Google Scholar] [CrossRef]
- Ogundele, A.D. Modeling and analysis of nonlinear spacecraft relative motion via harmonic balance and Lyapunov function. Aerosp. Sci. Technol. 2020, 99, 105761. [Google Scholar] [CrossRef]
- Zhang, S.; Duan, H. Gaussian pigeon-inspired optimization approach to orbital spacecraft formation reconfiguration. Chin. J. Aeronaut. 2015, 28, 200–205. [Google Scholar] [CrossRef]
- Yang, W.W.; Zhao, Y.; Chen, X.Q.; Wang, Z.G. Progress in calculation methods for collision probability of spacecraft. Chin. Space Sci. Technol. 2012, 32, 8–15. [Google Scholar] [CrossRef]
- Dolado-Perez, J.; Pardini, C.; Anselmo, L. Review of uncertainty sources affecting the long-term predictions of space debris evolutionary models. Acta Astronaut. 2015, 113, 51–65. [Google Scholar] [CrossRef]
- Yu, W.; Zhao, P.; Chen, W. Analytical solutions to aeroassisted orbital transfer problem. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3502–3515. [Google Scholar] [CrossRef]
- Mark, C.P.; Kamath, S. Review of active space debris removal methods. Space Policy 2019, 47, 194–206. [Google Scholar] [CrossRef]
- Letizia, F.; Colombo, C.; Lewis, H.; Krag, H. Extending the ECOB space debris index with fragmentation risk estimation. In Proceedings of the 7th European Conference on Space Debris, Darmstadt, Germany, 17–21 April 2017. [Google Scholar]
- Gonzalo, J.L.; Colombo, C.; Di Lizia, P. Analytical framework for space debris collision avoidance maneuver design. J. Guid. Control Dyn. 2021, 44, 469–487. [Google Scholar] [CrossRef]
- Hall, D.T. Implementation recommendations and usage boundaries for the two-dimensional probability of collision calculation. In Proceedings of the 2019 AAS/AIAA Astrodynamics Specialist Conference, Portland, Maine, 11–15 August 2019. [Google Scholar]
- Hua, B.; Liu, R.P.; Sun, S.G.; Wu, Y.H.; Chen, Z.M. Spacecraft cluster orbit planning method based on adaptive population mutated pigeon group optimization. Sci. Sin. Technol. 2020, 50, 453–460. [Google Scholar]
- Zhang, Q.; Pang, G.; Wang, G. A novel sequential three-way decisions model based on penalty function. Knowl.-Based Syst. 2020, 192, 105350. [Google Scholar] [CrossRef]
- Li, C.; Luo, G.; Qin, K.; Li, C. An image encryption scheme based on chaotic tent map. Nonlinear Dyn. 2017, 87, 127–133. [Google Scholar] [CrossRef]
- Wang, H.; Wu, Z.; Rahnamayan, S.; Liu, Y.; Ventresca, M. Enhancing particle swarm optimization using generalized opposition-based learning. Inf. Sci. 2011, 181, 4699–4714. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; Volume 3, pp. 1945–1950. [Google Scholar]
- Duan, H.B.; Yang, Z.Y. Large civil aircraft receding horizon control based on Cauthy mutation pigeon inspired optimization. Sci. Sin. Technol. 2018, 48, 277–288. [Google Scholar]
- Hua, B.; Sun, S.; Wu, Y.; Chen, Z. Path planning method for spacecraft formation reconfiguration based on CGAPIO. J. Beijing Univ. Aeronaut. Astronaut. 2021, 47, 223–230. [Google Scholar] [CrossRef]


| Parameter | Expression | Value |
|---|---|---|
| a | Mapping parameter of Tent Map | 1 |
| Initial value of Tent Map | 0.32 | |
| Minimum value of weighting factor | 0.40 | |
| Maximum value of weighting factor | 0.90 | |
| Parameters of weighting factor | 2.50 | |
| R | Compass factor | 0.30 |
| Number of iterations of Map and Compass Operator | 60 | |
| Number of iterations of the Landmark Operator | 40 |
| Functions | Expression | Range | Min |
|---|---|---|---|
| Sphere | 0 | ||
| Schwefel_2.21 | 0 | ||
| Schwefel_2.22 | 0 | ||
| Setp | 0 | ||
| Rastrigin | 0 | ||
| Ackley | 0 | ||
| Griewank | 0 | ||
| Rosenbrock | 0 | ||
| Apline | 0 |
| Functions | Algorithm | Min | STD |
|---|---|---|---|
| Sphere | PSO PIO CGAPIO ALPIO | 2.22 1.21 6.17 8.94 | 3.27 2.65 2.83 1.22 |
| Schwefel_2.21 | PSO PIO CGAPIO ALPIO | 9.16 6.22 5.60 6.58 | 2.18 3.58 5.82 6.19 |
| Schwefel_2.22 | PSO PIO CGAPIO ALPIO | 5.99 2.65 2.45 1.28 | 7.32 3.82 2.54 7.21 |
| Setp | PSO PIO CGAPIO ALPIO | 4.75 9.89 2.87 2.95 | 3.68 5.49 3.27 2.87 |
| Rastrigin | PSO PIO CGAPIO ALPIO | 1.00 2.12 9.95 3.49 | 6.94 2.45 1.95 8.45 |
| Ackley | PSO PIO CGAPIO ALPIO | 1.68 1.77 4.37 5.01 | 3.31 1.29 5.58 6.86 |
| Griewank | PSO PIO CGAPIO ALPIO | 7.34 1.19 1.51 5.31 | 1.97 6.57 1.36 2.81 |
| Rosenbrock | PSO PIO CGAPIO ALPIO | 1.18 2.83 1.90 1.00 | 1.84 2.65 1.02 1.32 |
| Apline | PSO PIO CGAPIO ALPIO | 3.96 4.13 5.98 4.25 | 5.25 1.47 4.89 3.67 |
| x/(km) | y/(km) | z/(km) | /(km/s) | /(km/s) | /(km/s) | |
|---|---|---|---|---|---|---|
| Spacecratf1 | 0 | 40 | 2 | −0.002 | 0 | |
| Spacecraft2 | −40 | 0 | 1.2 | 0.002 | 0.002 | |
| Spacecratf3 | 0 | −40 | 2 | −0.002 | 0 | |
| Spacecratf4 | 40 | 0 | 2.8 | 0 | −0.002 | |
| Obstacle1 | 0 | 27 | 0 | −0.002 | 0 | |
| Obstacle2 | −26 | 0 | 0 | 0.002 | 0.002 | |
| Obstacle3 | 0 | −28 | 0 | −0.002 | 0 | |
| Obstacle4 | 25 | 0 | 0 | 0 | −0.002 |
| x/(km) | y/(km) | z/(km) | /(km/s) | /(km/s) | /(km/s) | |
|---|---|---|---|---|---|---|
| Spacecratf1 | 14.14 | −14.14 | −1.71 | 0 | 0 | 0 |
| Spacecraft2 | 14.14 | 14.14 | −1.71 | 0 | 0 | 0 |
| Spacecratf3 | −14.14 | 14.14 | −2.28 | 0 | 0 | 0 |
| Spacecratf4 | −14.14 | −14.14 | −2.28 | 0 | 0 | 0 |
| Parameter | Expression | Value |
|---|---|---|
| J | Penalty factor | 100 |
| Threshold of collision probability | ||
| n | Orbital angular velocity | rad/s |
| t | Reconstruction time | ≤40 min |
| Safe distance | 30 m | |
| Acceleration components | m/s |
| Algorithm | /(km/s) | ||||
|---|---|---|---|---|---|
| Spacecraft 1 | Spacecraft 2 | Spacecraft 3 | Spacecraft 4 | Total | |
| PSO | 0.143930 | 0.179476 | 0.151393 | 0.197614 | 0.672413 |
| PIO | 0.141176 | 0.175323 | 0.141251 | 0.177637 | 0.635388 |
| CGAPIO | 0.140877 | 0.173518 | 0.140907 | 0.175290 | 0.630592 |
| ALPIO | 0.140823 | 0.173353 | 0.140866 | 0.175288 | 0.630333 |
| Algorithm | /(km/s) | ||||
|---|---|---|---|---|---|
| Spacecraft 1 | Spacecraft 2 | Spacecraft 3 | Spacecraft 4 | Total | |
| PSO | 0.154627 | 0.210988 | 0.162819 | 0.200227 | 0.728661 |
| PIO | 0.157961 | 0.193940 | 0.156199 | 0.192466 | 0.700566 |
| CGAPIO | 0.150595 | 0.182973 | 0.157982 | 0.198670 | 0.690220 |
| ALPIO | 0.146349 | 0.176344 | 0.144906 | 0.194798 | 0.662397 |
| Algorithm | /(km/s) | ||||
|---|---|---|---|---|---|
| Spacecraft 1 | Spacecraft 2 | Spacecraft 3 | Spacecraft 4 | Total | |
| PSO | 0.193661 | 0.271571 | 0.179255 | 0.212045 | 0.856532 |
| PIO | 0.163336 | 0.197146 | 0.163789 | 0.200310 | 0.724581 |
| CGAPIO | 0.163417 | 0.192411 | 0.157560 | 0.202538 | 0.715926 |
| ALPIO | 0.156120 | 0.183607 | 0.149306 | 0.200546 | 0.689579 |
| Algorithm | Running Time/(s) | ||
|---|---|---|---|
| Four-Impulse | Five-Impulse | Six-Impulse | |
| PSO | 7.76 | 9.89 | 12.39 |
| PIO | 5.48 | 6.73 | 10.28 |
| CGAPIO | 5.29 | 6.55 | 9.96 |
| ALPIO | 5.12 | 6.34 | 9.52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hua, B.; Yang, G.; Wu, Y.; Chen, Z. Path Planning of Spacecraft Cluster Orbit Reconstruction Based on ALPIO. Remote Sens. 2022, 14, 4768. https://doi.org/10.3390/rs14194768
Hua B, Yang G, Wu Y, Chen Z. Path Planning of Spacecraft Cluster Orbit Reconstruction Based on ALPIO. Remote Sensing. 2022; 14(19):4768. https://doi.org/10.3390/rs14194768
Chicago/Turabian StyleHua, Bing, Guang Yang, Yunhua Wu, and Zhiming Chen. 2022. "Path Planning of Spacecraft Cluster Orbit Reconstruction Based on ALPIO" Remote Sensing 14, no. 19: 4768. https://doi.org/10.3390/rs14194768
APA StyleHua, B., Yang, G., Wu, Y., & Chen, Z. (2022). Path Planning of Spacecraft Cluster Orbit Reconstruction Based on ALPIO. Remote Sensing, 14(19), 4768. https://doi.org/10.3390/rs14194768






