1. Introduction
Remote sensing images are a valuable data source for observing the earth surface [
1]. The rapid development of remote sensing instruments provides us with opportunities to obtain high-resolution images. Remote sensing technology has been widely used in many practical applications, such as remote sensing image scene classification (RSISC) [
2], object detection [
3], semantic segmentation [
4], change detection [
5], and image fusion [
6,
7]. Scene classification is an active research topic in the intelligent interpretation of remote sensing images, and it aims to distinguish a predefined semantic category. For the last few decades, extensive research work on RSISC has been undertaken, driven by its real-world applications, such as urban planning [
8], natural hazard detection [
9], and geospatial object detection [
10]. As the resolution of remote sensing images increases, RSISC has become an important and challenging task.
It is important for RSISC to establish contextual information [
11]. For example, pixel-based classification methods can distinguish the basic land-cover types such as vegetation, water, buildings, etc. When contextual information is considered, scene classification can distinguish high-level semantic information such as residential areas, industrial areas, etc. Convolutional neural networks (CNNs) expand the receptive field by stacking convolutional layers. However, the global interactions of the local elements in the image are not directly modeled when using stacked receptive fields. Differing from CNNs, Vision Transformer (ViT) [
12] directly establishes contextual information between different patches via a self-attention mechanism and achieves remarkable performance in the field of computer vision. ViT is also used for scene classification [
13,
14] and achieved state-of-the-art (SOTA). Unfortunately, self-attention has quadratic computation complexity, and it focuses too much on global semantic information while ignoring local structural features, such as those extracted by convolution. The recent work on multi-layer perceptron (MLP) [
15,
16,
17,
18] comparisons shows that self-attention is not critical for ViT, as MLP can also directly establish contextual dependencies and achieve similar accuracy to ViT. MLP achieves local and global semantic information extraction by alternately stacking MLP layers along spatial and channels, respectively. It is a competitive but conceptually and technically simple alternative that does not rely on self-attention. There is less research on MLP in RSISC. To our knowledge, we are the first to introduce MLP work into RSISC, and we hope that the insights extracted from this article can help promote the development of MLP in RSISC.
Remote sensing images are extremely different from conventional images due to their unique capture methods. On the one hand, remote sensing images often have the characteristics of broad independent coverage, high resolution, and complex components, which causes difficulties in scene classification [
1]. As shown in
Figure 1a, each image contains multiple ground objects. On the other hand, scene images of different categories may have high similarities. Such “dense residential” and “medium residential” areas, as shown in
Figure 1b, have the same components; the distribution of densities causes them to be slightly different. Extracting discriminative features is the key to solving such problems. How to enhance the local semantic representation capability and extract more discriminative features for aerial scenes remains to be investigated [
19]. Another critical challenge for scene classification is the lack of data due to the difficulty of dataset labelling and the limitation of sensor characteristics [
1]. Although a series of new datasets have been made public recently, the number of images and object categories are still relatively small compared with the natural scene dataset. Mining more supervision information becomes a way to solve such problems.
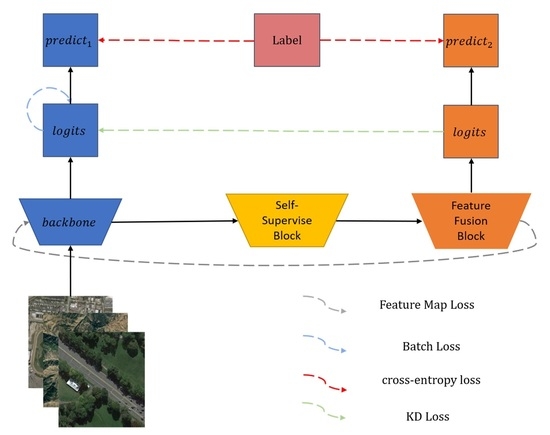
When the number of training samples is limited, acquiring more labels to supervise the network is an effective solution to alleviate the lack of data. We design a self-supervised branch that takes the feature maps of the backbone network as labels and uses self-supervised methods to process the feature maps of the backbone network as the input of the branch network, and the output of the branch network is used as the prediction result. Specifically, it includes a self-supervised block and a feature fusion block. The self-supervised block uses two methods to preprocess the feature maps. One is to shuffle the feature map after dividing the region. Noroozi et al. [
21] argues that solving jigsaw puzzles can be used to teach a system that an object is made of parts and what these parts are. It is beneficial for the network to understand the relative position information between different image patches. The other is to mask the background region [
15,
22]. Remote sensing scene images often contain a large amount of background information, and background masking can mask redundant backgrounds and enhance the discriminative ability of the branch network. This is an efficient solution to address the challenge of discriminative feature extraction. Different from SKAL [
22], we propose masking the background by dividing the patch. Subsequent experiments show that this masking method is relatively flexible.
We adopt a feature pyramid network (FPN) [
23] structure as the feature fusion block. The FPN structure has been used extensively in remote sensing [
24,
25]. It adopts a top-down method to fuse feature maps from different stages, and high-level features play a guiding role for low-level features. However, low-level and mid-level features are also essential for improving the features extracted in deep layers from a coarse level to a fine level [
26]. Thus, we add a bottom-up fusion process to the branch network. Different locations in the image should have different attention weights, and due to the inherent density advantage of the image, the adjacent regions tend to have similar attention weight. Motivated by this, we propose a feature fusion module; it dynamically weights the feature map by assigning different attention weights to the patches.
The large memory and computation cost of branch structure cannot be ignored, so we embed the knowledge distillation method in SSKDNet. Inspired by FRSKD [
27] and BAKE [
28], the branch labels are served as soft logits to distil knowledge to the backbone, and the backbone integrates sample-similarity-level soft logits to guide itself. We only adopt the backbone during inference to reduce the computational load.
The main contributions of this article are summarized as follows:
- 1.
The performance of the Cycle MLP [
18] model in RSISC is explored, and the SSKDNet model is proposed, enhancing the discriminative ability of Cycle MLP through self-supervised learning and knowledge distillation.
- 2.
We propose a self-supervised learning branch to learn the backbone feature maps. It includes a self-supervised block and a feature fusion block. The self-supervised block masks background regions by an attention mechanism and shuffles the feature map after dividing the region to improve the discriminative ability of the branch. The feature fusion block dynamically weights the feature maps of different stages, enhancing the high-level features from a coarse level to a fine level.
- 3.
The backbone integrates the “dark knowledge” of the branch via knowledge distillation to reduce the computation of the inference. It ensembles the sample-similarity-level soft logits to guide itself, which fully uses the similarity information between samples. Moreover, SSKDNet dynamically weights multiple losses via a principled loss function [
29] to reduce training costs.
The remainder of this article is organized as follows.
Section 2 presents related work on RSISC, MLP, self-supervised learning and knowledge distillation. In
Section 3, our proposed model is described in detail. In
Section 4, the effectiveness of SSKDNet is demonstrated through experiments on three datasets.
Section 5 discusses the advantages of our self-supervised branch.
Section 6 provides the concluding remarks.
3. Materials and Methods
This section explains the specific details of the proposed SSKDNet for RSISC. The overall structure of the SSKDNet model is displayed in
Figure 2. It consists of a backbone and a self-supervised branch. The backbone adopts Cycle MLP [
18], and the self-supervised branch includes a self-supervised block and a feature fusion block. We present the backbone in
Section 3.1, the self-supervised branch in
Section 3.2, knowledge distillation in
Section 3.3, and loss functions of SSKDNet in
Section 3.4.
3.1. Backbone
Cycle MLP [
18] is used as our backbone in the feature extraction stage. We denote stage1-stage5 as
–
.
represents patch embedding, which downsamples a quarter of the original input spatial dimension.
–
stack 3, 4, 24, and 3 cycle fully connected (FC) layers (
Section 3.1.1), respectively. The outputs have 96, 192, 384, and 768 channel dimensions, respectively. After each stage, the spatial dimension is downsampled by half. The feature maps of the backbone can be formulated as follows.
where
is the output feature map of
, and
is the feature map from the former layer. Specifically, the feature map
is the input image. For the j-th sample, the predictive probability vector
can be obtained via a softmax function on the logits
, where
M is the category number. The probability of class
k can be formulated as follows.
3.1.1. Cycle MLP
We denote the input feature map as
, where
H,
W,
C are the height of the feature map, the width of the feature map and the number of channels. As shown in
Figure 3a, channel FC allows communication between different channels, and it can handle various input scales. However, it cannot provide spatial information interactions. As shown in
Figure 3b, spatial FC allows communication between different spatial locations. However, its computational complexity is quadratic with the image scale. As shown in
Figure 3c, Cycle FC allows communication between channels and spatial locations by adding a shift operation, and it has linear complexity.
We use subscripts to index the feature map. For example,
is the value of the
c-th channel at the spatial position
, and
are values of all channels at the spatial position
. The Cycle FC can be formulated as follows.
where
and
are
along with the height and width dimensions, respectively.
and
are spatial offsets on the
c-th channel.
and
are parameters of Cycle FC.
Figure 3d shows the Cycle FC when
and
.
3.2. Self-Supervised Branch
The self-supervised branch includes a self-supervised block and a feature fusion block. The self-supervised block is shown in
Figure 4. This block performs patch embedding on the backbone feature maps
–
, and then feeds the features into the gMLP [
15] to extract local information
–
. The final feature maps
–
are obtained by passing the adjacent
–
through a Cross MLP, which is an information interaction module. Notably,
–
are processed differently.
masks a part of the background by background masking.
shuffles the regions after dividing the regions by jigsaw puzzle.
is fed directly into the gMLP after patch embedding.
is utilized to calculate the attention map. The feature fusion block is shown at the bottom of
Figure 2, which is achieved by a top-down and bottom-up bidirectional fusion. We use a feature fusion module to fuse adjacent feature maps and use the feature maps
–
as the self-supervised prediction results.
3.2.1. Background Masking
Masking background regions is an effective way to extract discriminative features [
22]. As shown in
Figure 4a,d, we calculate the attention map of the high-level feature map
. The attention map
for each position
is calculated as follows.
where
is the element of
, and
C is the number of channels of
. We upsample the attention map
to the same spatial shape as
by the nearest interpolation, record the positions of
of feature points with the lowest attention weights, and then delete the corresponding tokens in the feature map
. We pad a vector
with an initial value of 1 to replace the deleted tokens. It is well known that high-level feature maps contain high-level semantic information, and the network tends to pay more attention to points with higher activation values. Thus, the channel means of the feature map
can effectively calculate the attention map of the network. Later experiments can also verify this.
3.2.2. Jigsaw Puzzle
We expect SSKDNet to learn more location information about images. Noroozi et al. [
21] proposed to divide the feature map into different regions, erase the edge information and randomly shuffle the regions. As shown in
Figure 4b, we adopt a similar method to divide the feature map into four regions, erase the edge information of the feature map, and then shuffle them randomly.
3.2.3. Cross MLP
Compared with convolution and transformer, gMLP [
15] alternately constructs FC layers along the channel dimension and the token dimension, which can extract global features easily. As shown in
Figure 5, we propose a Cross MLP module to obtain more complete semantic information from adjacent feature maps. The Cross MLP has two parallel gMLP with a larger receptive field. It can be formulated as follows.
where
and
are the input feature maps.
represents patch embedding with
.
and
are split tokens,
,
, where N is the number of tokens. We concatenate
and
along the channel dimension and token dimension to obtain
and
by
, respectively. gMLP [
15] is used for information interaction between channels and tokens, and
and
are FC layers along the channel dimension and token dimension to adjust the size of
and
, respectively.
As shown in
Figure 4, the feature maps
–
are the input. We can obtain the self-supervised block output
–
from the following formula.
Before Cross MLP, the feature maps and are adjusted to be the same as the spatial size of the by upsample or downsample. The upsample adopts nearest interpolation, and the downsample adopts convolution with kernel size and stride = 2, where denotes a convolutional layer. We adjust the output – to the same size as – by upsample and .
As shown in
Table 1, we show the parameter settings for patch embedding in the self-supervised block, where
and
are patch size and the number of channels, respectively, and (a)–(d) correspond to the different branchs of
Figure 4.
3.2.4. Feature Fusion Block
We dynamically weight adjacent feature maps by setting a weight for each patch of the feature map. As shown in
Figure 6, for the input
and
, the feature fusion module can be formulated as follows.
where
denotes a
convolutional layer, and
is the nearest interpolation. We adjust
to the same spatial and channel shape as
by
and
(when the spatial size of
is greater than
, replace the
with the
). Then the feature maps
and
are split into fixed-size tokens by
.
, and
, where N is the number of tokens.
is the feature map after fusion of
and
. We adjust the weight of the tokens by setting a pair of learnable vectors
and
. Specifically, the j-th token
is calculated as follows.
Dividing the feature map into patches allows the network to flexibly assign different attention weights to patches.
The top-down feature maps
can be formulated as follows.
Similarly, the bottom-up feature maps
can be formulated as follows.
The difference between and is that upsample is substituted by downsample, and the downsample adopts convolution with kernel size and stride = 2.
For the setting of parameters
and
, we initialize
and
to 1 and normalize them by the softmax function. It can be formulated as follows.
The weights are normalized to the range 0 to 1 by softmax to represent the importance of each input, which is an efficient attention calculation method. In the feature fusion block, we set the patch size of the patch embedding to 6, 8, and 16 in the top-down approach and set the patch size to 8, 4, and 2 in the bottom-up approach, respectively. The other settings are the same as FRSKD [
27].
3.2.5. Feature Map Loss
For the backbone feature map
, we denote
as the channel mean of
.
and
are the mean and variance of
, respectively. The normalization process can be formulated as follows.
Similarly, for the branch feature map
, we can calculate the normalized feature map
. The feature map loss can be formulated as follows.
The gradients through are not propagated to avoid the model collapse issue.
3.3. Knowledge Distillation
Knowledge distillation can be viewed as normalizing the training of the student network with soft targets that carry the “dark knowledge” of the teacher network. We combine two knowledge distillation methods so that the backbone can obtain knowledge from the branch and itself. The knowledge distillation methods include soft logit distillation and batch distillation.
We denote as the logit vectors of the backbone in the same batch. For the j-th sample, the backbone logit vector , where M is the number of categories, and N is the number of samples in a batch.
3.3.1. Soft Logits Distillation
The soft logit output by the network contains more information about sample than just the class label. For the j-th sample, the backbone soft logits
can be obtained by a softmax function, and the soft logits of the
k-th class can be formulated as follows.
The
is the temperature hyper-parameter which is used to soften the logits. Similarly, we can obtain the branch soft logits
. The Kullback–Leibler (
KL) loss is used to measure the similarity of two distributions. The
KL loss can be formulated as follows.
3.3.2. Batch Distillation
Samples with high visual similarities are expected to make more consistent predictions about their predicted class probabilities, regardless of these truth labels. In this part, the batch knowledge ensembling (BAKE) [
28] is introduced to obtain excellent soft logits. It achieves knowledge ensembling by aggregating the “dark knowledge” from different samples in the same batch. We can obtain the pairwise similarity matrix
by the dot product of the logits.
represents the affinity between the samples with indexes i and j, and it can be formulated as follows.
where
. We normalize each row of the affinity matrix
to obtain
,
For the i-th sample, the soft logits
, we denote the soft logits of samples within the same batch as
. Based on Equations (
17) and (
18), we can obtain the soft logits
aggregated from the sample information,
where
is the weighting factor. For the j-th sample, the batch
KL loss can be formulated as follows.
Notably, in Equation (
20),
is different from Equation (
16). The parameters for knowledge distillation are set the same as in BAKE [
28].
3.4. Loss Function of SSKDNet
The SSKDNet is optimized by minimizing the loss function. Our loss function consists of three parts, including knowledge distillation loss (Equations (
16) and (
20)), cross-entropy loss (Equations (
22) and (
23)), and feature map loss (Equation (
14)). The total loss can be formulated as follows.
where
and
are the backbone and branch predictions, respectively.
and
represent the cross-entropy loss functions from the backbone and self-supervised branch.
and
are the weight coefficients. We introduce a multi-task loss function [
29] to reduce the extra cost of hyperparameters. Specifically, we set the weight coefficients as learnable variables and optimize them using the following formula.
where
and
are learnable parameters. This loss function is smoothly differentiable and is well-formed such that the task weights do not converge to zero. In contrast, directly learning the weights using a simple linear sum of losses would result in weights that quickly converge to zero.
5. Discussion
In SSKDNet, the backbone and branch are optimized together. On the one hand, the self-supervised branch learns the feature map of the backbone by feature map loss. On the other hand, the backbone integrates the “dark knowledge” of the branch via soft logits. This is a mutual learning process.
We visualized the background masking module on the UCM dataset.
Figure 14 and
Figure 15 show our background masking results on the original images with 75% and 50% scales, respectively. By the 30th epoch, the network can already accurately determine the background location. These results show that the branch can detect the background and discriminative region locations significantly. SKAL [
22] uses a similar method to calculate the discriminative regions. The difference is that they can only crop out a continuous square region. In contrast, we use patch embedding to process each token attention information, and the extracted tokens can be discontinuous in spatial position, which is relatively flexible.
We also selected the UCM dataset to generate the energy maps of
–
at different training stages to explore the branch learning process. As shown in
Figure 16 and
Figure 17, the attention of the feature map gradually transfers to the discriminative area as the training progresses. Additionally, even the low-level feature map
can focus on the discriminative area. The results show that our network can extract accurate discriminative regional features and further verify the effectiveness of the self-supervised branch.
To further demonstrate the classification results of our SSKDNet, we used T-SNE [
72] to map the prediction vectors in the high-dimensional space to the low-dimensional space. In addition, we visualize Cycle MLP and SSKDNet by randomly selecting 1000 test samples on the AID and UCM datasets, respectively.
Figure 18a,b represent the visualization results of Cycle MLP and SSKDNet on the AID dataset, respectively.
Figure 18c,d represent the visualization results of SSKDNet on the UCM dataset, respectively. It can be seen that SSKDNet has smaller intraclass distance and larger interclass distance than Cycle MLP.
6. Conclusions
This article investigated the Cycle MLP models for RSISC. We have also proposed the SSKDNet model to improve the discriminative ability of the Cycle MLP model. First, a self-supervised branch is introduced, which generates labels through feature maps to alleviate the problem of insufficient training data. Second, an attention-based feature fusion module is introduced to fuse adjacent feature maps dynamically. Finally, a knowledge distillation method is proposed to distil the “dark knowledge” of the branch to the backbone. Moreover, a multi-task loss function weighting method is introduced to weight the SSKDNet loss function dynamically. We evaluate the performance of our model on three public datasets, achieving 99.62%, 95.96%, and 92.77% accuracy on the UCM, AID, and NWPU datasets, respectively. Results on multiple datasets show that SSKDNet has more competitive classification accuracy than some SOTA methods, and MLP can achieve a similar effect to the self-attention mechanism. For future work, we will try to reduce the time consumption of the SSKDNet method in the training phase and further improve the performance on small-scale datasets.