Permafrost Early Deformation Signals before the Norilsk Oil Tank Collapse in Russia
Abstract
:1. Introduction
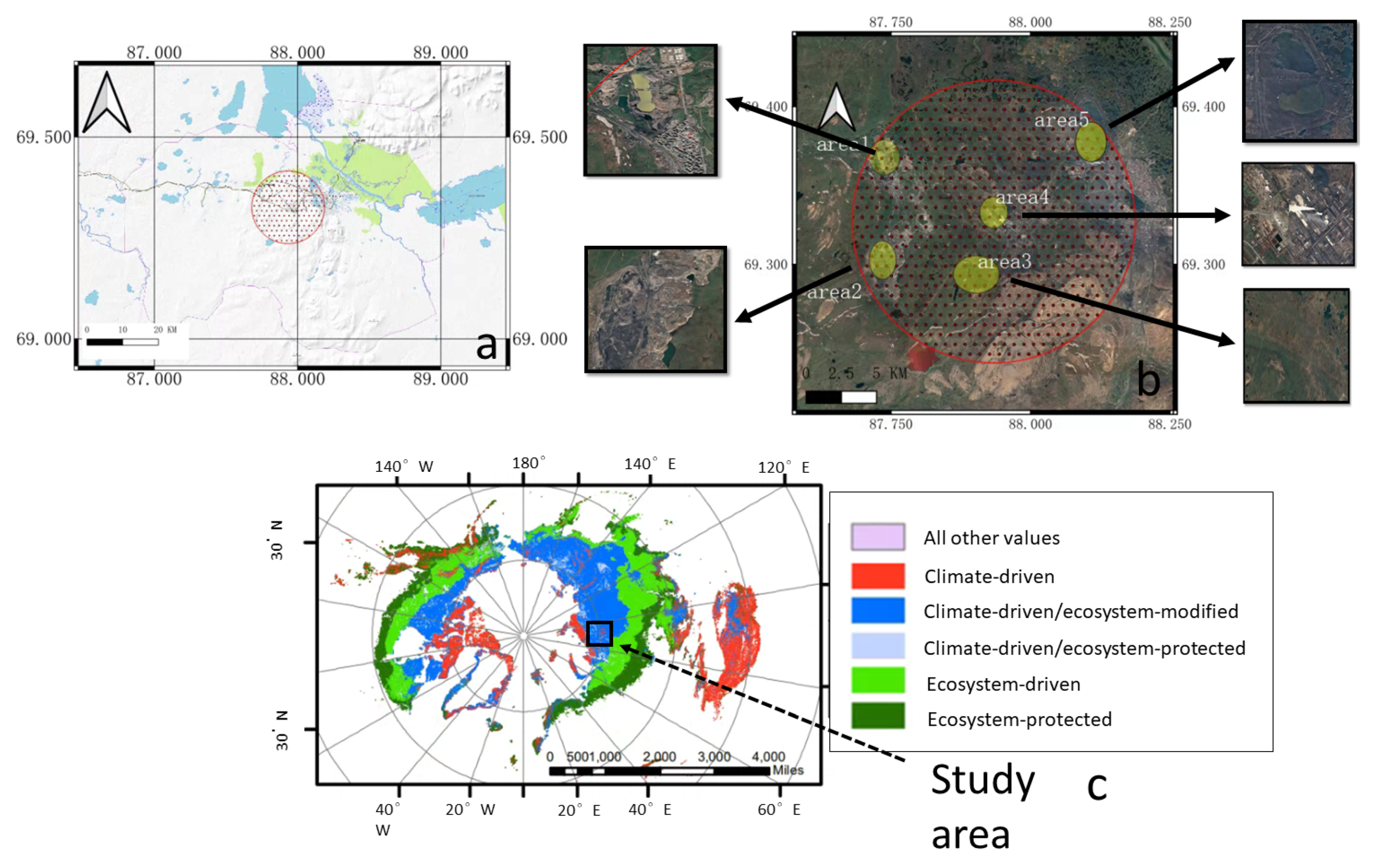
2. Study Area and Materials
3. Methods
3.1. Long-Term Surface Deformation Monitoring
3.2. Interannual and Seasonal Deformation Decomposition
3.3. Calculation of Thermal Conductivity
3.4. Calculation of Melting Depth
4. Results
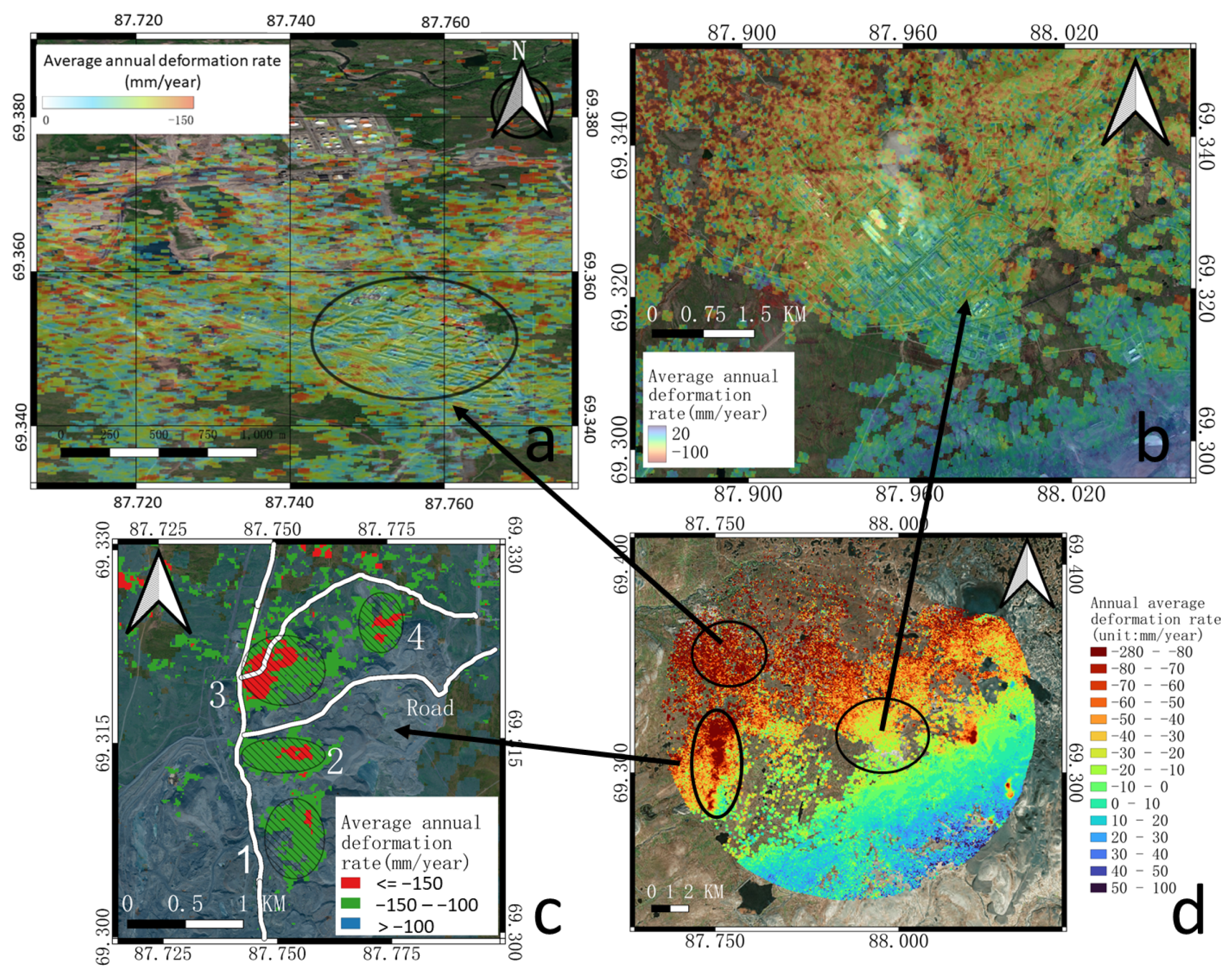
4.1. Surface Deformation Rate Distribution
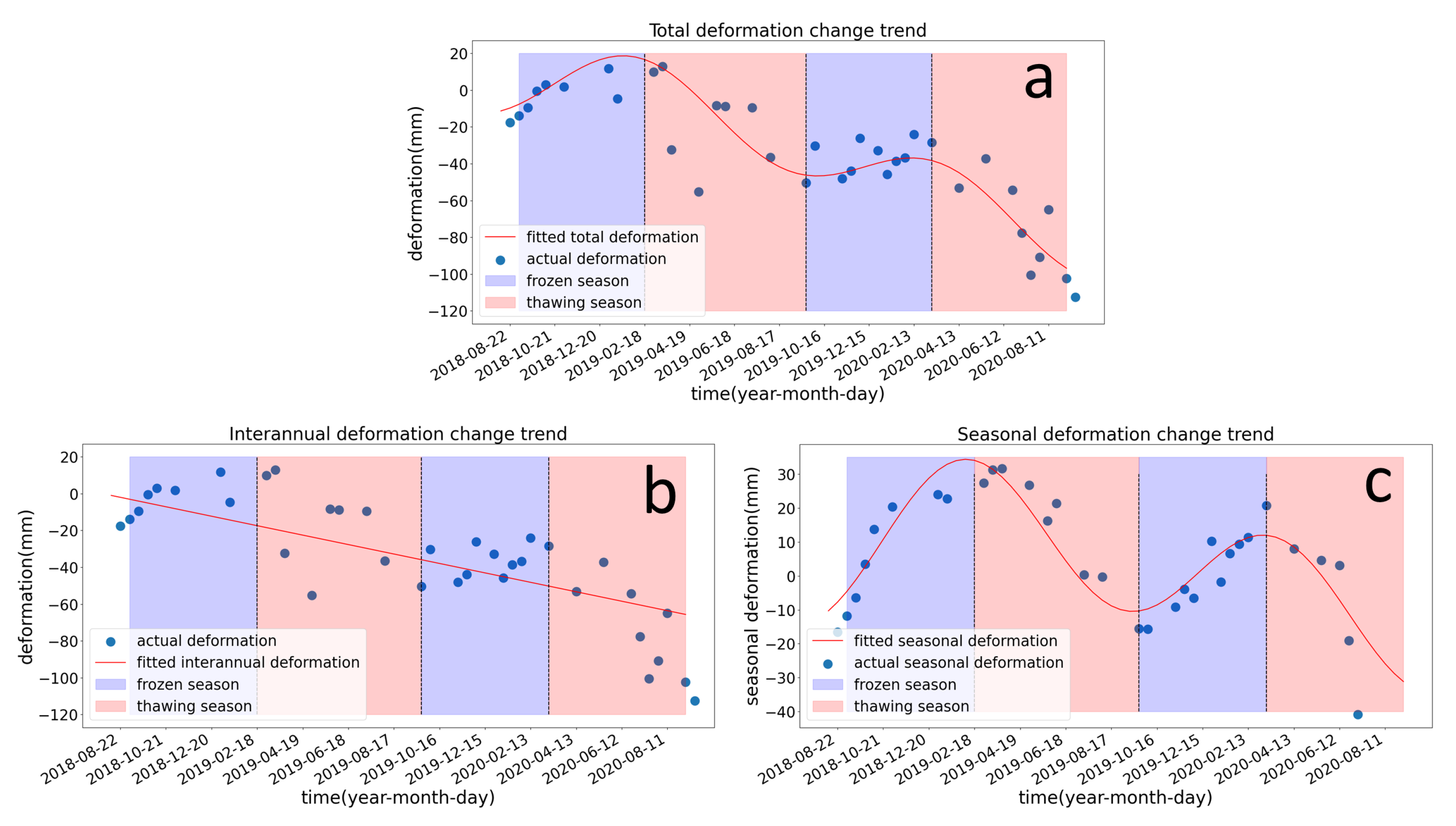
4.2. Interannual Deformation and Seasonal Deformation Decomposition
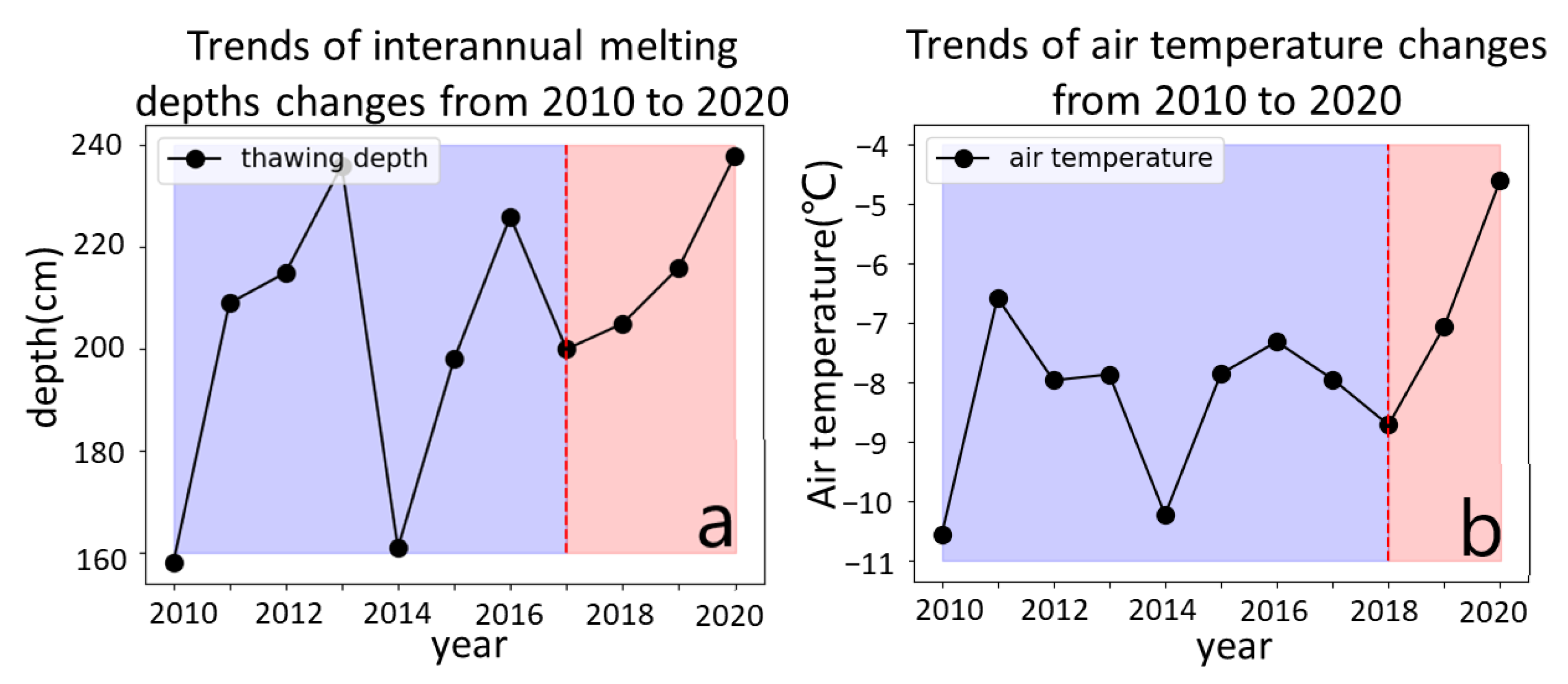
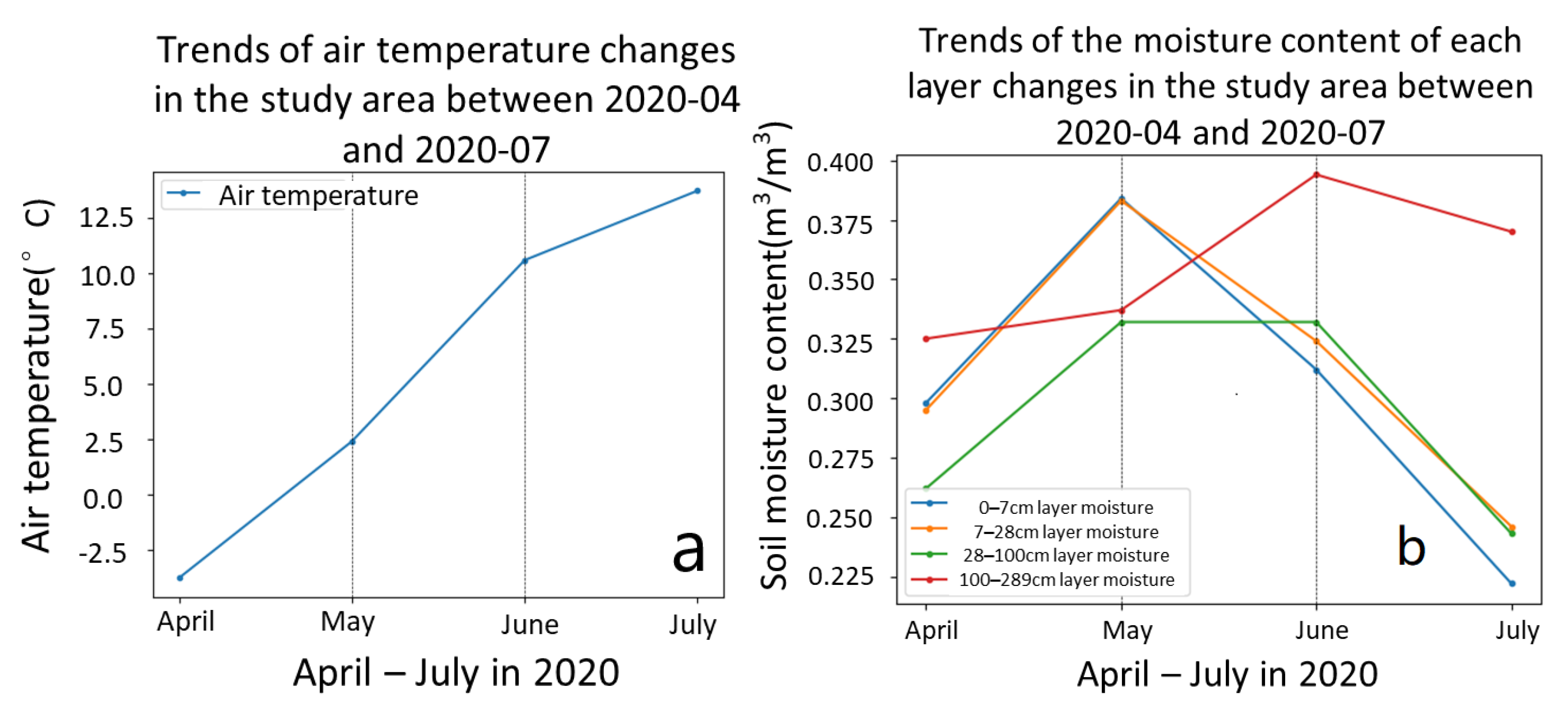
4.3. Effect of Annual Average Air Temperature on Interannual Melting Depth
4.4. Subsurface Ice Melting Process during the Summer Thawing Period
4.5. Effect of Terrain Slope on the Rate of Surface Deformation
5. Discussion
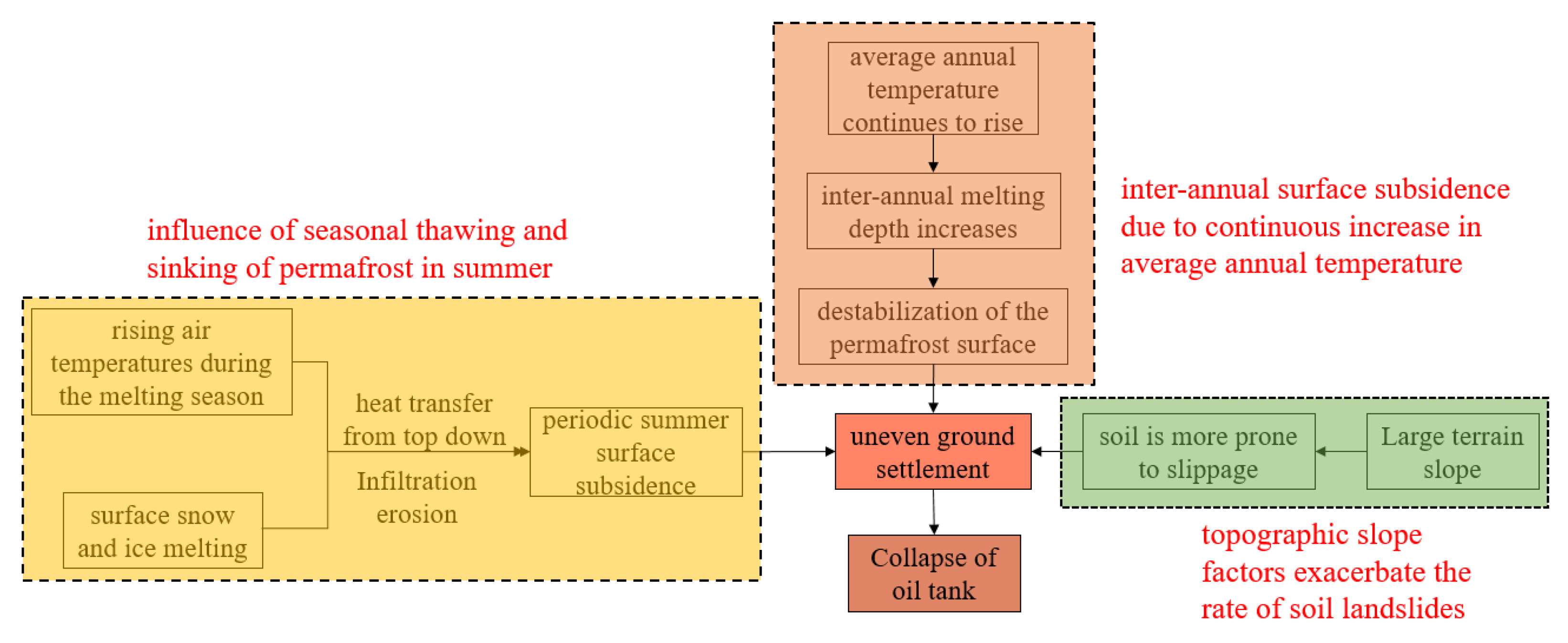
5.1. Permafrost Surface Deformation Mechanisms
5.2. Permafrost Early Deformation Signals
5.3. Comparison with Previous Studies
5.4. Limitation and Future Reasearch
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, S.; Zhao, L.; Wang, L.; Zhou, H.; Zou, D.; Sun, Z.; Xie, C.; Qiao, Y. Intra-Annual Ground Surface Deformation Detected by Site Observation, Simulation and InSAR Monitoring in Permafrost Site of Xidatan, Qinghai-Tibet Plateau. Geophys. Res. Lett. 2022, 49, e2021GL095029. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, L.; Zhou, H.; Liu, S.; Du, E.; Zou, D.; Liu, G.; Wang, C.; Li, Y. Permafrost Ground Ice Melting and Deformation Time Series Revealed by Sentinel-1 InSAR in the Tanggula Mountain Region on the Tibetan Plateau. Remote Sens. 2022, 14, 811. [Google Scholar] [CrossRef]
- Meng, Q.; Intrieri, E.; Raspini, F.; Peng, Y.; Liu, H.; Casagli, N. Satellite-based interferometric monitoring of deformation characteristics and their relationship with internal hydrothermal structures of an earthflow in Zhimei, Yushu, Qinghai-Tibet Plateau. Remote Sens. Environ. 2022, 273, 112987. [Google Scholar] [CrossRef]
- IPCC Climate Change. The physical science basis. In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2013; Volume 1535, p. 2013. [Google Scholar]
- Schuur, E.A.; McGuire, A.D.; Schädel, C.; Grosse, G.; Harden, J.W.; Hayes, D.J.; Hugelius, G.; Koven, C.D.; Kuhry, P.; Lawrence, D.M.; et al. Climate change and the permafrost carbon feedback. Nature 2015, 520, 171–179. [Google Scholar] [CrossRef] [PubMed]
- Walter Anthony, K.; Schneider von Deimling, T.; Nitze, I.; Frolking, S.; Emond, A.; Daanen, R.; Anthony, P.; Lindgren, P.; Jones, B.; Grosse, G. 21st-century modeled permafrost carbon emissions accelerated by abrupt thaw beneath lakes. Nat. Commun. 2018, 9, 3262. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, H.; Zhu, Q.; Peng, C.; Wu, N.; Wang, Y.; Fang, X.; Gao, Y.; Zhu, D.; Yang, G.; Tian, J.; et al. The impacts of climate change and human activities on biogeochemical cycles on the Q inghai-T ibetan P lateau. Glob. Chang. Biol. 2013, 19, 2940–2955. [Google Scholar] [CrossRef]
- Woodcroft, B.J.; Singleton, C.M.; Boyd, J.A.; Evans, P.N.; Emerson, J.B.; Zayed, A.A.; Hoelzle, R.D.; Lamberton, T.O.; McCalley, C.K.; Hodgkins, S.B.; et al. Genome-centric view of carbon processing in thawing permafrost. Nature 2018, 560, 49–54. [Google Scholar] [CrossRef] [PubMed]
- Qhma, B.; Ji, C.; Jcw, C.; Xin, H.; Jyz, A.; Shz, C.; C, H.; Jwga, B. Strengthening effect of crushed rock revetment and thermosyphons in a traditional embankment in permafrost regions under warming climate. Adv. Clim. Chang. Res. 2021, 12, 66–75. [Google Scholar]
- Wang, S.; Niu, F.; Chen, J.; Dong, Y. Permafrost research in China related to express highway construction. Permafr. Periglac. Process. 2020, 31, 406–416. [Google Scholar] [CrossRef]
- Zhong, W.; Zhang, T.; Chen, J.; Shang, J.; Wang, S.; Mu, C.; Fan, C. Seasonal deformation monitoring over thermokarst landforms using terrestrial laser scanning in Northeastern Qinghai-Tibetan Plateau. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102501. [Google Scholar] [CrossRef]
- Li, R.; Li, Z.; Han, J.; Lu, P.; Qiao, G.; Meng, X.; Hao, T.; Zhou, F. Monitoring surface deformation of permafrost in Wudaoliang Region, Qinghai–Tibet Plateau with ENVISAT ASAR data. Int. J. Appl. Earth Obs. Geoinf. 2021, 104, 102527. [Google Scholar] [CrossRef]
- Howard, H.R.; Manandhar, S.; Wang, Q.; Mcmillan, J.M.; Qie, G.; Liu, X.; Thapa, K.; Xu, X.; Wang, G. Spatially characterizing land surface deformation and permafrost active layer thickness for Donnelly installation of Alaska using DInSAR and MODIS data. Cold Reg. Sci. Technol. 2022, 196, 103510. [Google Scholar] [CrossRef]
- Luo, L.; Zhuang, Y.; Zhang, M.; Zhang, Z.; Ma, W.; Zhao, W.; Zhao, L.; Wang, L.; Shi, Y.; Zhang, Z.; et al. An integrated observation dataset of the hydrological and thermal deformation in permafrost slopes and engineering infrastructure in the Qinghai–Tibet Engineering Corridor. Earth Syst. Sci. Data 2021, 13, 4035–4052. [Google Scholar] [CrossRef]
- Chai, M.; Li, G.; Ma, W.; Cao, Y.; Wu, G.; Mu, Y.; Chen, D.; Zhang, J.; Zhou, Z.; Zhou, Y.; et al. Assessment of freeze–thaw hazards and water features along the China–Russia Crude Oil Pipeline in permafrost regions. Remote Sens. 2020, 12, 3576. [Google Scholar] [CrossRef]
- Shi, X.; Jiang, L.; Jiang, H.; Wang, X.; Xu, J. Geohazards Analysis of the Litang–Batang Section of Sichuan–Tibet Railway Using SAR Interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 11998–12006. [Google Scholar] [CrossRef]
- Shan, W.; Hu, Z.; Jiang, H.; Guo, Y.; Wang, C. Environmental and Engineering Geology of the Bei’an to Heihe Expressway in China with a Focus on Climate Change. In Engineering Geology for Society and Territory; Springer: Cham, Switzerland, 2015; Volume 1, pp. 271–277. [Google Scholar]
- Qi, J.; Sheng, Y.; Zhang, J.; Wen, Z. Settlement of embankments in permafrost regions in the Qinghai-Tibet Plateau. Nor. Geogr. Tidsskr.-Nor. J. Geogr. 2007, 61, 49–55. [Google Scholar]
- Yuan, C.; Yu, Q.; You, Y.; Guo, L. Deformation mechanism of an expressway embankment in warm and high ice content permafrost regions. Appl. Therm. Eng. 2017, 121, 1032–1039. [Google Scholar] [CrossRef]
- Luo, X.; Yu, Q.; Ma, Q.; Guo, L. Study on the heat and deformation characteristics of an expressway embankment with shady and sunny slopes in warm and ice-rich permafrost regions. Transp. Geotech. 2020, 24, 100390. [Google Scholar] [CrossRef]
- Wang, S.; Chen, Z.; Qin, W.; Liu, Y.; Liu, F.; Jin, G. Using DInSAR to Monitor Frost Heaving and Thaw Settlement Deformation of Highway Subgrade in Seasonal Frozen Soil Zone. J. Wuhan Univ. Technol. (Transp. Sci. Eng.) 2018, 42, 58–62. [Google Scholar]
- Wang, H.; Qi, Y.; Zhang, J.; Zhang, J.; Yang, R.; Guo, J.; Luo, D.; Wu, J.; Zhou, S. Influence of Open-Pit Coal Mining on Ground Surface Deformation of Permafrost in the Muli Region in the Qinghai-Tibet Plateau, China. Remote Sens. 2022, 14, 2352. [Google Scholar] [CrossRef]
- Luo, L.; Ma, W.; Zhang, Z.; Zhuang, Y.; Zhang, Y.; Yang, J.; Cao, X.; Liang, S.; Mu, Y. Freeze/thaw-induced deformation monitoring and assessment of the slope in permafrost based on terrestrial laser scanner and GNSS. Remote Sens. 2017, 9, 198. [Google Scholar] [CrossRef] [Green Version]
- Kenyi, L.W.; Kaufmann, V. Estimation of rock glacier surface deformation using SAR interferometry data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1512–1515. [Google Scholar] [CrossRef]
- Echelard, T.; Krysiecki, J.M.; Gay, M.; Schoeneich, P. Rockglacier movements detection by Differential lnterferometric Synthetic Aperture Radar D-InSAR in French Alps using ERS (European Remote Sensing) archive data. Geomorphol.-Relief Process. Environ. 2013, 3, 231–242. [Google Scholar] [CrossRef]
- Kunz, J.; Ullmann, T.; Kneisel, C. Internal structure and recent dynamics of a moraine complex in an alpine glacier forefield revealed by geophysical surveying and Sentinel-1 InSAR time series. Geomorphology 2022, 398, 108052. [Google Scholar] [CrossRef]
- Zou, L.; Wang, C.; Tang, Y.; Zhang, B.; Zhang, H.; Dong, L. Interferometric SAR Observation of Permafrost Status in the Northern Qinghai-Tibet Plateau by ALOS, ALOS-2 and Sentinel-1 between 2007 and 2021. Remote Sens. 2022, 14, 1870. [Google Scholar] [CrossRef]
- LI, S.S.; LI, Z.W.; Hu, J.; Sun, Q.; YU, X.Y. Investigation of the seasonal oscillation of the permafrost over Qinghai-Tibet Plateau with SBAS-InSAR algorithm. Chin. J. Geophys. 2013, 56, 1476–1486. [Google Scholar]
- Chen, J.; Wu, T.; Zou, D.; Liu, L.; Wu, X.; Gong, W.; Zhu, X.; Li, R.; Hao, J.; Hu, G.; et al. Magnitudes and patterns of large-scale permafrost ground deformation revealed by Sentinel-1 InSAR on the central Qinghai-Tibet Plateau. Remote Sens. Environ. 2022, 268, 112778. [Google Scholar] [CrossRef]
- Weise, E.; Karina Zaiets, K.G. Russia Declares State of Emergency over Arctic Circle Oil Spill Caused by Melting Permafrost. (USA TODAY). 2020. Available online: https://www.usatoday.com/in-depth/graphics/2020/06/05/oil-spill-red-river-permafrost-tied-russian-arctic-circle-emergency-diesel/3143679001/ (accessed on 6 June 2020).
- Seddon, M. Siberia Fuel Spill Threatens Moscow’s Arctic Ambitions. (Financial Times). 2020. Available online: https://www.ft.com/content/fa9c20a0-2dad-4992-9686-0ec98b44faa8 (accessed on 4 June 2020).
- Kozhevnikov, D. Diesel Fuel Spill in Norilsk in Russia’s Arctic Contained. (TASS, Moscow, Russia). 2020. Available online: https://tass.com/emergencies/1164423#:~:text=Cleanup%20workers%20have%20contained%20the,collected%2C%22%20the%20ministry%20said (accessed on 5 June 2020).
- Rajendran, S.; Sadooni, F.N.; Al-Kuwari, H.A.S.; Oleg, A.; Govil, H.; Nasir, S.; Vethamony, P. Monitoring oil spill in Norilsk, Russia using satellite data. Sci. Rep. 2021, 11, 3817. [Google Scholar] [CrossRef]
- Iljin, K. Remediation after Oil Spill in Norilsk Will Cost $2 Billion. (BBC News Russia). 2020. Available online: https://www.bbc.com/russian/features-53282724 (accessed on 18 October 2020).
- Shur, Y.L.; Jorgenson, M.T. Patterns of permafrost formation and degradation in relation to climate and ecosystems. Permafr. Periglac. Process. 2007, 18, 7–19. [Google Scholar] [CrossRef]
- Ran, Y.; Jorgenson, M.T.; Li, X.; Jin, H.; Wu, T.; Li, R.; Cheng, G. A Biophysical Permafrost Zonation Map in the Northern Hemisphere (2000–2016); National Tibetan Plateau Data Center: Beijing, China, 2021. [Google Scholar] [CrossRef]
- Ran, Y.; Jorgenson, M.T.; Li, X.; Jin, H.; Wu, T.; Li, R.; Cheng, G. Biophysical permafrost map indicates ecosystem processes dominate permafrost stability in the Northern Hemisphere. Environ. Res. Lett. 2021, 16, 095010. [Google Scholar] [CrossRef]
- Ran, Y.; Li, X.; Cheng, G.; Che, J.; Aalto, J.; Karjalainen, O.; Hjort, J.; Luoto, M.; Jin, H.; Obu, J.; et al. New high-resolution estimates of the permafrost thermal state and hydrothermal conditions over the Northern Hemisphere. Earth Syst. Sci. Data 2022, 14, 865–884. [Google Scholar] [CrossRef]
- Dai, Y.; Wei, N.; Yuan, H.; Zhang, S.; Shangguan, W.; Liu, S.; Lu, X.; Xin, Y. Evaluation of soil thermal conductivity schemes for use in land surface modeling. J. Adv. Model. Earth Syst. 2019, 11, 3454–3473. [Google Scholar] [CrossRef]
- Dai, Y.; Xin, Q.; Wei, N.; Zhang, Y.; Shangguan, W.; Yuan, H.; Zhang, S.; Liu, S.; Lu, X. A Global High-Resolution Data Set of Soil Hydraulic and Thermal Properties for Land Surface Modeling. J. Adv. Model. Earth Syst. 2019, 11, 2996–3023. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef] [Green Version]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef] [Green Version]
- Goldstein, R.M.; Zebker, H.A.; Werner, C.L. Satellite radar interferometry: Two-dimensional phase unwrapping. Radio Sci. 1988, 23, 713–720. [Google Scholar] [CrossRef] [Green Version]
- Costantini, M. A novel phase unwrapping method based on network programming. IEEE Trans. Geosci. Remote Sens. 1998, 36, 813–821. [Google Scholar] [CrossRef]
- Daout, S.; Doin, M.P.; Peltzer, G.; Socquet, A.; Lasserre, C. Large-scale InSAR monitoring of permafrost freeze-thaw cycles on the Tibetan Plateau. Geophys. Res. Lett. 2017, 44, 901–909. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, R.; Hu, J.; Wen, L.; Feng, G.; Zhang, Z.; Wang, Q. InSAR analysis of surface deformation over permafrost to estimate active layer thickness based on one-dimensional heat transfer model of soils. Sci. Rep. 2015, 5, 15542. [Google Scholar] [CrossRef] [Green Version]
- Johansen, O. Thermal Conductivity of Soils. Ph.D. Thesis, Trondheim University, Trondheim, Norway, 1977. [Google Scholar]
- Kersten, M.S. Laboratory Research for the Determination of Thermal Properties of Soils; Arctic Construction and Frost Effects Laboratory (US): Boston, MA, USA, 1949. [Google Scholar]
- Balland, P.V. Modeling soil thermal conductivities over a wide range of conditions. J. Environ. Eng. Sci. 2005, 4, 549–558. [Google Scholar] [CrossRef]
- Stefan, J. Über die Theorie der Eisbildung, insbesondere über die Eisbildung im Polarmeere. Ann. Phys. 1891, 278, 269–286. [Google Scholar] [CrossRef] [Green Version]
- Klene, A.E.; Nelson, F.E.; Shiklomanov, N.I.; Hinkel, K.M. The n-factor in natural landscapes: Variability of air and soil-surface temperatures, Kuparuk River Basin, Alaska, USA. Arctic Antarct. Alp. Res. 2001, 33, 140–148. [Google Scholar] [CrossRef]
- Lunardini, V.J. Heat Transfer in Cold Climates; Van Nostrand Reinhold Company: New York, NY, USA, 1981. [Google Scholar]
- Kurylyk, B.L.; McKenzie, J.M.; MacQuarrie, K.T.; Voss, C.I. Analytical solutions for benchmarking cold regions subsurface water flow and energy transport models: One-dimensional soil thaw with conduction and advection. Adv. Water Resour. 2014, 70, 172–184. [Google Scholar] [CrossRef]
- Jumikis, A.R. Thermal geotechnics. Soil Sci. 1978, 125, 393. [Google Scholar] [CrossRef]
- Rouyet, L.; Karjalainen, O.; Niittynen, P.; Aalto, J.; Luoto, M.; Lauknes, T.R.; Larsen, Y.; Hjort, J. Environmental Controls of InSAR-Based Periglacial Ground Dynamics in a Sub-Arctic Landscape. J. Geophys. Res. Earth Surf. 2021, 126, e2021JF006175. [Google Scholar] [CrossRef]
- Qi, Y.; Li, S.; Ran, Y.; Wang, H.; Wu, J.; Lian, X.; Luo, D. Mapping frozen ground in the Qilian Mountains in 2004–2019 using Google earth engine cloud computing. Remote Sens. 2021, 13, 149. [Google Scholar] [CrossRef]
- Cao, H.; Gao, B.; Gong, T.; Wang, B. Analyzing changes in frozen soil in the source region of the yellow river using the modis land surface temperature products. Remote Sens. 2021, 13, 180. [Google Scholar] [CrossRef]
- Ma, W.; Mu, Y.; Wu, Q.; Sun, Z.; Liu, Y. Characteristics and mechanisms of embankment deformation along the Qinghai–Tibet Railway in permafrost regions. Cold Reg. Sci. Technol. 2011, 67, 178–186. [Google Scholar] [CrossRef]
- Ming, F.; Yu, Q.h.; Li, D.Q. Investigation of embankment deformation mechanisms in permafrost regions. Transp. Geotech. 2018, 16, 21–28. [Google Scholar] [CrossRef]
- Yu, F.; Qi, J.; Lai, Y.; Sivasithamparam, N.; Yao, X.; Zhang, M.; Liu, Y.; Wu, G. Typical embankment settlement/heave patterns of the Qinghai–Tibet highway in permafrost regions: Formation and evolution. Eng. Geol. 2016, 214, 147–156. [Google Scholar] [CrossRef]
- Tai, B.; Wu, Q.; Zhang, Z.; Xu, X. Cooling performance and deformation behavior of crushed-rock embankments on the Qinghai-Tibet Railway in permafrost regions. Eng. Geol. 2020, 265, 105453. [Google Scholar] [CrossRef]





| Attributes | Unit |
|---|---|
| Volumetric fraction of gravels | cm/cm |
| Volumetric fraction of soil organic matters (SOM) | cm/cm |
| Volumetric fraction of sand | cm/cm |
| Thermal conductivity of unfrozen saturated soils | W·m·K |
| Thermal conductivity of frozen saturated soils | W·m·K |
| Thermal conductivity of dry soils | W·m·K |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Chen, Y.; Ran, Y.; Chen, Y. Permafrost Early Deformation Signals before the Norilsk Oil Tank Collapse in Russia. Remote Sens. 2022, 14, 5036. https://doi.org/10.3390/rs14195036
Zhang P, Chen Y, Ran Y, Chen Y. Permafrost Early Deformation Signals before the Norilsk Oil Tank Collapse in Russia. Remote Sensing. 2022; 14(19):5036. https://doi.org/10.3390/rs14195036
Chicago/Turabian StyleZhang, Peng, Yan Chen, Youhua Ran, and Yunping Chen. 2022. "Permafrost Early Deformation Signals before the Norilsk Oil Tank Collapse in Russia" Remote Sensing 14, no. 19: 5036. https://doi.org/10.3390/rs14195036
APA StyleZhang, P., Chen, Y., Ran, Y., & Chen, Y. (2022). Permafrost Early Deformation Signals before the Norilsk Oil Tank Collapse in Russia. Remote Sensing, 14(19), 5036. https://doi.org/10.3390/rs14195036









