Fusion Retrieval of Sea Surface Barometric Pressure from the Microwave Humidity and Temperature Sounder and Microwave Temperature Sounder-II Onboard the Fengyun-3 Satellite
Abstract
:1. Introduction
2. Data Description and Pre-Processing
2.1. Instrument Characteristics
2.2. Date Description and Pre-Processing
3. The Principle of Measuring SSP by Satellite-Based Microwave Radiometer
3.1. Theoretical Basis
3.2. The Sensitivity Test of MWHTS and MWTS-II to SSP
4. Algorithm and Experiment Design
4.1. Neural-Network-Based Retrieval Algorithm
4.2. Design of Retrieval Experiment
5. Experimental Results
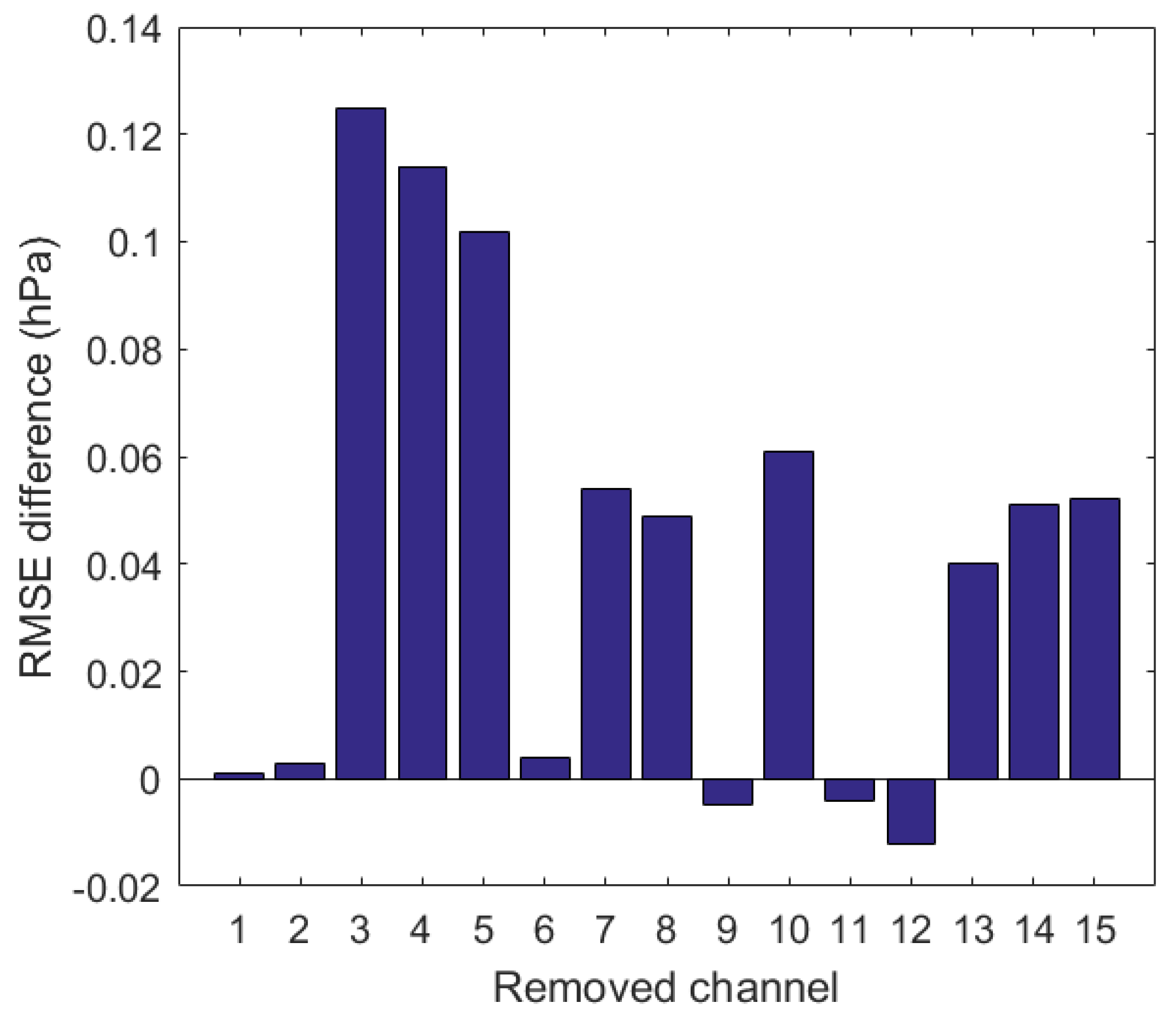
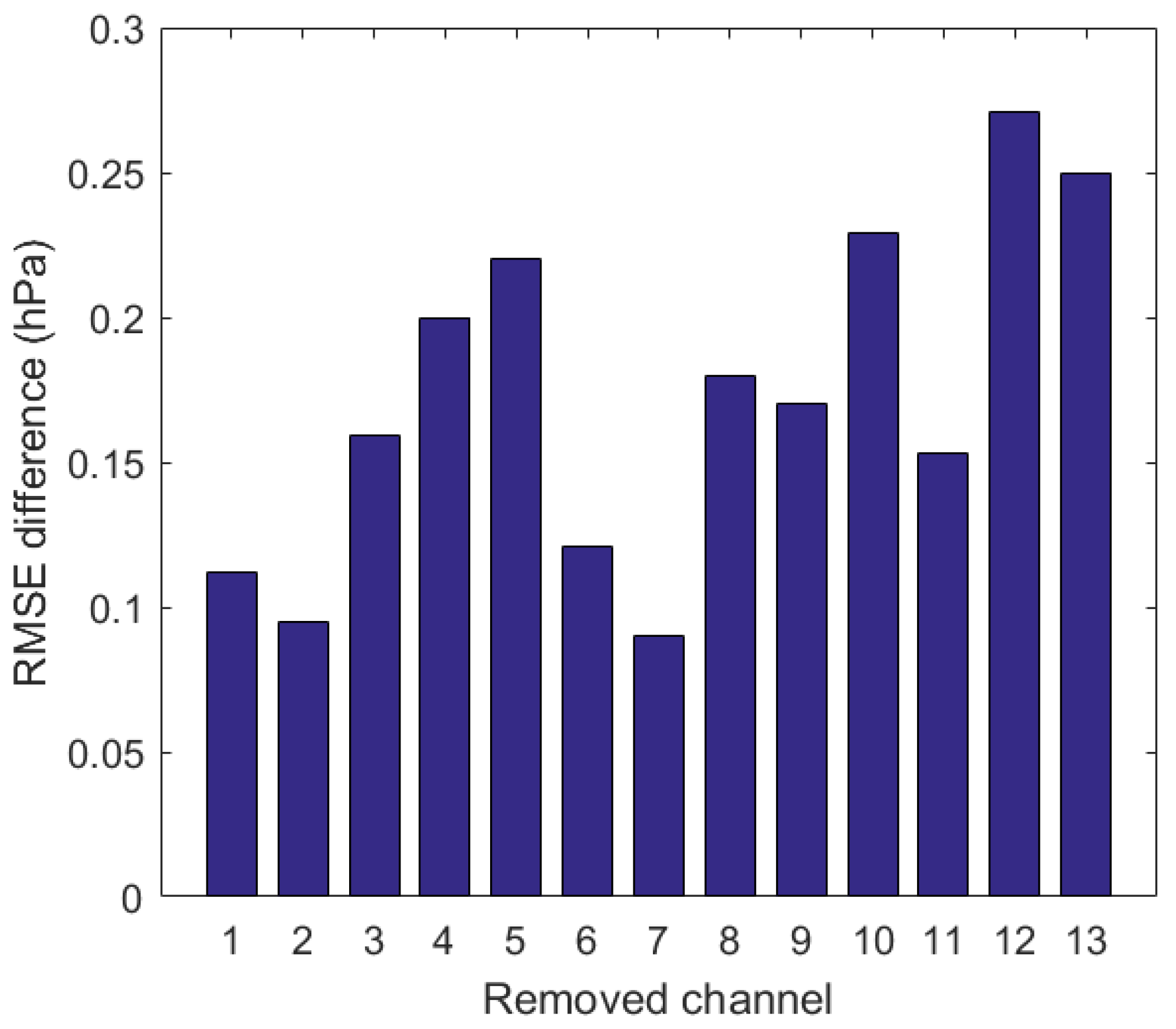
5.1. The Test Results of the Contribution of Each Channel to the SSP Retrieval
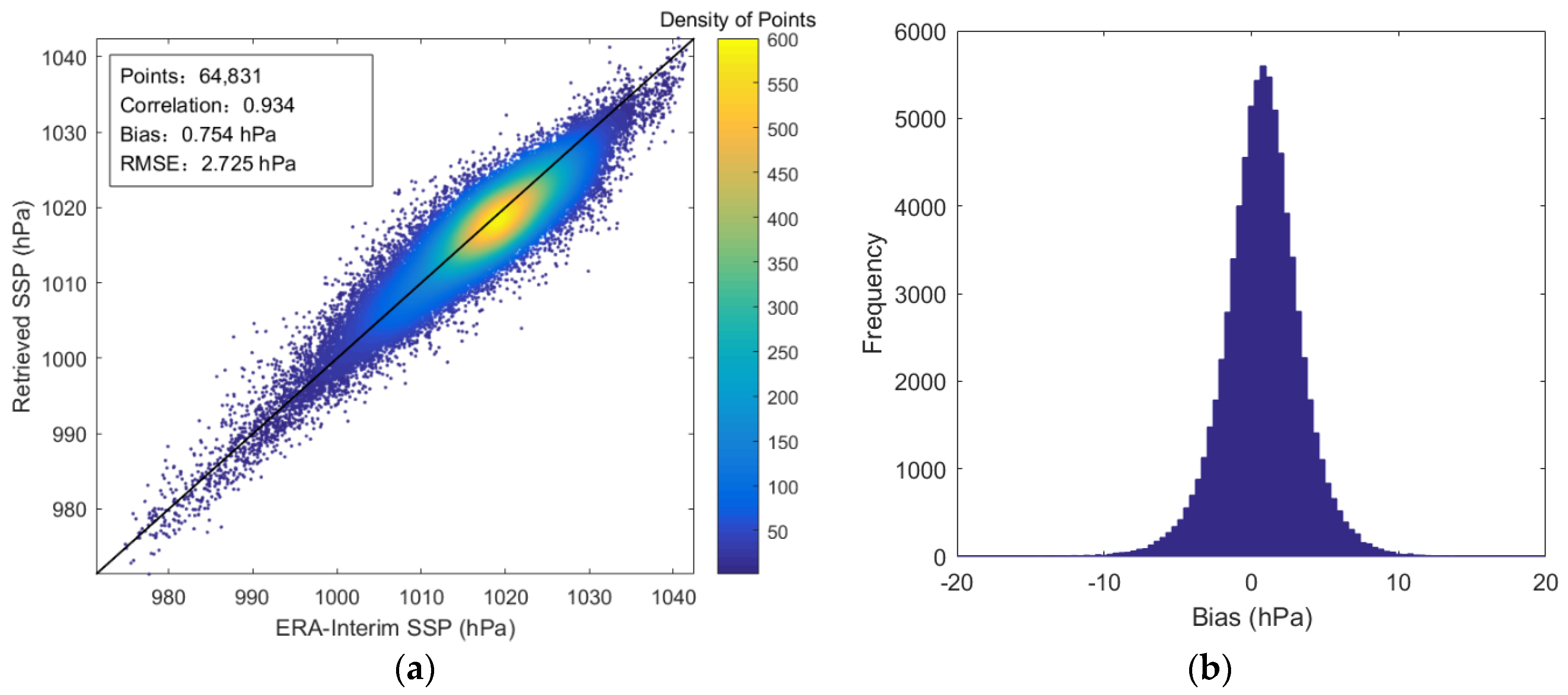
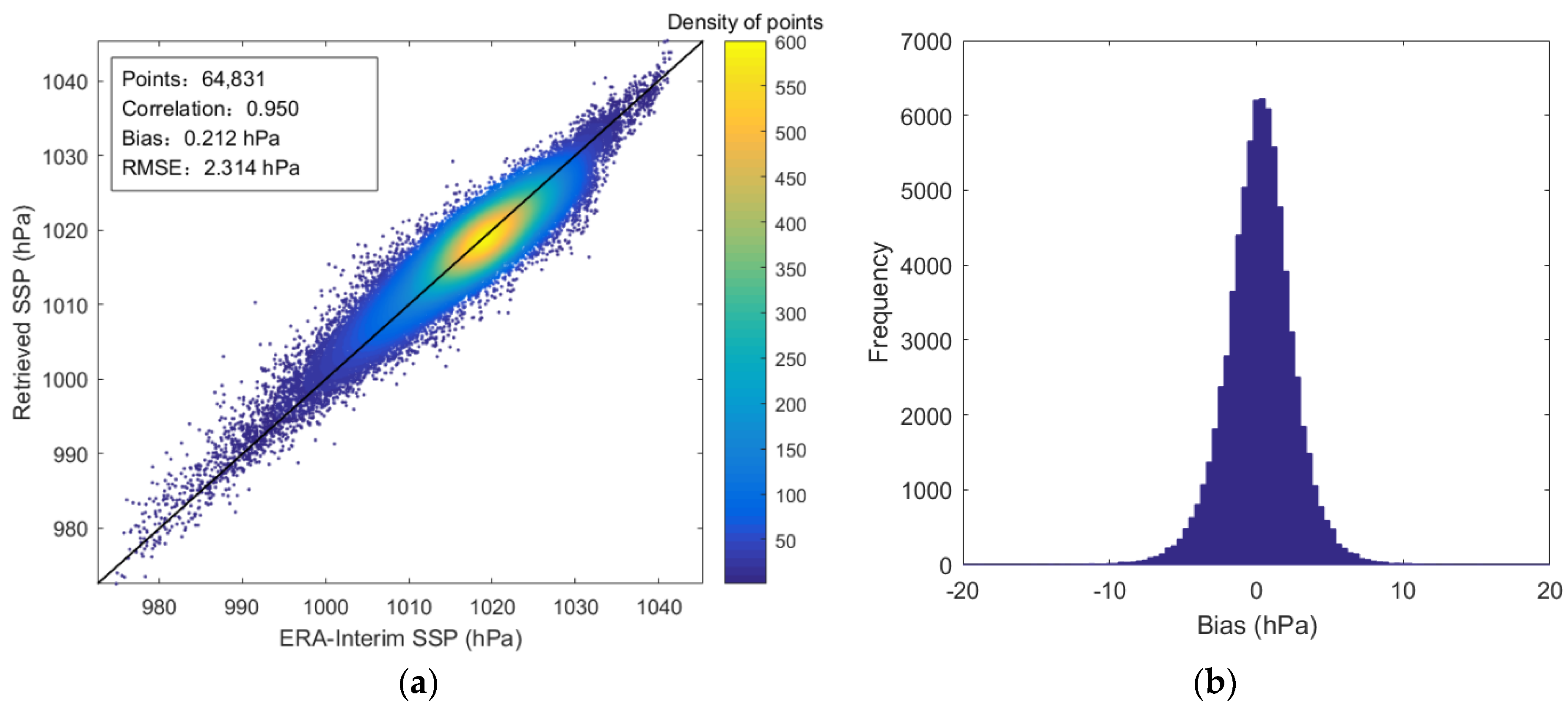
5.2. The Fusion Retrieval Results of SSP from MWHTS and MWTS-II
6. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Flasar, F.M.; Baines, K.H.; Bird, M.K.; Tokano, T.; West, R.A. Atmospheric Dynamics and Meteorology; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar] [CrossRef]
- Lorenc, A.C. Analysis methods for numerical weather prediction. Q. J. R. Meteorol. Soc. 2010, 112, 1177–1194. [Google Scholar] [CrossRef]
- Min, Q.; Gong, W.; Lin, B.; Hu, Y. Application of surface pressure measurements from O2-band differential absorption radar system in three-dimensional data assimilation on hurricane: Part I. An observing system simulation experiments study. J. Quant. Spectrosc. Radiat. Transf. 2011, 150, 148–165. [Google Scholar] [CrossRef] [Green Version]
- Lin, B.; Hu, Y.; Harrah, S.; Neece, R.; Lawrence, R.; Fralick, D. The Feasibility of Radar-Based Remote Sensing of Barometric Pressure; Hampton, V.A., Ed.; NASA Langley Research Center: Hampton, VA, USA, 2006.
- Liu, H.; Duan, M.; Lü, D.; Zhang, Y. Algorithm for retrieving surface pressure from hyperspectral measurements in oxygen A-band. Chin. Sci. Bull. 2014, 59, 1492–1498. [Google Scholar] [CrossRef]
- O’Brien, D.M.; Mitchell, R.M.; English, S.A.; da Costa, G.A. Airborne measurements of air mass from O2 A-band absorption spectral. J. Atmos. Ocean. Technol. 1998, 15, 1272–1286. [Google Scholar] [CrossRef]
- Healy, S.B. Surface pressure information retrieved from GPS radio occultation measurements. Q. J. R. Meteorol. Soc. 2013, 139, 2108–2118. [Google Scholar] [CrossRef]
- Hsu, C.S.; Liu, W.T. Wind and pressure fields near tropical cyclone Oliver derived from scatterometer observations. J. Geophys. Res. 1996, 101, 17021–17027. [Google Scholar] [CrossRef]
- Patoux, J.; Foster, R.C.; Brown, R.A. An evaluation of scatterometer-derived oceanic surface pressure fields. J. Appl. Meteorol. Clim. 2008, 47, 835–852. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Huang, S.; Du, H. A new method of retrieving typhoon’s sea level pressure fields and central positions from scatterometer-derived sea surface winds. Acta Phys. Sin. 2011, 60, 119202. [Google Scholar] [CrossRef]
- Van Zadelhoff, G.J.; Stoffelen, A.; Vachon, P.W.; Wolfe, J.; Horstmann, J.; Belmonte Rivas, M. Retrieving hurricane wind speeds using C-band measurements. Atmos. Meas. Tech. 2014, 7, 437–449. [Google Scholar] [CrossRef] [Green Version]
- Kidder, S.Q.; Goldberg, M.D.; Zehr, R.M.; Demaria, M.; Purdom, J.F.W.; Velden, C.S.; Grody, N.C.; Kusselson, S.J. Satellite analysis of Tropical cyclones using the advanced Microwave Sounding Unit (AMSU). Bull. Amer. Meteor. Soc. 2000, 81, 1241–1260. [Google Scholar] [CrossRef] [Green Version]
- Elachi, C.; van Zyl, J. Introduction to the Physics and Techniques of Remote Sensing; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive; Addison-Wesley: Reading, MA, USA, 1981. [Google Scholar]
- Zhang, Z. Study on the Retrieval Theory and Method of Sea Surface Pressure Basing on Passive Microwave Observations. Ph.D. Thesis, Chinese Academy of Science, Beijing, China, 2019. [Google Scholar]
- Zhang, Z.; Dong, X.; Liu, L.; He, J. Retrieval of barometric pressure from satellite passive microwave observations over the oceans. J. Geophys. Res. 2018, 123, 4360–4372. [Google Scholar] [CrossRef]
- He, J.; Zhang, S. Regional profiles and precipitation retrievals and analysis using FY-3C MWHTS. Atmos. Clim. Sci. 2016, 6, 273–284. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Lu, N.; Qi, C.; Gu, S.; Xu, J. Calibration and validation of microwave humidity and temperature sounder onboard FY-3C satellite. Chin. J. Geophys. Chin. 2015, 58, 20–31. [Google Scholar] [CrossRef]
- He, Q.; Wang, Z.; He, J. Bias correction for retrieval of atmospheric parameters from the Microwave Humidity and Temperature Sounder onboard the Fengyun-3C satellite. Atmosphere 2016, 7, 156. [Google Scholar] [CrossRef] [Green Version]
- Liebe, H.J.; Hufford, G.A.; Cotton, M.G. Propagation modeling of moist air and suspended water/ice particles at frequencies below 1000 GHz. In Proceedings of the AGARD 52nd Specialists Meeting of Electromagnetic Wave Propagation Panel, Palma De Mallorca, Spain, 17–21 May 1993. [Google Scholar]
- Berrisford, P.; Dee, D.; Poli, P.; Brugge, R.; Fielding, K.; Fuentes, M.; Kallberg, P.; Kobayashi, S. The ERA-Interim Archive Version 2.0; ERA Report Series 1; ECMWF: Reading, UK, 2011. [Google Scholar]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Saunders, R.; Hocking, J.; Rundle, D.; Rayer, P.; Matricardi, M.; Geer, A.; Lupu, C.; Brunel, P.; Vidot, J. RTTOV-11 Science and Validation Report; NWP-SAF Report; Met Office: Exeter, UK, 2013; pp. 1–62.
- Saunders, R.; Hocking, J.; Turner, E.; Rayer, P.; Rundle, D.; Brunel, P.; Vidot, J.; Roquet, P.; Matricardi, M.; Geer, A.; et al. An update on the RTTOV fast radiative transfer model (currently at version 12). Geosci. Model Dev. 2018, 11, 2717–2737. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.R.; Chang, L.A. Retrieval of water vapor profiles from microwave radiometric measurements near 90 and 183 GHz. J. Appl. Meteorol. 1990, 29, 1005–1013. [Google Scholar] [CrossRef] [Green Version]
- Boukabara, S.A.; Garrett, K.; Chen, W.; Iturbide-Sanchez, F.; Grassotti, C.; Kongoli, C.; Chen, R.; Liu, Q.; Yan, B.; Weng, F.; et al. MiRS: An all-weather 1DVAR satellite data assimilation and retrieval system. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3249–3272. [Google Scholar] [CrossRef]
- Weng, F.; Zou, X.; Qin, Z. Uncertainty of AMSU-A derived temperature trends in relationship with clouds and precipitation over ocean. Clim. Dyn. 2014, 43, 1439–1448. [Google Scholar] [CrossRef]
- Moradi, I.; Ferraro, R.R.; Soden, B.J.; Eriksson, P.; Arkin, P. Retrieving Layer-Averaged Tropospheric Humidity from Advanced Technology Microwave Sounder Water Vapor Channels. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6675–6688. [Google Scholar] [CrossRef] [Green Version]
- Navas-Guzmán, F.; Stähli, O.; Kämpfer, N. An integrated approach toward the incorporation of clouds in the temperature retrievals from microwave measurements. Atmos. Meas. Technol. 2014, 7, 1619–1628. [Google Scholar] [CrossRef] [Green Version]
- Han, Y.; Van Delst, P.; Liu, Q.H.; Weng, F.Z.; Yan, B.; Treadon, R.; Derber, J. Community Radiative Transfer Model (CRTM),-Version 1; NOAA Technical Report 122; Department of Commerce/NOAA/NESDIS: Washington, DC, USA, 2006.
- Buehler, S.A.; Mendrok, J.; Eriksson, P.; Perrin, A.; Larsson, R.; Lemke, O. ARTS, the Atmospheric Radiative Transfer Simulator—version 2.2, the planetary toolbox edition. Geosci. Model Deve. 2018, 11, 1537–1556. [Google Scholar] [CrossRef] [Green Version]
- Dee, D.P. Bias and data assimilation. Q. J. R. Meteorol. Soc. 2005, 131, 3323–3343. [Google Scholar] [CrossRef] [Green Version]
- Auligné, T.; McNally, A.P.; Dee, D.P. Adaptive bias correction for satellite data in a numerical weather prediction system. Q. J. R. Meteorol. Soc. 2007, 133, 631–642. [Google Scholar] [CrossRef]
- Golubkov, G.V.; Manzhelii, M.I.; Berlin, A.A.; Eppelbaum, L.V.; Lushnikov, A.A.; Morozov, I.I.; Dmitriev, A.V.; Adamson, S.O.; Dyakov, Y.A.; Morozov, A.N.; et al. The Problems of Passive Remote Sensing of the Earth’s Surface in the Range of 1.2–1.6 GHz. Atmosphere 2020, 11, 650. [Google Scholar] [CrossRef]
- He, Q.; Wang, Z.; Li, J. Application of the deep neural network in retrieving the atmospheric temperature and humidity profiles from the Microwave Humidity and Temperature Sounder onboard the Feng-Yun-3 satellite. Sensors-Basel 2021, 21, 4673. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Grasstotti, C. Development of a machine learning-based radiometric bias correction for NOAA’s Microwave integrated retrieval system (MIRS). Remote Sens. 2020, 12, 3160. [Google Scholar] [CrossRef]
- Yan, X.; Liang, C.; Jiang, Y.; Luo, N.; Zang, Z.; Li, Z. A deep learning approach to improve the retrieval of temperature and humidity profiles from a ground-based microwave radiometer. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8427–8437. [Google Scholar] [CrossRef]
- Blackwell, W.J.; Chen, F.W. Neural Networks in Atmospheric Remote Sensing; Artech House: Norwood, MA, USA, 2009. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Lee, Y.; Han, D.; Ahn, M.H.; Im, J.; Lee, S.J. Retrieval of total precipitable water from Himawari-8 AHI data: A comparison of random forest, extreme gradient boosting, and deep neural network. Remote Sens. 2019, 11, 1741. [Google Scholar] [CrossRef] [Green Version]
- Lu, Q.; Hu, J.; Wu, C.; Qi, C.; Wu, S.; Xu, N.; Sun, L.; Li, X.; Liu, H.; Guo, Y.; et al. Monitoring the performance of the Fengyun satellite instruments using radiative transfer models and NWP fields. J. Quant. Spectrosc. Radiat. Transf. 2020, 225, 107239. [Google Scholar] [CrossRef]
- Carminati, F.; Migliorini, S. All-sky Data Assimilation of MWTS-2 and MWHS-2 in the Met Office Global NWP System. Adv. Atmos. Sci. 2021, 38, 1682–1694. [Google Scholar] [CrossRef]
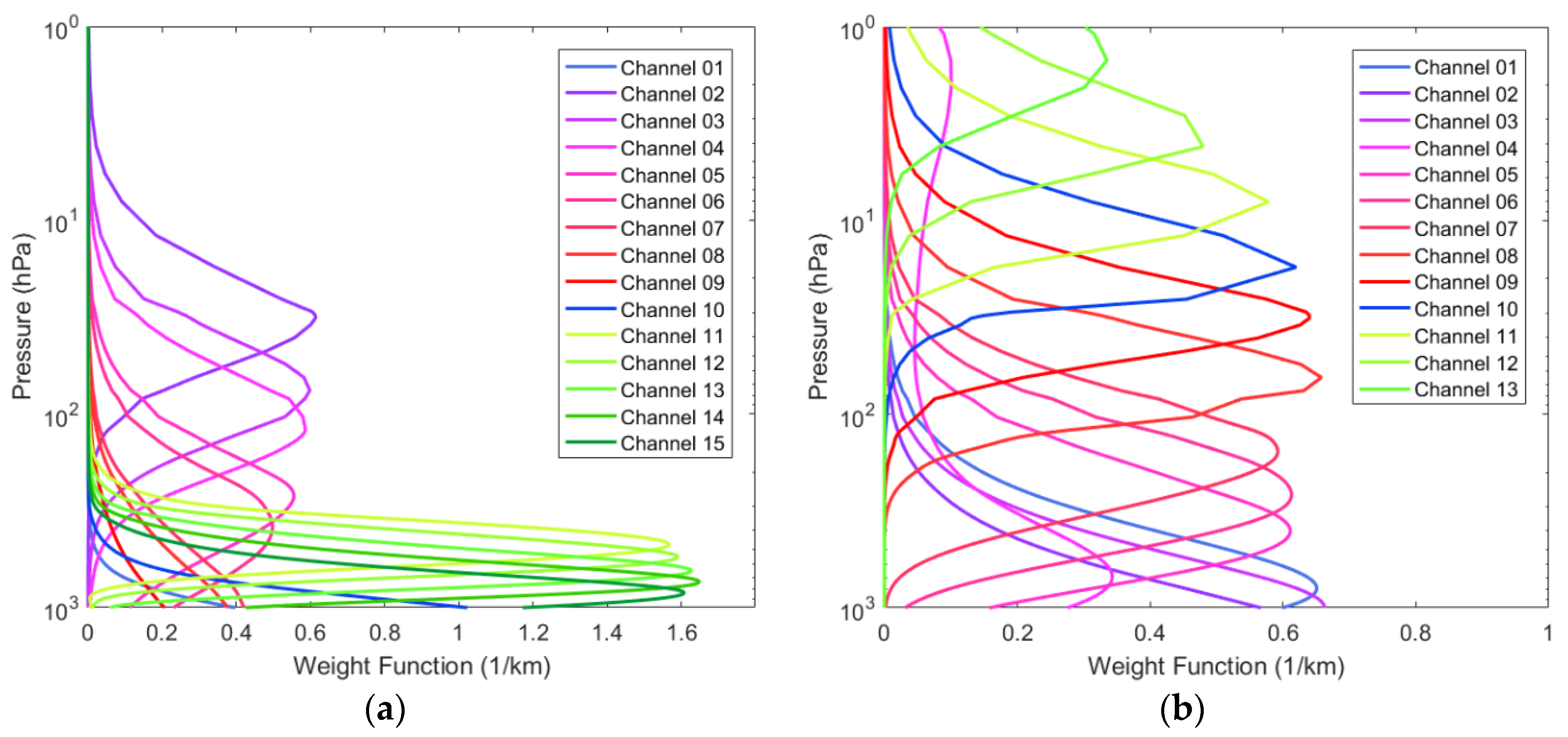

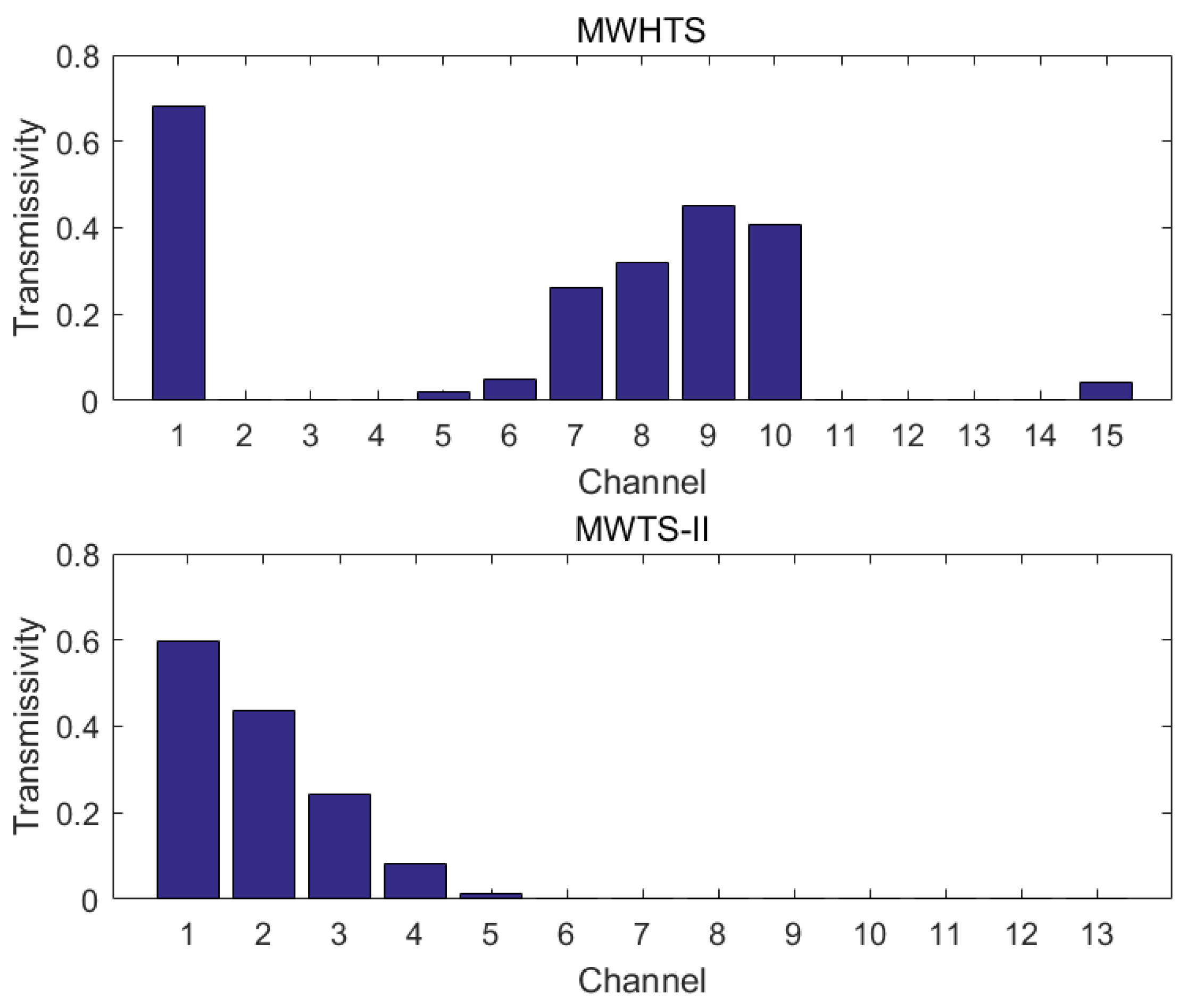

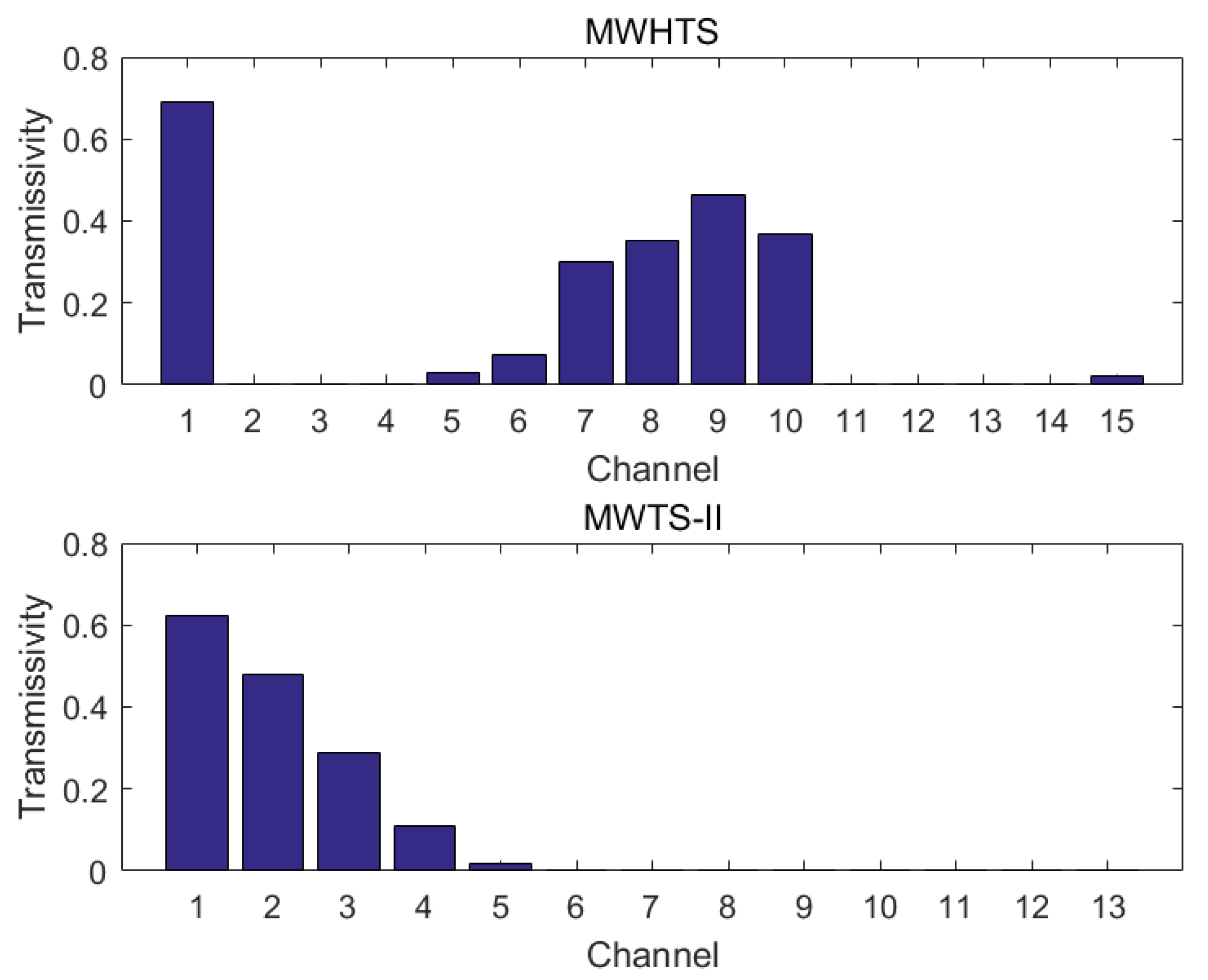



| Channel | Frequency (GHz) | Sensitivity Requirements (K) | On-Orbit Sensitivity (K) | Calibration Accuracy (K) | Peak WF Height (hPa) |
|---|---|---|---|---|---|
| 1 | 89.0 | 1.0 | 0.23 | 1.3 | surface |
| 2 | 118.75 ± 0.08 | 3.6 | 1.62 | 2.0 | 30 |
| 3 | 118.75 ± 0.2 | 2.0 | 0.75 | 2.0 | 50 |
| 4 | 118.75 ± 0.3 | 1.6 | 0.59 | 2.0 | 100 |
| 5 | 118.75 ± 0.8 | 1.6 | 0.65 | 2.0 | 250 |
| 6 | 118.75 ± 1.1 | 1.6 | 0.52 | 2.0 | 350 |
| 7 | 118.75 ± 2.5 | 1.6 | 0.49 | 2.0 | surface |
| 8 | 118.75 ± 3.0 | 1.0 | 0.27 | 2.0 | surface |
| 9 | 118.75 ± 5.0 | 1.0 | 0.27 | 2.0 | surface |
| 10 | 150.0 | 1.0 | 0.34 | 1.3 | surface |
| 11 | 183.31 ± 1.0 | 1.0 | 0.47 | 1.3 | 300 |
| 12 | 183.31 ± 1.8 | 1.0 | 0.34 | 1.3 | 400 |
| 13 | 183.31 ± 3.0 | 1.0 | 0.30 | 1.3 | 500 |
| 14 | 183.31 ± 4.5 | 1.0 | 0.22 | 1.3 | 700 |
| 15 | 183.31 ± 7.0 | 1.0 | 0.27 | 1.3 | 800 |
| Channel | Frequency (GHz) | Sensitivity Requirements (K) | On-Orbit Sensitivity (K) | Calibration Accuracy (K) | Peak WF Height (hPa) |
|---|---|---|---|---|---|
| 1 | 53.30 | 1.5 | 0.26 | 1.5 | surface |
| 2 | 51.760 | 0.9 | 0.20 | 1.5 | surface |
| 3 | 52.800 | 0.9 | 0.21 | 1.5 | 950 |
| 4 | 53.596 | 0.9 | 0.18 | 1.5 | 700 |
| 5 | 54.400 | 0.9 | 0.19 | 1.5 | 400 |
| 6 | 54.940 | 0.9 | 0.19 | 1.5 | 250 |
| 7 | 55.500 | 0.9 | 0.23 | 1.5 | 180 |
| 8 | 57.290(f0) | 0.9 | 0.74 | 1.5 | 90 |
| 9 | f0 ± 0.217 | 1.5 | 0.66 | 1.5 | 50 |
| 10 | f0 ± 0.322 ± 0.048 | 1.5 | 0.49 | 1.5 | 25 |
| 11 | f0 ± 0.322 ± 0.022 | 2.3 | 0.53 | 1.5 | 10 |
| 12 | f0 ± 0.322 ± 0.010 | 3.0 | 0.93 | 1.5 | 6 |
| 13 | f0 ± 0.322 ± 0.005 | 4.5 | 2.11 | 1.5 | 3 |
| Correlation Coefficient | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Channel | H-1 | H-5 | H-6 | H-7 | H-8 | H-9 | H-10 | H-15 | T-1 | T-2 | T-3 | T-4 | T-5 |
| H-2 | 0.38 | −0.22 | −0.17 | 0.22 | 0.28 | 0.36 | 0.32 | −0.10 | 0.39 | 0.38 | 0.21 | −0.09 | −0.16 |
| H-3 | −0.03 | −0.09 | −0.23 | −0.25 | −0.20 | −0.09 | −0.15 | −0.40 | 0.02 | −0.06 | −0.41 | −0.35 | −0.21 |
| H-4 | −0.31 | 0.15 | −0.09 | −0.47 | −0.45 | −0.38 | −0.41 | −0.49 | −0.30 | −0.41 | −0.56 | −0.28 | −0.06 |
| H-11 | −0.18 | 0.38 | 0.40 | 0.08 | −0.01 | −0.13 | −0.08 | 0.62 | −0.26 | −0.20 | 0.12 | −0.32 | 0.37 |
| H-12 | −0.12 | 0.42 | 0.47 | 0.18 | 0.10 | −0.04 | 0.01 | 0.74 | −0.24 | −0.16 | 0.22 | −0.26 | 0.43 |
| H-13 | −0.06 | 0.42 | 0.49 | 0.25 | 0.17 | 0.02 | 0.08 | 0.83 | −0.20 | −0.11 | 0.30 | −0.22 | 0.46 |
| H-14 | −0.01 | 0.44 | 0.54 | 0.32 | 0.24 | 0.09 | 0.15 | 0.90 | −0.20 | −0.09 | 0.37 | −0.17 | 0.50 |
| T-6 | −0.19 | 0.98 | 0.91 | 0.16 | 0.04 | −0.11 | −0.03 | 0.29 | −0.67 | −0.60 | 0.10 | 0.76 | 0.92 |
| T-7 | −0.42 | 0.68 | 0.45 | −0.33 | −0.39 | −0.43 | −0.40 | −0.20 | −0.65 | −0.67 | −0.42 | 0.18 | 0.47 |
| T-8 | −0.15 | −0.10 | −0.29 | −0.40 | −0.35 | −0.23 | −0.29 | −0.44 | −0.05 | −0.17 | −0.54 | −0.42 | −0.26 |
| T-9 | 0.22 | −0.20 | −0.25 | −0.01 | 0.05 | 0.16 | 0.10 | −0.22 | 0.26 | 0.21 | −0.06 | −0.27 | −0.23 |
| T-10 | 0.47 | −0.27 | −0.19 | 0.30 | 0.37 | 0.45 | 0.41 | −0.06 | 0.47 | 0.48 | 0.29 | −0.07 | −0.18 |
| T-11 | 0.50 | −0.34 | −0.20 | 0.38 | 0.44 | 0.51 | 0.49 | 0.08 | 0.52 | 0.54 | 0.38 | −0.03 | −0.19 |
| T-12 | 0.47 | −0.28 | −0.12 | 0.40 | 0.44 | 0.48 | 0.48 | 0.16 | 0.46 | 0.50 | 0.42 | 0.06 | −0.11 |
| T-13 | 0.37 | −0.02 | 0.13 | 0.41 | 0.41 | 0.40 | 0.42 | 0.25 | 0.26 | 0.32 | 0.44 | 0.25 | 0.11 |
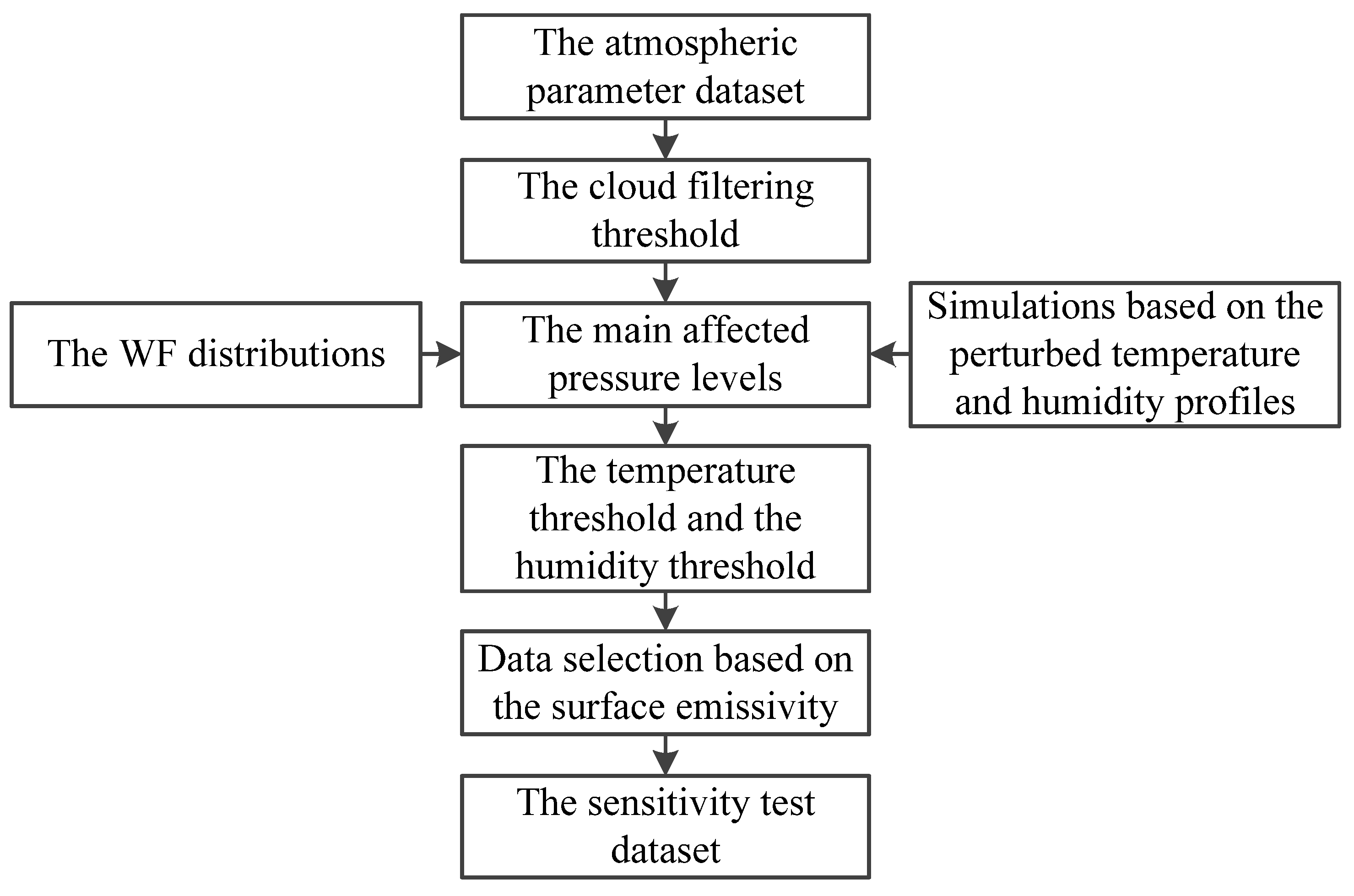
| Channel | Main Affected Pressure Levels | Temperature Threshold (K) | Humidity Threshold (%) | Number of Samples |
|---|---|---|---|---|
| H-1, H-7, H-8, H-9, H-10, T-1, T-2 | 825–1000 | 1.20 | 8 | 468 |
| H-2, T-10 | 3–150 | 0.45 | - | 163 |
| H-3, H-4, T-8, T-9 | 5–225 | 0.50 | - | 152 |
| H-5, H-6 | 100–1000 | 1.20 | 25 | 181 |
| T-3, T-4 | 200–975 | 0.95 | - | 115 |
| T-5, T-6 | 50–825 | 0.85 | - | 212 |
| T-7 | 5–550 | 0.65 | - | 133 |
| T-11 | 2–100 | 0.45 | - | 148 |
| T-12 | 2–50 | 0.40 | - | 188 |
| T-13 | 1–10 | 0.35 | - | 265 |
| H-11, H-12 | 150–650 | 1.50 | 3 | 238 |
| H-13, H-14, H-15 | 200–950 | 1.80 | 5 | 260 |
| Channel Combination | Channel |
|---|---|
| The theoretical channel combination | MWHTS channels: 1–15, |
| MWTS-II channels: 1–13 | |
| The optimal theoretical channel combination | MWHTS channels: 3–5, 7–8, 10, 13–15, |
| MWTS-II channels: 1–13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Q.; Wang, Z.; Li, J. Fusion Retrieval of Sea Surface Barometric Pressure from the Microwave Humidity and Temperature Sounder and Microwave Temperature Sounder-II Onboard the Fengyun-3 Satellite. Remote Sens. 2022, 14, 276. https://doi.org/10.3390/rs14020276
He Q, Wang Z, Li J. Fusion Retrieval of Sea Surface Barometric Pressure from the Microwave Humidity and Temperature Sounder and Microwave Temperature Sounder-II Onboard the Fengyun-3 Satellite. Remote Sensing. 2022; 14(2):276. https://doi.org/10.3390/rs14020276
Chicago/Turabian StyleHe, Qiurui, Zhenzhan Wang, and Jiaoyang Li. 2022. "Fusion Retrieval of Sea Surface Barometric Pressure from the Microwave Humidity and Temperature Sounder and Microwave Temperature Sounder-II Onboard the Fengyun-3 Satellite" Remote Sensing 14, no. 2: 276. https://doi.org/10.3390/rs14020276
APA StyleHe, Q., Wang, Z., & Li, J. (2022). Fusion Retrieval of Sea Surface Barometric Pressure from the Microwave Humidity and Temperature Sounder and Microwave Temperature Sounder-II Onboard the Fengyun-3 Satellite. Remote Sensing, 14(2), 276. https://doi.org/10.3390/rs14020276






