Region-Level Traffic Prediction Based on Temporal Multi-Spatial Dependence Graph Convolutional Network from GPS Data

Abstract

Region-level traffic information can characterize dynamic changes of urban traffic at the macro level. Real-time region-level traffic prediction help city traffic managers with traffic demand analysis, traffic congestion control, and other activities, and it has become a research hotspot. As more vehicles are equipped with GPS devices, remote sensing data can be collected and used to conduct data-driven region-level-based traffic prediction. However, due to dynamism and randomness of urban traffic and the complexity of urban road networks, the study of such issues faces many challenges. This paper proposes a new deep learning model named TmS-GCN to predict region-level traffic information, which is composed of Graph Convolutional Network (GCN) and Gated Recurrent Unit (GRU). The GCN part captures spatial dependence among regions, while the GRU part captures the dynamic change of traffic within the region. Model verification and comparison are carried out using real taxi GPS data from Shenzhen. The experimental results show that the proposed model outperforms both the classic time series prediction model and the deep learning model at different scales.

1. Introduction

Region-level traffic prediction has received increasing attention in the field of Intelligent Transportation System (ITS). It is a key aspect of urban traffic management. With the widespread use of remote sensing equipment, such as the Global Positioning System (GPS), radar, and other sensors, remote sensing data-driven-based region-level traffic predictions has become popular [1,2,3]. Vehicles equipped with GPS devices that travel on urban roads can dynamically upload their latitude, longitude, velocity, and other data to a server. When the number of such vehicles reaches tens of thousands, traffic managers can obtain dynamic traffic information of urban roads, such as traffic flow and traffic speed, to support various research and applications in the field of Intelligent Transportation System. For instance, identifying areas of interest (AOIs) based on taxi GPS in New York City [4], estimating urban network-wide traffic speed estimation based on massive ride-sourcing GPS traces [5], assessing individual activity-related exposures to traffic congestion using GPS trajectory data [6], and so on. Therefore, using GPS data to perform region-level traffic prediction is reasonable and representative. Region-level traffic prediction, on the one hand, can support the development of real-time traffic management applications such as traffic control and traffic guidance, and, on the other hand, it can also help carry out real-time OD estimation [7]. For instance, using the average speed of a specific region deviates from the average value, and the traffic manager can reschedule the traffic signal in advance or send the police to divert traffic. With region-level dynamic traffic flow information, which represents travel demand, companies can dispatch vehicles based on this forecast information to obtain greater economic benefits.

However, due to the complexity and relevance of the traffic state in both the time and space dimensions, traffic prediction at the region level is of a great challenge. Firstly, traffic prediction is a time-series task that uses historical traffic information in the region to forecast future traffic information. As a result, many studies based on time series models, such as the Autoregressive Integrated Moving Average (ARRIMA) model [8], the Kalman filtering model [9], Bayesian network [10], Neural Network [11], Recurrent Neural Network [12], and so on, have been proposed. However, these models only consider temporal dependence and ignore spatial dependence of adjacent regions, which has an impact on prediction result. In recent years, some studies have proposed new hybrid models based on the time-series model and spatial feature mining model to comprehensively use the temporal dependence of the predicted region and spatial dependence from adjacent regions to forecast traffic information [13,14].

Furthermore, regular regions divided by square grids and hexagons cannot accurately describe the evolution of traffic conditions due to the complexity of the road network and randomness of traffic. Although irregularly divided regions based on natural boundaries, such as roads, can accurately describe the evolution of the traffic state, it is difficult to extract spatial dependence from non-Euclidean distance data (irregularly regions). With the application of Graph Convolutional Network, it is now possible to extract spatial features from non-Euclidean distance data [15,16]. Most studies based on GCN assumed that adjacent regions have the same effect on the predicted region, which is imprecise. There are two errors, as shown in Figure 1: (1) g1 and g2 are adjacent grids of g4, and the traffic flow from g2 to g4 is obviously greater than the one from g1 to g4; therefore, it is reasonable that the influence of g2 is greater than that of g1 when extracting spatial features of g4; (2) g3 and g5 are adjacent regions of g4, and $d_{34}$ and $d_{45}$ are the distances from the centroid of GPS points located in g3 to the centroid of GPS points located in g4 and from the centroid of GPS points located in g5 to the centroid of GPS points located in g4, respectively. Due to the fact that $d_{34}$ is greater than $d_{45}$, it is reasonable that the influence of g5 is greater than that of g3 when extracting the spatial features of g4. However, most existing models cannot consider these spatial dependencies, resulting in poor prediction results.

In order to solve the above problems, we propose a new traffic state prediction method called the temporal multi-spatial dependence graph convolutional network (TmS-GCN) to forecast region-level traffic states. Our main contributions in this study are summarized as follows:

• We proposed the TmS-GCN model, which integrates Gated Recurrent Units (GRU) and GCN. GRU is used to obtain temporal dependence based on historical traffic state data. GCN is used to capture spatial dependence based on the graph of irregular regions.
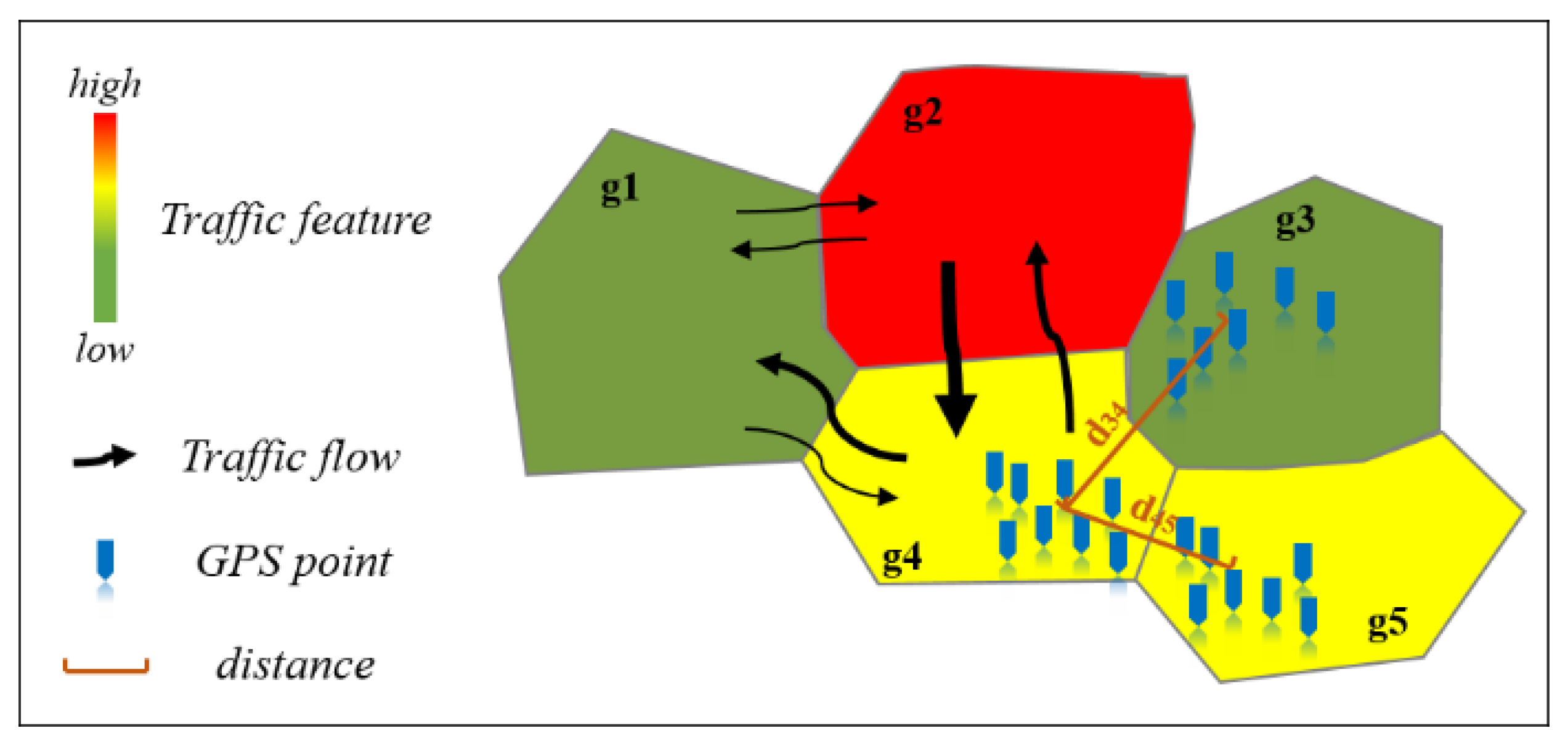
• The TmS-GCN model fully takes into account multiple types of spatial dependencies. Compared with the classic GCN model, which assumed that adjacent regions have the same effect on the predicted region, our model also considers traffic flow propagation and spatial distance among regions.
• We evaluate our method using real-world GPS data collected from Taxi vehicles in Shenzhen, China. The results show that our method outperforms baseline methods.

The rest of the paper is organized as follows. Section 2 reviews relevant research on traffic state prediction. Section 3 introduces the details of the method, including problem description, method overall framework, spatial dependence modeling, and temporal dependence modeling. In Section 4, we use real-world GPS dataset to evaluate the TmS-GCN model. Finally, we conclude the paper in Section 5.

2. Related Work

Region-level traffic states provide a macro view of urban traffic, which is useful for traffic control, traffic guidance, and other applications. Region-level traffic state prediction has become the hotspot in the Intelligent Transportation System, and it can be divided into model-driven research and data-driven research. The existing researches on traffic prediction are shown in

Table 1. Existing research on traffic prediction.

Category		Models	Contribution	Shortcomings
Model-driven		car-following model [13], queuing theory [1,4], cell transmission model [15], three-phase traffic theory [16]	Establish a microscopic mathematical model for traffic forecasting; work better in micro scenes	based on a variety of assumptions and ideal conditions; with extremely high application scenario requirements
Data-driven	Parametric model	ARIMA [17], Kalman filter [18], Bayesian model [19]	treat traffic prediction as time-series task; work better in a single region scene	not consider the impact of spatial characteristics on traffic prediction
	Deep learning model	ARIMA-GARCH [20], LSTM-ARIMA [5], IBCM-DL [7], RNN [21], LSTM [22], CNN [23,24], APTN [25]	considering not only temporal characteristics but also spatial characteristics	only applicable to regular Euclidean datasets
		GATCN [9], T-GCN [10], GCN [26]	applicable to irregular non-Euclidean datasets	assume that adjacent regions have the same effect on the predicted region

. Model-driven research is typically based on a variety of assumptions and ideal conditions, with extremely high application scenario requirements. Typical model-driven research includes the following: car-following model [17], queuing theory [18], cell transmission model [19], three-phase traffic theory [20], etc. Data-driven research, on the other hand, considers both feasibility and accuracy in practical applications; thus, it has received more attention from researchers.

Many data-driven studies were carried out using time series models due to the periodicity and tendency of urban traffic flow in the time dimension. Parametric models and deep learning models are two types of prediction research based on time series features. The parametric model assumes that the regression function conforms to traffic flow distribution; then, it uses historical data to fit the function’s parameters. As early as 1970s, researchers used classic ARIMA [21], Kalman filter [22], Bayesian model [23], and Network Fundamental Diagram (NFD) [24] to conduct traffic prediction research, followed by studies using variants of these models. For example, Chen et al. proposed an Autoregressive Integrated Moving Average with Generalized Autoregressive Conditional Heteroscedasticity (ARIMA-GARCH) model for traffic flow prediction [25]; Azari et al. employed a machine learning and statistical learning time-series prediction method based on long short-term memory and ARIMA to predict cellular network traffic, with a fix-point algorithm embedded to update posterior estimations of maximum correntropy-deduced Kalman filter. Cai et al. achieved better traffic forecasting [9]. Gu et al. proposed an improved Bayesian combination model with deep learning (IBCM-DL) for traffic flow prediction and proved it outperforms other state-of-the-art methods in terms of accuracy and stability [10]. Deep learning models, such as Artificial Neural Network [11], Recurrent Neural Network (RNN) [26], Long Short-term Memory (LSTM) [27], etc., have also performed well in terms of prediction.

Due to the connectivity of the urban road network, the traffic state of a region can be influenced by traffic states of its neighboring regions. As a result, many studies forecast traffic states by extracting both temporal and spatial features. For example, Ma et al. proposed a convolutional neural network (CNN)-based method that learns traffic as images and predicts large-scale, network-wide traffic speed with high accuracy [28]. Zhang et al. proposed a short-term traffic-flow prediction model based on a Convolution Neural Network (CNN) deep learning framework [29]. Shi et al. proposed a novel Attention-based Periodic-Temporal neural Network (APTN), which is an end-to-end solution for traffic foresting that captures spatial, short-term, and long-term periodical dependencies [30]. However, region-level traffic state prediction still faces challenges: (1) The topological structure of the city’s complex road network is destroyed when regions are divided into squares or hexagons, and it is difficult to extract accurate spatial features of these regions; (2) irregular regions based on natural roads, administrative divisions, and other factors are typically non-Euclidean distance data. The classic CNN model is difficult to apply to this type of data.

With the rise of Graph Convolutional Network (GCN), we can capture exactly spatial features from irregular regions [15,16]. Researchers tried to employ GCN and time series model to forecast traffic state. For example, Zhao et al. proposed a temporal graph convolutional network (T-GCN) model, which is combined with the graph convolutional network (GCN) and the gated recurrent unit (GRU), for traffic prediction [14]. Yu et al. devised a novel graph-based neural network that expanded the existing GCN to predict road traffic speeds [31]. Zhang et al. proposed a novel end-to-end deep learning framework named Graph Attention Temporal Convolutional Network (GATCN) for traffic speed forecasting [13], etc. Most studies based on GCN assumed that adjacent regions have the same effect on the predicted region, which is imprecise. As discussed in Section 1, the features of traffic flow propagation and distance between regions should also be considered.

In this context, we propose a new deep learning method that can capture complex temporal and spatial features from remote sensing data in this research and can be used for traffic state forecasting based on irregular region graph.

3. Methodology

In order to capture not only the temporal features of traffic flow, but also the spatial dependencies of the irregular non-Euclidean distance graph structure, we propose the TmS-GCN model. Figure 2 shows the step-by-step diagram of the method. Firstly, the urban area is divided into regions, and a region graph is conducted, and traffic information (i.e., traffic speed, traffic demand, and etc.) in each region are obtained. Secondly, the graph convolutional neural network is used to capture the spatial features. Finally, the outputs of the GCN part are inputed into GRU part to forecast future traffic information.

3.1. Problem Definition

For region-level traffic state prediction, we first define several parameters as follows:

Definition 1.

region graph$G$. $G=\left(V,E\right)$, where$V$is the set of nodes. In our research, each region represents a node;$E$is the set of edges that defines the topology of$G$, which is described by adjacency matrix$A$.

Definition 2.

feature matrix$X\in R^{N\times P}$. $X$represents the feature matrix of all regions,$N$is the number of regions, and$P$is the number of historical time series.$X_m=\left[x_m^{t-P},x_m^{t-P+1},\dots ,x_m^t\right]$represents traffic feature information, such as traffic flow, traffic speed, and traffic density, from time series$t-P$to time series$t$in the$mth$region.

Therefore, region-level traffic state prediction can be defined as follows:

$$\left[X_{t+1},X_{t+2},\dots ,X_{t+T}\right]=f\left(\left[X_{t-P},X_{t-P+1},\dots ,X_t\right];G\right)$$

(1)

which is learning the function $f$ to mapping from historical traffic feature matrix $\left[X_{t-P},X_{t-P+1},\dots ,X_t\right]$ to future traffic feature matrix $\left[X_{t+1},X_{t+2},\dots ,X_{t+T}\right]$ based on graph $G$.

3.2. Overall Framework

Figure 3 shows the framework of the proposed TmS-GCN model consisting of two parts: Grated Recurrent Units and Graph Convolutional Network. Firstly, the GCN part uses the historical traffic state data, i.e., feature matrix $\left[X_{t-P},X_{t-P+1},\dots ,X_t\right]$, and three types of convolutional filter to obtain the intermediate feature matrix $\left[{\tilde{X}}_{t-P},{\tilde{X}}_{t-P+1},\dots ,{\tilde{X}}_t\right]$. Secondly, intermediate feature matrix $\left[{\tilde{X}}_{t-P},{\tilde{X}}_{t-P+1},\dots ,{\tilde{X}}_t\right]$ is input to GRU part to obtain future traffic feature matrix $\left[X_{t+1},X_{t+2},\dots ,X_{t+T}\right]$.

3.3. Spatial Dependence Modeling

The datasets used in many deep learning studies are Euclidean distance datasets with regular shapes, such as images, videos, and audios. The classic Convolutional Neural Network (CNN) model can be used to extract effective features from these datasets [28,32]. However, classic CNN models cannot be deployed on irregular non-Euclidean distance datasets, such as social networks and road networks. In recent years, researchers have tried to use graph convolutional neural networks to capture features from irregular graph structure, such as the following: identifying disease-gene association [33], forecasting road traffic speeds [31], classifying node [34], etc. Given a graph $G=\left(V,E\right)$, an adjacency matrix $A$ and feature matrix $X$ can be obtained. The GCN model defines convolutional operation in the Fourier domain. The convolutional filter captures spatial features of each node from its first-order neighborhood and itself. A typical multi-layered GCN is shown in Figure 4, in which the relationship between two adjacency layers can be expressed as follows:

$$H^{\left(l+1\right)}=\sigma \left({\tilde{D}}^{-\frac{1}{2}}\widehat{A}{\tilde{D}}^{-\frac{1}{2}}{H}^{\left(l\right)}{\theta }^{\left(l\right)}\right)$$

(2)

$$\widehat{A}=A+I_N$$

(3)

where $A$ represents adjacency matrix, $I$ is the identity matrix, $\tilde{D}$ is the degree matix, $H^{\left(l\right)}$ and $H^{\left(l+1\right)}$ are the outputs of $l$ and $l+1$ layer, ${\theta }^{\left(l\right)}$ represents all parameters of $l$ layer, and $\sigma \left(\right)$ is the activation function.

We stated in the first section that the spatial dependence of region-level traffic states cannot only rely on adjacency matrix, which result in poor prediction. Thus, here, we introduce two more special adjacency matrices $A^P$ and $A^d$ to capture richer spatial dependencies.

(1) Traffic flow propagating matrix $A^P$ captures the features of traffic flow propagating between regions, which is defined as follows:

$$A_{ij}^P=\{\begin{array}{cc}0& \mathrm{no}\mathrm{vehicle}\mathrm{travel}\mathrm{from}\mathrm{region}i\mathrm{to}\mathrm{region}j\\ \frac{{\overline{Q}}_{ij}}{{\overline{Q}}_j}& \mathrm{otherwise}\end{array}$$

(4)

where ${\overline{Q}}_j$ is the average number of vehicles located in region $j$, and ${\overline{Q}}_{ij}$ represents the average number of vehicles travelling from region $i$ to region $j$. According to Equation (4), a greater value of $A_{ij}^P$ indicates that region $i$ provides more information than other regions for capturing spatial features of region $j$. As shown in Figure 1, $A_{24}^P$ is greater than $A_{14}^P$.

(2) Centroid distance matrix $A^d$ captures the feature of distance of GPS points’ centroid between regions, which is defined as follows:

$$A_{ij}^d=\{\begin{array}{cc}0& \mathrm{if}\mathrm{region}j\mathrm{and}\mathrm{region}i\mathrm{is}\mathrm{not}\mathrm{adjacent}\\ \frac{1}{\phi \left(La{t}^i,La{t}^j,Ln{g}^i,Ln{g}^j\right)}& \mathrm{otherwise}\end{array}$$

(5)

where $\phi \left(\right)$ represents the function to calculate distance based on latitude and longitude coordinates, $La{t}^i$ and $Ln{g}^i$ are the latitude and longitude coordinates of the GPS points’ centroid in region $i$, and $La{t}^j$ and $Ln{g}^j$ are the latitude and longitude coordinates of the GPS points centroid in region $j$. A greater value of $A_{ij}^d$ indicates that region $i$ provides more information than other regions for capturing spatial features of region $j$. As shown in Figure 1, $A_{54}^d$ is greater than $A_{34}^d$.

3.4. Temporal Dependence Modeling

Traffic state prediction is a typical time series task, and some classic time series model can be employed to this task, such as Moving Average (MA) model, Auto Regressive (AR) model, ARIMA, etc. With the rise of deep learning methods, Recurrent Neural Network (RNN) models with better prediction effects on time-series tasks have been proposed. However, the RNN model has been replaced by Long Short-Term Memory (LSTM) [35] and GRU [36] because it is prone to gradient disappearance and gradient explosion problems. The GRU model has a small number of parameters, which speeds up model convergence without sacrificing prediction accuracy. As a result, we employ the GRU model to extract the traffic state’s dynamic change characteristics from time series.

Figure 5 shows the structure of GRU, where $h_{\left(t-1\right)}$ and $h_t$ are the latent state at $t-1$ and $t$, $X_t$ represents the input of GRU at $t$, i.e., traffic state information, ${\widehat{Y}}_t$ is the output at $t$, which is the predicted traffic state information. Overall, the model is capable of predicting future traffic states by combining both traffic state information and hidden state information from previous time intervals. There are two important gate controls added to the model, including reset gate $r_t$ and update gate $z_t$. $r_t$ and $z_t$ are defined in Formulas (7) and (8), respectively. With the two gates, GRU is able to control whether current traffic state information and previous hidden state information can be imported. In addition, the sigmoid activation function is added to the two gates to make sure that input size is controlled in the range of 0% to 100%.

$$r_t=\sigma \left(W_r\left[f\left(A,X_t\right),h_{\left(t-1\right)}\right]+b_r\right)$$

(6)

$$z_t=\sigma \left(W_u\left[f\left(A,X_t\right),h_{\left(t-1\right)}\right]+b_u\right)$$

(7)

$${\tilde{h}}_t=tanh\left(W_{\tilde{h}}\left[f\left(A,X_t\right),(r_t\odot h_{\left(t-1\right)})\right]+b_{\tilde{h}}\right)$$

(8)

$$h_t=z_t\odot h_{\left(t-1\right)}+\left(1-z_t\right)\odot {\tilde{h}}_t$$

(9)

4. Experiment

4.1. Data Description

The dataset for this paper was derived from taxi GPS data collected in Shenzhen, China, in January 2019. There are about 30,000 taxis in total and over 900 million positioning points. The sampling rate of GPS is 1–3 s, and the average penetration rate of GPS is above 5%. Our research is similar to other studies using GPS data from taxis, such as mining Urban Recurrent Congestion Evolution Patterns [1], forecasting Citywide Traffic Congestion [2], and identifying areas of interest [4], which all reflect urban traffic status from a macro level. Compared with other types of vehicles, taxis perform better in terms of overall number, sampling rate, penetration rate, and other indicators. Therefore, it is reasonable and representative to carry out verification of this paper based on taxi GPS data.

Before placing data into the model for training, some pre-processing work was performed: (1) Weekend data and holiday data were removed, leaving only 22 workdays; (2) incorrect and redundant data, such as one vehicle’s GPS data located in one region for an unreasonable amount of time, were deleted. (3) Average speed values of all vehicles, which represent region-level traffic features, were aggregated every 15 min in each region. (4) The 22-day dataset was divided into a training dataset and a test dataset at a ratio of 8:2. The test dataset includes data on 21–24 January 2019. Moreover, the rest part is the training dataset.

The urban area of Shenzhen is divided into 78 regions according to administrative zip code, as shown in Figure 6. Adjacent matrix $A$, traffic flow propagating matrix $A^P$, and Centroid distance matrix $A^d$ were obtained based on the connectivity of graph generated by regions, Equation (4), and Equation (5), respectively.

4.2. Benchmark Model and Evaluation Measurement

We evaluate the performance of the TmS-GCN model with the following benchmark models:

• Historical average (HA) [37] uses the average value of historical state traffic information as the prediction result.
• Auto-Regressive Moving Average (ARIMA) [25] is a parameter model widely used in various traffic prediction research.
• Multiple Layer Perceptron (MLP) [38] is a classic feedforward neural network model.
• Graph Convolutional Network model (GCN) [39] is described in Section 3.3.
• Gated Recurrent Unit model (GRU) [40] is described in Section 3.4.
• Long Short-Term Memory (LSTM) [27] is similar to the GRU model and widely used in traffic prediction areas. The settings of LSTM are the same as GRU.
• Temporal Graph Convolutional Network (T-GCN) [14] captures both temporal and spatial dependencies to forecast short-term traffic flow.

Three common indicators are used to compare the performance of the TmS-GCN model and benchmark models:

(1) Mean Absolute Error (MAE):

$$MAE=\frac{1}{N}{\displaystyle \sum _{i=1}^N\left|y_i-\widehat{y_i}\right|}$$

(10)

(2) Mean Absolute Percentage Error (MAPE):

$$MAPE=\frac{1}{N}{\displaystyle \sum _{i=1}^N\frac{\left|y_i-\widehat{y_i}\right|}{y_i}}$$

(11)

(3) Root Mean Square Error (RMSE):

$$RMSE=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N\left(y_i-\widehat{y_i}\right)}}$$

(12)

where $y_i$ and $\widehat{y_i}$ represent the $i^{th}$ real value and predicted value. The smaller MAE, MAPE, and RMSE values are, the higher the accuracy of the model and the better prediction performance will be.

We use Pytorch to implement the TmS-GCN model and other benchmark models. Some parameters involved in the TmS-GCN model are as follows: the learning rate is set to 0.001, the batch size is set to 32, and the training Epoch is 600. The L2 loss function is used to calculate the difference between true and predicted values.

4.3. Results

Table 2. Comparison of prediction performance.

Prediction Horizons	Indicator	Models
		HA	ARIMA	GCN	GRU	T-GCN	TmS-GCN
15 min	MAE	4.9444	4.7388	6.4901	4.6163	4.3459	4.1558
	MAPE	22.1308	15.4636	30.3969	18.6844	17.8520	17.5257
	RMSE	9.4545	8.7343	10.4114	8.5333	7.9872	7.7170
30 min	MAE	4.9444	6.3588	6.5580	4.6815	4.2521	4.2626
	MAPE	22.1308	19.9847	30.6031	19.4643	18.6607	17.9527
	RMSE	9.4545	10.4867	10.5076	8.9123	7.7833	7.7935
45 min	MAE	4.9444	6.0853	6.5832	4.8029	4.4019	4.3449
	MAPE	22.1308	21.5859	30.7334	19.6285	18.9232	18.8494
	RMSE	9.4545	9.8143	10.5497	9.3611	7.9631	7.8322
60 min	MAE	4.9444	6.8783	6.5979	4.7871	4.7776	4.2945
	MAPE	22.1308	25.6076	30.8103	18.6647	21.3096	17.9971
	RMSE	9.4545	11.2398	10.5686	10.5902	8.2070	7.8740

shows the prediction performance of the TmS-GCN model and other benchmark models for 5 min, 15 min, 30 min, 45 min, and 60 min. It can be observed that the proposed TmS-GCN model has the best prediction performance for all prediction horizons.

We can deduce the following information from Table 2: (1) For all prediction horizons, the GCN model, which simply considers spatial dependencies, is the worst. It shows that in the study of regional traffic state prediction, temporal dependencies have a greater impact than spatial dependencies. (2) The deep learning model outperforms the traditional time series model. The GRU model that ignores spatial dependencies outperforms HA and ARIMA models for all prediction horizons. (3) The T-GCN model and TmS-GCN models, considering both spatial and temporal dependencies, outperform not only the GCN model but also the GRU model. (4) The TmS-GCN model outperforms T-GCN model for most prediction horizons, which demonstrating the validity of our hypothesis that adding two more special adjacency matrices $A^P$ and $A^d$ to capture richer spatial dependencies improves forecasting performance.

4.4. Discussion

4.4.1. Results Analysis

We analyze the prediction results of the TmS-GCN model from the time dimension and space dimension.

In Figure 7, the true traffic feature value of Region 60 (i.e., Longhua subdistinct, the red region in Figure 6) is compared to the predicted values of 15 min, 30 min, 45 min, and 60 min, respectively. The following conclusions can be drawn: (1) The TmS-GCN model performs better in short-term prediction tasks than in long-term prediction tasks, which are determined by GRU features. (2) The model does not perform well when regional traffic speed increases or decreases sharply. This is due to the fact that our model ignores the random effect induced by a lack of taxi vehicles. In the future, other GPS data sources could be collected to improve it.

Figure 8 shows the comparison of prediction results for 78 regions. We can draw the following conclusions:

• Figure 8a shows that the majority of the locations with good prediction results are in the city center, such as Nanshan District, Futian District, Bao’an District, and so on. However, suburban areas such as Guangming District in the northwest corner and Longgang District in the southeast corner have a poor prediction results. This is due to the fact that suburb regions have less adjacent regions, making it difficult to acquire effective spatial dependencies. Furthermore, the amount of taxi GPS data in the suburbs is tiny, resulting in randomness.
• Figure 8 shows that the number of taxi GPS points has a significant impact on prediction effect. When there are a few taxi vehicles between 3:00 and 4:00 a.m. every day, the prediction results of practically all regions are smaller than in other time periods. The increase in the number of taxi GPS points between 12:00 and 13:00 improves forecasting results of all regions.

4.4.2. Analysis of Influencing Factors

• Type and number of GPS points

There are nearly 30,000 taxis in Shenzhen cruising on roads at any time of the day. Each taxi vehicle uploads location information every 3 s, including latitude, longitude, and instantaneous speed. These data can comprehensively and accurately reflect travel demand, traffic flow speed, and other information of the divided regions. GPS data of other vehicles can also be applied to the TmS-GCN model, such as online car-hailing vehicles, bus, private car, etc.

Intuitively, the number of GPS points within the region has an impact on prediction results. Figure 9 shows the results of regional traffic prediction at various GPS points. We observe that when the average number of GPS points within a region in 15 min exceeds 600, the values of MAE, MAPE, and RMSE are obviously smaller and more stable, and the prediction effect is greatly improved. Therefore, in order to achieve better prediction, the average number of GPS points in each region needs to reach 600 every 15 min.

• Time interval

In this paper, we set the time interval to 15 min. In terms of calculation, the smaller the time interval, the more calculations are required. The calculation amount for a 5-min scale forecast, for example, is three times that of a 15-min forecast. However, the 5-min forecast is more relevant than the 15-min forecast in terms of application. We compared prediction impacts over different time intervals, as shown in Figure 10. As the time interval becomes larger, the values of MAE, MAPE, and RMSE also increase correspondingly, which means that the prediction effect becomes worse. Compared with the prediction results on the 5-min scale, MAE, MAPE, and RMSE values on the 15-min scale only increased by 8.2%, 15%, and 12.6%, respectively. If calculation efficiency is not considered, it is recommended to perform a 5-min traffic forecast. However, 15-min traffic forecasting is the most appropriate if computing efficiency, practicability, and forecasting consequences are all taken into account.

4.4.3. Potential Application Direction

Since the average speed values of all regions can be obtained, the most direct application is to provide a macroscopic visual display of traffic operation status in the ITS system. If the average speed of a specific region deviates from the average value of all regions, the traffic manager can reschedule the traffic signal in advance or send the police to divert the traffic. Furthermore, if the speed of traffic in a certain location is. reduced, this information can be displayed on a public information platform. Furthermore, if the traffic speed in a specific region decreases, an individual can use this knowledge to choose the subway instead of a private car, or the individual can adjust travel time to avoid wasting time.

In this research study, we verified traffic speed prediction within the region. In fact, our model can also predict region-level traffic flow as long as traffic speed is replaced by traffic flow. Thus, the most direct application is to estimate the OD matrix at the regional level. Furthermore, if we know where and when a taxi picks up passengers, we can incorporate this type of location information into our model and forecast the demand for individuals to travel by taxi. Taxi companies can dispatch vehicles based on this forecast information to obtain greater economic benefits. These applications are also applicable to private cars, online car-hailing, shared bicycles, etc.

5. Conclusions

This paper proposes a deep learning model for predicting region-level traffic state called TmS-GCN, including the following two parts: GRU and GCN. In the GCN part, not only adjacency matrix information but also traffic propagation features between regions and GPS positioning points’ centroid distance feature are used to capture spatial dependencies of the region’s graph. In the GRU part, temporal dependencies are captured in order to predict region-level traffic state for prediction horizons of 15 min, 30 min, 45 min, and 60 min. Using real GPS data from Shenzhen taxis, the model is evaluated and compared to HA, ARIMA, MLP, GCN, GRU, and T-GCN. In most regions and prediction horizons, the model outperforms other benchmark models. Our model is expected to be used to analyze and capture spatio-temporal features at the regional level in other scenarios.

The contributions of this article are listed as follows:

• We propose a complete region-level traffic prediction method named TmS-GCN composed of GCN and GRU. Based on GCN, TmS-GCN can capture multi-spatial correlation features of regions on non-Euclidean distance data composed of divided regions. In addition, based on GRU, TmS-GCN can capture temporal features of traffic parameters within the region.
• We validate the TmS-GCN model by using real taxi GPS data from Shenzhen. The findings show that the model produces the desired impact and that the model’s effect is much better when traffic flow propagation information and centroid distance information are included. TmS-GCN outperforms baseline models of HA, ARIMA, MLP, GCN, GRU, and T-GCN on prediction scales of 15 min, 30 min, 45 min, and 60 min. The MAE, MAPE, and RMSE of the model’s prediction outcomes are 4.1558, 17.5257, and 7.7170, respectively, on a 15-min prediction scale.

This study can provide support for better understanding and carrying out region-level traffic prediction. The research’s findings, in particular, are extremely useful for decision making in Intelligent Transportation Systems. For example, using forecasted dynamic region-level traffic demand, managers can dispatch vehicles to balance traffic demand. Using information on abnormal changes in region-level traffic speeds, managers can implement traffic control or traffic guidance to relieve traffic congestion. Although the model in this paper has a good prediction effect in most regions and for most of the time period, it fails to respond well to the impact of severe weather and traffic accidents. Future research and improvement ideas include two types: one is to design an adaptive model for a specific shock event, and the other is to consider the impact of shock events by using the existing TmS-GCN model, such as time, location, and scale of shock events, as input features into the neural network.