Region-Level Traffic Prediction Based on Temporal Multi-Spatial Dependence Graph Convolutional Network from GPS Data
Abstract
:1. Introduction
- We proposed the TmS-GCN model, which integrates Gated Recurrent Units (GRU) and GCN. GRU is used to obtain temporal dependence based on historical traffic state data. GCN is used to capture spatial dependence based on the graph of irregular regions.
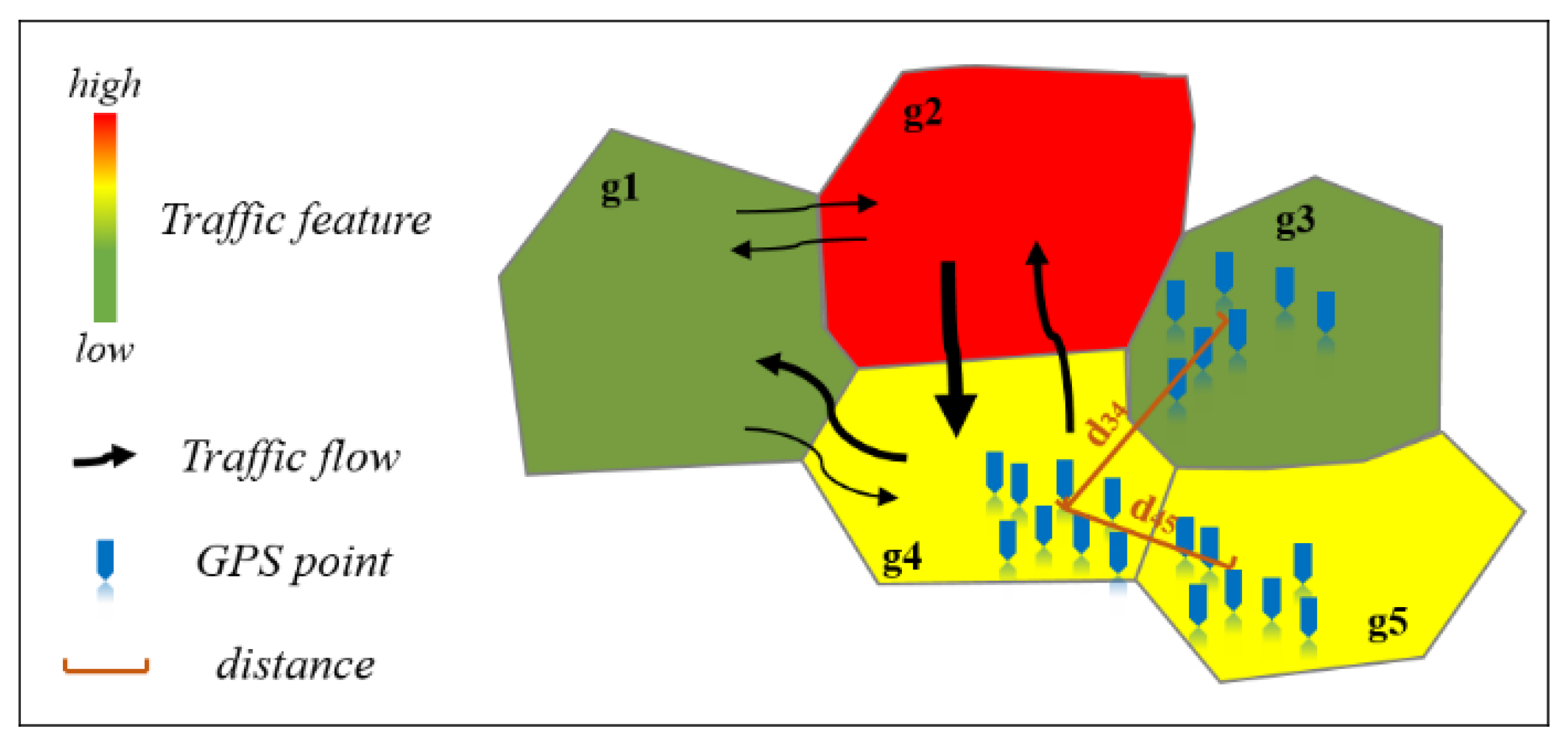
- The TmS-GCN model fully takes into account multiple types of spatial dependencies. Compared with the classic GCN model, which assumed that adjacent regions have the same effect on the predicted region, our model also considers traffic flow propagation and spatial distance among regions.
- We evaluate our method using real-world GPS data collected from Taxi vehicles in Shenzhen, China. The results show that our method outperforms baseline methods.
2. Related Work
3. Methodology
3.1. Problem Definition
3.2. Overall Framework
3.3. Spatial Dependence Modeling
3.4. Temporal Dependence Modeling
4. Experiment
4.1. Data Description
4.2. Benchmark Model and Evaluation Measurement
- Historical average (HA) [37] uses the average value of historical state traffic information as the prediction result.
- Auto-Regressive Moving Average (ARIMA) [25] is a parameter model widely used in various traffic prediction research.
- Multiple Layer Perceptron (MLP) [38] is a classic feedforward neural network model.
- Graph Convolutional Network model (GCN) [39] is described in Section 3.3.
- Gated Recurrent Unit model (GRU) [40] is described in Section 3.4.
- Long Short-Term Memory (LSTM) [27] is similar to the GRU model and widely used in traffic prediction areas. The settings of LSTM are the same as GRU.
- Temporal Graph Convolutional Network (T-GCN) [14] captures both temporal and spatial dependencies to forecast short-term traffic flow.
4.3. Results
4.4. Discussion
4.4.1. Results Analysis
- Figure 8a shows that the majority of the locations with good prediction results are in the city center, such as Nanshan District, Futian District, Bao’an District, and so on. However, suburban areas such as Guangming District in the northwest corner and Longgang District in the southeast corner have a poor prediction results. This is due to the fact that suburb regions have less adjacent regions, making it difficult to acquire effective spatial dependencies. Furthermore, the amount of taxi GPS data in the suburbs is tiny, resulting in randomness.
- Figure 8 shows that the number of taxi GPS points has a significant impact on prediction effect. When there are a few taxi vehicles between 3:00 and 4:00 a.m. every day, the prediction results of practically all regions are smaller than in other time periods. The increase in the number of taxi GPS points between 12:00 and 13:00 improves forecasting results of all regions.
4.4.2. Analysis of Influencing Factors
- Type and number of GPS points
- Time interval
4.4.3. Potential Application Direction
5. Conclusions
- We propose a complete region-level traffic prediction method named TmS-GCN composed of GCN and GRU. Based on GCN, TmS-GCN can capture multi-spatial correlation features of regions on non-Euclidean distance data composed of divided regions. In addition, based on GRU, TmS-GCN can capture temporal features of traffic parameters within the region.
- We validate the TmS-GCN model by using real taxi GPS data from Shenzhen. The findings show that the model produces the desired impact and that the model’s effect is much better when traffic flow propagation information and centroid distance information are included. TmS-GCN outperforms baseline models of HA, ARIMA, MLP, GCN, GRU, and T-GCN on prediction scales of 15 min, 30 min, 45 min, and 60 min. The MAE, MAPE, and RMSE of the model’s prediction outcomes are 4.1558, 17.5257, and 7.7170, respectively, on a 15-min prediction scale.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- An, S.; Yang, H.; Wang, J.; Cui, N.; Cui, J. Mining Urban Recurrent Congestion Evolution Patterns from GPS-Equipped Vehicle Mobility Data. Inf. Sci. 2016, 373, 515–526. [Google Scholar] [CrossRef]
- Guo, J.; Liu, Y.; Yang, Q.; Wang, Y.; Fang, S. GPS-Based Citywide Traffic Congestion Forecasting Using CNN-RNN and C3D Hybrid Model. Transp. A: Transp. Sci. 2021, 17, 190–211. [Google Scholar] [CrossRef]
- Tang, J.; Liang, J.; Liu, F.; Hao, J.; Wang, Y. Multi-Community Passenger Demand Prediction at Region Level Based on Spatio-Temporal Graph Convolutional Network. Transp. Res. Part C Emerg. Technol. 2021, 124, 102951. [Google Scholar] [CrossRef]
- Liu, Y.; Singleton, A.; Arribas-bel, D.; Chen, M. Identifying and Understanding Road-Constrained Areas of Interest (AOIs) through Spatiotemporal Taxi GPS Data: A Case Study in New York City. Comput. Environ. Urban Syst. 2021, 86, 101592. [Google Scholar] [CrossRef]
- Yu, J.; Stettler, M.E.J.; Angeloudis, P.; Hu, S.; Chen, X. Urban Network-Wide Traffic Speed Estimation with Massive Ride-Sourcing GPS Traces. Transp. Res. Part C Emerg. Technol. 2020, 112, 136–152. [Google Scholar] [CrossRef]
- Kan, Z.; Kwan, M.-P.; Liu, D.; Tang, L.; Chen, Y.; Fang, M. Assessing Individual Activity-Related Exposures to Traffic Congestion Using GPS Trajectory Data. J. Transp. Geogr. 2022, 98, 103240. [Google Scholar] [CrossRef]
- Cascetta, E. Transportation Systems Analysis: Models and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; Volume 29. [Google Scholar]
- Azari, A.; Papapetrou, P.; Denic, S.; Peters, G. Cellular Traffic Prediction and Classification: A Comparative Evaluation of LSTM and ARIMA. In Proceedings of the Discovery Science; Kralj Novak, P., Šmuc, T., Džeroski, S., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 129–144. [Google Scholar]
- Cai, L.; Zhang, Z.; Yang, J.; Yu, Y.; Zhou, T.; Qin, J. A Noise-Immune Kalman Filter for Short-Term Traffic Flow Forecasting. Phys. A Stat. Mech. Its Appl. 2019, 536, 122601. [Google Scholar] [CrossRef]
- Gu, Y.; Lu, W.; Xu, X.; Qin, L.; Shao, Z.; Zhang, H. An Improved Bayesian Combination Model for Short-Term Traffic Prediction With Deep Learning. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1332–1342. [Google Scholar] [CrossRef]
- Chen, X.; Lu, J.; Zhao, J.; Qu, Z.; Yang, Y.; Xian, J. Traffic Flow Prediction at Varied Time Scales via Ensemble Empirical Mode Decomposition and Artificial Neural Network. Sustainability 2020, 12, 3678. [Google Scholar] [CrossRef]
- Azzouni, A.; Pujolle, G. A Long Short-Term Memory Recurrent Neural Network Framework for Network Traffic Matrix Prediction. arXiv 2017, arXiv:1705.05690. [Google Scholar]
- Zhang, K.; He, F.; Zhang, Z.; Lin, X.; Li, M. Graph Attention Temporal Convolutional Network for Traffic Speed Forecasting on Road Networks. Transp. B Transp. Dyn. 2021, 9, 153–171. [Google Scholar] [CrossRef]
- Zhao, L.; Song, Y.; Zhang, C.; Liu, Y.; Wang, P.; Lin, T.; Deng, M.; Li, H. T-GCN: A Temporal Graph Convolutional Network for Traffic Prediction. IEEE Trans. Intell. Transport. Syst. 2020, 21, 3848–3858. [Google Scholar] [CrossRef] [Green Version]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2017, arXiv:1609.02907. [Google Scholar]
- Zhang, S.; Tong, H.; Xu, J.; Maciejewski, R. Graph Convolutional Networks: A Comprehensive Review. Comput. Soc. Netw. 2019, 6, 11. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Wang, X.; Ouyang, Y. Prediction and Field Validation of Traffic Oscillation Propagation under Nonlinear Car-Following Laws. Transp. Res. Part B: Methodol. 2012, 46, 409–423. [Google Scholar] [CrossRef]
- Lartey, J.D. Predicting Traffic Congestion: A Queuing Perspective. Open J. Model. Simul. 2014, 2, 57. [Google Scholar] [CrossRef]
- Hu, X.; Wang, W.; Sheng, H. Urban Traffic Flow Prediction with Variable Cell Transmission Model. J. Transp. Syst. Eng. Inf. Technol. 2010, 10, 73–78. [Google Scholar] [CrossRef]
- Wegerle, D.; Kerner, B.S.; Schreckenberg, M.; Klenov, S.L. Prediction of Moving Bottleneck through the Use of Probe Vehicles: A Simulation Approach in the Framework of Three-Phase Traffic Theory. J. Intell. Transp. Syst. 2020, 24, 598–616. [Google Scholar] [CrossRef]
- Kinney, W.R. ARIMA and Regression in Analytical Review: An Empirical Test. Account. Rev. 1978, 53, 48–60. [Google Scholar]
- Ghosh, D.; Knapp, C.H. Estimation of Traffic Variables Using a Linear Model of Traffic Flow. Transp. Res. 1978, 12, 395–402. [Google Scholar] [CrossRef]
- Levin, M.; Krause, G.M. Incident Detection: A Bayesian Approach. Transp. Res. Rec. 1978, 682, 52–58. [Google Scholar]
- Alonso, B.; Pòrtilla, Á.I.; Musolino, G.; Rindone, C.; Vitetta, A. Network Fundamental Diagram (NFD) and Traffic Signal Control: First Empirical Evidences from the City of Santander. Transp. Res. Procedia 2017, 27, 27–34. [Google Scholar] [CrossRef]
- Chen, C.; Hu, J.; Meng, Q.; Zhang, Y. Short-Time Traffic Flow Prediction with ARIMA-GARCH Model. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; pp. 607–612. [Google Scholar]
- Zhene, Z.; Hao, P.; Lin, L.; Guixi, X.; Du, B.; Bhuiyan, M.Z.A.; Long, Y.; Li, D. Deep Convolutional Mesh RNN for Urban Traffic Passenger Flows Prediction. In Proceedings of the 2018 IEEE SmartWorld, Ubiquitous Intelligence Computing, Advanced Trusted Computing, Scalable Computing Communications, Cloud Big Data Computing, Internet of People and Smart City Innovation (SmartWorld/SCALCOM/UIC/ATC/CBDCom/IOP/SCI), Guangzhou, China, 8–12 October 2018; pp. 1305–1310. [Google Scholar]
- Zhao, Z.; Chen, W.; Wu, X.; Chen, P.C.Y.; Liu, J. LSTM Network: A Deep Learning Approach for Short-term Traffic Forecast. IET Intell. Transp. Syst. 2017, 11, 68–75. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.; Dai, Z.; He, Z.; Ma, J.; Wang, Y.; Wang, Y. Learning Traffic as Images: A Deep Convolutional Neural Network for Large-Scale Transportation Network Speed Prediction. Sensors 2017, 17, 818. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, W.; Yu, Y.; Qi, Y.; Shu, F.; Wang, Y. Short-Term Traffic Flow Prediction Based on Spatio-Temporal Analysis and CNN Deep Learning. Transp. A Transp. Sci. 2019, 15, 1688–1711. [Google Scholar] [CrossRef]
- Shi, X.; Qi, H.; Shen, Y.; Wu, G.; Yin, B. A Spatial–Temporal Attention Approach for Traffic Prediction. IEEE Trans. Intell. Transp. Syst. 2021, 22, 4909–4918. [Google Scholar] [CrossRef]
- Yu, B.; Lee, Y.; Sohn, K. Forecasting Road Traffic Speeds by Considering Area-Wide Spatio-Temporal Dependencies Based on a Graph Convolutional Neural Network (GCN). Transp. Res. Part C Emerg. Technol. 2020, 114, 189–204. [Google Scholar] [CrossRef]
- Li, X.; Li, J.; Hu, X.; Yang, J. Line-CNN: End-to-End Traffic Line Detection With Line Proposal Unit. IEEE Trans. Intell. Transp. Syst. 2020, 21, 248–258. [Google Scholar] [CrossRef]
- Han, P.; Yang, P.; Zhao, P.; Shang, S.; Liu, Y.; Zhou, J.; Gao, X.; Kalnis, P. GCN-MF: Disease-Gene Association Identification By Graph Convolutional Networks and Matrix Factorization. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 705–713. [Google Scholar]
- Abu-El-Haija, S.; Kapoor, A.; Perozzi, B.; Lee, J. N-GCN: Multi-Scale Graph Convolution for Semi-Supervised Node Classification. In Proceedings of the 35th Uncertainty in Artificial Intelligence Conference, Tel Aviv, Israel, 22–25 July 2019; pp. 841–851. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations Using RNN Encoder-Decoder for Statistical Machine Translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Kamarianakis, Y.; Prastacos, P. Forecasting Traffic Flow Conditions in an Urban Network: Comparison of Multivariate and Univariate Approaches. Transp. Res. Rec. 2003, 1857, 74–84. [Google Scholar] [CrossRef]
- Chen, H.; Grant-Muller, S.; Mussone, L.; Montgomery, F. A Study of Hybrid Neural Network Approaches and the Effects of Missing Data on Traffic Forecasting. NCA 2001, 10, 277–286. [Google Scholar] [CrossRef]
- Chen, Z.; Zhao, B.; Wang, Y.; Duan, Z.; Zhao, X. Multitask Learning and GCN-Based Taxi Demand Prediction for a Traffic Road Network. Sensors 2020, 20, 3776. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, J.; Shao, C.; Dong, C.; Yin, C. Truck Traffic Flow Prediction Based on LSTM and GRU Methods With Sampled GPS Data. IEEE Access 2020, 8, 208158–208169. [Google Scholar] [CrossRef]









| Category | Models | Contribution | Shortcomings | |
|---|---|---|---|---|
| Model-driven | car-following model [13], queuing theory [1,4], cell transmission model [15], three-phase traffic theory [16] | Establish a microscopic mathematical model for traffic forecasting; work better in micro scenes | based on a variety of assumptions and ideal conditions; with extremely high application scenario requirements | |
| Data-driven | Parametric model | ARIMA [17], Kalman filter [18], Bayesian model [19] | treat traffic prediction as time-series task; work better in a single region scene | not consider the impact of spatial characteristics on traffic prediction |
| Deep learning model | ARIMA-GARCH [20], LSTM-ARIMA [5], IBCM-DL [7], RNN [21], LSTM [22], CNN [23,24], APTN [25] | considering not only temporal characteristics but also spatial characteristics | only applicable to regular Euclidean datasets | |
| GATCN [9], T-GCN [10], GCN [26] | applicable to irregular non-Euclidean datasets | assume that adjacent regions have the same effect on the predicted region | ||
| Prediction Horizons | Indicator | Models | |||||
|---|---|---|---|---|---|---|---|
| HA | ARIMA | GCN | GRU | T-GCN | TmS-GCN | ||
| 15 min | MAE | 4.9444 | 4.7388 | 6.4901 | 4.6163 | 4.3459 | 4.1558 |
| MAPE | 22.1308 | 15.4636 | 30.3969 | 18.6844 | 17.8520 | 17.5257 | |
| RMSE | 9.4545 | 8.7343 | 10.4114 | 8.5333 | 7.9872 | 7.7170 | |
| 30 min | MAE | 4.9444 | 6.3588 | 6.5580 | 4.6815 | 4.2521 | 4.2626 |
| MAPE | 22.1308 | 19.9847 | 30.6031 | 19.4643 | 18.6607 | 17.9527 | |
| RMSE | 9.4545 | 10.4867 | 10.5076 | 8.9123 | 7.7833 | 7.7935 | |
| 45 min | MAE | 4.9444 | 6.0853 | 6.5832 | 4.8029 | 4.4019 | 4.3449 |
| MAPE | 22.1308 | 21.5859 | 30.7334 | 19.6285 | 18.9232 | 18.8494 | |
| RMSE | 9.4545 | 9.8143 | 10.5497 | 9.3611 | 7.9631 | 7.8322 | |
| 60 min | MAE | 4.9444 | 6.8783 | 6.5979 | 4.7871 | 4.7776 | 4.2945 |
| MAPE | 22.1308 | 25.6076 | 30.8103 | 18.6647 | 21.3096 | 17.9971 | |
| RMSE | 9.4545 | 11.2398 | 10.5686 | 10.5902 | 8.2070 | 7.8740 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Zhang, X.; Li, Z.; Cui, J. Region-Level Traffic Prediction Based on Temporal Multi-Spatial Dependence Graph Convolutional Network from GPS Data. Remote Sens. 2022, 14, 303. https://doi.org/10.3390/rs14020303
Yang H, Zhang X, Li Z, Cui J. Region-Level Traffic Prediction Based on Temporal Multi-Spatial Dependence Graph Convolutional Network from GPS Data. Remote Sensing. 2022; 14(2):303. https://doi.org/10.3390/rs14020303
Chicago/Turabian StyleYang, Haiqiang, Xinming Zhang, Zihan Li, and Jianxun Cui. 2022. "Region-Level Traffic Prediction Based on Temporal Multi-Spatial Dependence Graph Convolutional Network from GPS Data" Remote Sensing 14, no. 2: 303. https://doi.org/10.3390/rs14020303
APA StyleYang, H., Zhang, X., Li, Z., & Cui, J. (2022). Region-Level Traffic Prediction Based on Temporal Multi-Spatial Dependence Graph Convolutional Network from GPS Data. Remote Sensing, 14(2), 303. https://doi.org/10.3390/rs14020303






