An Improved Fast Estimation of Satellite Phase Fractional Cycle Biases
Abstract
:1. Introduction
2. Methods
2.1. PPP Model of BDS-3
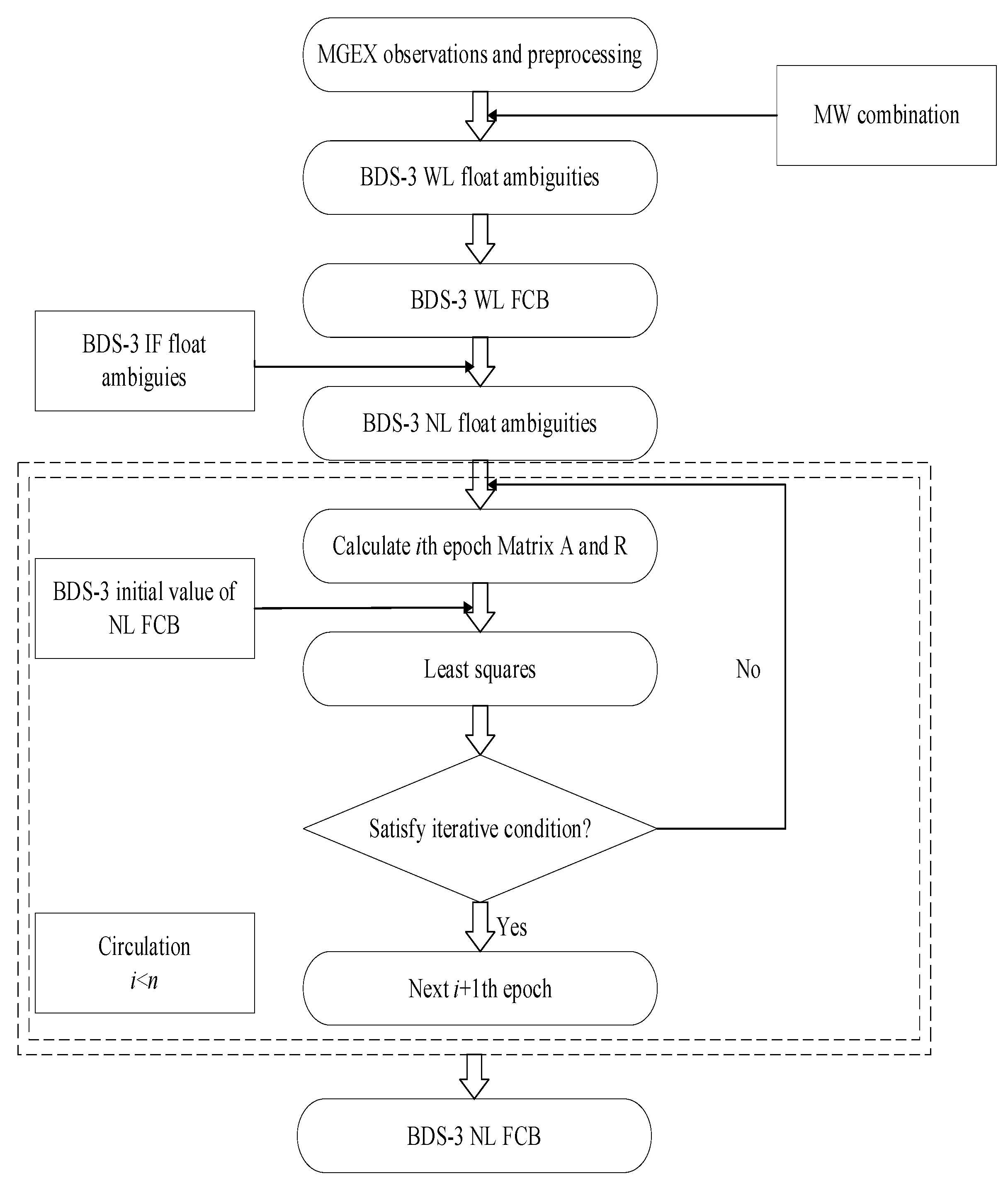
2.2. Improved Fast Estimation of FCB
2.2.1. Estimation of WL FCB
2.2.2. Traditional Estimation of NL FCB
2.2.3. Improved Estimation of NL FCB
3. Results and Discussion
3.1. FCB Experiment
3.2. PPP–AR Experiment
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zumberge, J.; Heflin, M.; Jefferson, D.; Watkins, M.; Webb, F. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef] [Green Version]
- Héroux, P.; Kouba, J. GPS precise point positioning using IGS orbit products. Phys. Chem. Earth Part A Solid Earth Geod. 2001, 26, 573–578. [Google Scholar] [CrossRef]
- Ye, S. Theory and Realization of GPS Precise Point Positioning Using Un-Differenced Phase Observation. Ph.D. Thesis, Wuhan University, Wuhan, China, 2002. [Google Scholar]
- Gao, Y.; Shen, X. Improving Ambiguity Convergence in Carrier Phase-Based Precise Point Positioning. In Proceedings of the 14th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 2001), Salt Lake City, UT, USA, 11–14 September 2001; pp. 1532–1539. [Google Scholar]
- Cai, C.; Gao, Y. Performance analysis of Precise Point Positioning based on combined GPS and GLONASS. In Proceedings of the 20th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2007), Fort Worth, TX, USA, 25–28 September 2007; pp. 858–865. [Google Scholar]
- Cai, C.; Gao, Y. Precise point positioning using combined GPS and GLONASS observations. Positioning 2007, 1, 13–22. [Google Scholar] [CrossRef] [Green Version]
- Cai, C.; Gao, Y. Modeling and assessment of combined GPS/GLONASS precise point positioning. GPS Solut. 2013, 17, 223–236. [Google Scholar] [CrossRef]
- Martín, A.; Anquela, A.; Capilla, R.; Berné, J. PPP technique analysis based on time convergence, repeatability, IGS products, different software processing, and GPS+ GLONASS constellation. J. Surv. Eng. 2011, 137, 99–108. [Google Scholar] [CrossRef]
- Li, P.; Zhang, X. Integrating GPS and GLONASS to accelerate convergence and initialization times of precise point positioning. GPS Solut. 2014, 18, 461–471. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Khachikyan, R.; Weber, G.; Langley, R.; Mervart, L.; Hugentobler, U. IGS-MGEX: Preparing the ground for multi-constellation GNSS science. Inside Gnss 2014, 9, 42–49. [Google Scholar]
- Xiaohong, Z.; Xingxing, L.; Pan, L. Review of GNSS PPP and its application. Acta Geod. Cartogr. Sin. 2017, 46, 1399. [Google Scholar] [CrossRef]
- Gabor, M.J.; Nerem, R.S. GPS Carrier Phase Ambiguity Resolution Using Satellite-Satellite Single Differences. In Proceedings of the 12th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1999), Nashville, TN, USA, 14–17 September 1999; pp. 1569–1578. [Google Scholar]
- Ge, M.; Gendt, G.; Rothacher, M.A.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Zhang, X.; Li, P.; Guo, F. Ambiguity resolution in precise point positioning with hourly data for global single receiver. Adv. Space Res. 2013, 51, 153–161. [Google Scholar] [CrossRef]
- Laurichesse, D.; Mercier, F.; Berthias, J.P.; Broca, P.; Cerri, L. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination. Navigation 2009, 56, 135–149. [Google Scholar] [CrossRef]
- Collins, P.; Bisnath, S.; Lahaye, F.; Héroux, P. Undifferenced GPS ambiguity resolution using the decoupled clock model and ambiguity datum fixing. NAVIGATION J. Inst. Navig. 2010, 57, 123–135. [Google Scholar] [CrossRef] [Green Version]
- Geng, J.; Meng, X.; Dodson, A.H.; Teferle, F.N. Integer ambiguity resolution in precise point positioning: Method comparison. J. Geod. 2010, 84, 569–581. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Gao, Y. A comparison of three PPP integer ambiguity resolution methods. GPS Solut. 2014, 18, 519–528. [Google Scholar] [CrossRef]
- Li, R.; Wang, N.; Li, Z.; Zhang, Y.; Wang, Z.; Ma, H. Precise orbit determination of BDS-3 satellites using B1C and B2a dual-frequency measurements. GPS Solut. 2021, 25, 95. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Liu, G.; Yuan, Y.; Zhou, F. BDS multi-frequency PPP ambiguity resolution with new B2a/B2b/B2a + b signals and legacy B1I/B3I signals. J. Geod. 2020, 94, 107. [Google Scholar] [CrossRef]
- Liang, Z.; Yang, H.; Yang, G.; Yao, Y.; Xu, C. Evaluation and analysis of real-time precise orbits and clocks products from different IGS analysis centers. Adv. Space Res. 2018, 61, 2942–2954. [Google Scholar] [CrossRef]
- Kouba, J. A Guide to Using International GNSS Service (IGS) Products. 2009. Available online: https://kb.igs.org/hc/en-us/articles/201271873-A-Guide-to-Using-the-IGS-Products (accessed on 14 October 2021).
- Hatch, R. The Synergism of GPS Code and Carrier Measurements. In Proceedings of the International Geodetic Symposium on Satellite Doppler Positioning, Las Cruces, NM, USA, 8–12 February 1982; pp. 1213–1231. [Google Scholar]
- Melbourne, W.G. The Case for Ranging in GPS-Based Geodetic Systems. In Proceedings of the First International Symposium on Precise Positioning with the Global Positioning System, Rockville, MD, USA, 15–19 April 1985; pp. 373–386. [Google Scholar]















| Processing Type | Correction Model |
|---|---|
| Satellite orbit error | Precise ephemeris products(CODE,15 min) |
| Satellite clock error | Precise clock products(CODE, 30 seconds) |
| Error caused by the rotation of the Earth | Erp products(CODE) |
| DCB | DCB product(CODE) |
| Tropospheric delay | Saastamoinen + GPT2w + Estimate |
| Ionospheric delay | IF model |
| PCO/PCV | IGS14 atx |
| Receiver clock error | Estimate |
| Phase wind-up | Model correction |
| Solid tide, extreme tide, and ocean tide | Model correction |
| Elevation mask angle | 7 |
| Stochastic model | Elevation model |
| Parameter estimation method | Kalman filter (constrained station coordinates) |
| Configuration of PC | Details |
|---|---|
| PC | Lenovo ThinkStation P340 |
| CPU | Intel Core i9-10900 @ 2.80GHz |
| GPU | NVIDIA Quadro P400 |
| Memory | 16G |
| Mainboard | Lenovo 1048 |
| Hard Disk Drive | 256G SSD + 1T HDD |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, K.; Dang, Y.; Xu, C.; Gu, S. An Improved Fast Estimation of Satellite Phase Fractional Cycle Biases. Remote Sens. 2022, 14, 334. https://doi.org/10.3390/rs14020334
Qi K, Dang Y, Xu C, Gu S. An Improved Fast Estimation of Satellite Phase Fractional Cycle Biases. Remote Sensing. 2022; 14(2):334. https://doi.org/10.3390/rs14020334
Chicago/Turabian StyleQi, Ke, Yamin Dang, Changhui Xu, and Shouzhou Gu. 2022. "An Improved Fast Estimation of Satellite Phase Fractional Cycle Biases" Remote Sensing 14, no. 2: 334. https://doi.org/10.3390/rs14020334
APA StyleQi, K., Dang, Y., Xu, C., & Gu, S. (2022). An Improved Fast Estimation of Satellite Phase Fractional Cycle Biases. Remote Sensing, 14(2), 334. https://doi.org/10.3390/rs14020334





