LiDAR-Based Hatch Localization
Abstract
:1. Introduction
2. Related Work
2.1. Sensor Choice
2.2. LiDAR Transloading Literature
2.3. Plane Extraction Literature
2.4. Point Cloud Rasterization Literature
3. Preliminary Information
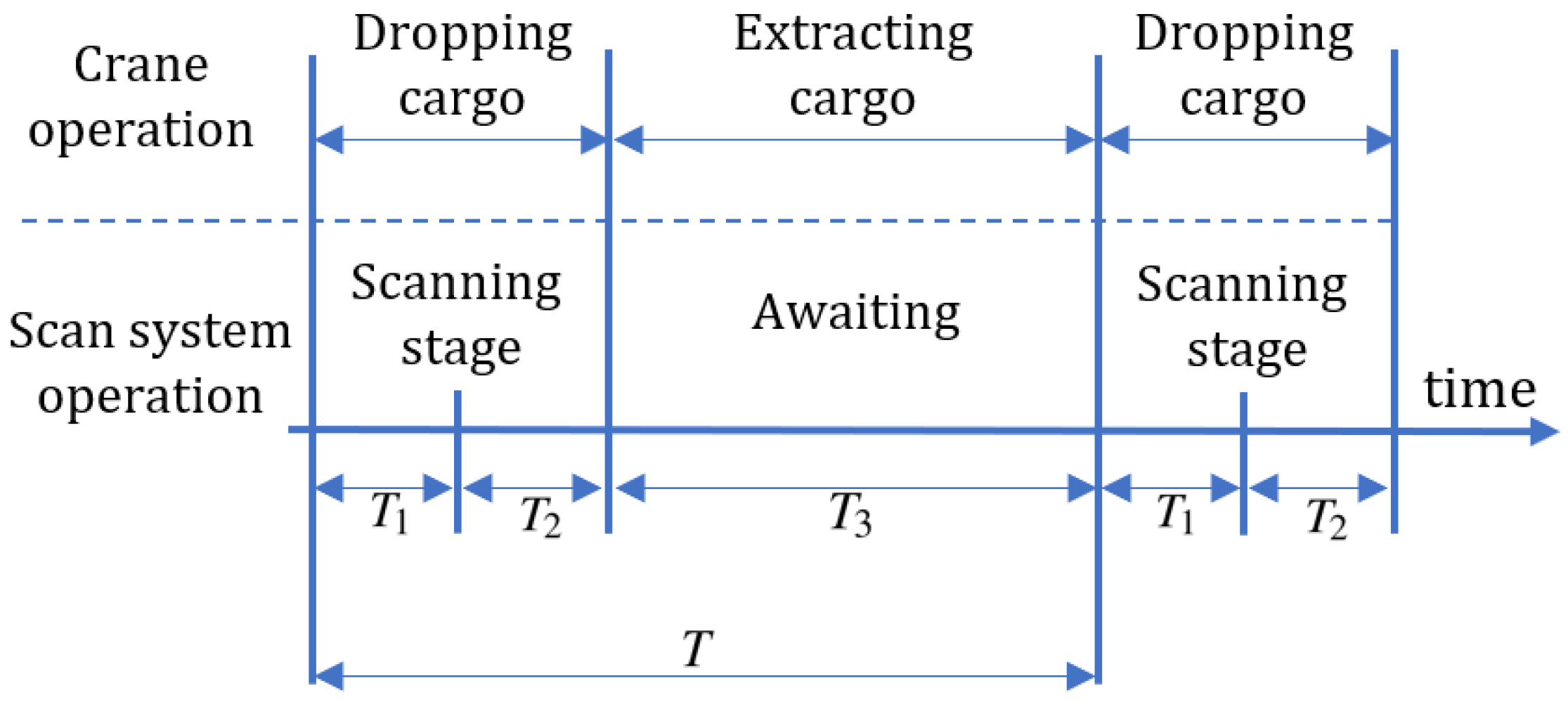
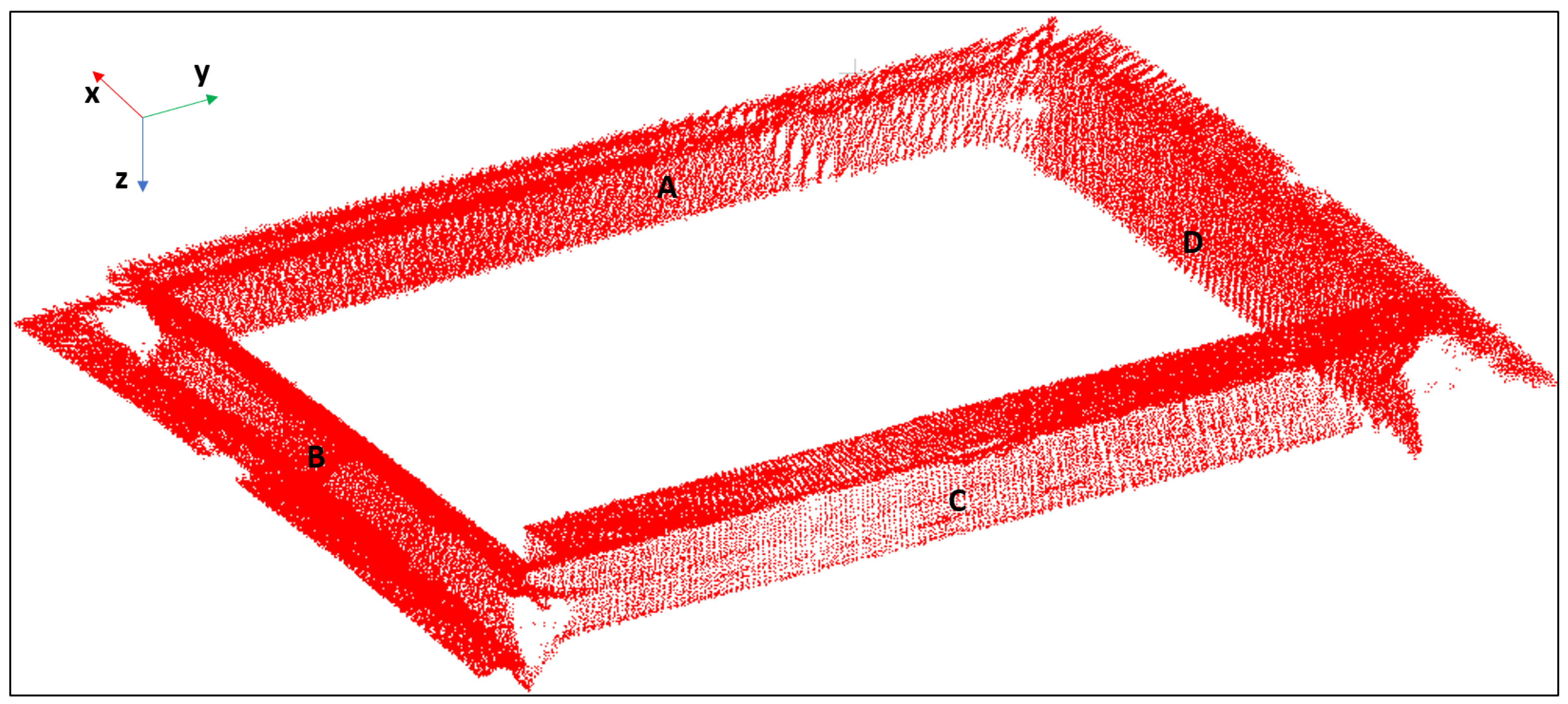
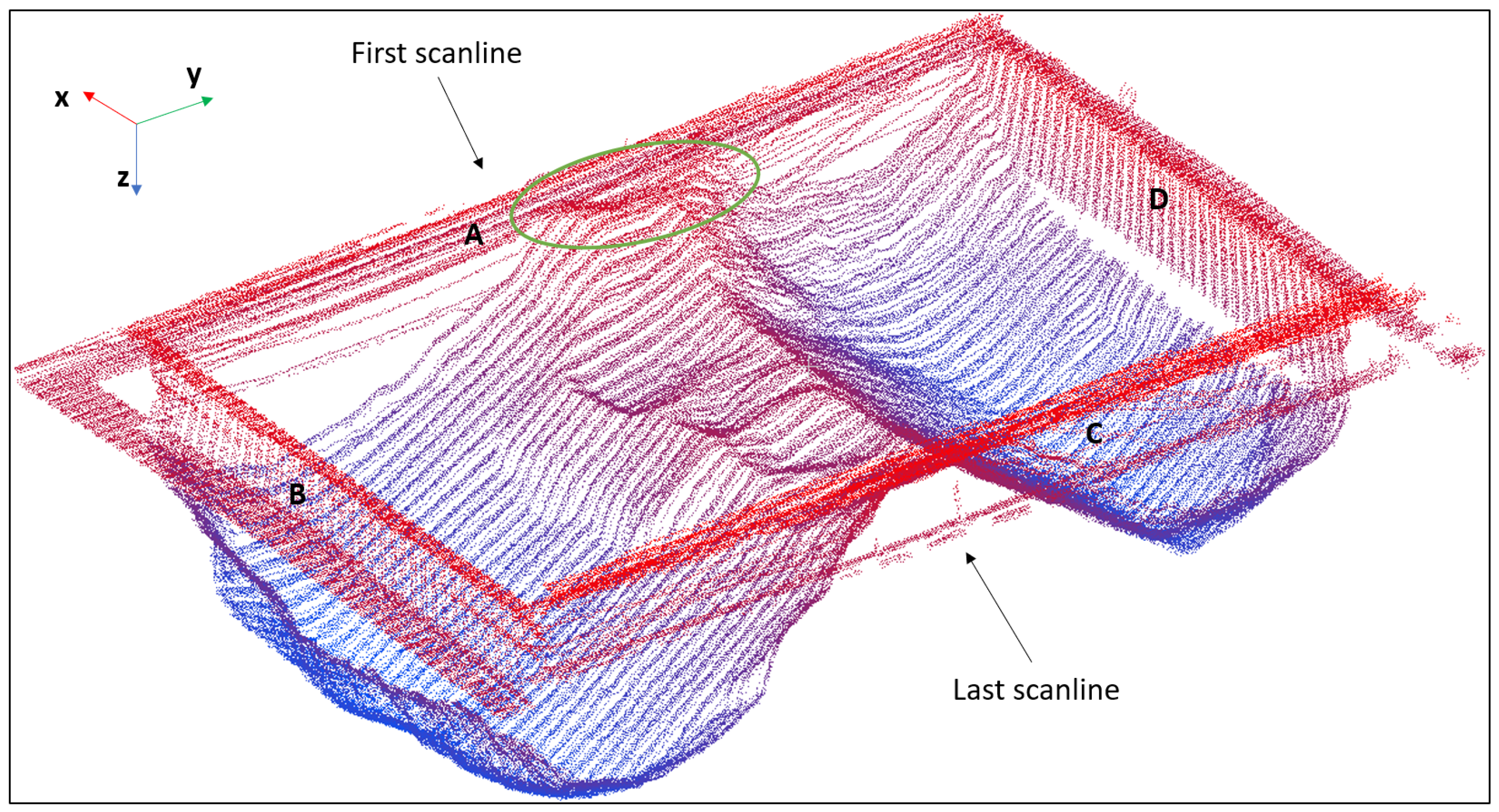
3.1. Scanning System Hardware
3.2. Frames of Reference
- World frame: The W-frame origin is a fixed point in the transloading field. The axes’ directions are selected to be parallel to the expected directions of the hatch edges. The cross-product of the orthogonal x and y axes defines a third vector N. By design, this vector N is expected to be approximately parallel to the normal part of the plane defined by the corners of the hatch. Encoders are installed on the carrier machine to measure the x and y coordinates of the P-frame origin relative to the W-frame origin (i.e., scanning system position) in the W-frame. Herein, the hatch localization results from each cycle are presented in W-frame.
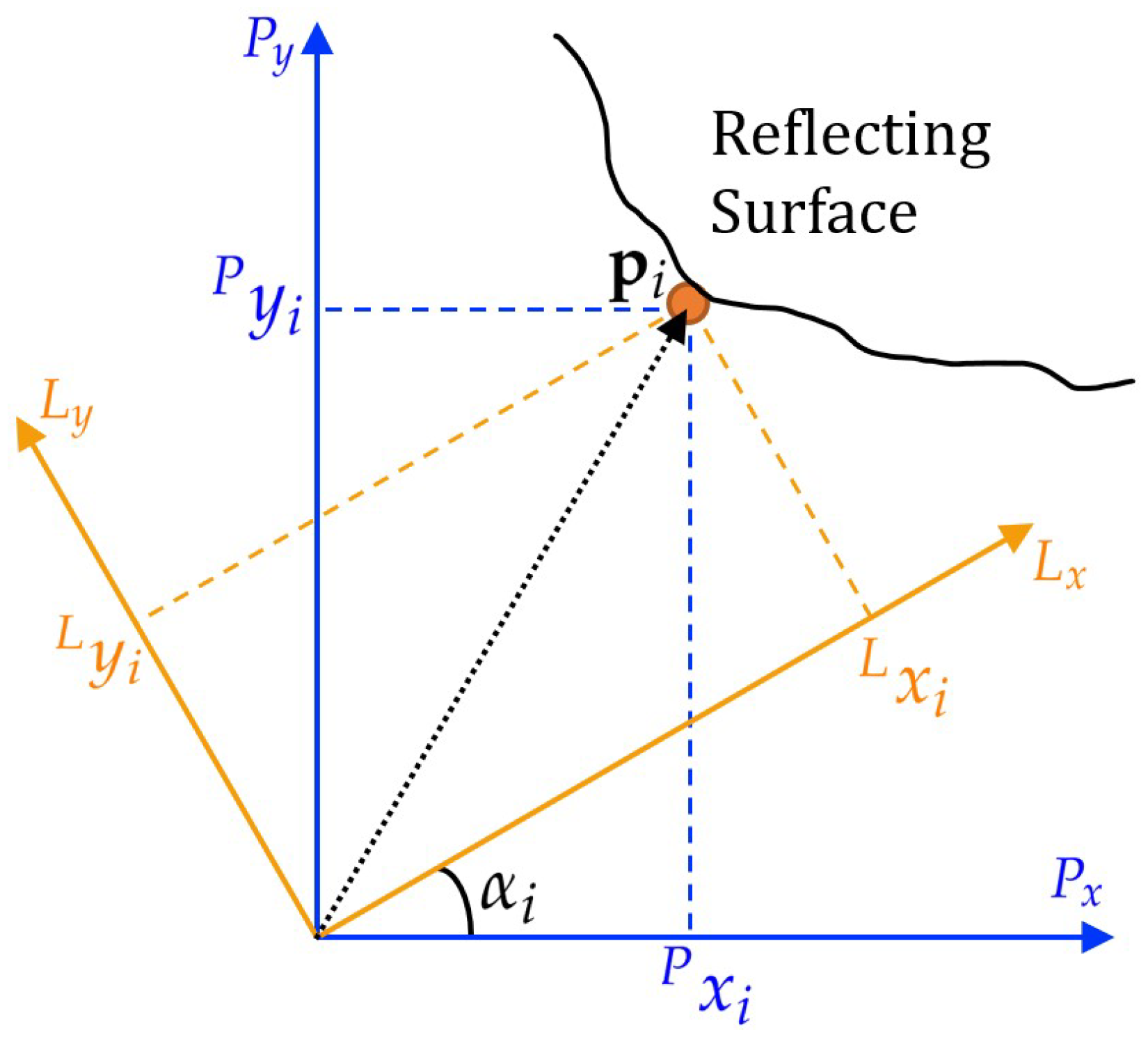
- PT frame: The P-origin is at the rotational center of the PT. The P-frame axes are fixed relative to the PT base. These axes do not rotate when the PT changes the pan angle () and tilt angle (). The P-frame axes are defined to be aligned to the W-frame axes. Herein, the input point cloud from each cycle is accumulated and processed in the P-frame.
- LiDAR frame: The L-frame is attached to the LiDAR. Its origin is at the effective measurement point of the LiDAR. The axes directions are manufacturer-specified.
3.3. Data Acquisition
4. Problem Statement
4.1. Objective and Notation
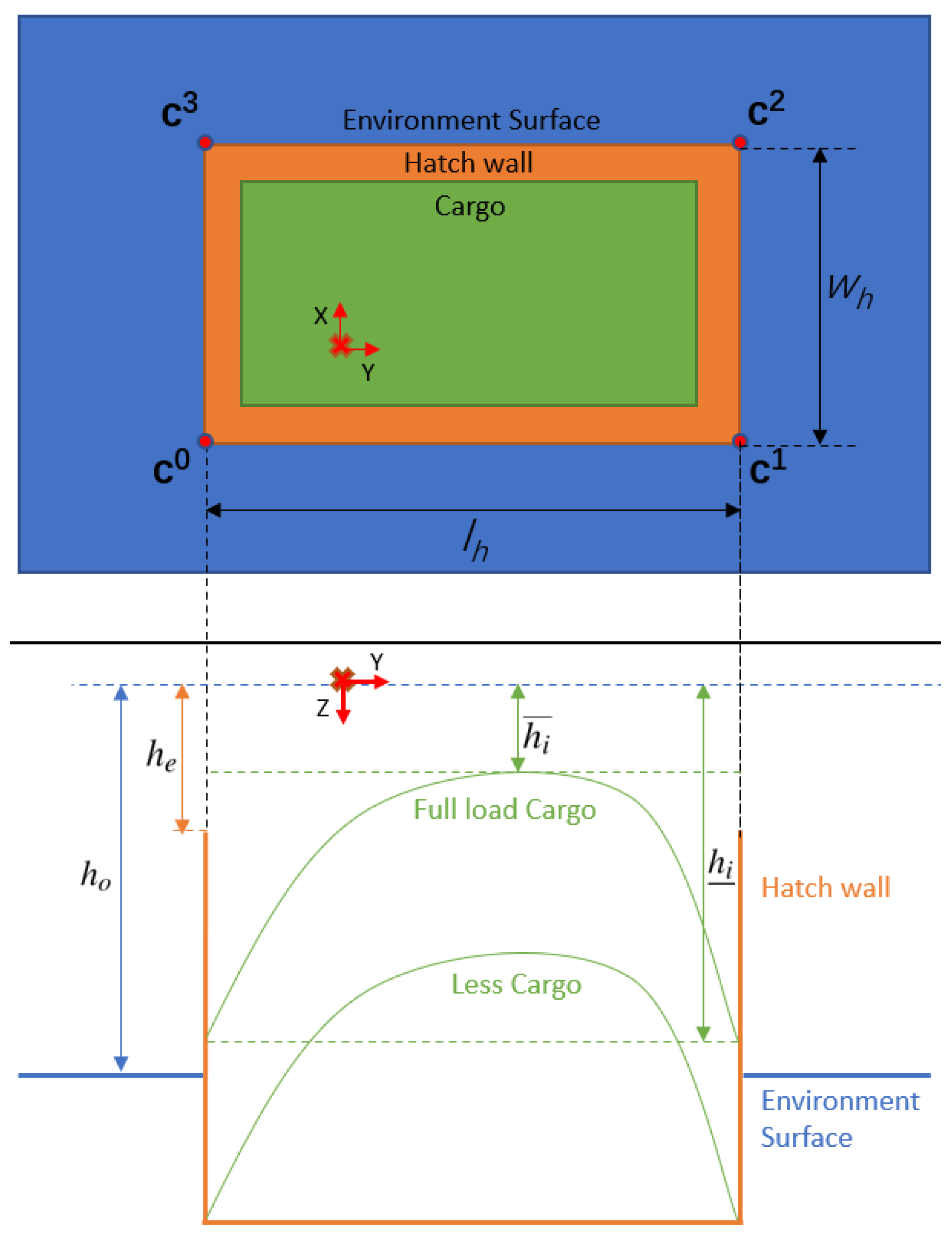
- The hatch is nearly empty, while the environment surface is low (i.e., and ), e.g., the red train car in Figure 1.
- The hatch is nearly (or beyond) full, while the environment surface is low (i.e., and ), e.g., the green train car in Figure 1.
- The hatch is nearly (or overly) full, while the environment surface is high (i.e., and ).
4.2. Assumptions
- The P-frame x–y plane is approximately parallel with the plane containing the top of the hatch. This is equivalent to stating that the P-frame z-axis points approximately perpendicular to the plane containing the top of the hatch (e.g., into the hatch).
- The P-frame origin, which is defined by the scanning system location, is within the x–y edges of the hatch so that it can scan all four hatch edge planes.
- Each hatch edge is a segment of a plane. Each plane defining an x-edge (y-edge) has a normal pointing approximately parallel to the P-frame y-axis (x-axis). This implies that the edges of the hatch rectangle are approximately aligned to the P-frame x and y axes. Therefore, the outline of the hatch in the P-frame x–y view is rectangular.
- The z-extent of the hatch edge plane is deep enough that the scanning system generates enough reflecting points on the hatch edge planes.
- Upper bounds and are known for the hatch length and width, respectively.
4.3. Subproblems
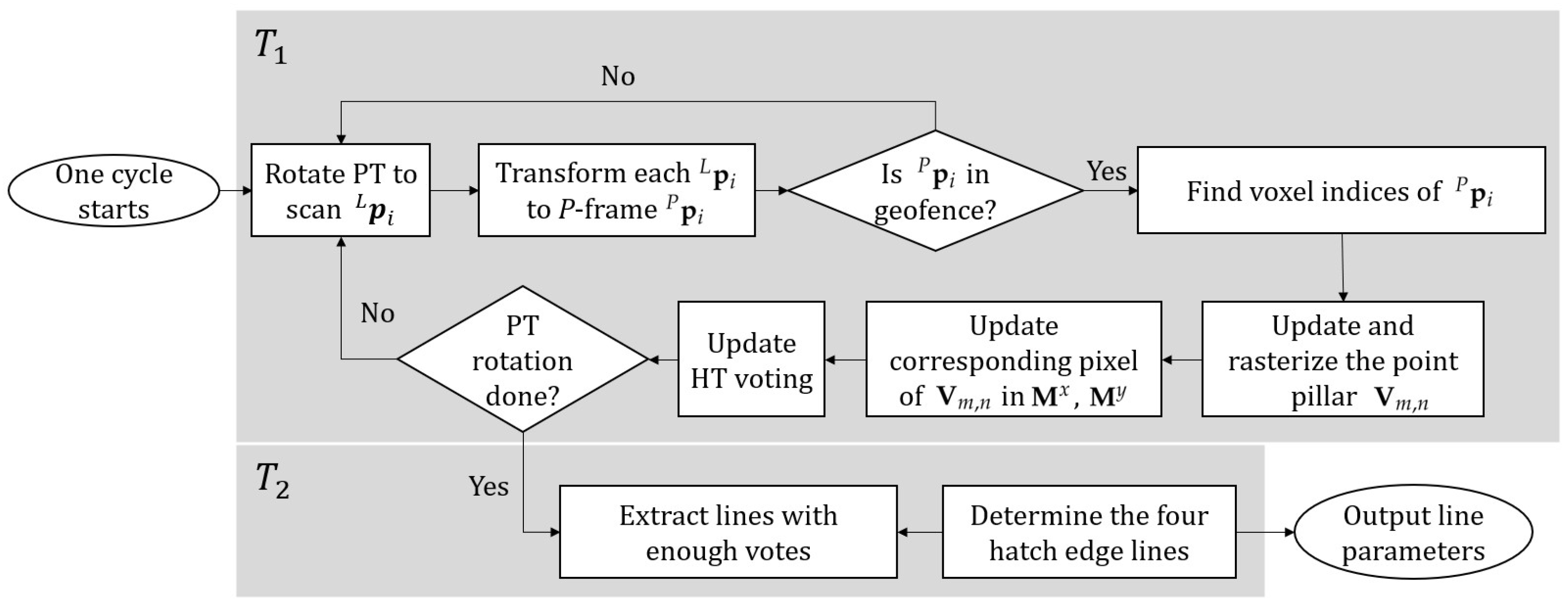
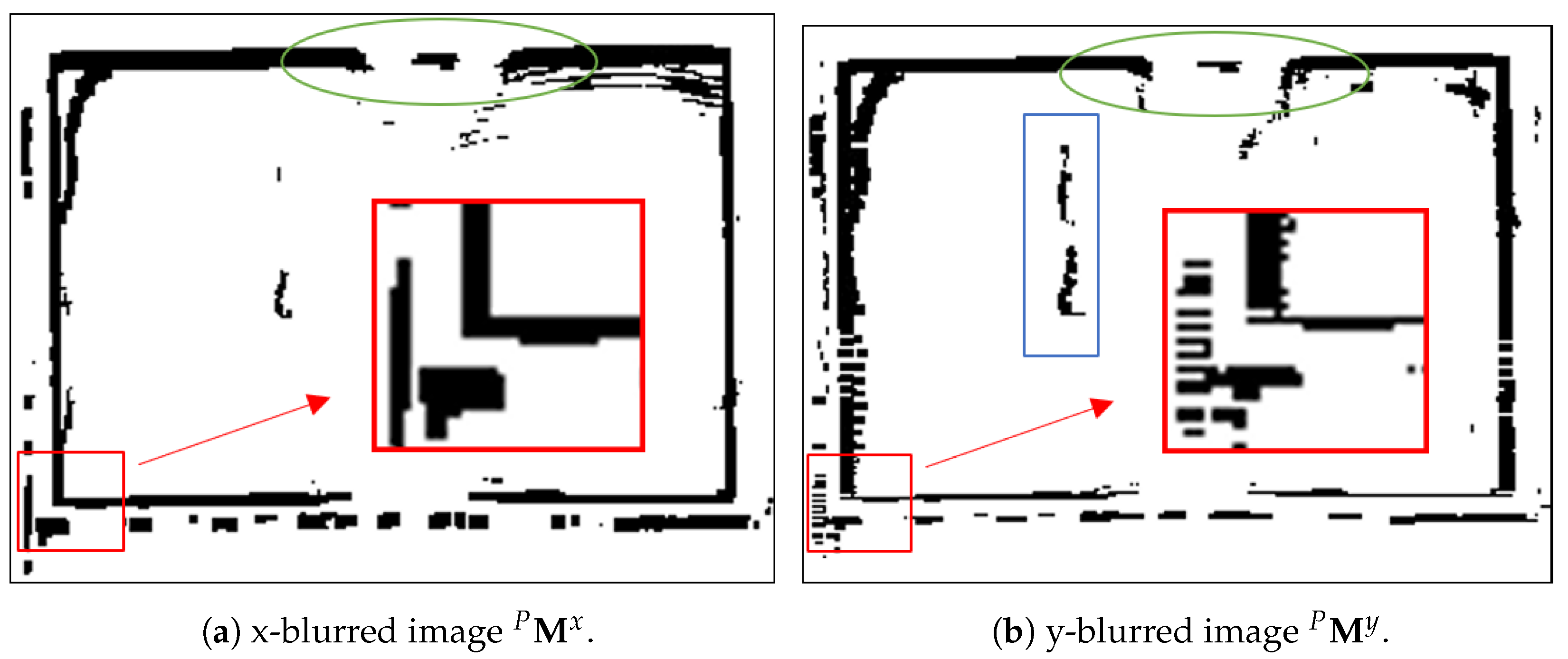
- Voxelization: Organize into occupancy matrices , , and . Each is defined as a 3D binary matrix with rows, columns, and layers. The physical extent of the three voxel structures can be determined by either the extent of or by a smaller geofence. Each entry of indicates whether () or not () any point of is located in the volume determined by the corresponding voxel. Herein, , and will be referred to as the occupancy matrix, and the x-blurred and y-blurred occupancy matrices. The blurred occupancy matrices have utility for improving performance in image-based edge detection [36,37]. Point cloud voxelization is discussed further in Section 5.1.
- Rasterization: Convert and from 3D occupancy matrices to 2D occupancy matrices (i.e., images) , and , such that the x and y coordinates of the hatch edges can be found by processing and . Rasterization is discussed further in Section 5.2.
- Hatch Edge extraction: Process and to extract lines approximately parallel to the P-frame x-axis and y-axis, and then calculate the edge position and the hatch size from the extracted lines. Hatch edge extraction is discussed further in Section 5.3.
5. Methodology
5.1. Voxelization
5.2. Rasterization
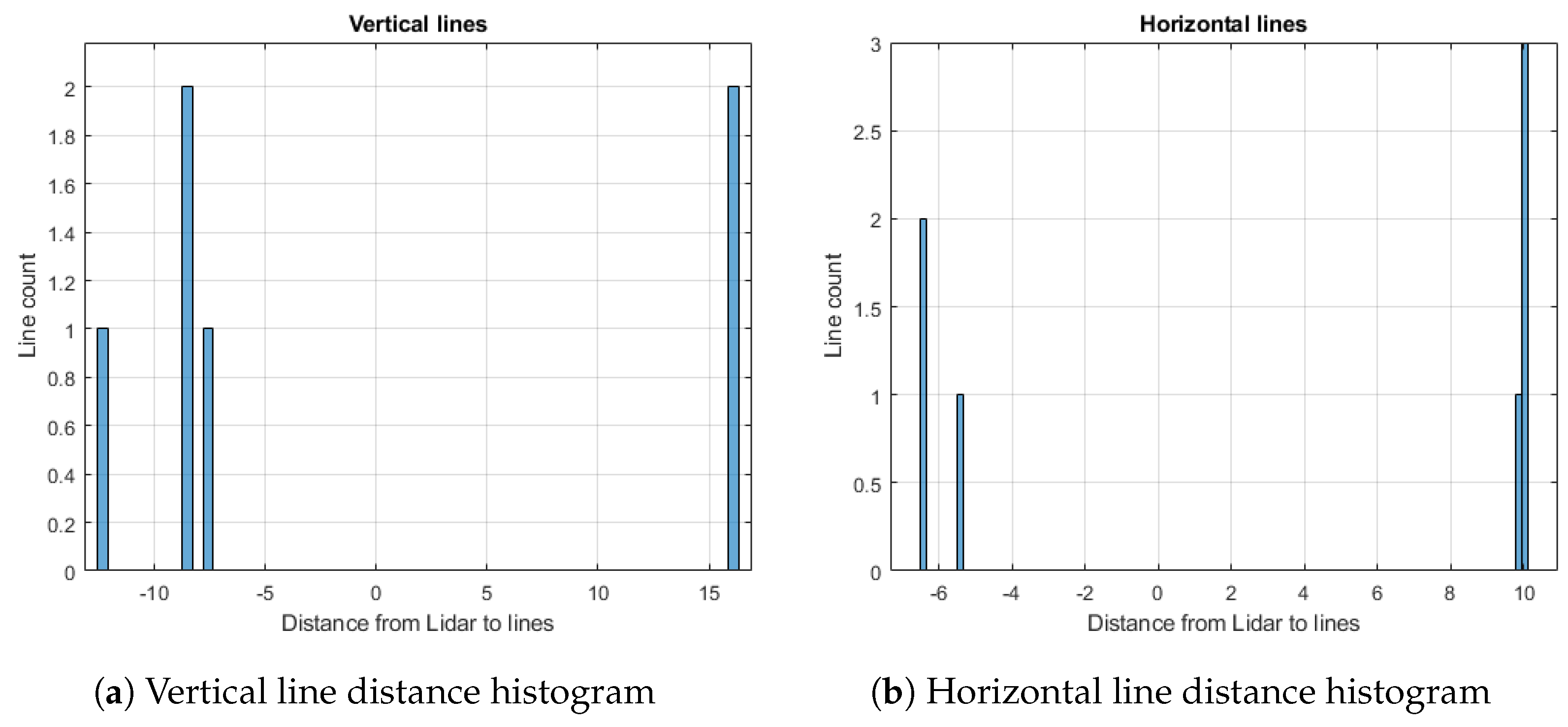
5.3. Hatch Edge Extraction
5.4. Summary of Constant Parameters
- Geofence parameters, , , , , : These constants are used in Equation (1) to define the geofence. The purpose is to remove points that are not relevant while retaining all hatch edge points even as the hatch moves between cycles. The values are user-defined based on local knowledge of hatch motion.
- Cell size: The cell size is used in the definition of the three occupancy matrices , , and . It determines the resolution of these voxelized point clouds. For a given point cloud region, the memory requirements of each occupancy matrix scales cubically with . Larger structures also require longer processing time. The cell size needs to be small enough to meet the localization accuracy requirement and large enough to be comparable with the accuracy of the raw data. Herein, the cell size is 5 cm through all experiments, which is comparable with the accuracy of the raw LiDAR range data.
- Parameters for gaps: : The purpose of these parameters is to improve edge extraction performance [36,37]. These constants are used in Section 5.1 and Section 5.2.
- Hatch edge plane depth lower bound : This constant is used in Equation (6) to check whether each occupancy vector (i.e., pillar) is deep enough in the z-direction to be regarded as a piece of a hatch edge plane. It needs to be large enough to reject small plane segments and small enough that hatch edge points are recognized.
- Hough transform angular search range : This constant is used in Section 5.3 to limit the HT angular search to the small range required due to Assumption 3. This constant must be large enough to account for misalignment of the hatch edges with the P-frame x and y axes. If it is too small, hatch edges could be missed. As it is increased, the HT computation time will increase.
6. Experimental Results
6.1. Scanning Patterns
6.1.1. Circular Scanning: Pan Rotation
6.1.2. Swipe Scanning: Tilt Rotation
6.1.3. Scanning Pattern Comparison
6.2. Processing of One Scan
6.3. Assessment Metrics
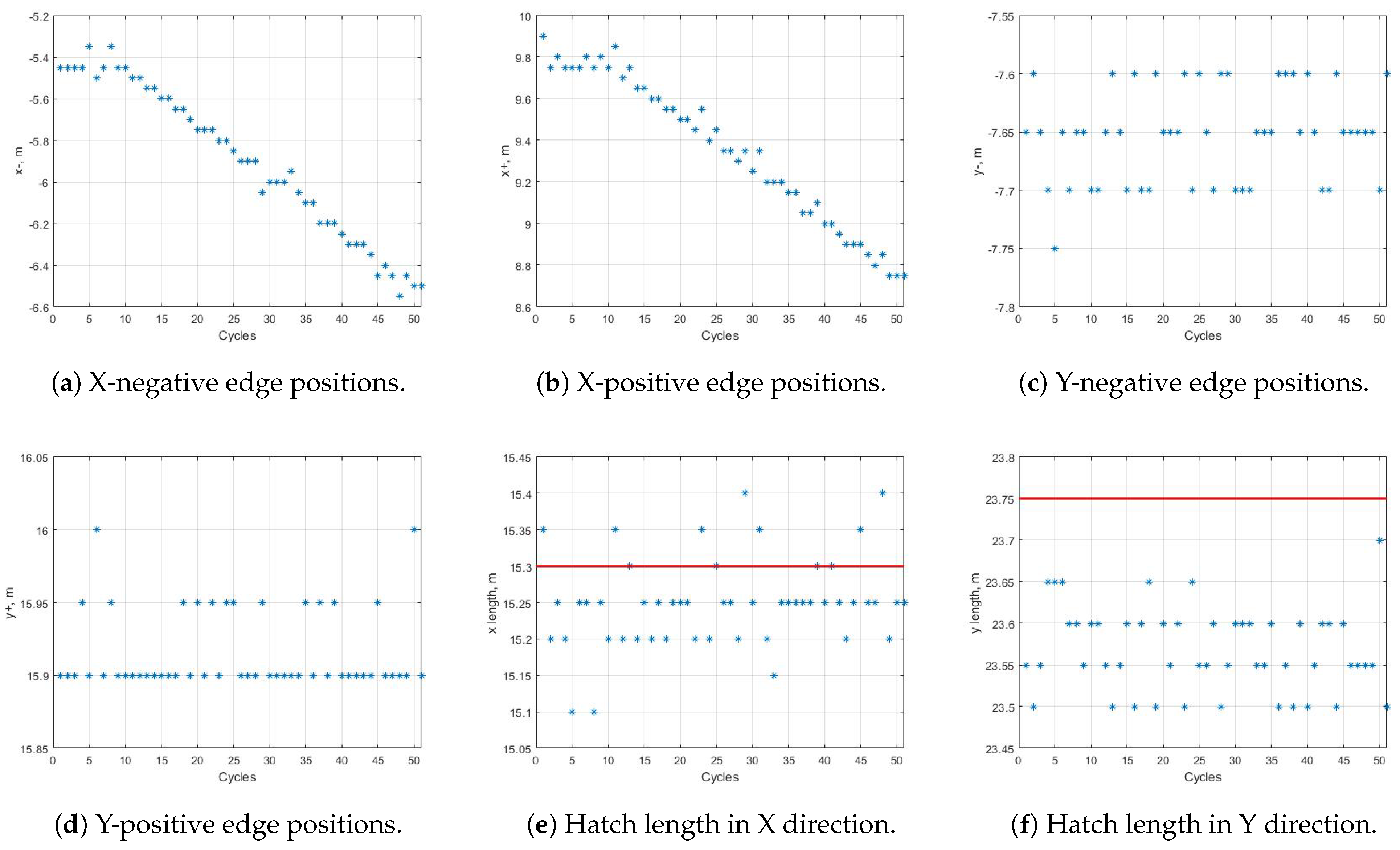
6.4. Tracking Motion over Sequential Scans
6.5. Statistical Results over Multiple Datasets
7. Discussion
7.1. PT Pattern Determination
7.2. Cargo-Hatch Overlap
7.3. Hatch Size Determination Strategy
8. Conclusions
- The case of an exactly full hatch is rare in transloading. When it occurs, it causes severe cargo-hatch overlap as discussed in Section 7.2. Currently, manual unloading proceeds until enough of the hatch edge is exposed. Potential ideas to solve this special case include the detection of point cloud features (e.g., surface roughness or curvature) that distinguish cargo from hatch or augmentation of an additional sensor (e.g., camera).
- The duration of a transloading task is usually long; therefore, it is interesting to develop the algorithm to filter across time as mentioned in Section 7.3.
- Both the development and the use of an active acoustic sensor able to resolve the range and angle of points along a reflecting surface relative to the sensor would be very interesting.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mi, C.; Zhang, Z.W.; Huang, Y.F.; Shen, Y. A fast automated vision system for container corner casting recognition. J. Mar. Sci. Technol. 2016, 24, 54–60. [Google Scholar] [CrossRef]
- Shen, Y.; Mi, W.; Zhang, Z. A Positioning Lockholes of Container Corner Castings Method Based on Image Recognition. Pol. Marit. Res. 2017, 24, 95–101. [Google Scholar] [CrossRef] [Green Version]
- Vaquero, V.; Repiso, E.; Sanfeliu, A. Robust and Real-Time Detection and Tracking of Moving Objects with Minimum 2D LiDAR Information to Advance Autonomous Cargo Handling in Ports. Sensors 2018, 19, 107. [Google Scholar] [CrossRef] [Green Version]
- Yoon, H.J.; Hwang, Y.C.; Cha, E.Y. Real-time container position estimation method using stereo vision for container auto-landing system. In Proceedings of the International Conference on Control, Automation and Systems, Gyeonggi-do, Korea, 27–30 October 2010; pp. 872–876. [Google Scholar] [CrossRef]
- Mi, C.; Huang, Y.; Liu, H.; Shen, Y.; Mi, W. Study on Target Detection & Recognition Using Laser 3D Vision Systems for Automatic Ship Loader. Sens. Transducers 2013, 158, 436–442. [Google Scholar]
- Mi, C.; Shen, Y.; Mi, W.; Huang, Y. Ship Identification Algorithm Based on 3D Point Cloud for Automated Ship Loaders. J. Coast. Res. 2015, 73, 28–34. [Google Scholar] [CrossRef]
- Miao, Y.; Li, C.; Li, Z.; Yang, Y.; Yu, X. A novel algorithm of ship structure modeling and target identification based on point cloud for automation in bulk cargo terminals. Meas. Control. 2021, 54, 155–163. [Google Scholar] [CrossRef]
- Lang, A.H.; Vora, S.; Caesar, H.; Zhou, L.; Yang, J.; Beijbom, O. PointPillars: Fast Encoders for Object Detection From Point Clouds. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 12689–12697. [Google Scholar] [CrossRef] [Green Version]
- Hackel, T.; Wegner, J.D.; Schindler, K. FAST SEMANTIC SEGMENTATION OF 3D POINT CLOUDS WITH STRONGLY VARYING DENSITY. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, III-3, 177–184. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Olson, E.B. A General Purpose Feature Extractor for Light Detection and Ranging Data. Sensors 2010, 10, 10356–10375. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Li, B.; Jiang, Y.; Wen, C.y. A Camera-Based Target Detection and Positioning UAV System for Search and Rescue (SAR) Purposes. Sensors 2016, 16, 1778. [Google Scholar] [CrossRef]
- Symington, A.; Waharte, S.; Julier, S.; Trigoni, N. Probabilistic target detection by camera-equipped UAVs. In Proceedings of the International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 4076–4081. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Liu, J.; Wang, C.; Luo, B.; Zhang, C. DV-LOAM: Direct Visual LiDAR Odometry and Mapping. Remote Sens. 2021, 13, 3340. [Google Scholar] [CrossRef]
- Hammer, M.; Hebel, M.; Borgmann, B.; Laurenzis, M.; Arens, M. Potential of LiDAR sensors for the detection of UAVs. In Proceedings of the Laser Radar Technology and Applitions XXIII, Orlando, FL, USA, 17–18 April 2018; p. 4. [Google Scholar] [CrossRef]
- Rachman, A.A. 3D-LIDAR Multi Object Tracking for Autonomous Driving: Multi-target Detection and Tracking under Urban Road Uncertainties. Master’s Thesis, TU Delft Mechanical, Maritime and Materials Engineering, Esbjerg, Danmark, 2017. [Google Scholar]
- Tarsha Kurdi, F.; Gharineiat, Z.; Campbell, G.; Awrangjeb, M.; Dey, E.K. Automatic Filtering of Lidar Building Point Cloud in Case of Trees Associated to Building Roof. Remote Sens. 2022, 14, 430. [Google Scholar] [CrossRef]
- Ren, Z.; Wang, L. Accurate Real-Time Localization Estimation in Underground Mine Environments Based on a Distance-Weight Map (DWM). Sensors 2022, 22, 1463. [Google Scholar] [CrossRef]
- Xue, G.; Wei, J.; Li, R.; Cheng, J. LeGO-LOAM-SC: An Improved Simultaneous Localization and Mapping Method Fusing LeGO-LOAM and Scan Context for Underground Coalmine. Sensors 2022, 22, 520. [Google Scholar] [CrossRef] [PubMed]
- Bocanegra, J.A.; Borelli, D.; Gaggero, T.; Rizzuto, E.; Schenone, C. A novel approach to port noise characterization using an acoustic camera. Sci. Total. Environ. 2022, 808, 151903. [Google Scholar] [CrossRef]
- Remmas, W.; Chemori, A.; Kruusmaa, M. Diver tracking in open waters: A low-cost approach based on visual and acoustic sensor fusion. J. Field Robot. 2021, 38, 494–508. [Google Scholar] [CrossRef]
- Svanstrom, F.; Englund, C.; Alonso-Fernandez, F. Real-Time Drone Detection and Tracking With Visible, Thermal and Acoustic Sensors. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 7265–7272. [Google Scholar] [CrossRef]
- Gong, L.; Zhang, Y.; Li, Z.; Bao, Q. Automated road extraction from LiDAR data based on intensity and aerial photo. In Proceedings of the 3rd International Congress on Image and Signal Processing, Yantai, China, 16–18 October 2010; pp. 2130–2133. [Google Scholar] [CrossRef]
- Raj, T.; Hashim, F.H.; Huddin, A.B.; Ibrahim, M.F.; Hussain, A. A Survey on LiDAR Scanning Mechanisms. Electronics 2020, 9, 741. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Yang, L.; Li, Y.; Li, X.; Meng, Z.; Luo, H. Efficient plane extraction using normal estimation and RANSAC from 3D point cloud. Comput. Stand. Interfaces 2022, 82, 103608. [Google Scholar] [CrossRef]
- Adams, R.; Bischof, L. Seeded region growing. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 641–647. [Google Scholar] [CrossRef] [Green Version]
- Ballard, D.H. Generalizing the Hough transform to detect arbitrary shapes. Pattern Recognit. 1981, 13, 111–122. [Google Scholar] [CrossRef] [Green Version]
- Duda, R.O.; Hart, P.E. Use of the Hough transformation to detect lines and curves in pictures. Commun. ACM 1972, 15, 11–15. [Google Scholar] [CrossRef]
- Hulik, R.; Spanel, M.; Smrz, P.; Materna, Z. Continuous plane detection in point-cloud data based on 3D Hough Transform. J. Vis. Commun. Image Represent. 2014, 25, 86–97. [Google Scholar] [CrossRef]
- Choi, S.; Kim, T.; Yu, W. Performance Evaluation of RANSAC Family. In Proceedings of the British Machine Vision Conference, London, UK, 7–10 September 2009; pp. 81.1–81.12. [Google Scholar] [CrossRef] [Green Version]
- Vo, A.V.; Truong-Hong, L.; Laefer, D.F.; Bertolotto, M. Octree-based region growing for point cloud segmentation. ISPRS J. Photogramm. Remote Sens. 2015, 104, 88–100. [Google Scholar] [CrossRef]
- Zhan, Q.; Liang, Y.; Xiao, Y. Color-based segmentation of point clouds. Laser Scanning 2009, 38, 155–161. [Google Scholar]
- Tarsha-Kurdi, F.; Landes, T.; Grussenmeyer, P. Hough-transform and extended ransac algorithms for automatic detection of 3D building roof planes from Lidar data. In Proceedings of the ISPRS Workshop on Laser Scanning and SilviLaser, Espoo, Finland, 12–14 September 2007; Volume 36, pp. 407–412. [Google Scholar]
- Ali, W.; Liu, P.; Ying, R.; Gong, Z. A Feature Based Laser SLAM Using Rasterized Images of 3D Point Cloud. IEEE Sens. J. 2021, 21, 24422–24430. [Google Scholar] [CrossRef]
- Guiotte, F.; Pham, M.T.; Dambreville, R.; Corpetti, T.; Lefevre, S. Semantic Segmentation of LiDAR Points Clouds: Rasterization Beyond Digital Elevation Models. IEEE Geosci. Remote Sens. Lett. 2020, 17, 2016–2019. [Google Scholar] [CrossRef] [Green Version]
- Basu, M. Gaussian-based edge-detection methods-a survey. IEEE Trans. Syst. Man Cybern. C 2002, 32, 252–260. [Google Scholar] [CrossRef] [Green Version]
- Elder, J.; Zucker, S. Local scale control for edge detection and blur estimation. IEEE Trans. Pattern Anal. Machine Intell. 1998, 20, 699–716. [Google Scholar] [CrossRef]
- Maturana, D.; Scherer, S. VoxNet: A 3D Convolutional Neural Network for real-time object recognition. In Proceedings of the International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 Septembe–2 October 2015; pp. 922–928. [Google Scholar] [CrossRef]
- Xu, Y.; Tong, X.; Stilla, U. Voxel-based representation of 3D point clouds: Methods, applications, and its potential use in the construction industry. Autom. Constr. 2021, 126, 103675. [Google Scholar] [CrossRef]



| Dataset | # Cycle | Hatch- Cargo Gap (m) | Hatch Size (m) | Hatch Edge Position (m) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X | Y | |||||||||||
| ASH | MSH | HSTD | ASH | MSH | HSTD | X- PSTD | X+ PSTD | Y- PSTD | Y+ PSTD | |||
| 1 | 6 | 7.15 | 0.03 | 0.05 | 0.03 | −0.01 | −0.05 | 0.02 | 0.03 | 0.00 | 0.03 | 0.03 |
| 2 | 7 | 7.15 | −0.22 | −0.30 | 0.06 | −0.21 | −0.25 | 0.05 | 0.03 | 0.05 | 0.02 | 0.04 |
| 3 | 10 | 8.35 | 0.03 | 0.08 | 0.03 | 0.07 | 0.10 | 0.03 | 0.03 | 0.02 | 0.03 | 0.00 |
| 4 | 12 | 5.45 | 0.03 | 0.10 | 0.03 | −0.05 | −0.10 | 0.03 | 0.03 | 0.01 | 0.02 | 0.03 |
| 5 | 13 | OL | −0.03 | −0.20 | 0.12 | −0.17 | −0.25 | 0.06 | 0.08 | 0.07 | 0.04 | 0.03 |
| 6 | 14 | 4.15 | −0.21 | −0.32 | 0.07 | −0.14 | −0.16 | 0.03 | 0.05 | 0.03 | 0.02 | 0.02 |
| 7 | 27 | 6.20 | −0.27 | −0.34 | 0.05 | −0.17 | −0.25 | 0.06 | 0.07 | 0.05 | 0.06 | 0.05 |
| 8 | 29 | 12.05 | −0.09 | −0.14 | 0.06 | 0.06 | 0.10 | 0.03 | 0.04 | 0.03 | 0.03 | 0.02 |
| 9 | 34 | 9.40 | −0.01 | −0.15 | 0.05 | 0.03 | 0.10 | 0.03 | 0.05 | 0.02 | 0.03 | 0.03 |
| 10 | 37 | 5.25 | 0.03 | 0.09 | 0.04 | 0.10 | 0.14 | 0.02 | 0.03 | 0.03 | 0.02 | 0.01 |
| 11 | 39 | 6.35 | −0.22 | −0.27 | 0.03 | 0.18 | 0.25 | 0.04 | 0.03 | 0.03 | 0.03 | 0.03 |
| 12 | 48 | 10.15 | 0.00 | 0.03 | 0.03 | 0.14 | 0.25 | 0.04 | 0.03 | 0.04 | 0.03 | 0.03 |
| 13 | 51 | 6.55 | −0.06 | −0.17 | 0.05 | −0.03 | −0.10 | 0.03 | 0.03 | 0.04 | 0.04 | 0.03 |
| 14 | 53 | 6.05 | −0.15 | −0.27 | 0.07 | −0.18 | −0.24 | 0.04 | 0.09 | 0.06 | 0.02 | 0.04 |
| 15 | 13 | 4.35 | 0.08 | 0.05 | 0.03 | −0.01 | −0.05 | 0.03 | 0.02 | 0.02 | 0.03 | 0.02 |
| 16 | 16 | 10.85 | 0.06 | 0.20 | 0.09 | 0.06 | 0.10 | 0.06 | 0.03 | 0.09 | 0.04 | 0.08 |
| 17 | 16 | 7.10 | −0.04 | −0.07 | 0.03 | 0.02 | 0.10 | 0.04 | 0.03 | 0.02 | 0.05 | 0.02 |
| 18 | 17 | 11.95 | 0.05 | 0.10 | 0.03 | 0.05 | 0.10 | 0.04 | 0.03 | 0.03 | 0.03 | 0.02 |
| 19 | 20 | OL | −0.07 | −0.25 | 0.11 | −0.15 | −0.25 | 0.05 | 0.09 | 0.05 | 0.03 | 0.03 |
| 20 | 23 | 7.00 | −0.21 | −0.27 | 0.03 | −0.14 | −0.20 | 0.05 | 0.03 | 0.03 | 0.04 | 0.04 |
| 21 | 29 | 6.10 | −0.09 | −0.16 | 0.04 | −0.02 | −0.06 | 0.03 | 0.04 | 0.03 | 0.02 | 0.02 |
| 22 | 29 | 8.45 | −0.01 | −0.05 | 0.03 | −0.06 | −0.10 | 0.04 | 0.06 | 0.06 | 0.06 | 0.04 |
| 23 | 32 | 6.30 | 0.04 | 0.10 | 0.05 | −0.01 | 0.10 | 0.04 | 0.03 | 0.03 | 0.03 | 0.03 |
| 24 | 33 | 8.30 | −0.05 | −0.12 | 0.04 | 0.04 | 0.11 | 0.03 | 0.04 | 0.03 | 0.02 | 0.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z.; Liu, X.; Ma, M.; Wu, G.; Farrell, J.A. LiDAR-Based Hatch Localization. Remote Sens. 2022, 14, 5069. https://doi.org/10.3390/rs14205069
Jiang Z, Liu X, Ma M, Wu G, Farrell JA. LiDAR-Based Hatch Localization. Remote Sensing. 2022; 14(20):5069. https://doi.org/10.3390/rs14205069
Chicago/Turabian StyleJiang, Zeyi, Xuqing Liu, Mike Ma, Guanlin Wu, and Jay A. Farrell. 2022. "LiDAR-Based Hatch Localization" Remote Sensing 14, no. 20: 5069. https://doi.org/10.3390/rs14205069
APA StyleJiang, Z., Liu, X., Ma, M., Wu, G., & Farrell, J. A. (2022). LiDAR-Based Hatch Localization. Remote Sensing, 14(20), 5069. https://doi.org/10.3390/rs14205069







