Nonlinear Unmixing via Deep Autoencoder Networks for Generalized Bilinear Model
Abstract
:1. Introduction
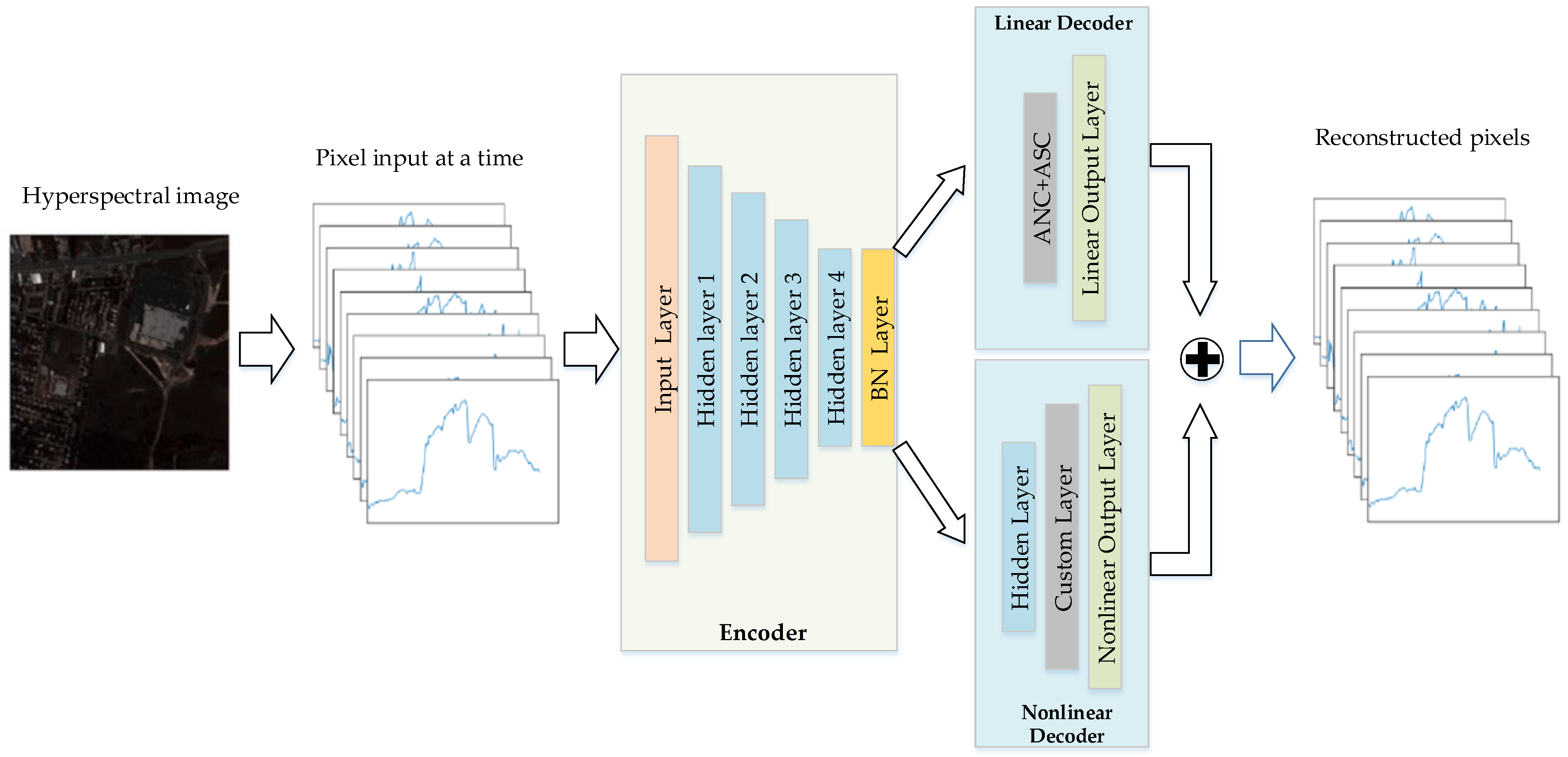
- Inspired by the widely used autoencoder network, we design a new deep autoencoder network structure based on the GBM, to achieve nonlinear unmixing. The deep encoder of the autoencoder is utilized to extract features. In the decoder part, the GBM is used to divide the decoder into a linear part and a nonlinear part. For the linear part of the decoder, we design a specific network layer to meet the constraints of ASC and ANC. For the nonlinear part of the decoder, the coefficients of nonlinear mixing terms are determined by a set of parameters, which can be learned during network training.
- To avoid overfitting, some regular constraint terms based on prior knowledge are added to the loss function. At the same time, we borrow some ideas from BCD’s (block-coordinate decent) method, and regard the optimization of nonlinear unmixing as two sub-problems. During the training process, the learnable parameters in the nonlinear decoder and the other part of the network are alternately trained. When training the linear decoder part, the parameters of the nonlinear decoder are fixed. The training for the nonlinear decoder is the same.
- Since the coefficients of the nonlinear parts are learned, the network can learn useful parameters adaptively for linear mixing data in HSI. To demonstrate the efficiency and superior performance of the proposed model, we conduct experiments on both linear and nonlinear synthetic data. In addition, we further verify the efficiency by using typical real HSIs.
2. Generalized Bilinear Mixing Model
3. Proposed Model
3.1. Encoder
3.2. Decoder
3.2.1. Linear Decoder
3.2.2. Nonlinear Decoder
3.3. Loss Function
4. Experiments
4.1. Experiments on Synthetic Data
- Additive white Gaussian noise: Add Gaussian noise with a signal-to-noise ratio (SNR) of 30 dB for all bands;
- Impulse noise: Add 20% Impulse noise to a 10% band, randomly selected.
4.1.1. Experiment on Synthetic Nonlinear Data and Linear Data
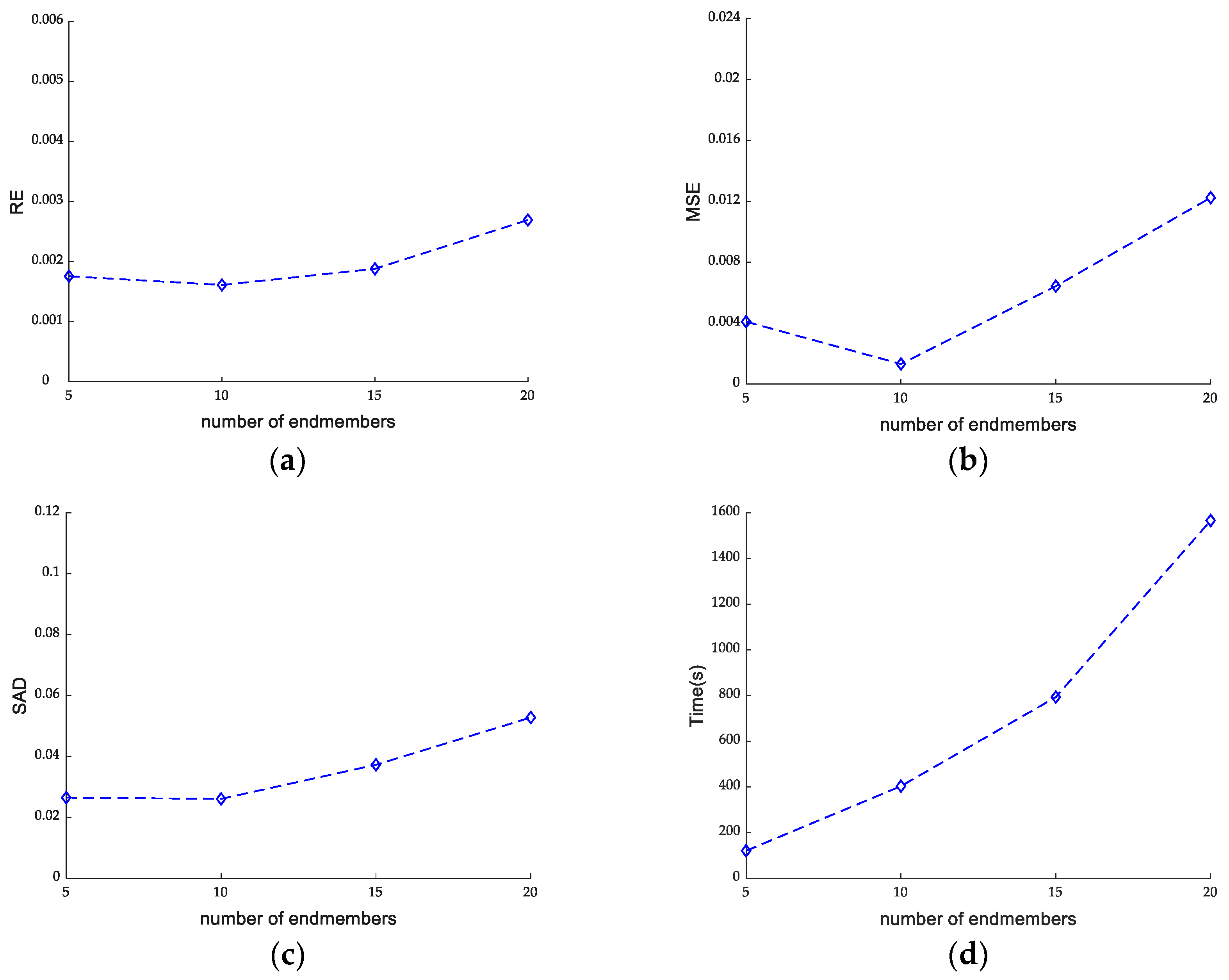
4.1.2. Effect of the Endmember Number
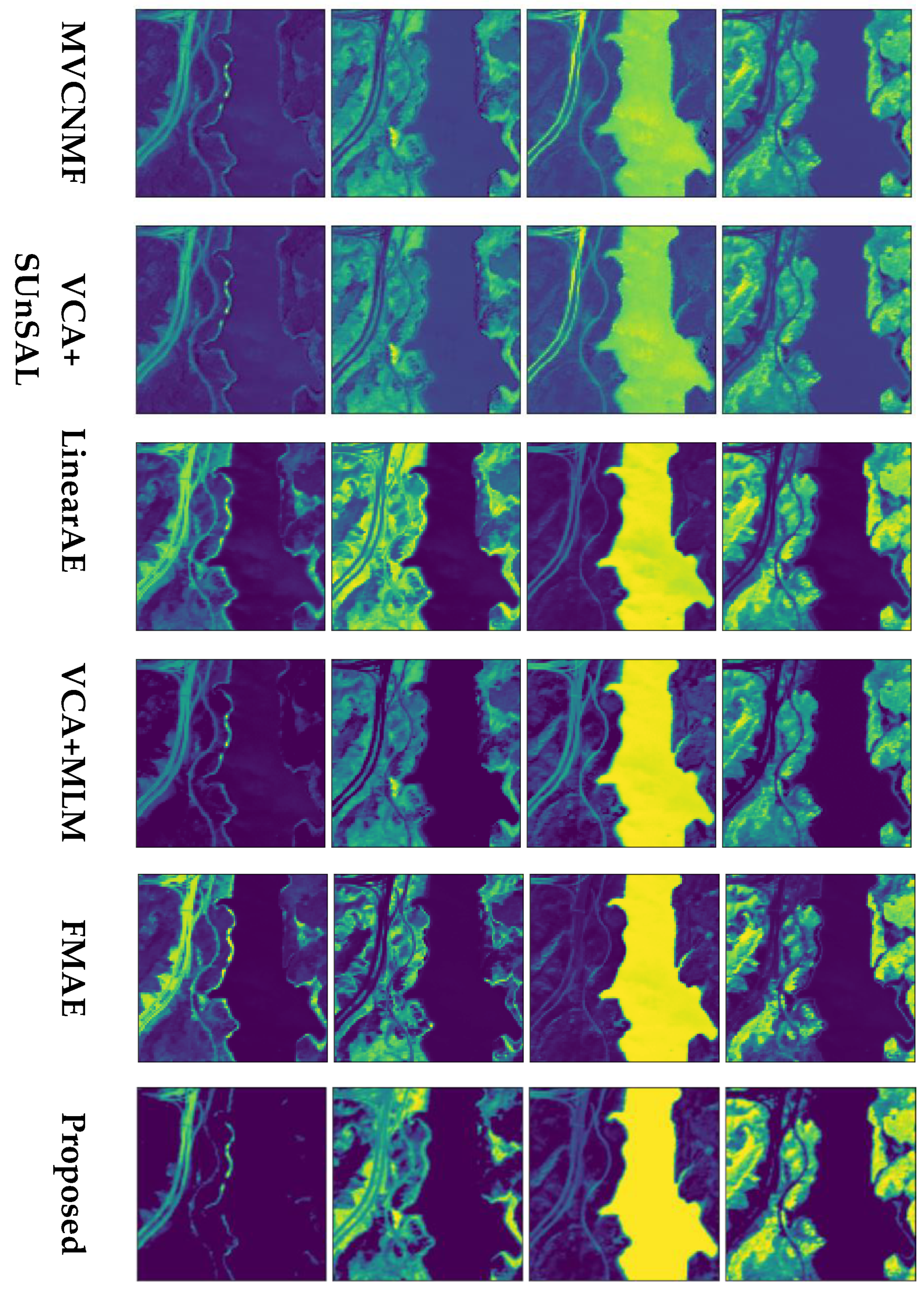
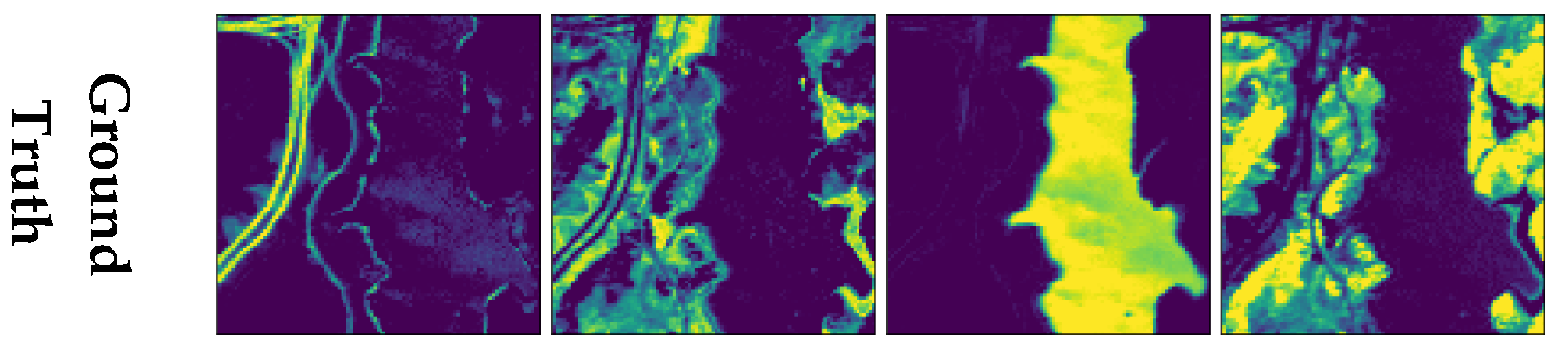
4.2. Experiments on Real Data
4.2.1. Jasper Ridge
4.2.2. Urban
4.2.3. AVIRIS Cuprite
4.3. Computational Complexity
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral Remote Sensing Data Analysis and Future Challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef] [Green Version]
- Bioucas-Dias, J.M.; Plaza, A. An overview on hyperspectral unmixing: Geometrical, statistical, and sparse regression based approaches. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 1135–1138. [Google Scholar]
- Keshava, N.; Mustard, J.F. Spectral unmixing. IEEE Signal Process. Mag. 2002, 19, 44–57. [Google Scholar] [CrossRef]
- Iordache, M.-D.; Bioucas-Dias, J.M.; Plaza, A. Sparse Unmixing of Hyperspectral Data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2014–2039. [Google Scholar] [CrossRef] [Green Version]
- Dópido, I.; Gamba, P.; Plaza, A. Spectral unmixing-based post-processing for hyperspectral image classification. In Proceedings of the 2013 5th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Gainesville, FL, USA, 26–28 June 2013; pp. 1–4. [Google Scholar]
- Andrejchenko, V.; Heylen, R.; Scheunders, P.; Philips, W.; Liao, W. Classification of hyperspectral images with very small training size using sparse unmixing. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5115–5117. [Google Scholar]
- Ibarrola-Ulzurrun, E.; Drumetz, L.; Chanussot, J.; Marcello, J.; Gonzalo-Martin, C. Classification Using Unmixing Models in Areas With Substantial Endmember Variability. In Proceedings of the 2018 9th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands, 23–26 September 2018; pp. 1–4. [Google Scholar]
- Hou, S.; Shi, H.; Cao, X.; Zhang, X.; Jiao, L. Hyperspectral Imagery Classification Based on Contrastive Learning. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Yokoya, N.; Iwasaki, A. Effect of unmixing-based hyperspectral super-resolution on target detection. In Proceedings of the 2014 6th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lausanne, Switzerland, 24–27 June 2014; pp. 1–4. [Google Scholar]
- Ziemann, A.K. Local spectral unmixing for target detection. In Proceedings of the 2016 IEEE Southwest Symposium on Image Analysis and Interpretation (SSIAI), Santa Fe, NM, USA, 6–8 March 2016; pp. 77–80. [Google Scholar]
- Glenn, T.; Dranishnikov, D.; Gader, P.; Zare, A. Subpixel target detection in hyperspectral imagery using piece-wise convex spatial-spectral unmixing, possibilistic and fuzzy clustering, and co-registered LiDAR. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium-IGARSS, Melbourne, Australia, 21–26 July 2013; pp. 1063–1066. [Google Scholar]
- Ma, J.; Zhou, H.; Zhao, J.; Gao, Y.; Jiang, J.; Tian, J. Robust Feature Matching for Remote Sensing Image Registration via Locally Linear Transforming. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6469–6481. [Google Scholar] [CrossRef]
- Cui, S.; Zhong, Y.; Ma, A.; Zhang, L. A novel robust feature descriptor for multi-source remote sensing image registration. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 919–922. [Google Scholar]
- Guo, Q.; He, M.; Li, A. High-Resolution Remote-Sensing Image Registration Based on Angle Matching of Edge Point Features. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2881–2895. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral Unmixing Overview: Geometrical, Statistical, and Sparse Regression-Based Approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef] [Green Version]
- Veganzones, M.A.; Drumetz, L.; Tochon, G.; Dalla Mura, M.; Plaza, A.; Bioucas-Dias, J.; Chanussot, J. A new extended linear mixing model to address spectral variability. In Proceedings of the 2014 6th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lausanne, Switzerland, 24–27 June 2014; pp. 1–4. [Google Scholar]
- Drumetz, L.; Veganzones, M.A.; Henrot, S.; Phlypo, R.; Chanussot, J.; Jutten, C. Blind Hyperspectral Unmixing Using an Extended Linear Mixing Model to Address Spectral Variability. IEEE Trans. Image Process. 2016, 25, 3890–3905. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, M.; Zhang, L.; Du, B.; Zhang, L. The linear mixed model constrained particle swarm optimization for hyperspectral endmember extraction from highly mixed data. In Proceedings of the 2016 8th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Los Angeles, CA, USA, 21–24 August 2016; pp. 1–4. [Google Scholar]
- Miao, L.; Qi, H. Endmember Extraction From Highly Mixed Data Using Minimum Volume Constrained Nonnegative Matrix Factorization. IEEE Trans. Geosci. Remote Sens. 2007, 45, 765–777. [Google Scholar] [CrossRef]
- Nascimento, J.M.P.; Dias, J.M.B. Vertex component analysis: A fast algorithm to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 898–910. [Google Scholar] [CrossRef]
- Afonso, M.V.; Bioucas-Dias, J.M.; Figueiredo, M.A. An augmented Lagrangian approach to the constrained optimization formulation of imaging inverse problems. IEEE Trans. Image Process. 2011, 20, 681–695. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bioucas-Dias, J.M.; Figueiredo, M.A. Alternating direction algorithms for constrained sparse regression: Application to hyperspectral unmixing. In Proceedings of the 2010 2nd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Reykjavik, Iceland, 14–16 June 2010; pp. 1–4. [Google Scholar]
- Heinz, D.C.; Chein, I.C. Fully constrained least squares linear spectral mixture analysis method for material quantification in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 529–545. [Google Scholar] [CrossRef] [Green Version]
- Izquierdo-Verdiguier, E.; Gomez-Chova, L.; Bruzzone, L.; Camps-Valls, G. Semisupervised Kernel Feature Extraction for Remote Sensing Image Analysis. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5567–5578. [Google Scholar] [CrossRef]
- Mateo-García, G.; Laparra, V.; Gómez-Chova, L. Optimizing Kernel Ridge Regression for Remote Sensing Problems. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 4007–4010. [Google Scholar]
- Hapke, B. Bidirectional reflectance spectroscopy: 1. Theory. J. Geophys. Res. Solid Earth 1981, 86, 3039–3054. [Google Scholar] [CrossRef] [Green Version]
- Hapke, B.; Wells, E. Bidirectional reflectance spectroscopy: 2. Experiments and observations. J. Geophys. Res. Solid Earth 1981, 86, 3055–3060. [Google Scholar] [CrossRef]
- Chen, W.; Cao, C.; Zhang, H.; Jia, H.; Ji, W.; Xu, M.; Gao, M.; Ni, X.; Zhao, J.; Zheng, S. Estimation of shrub canopy cover based on a geometric-optical model using HJ-1 data. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 1922–1925. [Google Scholar]
- Altmann, Y.; Dobigeon, N.; Tourneret, J.-Y. Bilinear models for nonlinear unmixing of hyperspectral images. In Proceedings of the 2011 3rd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lisbon, Portugal, 6–9 June 2011; pp. 1–4. [Google Scholar]
- Nascimento, J.M.; Bioucas-Dias, J.M. Nonlinear mixture model for hyperspectral unmixing. In Proceedings of the Image and Signal Processing for Remote Sensing XV, Berlin, Germany, 31 August–3 September 2009; pp. 157–164. [Google Scholar]
- Fan, W.; Hu, B.; Miller, J.; Li, M. Comparative study between a new nonlinear model and common linear model for analysing laboratory simulated-forest hyperspectral data. Int. J. Remote Sens. 2009, 30, 2951–2962. [Google Scholar] [CrossRef]
- Halimi, A.; Altmann, Y.; Dobigeon, N.; Tourneret, J.-Y. Nonlinear Unmixing of Hyperspectral Images Using a Generalized Bilinear Model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4153–4162. [Google Scholar] [CrossRef] [Green Version]
- Halimi, A.; Altmann, Y.; Dobigeon, N.; Tourneret, J.-Y. Unmixing hyperspectral images using the generalized bilinear model. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 1886–1889. [Google Scholar]
- Yokoya, N.; Chanussot, J.; Iwasaki, A. Nonlinear Unmixing of Hyperspectral Data Using Semi-Nonnegative Matrix Factorization. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1430–1437. [Google Scholar] [CrossRef] [Green Version]
- Plaza, J.; Plaza, A.J.; Martinez, P.; Perez, R.M. Nonlinear mixture models for analyzing laboratory simulated-forest hyperspectral data. In Proceedings of the Image and Signal Processing for Remote Sensing IX, Barcelona, Spain, 9–12 September 2003; pp. 480–487. [Google Scholar]
- Licciardi, G.A.; Del Frate, F. Pixel Unmixing in Hyperspectral Data by Means of Neural Networks. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4163–4172. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, Y.; Zhang, J.; Wu, P.; Jiao, L. Hyperspectral Unmixing via Deep Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1755–1759. [Google Scholar] [CrossRef]
- Su, Y.; Li, J.; Plaza, A.; Marinoni, A.; Gamba, P.; Chakravortty, S. DAEN: Deep Autoencoder Networks for Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4309–4321. [Google Scholar] [CrossRef]
- Palsson, B.; Ulfarsson, M.O.; Sveinsson, J.R. Convolutional autoencoder for spatial-spectral hyperspectral unmixing. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 357–360. [Google Scholar]
- Min, A.; Guo, Z.; Li, H.; Peng, J. JMnet: Joint Metric Neural Network for Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5505412. [Google Scholar] [CrossRef]
- Wang, M.; Zhao, M.; Chen, J.; Rahardja, S. Nonlinear Unmixing of Hyperspectral Data via Deep Autoencoder Networks. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1467–1471. [Google Scholar] [CrossRef]
- Su, Y.; Xu, X.; Li, J.; Qi, H.; Gamba, P.; Plaza, A. Deep Autoencoders With Multitask Learning for Bilinear Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8615–8629. [Google Scholar] [CrossRef]
- Li, H.; Borsoi, R.A.; Imbiriba, T.; Closas, P.; Bermudez, J.C.M.; Erdogmus, D. Model-Based Deep Autoencoder Networks for Nonlinear Hyperspectral Unmixing. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5506105. [Google Scholar] [CrossRef]
- Dobigeon, N.; Tourneret, J.-Y.; Richard, C.; Bermudez, J.C.M.; McLaughlin, S.; Hero, A.O. Nonlinear Unmixing of Hyperspectral Images: Models and Algorithms. IEEE Signal Process. Mag. 2014, 31, 82–94. [Google Scholar] [CrossRef] [Green Version]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Keskar, N.S.; Mudigere, D.; Nocedal, J.; Smelyanskiy, M.; Tang, P.T.P. On large-batch training for deep learning: Generalization gap and sharp minima. arXiv 2016, arXiv:1609.04836. [Google Scholar]
- Masters, D.; Luschi, C. Revisiting small batch training for deep neural networks. arXiv 2018, arXiv:1804.07612. [Google Scholar]
- Palsson, B.; Sigurdsson, J.; Sveinsson, J.R.; Ulfarsson, M.O. Hyperspectral Unmixing Using a Neural Network Autoencoder. IEEE Access 2018, 6, 25646–25656. [Google Scholar] [CrossRef]
- Wei, Q.; Chen, M.; Tourneret, J.-Y.; Godsill, S. Unsupervised Nonlinear Spectral Unmixing Based on a Multilinear Mixing Model. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4534–4544. [Google Scholar] [CrossRef] [Green Version]
- Mei, X.; Ma, Y.; Li, C.; Fan, F.; Huang, J.; Ma, J. Robust GBM hyperspectral image unmixing with superpixel segmentation based low rank and sparse representation. Neurocomputing 2018, 275, 2783–2797. [Google Scholar] [CrossRef]
- Zhu, F. Hyperspectral unmixing: Ground truth labeling, datasets, benchmark performances and survey. arXiv 2017, arXiv:1708.05125. [Google Scholar]
- Wang, X.; Zhong, Y.; Zhang, L.; Xu, Y. Blind Hyperspectral Unmixing Considering the Adjacency Effect. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6633–6649. [Google Scholar] [CrossRef]










| Layers | Activation | Units | Bias | ||
|---|---|---|---|---|---|
| Encoder | Input layer | - | L | No | |
| Hidden layer 1 | Leaky ReLU | 9∗M | No | ||
| Hidden layer 2 | Leaky ReLU | 6∗M | No | ||
| Hidden layer 3 | Leaky ReLU | 3∗M | No | ||
| Hidden layer 4 | Leaky ReLU | M | No | ||
| Batch Normalization | - | M | - | ||
| Decoder | Linear part | ANC + ASC | - | M | - |
| Linear output layer | - | L | No | ||
| Nonlinear part | Hidden layer | M(M − 1)/2 | No | ||
| Custom layer | - | M(M − 1)/2 | No | ||
| Nonlinear output layer | - | L | No | ||
| MVCNMF | VCA + SUnSAL | LinearAE | VCA + MLM | FMAE | Proposed | |
|---|---|---|---|---|---|---|
| MSE | 0.0115 | 0.0147 | 0.0142 | 0.0110 | 0.0111 | 0.0030 |
| AAD | 0.2764 | 0.2959 | 0.3511 | 0.2676 | 0.3211 | 0.1486 |
| SAD | 0.0721 | 0.0801 | 0.0731 | 0.0672 | 0.0918 | 0.0377 |
| RE | 0.0042 | 0.0031 | 0.0041 | 0.0068 | 0.0023 | 0.0019 |
| MVCNMF | VCA + SUnSAL | LinearAE | VCA + MLM | FMAE | Proposed | |
|---|---|---|---|---|---|---|
| MSE | 0.0112 | 0.0111 | 0.0107 | 0.0158 | 0.0120 | 0.0092 |
| AAD | 0.2736 | 0.2731 | 0.2956 | 0.3035 | 0.3137 | 0.2921 |
| SAD | 0.0587 | 0.0801 | 0.0643 | 0.0817 | 0.0911 | 0.0322 |
| RE | 0.0003 | 0.0012 | 0.0054 | 0.0035 | 0.0059 | 0.0018 |
| MVCNMF | VCA + SUnSAL | LinearAE | VCA + MLM | FMAE | Proposed | |
|---|---|---|---|---|---|---|
| MSE | 0.0264 | 0.0241 | 0.0216 | 0.0234 | 0.0260 | 0.0185 |
| AAD | 0.4617 | 0.4300 | 0.4274 | 0.3246 | 0.4363 | 0.2134 |
| SAD | 0.1773 | 0.1726 | 0.3161 | 0.2413 | 0.1275 | 0.0869 |
| RE | 0.0029 | 0.0028 | 0.0030 | 0.0028 | 0.0022 | 0.0005 |
| MVCNMF | VCA + SUnSAL | LinearAE | VCA + MLM | FMAE | Proposed | |
|---|---|---|---|---|---|---|
| MSE | 0.0739 | 0.0573 | 0.0452 | 0.0864 | 0.0511 | 0.0336 |
| AAD | 0.8452 | 0.6702 | 0.6104 | 0.7525 | 0.5751 | 0.4951 |
| SAD | 0.3032 | 0.3641 | 0.2031 | 0.2667 | 0.1958 | 0.1908 |
| RE | 0.0061 | 0.0058 | 0.0050 | 0.0047 | 0.0015 | 0.0015 |
| MVCNMF | VCA + SUnSAL | LinearAE | VCA + MLM | FMAE | Proposed | |
|---|---|---|---|---|---|---|
| SAD | 0.1172 | 0.1212 | 0.1393 | 0.1052 | 0.1038 | 0.0937 |
| RE | 3.41 | 4.01 | 1.54 | 1.07 | 7.56 | 3.05 |
| Syn Linear | Syn Nonlinear | Jasper Ridge | Urban | Cuprite | |
|---|---|---|---|---|---|
| MVCNMF | 10 | 34 | 396 | 31 | 559 |
| VCA + SUnSAL | 1 | 1 | 6 | 1 | 5 |
| LinearAE | 68 | 66 | 230 | 28 | 181 |
| VCA + MLM | 128 | 98 | 487 | 37 | 54 |
| FMAE | 203 | 211 | 1175 | 176 | 774 |
| GBM_AE | 142 | 154 | 558 | 50 | 689 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Zhang, X.; Meng, H.; Sun, C.; Wang, L.; Cao, X. Nonlinear Unmixing via Deep Autoencoder Networks for Generalized Bilinear Model. Remote Sens. 2022, 14, 5167. https://doi.org/10.3390/rs14205167
Zhang J, Zhang X, Meng H, Sun C, Wang L, Cao X. Nonlinear Unmixing via Deep Autoencoder Networks for Generalized Bilinear Model. Remote Sensing. 2022; 14(20):5167. https://doi.org/10.3390/rs14205167
Chicago/Turabian StyleZhang, Jinhua, Xiaohua Zhang, Hongyun Meng, Caihao Sun, Li Wang, and Xianghai Cao. 2022. "Nonlinear Unmixing via Deep Autoencoder Networks for Generalized Bilinear Model" Remote Sensing 14, no. 20: 5167. https://doi.org/10.3390/rs14205167
APA StyleZhang, J., Zhang, X., Meng, H., Sun, C., Wang, L., & Cao, X. (2022). Nonlinear Unmixing via Deep Autoencoder Networks for Generalized Bilinear Model. Remote Sensing, 14(20), 5167. https://doi.org/10.3390/rs14205167








