Can Data Assimilation Improve Short-Term Prediction of Land Surface Variables?
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.2. Noah-MP Model
2.3. Multi-Pass Land Data Assimilation Scheme
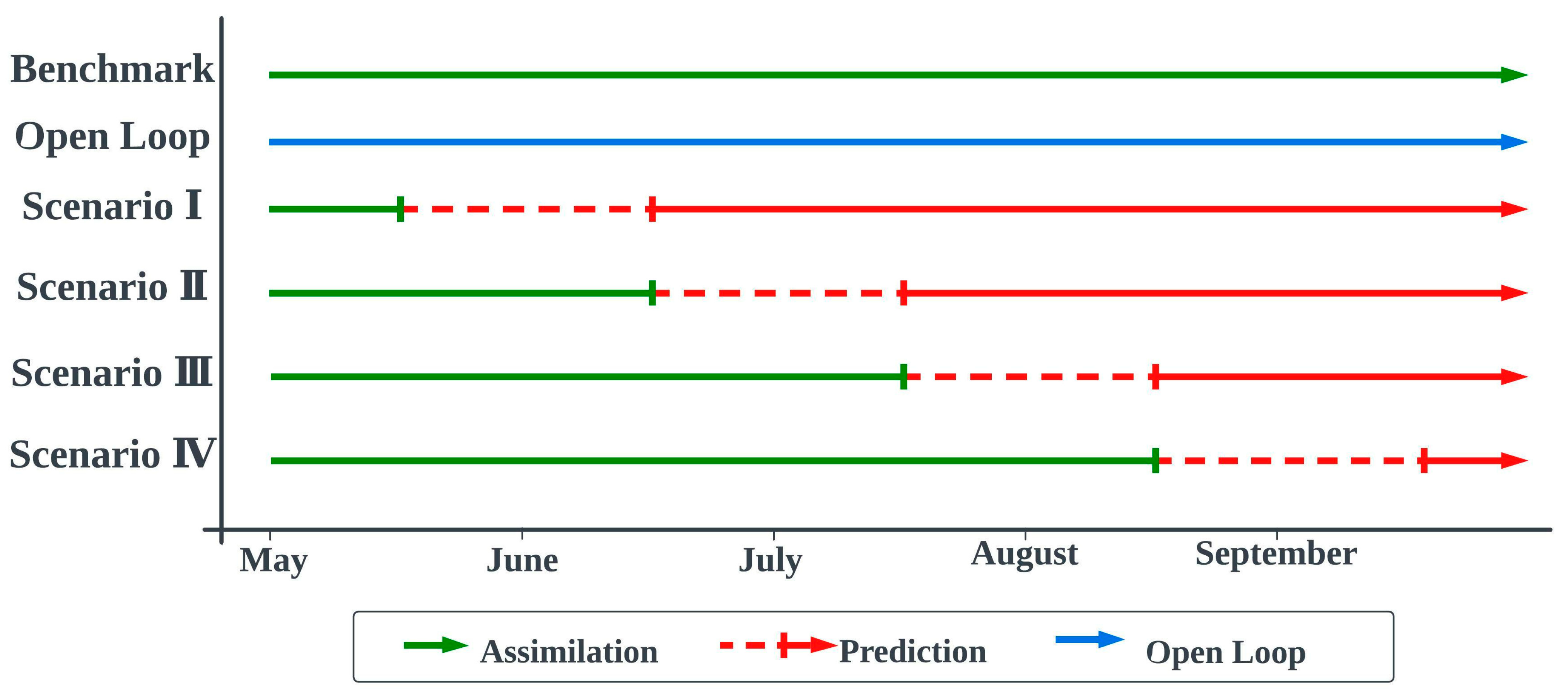
2.4. Experiments Setup
3. Results
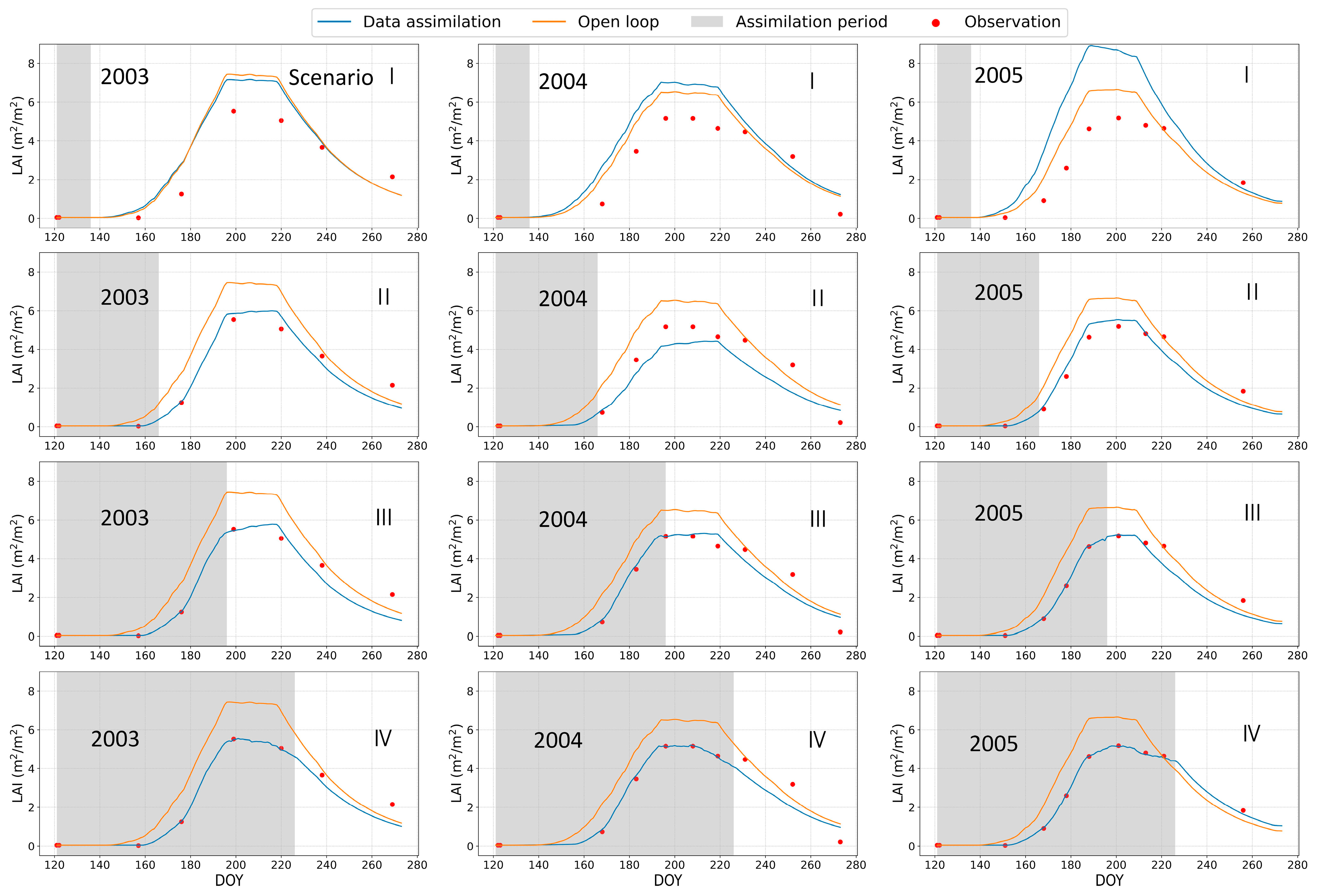
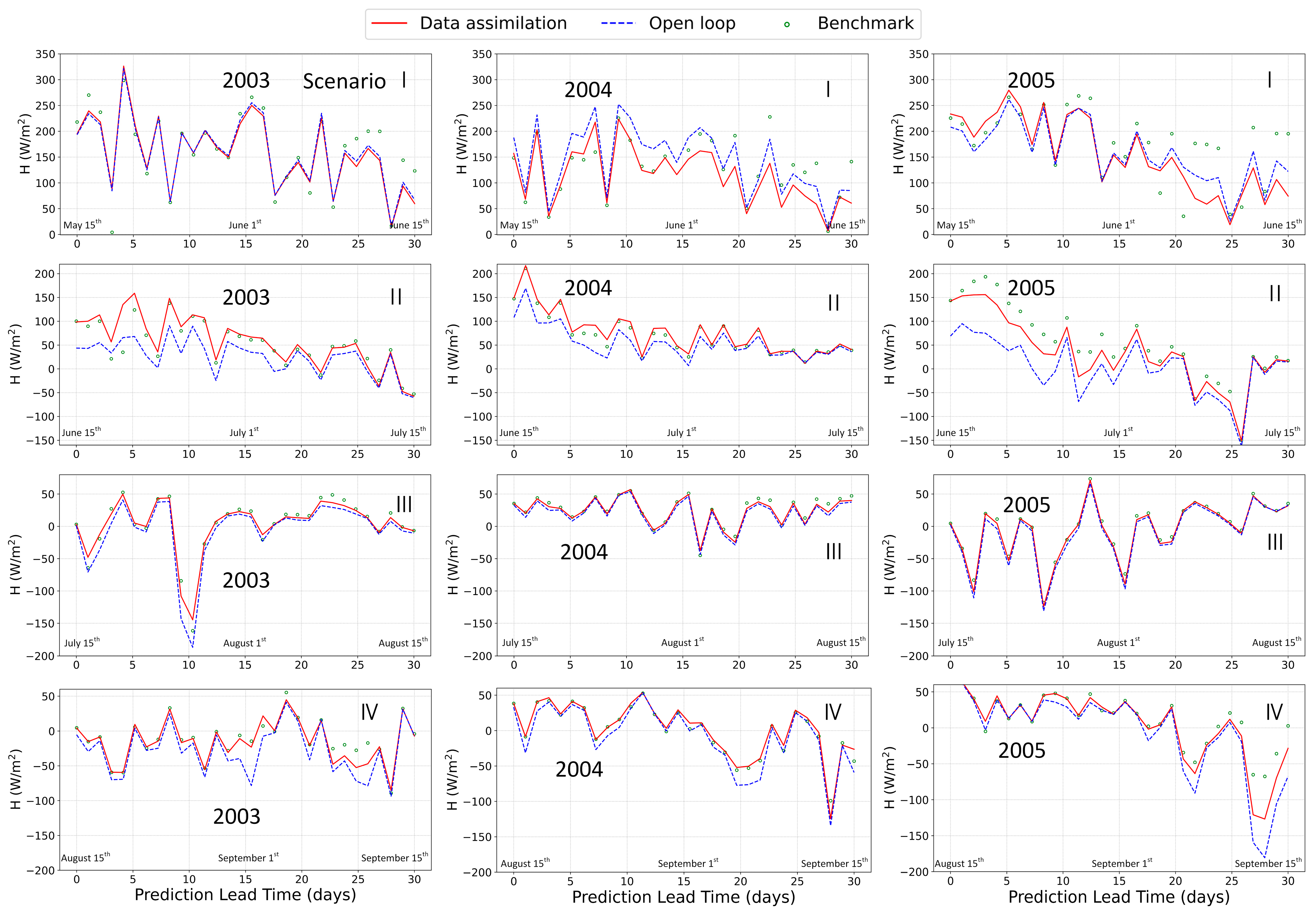
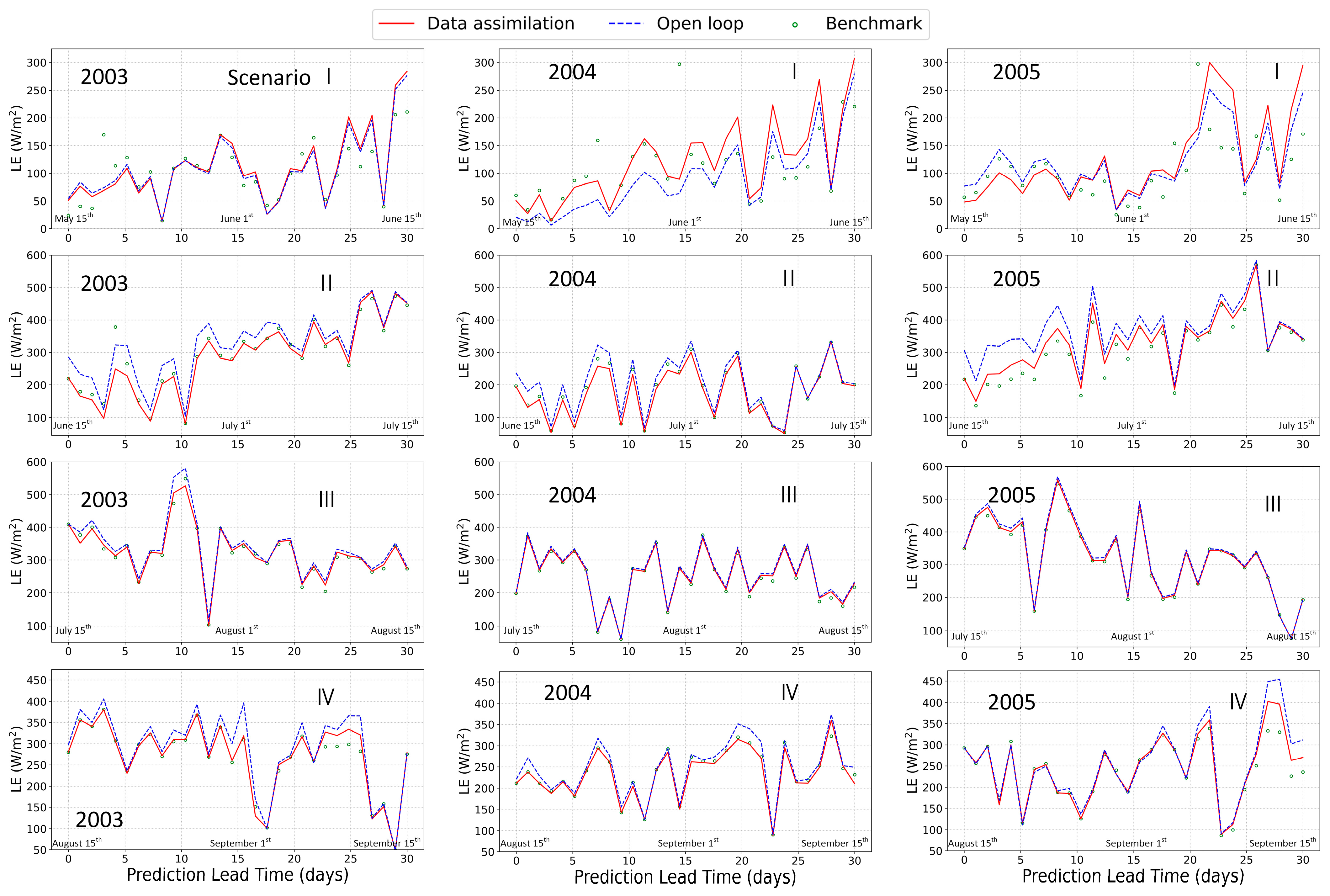
3.1. Impacts of Assimilation on Land Surface Variables Prediction
3.1.1. Leaf Area Index
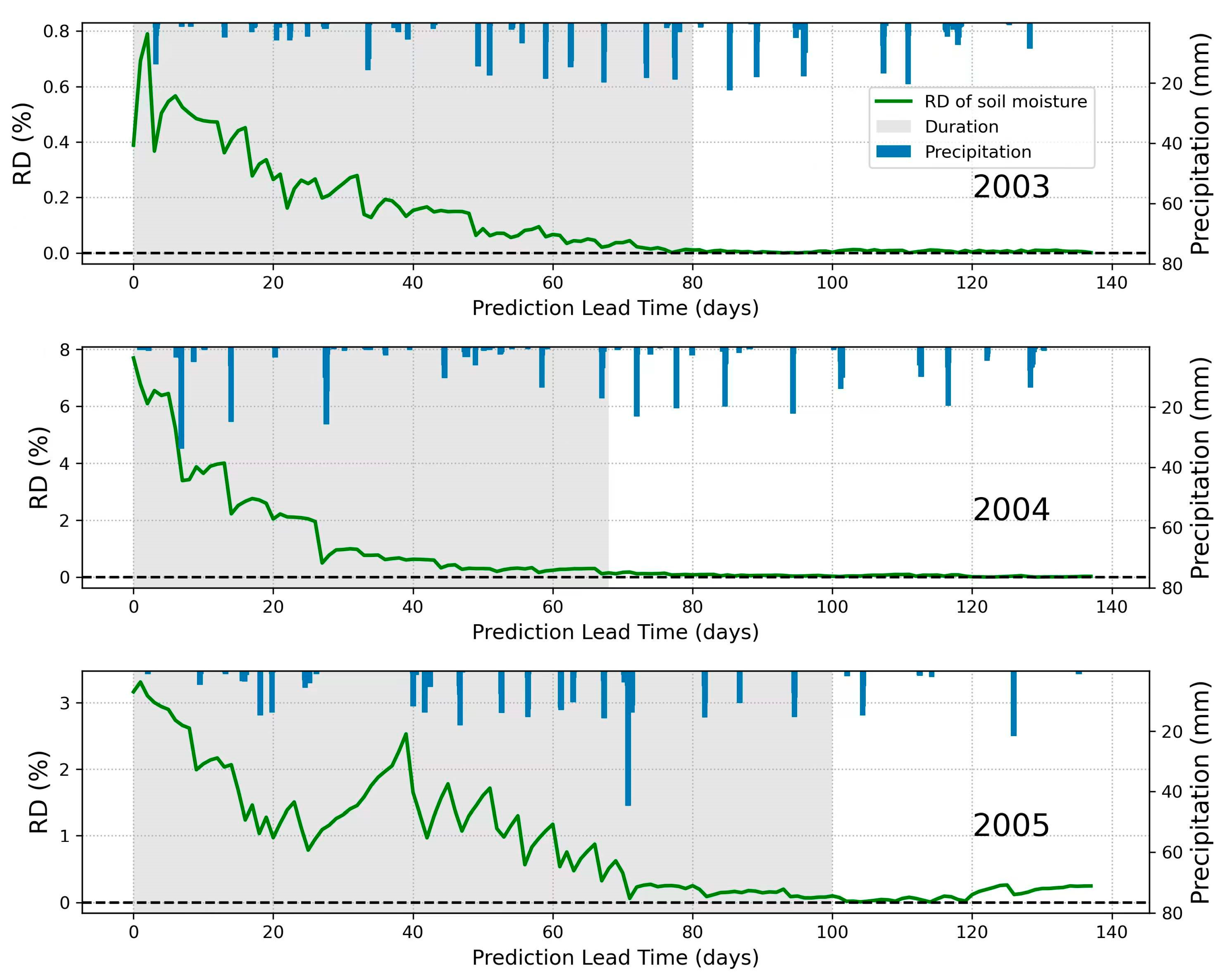
3.1.2. Soil Moisture
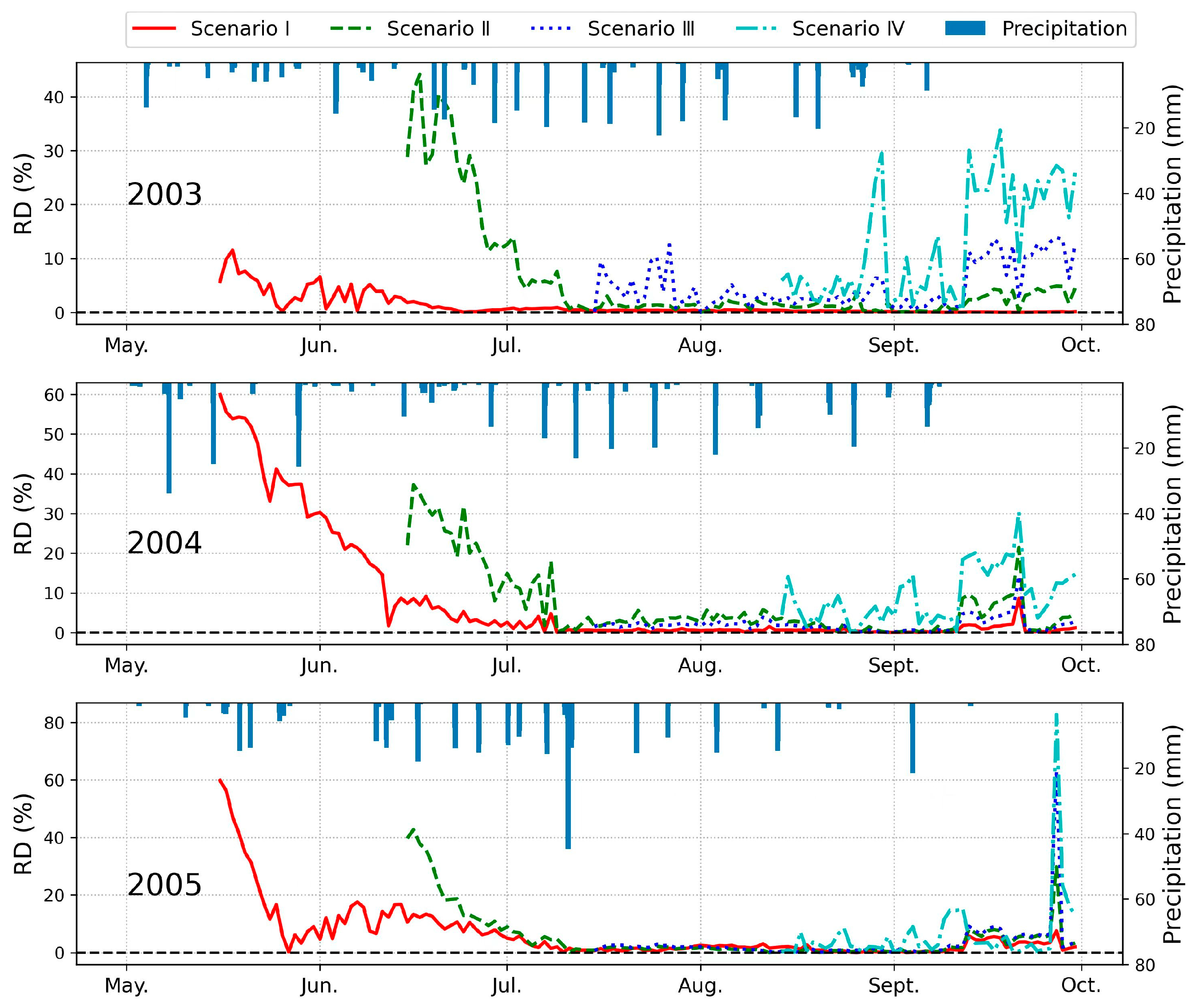
3.1.3. Sensible Heat Flux
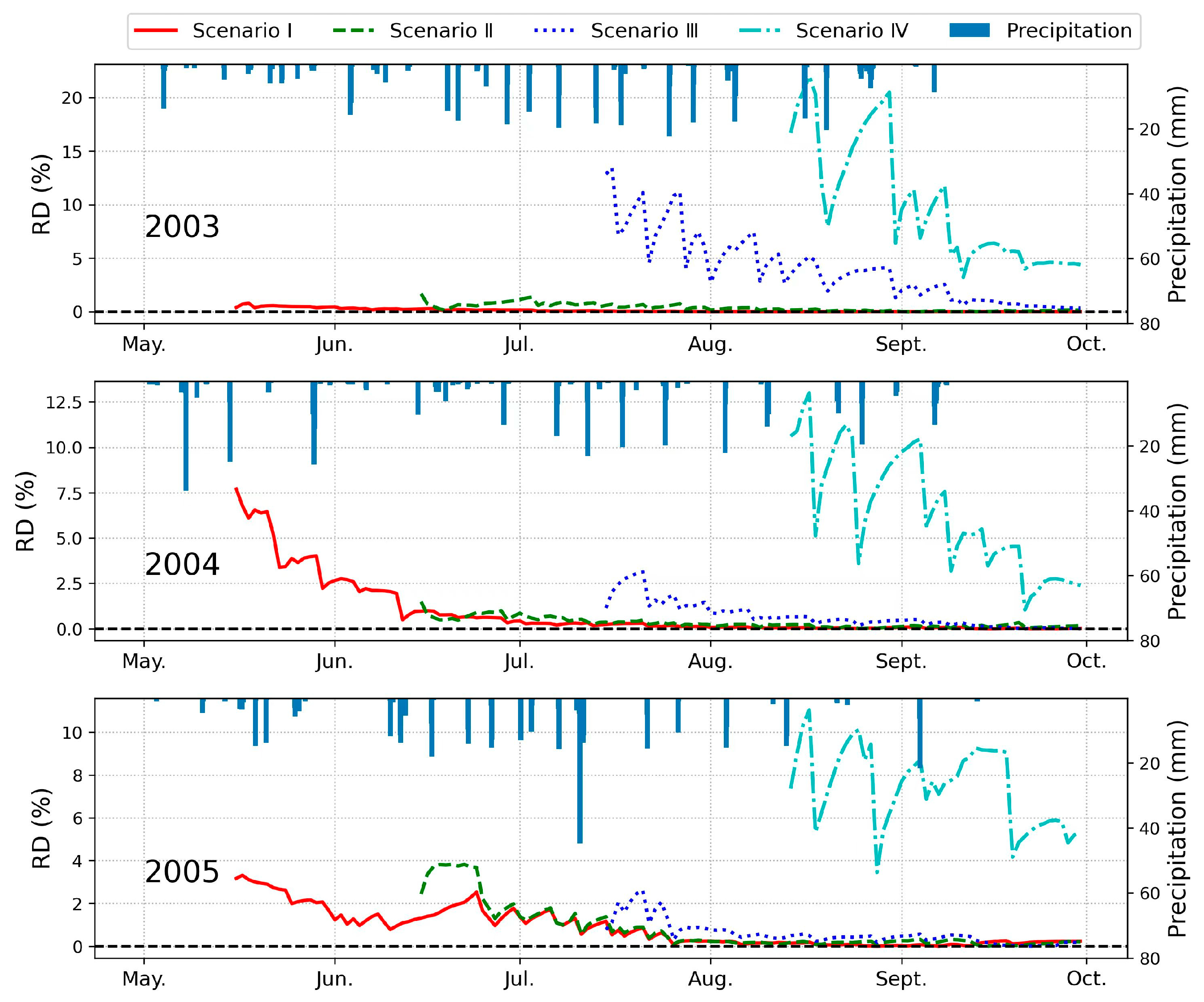
3.1.4. Latent Heat Flux
3.2. Duration of Impact of Data Assimilation on Prediction
4. Discussion
4.1. Can MLDAS Improve the near Future Prediction Performance?
4.2. How Long Does the Influence of Assimilation Exist?
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, X.; Xu, T.; Xia, Y.; Bateni, S.M.; Guo, Z.; Liu, S.; Mao, K.; Zhang, Y.; Feng, H.; Zhao, J. A Bayesian Three-Cornered Hat (BTCH) method: Improving the terrestrial evapotranspiration estimation. Remote Sens. 2020, 12, 878. [Google Scholar] [CrossRef] [Green Version]
- Lokupitiya, E.; Denning, A.S.; Schaefer, K.; Ricciuto, D.; Anderson, R.; Arain, M.A.; Baker, I.; Barr, A.G.; Chen, G.; Chen, J.M.; et al. Carbon and energy fluxes in cropland ecosystems: A model-data comparison. Biogeochemistry 2016, 129, 53–76. [Google Scholar] [CrossRef] [Green Version]
- Xu, T.; Guo, Z.; Liu, S.; He, X.; Meng, Y.; Xu, Z.; Xia, Y.; Xiao, J.; Zhang, Y.; Ma, Y.; et al. Evaluating different machine learning methods for upscaling evapotranspiration from flux towers to the regional scale. J. Geophys. Res. Atmos. 2018, 123, 8674–8690. [Google Scholar] [CrossRef]
- Yang, Z.L.; Niu, G.Y.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Longuevergne, L.; Manning, K.; Niyogi, D.; Tewari, M.; et al. The community noah land surface model with multiparameterization options (Noah-MP): 2. Evaluation over global river basins. J. Geophys. Res. Atmos. 2011, 116, D12110. [Google Scholar] [CrossRef]
- Niu, G.Y.; Yang, Z.L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The community noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. Atmos. 2011, 116, D12109. [Google Scholar] [CrossRef] [Green Version]
- Mucia, A.; Bonan, B.; Zheng, Y.; Albergel, C.; Calvet, J.C. From monitoring to forecasting land surface conditions using a land data assimilation system: Application over the contiguous United States. Remote Sens. 2020, 12, 2020. [Google Scholar] [CrossRef]
- Wood, A.W.; Lettenmaier, D.P. An ensemble approach for attribution of hydrologic prediction uncertainty. Geophys. Res. Lett. 2008, 35, L14401. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Barlage, M.; Chen, F.; Li, Y.; Helgason, W.; Xu, X.; Liu, X.; Li, Z. joint modeling of crop and irrigation in the central United States using the Noah-MP land surface model. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002159. [Google Scholar] [CrossRef]
- Xu, X.; Chen, F.; Barlage, M.; Gochis, D.; Miao, S.; Shen, S. Lessons learned from modeling irrigation from field to regional scales. J. Adv. Model. Earth Syst. 2019, 11, 2428–2448. [Google Scholar] [CrossRef] [Green Version]
- Xu, T.R.; Liu, S.M.; Xu, Z.W.; Liang, S.L.; Xu, L. A dual-pass data assimilation scheme for estimating surface fluxes with FY3A-VIRR land surface temperature. Sci. China Earth Sci. 2015, 58, 211–230. [Google Scholar] [CrossRef]
- Kumar, S.V.; Mocko, D.M.; Wang, S.; Peters-Lidard, C.D.; Borak, J. Assimilation of remotely sensed leaf area index into the Noah-Mp land surface model: Impacts on water and carbon fluxes and states over the continental United States. J. Hydrometeorol. 2019, 20, 1359–1377. [Google Scholar] [CrossRef]
- He, X.; Liu, S.; Xu, T.; Yu, K.; Gentine, P.; Zhang, Z.; Xu, Z.; Jiao, D.; Wu, D. Improving predictions of evapotranspiration by integrating multi-source observations and land surface model. Agric. Water Manag. 2022, 272, 107827. [Google Scholar] [CrossRef]
- Xu, T.; He, X.; Bateni, S.M.; Auligne, T.; Liu, S.; Xu, Z.; Zhou, J.; Mao, K. Mapping regional turbulent heat fluxes via variational assimilation of land surface temperature data from polar orbiting satellites. Remote Sens. Environ. 2019, 221, 444–461. [Google Scholar] [CrossRef]
- Pinnington, E.; Quaife, T.; Black, E. Impact of remotely sensed soil moisture and precipitation on soil moisture prediction in a data assimilation system with the JULES land surface model. Hydrol. Earth Syst. Sci. 2018, 22, 2575–2588. [Google Scholar] [CrossRef] [Green Version]
- Tian, S.; Tregoning, P.; Renzullo, L.J.; van Dijk, A.I.J.M.; Walker, J.P.; Pauwels, V.R.N.; Allgeyer, S. Improved water balance component estimates through joint assimilation of GRACE water storage and SMOS soil moisture retrievals. Water Resour. Res. 2017, 53, 1820–1840. [Google Scholar] [CrossRef]
- Albergel, C.; Munier, S.; Jennifer Leroux, D.; Dewaele, H.; Fairbairn, D.; Lavinia Barbu, A.; Gelati, E.; Dorigo, W.; Faroux, S.; Meurey, C.; et al. Sequential assimilation of satellite-derived vegetation and soil moisture products using SURFEX-v8.0: LDAS-Monde Assessment over the Euro-Mediterranean Area. Geosci. Model Dev. 2017, 10, 3889–3912. [Google Scholar] [CrossRef] [Green Version]
- Xu, T.; Chen, F.; He, X.; Barlage, M.; Zhang, Z.; Liu, S.; He, X. Improve the performance of the Noah-MP-pCro Model by jointly assimilating soil moisture and vegetation phenology data. J. Adv. Model. Earth Syst. 2021, 13, e2020MS002394. [Google Scholar] [CrossRef]
- Sawada, Y.; Koike, T.; Ikoma, E.; Kitsuregawa, M. Monitoring and predicting agricultural droughts for a water-limited subcontinental region by integrating a land surface model and microwave remote sensing. IEEE Trans. Geosci. Remote Sens. 2020, 58, 14–33. [Google Scholar] [CrossRef]
- Verma, S.B.; Dobermann, A.; Cassman, K.G.; Walters, D.T.; Knops, J.M.; Arkebauer, T.J.; Suyker, A.E.; Burba, G.G.; Amos, B.; Yang, H.; et al. Annual carbon dioxide exchange in irrigated and rainfed maize-based agroecosystems. Agric. Meteorol. 2005, 131, 77–96. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Joiner, J.; Hamed Alemohammad, S.; Zhou, S.; Gentine, P. A global spatially contiguous solar-induced fluorescence (CSIF) dataset using neural networks. Biogeosciences 2018, 15, 5779–5800. [Google Scholar] [CrossRef]
- Chen, F.; Mitchell, K.; Schaake, J.; Xue, Y.; Pan, H.L.; Koren, V.; Duan, Q.Y.; Ek, M.; Betts, A. Modeling of land surface evaporation by four schemes and comparison with FIFE observations. J. Geophys. Res. Atmos. 1996, 101, 7251–7268. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Chen, F.; Barlage, M.; Zhou, G.; Niyogi, D. Noah-MP-Crop: Introducing dynamic crop growth in the Noah-MP land surface model. J. Geophys. Res. Atmos. 2016, 121, 13953–13972. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Guanter, L.; Berry, J.A.; Joiner, J.; van der Tol, C.; Huete, A.; Gitelson, A.; Voigt, M.; Köhler, P. Estimation of vegetation photosynthetic capacity from space-based measurements of chlorophyll fluorescence for terrestrial biosphere models. Glob. Chang. Biol. 2014, 20, 3727–3742. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kumar, S.V.; Reichle, R.H.; Koster, R.D.; Crow, W.T.; Peters-Lidard, C.D. Role of subsurface physics in the assimilation of surface soil moisture observations. J. Hydrometeorol. 2009, 10, 1534–1547. [Google Scholar] [CrossRef]
- Shokri, N.; Lehmann, P.; Or, D. Characteristics of evaporation from partially wettable porous media. Water Resour. Res. 2009, 45, W02415. [Google Scholar] [CrossRef] [Green Version]
- Shokri, N.; Lehmann, P.; Vontobel, P.; Or, D. Drying front and water content dynamics during evaporation from sand delineated by neutron radiography. Water Resour. Res. 2008, 44, W06418. [Google Scholar] [CrossRef] [Green Version]
- Donegan, S.; Murphy, C.; Harrigan, S.; Broderick, C.; Foran Quinn, D.; Golian, S.; Knight, J.; Matthews, T.; Prudhomme, C.; Scaife, A.A.; et al. Conditioning ensemble streamflow prediction with the North Atlantic oscillation improves skill at longer lead times. Hydrol. Earth Syst. Sci. 2021, 25, 4159–4183. [Google Scholar] [CrossRef]
- Shukla, S.; Sheffield, J.; Wood, E.F.; Lettenmaier, D.P. On the sources of global land surface hydrologic predictability. Hydrol. Earth Syst. Sci. 2013, 17, 2781–2796. [Google Scholar] [CrossRef] [Green Version]
- Drusch, M.; Viterbo, P. Assimilation of screen-level variables in ECMWF’s integrated forecast system: A study on the impact on the forecast quality and analyzed soil moisture. Mon. Weather Rev. 2007, 135, 300–314. [Google Scholar] [CrossRef]
- De Rosnay, P.; Balsamo, G.; Albergel, C.; Muñoz-Sabater, J.; Isaksen, L. Initialisation of land surface variables for numerical weather prediction. Surv. Geophys. 2014, 35, 607–621. [Google Scholar] [CrossRef]
- Van den Hurk, B.; Ettema, J.; Viterbo, P. Analysis of soil moisture changes in europe during a single growing season in a new ECMWF soil moisture assimilation system. J. Hydrometeorol. 2008, 9, 116–131. [Google Scholar] [CrossRef]
- Weisheimer, A.; Doblas-Reyes, F.J.; Jung, T.; Palmer, T.N. On the predictability of the extreme summer 2003 over Europe. Geophys. Res. Lett. 2011, 38, L05704. [Google Scholar] [CrossRef]

| Year | 2003 | 2004 | 2005 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSDModel (m3/m3) | RMSDAnalysis (m3/m3) | NICRMSD (%) | RMSDModel (m3/m3) | RMSDAnalysis (m3/m3) | NICRMSD (%) | RMSDModel (m3/m3) | RMSDAnalysis (m3/m3) | NICRMSD (%) | |
| Scenario I | 0.0102 | 0.0106 | −3.87 | 0.0233 | 0.0115 | 50.51 | 0.0084 | 0.0106 | −26.50 |
| Scenario II | 0.0138 | 0.0136 | 1.23 | 0.0121 | 0.0136 | −12.08 | 0.0469 | 0.0402 | 14.26 |
| Scenario III | 0.0386 | 0.0245 | 36.35 | 0.0224 | 0.0201 | 10.10 | 0.0251 | 0.0225 | 10.15 |
| Scenario IV | 0.0540 | 0.0214 | 60.41 | 0.0244 | 0.0166 | 31.93 | 0.0411 | 0.0227 | 44.83 |
| Year | 2003 | 2004 | 2005 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSDModel (W/m2) | RMSDAnalysis (W/m2) | NICRMSD (%) | RMSDModel (W/m2) | RMSDAnalysis (W/m2) | NICRMSD (%) | RMSDModel (W/m2) | RMSDAnalysis (W/m2) | NICRMSD (%) | |
| Scenario I | 26.716 | 29.411 | −10.09 | 48.168 | 46.886 | 2.66 | 36.926 | 52.082 | −41.04 |
| Scenario II | 32.043 | 21.718 | 32.22 | 20.031 | 7.822 | 60.95 | 63.834 | 25.284 | 60.39 |
| Scenario III | 15.021 | 7.552 | 49.72 | 7.961 | 5.210 | 34.56 | 9.853 | 5.745 | 41.70 |
| Scenario IV | 22.453 | 9.640 | 57.07 | 12.422 | 6.484 | 47.80 | 34.707 | 18.198 | 47.57 |
| Year | 2003 | 2004 | 2005 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSDModel (W/m2) | RMSDAnalysis (W/m2) | NICRMSD (%) | RMSDModel (W/m2) | RMSDAnalysis (W/m2) | NICRMSD (%) | RMSDModel (W/m2) | RMSDAnalysis (W/m2) | NICRMSD (%) | |
| Scenario I | 31.121 | 33.785 | −8.56 | 56.808 | 54.251 | 4.50 | 44.714 | 59.053 | −32.07 |
| Scenario II | 36.858 | 27.390 | 25.69 | 22.309 | 9.517 | 57.34 | 69.300 | 26.642 | 61.56 |
| Scenario III | 21.382 | 11.165 | 47.79 | 11.749 | 7.763 | 33.93 | 13.545 | 8.009 | 40.87 |
| Scenario IV | 32.459 | 13.608 | 58.08 | 17.408 | 9.235 | 46.95 | 39.647 | 21.527 | 45.70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Y.; Xu, T.; Chen, F.; He, X.; Li, S. Can Data Assimilation Improve Short-Term Prediction of Land Surface Variables? Remote Sens. 2022, 14, 5172. https://doi.org/10.3390/rs14205172
Tian Y, Xu T, Chen F, He X, Li S. Can Data Assimilation Improve Short-Term Prediction of Land Surface Variables? Remote Sensing. 2022; 14(20):5172. https://doi.org/10.3390/rs14205172
Chicago/Turabian StyleTian, Yingze, Tongren Xu, Fei Chen, Xinlei He, and Shi Li. 2022. "Can Data Assimilation Improve Short-Term Prediction of Land Surface Variables?" Remote Sensing 14, no. 20: 5172. https://doi.org/10.3390/rs14205172
APA StyleTian, Y., Xu, T., Chen, F., He, X., & Li, S. (2022). Can Data Assimilation Improve Short-Term Prediction of Land Surface Variables? Remote Sensing, 14(20), 5172. https://doi.org/10.3390/rs14205172








