Dithered Depth Imaging for Single-Photon Lidar at Kilometer Distances
Abstract
:1. Introduction
2. Method
2.1. Data Processing Method
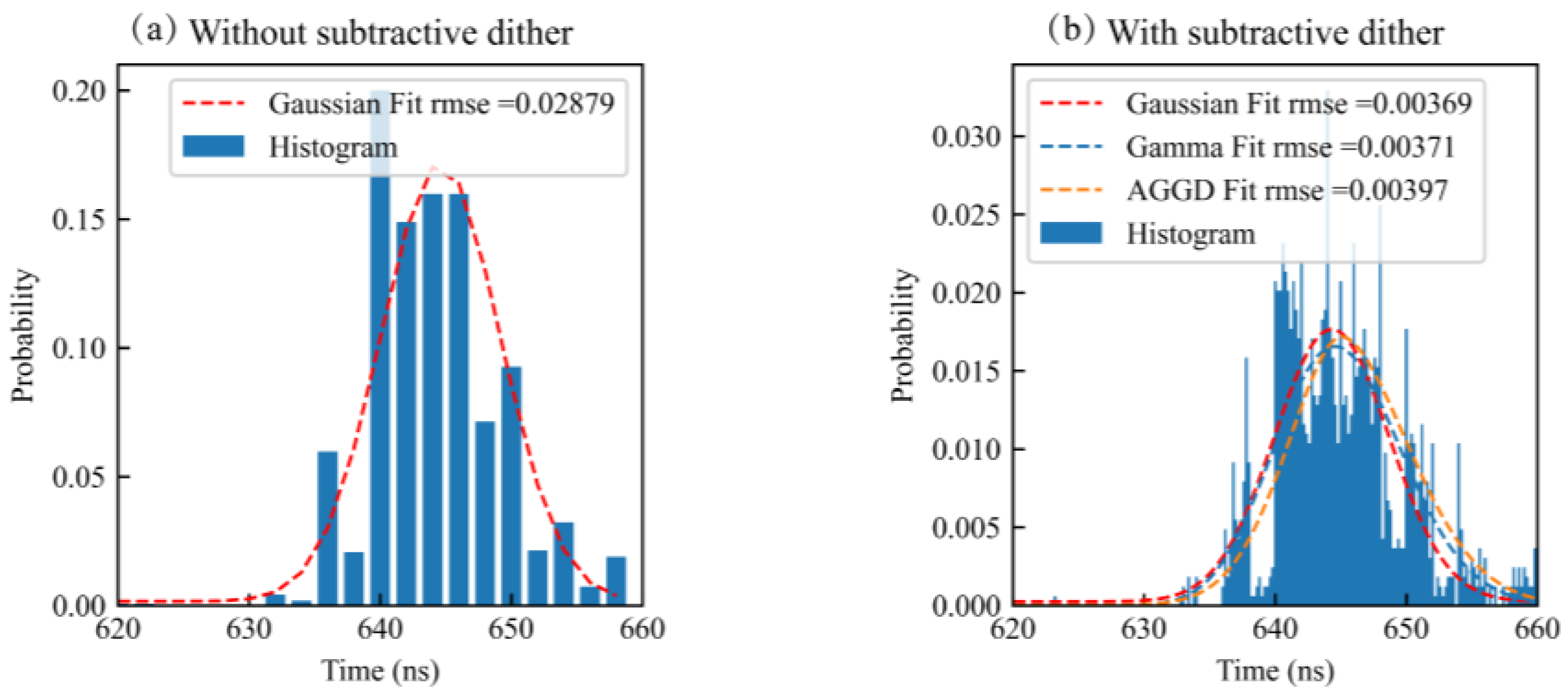
2.1.1. Subtractive Dither Depth Estimation
2.1.2. Censoring of Photon Data
2.1.3. Depth Image Restoration
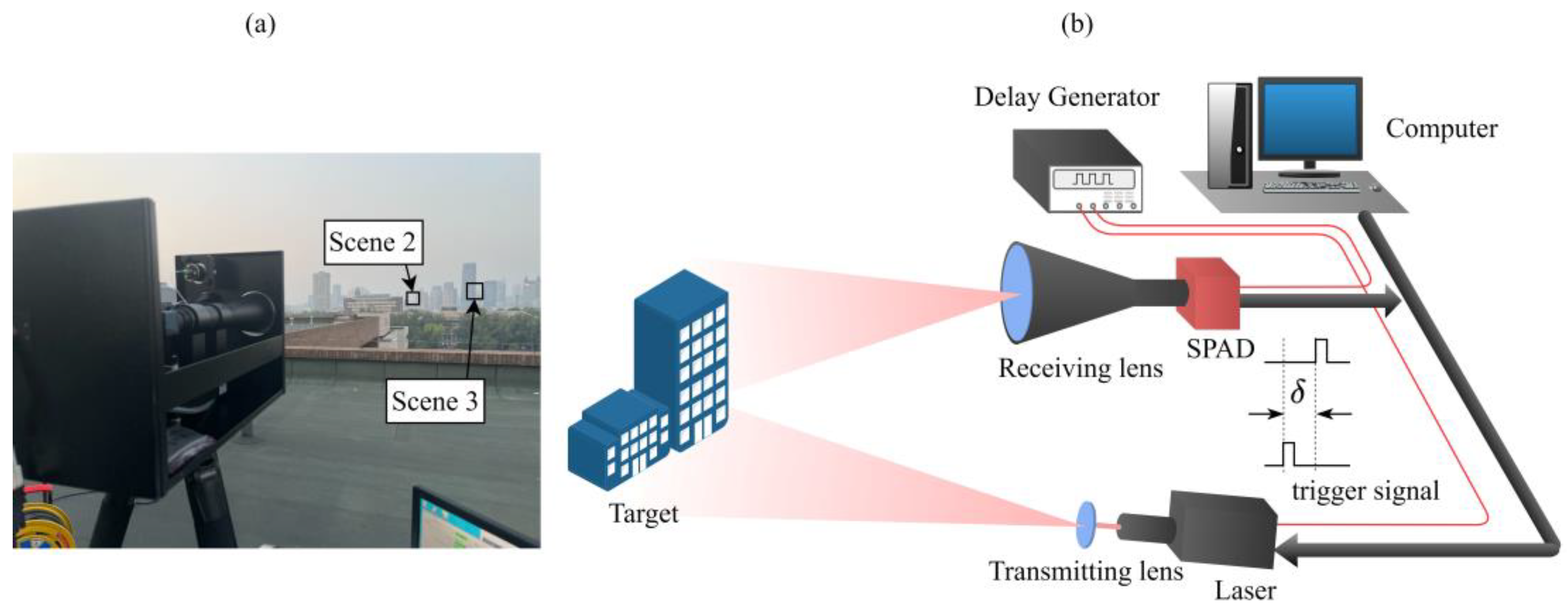
2.2. Dithered Single-Photon Lidar Measurement Setup
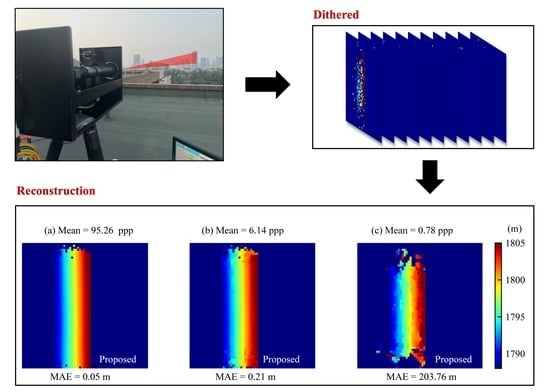
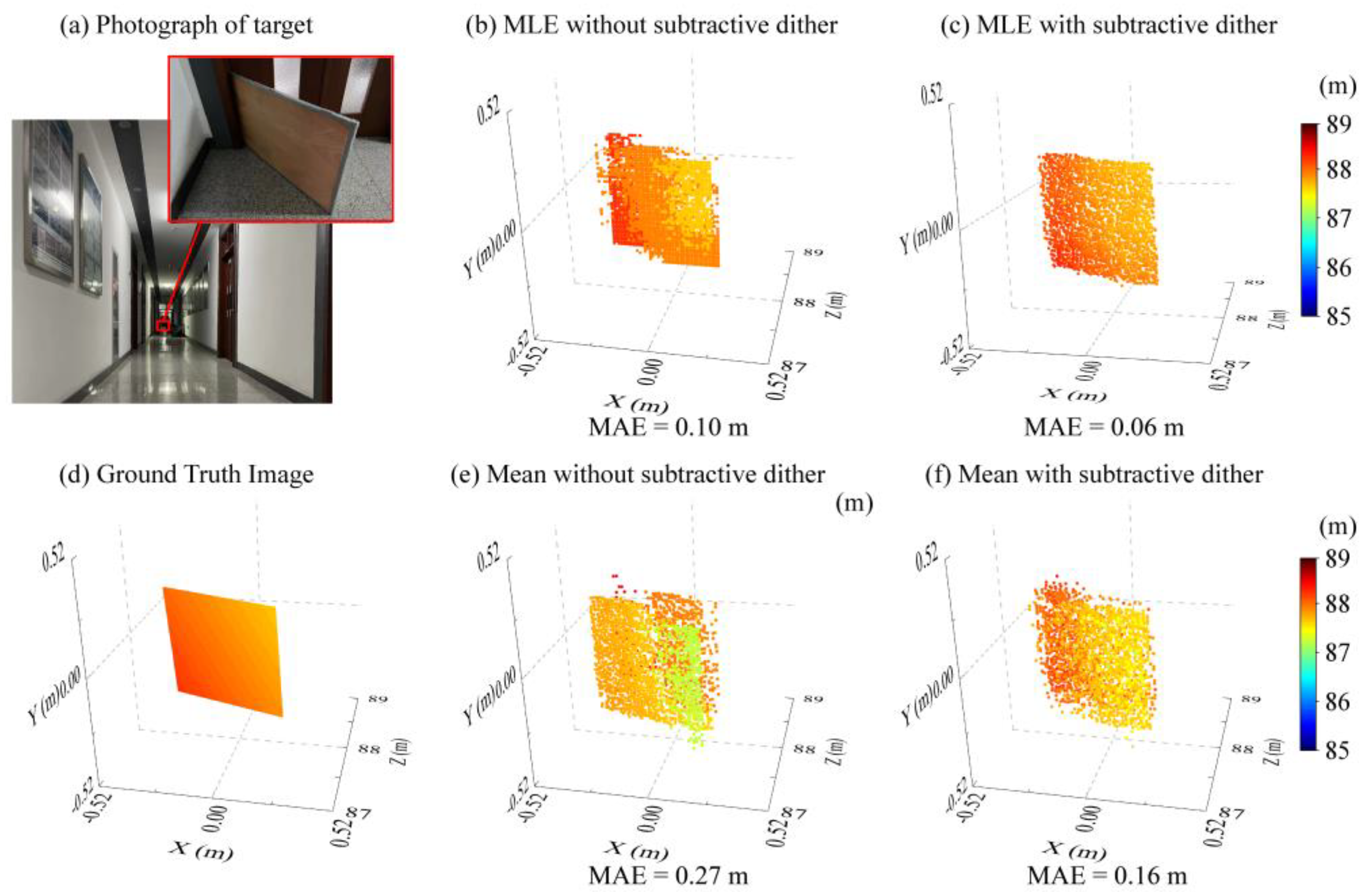
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Albota, M.; Gurjar, R.; Mangognia, A.; Dumanis, D.; Edwards, B. The Airborne Optical Systems Testbed (AOSTB). In Military Sensing Symp; MIT Lincoln Laboratory Lexington United States: Lexington, MA, USA, 2017. [Google Scholar]
- Clifton, W.E.; Steele, B.; Nelson, G.; Truscott, A.; Itzler, M.; Entwistle, M. Medium altitude airborne geiger-mode mapping lidar system. In Laser Radar Technology and Applications XX; and Atmospheric Propagation XII; SPIE: Bellingham, WA, USA, 2015; p. 9465. [Google Scholar]
- Rapp, J.; Tachella, J.; Altmann, Y.; McLaughlin, S.; Goyal, V.K. Advances in single-photon lidar for autonomous vehicles: Working principles, challenges, and recent advances. IEEE Signal Process. Mag. 2020, 37, 62–71. [Google Scholar] [CrossRef]
- Maccarone, A.; Acconcia, G.; Steinlehner, U.; Labanca, I.; Newborough, D.; Rech, I.; Buller, G. Custom-Technology Single-Photon Avalanche Diode Linear Detector Array for Underwater Depth Imaging. Sensors 2021, 21, 4850. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.-P.; Ye, J.-T.; Huang, X.; Jiang, P.-Y.; Cao, Y.; Hong, Y.; Yu, C.; Zhang, J.; Zhang, Q.; Peng, C.-Z.; et al. Single-photon imaging over 200 km. Optica 2021, 8, 344. [Google Scholar] [CrossRef]
- Shen, G.; Zheng, T.; Li, Z.; Yang, L.; Wu, G. Self-gating single-photon time-of-flight depth imaging with multiple repetition rates. Opt. Lasers Eng. 2021, 151, 106908. [Google Scholar] [CrossRef]
- Shen, G.; Zheng, T.; Li, Z.; Wu, E.; Yang, L.; Tao, Y.; Wang, C.; Wu, G. High-speed airborne single-photon LiDAR with GHz-gated single-photon detector at 1550 nm. Opt. Laser Technol. 2021, 141, 107109. [Google Scholar] [CrossRef]
- Liu, D.; Sun, J.; Gao, S.; Ma, L.; Jiang, P.; Guo, S.; Zhou, X. Single-parameter estimation construction algorithm for Gm-APD ladar imaging through fog. Opt. Commun. 2020, 482, 126558. [Google Scholar] [CrossRef]
- Xu, W.; Zhen, S.; Xiong, H.; Zhao, B.; Liu, Z.; Zhang, Y.; Ke, Z.; Zhang, B. Design of 128 × 32 GM-APD array ROIC with multi-echo detection for single photon 3D LiDAR. Proc. SPIE 2021, 11763, 117634A. [Google Scholar]
- Padmanabhan, P.; Zhang, C.; Cazzaniga, M.; Efe, B.; Ximenes, A.R.; Lee, M.-J.; Charbon, E. 7.4 A 256 × 128 3D-Stacked (45 nm) SPAD FLASH LiDAR with 7-Level Coincidence Detection and Progressive Gating for 100 m Range and 10klux Background Light. Proc. IEEE Int. Solid-State Circuits Conf. 2021, 64, 111–113. [Google Scholar]
- Mizuno, T.; Ikeda, H.; Makino, K.; Tamura, Y.; Suzuki, Y.; Baba, T.; Adachi, S.; Hashi, T.; Mita, M.; Mimasu, Y.; et al. Geiger-mode three-dimensional image sensor for eye-safe flash LIDAR. IEICE Electron. Express 2020, 17, 20200152. [Google Scholar] [CrossRef]
- Jahromi, S.S.; Jansson, J.-P.; Keränen, P.; Avrutin, E.A.; Ryvkin, B.S.; Kostamovaara, J.T. Solid-state block-based pulsed laser illuminator for single-photon avalanche diode detection-based time-of-flight 3D range imaging. Opt. Eng. 2021, 60, 054105. [Google Scholar] [CrossRef]
- Henriksson, M.; Allard, L.; Jonsson, P. Panoramic single-photon counting 3D lidar. Proc. SPIE 2018, 10796, 1079606. [Google Scholar]
- Raghuram, A.; Pediredla, A.; Narasimhan, S.G.; Gkioulekas, I.; Veeraraghavan, A. STORM: Super-resolving Transients by OveRsampled Measurements. Proc. IEEE Int. Conf. Comput. Photog. 2019, 44–54. [Google Scholar] [CrossRef]
- Wu, J.; Qian, Z.; Zhao, Y.; Yu, X.; Zheng, L.; Sun, W. 64 × 64 GM-APD array-based readout integrated circuit for 3D imaging applications. Sci. China Inf. Sci. 2019, 62, 62407. [Google Scholar] [CrossRef]
- Tan, C.; Kong, W.; Huang, G.; Hou, J.; Jia, S.; Chen, T.; Shu, R. Design and Demonstration of a Novel Long-Range Photon-Counting 3D Imaging LiDAR with 32 × 32 Transceivers. Remote Sens. 2022, 14, 2851. [Google Scholar] [CrossRef]
- Yuan, P.; Sudharsanan, R.; Bai, X.; Boisvert, J.; McDonald, P.; Labios, E.; Morris, B.; Nicholson, J.P.; Stuart, G.M.; Danny, H.; et al. Geiger-mode ladar cameras. Proc. SPIE 2011, 8037, 803712. [Google Scholar]
- Pawlikowska, A.M.; Halimi, A.; Lamb, R.A.; Buller, G.S. Single-photon three-dimensional imaging at up to 10 kilometers range. Opt. Express 2017, 25, 11919–11931. [Google Scholar] [CrossRef]
- Li, Z.-P.; Huang, X.; Cao, Y.; Wang, B.; Li, Y.-H.; Jin, W.; Yu, C.; Zhang, J.; Zhang, Q.; Peng, C.-Z.; et al. Single-photon computational 3D imaging at 45 km. Photonics Res. 2020, 8, 1532. [Google Scholar] [CrossRef]
- Chen, Z.; Fan, R.; Li, X.; Dong, Z.; Zhou, Z.; Ye, G.; Chen, D. Accuracy improvement of imaging lidar based on time-correlated single-photon counting using three laser beams. Opt. Commun. 2018, 429, 175–179. [Google Scholar] [CrossRef]
- Rapp, J.; Dawson, R.M.A.; Goyal, V.K. Dither-Enhanced Lidar. In Applications of Lasers for Sensing and Free Space Communications; Optica Publishing Group: Hong Kong, China, 2018; p. JW4A-38. [Google Scholar]
- Rapp, J.; Dawson, R.M.A.; Goyal, V.K. Improving Lidar Depth Resolution with Dither. Proc. IEEE Int. Conf. Image Process. 2018, 1553–1557. [Google Scholar] [CrossRef]
- Rapp, J.; Dawson, R.M.A.; Goyal, V.K. Estimation From Quantized Gaussian Measurements: When and How to Use Dither. IEEE Trans. Signal Process. 2019, 67, 3424–3438. [Google Scholar] [CrossRef]
- Rapp, J.; Dawson, R.M.A.; Goyal, V.K. Dithered Depth Imaging. Opt. Express 2020, 28, 35143–35157. [Google Scholar] [CrossRef] [PubMed]
- Yan, K.; Lifei, L.; Xuejie, D.; Tongyi, Z.; Dongjian, L.; Wei, Z. Photon-limited depth and reflectivity imaging with sparsity regularization. Opt. Commun. 2017, 392, 25–30. [Google Scholar] [CrossRef]
- Altmann, Y.; Ren, X.; McCarthy, A.; Buller, G.S.; McLaughlin, S. Lidar Waveform-Based Analysis of Depth Images Constructed Using Sparse Single-Photon Data. IEEE Trans. Image Process. 2016, 25, 1935–1946. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tachella, J.; Altmann, Y.; Marquez, M.; Arguello-Fuentes, H.; Tourneret, J.-Y.; McLaughlin, S. Bayesian 3D Reconstruction of Subsampled Multispectral Single-Photon Lidar Signals. IEEE Trans. Comput. Imaging 2019, 6, 208–220. [Google Scholar] [CrossRef]
- Kirmani, A.; Venkatraman, D.; Shin, D.; Colaço, A.; Wong, F.N.C.; Shapiro, J.H.; Goyal, V.K. First-Photon Imaging. Science 2014, 343, 58–61. [Google Scholar] [CrossRef]
- Shin, D.; Xu, F.; Venkatraman, D.; Lussana, R.; Villa, F.; Zappa, F.; Goyal, V.K.; Wong, F.N.C.; Shapiro, J.H. Photon-efficient imaging with a single-photon camera. Nat. Commun. 2016, 7, 12046. [Google Scholar] [CrossRef] [Green Version]
- Shin, D.; Shapiro, J.H.; Goyal, V.K. Single-Photon Depth Imaging Using a Union-of-Subspaces Model. IEEE Signal Process. Lett. 2015, 22, 2254–2258. [Google Scholar] [CrossRef] [Green Version]
- Harmany, Z.T.; Marcia, R.F.; Willett, R.M. This is SPIRAL-TAP: Sparse Poisson Intensity Reconstruction ALgorithms—Theory and Practice. IEEE Trans. Image Process. 2011, 21, 1084–1096. [Google Scholar] [CrossRef] [Green Version]
- Huang, P.; He, W.; Gu, G.; Chen, Q. Depth imaging denoising of photon-counting lidar. Appl. Opt. 2019, 58, 4390–4394. [Google Scholar] [CrossRef]
- Umasuthan, M.; Wallace, A.; Massa, J.; Buller, G.; Walker, A. Processing time-correlated single photon counting data to acquire range images. IEE Proc. Vis. Image Signal Process. 1998, 145, 237–243. [Google Scholar] [CrossRef] [Green Version]
- Kang, Y.; Li, L.; Li, D.; Liu, D.; Zhang, T.; Zhao, W. Performance analysis of different pixel-wise processing methods for depth imaging with single photon detection data. J. Mod. Opt. 2019, 66, 976–985. [Google Scholar] [CrossRef]

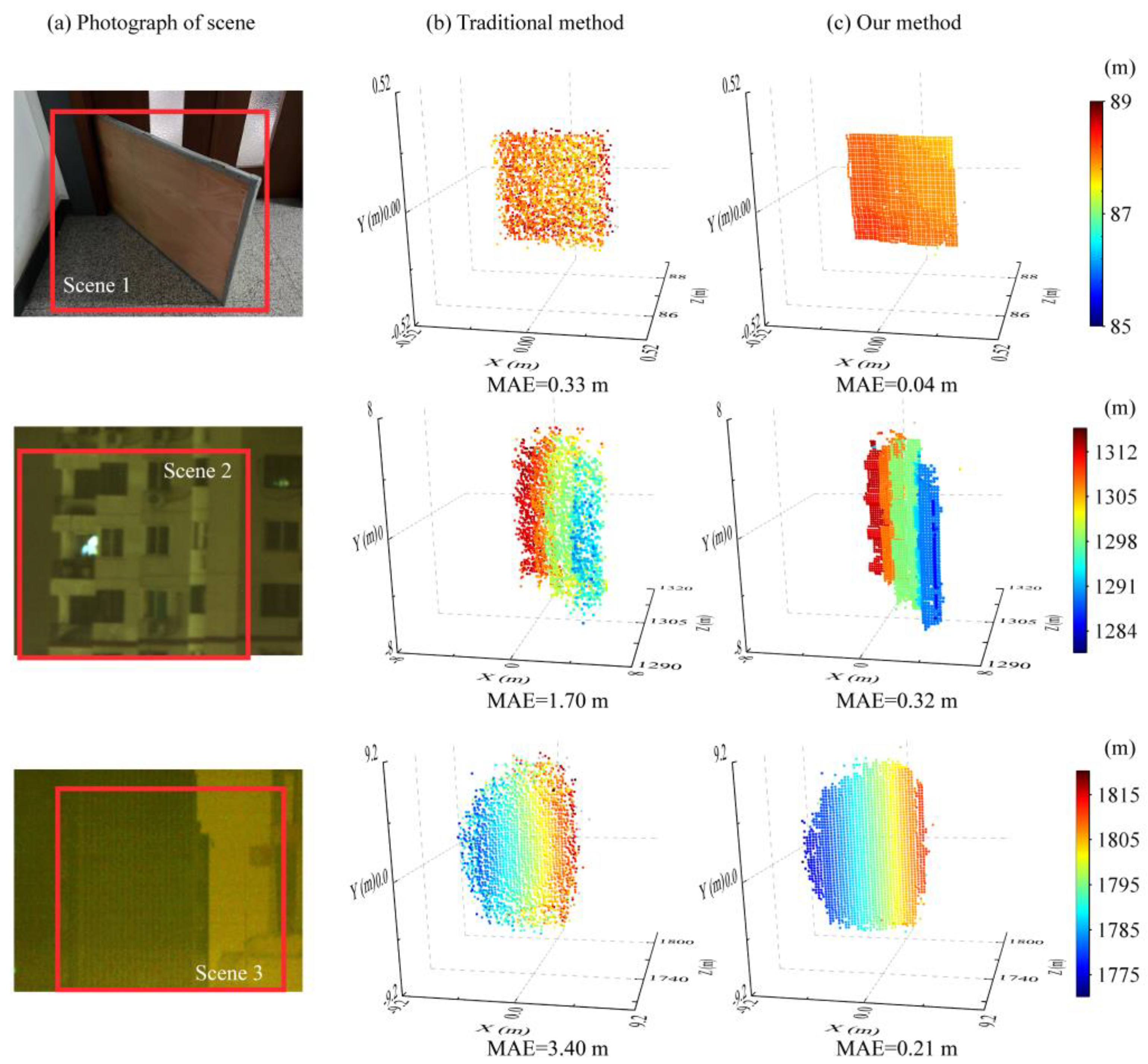


| MAE (m) | |||||
|---|---|---|---|---|---|
| without Subtractive Dither | with Subtractive Dither | ||||
| Scene | MLE | Mean | TV Regularized MLE | RSPE without TV | RSPE |
| scene 1 | 0.33 | 0.35 | 0.16 | 0.21 | 0.04 |
| scene 2 | 1.70 | 1.70 | 1.66 | 0.38 | 0.32 |
| scene 3 | 3.40 | 3.40 | 3.39 | 0.26 | 0.21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, J.; Li, J.; Chen, K.; Liu, S.; Wang, Y.; Zhong, K.; Xu, D.; Yao, J. Dithered Depth Imaging for Single-Photon Lidar at Kilometer Distances. Remote Sens. 2022, 14, 5304. https://doi.org/10.3390/rs14215304
Chang J, Li J, Chen K, Liu S, Wang Y, Zhong K, Xu D, Yao J. Dithered Depth Imaging for Single-Photon Lidar at Kilometer Distances. Remote Sensing. 2022; 14(21):5304. https://doi.org/10.3390/rs14215304
Chicago/Turabian StyleChang, Jiying, Jining Li, Kai Chen, Shuai Liu, Yuye Wang, Kai Zhong, Degang Xu, and Jianquan Yao. 2022. "Dithered Depth Imaging for Single-Photon Lidar at Kilometer Distances" Remote Sensing 14, no. 21: 5304. https://doi.org/10.3390/rs14215304
APA StyleChang, J., Li, J., Chen, K., Liu, S., Wang, Y., Zhong, K., Xu, D., & Yao, J. (2022). Dithered Depth Imaging for Single-Photon Lidar at Kilometer Distances. Remote Sensing, 14(21), 5304. https://doi.org/10.3390/rs14215304