Comparison of Mean Dynamic Topography Modeling from Multivariate Objective Analysis and Rigorous Least Squares Method
Abstract
1. Introduction
2. Method
2.1. Rigorous Least Squares Method
2.2. Multivariate Objective Analysis
3. Data and Study Area
3.1. Mean Sea Surface Model
3.2. Global Geopotential Model
3.3. Synthetic/Ocean MDT Models
3.4. Drifting Buoy Data
4. Results
4.1. MDT Modeling from the MOA and LS Method
4.2. Assessment of MDTs Computed from MOA and LS Method
4.3. Formal Errors of the MDTs Estimated by MOA and LS Method
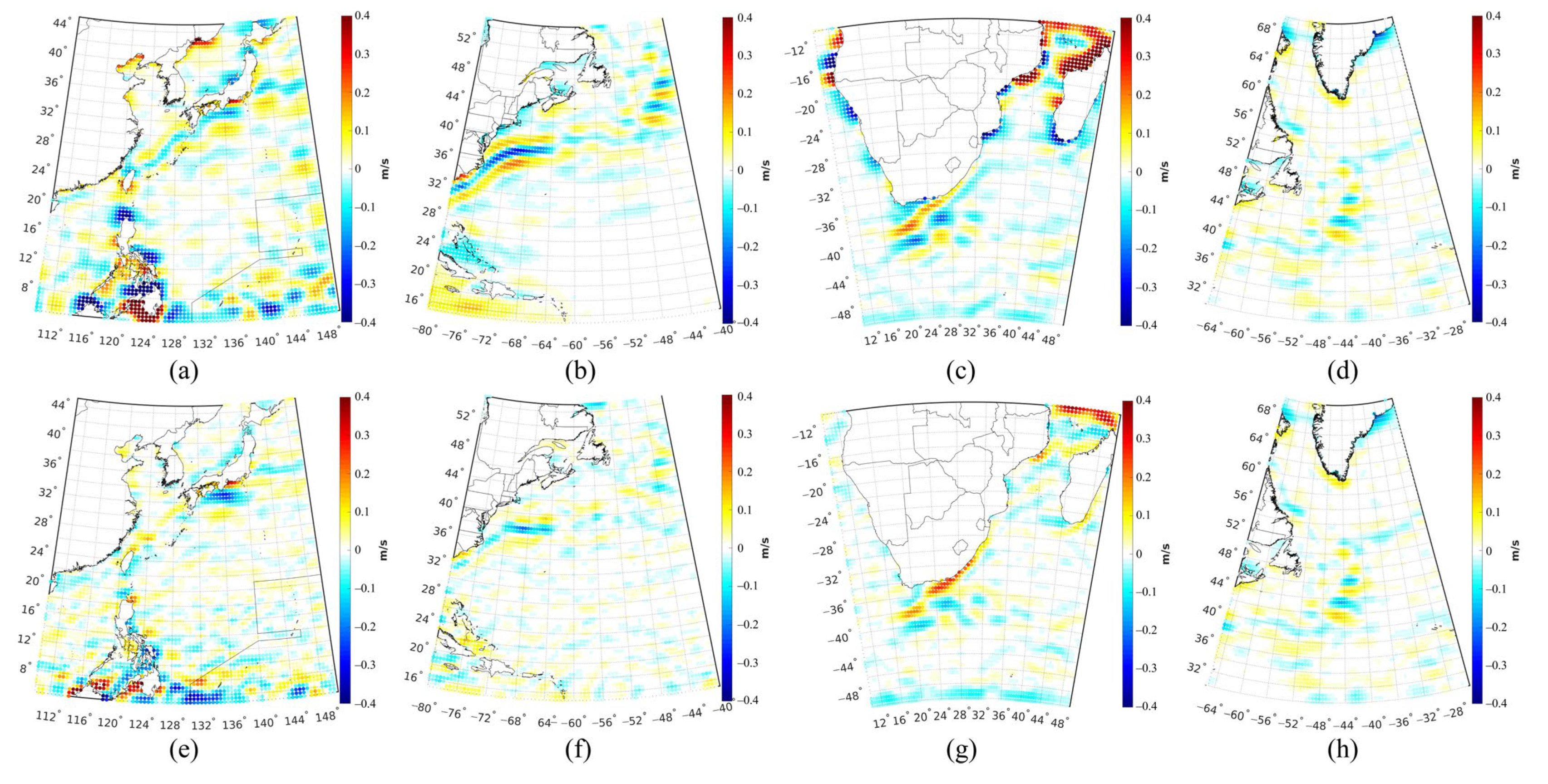
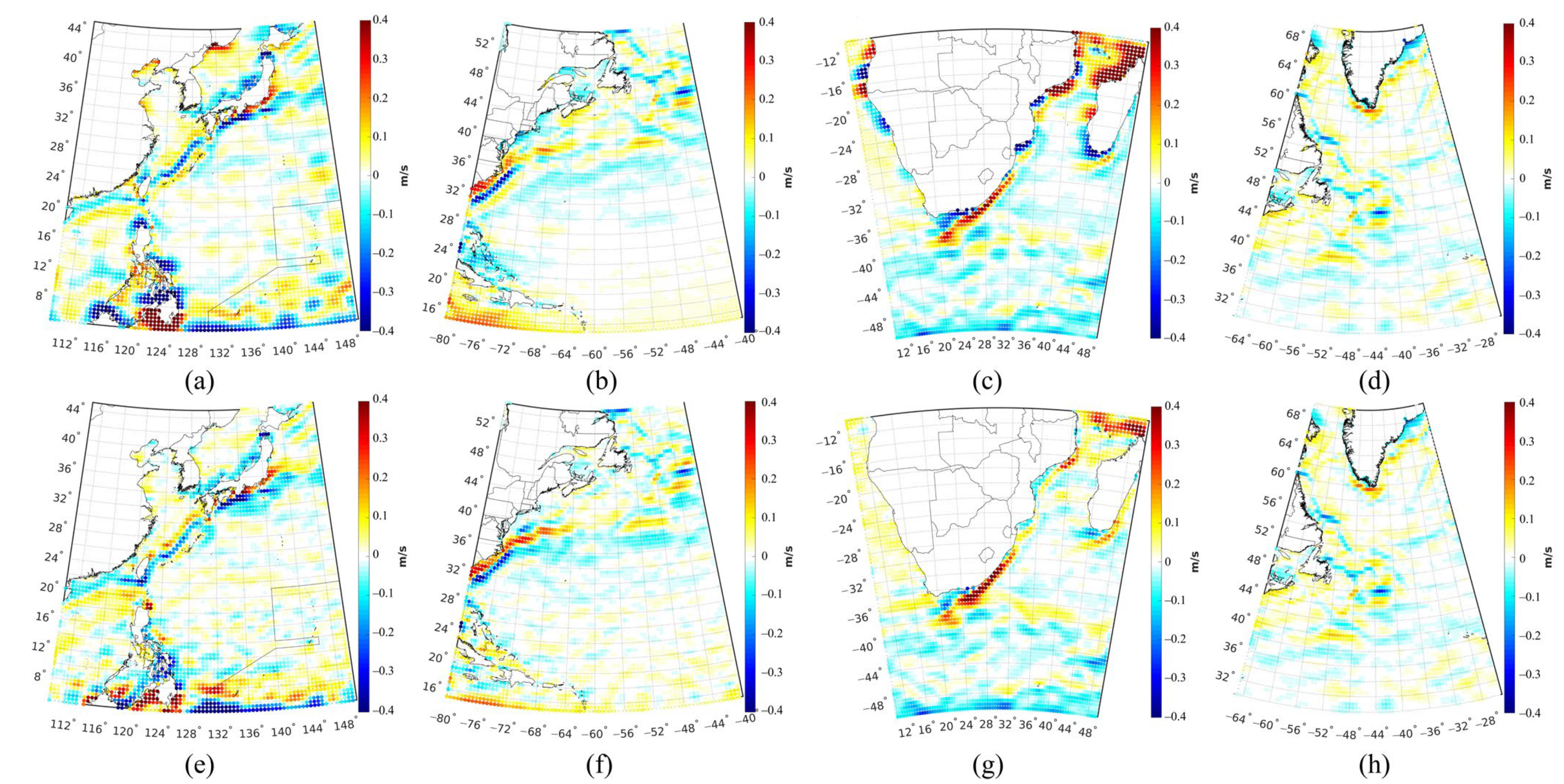
4.4. Comparison of Geostrophic Velocities Estimated by MDTs Derived from Different Methods
5. Discussion
6. Conclusions
- (1)
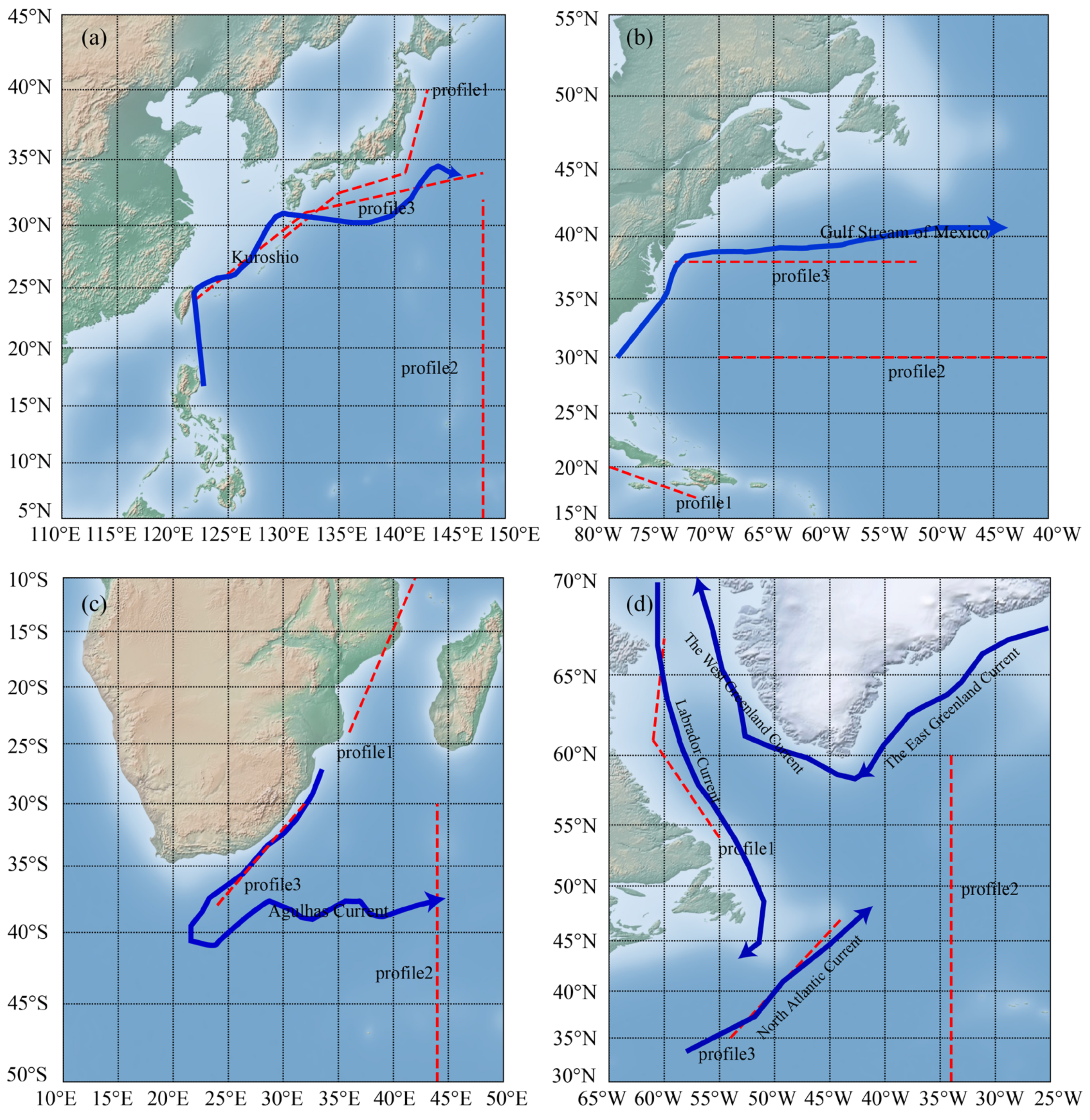
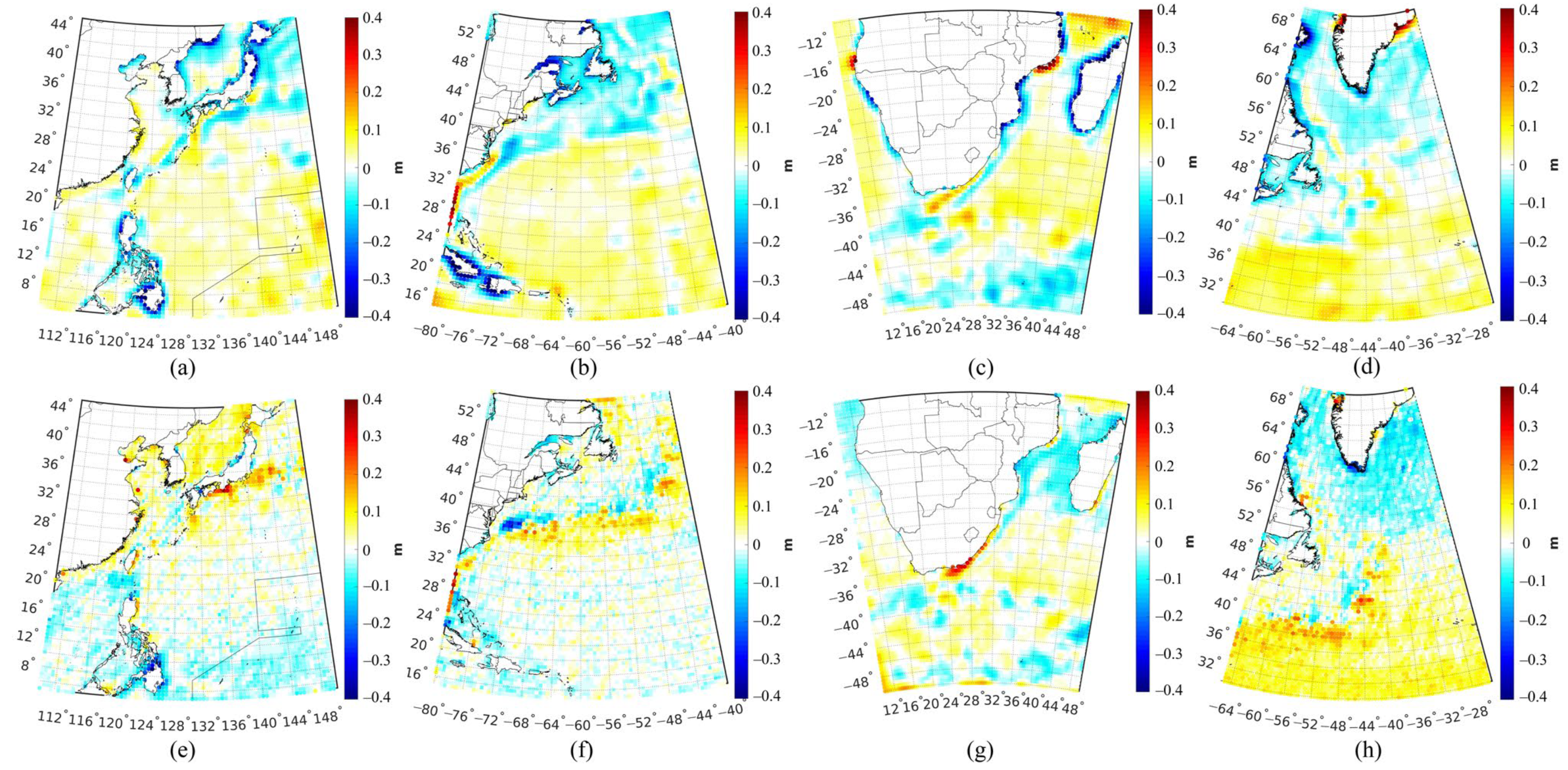
- The MDT derived from the LS method outperformed the MDT computed from the MOA method, especially over coastal areas and ocean current areas. The RMSs of the discrepancies between the LS-derived MDT and ocean data were 4.8 cm, 4.7 cm, 4.9 cm and 7.2 cm, for the Kuroshio Current area, Gulf Current area, Agulhas Current area and Greenland Current area, respectively, which were lower than those of the MOA-derived MDT, by a magnitude of 1.4 cm, 2.2 cm, 2.6 cm and −0.5 cm, respectively. The reason is that the LS method constructs the design matrix segmentally based on the error characteristics of the GGM, and then the signals are processed and constrained in different frequency bands to suppress high-frequency noise, which improves the quality of the estimated MDT;
- (2)
- The formal error of the MDT estimated by the LS method was more reasonable than that estimated by the MOA method. The errors of the MDT estimated by the LS method were prominent over coastal areas, which have larger magnitude, than estimated by the MOA method. The patterns of the formal errors of the LS-derived MDT were more realistic, since the errors of MSS models usually exceeded decimeter level along the coast, indicating the formal error of MDT computed from the MSS and geoid has at least the same magnitude of error as MSS, through error propagation;
- (3)
- Moreover, the geostrophic velocity derived from the LS-derived MDT was better than from the MOA-derived MDT, especially over coastal regions and ocean current areas. The RMSs of the discrepancies between the zonal (meridional) velocities calculated by the LS-derived MDT and the buoy data were 0.4 cm/s (2.0 cm/s), 0.2 cm/s (0.3 cm/s) and 1.1 cm/s (2.3 cm/s) smaller than of the velocities calculated by the MOA-derived MDT over the Kuroshio Current area, Gulf Current area and Agulhas Current area, respectively. The comparison between geostrophic velocities estimated by MDTs derived from different methods and the ocean models showed similar results. The results indicate that the LS-derived MDT outperforms the MOA-derived MDT.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Filmer, M.S.; Hughes, C.W.; Woodworth, P.L.; Featherstone, W.E.; Bingham, R.J. Comparison between geodetic and oceanographic approaches to estimate mean dynamic topography for vertical datum unification: Evaluation at Australian tide gauges. J. Geod. 2018, 12, 1413–1437. [Google Scholar] [CrossRef]
- Chaigneau, A.A.; Reffray, G.; Voldoire, A.; Melet, A. IBI-CCS: A regional high-resolution model to simulate sea level in western Europe. Geosci. Model Dev. 2022, 5, 2035–2062. [Google Scholar] [CrossRef]
- Lin, H.; Thompson, K.R.; Huang, J.; Véronneau, M. Tilt of mean sea level along the Pacific coasts of North America and Japan. J. Geophys. Res. Oceans 2015, 120, 6815–6828. [Google Scholar] [CrossRef]
- Song, X. The importance of including sea surface current when estimating air–sea turbulent heat fluxes and wind stress in the Gulf Stream region. J. Atmos. Ocean. Tech. 2021, 1, 119–138. [Google Scholar] [CrossRef]
- Onink, V.; Wichmann, D.; Delandmeter, P.; van Sebille, E. The role of Ekman currents, geostrophy, and stokes drift in the accumulation of floating microplastic. J. Geophys. Res. Oceans 2019, 3, 1474–1490. [Google Scholar] [CrossRef]
- Wu, Y.; Abulaitijiang, A.; Featherstone, W.E.; McCubbine, J.C.; Andersen, O.B. Coastal gravity field refinement by combining airborne and ground-based data. J. Geod. 2019, 93, 2569–2584. [Google Scholar] [CrossRef]
- Wu, Y.; Huang, J.; Shi, H.; He, X. Mean Dynamic Topography Modeling Based on Optimal Interpolation from Satellite Gravimetry and Altimetry Data. Appl. Sci. 2021, 11, 5286. [Google Scholar] [CrossRef]
- Bingham, R.J.; Haines, K.; Hughes, C.W. Calculating the ocean’s mean dynamic topography from a mean sea surface and a geoid. J. Atmos. Ocean. Tech. 2008, 10, 1808–1822. [Google Scholar] [CrossRef]
- Knudsen, P.; Bingham, R.; Andersen, O.; Rio, M.H. A global mean dynamic topography and ocean circulation estimation using a preliminary GOCE gravity model. J. Geod. 2011, 85, 861–879. [Google Scholar] [CrossRef]
- Zhang, Z.; Lu, Y.; Hsu, H. Detecting surface geostrophic currents using wavelet filter from satellite geodesy. Sci. China Ser. D-Earth Sci. 2007, 50, 918–926. [Google Scholar] [CrossRef]
- Vianna, M.L.; Menezes, V.V.; Chambers, D.P. A high resolution satellite-only GRACE-based mean dynamic topography of the South Atlantic Ocean. Geophys. Res. Lett. 2007, 34, L24604. [Google Scholar] [CrossRef]
- Bingham, R.J.; Knudsen, P.; Andersen, O.; Pail, R. An initial estimate of the North Atlantic steady-state geostrophic circulation from GOCE. Geophys. Res. Lett. 2011, 38, L01606. [Google Scholar] [CrossRef][Green Version]
- Becker, S.; Freiwald, G.; Losch, M.; Schuh, W.D. Rigorous Fusion of Gravity Field, Altimetry and Stationary Ocean Models. J. Geodyn. 2012, 60, 99–110. [Google Scholar] [CrossRef]
- Becker, S.; Brockmann, J.M.; Schuh, W.D. Mean Dynamic Topography Estimates Purely Based on GOCE Gravity Field Models and Altimetry. Geophys. Res. Lett. 2014, 41, 2063–2069. [Google Scholar] [CrossRef]
- Shi, H.; He, X.; Wu, Y.; Huang, J. The parameterization of mean dynamic topography based on the Lagrange basis functions. Adv. Space Res. 2020, 9, 2122–2140. [Google Scholar] [CrossRef]
- Rio, M.H.; Hernandez, F.A. Mean dynamic topography computed over the world ocean from altimetry, in situ measurements, and a geoid model. J. Geophys. Res. Oceans 2004, 109, C12032. [Google Scholar] [CrossRef]
- Rio, M.H.; Guinehut, S.; Larnicol, G. New CNES-CLS09 global mean dynamic topography computed from the combination of GRACE data, altimetry, and in situ measurements. J. Geophys. Res. Oceans 2011, 116, C07018. [Google Scholar] [CrossRef]
- Rio, M.-H.; Mulet, S.; Picot, N. Beyond GOCE for the ocean circulation estimate: Synergetic use of altimetry, gravimetry, and in situ data provides new insight into geostrophic and Ekman currents. Geophys. Res. Lett. 2014, 41, 8918–8925. [Google Scholar] [CrossRef]
- Lefèvre, F.; Lyard, F.H.; Le Provost, C. FES98: A new global tide finite element solution independent of altimetry. Geophys. Res. Lett. 2000, 17, 2717–2720. [Google Scholar] [CrossRef]
- Shi, H.; He, X.; Wu, Y.; Andersen, O.B.; Knudsen, P.; Liu, Y.; Zhang, Z. Spectrally Consistent Mean Dynamic Topography by Combining Mean Sea Surface and Global Geopotential Model Through a Least Squares-Based Approach. Front. Earth Sci. 2022, 10, 795935. [Google Scholar] [CrossRef]
- Wu, Y.; Huang, J.; He, X.; Luo, Z.; Wang, H. Coastal Mean Dynamic Topography Recovery Based on Multivariate Objective Analysis by Combining Data from Synthetic Aperture Radar Altimeter. Remote Sens. 2022, 14, 240. [Google Scholar] [CrossRef]
- Bretherton, F.P.; Davis, R.E.; Fandry, C.B. A technique for objective analysis and design of oceanographic experiments applied to MODE-73. Deep Sea Res. Oceanogr. Abstr. 1976, 23, 559–582. [Google Scholar] [CrossRef]
- Arhan, M.; De Verdiére, A.C. Dynamics of eddy motions in the eastern North Atlantic. J. Phys. Oceanogr. 1985, 15, 153–170. [Google Scholar] [CrossRef]
- Oka, E.; Kawabe, M. Dynamic Structure of the Kuroshio South of Kyushu in Relation to the Kuroshio Path Variations. J. Geophys. Res. 2003, 59, 595–608. [Google Scholar] [CrossRef]
- Oey, L.Y.; Ezer, T.; Forristall, G.; Cooper, C.; DiMarco, S.; Fan, S. An exercise in forecasting loop current and eddy frontal positions in the Gulf of Mexico. Geophys. Res. Lett. 2005, 12, L12611. [Google Scholar] [CrossRef]
- Franzese, A.M.; Hemming, S.R.; Goldstein, S.L.; Anderson, R.F. Reduced Agulhas Leakage during the Last Glacial Maximum inferred from an integrated provenance and flux study. Earth Planet. Sci. Lett. 2006, 1–2, 72–88. [Google Scholar] [CrossRef]
- Schlichtholz, P.; Houssais, M.N. An investigation of the dynamics of the East Greenland Current in Fram Strait based on a simple analytical model. J. Phys. Oceanogr. 1999, 29, 2240–2265. [Google Scholar] [CrossRef]
- Jiang, L.; Nielsen, K.; Dinardo, S.; Andersen, O.B.; Bauer-Gottwein, P. Evaluation of Sentinel-3 SRAL SAR altimetry over Chinese rivers. Remote Sens. Environ. 2020, 237, 111546. [Google Scholar] [CrossRef]
- Andersen, O.B.; Abulaitijiang, A.; Zhang, S.; Rose, S.K. A new high resolution Mean Sea Surface (DTU21MSS) for improved sea level monitoring. In Proceedings of the EGU General Assembly 2021, Göttingen Germany, 19–30 April 2021. EGU21-16084. [Google Scholar] [CrossRef]
- Förste, C.; Abrykosov, O.; Bruinsma, S.; Dahle, C.; König, R.; Lemoine, J.M. ESA’s Release 6 GOCE Gravity Field Model by Means of the Direct Approach Based on Improved Filtering of the Reprocessed Gradients of the Entire Mission; Data Publication; GFZ Data Services: Potsdam, Germany, 2019. [Google Scholar] [CrossRef]
- Carton, J.A.; Chepurin, G.A.; Chen, L. SODA3: A New Ocean Climate Reanalysis. J. Clim. 2018, 31, 6967–6983. [Google Scholar] [CrossRef]
- Zuo, H.; Balmaseda, M.A.; Tietsche, S.; Mogensen, K.; Mayer, M. The ECMWF operational ensemble reanalysis–analysis system for ocean and sea ice: A description of the system and assessment. Ocean Sci. 2019, 15, 779–808. [Google Scholar] [CrossRef]
- Mulet, S.; Rio, M.-H.; Etienne, H.; Artana, C.; Cancet, M.; Dibarboure, G.; Feng, H.; Husson, R.; Picot, N.; Provost, C.; et al. The new CNES-CLS18 global mean dynamic topography. Ocean Sci. 2021, 17, 789–808. [Google Scholar] [CrossRef]
- Mayer-Gürr, T.; Kvas, A.; Klinger, B.; Rieser, D.; Zehentner, N.; Pail, R. The combined satellite gravity field model GOCO05s. In Proceedings of the EGU General Assembly, Vienna, Austria, 12–17 April 2015. [Google Scholar]
- Bingham, R.J.; Haines, K. Mean dynamic topography: Intercomparisons and errors. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 903–916. [Google Scholar] [CrossRef]
- Ophaug, V.; Breili, K.; Gerlach, C. A comparative assessment of coastal mean dynamic topography in Norway by geodetic and ocean approaches. J. Geophys. Res. Oceans 2015, 120, 7807–7826. [Google Scholar] [CrossRef]
- Idžanović, M.; Ophaug, V.; Andersen, O.B. The coastal mean dynamic topography in Norway observed by CryoSat-2 and GOCE. Geophys. Res. Lett. 2017, 44, 5609–5617. [Google Scholar] [CrossRef]
- Wu, Y.; Abulaitijiang, A.; Andersen, O.B.; He, X.; Luo, Z.; Wang, H. Refinement of Mean Dynamic Topography Over Island Areas Using Airborne Gravimetry and Satellite Altimetry Data in the Northwestern South China Sea. J. Geophys. Res. Solid Earth 2021, 126, e2021JB021805. [Google Scholar] [CrossRef]
- Lumpkin, R.; Johnson, G.C. Global ocean surface velocities from drifters: Mean, variance, El Niño-Southern Oscillation response, and seasonal cycle. J. Geophys. Res. Oceans 2013, 118, 2992–3006. [Google Scholar] [CrossRef]
- Zingerle, P.; Pail, R.; Gruber, T.; Oikonomidou, X. The combined global gravity field model XGM2019e. J. Geod. 2020, 94, 66. [Google Scholar] [CrossRef]
- Lawson, C.L.; Hanson, R.J. Solving Least Squares Problems; Society for Industrial and Applied Mathematics: New York, NY, USA, 1995. [Google Scholar]
- Hwang, C.; Chen, S.A. Circulations and eddies over the South China Sea derived from TOPEX/Poseidon altimetry. J. Geophys. Res. Space Phys. 2000, 105, 23943–23965. [Google Scholar] [CrossRef]





| Area | Method | Min | Max | RMS |
|---|---|---|---|---|
| Kuroshio Current area | MOA | −54.6 | 15.3 | 6.2 |
| LS | −42.4 | 33.6 | 4.8 | |
| Gulf Current area | MOA | −75.4 | 40.4 | 6.9 |
| LS | −36.0 | 39.9 | 4.7 | |
| Agulhas Current area | MOA | −59.7 | 59.6 | 7.5 |
| LS | −36.5 | 32.2 | 4.9 | |
| Greenland Current area | MOA | −58.8 | 65.3 | 6.7 |
| LS | −29.8 | 28.9 | 7.2 |
| Study Area | Method | Geostrophic Velocities | Min | Max | RMS |
|---|---|---|---|---|---|
| Kuroshio Current area | MOA | u | −104.7 | 99.0 | 16.1 |
| v | −103.7 | 169.1 | 15.4 | ||
| LS | u | −116.6 | 75.1 | 15.7 | |
| v | −98.9 | 95.0 | 13.4 | ||
| Gulf Current area | MOA | u | −66.9 | 51.9 | 10.1 |
| v | −156.1 | 51.7 | 12.1 | ||
| LS | u | −63.6 | 50.4 | 9.9 | |
| v | −151.2 | 61.1 | 11.8 | ||
| Agulhas Current area | MOA | u | −126.3 | 110.9 | 19.7 |
| v | −171.8 | 129.2 | 23.3 | ||
| LS | u | −124.9 | 113.3 | 18.6 | |
| v | −119.0 | 123.6 | 21.0 | ||
| Greenland Current area | MOA | u | −77.5 | 48.6 | 8.4 |
| v | −58.7 | 68.6 | 9.0 | ||
| LS | u | −77.5 | 48.6 | 8.4 | |
| v | −58.7 | 68.6 | 9.0 |
| Study Area | Method | Geostrophic Velocities | Min | Max | RMS |
|---|---|---|---|---|---|
| Kuroshio Current area | MOA | u | −95.8 | 123.7 | 9.7 |
| v | −127.1 | 115.4 | 10.9 | ||
| LS | u | −45.3 | 74.7 | 5.9 | |
| v | −54.6 | 48.9 | 5.9 | ||
| Gulf Current area | MOA | u | −29.3 | 26.2 | 4.3 |
| v | −72.1 | 22.3 | 4.5 | ||
| LS | u | −21.4 | 13.9 | 2.7 | |
| v | −68.9 | 16.3 | 3.8 | ||
| Agulhas Current area | MOA | u | −79.1 | 140.2 | 10.7 |
| v | −176.1 | 125.3 | 14.0 | ||
| LS | u | −14.9 | 36.3 | 4.6 | |
| v | −28.2 | 29.3 | 3.7 | ||
| Greenland Current area | MOA | u | −26.1 | 14.6 | 2.9 |
| v | −29.6 | 26.4 | 2.7 | ||
| LS | u | −19.7 | 12.6 | 2.7 | |
| v | −12.2 | 15.8 | 2.4 |
| Study Area | Method | Geostrophic Velocities | Min | Max | RMS |
|---|---|---|---|---|---|
| Kuroshio Current area | MOA | u | −106.4 | 151.5 | 12.2 |
| v | −133.7 | 155.1 | 13.4 | ||
| LS | u | −59.0 | 74.9 | 9.1 | |
| v | −64.2 | 99.3 | 8.9 | ||
| Gulf Current area | MOA | u | −60.7 | 33.5 | 5.4 |
| v | −108.0 | 33.0 | 7.2 | ||
| LS | u | −67.1 | 33.6 | 5.3 | |
| v | −96.7 | 41.2 | 6.7 | ||
| Agulhas Current area | MOA | u | −77.2 | 136.2 | 12.4 |
| v | −192.7 | 121.7 | 15.0 | ||
| LS | u | −29.2 | 59.6 | 7.5 | |
| v | −58.3 | 52.9 | 6.9 | ||
| Greenland Current area | MOA | u | −28.0 | 23.8 | 3.9 |
| v | −30.3 | 26.7 | 4.1 | ||
| LS | u | −28.1 | 26.7 | 3.7 | |
| v | −19.3 | 22.5 | 3.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; He, X.; Huang, J.; Shi, H.; Wang, H.; Wu, Y.; Ding, Y. Comparison of Mean Dynamic Topography Modeling from Multivariate Objective Analysis and Rigorous Least Squares Method. Remote Sens. 2022, 14, 5330. https://doi.org/10.3390/rs14215330
Wu Y, He X, Huang J, Shi H, Wang H, Wu Y, Ding Y. Comparison of Mean Dynamic Topography Modeling from Multivariate Objective Analysis and Rigorous Least Squares Method. Remote Sensing. 2022; 14(21):5330. https://doi.org/10.3390/rs14215330
Chicago/Turabian StyleWu, Yihao, Xiufeng He, Jia Huang, Hongkai Shi, Haihong Wang, Yunlong Wu, and Yuan Ding. 2022. "Comparison of Mean Dynamic Topography Modeling from Multivariate Objective Analysis and Rigorous Least Squares Method" Remote Sensing 14, no. 21: 5330. https://doi.org/10.3390/rs14215330
APA StyleWu, Y., He, X., Huang, J., Shi, H., Wang, H., Wu, Y., & Ding, Y. (2022). Comparison of Mean Dynamic Topography Modeling from Multivariate Objective Analysis and Rigorous Least Squares Method. Remote Sensing, 14(21), 5330. https://doi.org/10.3390/rs14215330







