Next Article in Journal
Advances in Remote Sensing of the Inland and Coastal Water Zones
Next Article in Special Issue
Individual Tree Detection in Coal Mine Afforestation Area Based on Improved Faster RCNN in UAV RGB Images
Previous Article in Journal
A Spatiotemporal Atmospheric Refraction Correction Method for Improving the Geolocation Accuracy of High-Resolution Remote Sensing Images
Previous Article in Special Issue
Semantic Segmentation Guided Coarse-to-Fine Detection of Individual Trees from MLS Point Clouds Based on Treetop Points Extraction and Radius Expansion
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 14
Issue 21
10.3390/rs14215345
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Refinement of Individual Tree Detection Results Obtained from Airborne Laser Scanning Data for a Mixed Natural Forest

by
Nenad Brodić
1,*,
Željko Cvijetinović
1,
Milutin Milenković
2,3,
Jovan Kovačević
1,
Nikola Stančić
1,
Momir Mitrović
4 and
Dragan Mihajlović
1
1
Faculty of Civil Engineering, University of Belgrade, Bulevar kralja Aleksandra 73, 11000 Belgrade, Serbia
2
International Institute for Applied Systems Analysis (IIASA), Novel Data Ecosystems for Sustainability (NODES), Schlossplatz 1, A-2361 Laxenburg, Austria
3
Laboratory of Geo-Information Science and Remote Sensing, Department of Environmental Sciences, Wageningen University, Droevendaalsesteeg 3, 6708PB Wageningen, The Netherlands
4
MapSoft d.o.o, Ustanička 64/7, 11000 Belgrade, Serbia
*
Author to whom correspondence should be addressed.
Remote Sens. 2022, 14(21), 5345; https://doi.org/10.3390/rs14215345
Submission received: 25 August 2022 / Revised: 15 October 2022 / Accepted: 19 October 2022 / Published: 25 October 2022
(This article belongs to the Special Issue Applications of Individual Tree Detection (ITD))
Browse Figures
Versions Notes

Abstract

:
Numerous semi- and fully-automatic algorithms have been developed for individual tree detection from airborne laser-scanning data, but different rates of falsely detected treetops also accompany their results. In this paper, we proposed an approach that includes a machine learning-based refinement step to reduce the number of falsely detected treetops. The approach involves the local maxima filtering and segmentation of the canopy height model to extract different segment-level features used for the classification of treetop candidates. The study was conducted in a mixed temperate forest, predominantly deciduous, with a complex topography and an area size of 0.6 km × 4 km. The classification model’s training was performed by five machine learning approaches: Random Forest (RF), Extreme Gradient Boosting, Artificial Neural Network, the Support Vector Machine, and Logistic Regression. The final classification model with optimal hyperparameters was adopted based on the best-performing classifier (RF). The overall accuracy (OA) and kappa coefficient (κ) obtained from the ten-fold cross validation for the training data were 90.4% and 0.808, respectively. The prediction of the test data resulted in an OA = 89.0% and a κ = 0.757. This indicates that the proposed method could be an adequate solution for the reduction of falsely detected treetops before tree crown segmentation, especially in deciduous forests.

1. Introduction

Remote-sensing technologies are used by foresters as common tools for collecting geometric and radiometric information in order to improve forest management. Especially in the last decades, LiDAR (Light Detection and Ranging), as a remote-sensing technology that provides high spatial resolution, has rapidly progressed and showed great potential for the measurement, mapping, or monitoring of forests [1].
An airborne laser scanner (ALS) system is a type of LiDAR system that is mounted on an aerial platform. ALS systems are a widely used technology in forestry, given that the collected data can be successfully used for 3D terrain model generation and tree height determination in forested areas.
When using ALS point clouds, it is possible to detect single trees and determine the characteristics of an individual tree, such as its height, location, and crown dimensions, which can then provide accurate estimates for the stem volume and mean height at the stand-level [2]. There have been numerous semi- and fully-automatic algorithms developed in the last two decades for individual tree crown detection and delineation [3]. Hyyppä et al. [2,4] started with Individual Tree Detection (ITD) in boreal forests by using ALS data. Afterwards, many authors developed ITD algorithms for coniferous, deciduous, and mixed temperate forests [5,6,7,8,9]. Achieving high ITD accuracy still remains a challenge, because many approaches that worked well on coniferous stands have demonstrated a lower accuracy for deciduous or mixed forests. This is especially the case in complex forests with high variation in tree spacing, age, or size, or when the tree crowns have a high degree of overlap [3]. Therefore, the problems occurring during some ITD approaches are not so trivial and multiple methods have been developed for this task which take into account diverse forest conditions [10,11,12,13]. The performance of ITD approaches also depends on object and point cloud characteristics. The object characteristics include the type of land cover (e.g., tree species, crown shape, and stem density) [14], the site conditions (e.g., topography and type of terrain) [14], and the point cloud characteristics related to the type of LiDAR sensor and mission parameters (e.g., flying height, scanning angle, scanning mode, footprint size, and point density) [15,16].
ITD algorithms work either directly on point clouds, on rasterized point clouds in the form of a Canopy Height Model (CHM), or by combining both datasets. The raster-based methods use a CHM for their input that is interpolated or aggregated from a point cloud. A CHM is often smoothed to minimize the occurrence of pits or spikes [17]. After that, Local Maxima (LM) filtering using a fixed or variable-sized window is applied [2,6,18]. With point cloud-based ITD methods, the focus is on the exploitation of individual 3D point measurements without transforming them into a raster [19,20]. There are also hybrid algorithms that combine different types of geospatial data with some a priori assumptions, e.g., on the expected crown size and stand density [21,22] or exploring some echo features of full-waveform ALS systems [23,24].
Most current ITD techniques are still inefficient for dense and complex forests due to high commission (falsely detected trees) and omission (reference trees not detected by the algorithm) rates [25]. Treetops’ detection must be performed carefully because treetops that are missing (false negative) or are falsely detected (false positive) will lead to the under- or over-segmentation of tree crowns at a later stage [17,26]. Over-segmentation happens when one tree crown is split into several clusters, while under-segmentation represents several tree crowns merged into one cluster. Over-segmentation occurs more often in deciduous forests [3], because mature deciduous trees have large height variations within the crown topography [27]. Therefore, some authors have tried to prevent or minimize under-segmentation and over-segmentation errors by using different methods [28,29,30].
Many authors performed different types of feature extraction based on ALS data, such as geometric features [30,31,32], 3D shape-fitting features [23,33], neighborhood features based on eigenvalues [34,35,36], and tree metrics [27,37,38]. Some of these features were used to identify correctly segmented crowns of individual trees.
The related research was more focused on reducing the effect of segmentation errors in order to evaluate the accuracy after the refinement [39,40,41]. This was performed mostly without reporting the accuracy for the detection of erroneous segments, or solely noting the percentage difference in the improvement achieved.
The most recent research is concentrated on the usage of machine learning (ML) techniques for detecting individual trees [37] and the classification of delineated segments into correctly segmented, over-segmented, or under-segmented categories [27,30]. Kathuria et al. [37] developed an ITD algorithm based on an LM-filtering approach that selects the optimal search radius from the ALS point cloud for the detected LM. They used LiDAR-derived metrics from local neighbourhood data points as predictor variables. For classification, they chose a logistic regression (LR) model made with simulated stands and composed of individual trees and afterwards performed application testing on a real Pinus radiata plantation. Dai et al. [30] classified segments into well-detected trees or those over-segmented with 84% accuracy using the Support Vector Machine classifier. Nine geometric features of crown segments were calculated and used as predictor variables in the classification. Lisiewicz et al. performed comprehensive research dealing with erroneous tree segments’ detection [27] and correction [42]. Lisiewicz et al. [27] invented a method to distinguish correct segments from erroneous ones resulting from the ITD method based on a CHM. They tested three machine learning methods for classification: Random Forest (RF), Support Vector Machine, and k-Nearest Neighbour (kNN), where RF showed the best results. The groups of predictors were based on the segment geometry as well as structural and intensity variables from the ALS point cloud. Lisiewicz et al. [42] went two steps further, correcting the under-segmentation errors and merging segments that were over-segmented with correct segments based on the specified conditions. Both studies were conducted with the data collected from one of the most complex and diverse forest in Poland.
As it can be seen, there is only a limited number of methods for correcting the results of the ITD algorithms. Therefore, we believe there is room for improvement in terms of the features that could be extracted from ALS data and ML techniques that could be used for the classification of detected treetops. The hypothesis of this study is the assumption that falsely detected treetops can be reduced by performing the classification of detected treetops by using some of the ML methods on features extracted from ALS point clouds.
The aim of this study is to develop an effective ML method to refine the detected treetops by reclassifying them into true and false detections based the information obtained from the corresponding tree segments of an ALS point cloud. Four groups of features were extracted to be used as predictor variables for classification: segment shape features, eigenvalue-based features, shape-fitting features, and tree metrics. The most important features were selected in order to perform a better separation between the true and false detections of treetops. This study considered classification models based on five different ML methods to identify the best-performing one for our study area: Random Forest (RF), Extreme Gradient Boosting (XGB), Artificial Neural Network (ANN), the Support Vector Machine (SVM), and Logistic Regression (LR). The classification has been performed for the area of a mixed temperate forest with a complex topography in the north-eastern part of Bosnia and Herzegovina.

2. Materials

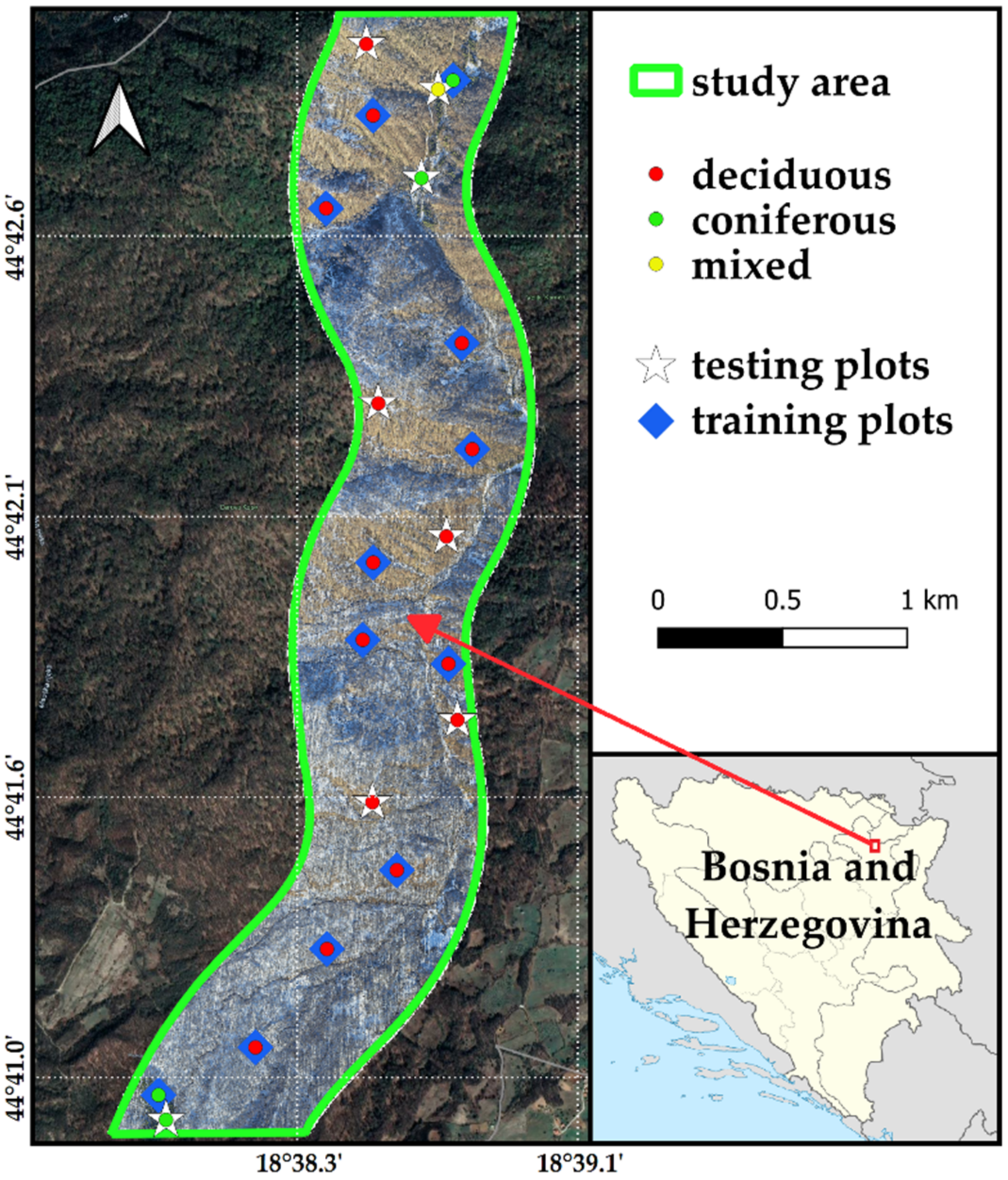
2.1. Study Area

The study area (44°42′40.8″N 18°38′12.7″E) covers 270 ha of forests located in the north-western part of the mountain Majevica in the north-eastern part of Bosnia and Herzegovina (Figure 1). Size of study area is around 0.6 × 4 km spreading in north–south direction. This area has hilly topography with significant elevation differences and steep slope (330–600 m above mean sea level).
Forests prevailing across the study area are mainly deciduous with a few coniferous forests. The major forest species in this part of the country include deciduous forests, namely, beech (Fagus sylvatica) and sessile oak (Quercus petraea), and mixed forests of deciduous and coniferous trees, specifically, beech and fir (Abies alba Mill.) forests with spruce (Picea abies).

2.2. Forest Plots

Target forest species in the study area belonged to the deciduous forests of beech, coniferous forests of fir with spruce, and mixed deciduous and coniferous forests, comprising beech and fir with spruce. A total of 20 circular sample plots with a diameter of 50 m were distributed throughout the study area as samples from the ALS point cloud. Reference trees were collected manually in stereo mode, or by observing profile sections of the ALS point cloud. Regarding this selection, 15 forest plots were deciduous, four were coniferous, and one contained mixed forest (Figure 1).
The forest plots were split into training and testing groups so that 8 plots were designated for testing while locations of other 12 plots were used to train the machine learning model. The test data contained five plots of deciduous forest, two plots of coniferous forest, and one plot of a mixed forest (Figure 1). Forest plot identification and classification was performed by visual interpretation of the orthophoto for this area, with ground-sampling distance of 5 cm. Categorization of the forest plots belonging to the test data was needed for later classification accuracy assessment for each type of forest.

2.3. ALS Data

The ALS data acquisition was performed at the end of January 2021 during the leaf-off period using the discrete-return signal system Galaxy T1000 (Teledyne Geospatial, Toronto, Canada) mounted on a fixed-wing aircraft. The system combines a 1000-kHz effective ground measurement rate with a constant swath width and seesaw scanning pattern. Flight was performed with an average flying height of 550 m above ground level, with 30% strip overlap and maximum scanning angle of ±45°. Generated point cloud has an average point density of 192 pts/m2 of all returns and 85 pts/m2 of last returns, with vertical and horizontal accuracy higher than 5 cm. This system can register up to 8 returns for each emitted laser pulse. The point cloud was acquired with a mean footprint size of 15 cm diameter. In order to cover the whole area of interest, 24 individual flight strips were performed.
The ALS data were received with the first, last, and intermediate returns for each laser pulse recorded. The points were processed, georeferenced, and classified by the service provider into ground and non-ground classes using Terrasolid TerraScan (Terrasolid, Helsinki, Finland) software, which implements the active TIN model algorithm. This method filters non-ground points based on the iterative-distance and iterative-angle method [43].
Point heights were normalized by subtracting the ground heights from the ALS heights, thereby providing points with heights relative to the ground level. Ground heights for each point were determined by linear interpolation using TIN model generated from points belonging to the ground class. The ALS data corresponding to each forest plot, including a 10 m buffer around each plot, were clipped and used for all further calculations. Mentioned buffer size was chosen in order to ensure that each tree crown is completely located inside this buffered area for each tree measured inside the forest plot.

2.4. Reference Tree Data

The reliability of reference tree locations is very important for ITD completeness and accuracy [3]. Locations of the trees were not measured in the field, but collected manually, through the digitization of a 3D point cloud by experienced operators. The field-measured tree locations are often inaccurate due to the significant shift between the treetop and the base of the tree that would arise because of the leaning trunk and highly inclined terrain. This particularly happens when working with deciduous tree species. In addition, there is a possibility of a bad tree location as a consequence of measurement unreliability due to the weak GNSS signal that can occur under dense tree canopies. Since ITD algorithms detect treetops, comparing this location with field-measured tree locations would not be suitable.
An inventory of all the trees (treetop locations and tree heights) inside the 20 forest plots was carried out in the stereo mode (using active shutter glasses) by a single operator with a high level of experience. Reference trees were also detected, where necessary, by observing profile sections of the point cloud (Figure 2). Only dominant trees were measured, whereas understory trees were not taken into account during digitization. This photointerpretation was performed in the Trimble Inpho software. An example of reference trees manually marked as a reference layer over point cloud is shown in Figure 2. A total of 923 reference trees were identified in 20 forest plots, wherein 615 were deciduous and 308 were conifers.

3. Methods

3.1. Methodology

The methodological framework developed for this research is shown in Figure 3.
First, CHM was generated, interpolated, and smoothed from the normalized ALS heights. Treetop candidates were detected using well-established ITD method with LM- filtering. These were used as seeds for deriving tree segments based on CHM. Treetop candidates were then validated with the reference data into true and false detections. Later, four groups of features for each segment were extracted. Class balancing and feature selection were performed for better separation between true and false detections of treetops. Selected features were used as a training data for classification using several ML methods. Finally, a classification model from the best-performing method was applied on the test data to distinguish true treetops from falsely detected ones and classification accuracy assessment was performed.

3.2. CHM Generation, ITD and Tree Crown Segmentation

The CHM with a grid size of 0.5 m was generated using procedure as described in Khosravipour et al. [17]. All ALS points above 2 m that represent first returns for each buffered forest plot were used for CHM generation. Pitfree CHM was created and post-processed in order to smooth CHM and fill its empty pixels.
Treetop candidates were detected by using LM-filtering with fixed window size in the shape of a square. This was performed using algorithm developed as described in Popescu and Wynne [44]. Here, we always used a filtering window that was a step smaller for each forest plot, which resulted in a greater number of treetop candidates. A treetop candidate is an ALS point with the largest height in a certain neighborhood. ITD also creates a unique identifier for each tree segment and assigns it as an attribute to each ALS point.
Algorithm developed by Silva et al. [8] was used for tree crown segmentation. This algorithm works on a CHM only; therefore, tree crown segments have jagged pixel boundaries as a product of raster to vector conversion.
CHM generation, ITD, and tree crown segmentation was performed using R package lidr [45,46] from R software environment (Version 4.1.1) [47] in RStudio (Version 1.4.1717) as an integrated development environment for R.

3.3. Feature Extraction

Four groups of features were derived to be used in this work: tree metrics, segment shape features, eigenvalue-based features, and shape-fitting features. Since the purpose of this paper is to distinguish treetops of individual trees in the upper tree canopy, features were calculated for all ALS points above half of the mean height of a forest plot.

3.3.1. Tree Metrics

Tree metrics represent descriptive statistics that are calculated for each of the segments of ALS points using function stdmetrics in R package lidr [45,46], function CrownMetrics implemented in R package rLidar [48], and by clipping the whole point cloud with segment polygons and calculating metrics for each of the segments of ALS points using function CloudMetrics in the software FUSION [49].
Tree metrics, together with a short description and the software used for their computation, are given in the Table 1.

3.3.2. Segment Shape Features

Segment shape features represent morphometric characteristics of segment polygons calculated using function poly_metrics from R package uavRst [52]. These features represent some of the global shape measurements [53,54].
List of segment shape features is given in Table 2.

3.3.3. Eigenvalue-Based Features

Eigenvalue-based features were determined using function stdshapemetrics from R package lidr [45,46] implemented as described in Lucas et al. [55]. This set of features, as well as additional parameters especially used for this research, describe the distribution of points of a neighborhood in space [34,35,36,56].
Mentioned features (linearity, planarity, and sphericity), as well as some additional features (anisotropy, curvature, omnivariance, eigentropy, and the sum of eigenvalues), were computed for each segment of ALS points using the formulas given in Table 3.

3.3.4. Shape-Fitting Features

Module ZonalFit of the software system OPALS (Orientation and Processing of Airborne Laser-scanning data) was used for the calculation of features based on fitting the second order polynomial surface to the points belonging to the tree segment [57,58]. Minimum, maximum, median, and RMS of point residuals were estimated using a strict least-squares adjustment, followed by a robust estimation, in order to eliminate outliers (features with robquad in their name).
Table 4 gives an overview of shape-fitting features determined using this software module.

3.4. Data Balancing and Feature Selection

Several steps were performed in order to reduce the number of variables and balance the classes in the dataset.
Due to the unbalanced number of trees in each class, generation of additional entities for minority class of falsely detected treetops was performed using SMOTE-based algorithm ADAptive SYNthetic sampling approach for imbalanced learning (ADASYN) [59]. SMOTE, Synthetic Majority Oversampling Technique, is an oversampling technique that synthesizes a new minority instance between one minority instance and its K nearest neighbors.
To select the most important predictor variables, we first eliminated highly correlated variables and then applied the Genetic Algorithms (GA) feature selection method. For the first step, Pearson correlation matrix was determined for the whole set of predictor variables. After that, predictor variables that had high pair-wise correlation were systematically removed. To select a subset of the most relevant features, we used the wrapper method of feature selection via Genetic Algorithms (GA) by calculating RF importance criterion. GA method belongs to a family of evolutionary algorithms based upon genetic evolution [60]. Feature selection based on GA performs supervised binary search of the predictor space using a genetic algorithm. Binary sequences are used to represent the inclusion or exclusion of a feature as genome. Their fitness is evaluated by accuracy of a certain classifier using repeated n-fold cross validation on each iteration.
For this methodology, we used 10-fold cross validation evaluated by accuracy of an RF classifier. In this case, for the first round, nine tenths of the data are used in the search while the remaining tenth is used to estimate the external performance. An external estimate provides better assessments because it is not used by the search, while internal estimation of the performance eventually overfits the subsets of the data.

3.5. Treetops Class Labelling

Calculated features were assigned to the treetop candidate that belongs to the tree segment (Figure 4). Labels specifying whether detected LM represents true or false treetops determined by comparison with reference trees (location proximity and height differences) are assigned to the treetop candidate. Following the strategy proposed by Reitberger et al. [23], we considered the state of treetop to be true if (1) the distance between the treetop candidate and the reference tree is smaller than 60% of the mean tree distance within the forest plot and (2) if the height difference between the treetop candidate and the reference tree is less than 20% of the top height of the plot. After this procedure, it was found that training data had 611 true and 343 false treetops while test data contained 289 true and 139 false treetops, which indicates a tree detection accuracy of 68% for the test data.

3.6. Classification Method Selection

In order to determine which method best suits and achieves highest accuracy, five machine learning (ML) methods were compared: Random Forest, Extreme Gradient Boosting, Artificial Neural Network, Support Vector Machine, and Logistic Regression.
Random Forest (RF) is an ensemble-based machine learning algorithm used for classification and regression [61]. It uses multiple decision tree classifiers to vote for the most popular class. Each tree is built by using the bootstrap aggregation (bagging) method where, to grow each tree, a random selection is made from the examples in the training set. Another ensemble method based on RF that adds randomization to the whole process is Extremely Randomized Trees (ERT) [62]. The main difference between these methods is in the selection of cut points to split the nodes. RF chooses the optimum split while ERT chooses it randomly so that ERT forest contains trees that are more variable, but less correlated than the RF forest. More details on ERT method can be found in Geurts et al. [62].
Extreme Gradient Boosting (XGB) is one of the widely popular boosting approaches that uses decision tree as a base estimator. The basic idea of boosting is to create/add models to an ensemble by considering the behavior of other models. In this way, on a model-by-model basis, iterative improvement (boosting) of the ensemble is carried out. XGB was developed by Chen and Guestrin [63], and it is a regularized extension of traditional boosting ensemble techniques, which makes it less prone to overfitting.
Artificial Neural Network (ANN) is a computational learning system that learns by using interconnected layers of small units called nodes. These are distributed across an input layer, single or multiple hidden layers, and an output layer. Nodes are linked to each other and associated with a particular weight and threshold. Once the output of a single node crosses its specified threshold, that particular node is activated, and its data are transmitted to the next layer in the network. In this study, feed-forward neural network with a single hidden layer algorithm is used for classification [64]. This is the simplest type of artificial neural network where connections between the nodes do not form a cycle or loop [65].
Support Vector Machine (SVM) is a supervised machine learning technique based on minimization principle, proposed by Cortes and Vapnik [66]. The algorithm aims to determine a classification hyperplane in order to split the data into a predefined number of classes. The split is performed using optimal maximum margin, with points on the margins called ‘support vectors’ pertaining to structural risk minimization. Kernel representations offer a solution to locating complex hyperplanes between classes [66,67]. The commonly used types of SVM kernels for classification include: linear, polynomial, radial basis function (RBF), and sigmoid [68].
Logistic Regression (LR) is a fundamental method that builds a logistic model [69] to find the probability of whether an event is occurring or not (the “odds” of an event), based on a given dataset of independent variables. It takes a linear combination of features and applies a nonlinear sigmoidal function. LR belongs to the class of generalized linear models, which are described in detail by Nelder and Wedderburn [70].

3.7. Accuracy Assessment

Average performance metrics for training data were estimated using 10-fold cross validation with 10 repeats. Performance metrics for test data were determined by training the model with training data and performing prediction of classes for each feature in the test data. Accuracy of classification using best-performing classifier was assessed using the confusion matrix and performance metrics: overall accuracy (OA), Kappa coefficient (κ), producer’s accuracy (PA), and user’s accuracy (UA) [71]. The reason why these metrics were used is due to the possibility to compare the results with those from other authors who used the same metrics in their research. We will also perform data balancing so that it will not be a problem if the used metrics are insensible to imbalanced datasets.

4. Results

4.1. Data Balancing and Feature Selection Results

As it was explained in Section 3.4, data were balanced using the SMOTE-based algorithm ADASYN. This algorithm is implemented as the function ADAS in the R package smotefamily [72]. The number of nearest neighbors (K) from the majority class used during oversampling process was five. After the data-balancing process was performed, the number of synthesized records for the minority class (false treetops) was 296. It was found that class balancing increased the OA almost 5% when using the 10-fold cross validation repeated 10 times (Figure 5).
In order to remove the predictor variables with a high correlation, a Pearson correlation matrix was determined for the whole set of predictor variables. Highly correlated variables were determined by using the function findCorrelation from the R package caret [73], which calculates the mean absolute correlation for each variable.
After that, the predictor variables that had a pair-wise correlation higher than 0.8 were removed. With this step performed, 37 predictor variables remained for further processing.
A feature selection based on GA was performed using the function gafs from the R package caret [73], which is based on the R package GA [74]. In this research, the fitness of the binary sequences was evaluated by the accuracy of an RF classifier using 10-fold cross validation repeated five times on each iteration. The parameters chosen for GA were 100 generations with 20 populations per generation, a crossover probability of 0.8, and a mutation probability of 0.1. The aim of the subset selection was to maximize the internal accuracy while the best iteration was chosen by maximizing the external performance achieved using the RF classifier.
The final subset selection was chosen at iteration 76, which yielded an external performance of 91.6% in terms of the OA and 0.832 for κ (Figure 6). There were 23 predictor variables selected at this iteration: N, Hentr, Phabhm, Phabx, Hq1, Hq5, Hpcum9, P2th, P3th, P5th, Hmod, Hmadmed, HL3, HL4, and Hprofarea from the group Tree metrics; Maxquad, Medquad, Minrobquad, Maxrobquad, Medrobquad, and RMSrobquad from the group Shape-fitting features; and EccEgn and Rect belonging to the group Segment shape features.

4.2. Optimal Hyperparameters Tuning

Optimal hyperparameter tuning was performed using training data by performing a separate grid search for each classification method. A 10-fold cross validation was repeated 10 times for the classification model’s training. OA was used as a measure of model performance given by the grid search combination of each classifier. The optimization of the classification models was performed using the R package caret [73].
The optimal hyperparameter values obtained by tuning the machine learning models, as well as the respective R packages, are given in the Table 5.

4.3. Machine Learning Method Selection

When comparing the accuracy achieved by different classifiers on the training data, it may be noted that RF, XGB, ANN, and SVM outperformed LR (Figure 7).
The same ranking of the mentioned classifiers was obtained when the trained model was applied to the test data, as seen in Table 6.
In the end, only RF gives an OA of over 90% and a κ of over 0.8 when using cross validation on the training data, as well as the highest accuracy when this model was applied on test data. Therefore, this classifier was chosen to distinguish between true and false treetops.

4.4. Classification Results

The OA and κ for the RF classifier obtained from the ten-fold cross validation applied to the training data were 90.4% and 0.808, respectively. When predicting the test data, it was possible to achieve an OA = 89.0% and κ = 0.757. The optimized parameters used for the RF model were splitrule = extratrees, ntree = 2000, min.node.size = 1, and mtry = 4. The calculated OA, κ, PA, and UA for the test data are shown in Table 7.
When splitting the predicted test data into plots that belong to different forest types (deciduous, coniferous, and mixed), we obtained results shown in Table 8.

4.5. Variable Importance

Feature selection was performed in order to reduce the number of data used. This shortened the processing time needed for classification, without sacrificing the significant performance of the model related to the accuracy achieved. After that, it was important to assess the importance of each variable participating in the classification.
The importance measure represents the node impurities from the splitting procedure applied to the variables, averaged over all trees. The node impurity was measured by the Gini measure. The Mean decrease in Gini is a measure of how much the Gini impurity metric is reduced by a variable for each class. It was chosen as a measure of importance since it was also used during GA feature selection. The scaled variable importance based on the Mean decrease in Gini measure is produced and plotted. The importance for only 15 predictor variables, out of the 23 selected ones for the final RF model, is given in Figure 8.
As it can be seen from Figure 8, the highest importance is given to the number of points belonging to each segment (N), followed by the predictor variables belonging to the group of shape-fitting features (Medquad and Medrobquad), and then the predictors belonging to the group of tree metrics (Hentr, Hprofarea, Phabx, Hpcum9), which were mixed with predictors from the group of segment shape features (Rect and EccEgn).

5. Discussion

5.1. The ITD Strategy and the Resulting Accuracy Improvements

The LM-filtering window was 1 m smaller than the optimal size for each forest plot in order to generate more treetop candidates. This was performed to ensure that all the trees within a plot contained the local maxima and to eliminate falsely detected treetops with our refinement method. Thus, we avoided under-segmentation later on, which happens when some of the treetop candidates are missing. Therefore, there is no need to define another class when LM were not detected, meaning that the corresponding segment contains more than one tree (under-segmentation). As the ITD accuracy for the test data was 68%, our improvement method increased the OA by 21%. However, the ITD results achieved were within the parameters set to generate a larger number of treetop candidates. When optimally parameterized, this ITD method reliably provides fewer treetop candidates, resulting in a higher OA. For LM-filtering, that would mean using a variable-sized window or a fixed-sized window with an optimal size. Persson et al. [9] managed to correctly detect 71% of the trees with one of the first automated tree extraction methods using a CHM generated from ALS data. The tree detection accuracy results were 70% for the dominant trees in heterogeneous forests in Pitkänen et al. [81]. Yu et al. [82] achieved an ITD accuracy of 69% for tree detection in various forest conditions (different forest densities, ages, site types, and tree species). Kaartinen et al. [83], in their international comparison of ITD results using ALS, found that manual processing can be used to find 70% of trees.

5.2. Machine Learning Method Selection

The XGB, ANN, and SVM classifiers showed to be just slightly inferior when compared to RF (Figure 7), but there are no significant differences between these methods (median OA for RF was 90.4%, for XGB it was 88.8%, for ANN it was 88.0%, and for SVM it was 85.6%, while their median κ values were 0.808, 0.776, 0.759, and 0.712, respectively). When comparing the performance of the mentioned classifiers on the test data (Table 6), it can be seen that the same ranking of the mentioned classifiers was obtained but with a bigger gap between the first two and last three. XGB showed almost the same level of accuracy in its performance as RF, but for XGB, much more computation time was needed for model training. It is also possible that ANN was overfit because of the large number of hidden units, so SVM may perform better than this classifier in some other case. An interesting finding in this research is that XGB and ANN were competitive with RF or even more suitable algorithms than SVM, considering that the researchers usually find that RF and SVM provide more advantageous results for ALS and other remote-sensing classification tasks [27,30,84,85,86].

5.3. Classification Results

In this research, we achieved high values for OA and κ when using the RF classifier with the ERT option. The OA obtained from the ten-fold cross validation applied to the training data was 90.4% and the κ was 0.808, whereas the prediction performed on the test data resulted in an OA = 89.0% and κ = 0.757.
There have been several studies dealing with the classification of tree segments using SVM classifiers [27,30]. They achieved similar results using SVM in terms of classification accuracy as we did in our study. Therefore, our results also confirmed that SVM continues to be a good benchmark method for classification because it has also outperformed RF in some cases of tree species classification [87,88].
In an approach based on an LR classifier developed by Kathuria et al. [37], it was found that LR yields a better OA in comparison with the RF-modelling technique (95% for RF and 98% for LR). We found that RF and other algorithms performed much better than the LR classifier, but a direct comparison of the results between the studies is difficult because our analysis was run on a complex, natural, and mostly deciduous forest while theirs was applied to a Pinus radiata coniferous plantation. Another reason why their OA values are so high could be the model’s training on simulated stands composed of individual trees derived from ALS point cloud data. Furthermore, the methodologies differ in several aspects. In our study, we used zonal statistics to calculate the features for tree segments belonging to each LM, while they used focal statistics in their method. Their approach also included feature selection based on a backward selection method with Akaike information criterion (AIC) [89], while we applied GA feature selection.
Lisiewicz et al. [27] tested several ML methods (RF, SVM, and kNN) to distinguish correct segments from erroneous ones resulting from the ITD method based on a CHM. With the RF classifier, they achieved high accuracy for the training (OA = 87.0% and κ = 0.794) and test data (OA = 85.3% and κ = 0.641). In our approach, we were more oriented towards separating the correct from the erroneous treetops, using the information obtained from the appropriate tree segments, while in their study, they tried to distinguish errors in a more comprehensive manner (correct-, over-, and under-segmentation) in order to identify all possible segmentation error scenarios. In our study, we achieved a higher accuracy for the training data with the RF approach based on ERT [62].
The accuracy results achieved for the test data from Lisiewicz et al. [27] are not comparable to ours because they used cross validation on the test dataset, while we performed the usual train/test split and then used the trained model for the prediction of the test data. The study area they used for research is also a natural forest, but with a higher proportion of coniferous than deciduous trees. The ALS data for our study were collected for mostly deciduous forests during the leaf-off season, which makes treetop detection more complicated. In addition, for classification, we used different features that were based on the shape of the tree segments, eigenvalues, the shape fitting of the points to a polynomial shape, and LiDAR-derived tree metrics. Unlike them, we did not compute or use any of the intensity variables because a proper radiometric correction of intensity data must be performed before any kind of analysis [90,91]. We had a similar approach with respect to removing highly correlated variables, but we additionally performed a feature selection using GA. In our study, we also used a class-balancing method based on the SMOTE algorithm, which increased accuracy by almost 5%.
To the best of our knowledge, XGB and ANN have never been used for this type of classification problem, and here it has been shown that XGB gives similar results as RF.

Classification Results Depending on the Forest Type

Table 8 showed that almost all the plots with different forest types gave an accuracy greater than 80%, except for UA regarding falsely detected treetops in deciduous forest plots and PA concerning falsely detected treetops in plots of mixed forest. The highest performance was achieved on the mixed forest plot. The reason for this result could be the small number of features in the forest plot, especially those belonging to the class of falsely detected treetops. Even one feature migrating from one class to another can highly influence the resulting accuracy.
It can be noticed that the classification accuracy performed on the deciduous plots was slightly lower than on the coniferous ones (Table 8). This has always been the case in the research conducted so far because a large number of studies have proven that the detection of individual trees and their delineation in coniferous forests is much more successful, as coniferous species have, in most cases, a clearly defined tree crown shape [92]. However, herein, the deciduous and coniferous plots had very similar results. Another important parameter is that forest plots usually contain dominant deciduous trees (birch), which were well-separated.

5.4. Variable Importance

The number of points in each tree segment (N) is an important variable due to the size of the tree. If a local maximum is detected for a tree segment area and the segmentation algorithm performs well, then the number of points for deciduous trees would have great significance. If there are several LM for a single tree crown, then non-treetop points would usually be falsely detected as treetops for that parts of the tree that usually represent tree branches [5]. When this predictor variable is not used in the training data, the OA obtained from ten-fold cross validation for the training data decreases by 2%. Kathuria et al. [37] also used the number of points that are above 2 m height as a predictor variable and they selected this to be an important non-correlated variable for the final model.
One of the most important predictor variables is the entropy of height distribution: the normalized Shannon vertical complexity index (Hentr). The entropy of height distribution is a measure for quantifying diversity and it is based on the number and frequency of species present [50]. This tree metric is applied to quantify the diversity and the evenness of the elevational distribution of ALS points. It, therefore, provides a good differentiation between a part of the tree resulting from over-segmentation and the correct segment covering the entire tree crown. When this predictor variable was omitted from the training data, the OA obtained from the ten-fold cross validation for the training data decreased by 1.5%.
Some features from a group of shape-fitting features (Medquad and Medrobquad) proved to be valuable for the classification based on the importance value. The median values of fitting a polynomial shape to the point cloud of a segmented tree canopy (first without and then with robust estimation for eliminating outliers) were ranked as second and third, respectively, when the predictor variables were ranked by their importance. In this case, if the whole tree is well-segmented, then the absolute median value of residuals from fitting a polynomial shape to the point cloud is greater than the value of the over-segmented part of the tree. One of the possible reasons is that the polynomial shape more adequately fits the points relating to a part of the tree than the points belonging to the whole tree due to the “peaky” distribution of points. This is an important conclusion because previous studies have not used this group of features for this kind of classification. When these shape-fitting features were not used in the training data, the OA obtained from the ten-fold cross validation for the training data decreased by 0.6%.
It is interesting to notice that the features from the group of eigenvalue-based features were not recognized as important for classification, so they were removed during feature selection.
Further studies may investigate refinement performance when working with UAV Laser-Scanning (ULS) data. This acquisition technique produces point clouds with a higher point density and, therefore, existing ITD algorithms would produce many more treetop candidates due to the much more detailed canopy surface. The problem of reducing the number of falsely detected treetops would be an even bigger challenge. The related future work would also be oriented towards determining additional features that could be useful for better classification, such as multispectral or full-waveform ALS data. Another task may be collecting more training data in order to be able to experiment with training data reduction procedures. This could lead to determining an optimal training/testing data ratio.

6. Conclusions

In this study, we presented an effective method to differentiate true and falsely detected treetops based on the information obtained from corresponding delineated tree segments of ALS point cloud data. The tree metrics, shape-fitting, eigenvalue-based, and segment shape groups of features were calculated for each tree segment in order to be used as predictor data for the ML model’s training. A SMOTE-based algorithm was used for data balancing and GA for feature selection. Five ML methods were tested for this classification, namely, RF, XGB, ANN, SVM, and LR, wherein the best-performing classifier was RF. The OA and κ obtained from the ten-fold cross validation of the training data were 90.4% and 0.808, respectively. When performing the prediction of the test data, it was possible to achieve an OA = 89.0% and a κ = 0.757.
One of the key steps for achieving this accuracy was ADASYN’s balancing of the data classes, which increased the OA by almost 5%. This experiment showed that the most important features for achieving this accuracy are the number of points in each segment (omitting this feature lowered the OA by 2%), the entropy of height distribution (omitting this feature lowered the OA by 1.5%), and the median values of fitting a polynomial shape to the point cloud (omitting these features would lower the OA by 0.6%).
When the classification results were assessed separately for each forest type, the OA was 88.3% for the deciduous forest plots predicted from the test data, 89.2% for the coniferous forest plots, and 91.7% for the forest plot that contained trees belonging to mixed forest types.
Further studies may investigate refinement performance when working with UAV Laser-Scanning (ULS) data. Another task would be testing additional features from other sources of data, such as multispectral or full-waveform ALS data.

Author Contributions

All authors worked equally on the research’s conceptualization, investigation, discussion, and data modelling. N.B. was involved in data preparation and case study implementation. All authors participated in the writing of the manuscript; however, N.B. took the lead. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Acknowledgments

This study was supported by the Ministry of Education, Science and Technological Development of the Republic of Serbia, Project No. 200092. The authors are thankful to the MapSoft d.o.o. for providing the datasets used in this research. The authors are also very thankful to the anonymous reviewers for constructive and valuable comments that improved the quality of this study.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Wulder, M.A.; Coops, N.C.; Hudak, A.T.; Morsdorf, F.; Nelson, R.; Newnham, G.; Vastaranta, M. Status and Prospects for LiDAR Remote Sensing of Forested Ecosystems. Can. J. Remote Sens. 2013, 39, 37–41. [Google Scholar] [CrossRef] [Green Version]
  2. Hyyppä, J.; Inkinen, M. Detecting and Estimating Attributes for Single Trees Using Laser Scanner. Photogramm. J. Finl. 1999, 16, 27–42. [Google Scholar]
  3. Zhen, Z.; Quackenbush, L.J.; Zhang, L. Trends in Automatic Individual Tree Crown Detection and Delineation—Evolution of LiDAR Data. Remote Sens. 2016, 8, 333. [Google Scholar] [CrossRef] [Green Version]
  4. Hyyppä, J.; Schardt, M.; Haggrén, H.; Koch, B.; Lohr, U.; Paananen, R.; Scherrer, H.; Luukkonen, H.; Ziegler, M.; Hyyppä, H.; et al. HIGH-SCAN: The First European-Wide Attempt to Derive Single-Tree Information from Laserscanner Data. Photogramm. J. Finl. 2001, 17, 58–68. [Google Scholar]
  5. Koch, B.; Heyder, U.; Weinacker, H. Detection of Individual Tree Crowns in Airborne Lidar Data. Photogramm. Eng. Remote Sens. 2006, 72, 357–363. [Google Scholar] [CrossRef] [Green Version]
  6. Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Estimating Plot-Level Tree Heights with Lidar: Local Filtering with a Canopy-Height Based Variable Window Size. Comput. Electron. Agric. 2002, 37, 71–95. [Google Scholar] [CrossRef]
  7. Ferraz, A.; Saatchi, S.; Mallet, C.; Meyer, V. Lidar Detection of Individual Tree Size in Tropical Forests. Remote Sens. Environ. 2016, 183, 318–333. [Google Scholar] [CrossRef]
  8. Silva, C.A.; Hudak, A.T.; Vierling, L.A.; Loudermilk, E.L.; O’Brien, J.J.; Hiers, J.K.; Jack, S.B.; Gonzalez-Benecke, C.; Lee, H.; Falkowski, M.J.; et al. Imputation of Individual Longleaf Pine (Pinus palustris Mill.) Tree Attributes from Field and LiDAR Data. Can. J. Remote Sens. 2016, 42, 554–573. [Google Scholar] [CrossRef]
  9. Persson, A.; Holmgren, J.; Soderman, U. Detecting and Measuring Individual Trees Using an Airborne Laser Scanner. Photogramm. Eng. Remote Sens. 2002, 68, 925–932. [Google Scholar]
  10. Hamraz, H.; Contreras, M.A.; Zhang, J. A Robust Approach for Tree Segmentation in Deciduous Forests Using Small-Footprint Airborne LiDAR Data. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 532–541. [Google Scholar] [CrossRef] [Green Version]
  11. Wu, B.; Yu, B.; Wu, Q.; Huang, Y.; Chen, Z.; Wu, J. Individual Tree Crown Delineation Using Localized Contour Tree Method and Airborne LiDAR Data in Coniferous Forests. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 82–94. [Google Scholar] [CrossRef]
  12. Wang, X.-H.; Zhang, Y.-Z.; Xu, M.-M. A Multi-Threshold Segmentation for Tree-Level Parameter Extraction in a Deciduous Forest Using Small-Footprint Airborne LiDAR Data. Remote Sens. 2019, 11, 2109. [Google Scholar] [CrossRef] [Green Version]
  13. Stereńczak, K.; Kraszewski, B.; Mielcarek, M.; Piasecka, Ż.; Lisiewicz, M.; Heurich, M. Mapping Individual Trees with Airborne Laser Scanning Data in an European Lowland Forest Using a Self-Calibration Algorithm. Int. J. Appl. Earth Obs. Geoinf. 2020, 93, 102191. [Google Scholar] [CrossRef]
  14. Khosravipour, A.; Skidmore, A.K.; Wang, T.; Isenburg, M.; Khoshelham, K. Effect of Slope on Treetop Detection Using a LiDAR Canopy Height Model. ISPRS J. Photogramm. Remote Sens. 2015, 104, 44–52. [Google Scholar] [CrossRef]
  15. Keränen, J.; Maltamo, M.; Packalen, P. Effect of Flying Altitude, Scanning Angle and Scanning Mode on the Accuracy of ALS Based Forest Inventory. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 349–360. [Google Scholar] [CrossRef]
  16. Liu, J.; Skidmore, A.K.; Jones, S.; Wang, T.; Heurich, M.; Zhu, X.; Shi, Y. Large Off-Nadir Scan Angle of Airborne LiDAR Can Severely Affect the Estimates of Forest Structure Metrics. ISPRS J. Photogramm. Remote Sens. 2018, 136, 13–25. [Google Scholar] [CrossRef]
  17. Khosravipour, A.; Skidmore, A.K.; Isenburg, M.; Wang, T.; Hussin, Y.A. Generating Pit-Free Canopy Height Models from Airborne Lidar. Photogramm. Eng. Remote Sens. 2014, 80, 863–872. [Google Scholar] [CrossRef]
  18. Chen, Q.; Baldocchi, D.; Gong, P.; Kelly, M. Isolating Individual Trees in a Savanna Woodland Using Small Footprint Lidar Data. Photogramm. Eng. Remote Sens. 2006, 72, 923–932. [Google Scholar] [CrossRef] [Green Version]
  19. Lee, H.; Slatton, K.C.; Roth, B.E.; Cropper, W.P. Adaptive Clustering of Airborne LiDAR Data to Segment Individual Tree Crowns in Managed Pine Forests. Int. J. Remote Sens. 2010, 31, 117–139. [Google Scholar] [CrossRef]
  20. Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A New Method for Segmenting Individual Trees from the Lidar Point Cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef] [Green Version]
  21. Heinzel, J.N.; Weinacker, H.; Koch, B. Prior-Knowledge-Based Single-Tree Extraction. Int. J. Remote Sens. 2011, 32, 4999–5020. [Google Scholar] [CrossRef]
  22. Ene, L.; Næsset, E.; Gobakken, T. Single Tree Detection in Heterogeneous Boreal Forests Using Airborne Laser Scanning and Area-Based Stem Number Estimates. Int. J. Remote Sens. 2012, 33, 5171–5193. [Google Scholar] [CrossRef]
  23. Reitberger, J.; Schnörr, C.; Krzystek, P.; Stilla, U. 3D Segmentation of Single Trees Exploiting Full Waveform LIDAR Data. ISPRS J. Photogramm. Remote Sens. 2009, 64, 561–574. [Google Scholar] [CrossRef]
  24. Gupta, S.; Weinacker, H.; Koch, B. Comparative Analysis of Clustering-Based Approaches for 3-D Single Tree Detection Using Airborne Fullwave Lidar Data. Remote Sens. 2010, 2, 968–989. [Google Scholar] [CrossRef] [Green Version]
  25. Dong, T.; Zhou, Q.; Gao, S.; Shen, Y. Automatic Detection of Single Trees in Airborne Laser Scanning Data through Gradient Orientation Clustering. Forests 2018, 9, 291. [Google Scholar] [CrossRef] [Green Version]
  26. Zhao, D.; Pang, Y.; Li, Z.; Sun, G. Filling Invalid Values in a Lidar-Derived Canopy Height Model with Morphological Crown Control. Int. J. Remote Sens. 2013, 34, 4636–4654. [Google Scholar] [CrossRef]
  27. Lisiewicz, M.; Kamińska, A.; Stereńczak, K. Recognition of Specified Errors of Individual Tree Detection Methods Based on Canopy Height Model. Remote Sens. Appl. Soc. Environ. 2022, 25, 100690. [Google Scholar] [CrossRef]
  28. Lindberg, E.; Eysn, L.; Hollaus, M.; Holmgren, J.; Pfeifer, N. Delineation of Tree Crowns and Tree Species Classification From Full-Waveform Airborne Laser Scanning Data Using 3-D Ellipsoidal Clustering. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3174–3181. [Google Scholar] [CrossRef] [Green Version]
  29. Liu, T.; Im, J.; Quackenbush, L.J. A Novel Transferable Individual Tree Crown Delineation Model Based on Fishing Net Dragging and Boundary Classification. ISPRS J. Photogramm. Remote Sens. 2015, 110, 34–47. [Google Scholar] [CrossRef]
  30. Dai, W.; Yang, B.; Dong, Z.; Shaker, A. A New Method for 3D Individual Tree Extraction Using Multispectral Airborne LiDAR Point Clouds. ISPRS J. Photogramm. Remote Sens. 2018, 144, 400–411. [Google Scholar] [CrossRef]
  31. Jing, L.; Hu, B.; Li, J.; Noland, T. Automated Delineation of Individual Tree Crowns from Lidar Data by Multi-Scale Analysis and Segmentation. Photogramm. Eng. Remote Sens. 2012, 78, 1275–1284. [Google Scholar] [CrossRef]
  32. Wolf (né Straub), B.-M.; Heipke, C. Automatic Extraction and Delineation of Single Trees from Remote Sensing Data. Mach. Vis. Appl. 2007, 18, 317–330. [Google Scholar] [CrossRef]
  33. Polewski, P.; Yao, W.; Heurich, M.; Krzystek, P.; Stilla, U. Free Shape Context Descriptors Optimized with Genetic Algorithm for the Detection of Dead Tree Trunks in ALS Point Clouds. In Proceedings of the ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, ISPRS Geospatial Week 2015, La Grande Motte, France, 28 September–3 October 2015; Volume II-3-W5. pp. 41–48. [Google Scholar]
  34. West, K.F.; Webb, B.N.; Lersch, J.R.; Pothier, S.; Triscari, J.M.; Iverson, A.E. Context-Driven Automated Target Detection in 3D Data. In Proceedings of the Automatic Target Recognition XIV, Bellingham, WA, USA, 21 September 2004; SPIE: Bellingham, WA, USA, 2004; Volume 5426, pp. 133–143. [Google Scholar]
  35. Chehata, N.; Guo, L.; Mallet, C. Airborne Lidar Feature Selection for Urban Classification Using Random Forests. In Proceedings of the Laserscanning, Paris, France, 1–2 September 2009. [Google Scholar]
  36. Weinmann, M.; Jutzi, B.; Mallet, C. Semantic 3D Scene Interpretation: A Framework Combining Optimal Neighborhood Size Selection with Relevant Features. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, II-3, 181–188. [Google Scholar] [CrossRef]
  37. Kathuria, A.; Turner, R.; Stone, C.; Duque-Lazo, J.; West, R. Development of an Automated Individual Tree Detection Model Using Point Cloud LiDAR Data for Accurate Tree Counts in a Pinus Radiata Plantation. Aust. For. 2016, 79, 126–136. [Google Scholar] [CrossRef]
  38. Wan Mohd Jaafar, W.S.; Woodhouse, I.H.; Silva, C.A.; Omar, H.; Abdul Maulud, K.N.; Hudak, A.T.; Klauberg, C.; Cardil, A.; Mohan, M. Improving Individual Tree Crown Delineation and Attributes Estimation of Tropical Forests Using Airborne LiDAR Data. Forests 2018, 9, 759. [Google Scholar] [CrossRef] [Green Version]
  39. Holmgren, J.; Lindberg, E. Tree Crown Segmentation Based on a Tree Crown Density Model Derived from Airborne Laser Scanning. Remote Sens. Lett. 2019, 10, 1143–1152. [Google Scholar] [CrossRef]
  40. Mongus, D.; Žalik, B. An Efficient Approach to 3D Single Tree-Crown Delineation in LiDAR Data. ISPRS J. Photogramm. Remote Sens. 2015, 108, 219–233. [Google Scholar] [CrossRef]
  41. Krzystek, P.; Serebryanyk, A.; Schnörr, C.; Červenka, J.; Heurich, M. Large-Scale Mapping of Tree Species and Dead Trees in Šumava National Park and Bavarian Forest National Park Using Lidar and Multispectral Imagery. Remote Sens. 2020, 12, 661. [Google Scholar] [CrossRef] [Green Version]
  42. Lisiewicz, M.; Kamińska, A.; Kraszewski, B.; Stereńczak, K. Correcting the Results of CHM-Based Individual Tree Detection Algorithms to Improve Their Accuracy and Reliability. Remote Sens. 2022, 14, 1822. [Google Scholar] [CrossRef]
  43. Axelsson, P. DEM Generation from Laser Scanner Data Using Adaptive TIN Models. Int. Arch. Photogramm. Remote Sens. 2000, 33, 110–117. [Google Scholar]
  44. Popescu, S.C.; Wynne, R.H. Seeing the Trees in the Forest. Photogramm. Eng. Remote Sens. 2004, 70, 589–604. [Google Scholar] [CrossRef] [Green Version]
  45. Roussel, J.-R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Meador, A.S.; Bourdon, J.-F.; de Boissieu, F.; Achim, A. LidR: An R Package for Analysis of Airborne Laser Scanning (ALS) Data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
  46. Roussel, J.-R.; Auty, D.; De Boissieu, F.; Meador, A.S.; Bourdon, J.-F.; Demetrios, G.; Steinmeier, L.; Adaszewski, S. lidR: Airborne LiDAR Data Manipulation and Visualization for Forestry Applications; Version 4.0.1; R Core Team: Vienna, Austria, 2022. [Google Scholar]
  47. R Core Team R. A language and environment for statistical computing; R Foundation for Statistical, Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 21 June 2022).
  48. Silva, C.A.; Crookston, N.L.; Hudak, A.T.; Vierling, L.A.; Klauberg, C.; Cardil, A.; Hamamura, C. rLiDAR: LiDAR Data Processing and Visualization; Version 0.1.5; R Core Team: Vienna, Austria, 2022. [Google Scholar]
  49. McGaughey, R.J. FUSION/LDV: Software for LIDAR Data Analysis and Visualization; Version 4.40; US Department of Agriculture, Forest Service, Pacific Northwest Research Station, University of Washington: Seattle, WA, USA, 2022.
  50. Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
  51. Woods, M.; Lim, K.; Treitz, P. Predicting Forest Stand Variables from LiDAR Data in the Great Lakes—St. Lawrence Forest of Ontario. For. Chron. 2008, 84, 827–839. [Google Scholar] [CrossRef]
  52. Detsch, F.; Meyer, H.; Möller, F.; Nauss, T.; Opgenoorth, L.; Reudenbach, C.; Environmental Informatics Marburg. uavRst: Unmanned Aerial Vehicle Remote Sensing Tools; Version 0.5.5. Available online: https://mran.microsoft.com/snapshot/2019-02-21/web/packages/uavRst/index.html (accessed on 21 June 2022).
  53. Rosin, P.L. Computing Global Shape Measures. In Handbook of Pattern Recognition and Computer Vision; World Scientific: Singapore, 2005; pp. 177–196. ISBN 978-981-256-105-3. [Google Scholar]
  54. Haralick, R.M. A Measure for Circularity of Digital Figures. IEEE Trans. Syst. Man Cybern. 1974, SMC-4, 394–396. [Google Scholar] [CrossRef]
  55. Lucas, C.; Bouten, W.; Koma, Z.; Kissling, W.D.; Seijmonsbergen, A.C. Identification of Linear Vegetation Elements in a Rural Landscape Using LiDAR Point Clouds. Remote Sens. 2019, 11, 292. [Google Scholar] [CrossRef] [Green Version]
  56. Hoppe, H.; DeRose, T.; Duchamp, T.; McDonald, J.; Stuetzle, W. Surface Reconstruction from Unorganized Points. SIGGRAPH Comput. Graph. 1992, 26, 71–78. [Google Scholar] [CrossRef]
  57. Pfeifer, N.; Mandlburger, G.; Otepka, J.; Karel, W. OPALS—A Framework for Airborne Laser Scanning Data Analysis. Comput. Environ. Urban Syst. 2014, 45, 125–136. [Google Scholar] [CrossRef]
  58. Mandlburger, G.; Otepka, J.; Karel, W.; Wagner, W.; Pfeifer, N. Orientation and Processing of Airborne Laser Scanning Data (OPALS)—Concept and First Results of a Comprehensive ALS Software. In Proceedings of the Laser Scanning 2009, IAPRS, Paris, France, 1–2 September 2009; Volume XXXVIII. Part 3/W8. [Google Scholar]
  59. He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive Synthetic Sampling Approach for Imbalanced Learning. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008; pp. 1322–1328. [Google Scholar]
  60. Mitchell, M. An Introduction to Genetic Algorithms; Complex Adaptive Systems; A Bradford Book: Cambridge, MA, USA, 1996; ISBN 978-0-262-13316-6. [Google Scholar]
  61. Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
  62. Geurts, P.; Ernst, D.; Wehenkel, L. Extremely Randomized Trees. Mach. Learn 2006, 63, 3–42. [Google Scholar] [CrossRef] [Green Version]
  63. Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
  64. Ripley, B.D. Pattern Recognition and Neural Networks; Cambridge University Press: Cambridge, UK, 1996; ISBN 978-0-521-71770-0. [Google Scholar]
  65. Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [Green Version]
  66. Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
  67. Kebede, T.A.; Hailu, B.T.; Suryabhagavan, K.V. Evaluation of Spectral Built-up Indices for Impervious Surface Extraction Using Sentinel-2A MSI Imageries: A Case of Addis Ababa City, Ethiopia. Environ. Chall. 2022, 8, 100568. [Google Scholar] [CrossRef]
  68. Gašparović, M.; Dobrinić, D. Green Infrastructure Mapping in Urban Areas Using Sentinel-1 Imagery. Croat. J. For. Eng. (Online) 2021, 42, 337–356. [Google Scholar] [CrossRef]
  69. Cox, D.R. The Regression Analysis of Binary Sequences. J. R. Stat. Society. Ser. B (Methodol.) 1958, 20, 215–242. [Google Scholar] [CrossRef]
  70. Nelder, J.A.; Wedderburn, R.W.M. Generalized Linear Models. J. R. Stat. Society. Ser. A (Gen.) 1972, 135, 370–384. [Google Scholar] [CrossRef]
  71. Story, M. Accuracy Assessment: A User’s Perspective. Photogramm. Eng. Remote Sens. 1986, 52, 397–399. [Google Scholar]
  72. CRAN—Package Smotefamily. Available online: https://cran.r-project.org/web/packages/smotefamily/index.html (accessed on 19 July 2022).
  73. Kuhn, M. Building Predictive Models in R Using the Caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef] [Green Version]
  74. Scrucca, L. GA: A Package for Genetic Algorithms in R. J. Stat. Softw. 2013, 53, 1–37. [Google Scholar] [CrossRef] [Green Version]
  75. Wright, M.N.; Ziegler, A. Ranger: A Fast Implementation of Random Forests for High Dimensional Data in C++ and R. J. Stat. Softw. 2017, 77, 1–17. [Google Scholar] [CrossRef] [Green Version]
  76. Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T.; et al. xgboost: Extreme Gradient Boosting; Version 1.6.0.1; R Core Team: Vienna, Austria, 2022. [Google Scholar]
  77. Karatzoglou, A.; Smola, A.; Hornik, K.; Zeileis, A. kernlab—An S4 Package for Kernel Methods in R. J. Stat. Softw. 2004, 11, 1–20. [Google Scholar] [CrossRef] [Green Version]
  78. Karatzoglou, A.; Smola, A.; Hornik, K.; Australia (NICTA); Maniscalco, M.; Teo, C.H. kernlab: Kernel-Based Machine Learning Lab; Version 0.9.29; R Core Team: Vienna, Austria, 2022. [Google Scholar]
  79. Venables, W.; Ripley, B. Modern Applied Statistics with S, 4th ed.; Springer: New York, NY, USA, 2002. [Google Scholar] [CrossRef]
  80. Kuhn, M.; Wing, J.; Weston, S.; Williams, A.; Keefer, C.; Engelhardt, A.; Cooper, T.; Mayer, Z.; Kenkel, B.; R Core Team; et al. caret: Classification and Regression Training; Version 6.0.92; R Core Team: Vienna, Austria, 2022. [Google Scholar]
  81. Pitkänen, J.; Maltamo, M.; Hyyppä, J.; Yu, X. Adaptive Methods for Individual Tree Detection on Airborne Laser Based Canopy Height Model. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 36, 187–191. [Google Scholar]
  82. Yu, X.; Hyyppä, J.; Vastaranta, M.; Holopainen, M.; Viitala, R. Predicting Individual Tree Attributes from Airborne Laser Point Clouds Based on the Random Forests Technique. ISPRS J. Photogramm. Remote Sens. 2011, 66, 28–37. [Google Scholar] [CrossRef]
  83. Kaartinen, H.; Hyyppä, J.; Yu, X.; Vastaranta, M.; Hyyppä, H.; Kukko, A.; Holopainen, M.; Heipke, C.; Hirschmugl, M.; Morsdorf, F.; et al. An International Comparison of Individual Tree Detection and Extraction Using Airborne Laser Scanning. Remote Sens. 2012, 4, 950–974. [Google Scholar] [CrossRef] [Green Version]
  84. Kamińska, A.; Lisiewicz, M.; Stereńczak, K.; Kraszewski, B.; Sadkowski, R. Species-Related Single Dead Tree Detection Using Multi-Temporal ALS Data and CIR Imagery. Remote Sens. Environ. 2018, 219, 31–43. [Google Scholar] [CrossRef]
  85. Immitzer, M.; Atzberger, C.; Koukal, T. Tree Species Classification with Random Forest Using Very High Spatial Resolution 8-Band WorldView-2 Satellite Data. Remote Sens. 2012, 4, 2661–2693. [Google Scholar] [CrossRef] [Green Version]
  86. Corte, A.P.D.; Souza, D.V.; Rex, F.E.; Sanquetta, C.R.; Mohan, M.; Silva, C.A.; Zambrano, A.M.A.; Prata, G.; Alves de Almeida, D.R.; Trautenmüller, J.W.; et al. Forest Inventory with High-Density UAV-Lidar: Machine Learning Approaches for Predicting Individual Tree Attributes. Comput. Electron. Agric. 2020, 179, 105815. [Google Scholar] [CrossRef]
  87. Ballanti, L.; Blesius, L.; Hines, E.; Kruse, B. Tree Species Classification Using Hyperspectral Imagery: A Comparison of Two Classifiers. Remote Sens. 2016, 8, 445. [Google Scholar] [CrossRef] [Green Version]
  88. Dalponte, M.; Bruzzone, L.; Gianelle, D. Tree Species Classification in the Southern Alps Based on the Fusion of Very High Geometrical Resolution Multispectral/Hyperspectral Images and LiDAR Data. Remote Sens. Environ. 2012, 123, 258–270. [Google Scholar] [CrossRef]
  89. Harrell, F.E. Regression Modeling Strategies, 2nd ed.; Springer: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
  90. Ahokas, E.; Kaasalainen, S.; Hyyppä, J.; Suomalainen, J. Calibration of the OPTECH ALTM 3100 Laser Scanner Intensity Data Using Brightness Targets. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 1–6. [Google Scholar]
  91. Kashani, A.G.; Olsen, M.J.; Parrish, C.E.; Wilson, N. A Review of LIDAR Radiometric Processing: From Ad Hoc Intensity Correction to Rigorous Radiometric Calibration. Sensors 2015, 15, 28099–28128. [Google Scholar] [CrossRef] [Green Version]
  92. Eysn, L.; Hollaus, M.; Lindberg, E.; Berger, F.; Monnet, J.-M.; Dalponte, M.; Kobal, M.; Pellegrini, M.; Lingua, E.; Mongus, D.; et al. A Benchmark of Lidar-Based Single Tree Detection Methods Using Heterogeneous Forest Data from the Alpine Space. Forests 2015, 6, 1721–1747. [Google Scholar] [CrossRef]
Remotesensing 14 05345 g001 550
Figure 1. The study area with selected forest plots with the orthophoto in background.
Figure 1. The study area with selected forest plots with the orthophoto in background.
Remotesensing 14 05345 g001
Remotesensing 14 05345 g002 550
Figure 2. Treetops of reference trees marked red in the profile section of forest plot.
Figure 2. Treetops of reference trees marked red in the profile section of forest plot.
Remotesensing 14 05345 g002
Remotesensing 14 05345 g003 550
Figure 3. Methodological framework.
Figure 3. Methodological framework.
Remotesensing 14 05345 g003
Remotesensing 14 05345 g004 550
Figure 4. Tree segments with detected treetops.
Figure 4. Tree segments with detected treetops.
Remotesensing 14 05345 g004
Remotesensing 14 05345 g005 550
Figure 5. Comparison of OA for the RF model before and after data balancing. The median is shown as black dot in the box, while first and third quartiles define the box. The whiskers define the minimum and maximum of the data while outliers are shown as blue circles.
Figure 5. Comparison of OA for the RF model before and after data balancing. The median is shown as black dot in the box, while first and third quartiles define the box. The whiskers define the minimum and maximum of the data while outliers are shown as blue circles.
Remotesensing 14 05345 g005
Remotesensing 14 05345 g006 550
Figure 6. Feature selection using GA with 100 iterations. Red dots represent external performance estimates while blue dots are estimates of mean internal performance of each iteration.
Figure 6. Feature selection using GA with 100 iterations. Red dots represent external performance estimates while blue dots are estimates of mean internal performance of each iteration.
Remotesensing 14 05345 g006
Remotesensing 14 05345 g007 550
Figure 7. Comparison of Overall Accuracy (OA) and kappa coefficient (κ) achieved by different classifiers on the training data.
Figure 7. Comparison of Overall Accuracy (OA) and kappa coefficient (κ) achieved by different classifiers on the training data.
Remotesensing 14 05345 g007
Remotesensing 14 05345 g008 550
Figure 8. The importance of selected variables expressed by scaled Mean decrease in Gini measure.
Figure 8. The importance of selected variables expressed by scaled Mean decrease in Gini measure.
Remotesensing 14 05345 g008
Table
Table 1. Overview of the tree metrics.
Table 1. Overview of the tree metrics.
Tree MetricsDescriptionSoftware
Nnumber of points in each tree segmentlidr
Areaapproximate actual area of a raster
Phabhmpercentage of returns above mean height
Hentrentropy of height distribution—the normalized Shannon vertical complexity index [50]
Phabxpercentage of returns above x
Hpcum (x = 1,…,9)
range = 1		cumulative percentage of return in the ith layer, according to Woods et al. [51]
P (x = 1,2,3,4,5) thpercentage of xth return
Hminminimum height rLidar
Hmaxmaximum height
Hmeanmean height
Hmedmedian height
Hmodheight mode
Hsdstandard deviation of height distribution
Hvarheight variance
Hcvcoefficient of variation of height
Hskewskewness of height distribution
Hkurtkurtosis of height distribution
Hq (x = 1,5,…,95,99) range = 5xth percentile (quantile) of height distribution
Ewidthtree crown width in eastern direction
Nwidthtree crown width in northern direction
Diqinterquartile distanceFUSION
HaadAverage Absolute Deviation of height
Hmadmedmedian of the absolute deviations from the overall median
Hmadmodmedian of the absolute deviations from the overall mode
HL (x = 1,2,3,4)L-moments (λ1, λ2, λ3, λ4)
HLcvL-moments coefficient of variation τ2 = λ1/λ2
HLskewL-moments skewness τ2 = λ3/λ2
HLkurt L - moments   kurtosis   τ 4   = λ4/λ2
Hcrrcanopy relief ratio ((Hmean − Hmin)/(Hmax − Hmin))
Hsqmsqgeneralized means for the 2nd power (height quadratic mean)
Hsqmcubegeneralized means for the 3rd power (height cubic mean)
Hprofareaarea under the height percentile profile or curve
Table
Table 2. Overview of the segment shape features.
Table 2. Overview of the segment shape features.
Segment Shape FeaturesDescription
Lngtlength—largest dimension of a polygon
Elngelongation—the ratio of the width and diameter of polygon
EccBBeccentricity-bounding box—ratio of the width and diameter of bounding box of polygon
Solidsolidity—the ratio of polygon area and area of the convex hull
EccEgneigenvalue of eccentricity matrix
Rectrectangularity—the ratio of the area of the segment to the area of its MBR
CircHarHaralick’s circularity of a shape
Convexconvexity—the ratio of the eigenvalues (inertia axis)
Table
Table 3. Overview of the eigenvalue-based features.
Table 3. Overview of the eigenvalue-based features.
Eigenvalue-Based FeaturesDescription
EgnLrglargest eigenvalue e1
EgnMdmmedium eigenvalue e2
EgnSmlsmallest eigenvalue e3
Lnrlinearity (e1 − e2)/e1
Plnrplanarity (e2 − e3)/e1
Sphsphericity e3/e1
Anstranisotropy (e1 − e3)/e1
Curvcurvature e3/(e1 + e2 + e3)
Omnivaromnivariance λ 1 λ 2 λ 3 3
EigentrEigen entropy—(e1 ln(e1) + e2 ln(e2) + e3 ln(e3))
Eigensumsum of eigenvalues e1 + e2 + e3
Table
Table 4. Overview of the shape-fitting features.
Table 4. Overview of the shape-fitting features.
Shape-Fitting FeaturesDescription
Minquadminimum of residuals fitting points to polynomial surface
Maxquadmaximum of residuals fitting points to polynomial surface
Medquadmedian of residuals fitting points to polynomial surface
RMSquadRMS of residuals fitting points to polynomial surface
Minrobquadrobust minimum of residuals fitting points to polynomial surface
Maxrobquadrobust maximum of residuals fitting points to polynomial surface
Medrobquadrobust median of residuals fitting points to polynomial surface
RMSrobquadrobust RMS of residuals fitting points to polynomial surface
Table
Table 5. Optimal hyperparameters for each machine learning algorithm and libraries used.
Table 5. Optimal hyperparameters for each machine learning algorithm and libraries used.
AlgorithmOptimal HyperparametersMethod/R Package
RFsplitrule = extratrees
ntree = 2000
min.node.size = 1
mtry = 4
num.random.splits = 3		Extremely Randomized Trees/ranger [75]
XGBnrounds = 1500
max_depth = 4
eta = 0.1
gamma = 0		xgboost [76]
ANNsize = 36
decay = 0.2		polynomial kernel/kernlab [77,78]
SVMdegree = 3
scale = 1
C = 0.1		feed-forward with single hidden layer/nnet [79]
LRfamily = binomialglm/caret [80]
Table
Table 6. Accuracy results of each classifier when predicted on test data.
Table 6. Accuracy results of each classifier when predicted on test data.
ClassifierOA [%]κ
RF89.00.757
XGB88.80.750
ANN84.10.657
SVM82.50.625
LR74.10.431
Table
Table 7. The confusion matrix and performance metrics of the RF classification based on the test dataset comprising 8 forest plots.
Table 7. The confusion matrix and performance metrics of the RF classification based on the test dataset comprising 8 forest plots.
Plot TypePred/RefTrueFalseUA
Mixed
(all 8 plots)		true2571594.5%
false3212479.5%
PA88.9%89.2%OA= 89.0%; κ = 0.757
Table
Table 8. The confusion matrix and performance metrics of the RF classification based on the test dataset with plots separated into deciduous, coniferous, and mixed forests.
Table 8. The confusion matrix and performance metrics of the RF classification based on the test dataset with plots separated into deciduous, coniferous, and mixed forests.
Plot TypePred/RefTrueFalseUA
Deciduous (5 plots)true113794.2%
false144676.7%
PA89.0%86.8%OA = 88.3%; κ = 0.730
Coniferous (2 plots) true118695.2%
false177180.7%
PA87.4%92.2%OA = 89.2%; κ = 0.772
Mixed (1 plot)true26292.9%
false1787.5%
PA96.3%77.8%OA = 91.7%; κ = 0.769
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Brodić, N.; Cvijetinović, Ž.; Milenković, M.; Kovačević, J.; Stančić, N.; Mitrović, M.; Mihajlović, D. Refinement of Individual Tree Detection Results Obtained from Airborne Laser Scanning Data for a Mixed Natural Forest. Remote Sens. 2022, 14, 5345. https://doi.org/10.3390/rs14215345

AMA Style

Brodić N, Cvijetinović Ž, Milenković M, Kovačević J, Stančić N, Mitrović M, Mihajlović D. Refinement of Individual Tree Detection Results Obtained from Airborne Laser Scanning Data for a Mixed Natural Forest. Remote Sensing. 2022; 14(21):5345. https://doi.org/10.3390/rs14215345

Chicago/Turabian Style

Brodić, Nenad, Željko Cvijetinović, Milutin Milenković, Jovan Kovačević, Nikola Stančić, Momir Mitrović, and Dragan Mihajlović. 2022. "Refinement of Individual Tree Detection Results Obtained from Airborne Laser Scanning Data for a Mixed Natural Forest" Remote Sensing 14, no. 21: 5345. https://doi.org/10.3390/rs14215345

APA Style

Brodić, N., Cvijetinović, Ž., Milenković, M., Kovačević, J., Stančić, N., Mitrović, M., & Mihajlović, D. (2022). Refinement of Individual Tree Detection Results Obtained from Airborne Laser Scanning Data for a Mixed Natural Forest. Remote Sensing, 14(21), 5345. https://doi.org/10.3390/rs14215345

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop