PU-WGCN: Point Cloud Upsampling Using Weighted Graph Convolutional Networks
Abstract
:1. Introduction
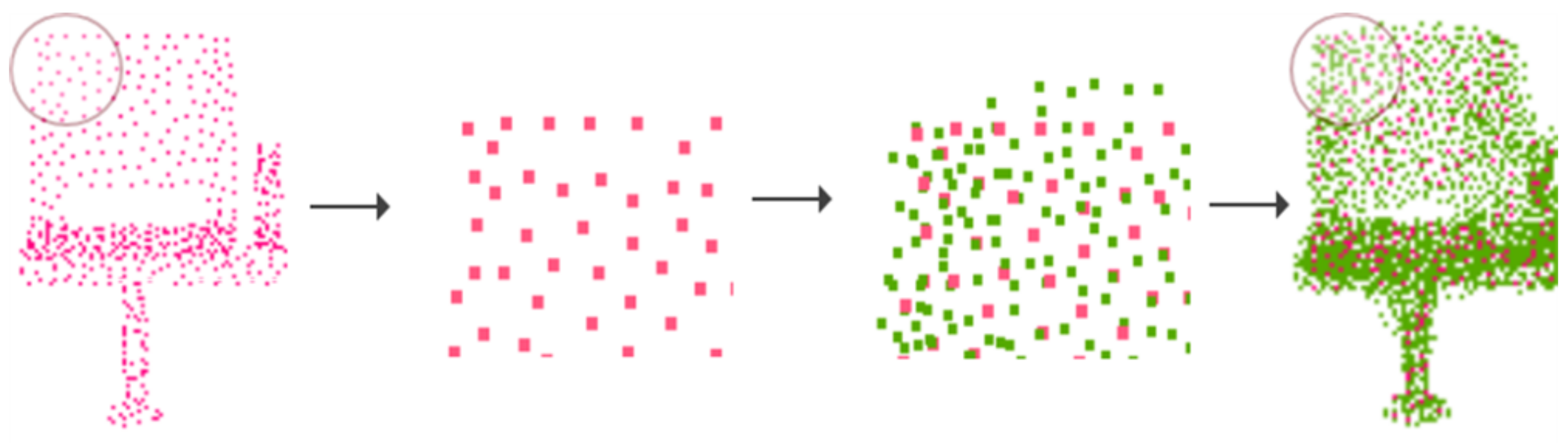
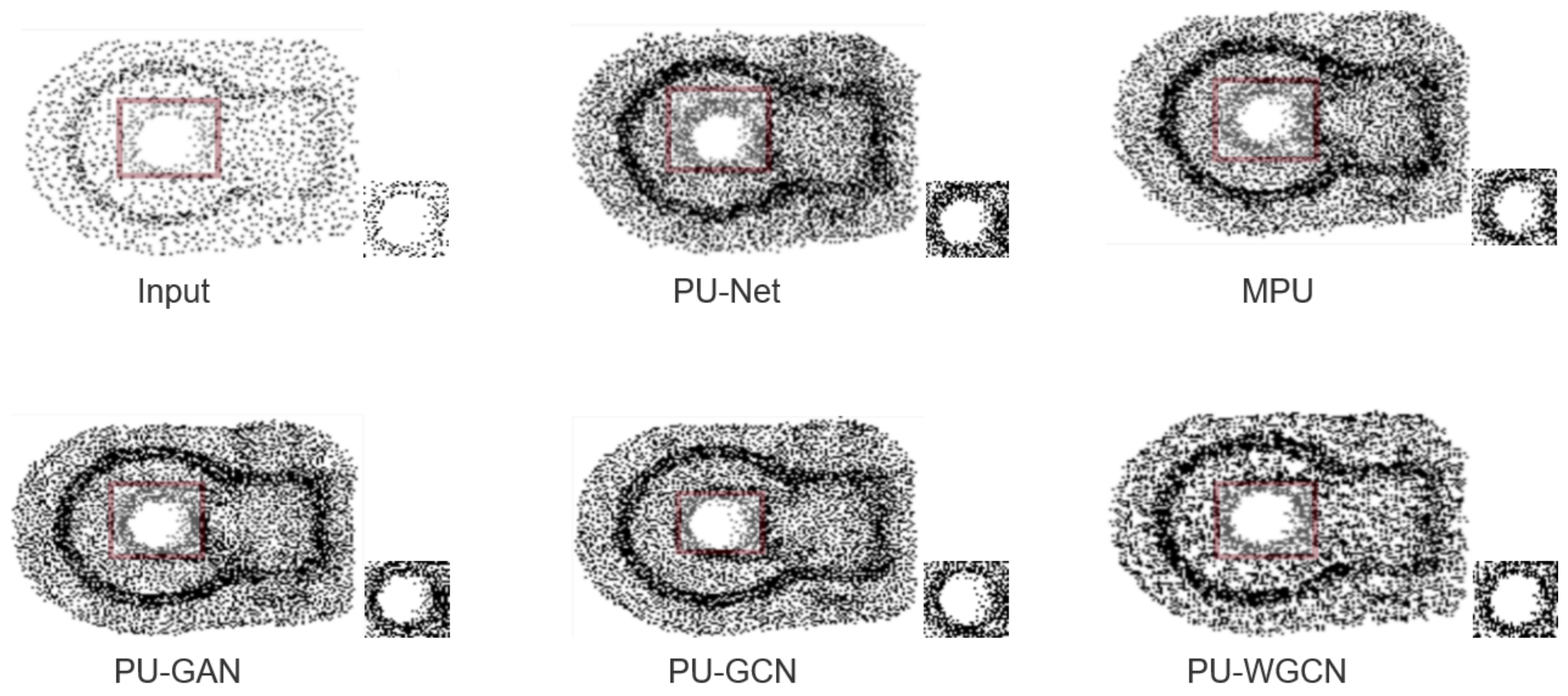
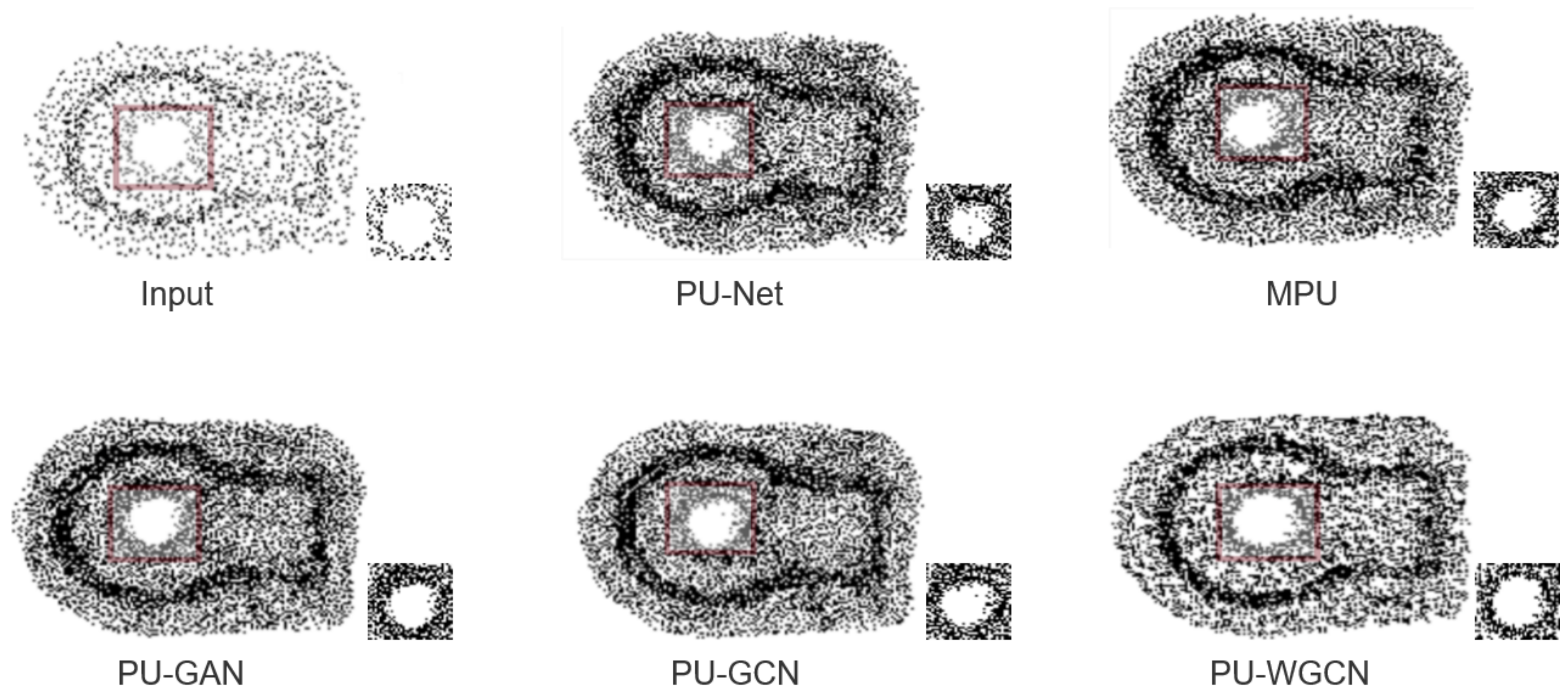
- Neighboring nodes with less variability and the aggregated neighborhood features operation treats all neighboring nodes equally. These two reasons lead to features of neighboring nodes that are too similar. When upsampling at the hole of the object, the network imposes uniform constraints on the upsampling points. As a result, the upsampling network creates the problem of holes being overfilled when increasing the number of points in this local neighborhood. Therefore, we enhance the graph feature information for the purpose of reducing the feature similarity of the point cloud.
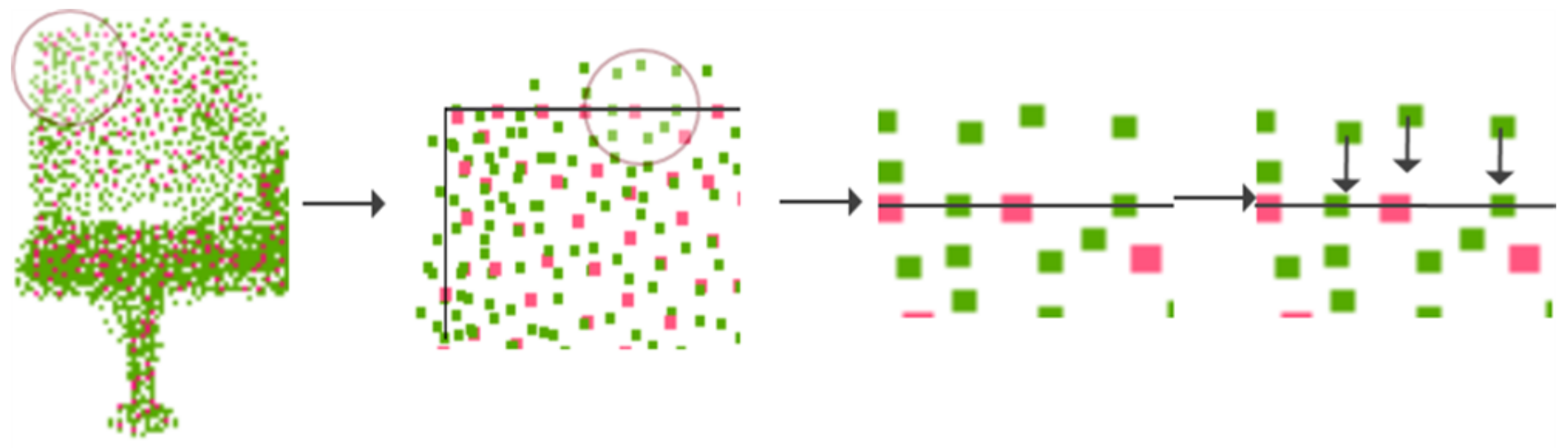
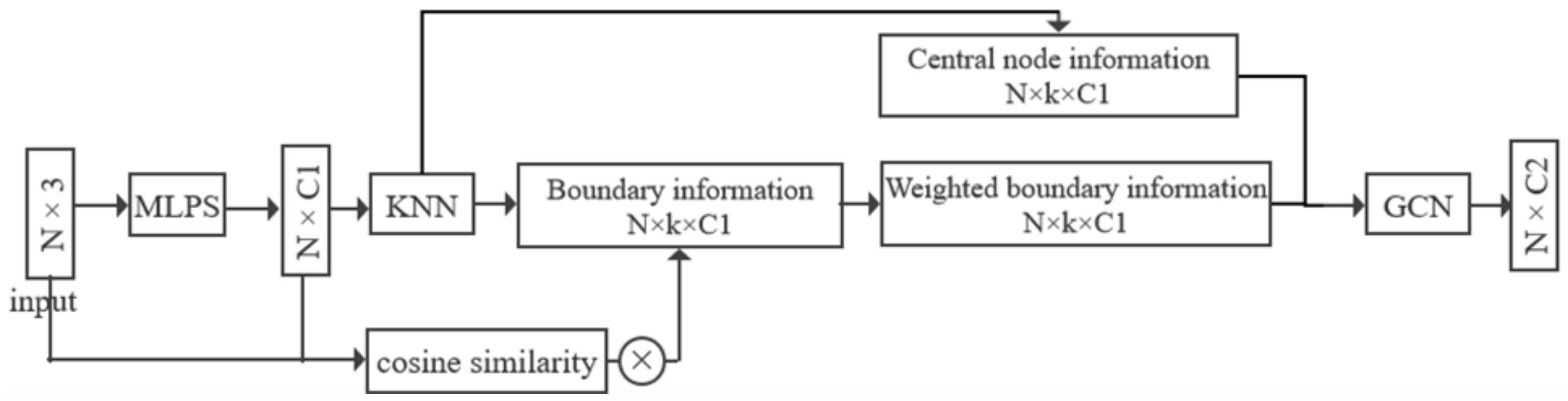
- The current upsampling network has no strict constraints on the boundary points. Moreover, the upsampling network uses uniform pattern to constrain the upsampling points in the point cloud graph. As a result, the boundary point cloud of the object generates outliers, which lead to boundary blurring. To solve this problem, we propose the boundary information weighting module. It weights the boundary information by calculating the point similarity. It makes the upsampling network more boundary-focused.
- The above two modules are combined with the upsampling module to form the upsampling network named PU-WGCN. PU-WGCN can solve the problems of hole overfilling and boundary blurring generated by upsampling.
2. Relation Work
2.1. Graph Convolutional Networks (GCNs)
2.2. Point Cloud Processing Based on Graph Neural Network
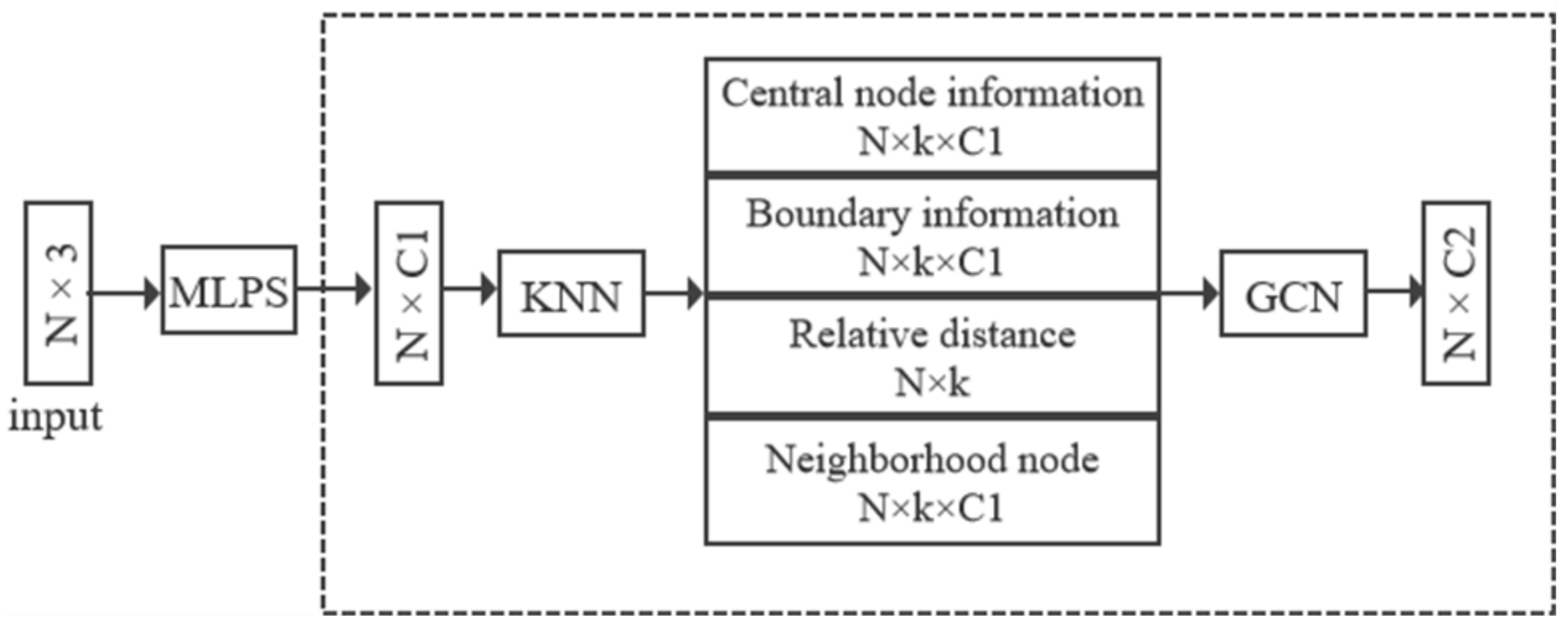
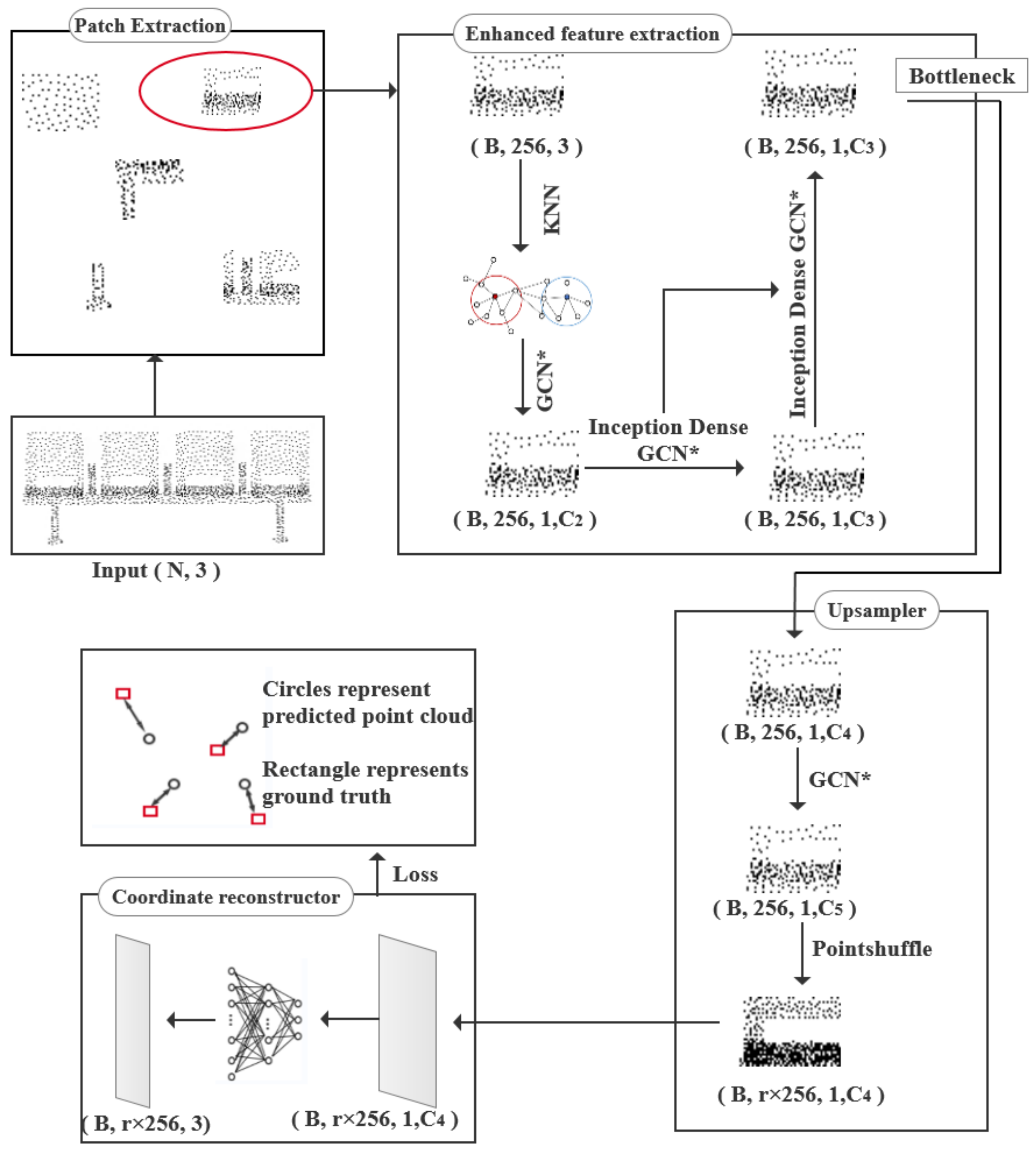
3. Materials and Methods
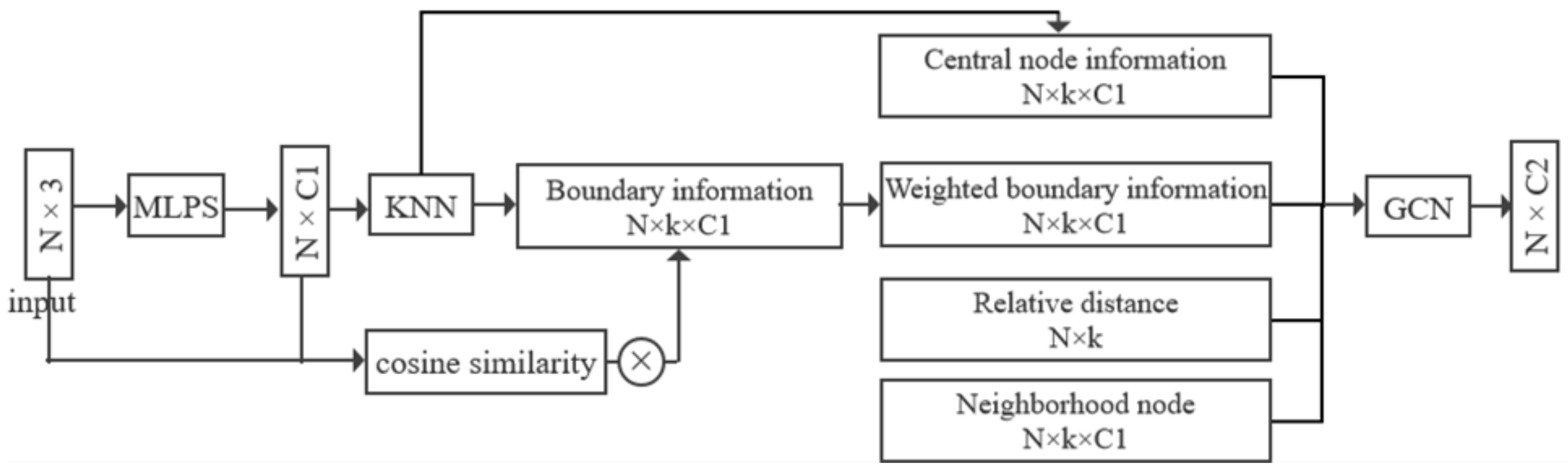
3.1. Weighted Graph Convolutional Networks (WGCN)
3.1.1. Graph Feature Enhancement Module
3.1.2. Boundary Information Weighting Module
3.2. PU-WGCN Architecture
4. Experiments and Results
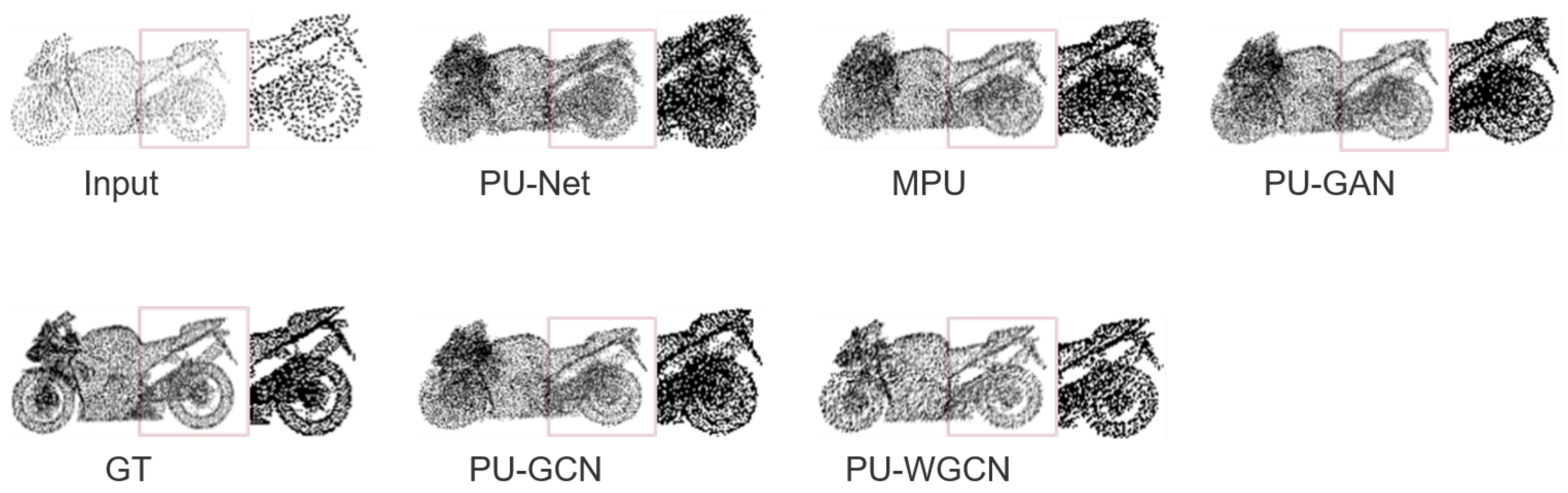
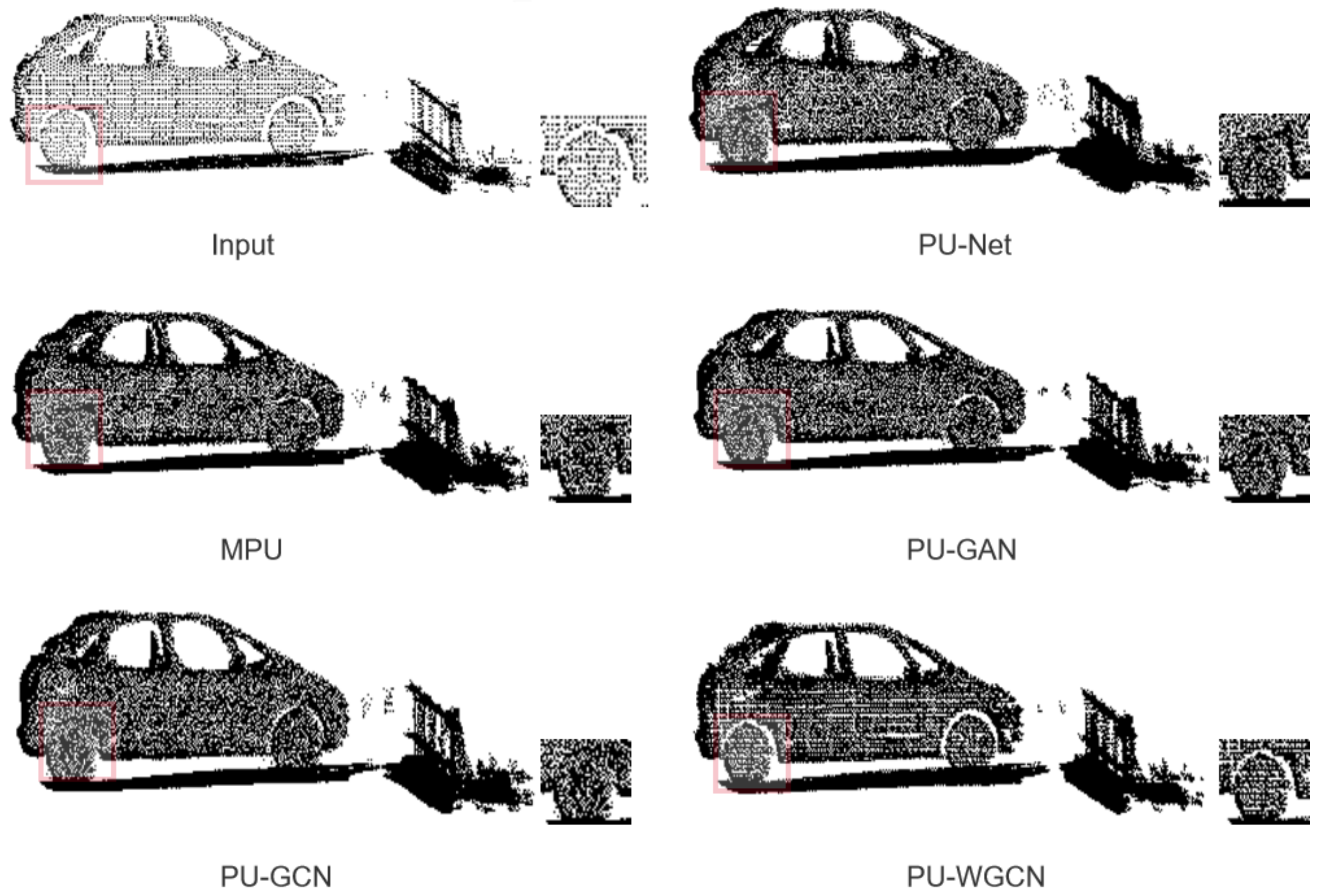
4.1. Results and Comparisons
4.2. Robustness to Real-Scanned Point Clouds
4.3. Ablation Study
4.4. Robustness of PU-WGCN
5. Discussion and Limitation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lv, C.; Lin, W.; Zhao, B. Voxel Structure-based Mesh Reconstruction from a 3D Point Cloud. IEEE Trans. Multimed. 2021, 24, 1815–1829. [Google Scholar] [CrossRef]
- Wu, J. A lidar point cloud encryption algorithm based on mobile least squares. Urban Geotech. Investig. Surv. 2019, 5, 110–115. [Google Scholar]
- Huang, K.Y.; Tang, J.C.; Zhou, X.J.; Chen, M.Y.; Fang, Y.M.; Lei, Z.Y. Poisson surface reconstruction algorithm based on improved normal orientation. Laser Optoelectron. Prog. 2019, 56, 88–95. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.C.; Guibas, L.J. PointNet: Deep learning on point sets for 3D classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Hawaii, HI, USA, 21–26 July 2017. [Google Scholar]
- Qi, C.R.; Li, Y.; Hao, S.; Guibas, L.J. PointNet++: Deep hierarchical feature learning on point sets in a metric space. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Hu, Q.Y.; Yang, B.; Xie, L.H.; Rosa, S.; Guo, Y.L.; Wang, Z.H.; Trigoni, N.; Markham, A. RandLA-Net: Efficient Semantic Segmentation of Large-Scale Point Clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Fan, S.Q.; Dong, Q.L.; Zhu, F.H.; LV, Y.S.; Ye, P.J.; Wang, F.Y. SCF-Net: Learning Spatial Contextual Features for Large-Scale Point Cloud Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Online, 19–25 June 2021. [Google Scholar]
- Nie, Y.Y.; Hou, J.; Han, X.G.; Niesner, M. RfD-Net: Point Scene Understanding by Semantic Instance Reconstruction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Online, 19–25 June 2021. [Google Scholar]
- He, T.; Huang, H.B.; Yi, L.; Zhou, Y.Q.; Wu, C.H.; Wang, J.; Soatto, S. GeoNet: Deep Geodesic Networks for Point Cloud Analysis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–21 June 2019. [Google Scholar]
- Yu, L.Q.; Li, X.Z.; Fu, C.W.; Cohen-Or, D.; Heng, P.A. PU-Net: Point cloud upsampling network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–21 June 2018. [Google Scholar]
- Wang, Y.F.; Wu, S.H.; Huang, H.; Cohen-Or, D.; Sorkine-Hornung, O. Patch-based progressive 3d point set upsampling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–21 June 2019. [Google Scholar]
- Li, R.H.; Li, X.Z.; Fu, C.W.; Cohen-Or, D.; Heng, P.A. PU-GAN: A point cloud upsampling adversarial network. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October 2019. [Google Scholar]
- Qian, Y.; Hou, J.H.; Kwong, S.; He, Y. PUGeo-Net: A geometry-centric network for 3d point cloud upsampling. In Proceedings of the European Conference on Computer Vision (ECCV), Online, 23–28 August 2020. [Google Scholar]
- Feng, W.Q.; Li, J.; Cai, H.R.; Luo, X.N.; Zhang, J.Y. Neural Points: Point Cloud Representation with Neural Fields for Arbitrary Upsampling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–24 June 2022. [Google Scholar]
- Qian, G.C.; Abualshour, A.; Li, G.H.; Thabet, A.; Ghanem, B. PU-GCN: Point cloud up sampling using graph convolutional networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Online, 19–25 June 2021. [Google Scholar]
- Li, Y.Y.; Bu, R.; Sun, M.C.; Wu, W.; Di, X.H.; Chen, B.Q. PointCNN: Convolution on X-Transformed Points. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Palais des Congrès de Montréal, Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Wu, W.X.; Qi, Z.A.; Li, F.X. PointConv: Deep Convolutional Networks on 3D Point Clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Liu, Y.C.; Fan, B.; Xiang, S.M.; Pan, C.H. Relation-Shape Convolutional Neural Network for Point Cloud Analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–21 June 2019. [Google Scholar]
- Wang, Y.; Sun, Y.B.; Liu, Z.W.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic Graph CNN for learning on point clouds. ACM Trans. Graph. 2019, 38, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Li, G.H.; Mvller, M.A.; Thabet, A.; Ghanem, B. DeepGCNs: Can GCNs Go as Deep as CNNs? In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October 2019. [Google Scholar]
- Li, D.L.; Shen, X.; Yu, Y.T.; Guan, H.Y.; Li, J.; Li, D. Building extraction from airborne multi-spectral lidar point clouds based on graph geometric moments convolutional neural networks. Remote Sens. 2020, 12, 3186. [Google Scholar] [CrossRef]
- Petar, V.; Guillem, C.; Arantxa, C.; Adriana, R.; Pietro, L.; Yoshua, B. Graph Attention Networks. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Zi, W.J.; Xiong, W.; Chen, H.; Li, J.; Jing, N. SGA-Net: Self-Constructing Graph Attention Neural Network for Semantic Segmentation of Remote Sensing Images. Remote Sens. 2021, 13, 4201. [Google Scholar] [CrossRef]
- Huang, W.B.; Rong, Y.; Xu, T.Y.; Sun, F.C.; Huang, J.Z. Tackling Over-Smoothing for General Graph Convolutional Networks. arXiv 2020, arXiv:2008.09864. [Google Scholar]
- Wu, S.W.; Sun, F.; Zhang, W.T.; Cui, B. Graph Neural Networks in Recommender Systems: A Survey. ACM Comput. Surv. 2022. [Google Scholar] [CrossRef]
- Tian, Q.Y.; Ding, M.; Yang, H.; Yue, C.B.; Zhong, Y.; Du, Z.Z.; Liu, D.Y.; Liu, J.L.; Deng, Y.F. Predicting drug-target affinity based on recurrent neural networks and graph convolutional neural networks. Comb. Chem. High Throughput Screen. 2022, 25, 634–641. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.N.; Yang, B.; Liu, D.Y. Distance Similarity Algorithm for Mining Communities from Complex Networks. J. Front. Comput. Sci. Technol. 2011, 5, 336–346. [Google Scholar]
- Wang, K.; Guang, H.; Liang, Z.W.; Ye, M.Y. Detecting community in weighted complex network based on similarities. J. Sichuan Univ. Sci. Ed. 2014, 51, 1170–1176. [Google Scholar]
- Yu, L.; Li, T.; Zhan, Q.M.; Yu, K. Segmentation of LiDAR point clouds based on similarity measures in multi-dimensional Euclidean Space. Remote Sens. Land Resour. 2014, 26, 31–36. [Google Scholar]
- An, Y.J.; Chen, X.X.; Sui, L.C.; Zhou, R.R. A Structural Road Extraction Method Based on Normal Vectors Similarity of Point Clouds. Bull. Surv. Mapp. 2018, 11, 69–72. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Chen, D.; Lin, Y.; Li, W.; Li, P.; Zhou, J.; Sun, X. Measuring and Relieving the Over-smoothing Problem for Graph NeuralNetworks from the Topological View. In Proceedings of the Association for the Advancement of Artificial Intelligence (AAAI), New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Kong, K.Z.; Li, G.H.; Ding, M.C.; Wu, Z.X.; Zhu, C.; Ghanem, B.; Taylor, G.; Goldstein, T. Robust Optimization as Data Augmentation for Large-scale Graphs. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–24 June 2022. [Google Scholar]
- Asiri, W.; Wang, Q. A New Perspective on “How Graph Neural NetWorks go Beyond Weisfeiler-Lehman?”. In Proceedings of the International Conference on Learning Representations (ICLR), Online, 25–29 April 2022. [Google Scholar]
- Shi, W.J.; Rajkumar, R. Point-GNN: Graph Neural Network for 3D Object Detection in a Point Cloud. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]




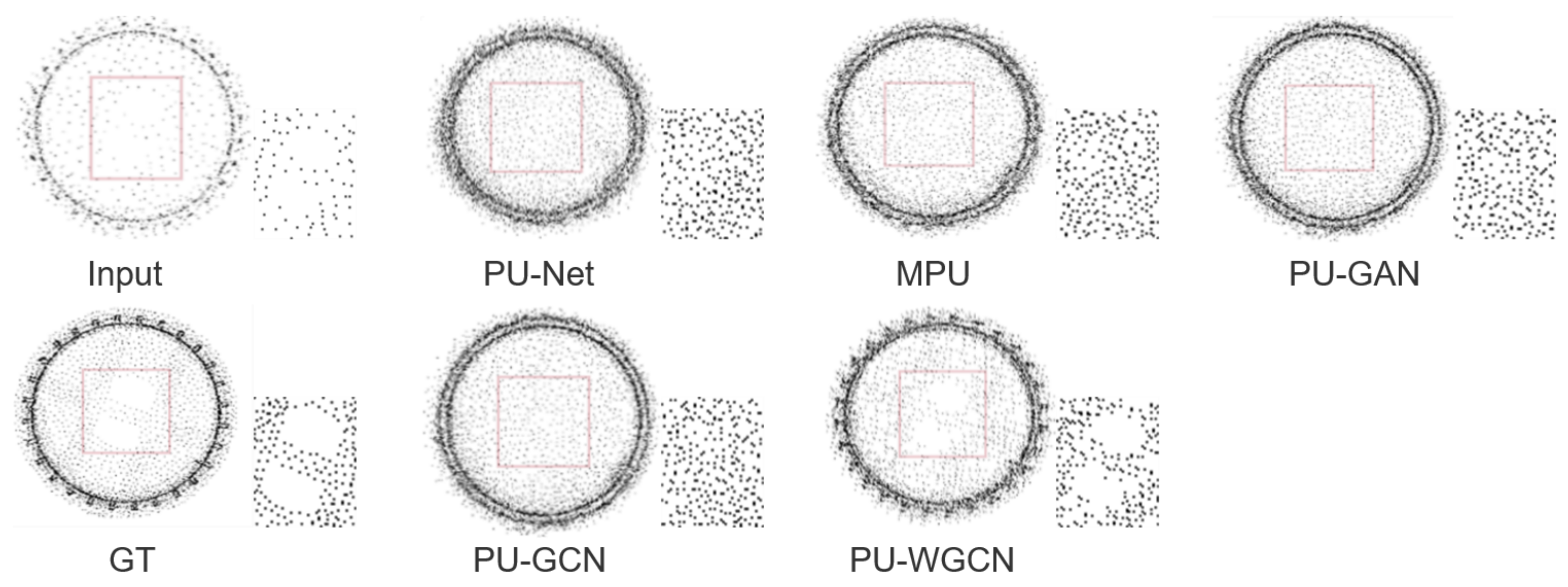

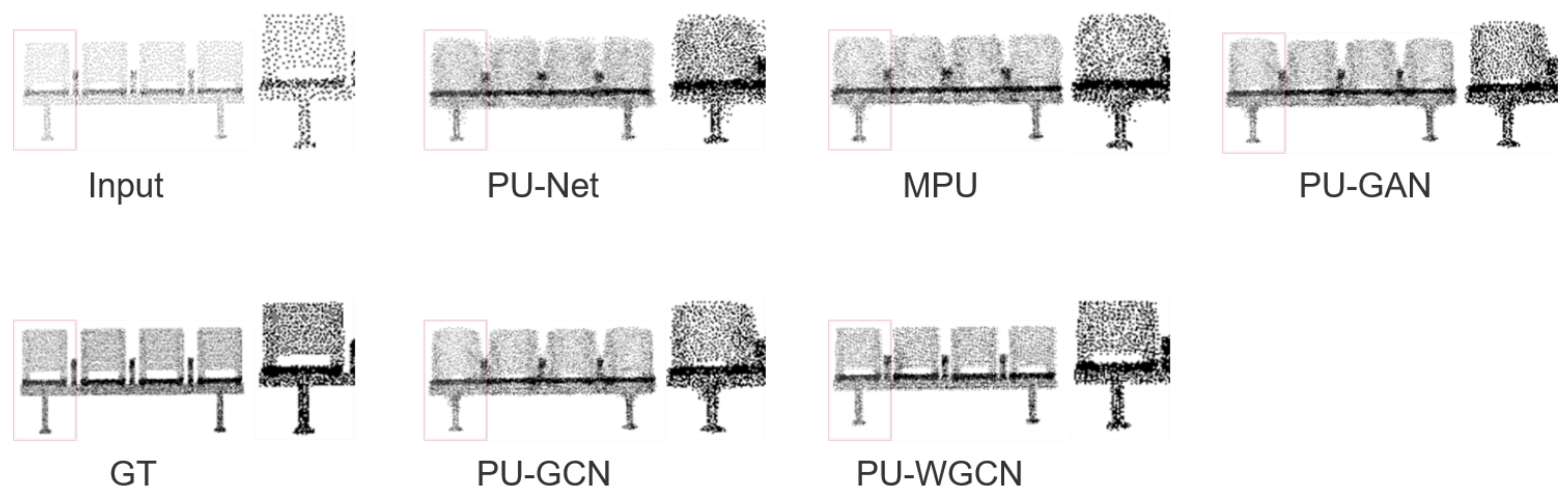




| Network | CD | HD | P2F |
|---|---|---|---|
| PU-Net | 4.569 | 49.431 | 15.645 |
| MPU | 3.821 | 38.123 | 7.513 |
| PU-GAN | 3.274 | 31.260 | 7.970 |
| PU-GCN | 3.186 | 31.884 | 7.724 |
| PU-WGCN | 2.936 | 29.567 | 7.265 |
| Network | CD | HD | P2F |
|---|---|---|---|
| PU-Net | 2.999 | 35.240 | 11.189 |
| MPU | 2.717 | 29.567 | 8.135 |
| PU-GAN | 2.085 | 21.862 | 6.949 |
| PU-GCN | 2.070 | 23.770 | 6.686 |
| PU-WGCN | 1.919 | 21.748 | 6.014 |
| Network | CD | HD | P2F |
|---|---|---|---|
| PU-Net | 1.886 | 24.310 | 7.407 |
| MPU | 1.602 | 19.722 | 5.350 |
| PU-GAN | 1.223 | 14.932 | 4.571 |
| PU-GCN | 1.144 | 15.546 | 4.312 |
| PU-WGCN | 1.087 | 13.351 | 3.820 |
| Network | CD | HD | P2F |
|---|---|---|---|
| PU-Net | 1.092 | 14.561 | 4.928 |
| MPU | 0.940 | 12.535 | 3.459 |
| PU-GAN | 0.738 | 10.074 | 2.992 |
| PU-GCN | 0.669 | 10.087 | 2.706 |
| PU-WGCN | 0.619 | 8.926 | 2.377 |
| Experiments | Graph Feature Enhancement Module | Boundary Information Weighting Module | CD | HD | P2F |
|---|---|---|---|---|---|
| Experiment 1 | 0.669 | 10.087 | 2.706 | ||
| Experiment 2 | √ | 0.626 | 8.809 | 2.550 | |
| Experiment 3 | √ | 0.608 | 9.458 | 2.451 | |
| Experiment 4 | √ | √ | 0.619 | 8.926 | 2.377 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, F.; Zhang, C.; Wang, H.; He, Q.; Huo, L. PU-WGCN: Point Cloud Upsampling Using Weighted Graph Convolutional Networks. Remote Sens. 2022, 14, 5356. https://doi.org/10.3390/rs14215356
Gu F, Zhang C, Wang H, He Q, Huo L. PU-WGCN: Point Cloud Upsampling Using Weighted Graph Convolutional Networks. Remote Sensing. 2022; 14(21):5356. https://doi.org/10.3390/rs14215356
Chicago/Turabian StyleGu, Fan, Changlun Zhang, Hengyou Wang, Qiang He, and Lianzhi Huo. 2022. "PU-WGCN: Point Cloud Upsampling Using Weighted Graph Convolutional Networks" Remote Sensing 14, no. 21: 5356. https://doi.org/10.3390/rs14215356
APA StyleGu, F., Zhang, C., Wang, H., He, Q., & Huo, L. (2022). PU-WGCN: Point Cloud Upsampling Using Weighted Graph Convolutional Networks. Remote Sensing, 14(21), 5356. https://doi.org/10.3390/rs14215356








