Linking Remote Sensing with APSIM through Emulation and Bayesian Optimization to Improve Yield Prediction
Abstract
1. Introduction
2. Materials and Methods
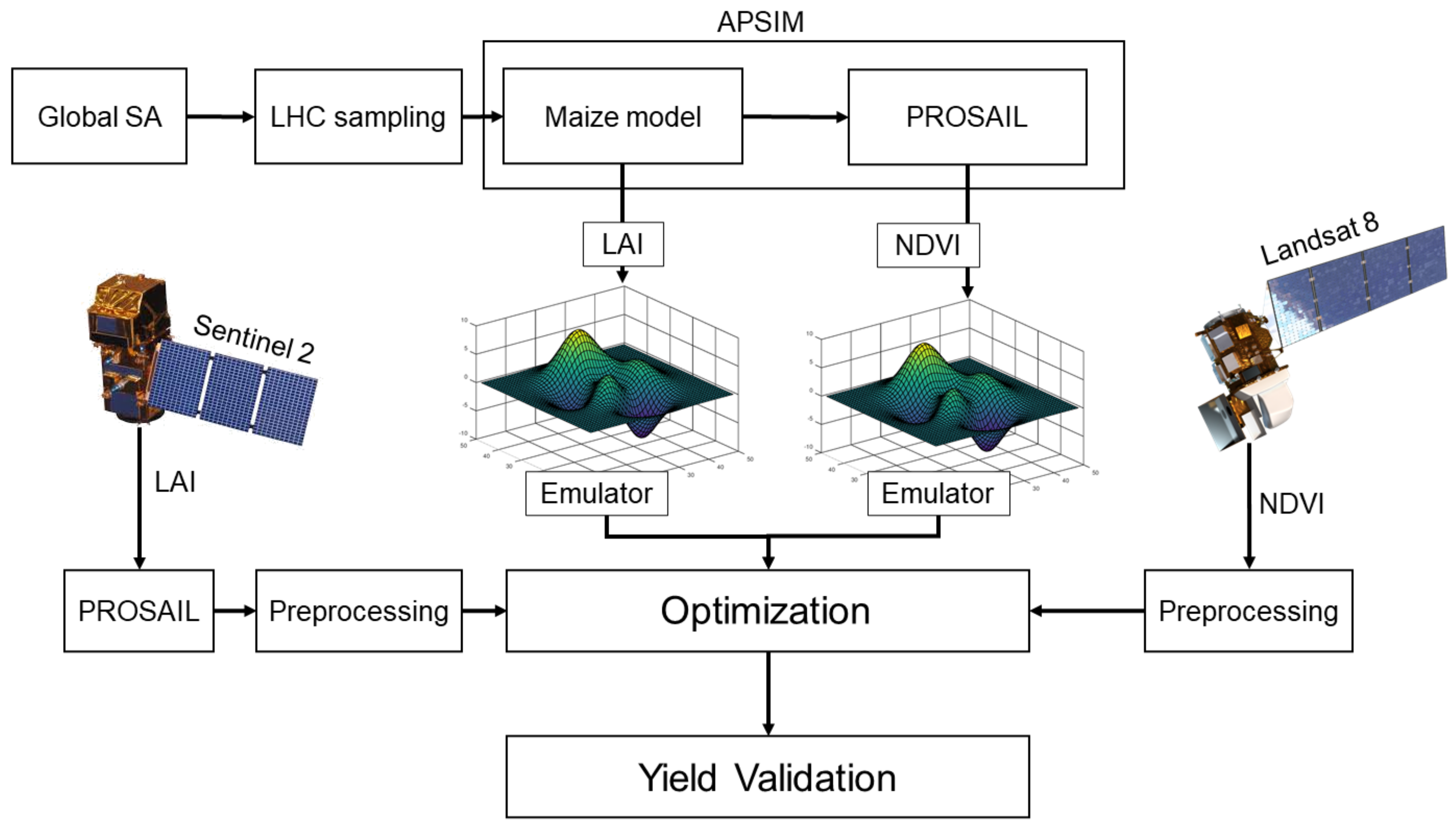
2.1. Overall Workflow
2.2. Study Sites
2.3. Data Collection
2.3.1. Weather and Soil
2.3.2. LAI and NDVI Retrieval and Data Processing
- Randomly sampled 400,000 combinations of PROSAIL input parameters with bounds shown in Table A2 and weights for the soil model.
- Using PROSAIL to compute top of canopy reflectance with the randomly sampled inputs and the simulated soil background.
- The simulated reflectance is convolved with the Sentinel-2 relative spectral response functions to simulate surface reflectance at different bands (addB02, B03, B04, B05, B06, B07, B08, B8A, B11, B12).
- Train NN for LAI by using the simulated reflectance over Sentinel-2 bands as inputs.
- The trained NN is then used to map from satellite surface reflectance to LAI.
2.3.3. Crop Growth Model
2.4. Model and Parameter Selection
2.5. Emulator Development
2.6. Optimization Schemes
3. Results
3.1. Sensitivity Analysis and Emulator Performance
3.2. Within Sample Prediction
3.3. Comparing Posterior Distributions
3.4. Out-of-Sample Prediction
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Library | Type | Reference |
|---|---|---|
| USGS v7 | Measurements | [59] |
| ICRAF-ISRIC | Measurements | [60] |
| Price | Soil model | [61] |
| Prosail | Soil model | [36] |
| Traits Type | Parameter | Symbol | Range | Unit |
|---|---|---|---|---|
| Canopy structure | leaf area index | 0–8 | m/m | |
| leaf angle distribution function | 0–90 | |||
| Leaf optical | chlorophyll a and b content | 0–120 | g/cm | |
| Carotenoid content | 0–25 | g/cm | ||
| Anthocyanin content | 0 | g/cm | ||
| leaf dry matter per leaf area | 0.002–0.01 | g/cm | ||
| leaf water content per leaf area | 0–0.04 | mg/cm | ||
| brown pigment content | 0–1 | - | ||
| mesophyll structure coefficient | N | 1–2.5 | - | |
| angles | solar zenith angle | sza | 0–80 | |
| viewing zenith angle | vza | 0–15 | ||
| relative azimuth angle | raa | 0–360 |
| Parameter | Upper Bound | Lower Bound |
|---|---|---|
| tt_flower_to_maturity | 1100 | 700 |
| tt_emerg_to_endjuv | 500 | 200 |
| tt_flower_to_start_grain | 400 | 100 |
| leaf_app_rate1 | 65 | 40 |
| leaf_app_rate2 | 50 | 20 |
| leaf_app_rate3 | 50 | 20 |
| largestLeafParams1 | −1 | −2 |
| largestLeafParams2 | 0.05 | 0.03 |
| y_lai_sla_max1 | 55,000 | 45,000 |
| y_lai_sla_max2 | 30,000 | 20,000 |
| leaf_init_rate | 30 | 15 |
| rue | 3 | 1.6 |
| grain_gth_rate | 11 | 8 |
| initial_tpla | 450 | 300 |





References
- Gill, H.S.; Halder, J.; Zhang, J.; Brar, N.K.; Rai, T.S.; Hall, C.; Bernardo, A.; Amand, P.S.; Bai, G.; Olson, E.; et al. Multi-Trait Multi-Environment Genomic Prediction of Agronomic Traits in Advanced Breeding Lines of Winter Wheat. Front. Plant Sci. 2021, 12, 1619. [Google Scholar] [CrossRef]
- Su, W.; Zhang, M.; Bian, D.; Liu, Z.; Huang, J.; Wang, W.; Wu, J.; Guo, H. Phenotyping of corn plants using unmanned aerial vehicle (UAV) images. Remote Sens. 2019, 11, 2021. [Google Scholar] [CrossRef]
- Dokoohaki, H.; Gheysari, M.; Mehnatkesh, A.; Ayoubi, S. Applying the CSM-CERES-Wheat model for rainfed wheat with specified soil characteristic in undulating area in Iran. Arch. Agron. Soil Sci. 2015, 61, 1231–1245. [Google Scholar] [CrossRef]
- Dietze, M. Ecological Forecasting; Princeton University Press: Princeton, NJ, USA, 2017. [Google Scholar]
- Kivi, M.S.; Blakely, B.; Masters, M.; Bernacchi, C.J.; Miguez, F.E.; Dokoohaki, H. Development of a data-assimilation system to forecast agricultural systems: A case study of constraining soil water and soil nitrogen dynamics in the APSIM model. Sci. Total Environ. 2022, 820, 153192. [Google Scholar] [CrossRef] [PubMed]
- Dokoohaki, H.; Gheisari, M.; Mousavi, S.F.; Mirlatifi, S.M. Estimation soil water content under deficit irrigation by using DSSAT. Water Irrig. Manag. 2012, 2, 1–14. [Google Scholar]
- Holzworth, D.P.; Huth, N.I.; deVoil, P.G.; Zurcher, E.J.; Herrmann, N.I.; McLean, G.; Chenu, K.; van Oosterom, E.J.; Snow, V.; Murphy, C.; et al. APSIM–evolution towards a new generation of agricultural systems simulation. Environ. Model. Softw. 2014, 62, 327–350. [Google Scholar] [CrossRef]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT cropping system model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Archontoulis, S.V.; Castellano, M.J.; Licht, M.A.; Nichols, V.; Baum, M.; Huber, I.; Martinez-Feria, R.; Puntel, L.; Ordóñez, R.A.; Iqbal, J.; et al. Predicting crop yields and soil-plant nitrogen dynamics in the US Corn Belt. Crop Sci. 2020, 60, 721–738. [Google Scholar] [CrossRef]
- Saddique, Q.; Zou, Y.; Ajaz, A.; Ji, J.; Xu, J.; Azmat, M.; ur Rahman, M.H.; He, J.; Cai, H. Analyzing the Performance and Application of CERES-Wheat and APSIM in the Guanzhong Plain, China. Trans. ASABE 2020, 63, 1879–1893. [Google Scholar] [CrossRef]
- Rai, T.; Kumar, S.; Nleya, T.; Sexton, P.; Hoogenboom, G. Simulation of maize and soybean yield using DSSAT under long-term conventional and no-till systems. Soil Res. 2022, 60, 520–533. [Google Scholar] [CrossRef]
- Dokoohaki, H.; Kivi, M.S.; Martinez-Feria, R.A.; Miguez, F.E.; Hoogenboom, G. A comprehensive uncertainty quantification of large-scale process-based crop modeling frameworks. Environ. Res. Lett. 2021, 16, 084010. [Google Scholar] [CrossRef]
- Sun, R.; Duan, Q.; Huo, X. Multi-Objective Adaptive Surrogate Modeling-Based Optimization for Distributed Environmental Models Based on Grid Sampling. Water Resour. Res. 2021, 57, e2020WR028740. [Google Scholar] [CrossRef]
- Wallach, D.; Palosuo, T.; Thorburn, P.; Hochman, Z.; Gourdain, E.; Andrianasolo, F.; Asseng, S.; Basso, B.; Buis, S.; Crout, N.; et al. The chaos in calibrating crop models: Lessons learned from a multi-model calibration exercise. Environ. Model. Softw. 2021, 145, 105206. [Google Scholar] [CrossRef]
- Fer, I.; Gardella, A.K.; Shiklomanov, A.N.; Campbell, E.E.; Cowdery, E.M.; De Kauwe, M.G.; Desai, A.; Duveneck, M.J.; Fisher, J.B.; Haynes, K.D.; et al. Beyond ecosystem modeling: A roadmap to community cyberinfrastructure for ecological data-model integration. Glob. Chang. Biol. 2021, 27, 13–26. [Google Scholar] [CrossRef]
- Post, H.; Vrugt, J.A.; Fox, A.; Vereecken, H.; Hendricks Franssen, H.J. Estimation of Community Land Model parameters for an improved assessment of net carbon fluxes at European sites. J. Geophys. Res. Biogeosci. 2017, 122, 661–689. [Google Scholar] [CrossRef]
- Fer, I.; Shiklomanov, A.N.; Novick, K.A.; Gough, C.M.; Arain, M.A.; Chen, J.; Murphy, B.; Desai, A.R.; Dietze, M.C. Capturing site-to-site variability through Hierarchical Bayesian calibration of a process-based dynamic vegetation model. bioRxiv 2021. [Google Scholar] [CrossRef]
- Dokoohaki, H.; Morrison, B.D.; Raiho, A.; Serbin, S.P.; Zarada, K.; Dramko, L.; Dietze, M. Development of an open-source regional data assimilation system in PEcAn v. 1.7. 2: Application to carbon cycle reanalysis across the contiguous US using SIPNET. Geosci. Model Dev. Discuss. 2022, 15, 1–28. [Google Scholar] [CrossRef]
- Huang, J.; Gómez-Dans, J.L.; Huang, H.; Ma, H.; Wu, Q.; Lewis, P.E.; Liang, S.; Chen, Z.; Xue, J.H.; Wu, Y.; et al. Assimilation of remote sensing into crop growth models: Current status and perspectives. Agric. For. Meteorol. 2019, 276, 107609. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Shiklomanov, A.N.; Dietze, M.C.; Fer, I.; Viskari, T.; Serbin, S.P. Cutting out the middleman: Calibrating and validating a dynamic vegetation model (ED2-PROSPECT5) using remotely sensed surface reflectance. Geosci. Model Dev. 2021, 14, 2603–2633. [Google Scholar] [CrossRef]
- Dokoohaki, H.; Miguez, F.E.; Archontoulis, S.; Laird, D. Use of inverse modelling and Bayesian optimization for investigating the effect of biochar on soil hydrological properties. Agric. Water Manag. 2018, 208, 268–274. [Google Scholar] [CrossRef]
- Akhavizadegan, F.; Ansarifar, J.; Wang, L.; Huber, I.; Archontoulis, S.V. A time-dependent parameter estimation framework for crop modeling. Sci. Rep. 2021, 11, 1–15. [Google Scholar]
- Dietzel, R.; Liebman, M.; Ewing, R.; Helmers, M.; Horton, R.; Jarchow, M.; Archontoulis, S. How efficiently do corn-and soybean-based cropping systems use water? A systems modeling analysis. Glob. Chang. Biol. 2016, 22, 666–681. [Google Scholar] [CrossRef] [PubMed]
- Sheng, M.; Liu, J.; Zhu, A.X.; Rossiter, D.G.; Liu, H.; Liu, Z.; Zhu, L. Comparison of GLUE and DREAM for the estimation of cultivar parameters in the APSIM-maize model. Agric. For. Meteorol. 2019, 278, 107659. [Google Scholar] [CrossRef]
- Malone, R.W.; Huth, N.; Carberry, P.; Ma, L.; Kaspar, T.C.; Karlen, D.L.; Meade, T.; Kanwar, R.S.; Heilman, P. Evaluating and predicting agricultural management effects under tile drainage using modified APSIM. Geoderma 2007, 140, 310–322. [Google Scholar] [CrossRef]
- Archontoulis, S.V.; Miguez, F.E.; Moore, K.J. Evaluating APSIM maize, soil water, soil nitrogen, manure, and soil temperature modules in the Midwestern United States. Agron. J. 2014, 106, 1025–1040. [Google Scholar] [CrossRef]
- Puntel, L.A.; Sawyer, J.E.; Barker, D.W.; Dietzel, R.; Poffenbarger, H.; Castellano, M.J.; Moore, K.J.; Thorburn, P.; Archontoulis, S.V. Modeling long-term corn yield response to nitrogen rate and crop rotation. Front. Plant Sci. 2016, 7, 1630. [Google Scholar] [CrossRef]
- Ojeda, J.J.; Volenec, J.J.; Brouder, S.M.; Caviglia, O.P.; Agnusdei, M.G. Modelling stover and grain yields, and subsurface artificial drainage from long-term corn rotations using APSIM. Agric. Water Manag. 2018, 195, 154–171. [Google Scholar] [CrossRef]
- Basche, A.D.; Archontoulis, S.V.; Kaspar, T.C.; Jaynes, D.B.; Parkin, T.B.; Miguez, F.E. Simulating long-term impacts of cover crops and climate change on crop production and environmental outcomes in the Midwestern United States. Agric. Ecosyst. Environ. 2016, 218, 95–106. [Google Scholar] [CrossRef]
- USDA National Agricultural Statistics Service. NASS—Quick Stats. USDA National Agricultural Statistics Service. Available online: https://data.nal.usda.gov/dataset/nass-quick-stats (accessed on 20 November 2021).
- Kang, Y.; Özdoğan, M. Field-level crop yield mapping with Landsat using a hierarchical data assimilation approach. Remote Sens. Environ. 2019, 228, 144–163. [Google Scholar] [CrossRef]
- Hengl, T.; Mendes de Jesus, J.; Heuvelink, G.B.; Ruiperez Gonzalez, M.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef] [PubMed]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Bolton, D.K.; Friedl, M.A. Forecasting crop yield using remotely sensed vegetation indices and crop phenology metrics. Agric. For. Meteorol. 2013, 173, 74–84. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT+ SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Müller, C.; Elliott, J.; Kelly, D.; Arneth, A.; Balkovic, J.; Ciais, P.; Deryng, D.; Folberth, C.; Hoek, S.; Izaurralde, R.C.; et al. The Global Gridded Crop Model Intercomparison phase 1 simulation dataset. Sci. Data 2019, 6, 50. [Google Scholar] [CrossRef]
- Martinez-Feria, R.; Nichols, V.; Basso, B.; Archontoulis, S. Can multi-strategy management stabilize nitrate leaching under increasing rainfall? Environ. Res. Lett. 2019, 14, 124079. [Google Scholar] [CrossRef]
- Keating, B.A.; Carberry, P.S.; Hammer, G.L.; Probert, M.E.; Robertson, M.J.; Holzworth, D.; Huth, N.I.; Hargreaves, J.N.; Meinke, H.; Hochman, Z.; et al. An overview of APSIM, a model designed for farming systems simulation. Eur. J. Agron. 2003, 18, 267–288. [Google Scholar] [CrossRef]
- Birch, C.; Hammer, G.; Rickert, K. Improved methods for predicting individual leaf area and leaf senescence in maize (Zea mays). Aust. J. Agric. Res. 1998, 49, 249–262. [Google Scholar] [CrossRef]
- Jones, C.A. CERES-Maize; a Simulation Model of Maize Growth and Development; Number 04; SB91. M2, J6.; Texas A&M University Press: College Station, TX, USA, 1986. [Google Scholar]
- Keating, B.; Wafula, B. Modelling the fully expanded area of maize leaves. Field Crop. Res. 1992, 29, 163–176. [Google Scholar] [CrossRef]
- Machwitz, M.; Giustarini, L.; Bossung, C.; Frantz, D.; Schlerf, M.; Lilienthal, H.; Wandera, L.; Matgen, P.; Hoffmann, L.; Udelhoven, T. Enhanced biomass prediction by assimilating satellite data into a crop growth model. Environ. Model. Softw. 2014, 62, 437–453. [Google Scholar] [CrossRef]
- Duan, S.B.; Li, Z.L.; Wu, H.; Tang, B.H.; Ma, L.; Zhao, E.; Li, C. Inversion of the PROSAIL model to estimate leaf area index of maize, potato, and sunflower fields from unmanned aerial vehicle hyperspectral data. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 12–20. [Google Scholar] [CrossRef]
- Richter, K.; Atzberger, C.; Vuolo, F.; D’Urso, G. Evaluation of sentinel-2 spectral sampling for radiative transfer model based LAI estimation of wheat, sugar beet, and maize. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 4, 458–464. [Google Scholar] [CrossRef]
- Fer, I.; Kelly, R.; Moorcroft, P.R.; Richardson, A.D.; Cowdery, E.M.; Dietze, M.C. Linking big models to big data: Efficient ecosystem model calibration through Bayesian model emulation. Biogeosciences 2018, 15, 5801–5830. [Google Scholar] [CrossRef]
- De Valpine, P.; Turek, D.; Paciorek, C.J.; Anderson-Bergman, C.; Lang, D.T.; Bodik, R. Programming with models: Writing statistical algorithms for general model structures with NIMBLE. J. Comput. Graph. Stat. 2017, 26, 403–413. [Google Scholar] [CrossRef]
- Dokoohaki, H.; Gheysari, M.; Mousavi, S.F.; Hoogenboom, G. Effects of different irrigation regimes on soil moisture availability evaluated by CSM-CERES-Maize model under semi-arid condition. Ecohydrol. Hydrobiol. 2017, 17, 207–216. [Google Scholar] [CrossRef]
- Pasley, H.; Nichols, V.; Castellano, M.; Baum, M.; Kladivko, E.; Helmers, M.; Archontoulis, S. Rotating maize reduces the risk and rate of nitrate leaching. Environ. Res. Lett. 2021, 16, 064063. [Google Scholar] [CrossRef]
- Martinez-Feria, R.A.; Licht, M.A.; Ordóñez, R.A.; Hatfield, J.L.; Coulter, J.A.; Archontoulis, S.V. Evaluating maize and soybean grain dry-down in the field with predictive algorithms and genotype-by-environment analysis. Sci. Rep. 2019, 9, 7167. [Google Scholar] [CrossRef]
- Dos Santos, C.L.; Abendroth, L.J.; Coulter, J.A.; Nafziger, E.D.; Suyker, A.; Yu, J.; Schnable, P.S.; Archontoulis, S.V. Maize Leaf Appearance Rates: A Synthesis From the United States Corn Belt. Front. Plant Sci. 2022, 13, 872738. [Google Scholar] [CrossRef]
- Clark, J.S. Why environmental scientists are becoming Bayesians. Ecol. Lett. 2005, 8, 2–14. Available online: http://xxx.lanl.gov/abs/https://onlinelibrary.wiley.com/doi/pdf/10.1111/j.1461-0248.2004.00702.x (accessed on 20 November 2021). [CrossRef]
- Van Oijen, M. Bayesian methods for quantifying and reducing uncertainty and error in forest models. Curr. For. Rep. 2017, 3, 269–280. [Google Scholar] [CrossRef]
- Oberpriller, J.; Cameron, D.R.; Dietze, M.C.; Hartig, F. Towards robust statistical inference for complex computer models. Ecol. Lett. 2021, 24, 1251–1261. [Google Scholar] [CrossRef] [PubMed]
- Cressie, N.; Calder, C.A.; Clark, J.S.; Hoef, J.M.V.; Wikle, C.K. Accounting for uncertainty in ecological analysis: The strengths and limitations of hierarchical statistical modeling. Ecol. Appl. 2009, 19, 553–570. [Google Scholar] [CrossRef] [PubMed]
- Sexton, J.; Everingham, Y.; Inman-Bamber, G. A theoretical and real world evaluation of two Bayesian techniques for the calibration of variety parameters in a sugarcane crop model. Environ. Model. Softw. 2016, 83, 126–142. [Google Scholar] [CrossRef]
- Makowski, D.; Wallach, D.; Tremblay, M. Using a Bayesian approach to parameter estimation; comparison of the GLUE and MCMC methods. Agronomie 2002, 22, 191–203. [Google Scholar] [CrossRef]
- Gao, F.; Zhang, X. Mapping crop phenology in near real-time using satellite remote sensing: Challenges and opportunities. J. Remote Sens. 2021, 2021, 8379391. [Google Scholar] [CrossRef]
- Pearson, N.C.; Livo, K.E.; Driscoll, R.L.; Lowers, H.A.; Hoefen, T.M.; Swayze, G.A.; Klein, A.J.; Kokaly, R.F.; Wise, R.A.; Benzel, W.M.; et al. USGS Spectral Library Version 7 Data. 2017. Available online: https://dx.doi.org/10.5066/F7RR1WDJ (accessed on 3 March 2020).
- Garrity, D.; Bindraban, P. A Globally Distributed Soil Spectral Library Visible Near Infrared Diffuse Reflectance Spectra; ICRAF (World Agroforestry Centre)/ISRIC (World Soil Information) Spectral Library: Nairobi, Kenya, 2004. [Google Scholar]
- Price, J.C. On the information content of soil reflectance spectra. Remote Sens. Environ. 1990, 33, 113–121. [Google Scholar] [CrossRef]








| Optimization Scheme | Model Definition | Hyperprior |
|---|---|---|
| Site-level | ||
| Hierarchical/HPDA | , | |
| Global/Joint |
| Month | Site-Level | Global | HPDA | ||||||
|---|---|---|---|---|---|---|---|---|---|
| d-Index | RMSE () | ME () | d-Index | RMSE () | ME () | d-Index | RMSE () | ME () | |
| May | 0.48 | 0.52 | −0.43 | 0.48 | 0.51 | −0.32 | 0.49 | 0.51 | −0.42 |
| June | 0.96 | 0.51 | −0.24 | 0.95 | 0.58 | −0.17 | 0.97 | 0.46 | −0.1 |
| July | 0.91 | 0.52 | 0.07 | 0.84 | 0.75 | −0.02 | 0.91 | 0.55 | 0.19 |
| Aug | 0.94 | 0.53 | −0.03 | 0.92 | 0.65 | 0.02 | 0.93 | 0.58 | 0.04 |
| Sep | 0.96 | 0.44 | −0.18 | 0.92 | 0.69 | 0.07 | 0.95 | 0.53 | −0.1 |
| Average | 0.85 | 0.5 | −0.16 | 0.82 | 0.63 | −0.08 | 0.85 | 0.52 | −0.07 |
| Year | HPDA | Global | ||||
|---|---|---|---|---|---|---|
| d-Index | RMSE () | ME () | d-Index | RMSE () | ME () | |
| 2014 (n = 61) | 0.52 | 1731 | −982 | 0.62 | 1260 | −154 |
| 2015 (n = 67) | 0.47 | 2017 | 465 | 0.54 | 1878 | 994 |
| 2016 (n = 50) | 0.27 | 4061 | −2670 | 0.35 | 2359 | −861 |
| 2017 (n = 64) | 0.49 | 2322 | −1428 | 0.49 | 1855 | −715 |
| Average | 0.44 | 2532 | −1153 | 0.50 | 1554 | −184 |
| 2018 (n = 51) | 0.7 | 1822 | −571 | 0.59 | 1625 | −72 |
| 2019 (n = 39) | 0.66 | 1823 | −448 | 0.71 | 1629 | 413 |
| Average | 0.68 | 1822 | −509 | 0.65 | 1627 | 170 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dokoohaki, H.; Rai, T.; Kivi, M.; Lewis, P.; Gómez-Dans, J.L.; Yin, F. Linking Remote Sensing with APSIM through Emulation and Bayesian Optimization to Improve Yield Prediction. Remote Sens. 2022, 14, 5389. https://doi.org/10.3390/rs14215389
Dokoohaki H, Rai T, Kivi M, Lewis P, Gómez-Dans JL, Yin F. Linking Remote Sensing with APSIM through Emulation and Bayesian Optimization to Improve Yield Prediction. Remote Sensing. 2022; 14(21):5389. https://doi.org/10.3390/rs14215389
Chicago/Turabian StyleDokoohaki, Hamze, Teerath Rai, Marissa Kivi, Philip Lewis, Jose L. Gómez-Dans, and Feng Yin. 2022. "Linking Remote Sensing with APSIM through Emulation and Bayesian Optimization to Improve Yield Prediction" Remote Sensing 14, no. 21: 5389. https://doi.org/10.3390/rs14215389
APA StyleDokoohaki, H., Rai, T., Kivi, M., Lewis, P., Gómez-Dans, J. L., & Yin, F. (2022). Linking Remote Sensing with APSIM through Emulation and Bayesian Optimization to Improve Yield Prediction. Remote Sensing, 14(21), 5389. https://doi.org/10.3390/rs14215389












