A Migratory Biomass Statistical Method Based on High-Resolution Fully Polarimetric Entomological Radar
Abstract
1. Introduction
2. Method of Calculating Migratory Biomass
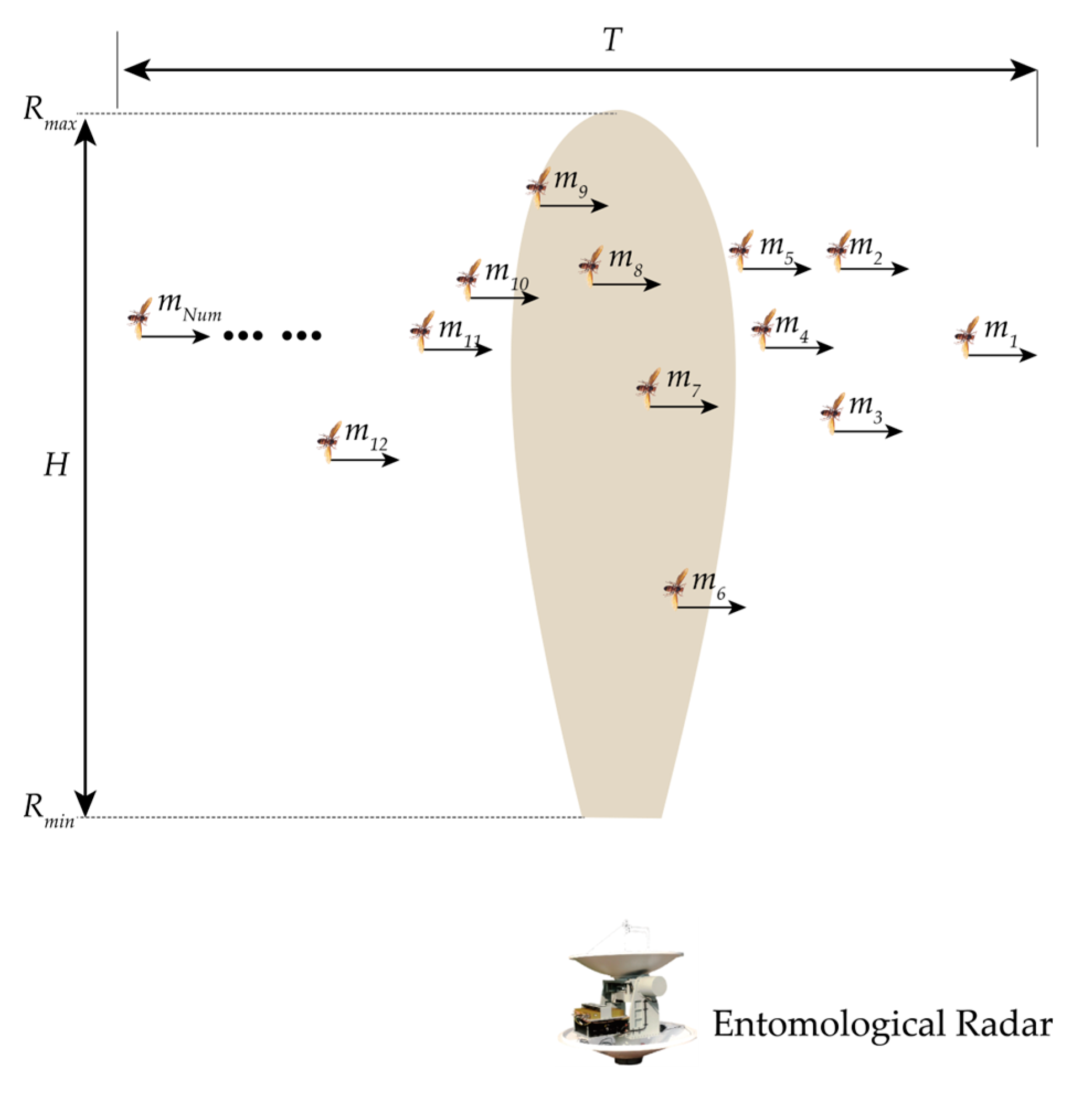
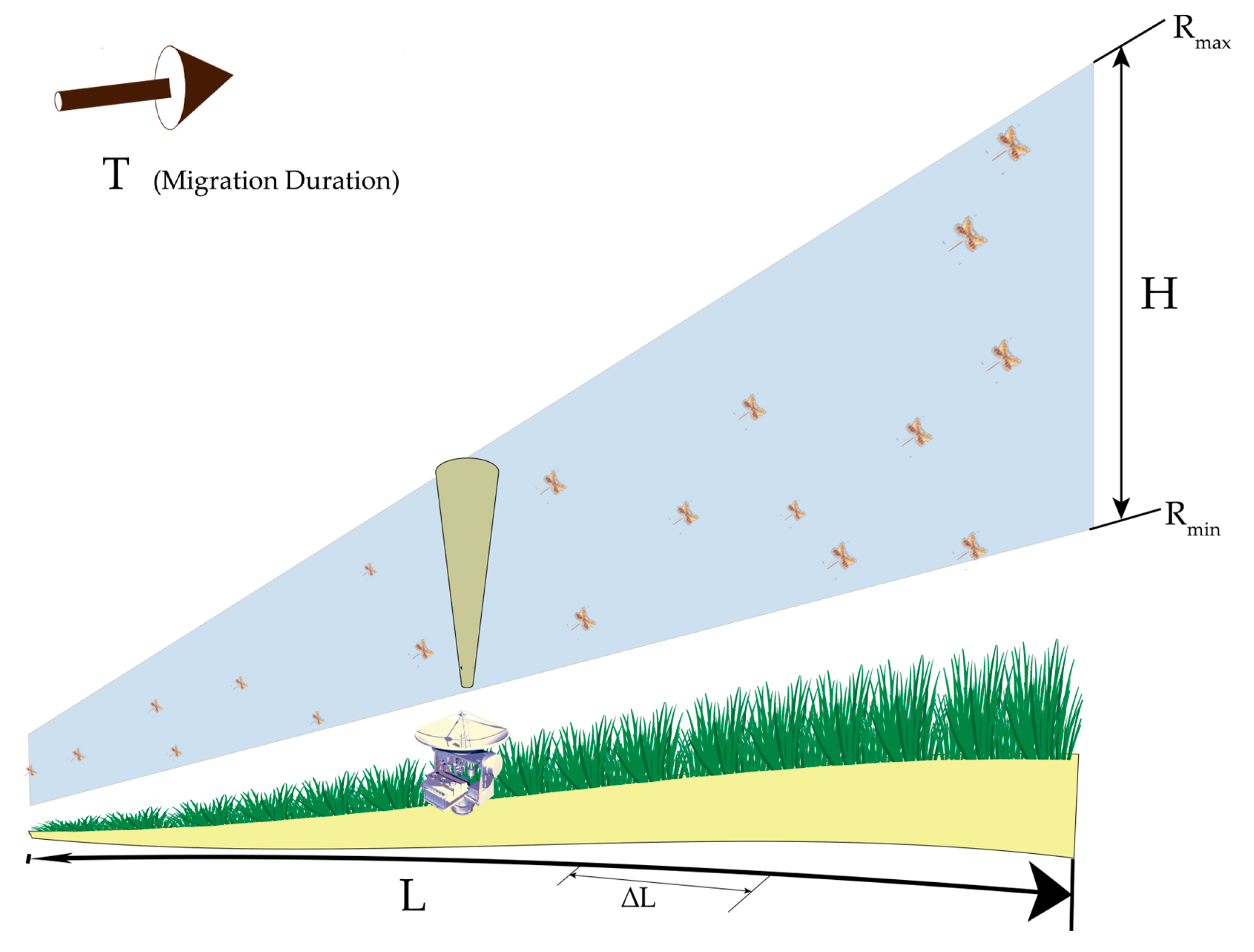
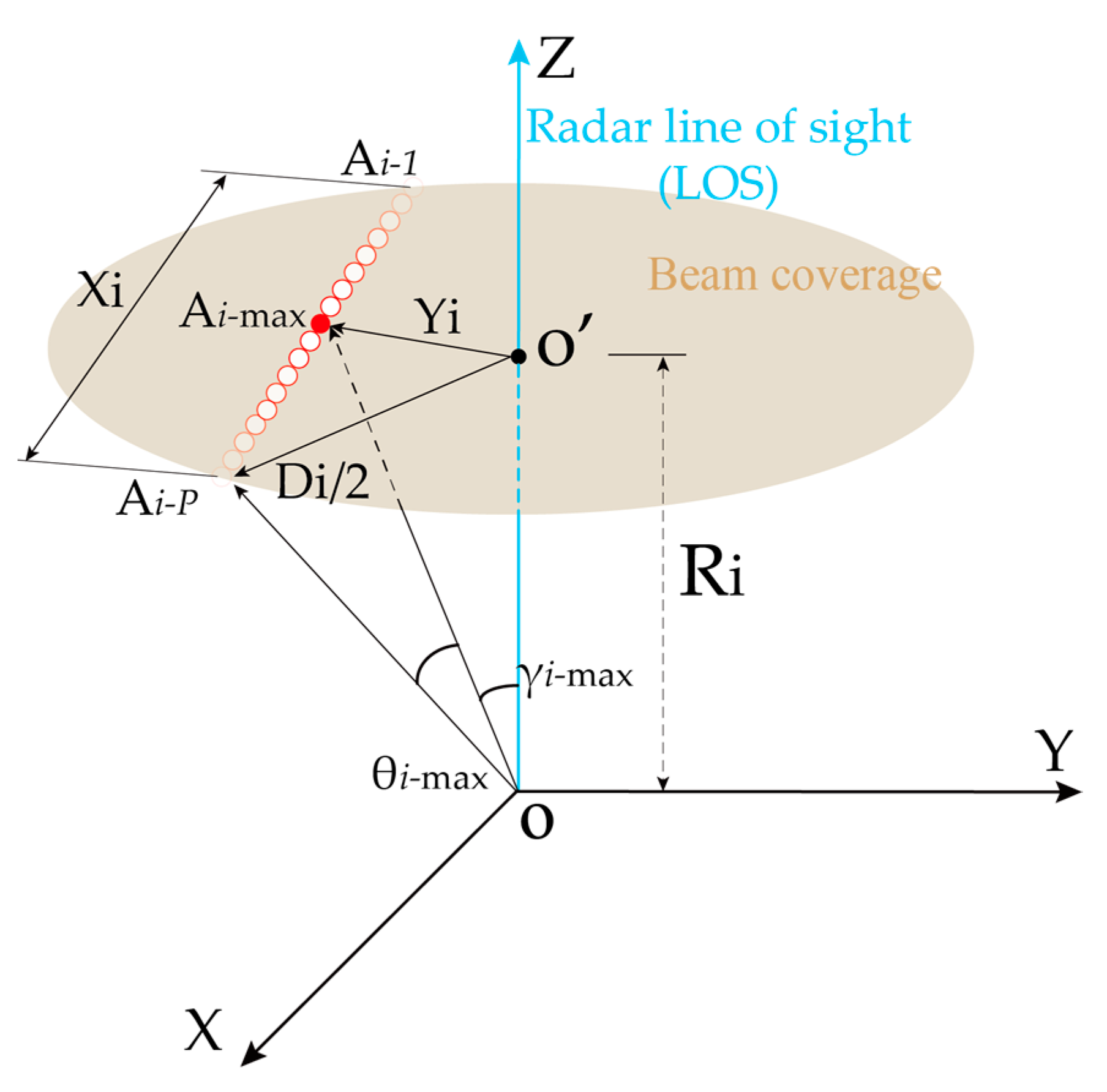
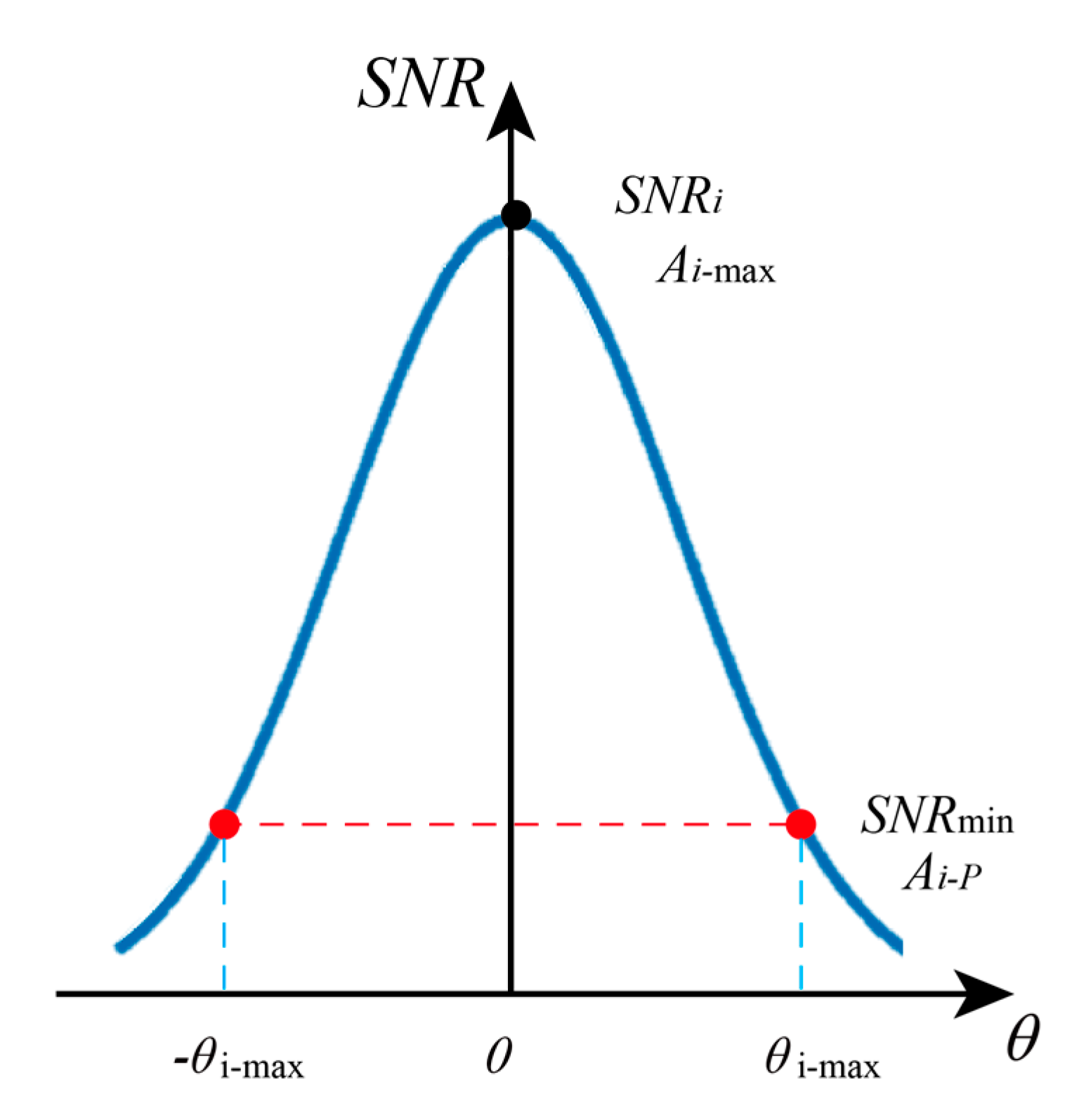
2.1. Model of Biomass Measurement
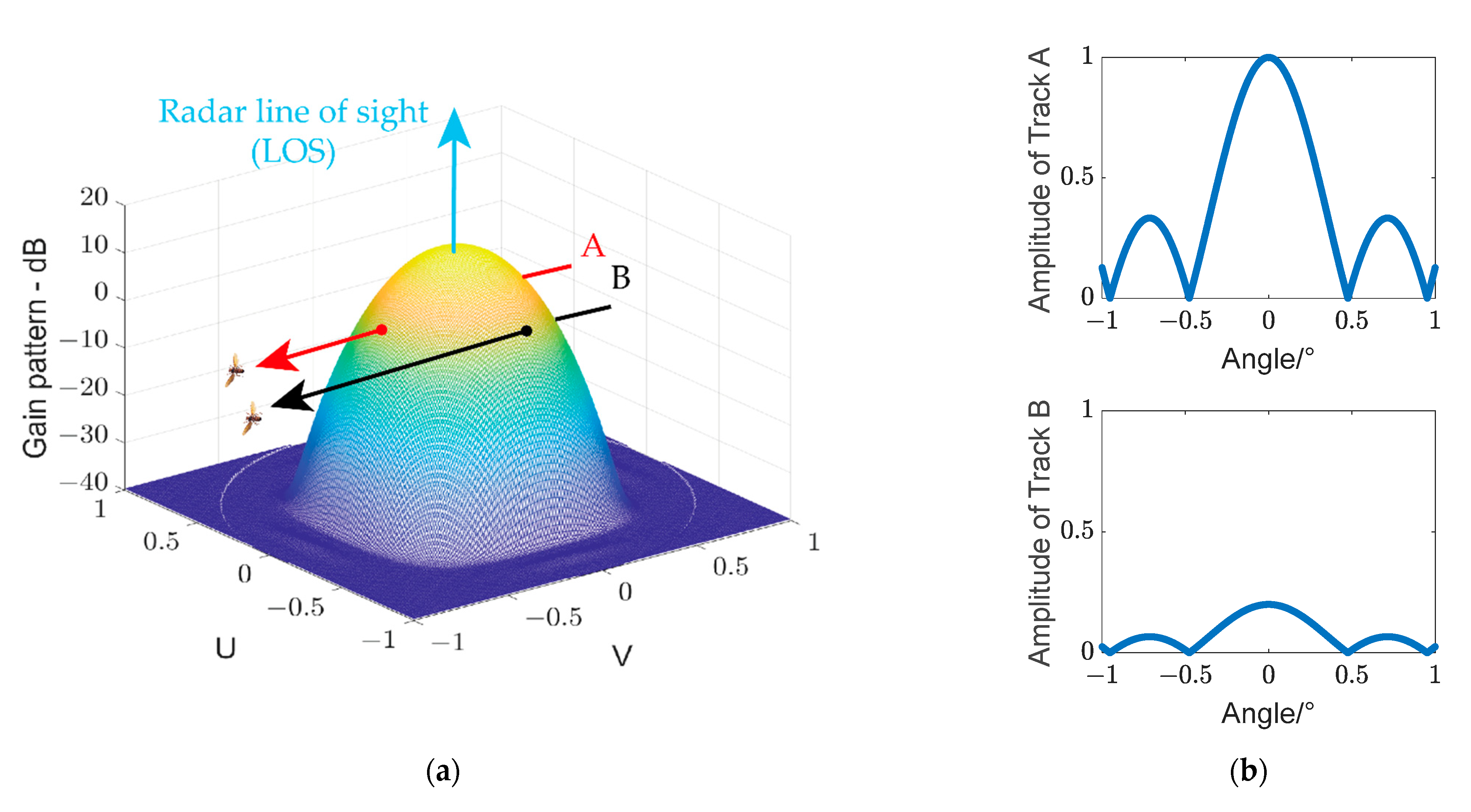
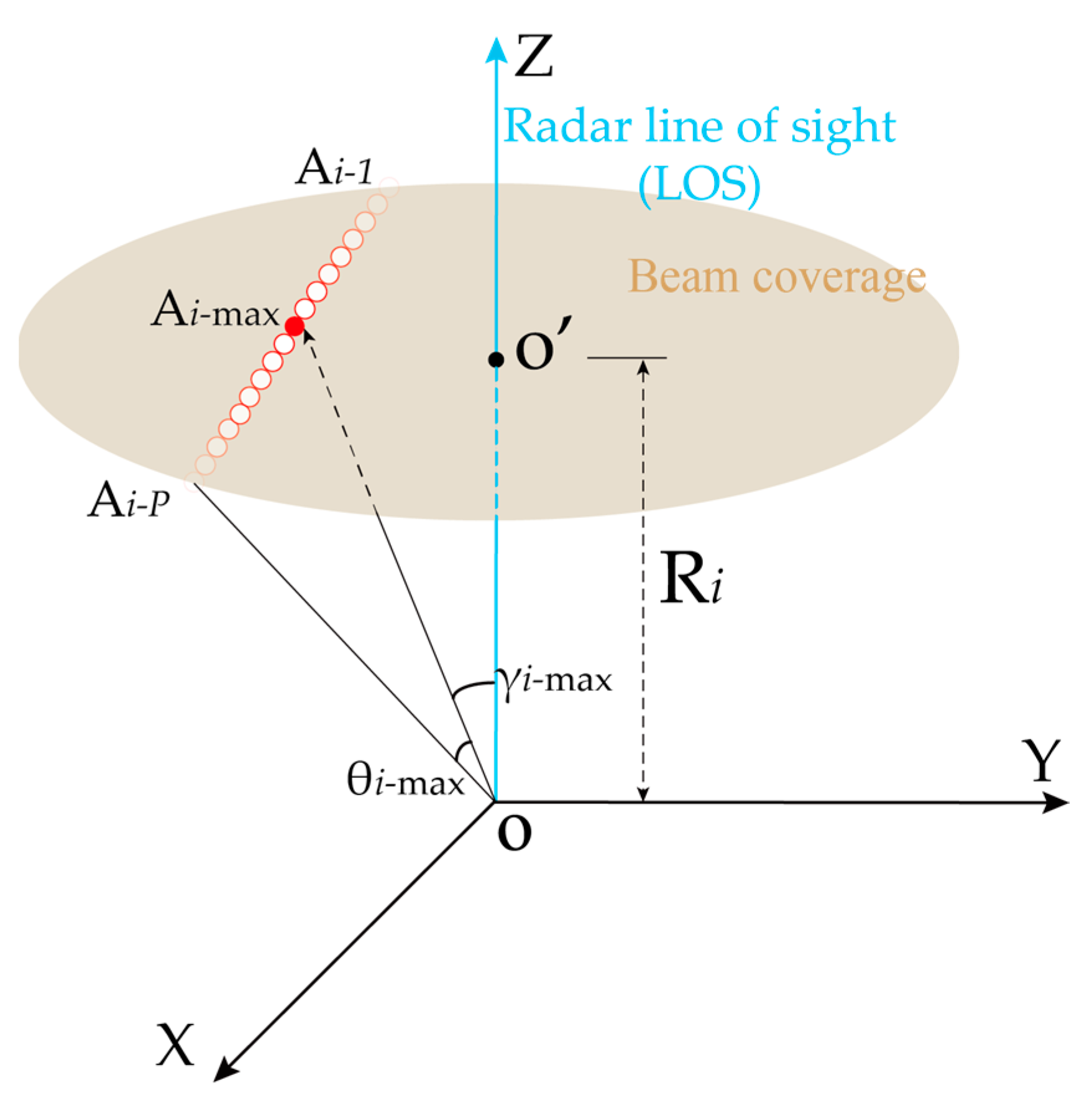
2.2. Method of Biomass Calculation
3. Results
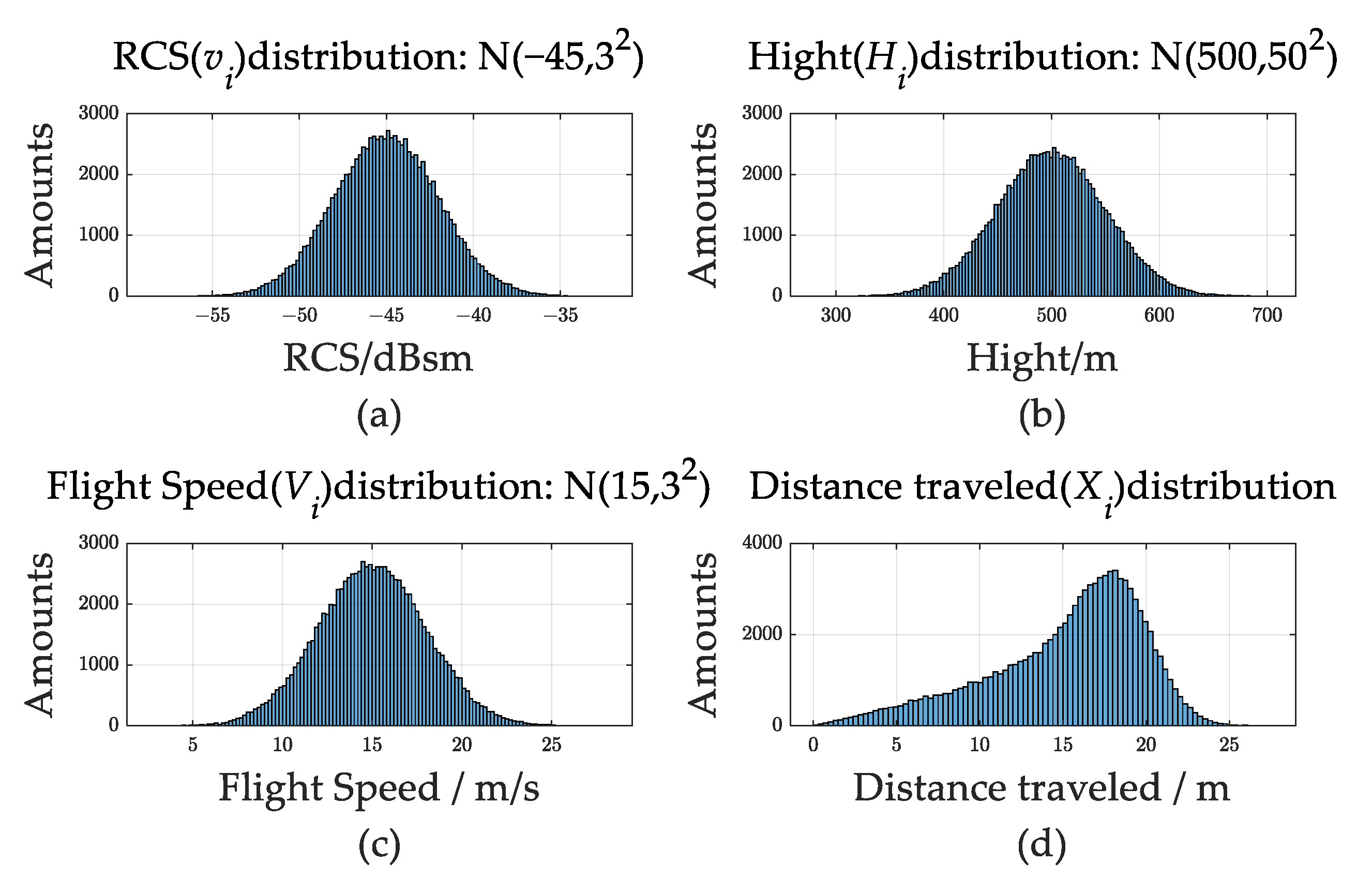
3.1. Simulation Analysis
3.1.1. RCS Expectation Accuracy Simulation
3.1.2. Simulation of the Accuracy of the Migratory Biomass Estimation
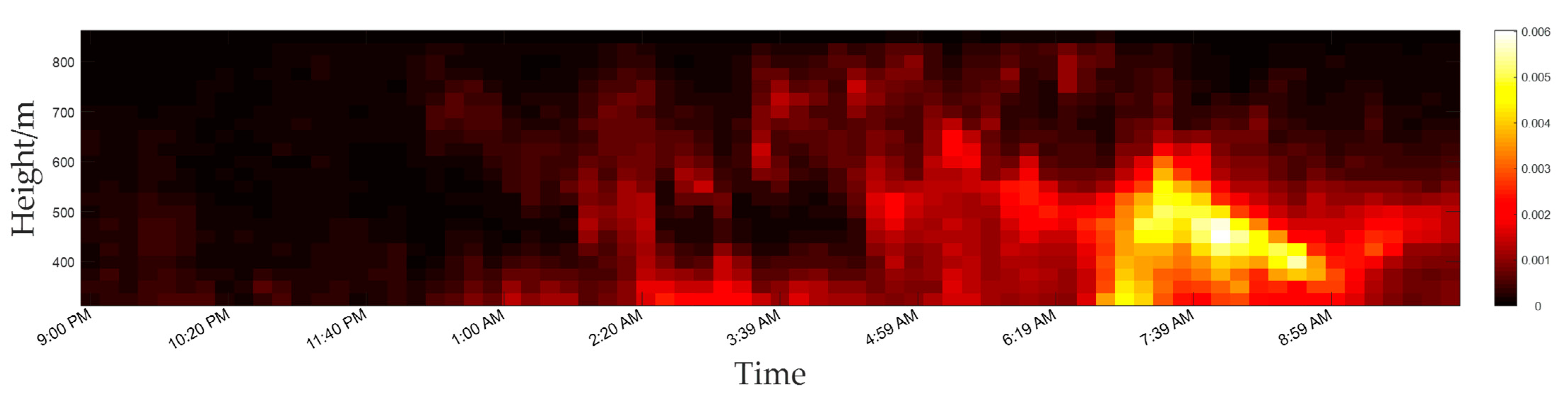
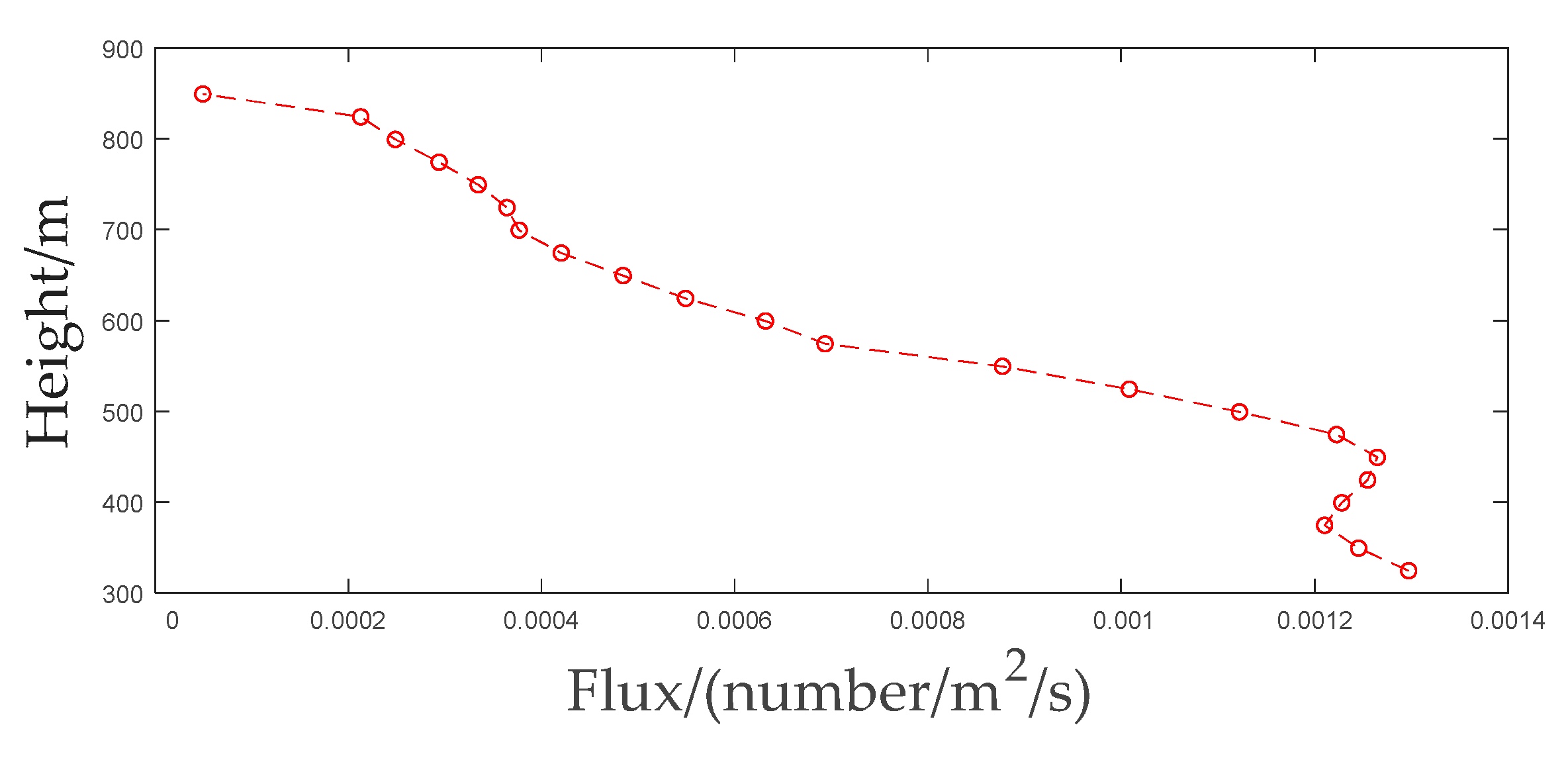
3.2. Experimental Verification
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Holland, R.A.; Wikelski, M.; Wilcove, D.S. How and why do insects migrate? Science Mad. 2006, 313, 794–796. [Google Scholar] [CrossRef] [PubMed]
- Hahn, S.; Bauer, S.; Liechti, F. The natural link between Europe and Africa–2.1 billion birds on migration. Oikos 2009, 118, 624–626. [Google Scholar] [CrossRef]
- Chapman, J.W.; Nesbit, R.L.; Burgin, L.E.; Reynolds, D.R.; Smith, A.D.; Middleton, D.R.; Hill, J.K. Flight orientation behaviors promote optimal migration trajectories in high-flying insects. Science 2010, 327, 682–685. [Google Scholar] [CrossRef] [PubMed]
- Chapman, J.W.; Bell, J.R.; Burgin, L.E.; Reynolds, D.R.; Pettersson, L.B.; Hill, J.K.; Bonsall, M.B.; Thomas, J.A. Seasonal migration to high latitudes results in major reproductive benefits in an insect. Proc. Natl. Acad. Sci. USA 2012, 109, 14924–14929. [Google Scholar] [CrossRef] [PubMed]
- Chapman, J.W.; Reynolds, D.R.; Wilson, K. Long-range seasonal migration in insects: Mechanisms, evolutionary drivers and ecological consequences. Ecol. Lett. 2015, 18, 287–302. [Google Scholar] [CrossRef]
- Kays, R.; Crofoot, M.C.; Jetz, W.; Wikelski, M. Terrestrial animal tracking as an eye on life and planet. Science 2015, 348, aaa2478. [Google Scholar] [CrossRef]
- Warrant, E.; Frost, B.; Green, K.; Mouritsen, H.; Dreyer, D.; Adden, A.; Brauburger, K.; Heinze, S. The Australian Bogong moth Agrotis infusa: A long-distance nocturnal navigator. Front. Behav. Neurosci. 2016, 10, 77. [Google Scholar] [CrossRef]
- Hu, G.; Lim, K.S.; Horvitz, N.; Clark, S.J.; Reynolds, D.R.; Sapir, N.; Chapman, J.W. Mass seasonal bioflows of high-flying insect migrants. Science 2016, 354, 1584–1587. [Google Scholar] [CrossRef]
- Wilcove, D.S.; Wikelski, M. Going, going, gone: Is animal migration disappearing. PLoS Biol. 2008, 6, e188. [Google Scholar] [CrossRef]
- Bauer, S.; Hoye, B.J. Migratory animals couple biodiversity and ecosystem functioning worldwide. Science 2014, 344, 1242552. [Google Scholar] [CrossRef]
- Landry, J.S.; Parrott, L. Could the lateral transfer of nutrients by outbreaking insects lead to consequential landscape-scale effects? Ecosphere 2016, 7, e01265. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Jiang, Y.; Wang, J.; Xie, A.; Yang, J. Current status of entomological radar development and application prospect in China. China Plant Prot. J. 2017, 37, 27–32. [Google Scholar]
- Hu, G.; Gao, B.; Feng, H.; Jiang, H.; Zhai, P.; Wu, K. Individual behavior, population dynamics and ecological effects of migrating insects. J. Chin. Sci. Found. 2020, 34, 456–463. [Google Scholar]
- Oerke, E.C. Crop losses to pests. J. Agr. Sci. Camb. 2006, 144, 31–43. [Google Scholar] [CrossRef]
- Bebber, D.P.; Holmes, T.; Gurr, S.J. The global spread of crop pests and pathogens. Global Ecol. Biogeogr. 2014, 23, 1398–1407. [Google Scholar] [CrossRef]
- Zhai, B. Tracking angels—30 years of radar entomology. Acta Entomol. Sin. 1999, 42, 315–326. [Google Scholar]
- Drake, V.A. Quantitative Observation and Analysis Procedures for a Manually Operated Entomological Radar; CSIRO: Melbourne, Australia, 1981.
- Wang, R.; Li, W.D.; Hu, C.; Li, M.Y.; Mao, H.F. Full-polarization entomological radar bioparametric inversion method and quantitative experimental validation in the external field. J. Signal. Process. 2021, 37, 199–208. [Google Scholar] [CrossRef]
- Hu, C.; Kong, S.; Wang, R.; Long, T.; Fu, X. Identification of Migratory Insects from their Physical Features using a Decision-Tree Support Vector Machine and its Application to Radar Entomology. Sci. Rep. 2018, 8, 5449. [Google Scholar] [CrossRef]
- Chapman, J.; Smith, A.; Woiwod, I.; Reynolds, D.; Riley, J. Development of vertical-looking radar technology for monitoring insect migration. Comput. Electron. Agric. 2002, 35, 95–110. [Google Scholar] [CrossRef]
- Chapman, J.W.; Reynolds, D.R.; Smith, A.D. Vertical-Looking Radar: A New Tool for Monitoring High-Altitude Insect Migration. BioScience 2003, 53, 503–511. [Google Scholar] [CrossRef]
- Wang, R.; Hu, C.; Liu, C.; Long, T.; Kong, S.; Lang, T.; Gould, P.J.L.; Lim, J.; Wu, K. Migratory Insect Multifrequency Radar Cross Sections for Morphological Parameter Estimation. IEEE Trans. Geosci. Electron. 2019, 57, 3450–3461. [Google Scholar] [CrossRef]
- Hu, C.; Kong, S.; Wang, R.; Zhang, F. Radar Measurements of Morphological Parameters and Species Identification Analysis of Migratory Insects. Remote Sens. 2019, 11, 1977. [Google Scholar] [CrossRef]
- Hu, C.; Kong, S.; Wang, R.; Zhang, F.; Wang, L. Insect Mass Estimation Based on Radar Cross Section Parameters and Support Vector Regression Algorithm. Remote Sens. 2020, 12, 1903. [Google Scholar] [CrossRef]
- Cai, J.; Yuan, Q.; Wang, R.; Liu, C.; Zhang, T. Insect detection and density estimation based on a Ku-band scanning entomological radar. J. Eng. 2019, 2019, 7636–7639. [Google Scholar] [CrossRef]
- Chao, Z.; Rui, W.; Hu, C. Equivalent Point Estimation for Small Target Groups Tracking based on MLE. Sci. China Inf. Sci 2019, 63, 8. [Google Scholar]
- Hu, C.; Li, W.; Wang, R.; Li, Y.; Li, W.; Zhang, T. Insect flight speed estimation analysis based on a full-polarization radar. Sci. China Inf. Sci 2018, 61, 1–3. [Google Scholar] [CrossRef]
- Yu, T.; Li, M.; Li, W.; Cai, J.; Wang, R.; Hu, C. Insect Migration Flux Estimation Based on Statistical Hypothesis for Entomological Radar. Remote Sens. 2022, 14, 2298. [Google Scholar] [CrossRef]
- Aldhous, A.C. An investigation of the polarisation dependence of insect radar cross sections at constant aspect. Cranfield University: Cranfield, UK, 1989. [Google Scholar]
- Li, W.D.; Wang, R.; Hu, C.; Zhang, N.; Liang, W.Z. Ku-band fully polarimetric radar insect body shape parameter inversion. Acta Elect Ronica Sin. 2021, 49, 1241–1248. [Google Scholar]
- Hu, C.; Li, W.; Wang, R.; Long, T.; Liu, C.; Drake, V.A. Insect Biological Parameter Estimation Based on the Invariant Target Parameters of the Scattering Matrix. IEEE Trans. Geosci. Electron. 2019, 57, 6212–6225. [Google Scholar] [CrossRef]
- Li, W.; Hu, C.; Wang, R.; Kong, S.; Zhang, F. Comprehensive analysis of polarimetric radar cross-section parameters for insect body width and length estimation. Sci. China Inf. Sci. 2021, 64, 11. [Google Scholar] [CrossRef]
- Hu, C.; Li, M.; Li, W.; Wang, R.; Yu, T. A Data-Driven Polarimetric Calibration Method for Entomological Radar. IEEE Trans. Geosci. Electron. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Song, X.J. Polarization feature-based radar target recognition technique. Radar Sci. Technol. 2016, 14, 7. [Google Scholar]
- Yu, T.; Li, M.; Li, W.; Mao, H.; Wang, R.; Hu, C.; Long, T. Polarimetric Calibration Technique for a Fully Polarimetric Entomological Radar Based on Antenna Rotation. Remote Sens. 2022, 14, 1551. [Google Scholar] [CrossRef]





| Insect Species | Average Mass | Quantity Proportion |
|---|---|---|
| Sarcopoliailloba (Butler, 1878) | 99 mg | 87.6% |
| Coccinella septempunctata (Linnaeus, 1758) | 29.7 mg | 7% |
| Apolygus lucorum (Meyer-Dür, 1843) | 5.2 mg | 3.2% |
| Gyllotalpa unispina (Sausure, 1874) | 1.01 g | 2.1% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, T.; Li, M.; Li, W.; Zhang, T.; Wang, R.; Hu, C. A Migratory Biomass Statistical Method Based on High-Resolution Fully Polarimetric Entomological Radar. Remote Sens. 2022, 14, 5426. https://doi.org/10.3390/rs14215426
Yu T, Li M, Li W, Zhang T, Wang R, Hu C. A Migratory Biomass Statistical Method Based on High-Resolution Fully Polarimetric Entomological Radar. Remote Sensing. 2022; 14(21):5426. https://doi.org/10.3390/rs14215426
Chicago/Turabian StyleYu, Teng, Muyang Li, Weidong Li, Tianran Zhang, Rui Wang, and Cheng Hu. 2022. "A Migratory Biomass Statistical Method Based on High-Resolution Fully Polarimetric Entomological Radar" Remote Sensing 14, no. 21: 5426. https://doi.org/10.3390/rs14215426
APA StyleYu, T., Li, M., Li, W., Zhang, T., Wang, R., & Hu, C. (2022). A Migratory Biomass Statistical Method Based on High-Resolution Fully Polarimetric Entomological Radar. Remote Sensing, 14(21), 5426. https://doi.org/10.3390/rs14215426








