Temporal Feature Learning and Pulse Prediction for Radars with Variable Parameters

Abstract

Many modern radars use variable pulse repetition intervals (PRI) to improve anti-reconnaissance and anti-jamming performance. Their PRI features are probably software-defined, but the PRI values at different time instants are variable. Previous statistical pattern analyzing methods are unable to extract such undetermined PRI values and features, which greatly increases the difficulty of Electronic Support Measures (ESM) against such radars. In this communication, we first establish a model to describe the temporal patterns of software-defined radar pulse trains, then introduce the recurrent neural network (RNN) to mine high-order relationships between successive pulses, and finally exploit the temporal features to predict the time of arrival of upcoming pulses. In the simulation part, we compare different time series prediction models to verify the RNN’s adaptability for pulse sequences of variable parameter radars. Moreover, behaviors of different RNN units in this task are compared, and the results show that the proposed method can learn complex PRI features in pulse trains even in the presence of significant data noises and agile PRIs.

1. Introduction

Variable parameter radar (VPR) usually refers to radars with variable inter-pulse time intervals, which is an important means of countering reconnaissance and jamming [1,2]. For a multi-function radar with variable parameters, whenever it shifts between different work modes, its pulse repetition intervals (PRIs) will change agilely within a certain range, and the changed PRIs can hardly be predicted by previous ones. This parameter variability places a great burden on Electronic Support Measures (ESM) and Electronic Counter Measures (ECM). However, for software-defined radars, a stable functional relationship hides in multiple PRIs of the same working mode and does not change with the agility of parameters, which is called PRI feature.

PRI feature is of great value to signal processing because it is a functional law about radar working mode. First, the known PRI feature can be used to predict subsequent pulses based on already intercepted pulses, which can be applied to online pulse deinterleaving in electronic support systems [3]. Second, we can identify the working modes of radar by judging PRI feature in the intercepted pulse train [4]. Although the temporal parameters of VPR are variable, PRI feature used to generate data at the bottom still shows stability. Based on the wide applications of PRI features, effective methods should be designed to learn them from intercepted pulse trains.

In the past, PRI information was learned mainly through statistical methods such as PRI estimation [5,6,7,8,9] and PRI pattern extraction [10,11,12]. These methods mine PRI values or pulse group structures in intercepted pulse trains mainly from a statistical perspective and have a good application effect for radar with fixed parameters. However, they ignore high-dimensional PRI patterns hidden among successive PRIs and are not suitable for VPRs having connotative PRI patterns. In recent years, neural networks have been introduced to process pulse data and have gained satisfying performance in many pulse deinterleaving and recognition tasks [13,14,15,16,17,18,19,20,21]. Liu recognized radars using the RNN at an early time, and he also proposed a state clustering method to identify MFR working modes [13,14]. In [15], a seq2seq LSTM was trained by fine-labeled pulse trains to identify working modes and their conversion boundaries. The Convolutional Neural Network could also be trained to recognize the signal waveform [16]. In [17], a multi-label classifier was designed using deep learning techniques for recognizing compound signals. In the deinterleaving field, Li utilized autoencoders to recover the original pulse train from its counterpart that was contaminated by data noises or interleaved with other signals, and finally realized the denoising and deinterleaving of pulse trains [18,19]. Zhu formulated temporal structures of radiation sources mathematically and abstracted the deinterleaving problem as the minimization of a cost function, which was solved by a trained Seq2seq network [20]. However, most of these neural network-based methods require sufficient manual tagged data to facilitate supervised learning, and the designed and learned model can only be used in specific application tasks, which weakens the practicability of neural networks in ESM.

In this communication, we first model the PRI feature in the software-defined pulse train as a high-dimensional function. Then, a self-supervised learning method is proposed through building an RNN structure to learn the PRI feature function in the unlabeled pulse trains. Finally, we carry out simulations to verify the performance of the proposed method in PRI feature learning and variable parameter prediction.

The main contributions of this communication are as follows:

(1)

The PRI feature hidden in the pulse train is formulated with a nonlinear function;

(2)

A self-supervised framework for learning PRI features is proposed based on RNN;

(3)

Temporal parameter prediction within pulse groups is realized based on the PRI feature function stored in the trained RNN;

(4)

The effects of many factors on PRI feature learning and prediction are investigated, including the agility range of PRIs, data noises in training pulse trains, and different recurrent units of RNNs.

2. Pulse Train Description

PRI is defined as the time interval between radar pulses, and it is the temporal element of pulse groups and pulse trains. Pulse groups constituted by different types of PRIs determine the working mode executed by a radar. For example, fire-control radars and airplane pulse-Doppler radars utilize constant PRIs that fall into different ranges to search targets at different distances and utilize stagger or jitter PRIs for ambiguity elimination and jamming deception [21,22]. Additionally, some advanced radars apply agile PRIs to escape from jamming [2]. Thus, extracting and utilizing PRI-related information has attracted great attention in the field of passive signal processing.

Each intercepted radar pulse can be represented by its parameters such as time of arrival (TOA) and radio frequency (RF) [23]. PRI features hide in the TOA sequence. In this communication, TOA is taken as the basic observation while other parameters are assumed to be fixed, so as to simplify data illustration and method description. However, relevant results can be extended directly to radars with jointly changing parameters.

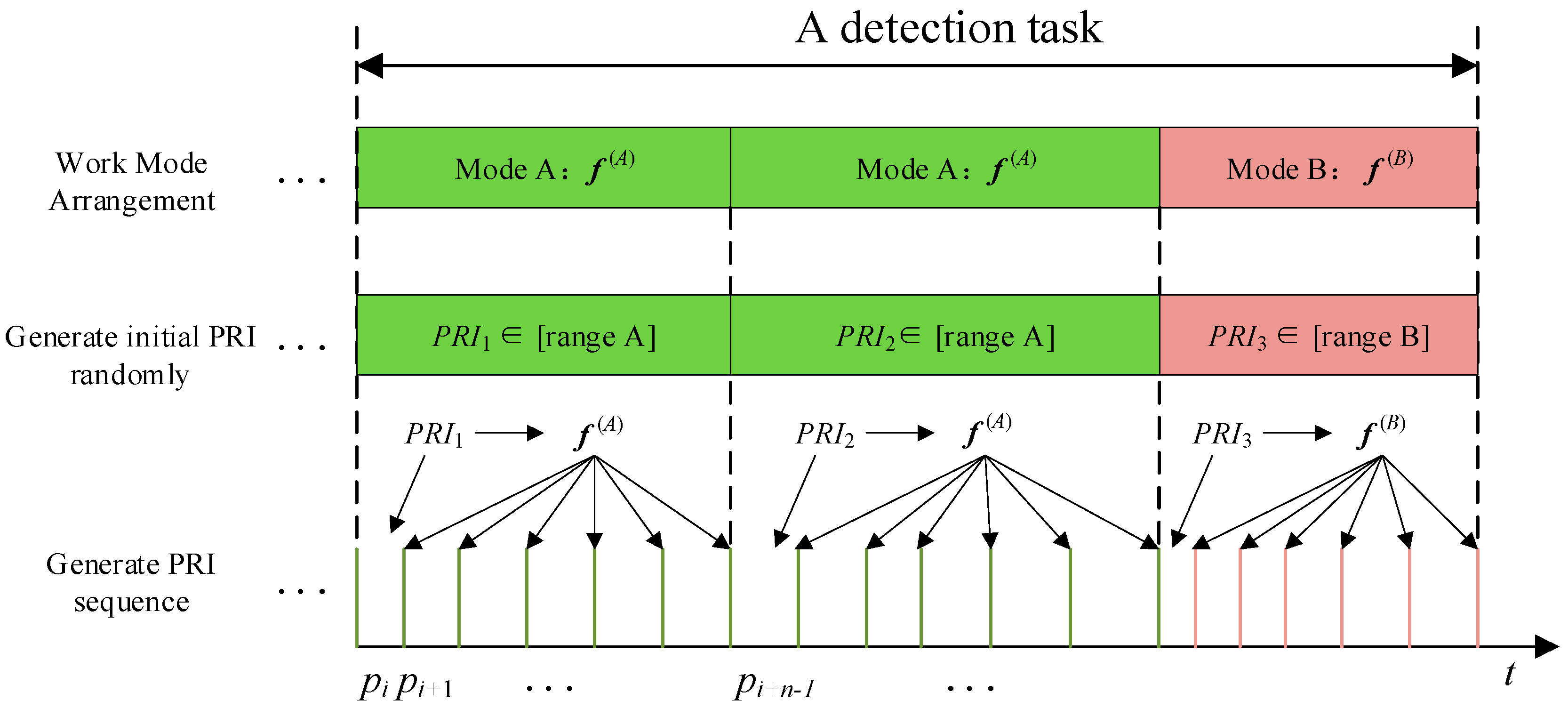
PRIs of a VPR at different time instants are variable. However, since many radars are software-defined to transmit pulses, PRIs during the same working mode are not independent of each other, but with a functional relationship, [24] called the PRI feature function. The pulse generation process of the VPR is shown in Figure 1. When a VPR transmits pulses to execute a certain working mode, it first generates an initial PRI randomly from a certain agility range, and other PRIs are determined by the PRI feature function. More concretely, if $f^{\left(i\right)}=\left[x,f_1^{\left(i\right)},f_2^{\left(i\right)},\cdots ,f_{N-1}^{\left(i\right)}\right]$ represents the PRI feature function set of the i-th working mode of a VPR, its PRI sequence is generated as:

$$p=f^{\left(i\right)}\left(PRI\right)=\left[PRI,f_1^{\left(i\right)}\left(PRI\right),f_2^{\left(i\right)}\left(PRI\right),\cdots ,f_{N-1}^{\left(i\right)}\left(PRI\right)\right]$$

(1)

where PRI ∈ [PRI_min, PRI_max] and is assumed to be uniformly distributed within this scope without loss of generality, PRI_max and PRI_min are the upper and lower bounds of the initial PRI, respectively. N represents the number of PRIs in the pulse sequence. For example, many radars use constant PRIs to search targets but have different PRIs each time they are powered on [25], so it can be regarded as a VPR. The PRI feature function of such VPR is $f_1^{\left(i\right)}=f_2^{\left(i\right)}=\cdots =f_{N-1}^{\left(i\right)}=x$.

In non-cooperative interception systems, the pulse train is initially represented by the TOA sequence, and inter-pulse differential time of arrival (DTOA) is usually calculated for PRI information mining. Without data noise, the first-order DTOA sequence is expressed as:

$$d=p=\left[d_1,d_2,\cdots ,d_n,\cdots ,d_N\right]$$

(2)

According to the process of VPR generating pulse train, PRI feature function can be exploited to predict upcoming DTOAs based on previous ones, which can be shown as:

$$d_{n+1}=g^{\left(i\right)}({\displaystyle \sum }_{i=0}^{n-1}{d}_i,d_n)$$

(3)

where $g^{\left(i\right)}(\cdot )$ represents the PRI feature function of the i-th working mode, which unifies the functions at different positions in $f^{\left(i\right)}$; d_n represents the n-th DTOA in Equation (2), and d₀ = 0 indicates the first pulse; ${\displaystyle \sum _{i=0}^{n-1}}{d}_i$ represents the DTOA between the (n − 1)-th and the first pulses to indicate the time state of (n − 1)-th pulse in pulse sequence. When d₀ = 0 and d₁ are input, the DTOA sequence could be predicted one by one according to the known PRI feature function $g^{\left(i\right)}(\cdot )$. We have ignored TOA measurement errors and will not consider them until the simulation part, so that we can focus on methodological contributions in the text.

In practical applications, the measured DTOA sequences are contaminated by data noises, such as missing pulses and interferential ones. As a result, the determined prediction output in Equation (3) should be modified to a probabilistic one to better describe noisy DTOA sequences as follows:

$$d_{pre}={\displaystyle \sum }_{j=n+1}^N{\rho }^{j-n-1}\left(1-\rho \right)\delta (d-{\displaystyle \sum }_{m=n+1}^j{d}_m),d_m\in d$$

(4)

where ρ ∈ [0,1) denotes the missing rate of pulses that are missed randomly and independently, $\delta$ is the impulse function, and $d_{pre}$ represents the predicted DTOA of the next pulse.

When the number of missing pulses increases, the probability that the corresponding DTOA emerges decreases. Moreover, the prediction probability of interferential pulses is 0 due to the impulse characteristic of the prediction in Equation (4) and the random emergence of interferential pulses. In particular, the result of predicting the first DTOA without preceding pulses is:

$$d_{pre}=g\left(0,0\right)=U({PRI}_{\min },{PRI}_{\max })$$

(5)

that is, the first predicted DTOA conforms to the uniform distribution of the initial PRI range.

The PRI feature function $g$ known in advance can be used to predict PRI parameters and further support applications of signal deinterleaving and working mode recognition. However, it is a very demanding task to rebuild the DTOA prediction function from non-cooperatively intercepted radar pulses due to various data noises. In this communication, we will work out a way to learn the approximate PRI feature function $\widehat{g}$ from intercepted pulse trains.

3. PRI Feature Learning

Due to the non-cooperation of interception, there is no tag indicating working modes, true or interferential pulses, etc. Thus, one has to realize the mining of PRI feature functions $\widehat{g}$ following a guideline of self-supervised learning.

The first-order DTOA sequences of intercepted pulse trains are used as inputs for rebuilding PRI feature functions. However, as intercepted pulse trains are contaminated with interferential pulses and missing ones, the function learning process should overcome some difficulties caused by various data noises. First, the process should be statistically robust against interferential pulses, which split true DTOAs irregularly due to their random occurrence times. Second, the process should also be comprehensive for missing pulses by adapting to high-order DTOAs other than expected first-order PRIs. Actually, we have taken missing pulses into account by formulating the output of $g$ as a probabilistic model in (4), and all the work left to us is finding out a way to approximate the PRI feature function $g$ by feeding noisy DTOA sequences to a model learning machine.

When the DTOA sequence is input sequentially, a good approximation of the PRI feature function, denoted by $\widehat{g}$, is expected to well predict the DTOA of the next pulse, i.e.,

$$DTO{A}_{n+1}{}_{pre}=\widehat{g}({\displaystyle \sum }_{i=0}^{n-1}DTO{A}_i,DTO{A}_n)$$

(6)

However, any deviation of the estimated $\widehat{g}$ from the real g leads to a bias between the predicted value and the real value of the next DTOA. Prediction loss is defined as the mean square error of each DTOA estimation to measure the difference between the estimated function and the real one, as presented below:

$$Loss=\frac{1}{N}{\displaystyle \sum }_{n=0}^{N-1}{(DTO{A}_{n+1}-DTO{A}_{n+1}{}_{pre})}^2$$

(7)

where N represents the number of DTOAs in the pulse sequence. The prediction loss can be used for optimizing the estimated function iteratively via back-propagation (BP) [26], as follows:

$$V^{\left(j+1\right)}=V^{\left(j\right)}+\eta \frac{\partial Loss}{\partial V}$$

(8)

where $V^{\left(j\right)}$ represents the parameters of the PRI feature function $\widehat{g}$ in the j-th iteration. η is the learning rate.

According to Equations (3)–(6), the PRI feature function may be nonlinear, and it can hardly be modeled and rebuilt analytically. By now, recurrent neural networks (RNN) have provided good representation abilities for such complex functions. The RNN is a deep learning framework designed for pulse sequence processing and has achieved a lot in applications such as machine translation and financial prediction. The RNN deals with sequential pulses one by one to extract the temporal feature or predict the parameters of subsequent pulses based on that of the former one. The pulse parameter prediction prospect forms a great inspiration for learning PRI features in pulse trains. To achieve this goal, we introduce a deep recurrent framework, as sketched in Figure 2, to mine PRI feature functions from DTOA sequences.

This is a self-supervised learning process, and the RNN processes the pulse sequence sequentially. After receiving each input, there will be a single-step prediction output. The DTOA_i and accumulated time of previous pulses are input into the RNN to get a predicted $DTO{A}_{{n+1}_{pre}}$ according to Equation (6). There is a deviation between the true DTOA_i+1 and the predicted one. The prediction loss is then calculated and accumulated according to Equation (7), and the BP algorithm [26] is then used to optimize the RNN parameters. The unfolded diagram of this process is shown in Figure 3.

In Figure 3, all layers and recurrent units could be regarded as mapping functions. The recurrent module can be realized with four types of gated units, including the simple RNN unit (SRU, no gate), minimum gated unit (MGU, a forget gate) [27], gated RNN unit (GRU, forget and input gates), and long short-term memory (LSTM, forget, input and output gates). Gated units help to mitigate the gradient disappearance and explosion caused by long-time dependence.

Through many learning iterations based on a large number of pulse trains, the learned PRI feature function is expected to approximate the true function relationship well, and the rebuilt function will be stored in the RNN in the form of a network structure and parameters.

4. Parameter Prediction Simulation

This part describes the PRI feature learning process exampled with a three-mode VPR. Then, based on the trained RNNs, a parameter prediction task is performed to verify the learning effect of PRI feature.

4.1. Data Set Simulation

To cope with different detection distances, the radar widely applies three working modes, namely low, medium, and high pulse repetition frequency (PRF) [1,28]. Thus, three types of pulse groups are included in the simulated data set. Each pulse group has an initial PRI range and a linear PRI feature function. The designed pulse group structure is shown as:

$$\begin{array}{l}PR{I}_1\in [220,280];PR{I}_2\in [450,500];PR{I}_3\in [700,780]\\ \left[\begin{array}{c}\left[PR{I}_1,PR{I}_1+20,PR{I}_1-30,PR{I}_1+10\right]\\ \left[PR{I}_2,PR{I}_2+30,PR{I}_2+60,PR{I}_2+20\right]\\ \left[PR{I}_3,PR{I}_3+40,PR{I}_3+80,PR{I}_3+40\right]\end{array}\right]us\end{array}$$

(9)

When generating pulse trains, the initial PRI of each pulse group is randomly determined in the variable interval range, and different kinds of pulse groups are switched with equal probability. The standard deviation of TOA is 2 us. There are 50–55 pulses in each pulse train, and 50000 pulse trains are generated in data set under same parameters. Pulses are lost randomly according to the missing pulse rate (MPR). The interferential pulses in the pulse train conform to Poisson distribution [29], and its parameter λ is regarded as the interferential pulse ratio (IPR).

4.2. Adaptation Verification to Pulse Trains with Variable Parameters

Prediction ability is an essential representation that a model understands the sequence pattern. To demonstrate that the RNN well adapts to VPR pulse trains, we compare the single-step prediction performances of four time series prediction models. The models used for performance comparison are ARIMA in Statsmodel, SVM in Sklearn, and CNN in Pytorch, and they are realized by third-party libraries in Python. We splice the unequal-length pulse trains and get a lengthy pulse train containing 10,000 pulses. The former 9900 pulses are taken as the training data and the last 100 pulses are used to test the prediction abilities of different models. The test results are shown in Figure 4 and

Table 1. Different prediction indicators of four prediction models.

Model	MAE↓	RMSE↓	MPE↓	MAPE↓	R2↑
ARIMA	70.232	102.359	−6.089	35.461	−0.292
SVM	38.512	58.354	4.54	16.834	0.604
CNN	35.211	58.057	−2.049	15.893	0.645
RNN	34.195	55.55	1.611	14.983	0.683

↓means that smaller is better for this indicator; otherwise, it is ↑. Bold values represented the best.

.

As shown in Figure 4, the four prediction models can well predict trends of the PRI sequence. There would be a sharp deviation between the predicted and true values at the conversion of pulse groups due to its randomness. Actually, the prediction ability in a pulse group is the main difference between different models. In Table 1, we measure the prediction performance through commonly used indicators such as MAE, RMSE, MPE, MAPE, and R2 (Their full names are shown in Appendix A). One can conclude easily from the results in Table 1 that the proposed RNN model realizes the prediction of VPR pulse trains best among the listed methods.

4.3. Neural Network Training

The data set is trained based on the framework in Figure 2 and Figure 3. To facilitate the loss calculation, each input DTOA is represented as a one-hot vector with 2001 dimensions [30], and the maximum DTOA that can be expressed is 2000us, and the DTOAs that exceed it are set to 0. An embedding layer compresses the inputted one-hot vector to 128 dimensions. The recurrent unit acts as a hidden layer to extract information, and its size is 128. Pytorch provides us with standard recurrent units. The output is the full connection layer with the same size as the input layer. Finally, through the activation function of SoftMax, a predicted probability spectrum of the next PRI is output. Batch training is adopted with 64 pulse trains per batch and 5000 batches are trained in all. The learning rate is set to 0.001. In different cases, the prediction loss of iterative training is shown in Figure 5.

We can see that the less data noise, the smaller the prediction loss. For different recurrent units, the models with gated units have lower prediction loss than that without gated units (SRU), and the more gated units, the better. However, the models with fewer gated units (SRU, MGU) have faster training convergence.

4.4. Parameter Prediction Task

For exhibiting the learning effect of PRI feature functions, we design a task of predicting pulse group parameters. That is, after obtaining the first DTOA (composed of two pulses) of a pulse group, we input it into the learned model to obtain a predicted DTOA, and continuously predict the remaining PRI parameters with the predicted value as the true value. An example of this process is shown in Figure 6.

At first, only one pulse does not form a DTOA, but the model already has an input. According to Equation (3), we input the defined $d_0=0$ into the trained RNN, and the output indicates the possible value of the first DTOA, as shown in Figure 6a. The first three ranges show initial PRI ranges of three set pulse groups, and remaining ranges with low probability are high-order DTOAs caused by missing pulses. This result conforms to Equation (5). Then, when the second pulse is intercepted, a first DTOA is obtained as 456 us, and its further prediction spectrum is shown in Figure 6b. Its predicted PRI is 487 us with the maximum possibility. After that, we input the predicted value into the RNN model to continue iterative predictions. Until we input the PRI (476 us) with the maximum probability in Figure 6c, the predicted PRI peak in Figure 6d is significantly lower than that in the last prediction, and there are multi-range peaks. This scene is caused by the uncertainty of the next DTOA during pulse group conversion, which means this pulse group has ended and we have finished the pulse group prediction.

In this way, once the second pulse or first DTOA is intercepted, we can complete the prediction of the whole pulse group. We call it a successful pulse group prediction if the PRI feature of predicted pulse group belongs to the patterns in Equation (9). Different first PRIs are intercepted to predict their pulse groups, and we will count the success rate to measure the performance of the PRI feature learning.

This task is of great significance to improve the real-time requirements of the electronic support system due to its sequential and online prediction.

4.5. Influence of Missing Pulse Rate (MPR) and Interferential Pulse Ratio (IPR)

The performance of PRI feature learning is tested under different MPRs and IPRs. The above pulse group prediction task is executed 100 times to obtain success rates as shown in Figure 7.

As can be seen from Figure 7a, when the IPR is fixed to 0.4, the prediction success rates of RNNs decrease with the increase in the MPR, which reflects that missing pulses increase the burden on RNNs to learn PRI features. When the IPR is 0.4 and the MPR does not exceed 0.4, RNNs can learn the PRI feature in pulse trains well, and their success rates of pulse group prediction can be close to 100%. While the MPR reaches 0.6, SRU, GRU and LSTM still achieve a success rate of more than 80%, but MGU has a significant decline of 29% in the pulse group prediction.

Figure 7b shows that interferential pulses have a similar effect on the PRI feature learning and predicting pulse groups with missing pulses. However, the influence of interferential pulses is smaller with success rates of four RNNs reaching more than 90% even when the IPR reaches 0.6. In general, LSTM and GRU can better learn PRI features in pulse trains and have a great stability against data noises. However, MGU with only a forgetting gate is not suitable for this prediction task with noises [27].

4.6. Influence of Parameter Variable Range

The PRI agility range is a key factor of the VPR. To explore its influence on PRI feature learning, we change the initial PRI range of each pulse group in Equation (9). Then, MPR and IPR are set as 0.4, and data sets are established for training four RNNs. The pulse group prediction task is executed 100 times to obtain the prediction success rates of different agility ranges, as shown in

Table 2. Influence of PRI agility range on PRI feature learning.

Agility Range of Initial PRIs/us	Agility Ratio	Success Rate of Pulse Group Prediction
		SRU	MGU	GRU	LSTM
PRI1 ∈ [285,315]; PRI2 ∈ [475,525]; PRI3 ∈ [760,840]	10%	100%	99%	100%	100%
PRI1 ∈ [270,330]; PRI2 ∈ [450,550]; PRI3 ∈ [720,880]	20%	87%	76%	95%	97%
PRI1 ∈ [255,345]; PRI2 ∈ [425,575]; PRI3 ∈ [680,920]	30%	51%	43%	60%	69%

.

In Table 2, when the agility ratio of initial PRIs is 10%, PRI features can be well learned by RNNs with prediction success rates of 100%. Although the agility ratio is 20%, the prediction success rates of GRU and LSTM are still over 95%, but the learning ability of RNN and MGU decreases significantly. Once the agility range reaches 30%, all four RNNs lose their ability to stably predict pulse group parameters, and LSTM has the highest success rate of 69%. Thus, RNNs can adapt to variable PRIs of the VPR to a certain context, its robustness needs to be further improved if the VPR has a much larger agility range.

5. Conclusions

In this communication, the PRI features hidden in variable parameter radar pulse trains are explored as feature functions, and a self-supervised learning framework is built to learn them using four RNNs with different recurrent units. By comparing different prediction models, we verify that RNN is capable of processing VPR pulse sequences. Then, we set a pulse group prediction task to verify the effect of PRI feature learning with RNNs. It shows that LSTM is more suitable for learning PRI features from pulse data of the variable parameter radar than other recurrent units, especially in the case of more complex data noises and larger parameter variable ranges. It is able to predict pulse parameters with a success rate of 96% when the IPR is 0.4 and MPR is 0.6, and it also can adapt to a PRI agility ratio of 20% with a success rate of 97%.