GPS-Derived Slant Water Vapor for Cloud Monitoring in Singapore
Abstract
1. Introduction
- A new methodology for cloud monitoring based on GPS-derived slant path water vapor is proposed. In particular, the normalized slant wet delay () and slant water vapor () are introduced, which are analyzed with respect to cloud formation. To the best of our knowledge, GPS-derived slant path water vapor has not been exploited before for cloud monitoring.
- Using the normalized or , this work demonstrates its usefulness and potential in cloud monitoring. The normalized is shown to be generally consistent with the cloud formation observed from whole sky imager spatially and temporally.
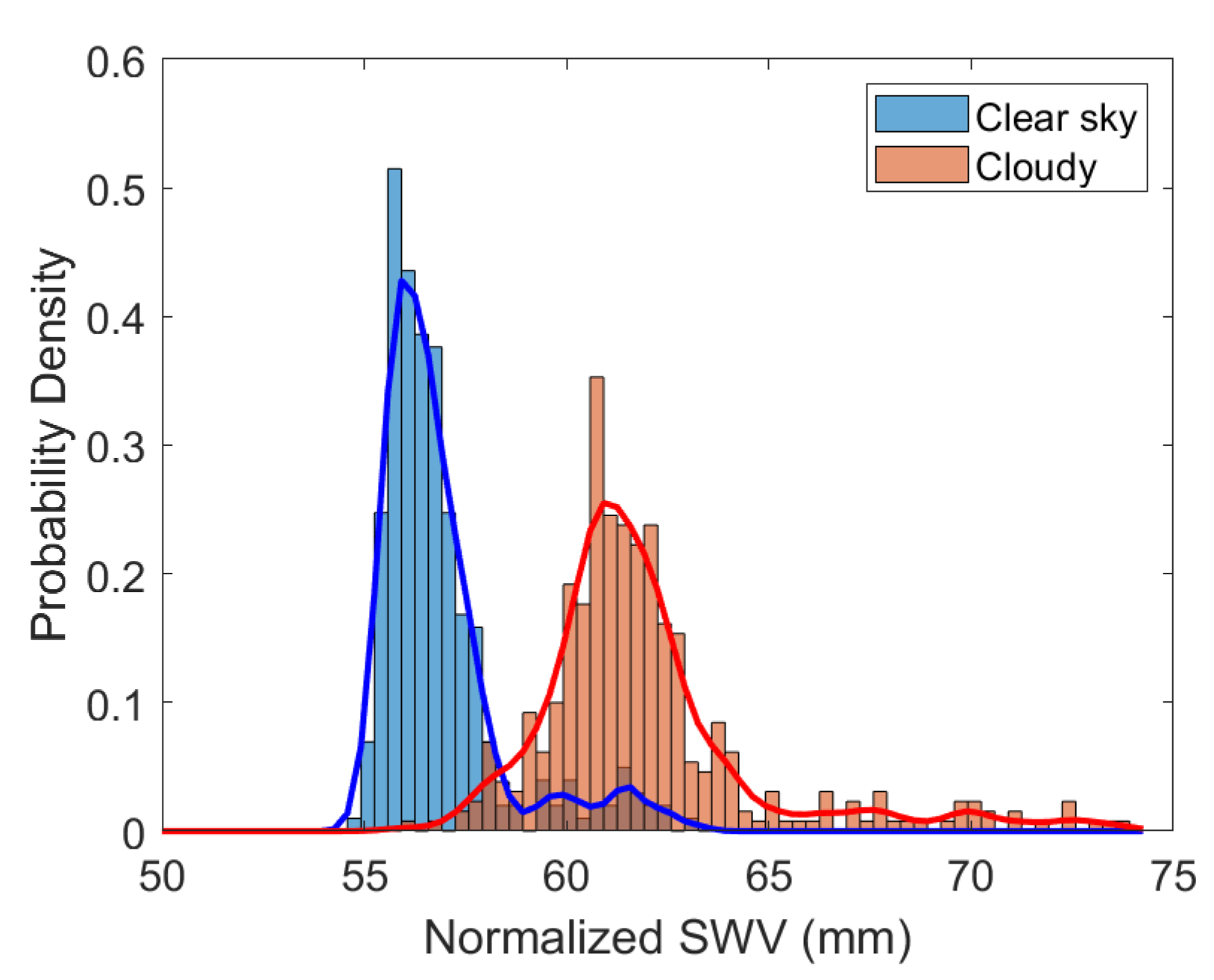
- The normalized values are quantified by obtaining the probability distributions associated with cloudy and clear sky conditions. It is shown that the mean values of the normalized associated with cloudy conditions are higher than those of clear sky conditions.
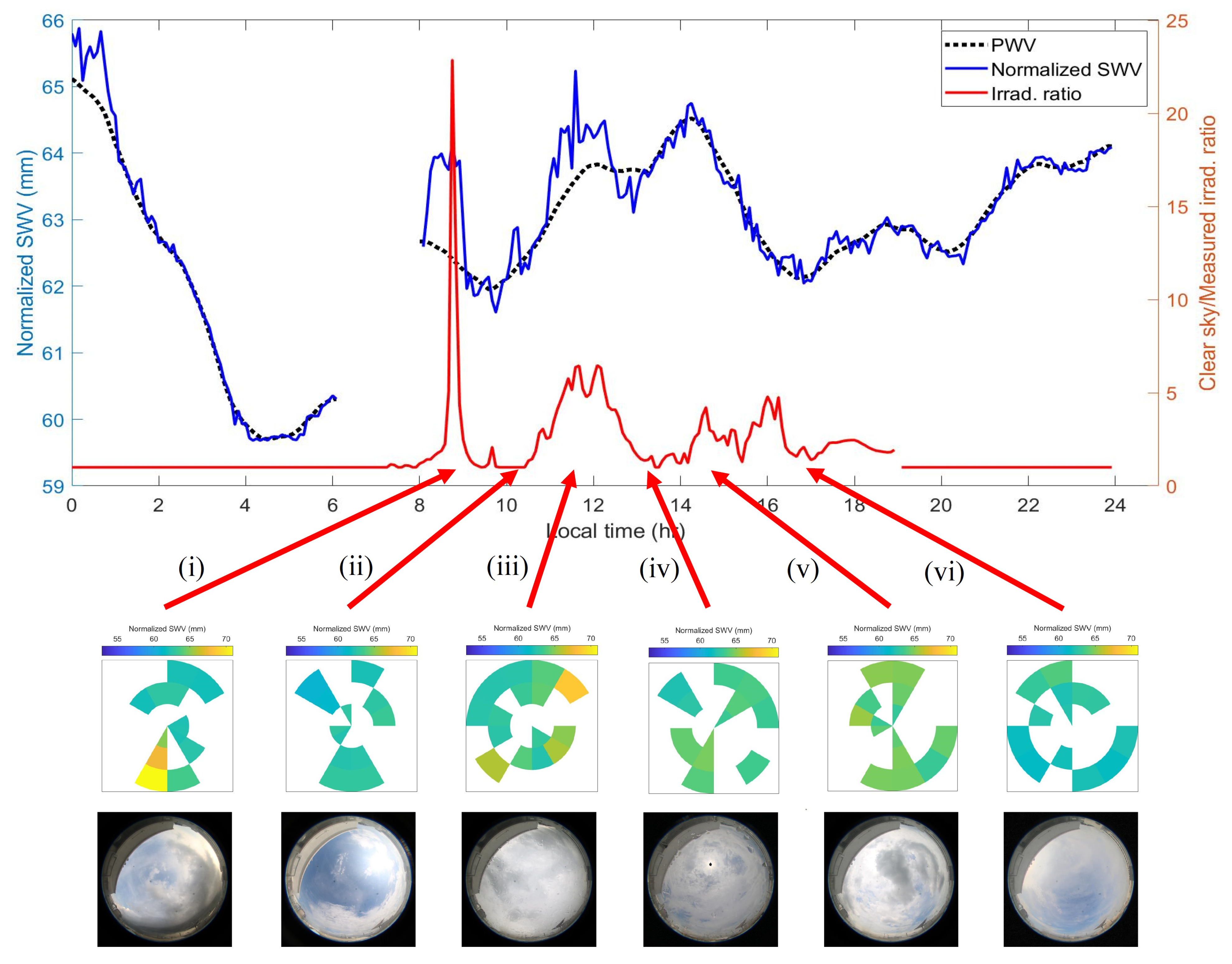
- As the cloud formation is closely related to the solar irradiance, the relations of the normalized with respect to the solar irradiance is also ascertained. It is shown that the time series of normalized is consistent with the temporal variation in solar irradiance.
2. Normalized Slant Wet Delay (SWD) and Slant Water Vapor (SWV)
3. Normalized SWV for Cloud Monitoring
3.1. Data and Methodology
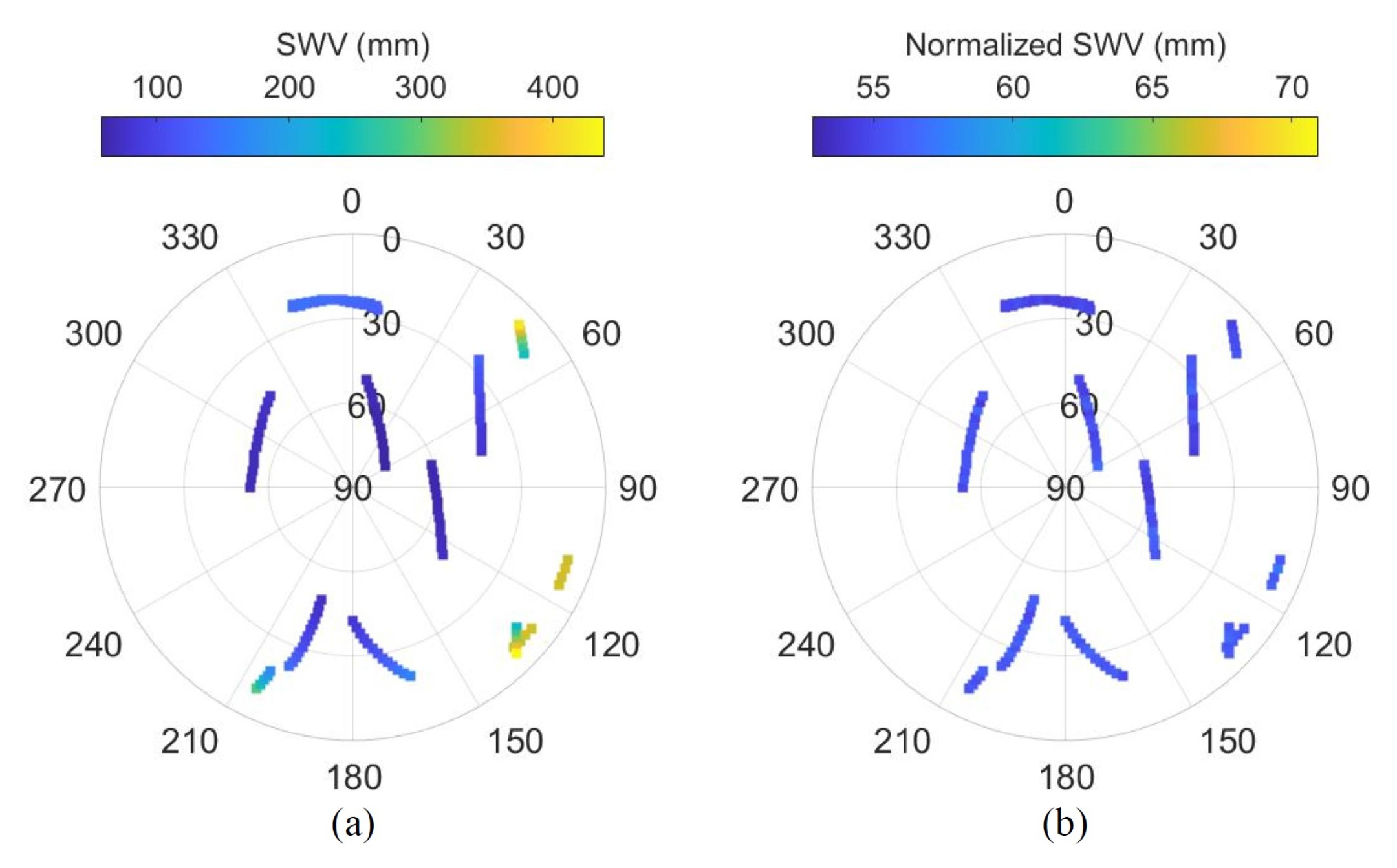
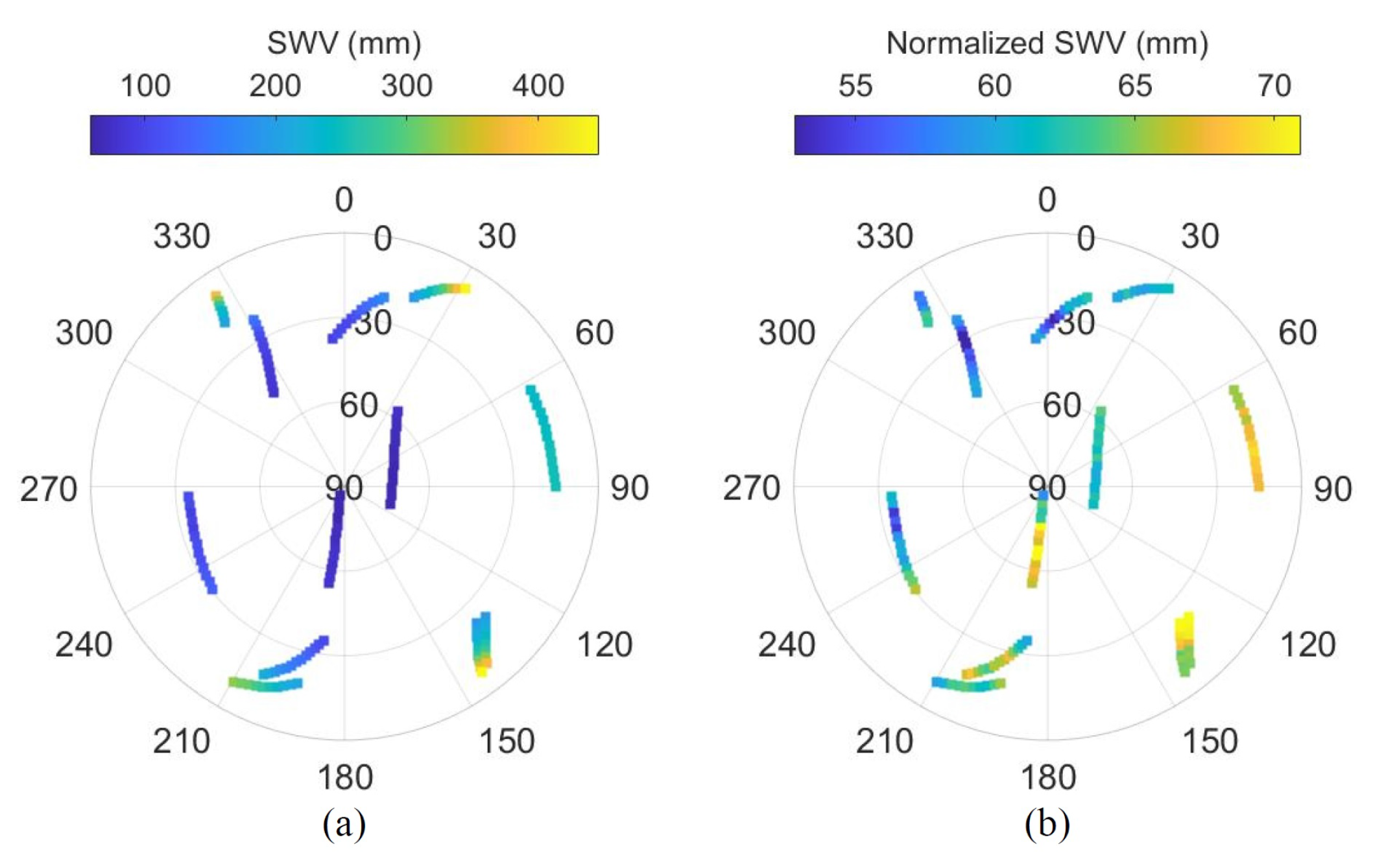
3.2. Comparison between and Normalized
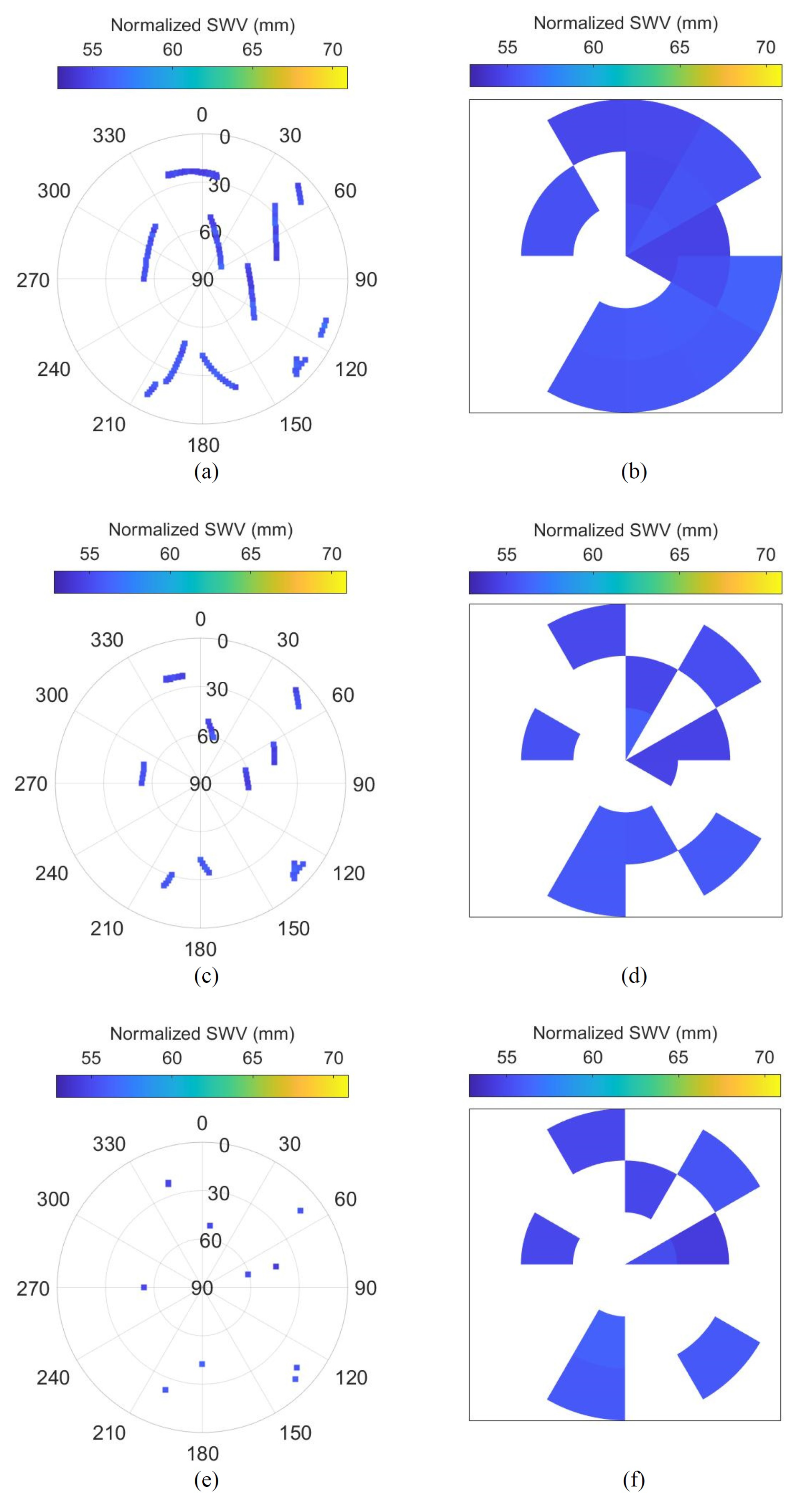
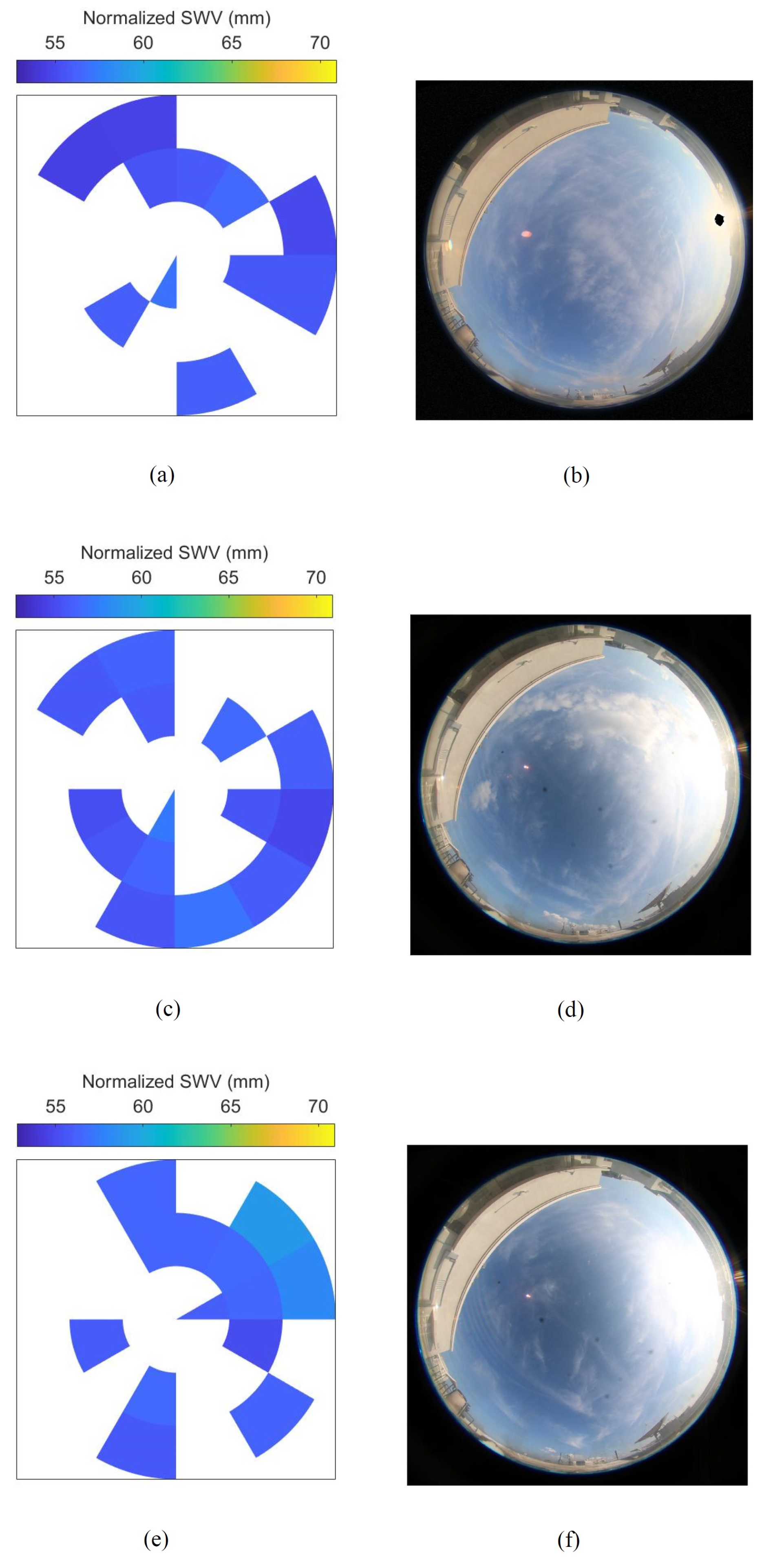
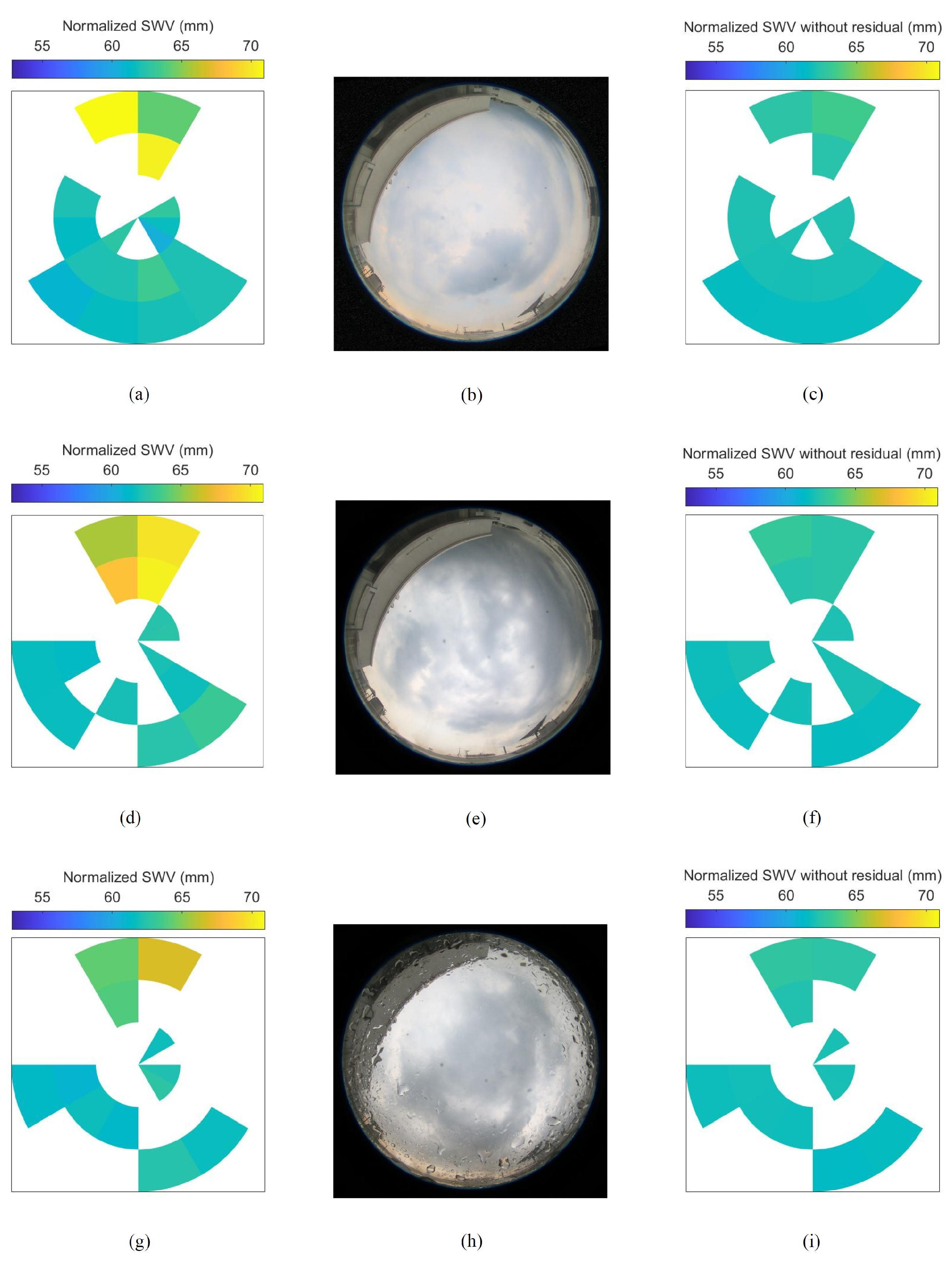
3.3. Analysis of Normalized Spatial Plots and Sky Images
3.4. Probability Distribution of Normalized Values for Clear Sky and Cloudy Conditions
3.5. Time Series of Normalized in Relation to Solar Irradiance
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Janiskova, M.; Fielding, M. Operational Assimilation of Space-Borne Radar and Lidar Cloud Profile Observations for Numerical Weather Prediction; ESA Contract Report; European Centre for Medium Range Weather Forecasts: Reading, UK, 2018; WP-6000; pp. 1–22. [Google Scholar]
- Tapakis, R.D.; Charalambides, A.G. Monitoring cloud motion in Cyprus for solar irradiance prediction. In Conference Papers in Science; Hindawi: London, UK, 2013; pp. 1–6. [Google Scholar]
- Sassen, K. Lidar monitoring of clouds and aerosols at the Facility for Atmospheric Remote Sensing. In Lidar Remote Sensing for Industry and Environment Monitoring; SPIE: Bellingham, WA, USA, 2001; Volume 4153, pp. 114–123. [Google Scholar]
- Brocard, E.; Schneebeli, M.; Mätzler, C. Detection of cirrus clouds using infrared radiometry. IEEE Trans. Geosci. Remote Sens. 2011, 49, 595–602. [Google Scholar] [CrossRef]
- Mahajan, S.; Fataniya, B. Cloud detection methodologies: Variants and development—A review. Complex Intell. Syst. 2020, 6, 251–261. [Google Scholar] [CrossRef]
- Letu, H.; Nagao, T.M.; Nakajima, T.Y.; Riedi, J.; Ishimoto, H.; Baran, A.J.; Shang, H.; Sekiguchi, M.; Kikuchi, M. Ice cloud properties from Himawari-8/AHI next-generation geostationary satellite: Capability of the AHI to monitor the DC cloud generation process. IEEE Trans. Geosci. Remote Sens. 2018, 57, 3229–3239. [Google Scholar] [CrossRef]
- Wagner, T.; Beirle, S.; Deutschmann, T.; Eigemeier, E.; Frankenberg, C.; Grzegorski, M.; Liu, C.; Marbach, T.; Platt, U.; De Vries, M.P. Monitoring of atmospheric trace gases, clouds, aerosols and surface properties from UV/vis/NIR satellite instruments. J. Opt. A Pure Appl. Opt. 2008, 10, 104019. [Google Scholar] [CrossRef]
- Ghosh, R.R.; Ali, M.S.; Hena, A.; Rahman, H. A simple cloud detection algorithm using NOAA-AVHRR satellite data. Int. J. Sci. Eng. Res. 2012, 3, 595–602. [Google Scholar]
- Sun, L.; Wei, J.; Wang, J.; Mi, X.; Guo, Y.; Lv, Y.; Yang, Y.; Gan, P.; Zhou, X.; Jia, C.; et al. A Universal Dynamic Threshold Cloud Detection Algorithm (UDTCDA) supported by a prior surface reflectance database. J. Geophys. Res. Atmos. 2016, 121, 7172–7196. [Google Scholar] [CrossRef]
- Murino, L.; Amato, U.; Carfora, M.F.; Antoniadis, A.; Huang, B.; Menzel, W.P.; Serio, C. Cloud detection of modis multispectral images. J. Atmos. Ocean. Technol. 2014, 31, 347–365. [Google Scholar] [CrossRef]
- Frey, R.A.; Ackerman, S.A.; Liu, Y.; Strabala, K.I.; Zhang, H.; Key, J.R.; Wang, X. Cloud detection with MODIS. Part I: Improvements in the MODIS cloud mask for collection 5. J. Atmos. Ocean. Technol. 2008, 25, 1057–1072. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Object-based cloud and cloud shadow detection in Landsat imagery. Remote Sens. Environ. 2012, 18, 83–94. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, S.; Woodcock, C.E. Improvement and expansion of the fmask algorithm: Cloud, cloud shadow, and snow detection for landsats 4–7, 8, and sentinel 2 images. Remote Sens. Environ. 2015, 159, 269–277. [Google Scholar] [CrossRef]
- Shields, J.E.; Karr, M.E.; Johnson, R.W.; Burden, A.R. Day/night whole sky imagers for 24-h cloud and sky assessment: History and overview. Appl. Opt. 2013, 52, 1605–1616. [Google Scholar] [CrossRef] [PubMed]
- Shields, J.E.; Karr, M.E.; Tooman, T.P.; Sowle, D.H.; Moore, S.T. The whole sky imager—A year of progress. In Proceedings of the 8th Atmospheric Radiation Measurement (ARM) Science Team Meeting, Tucson, Arizona, 23–27 March 1998; pp. 23–27. [Google Scholar]
- Chauvin, R.; Nou, J.; Thil, S.; Traore, A.; Grieu, S. Cloud detection methodology based on a sky-imaging system. Energy Procedia 2019, 69, 1970–1980. [Google Scholar] [CrossRef]
- Chauvin, R.; Nou, J.; Thil, S.; Grieu, S. Cloud motion estimation using a sky imager. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2016; Volume 1734, p. 150003. [Google Scholar]
- Adam, J.; Buss, J.; Brügge, K.; Nöthe, M.; Rhode, W. Cloud detection and prediction with all sky cameras. In EPJ Web of Conferences; EDP Sciences: Ulis, France, 2017; Volume 144, p. 01004. [Google Scholar]
- Azhar, M.A.D.M.; Hamid, N.S.A.; Kamil, W.M.A.W.M.; Mohamad, N.S. Daytime cloud detection method using the all-sky imager over PERMATApintar observatory. Universe 2021, 7, 41. [Google Scholar] [CrossRef]
- Alonso-Montesinos, J. Real-time automatic cloud detection using a low-cost sky camera. Remote Sens. 2020, 12, 1382. [Google Scholar] [CrossRef]
- Dev, S.; Savoy, F.M.; Lee, Y.H.; Winkler, S. WAHRSIS: A low-cost, high-resolution whole sky imager with near-infrared capabilities. In Infrared Imaging Systems: Design, Analysis, Modeling, and Testing XXV; SPIE: Bellingham, WA, USA, 2014. [Google Scholar]
- Dev, S.; Lee, Y.H.; Winkler, S. Color-based segmentation of sky/cloud images from ground-based cameras. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 231–242. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the global positioning system. J. Geophys. Res. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Arief, S.; Kosuke, H. GNSS meteorology for disastrous rainfalls in 2017–2019 summer in SW Japan: A new approach utilizing atmospheric delay gradients. Front. Earth Sci. 2020, 8, 182. [Google Scholar] [CrossRef]
- Westwater, E.R.; Han, Y.; Shupe, M.D.; Matrosov, S.Y. Analysis of integrated cloud liquid and precipitable water vapor retrievals from microwave radiometers during the Surface Heat Budget of the Arctic Ocean project. J. Geophys. Res. 2001, 106, 32019–32030. [Google Scholar] [CrossRef]
- Solheim, F.S.; Vivekanandan, J.; Ware, R.H.; Rocken, C. Propagation delays induced in GPS signals by dry air, water vapor, hydrometeors, and other particulates. J. Geophys. Res. 1999, 104, 9663–9670. [Google Scholar] [CrossRef]
- Brenot, H.; Ducrocq, V.; Walpersdorf, A.; Champollion, C.; Caumont, O. GPS zenith delay sensitivity evaluated from high-resolution numerical weather prediction simulations of the 8–9 September 2002 flash flood over southeastern France. J. Geophys. Res. 2006, 111, D15105. [Google Scholar] [CrossRef]
- Manandhar, S.; Lee, Y.H.; Meng, Y.S.; Yuan, F.; Ong, J.T. GPS derived PWV for rainfall nowcasting in tropical region. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4835–4844. [Google Scholar] [CrossRef]
- Manandhar, S.; Lee, Y.H.; Meng, Y.S. GPS-PWV based improved long-term rainfall prediction algorithm for tropical regions. Remote Sens. 2019, 11, 2643. [Google Scholar] [CrossRef]
- Biswas, A.N.; Lee, Y.H.; Manandhar, S. Rainfall forecasting using GPS derived atmospheric gradient and residual for tropical region. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–10. [Google Scholar] [CrossRef]
- Yuan, F.; Lee, Y.H.; Meng, Y.S.; Manandhar, S.; Ong, J.T. High-resolution ITU-R cloud attenuation model for satellite communications in tropical region. IEEE Trans. Antennas Propag. 2019, 67, 6115–6122. [Google Scholar] [CrossRef]
- Kumar, L.S.; Manandhar, S.; Lee, Y.H.; Meng, Y.S. GPS derived PWV for monitoring cloud evolution. In Proceedings of the 2017 Progress in Electromagnetics Research Symposium-Fall (PIERS-FALL), Singapore, 19–22 November 2017. [Google Scholar]
- Heh, D.Y.; Lee, Y.H.; Koh, L.M. Cloud monitoring in Singapore using GPS residuals. In Proceedings of the 2021 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting (APS/URSI), Singapore, 4–10 December 2021. [Google Scholar]
- Manandhar, S.; Tan, J.H.; Lee, Y.H.; Meng, Y.S. GPS slant path residuals for rainfall detection. In Proceedings of the 2019 USNC-URSI Radio Science Meeting (Joint with AP-S Symposium), Atlanta, GA, USA, 7–12 July 2019. [Google Scholar]
- Zus, F.; Dousa, J.; Kacmarik, M.; Vaclavovic, P.; Dick, G.; Wickert, J. Estimating the impact of global navigation satellite system horizontal delay gradients in variational data assimilation. Remote Sens. 2019, 11, 41. [Google Scholar] [CrossRef]
- Shoji, Y. Retrieval of water vapor inhomogeneity using the japanese nationwide GPS array and its potential for prediction of convective precipitation. J. Meteorol. Soc. Jpn. 2013, 91, 43–62. [Google Scholar] [CrossRef][Green Version]
- Elosegui, P.; Davis, J.L.; Gradinarsky, L.P.; Elgered, G.; Johansson, J.M.; Tahmoush, D.A.; Rius, A. Sensing atmospheric structure using small-scale space geodetic networks. Geophys. Res. Lett. 1999, 26, 2445–2448. [Google Scholar] [CrossRef]
- Flouzat, M.; Bettinelli, P.; Willis, P.; Avouac, J.P.; Héritier, T.; Gautam, U. Investigating tropospheric effects and seasonal position variations in GPS and DORIS time-series from the Nepal Himalaya. Geophys. J. Int. 2009, 178, 1246–1259. [Google Scholar] [CrossRef]
- Masoumi, S.; McClusky, S.; Koulali, A.; Tregoning, P. A directional model of tropospheric horizontal gradients in Global Positioning Systemand its application for particular weather scenarios. J. Geophys. Res. Atmos. 2017, 122, 4401–4425. [Google Scholar] [CrossRef]
- Gegout, P.; Biancale, R.; Soudarin, L. Adaptive mapping functions to the azimuthal anisotropy of the neutral atmosphere. J. Geod. 2011, 85, 661–677. [Google Scholar] [CrossRef]
- Davis, J.L.; Elgered, G.; Niell, A.E.; Kuehn, C.E. Ground-based measurement of gradients in the “wet” radio refractivity of air. Rad. Sci. 1993, 28, 1003–1018. [Google Scholar] [CrossRef]
- Manandhar, S.; Lee, Y.H.; Meng, Y.S.; Ong, J.T. A simplified model for the retrieval of precipitable water vapor from GPS signal. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6245–6253. [Google Scholar] [CrossRef]
- Shoji, Y.; Nakamura, H.; Iwabuchi, T.; Aonashi, K.; Seko, H.; Mishima, K.; Itagaki, A.; Ichikawa, R.; Ohtani, R. Tsukuba GPS Dense Net Campaign Observation: Improvement of GPS analysis of slant path delay by stacking one-way postfit phase residuals. J. Meteorol. Soc. Jpn. 2004, 82, 301–314. [Google Scholar] [CrossRef]
- Kačmařík, M.; Douša, J.; Dick, G.; Zus, F.; Brenot, H.; Möller, G.; Pottiaux, E.; Kapłon, J.; Hordyniec, P.; Václavovic, P.; et al. Inter-technique validation of tropospheric slant total delays. Atmos. Meas. Tech. 2017, 10, 2183–2208. [Google Scholar] [CrossRef]
- Niell, A.E. Global mapping functions for the atmosphere delay at radio wavelengths. J. Geophy. Res. 1996, 101, 3227–3246. [Google Scholar] [CrossRef]
- Site Information for Singapore. Available online: http://gnss1.tudelft.nl/dpga/station/Singapore.html (accessed on 1 September 2022).
- Dev, S. 2D and 3D Image Analysis and Its Application to Sky/Cloud Imaging. Ph.D. Thesis, Nanyang Technological University, Singapore, 2017. [Google Scholar]
- Yang, D.; Jirutitijaroen, P.; Walsh, W.M. The estimation of clear sky global horizontal irradiance at the equator. Energy Procedia 2012, 25, 141–148. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heh, D.Y.; Lee, Y.H.; Biswas, A.N.; Koh, L.M. GPS-Derived Slant Water Vapor for Cloud Monitoring in Singapore. Remote Sens. 2022, 14, 5459. https://doi.org/10.3390/rs14215459
Heh DY, Lee YH, Biswas AN, Koh LM. GPS-Derived Slant Water Vapor for Cloud Monitoring in Singapore. Remote Sensing. 2022; 14(21):5459. https://doi.org/10.3390/rs14215459
Chicago/Turabian StyleHeh, Ding Yu, Yee Hui Lee, Anik Naha Biswas, and Liang Mong Koh. 2022. "GPS-Derived Slant Water Vapor for Cloud Monitoring in Singapore" Remote Sensing 14, no. 21: 5459. https://doi.org/10.3390/rs14215459
APA StyleHeh, D. Y., Lee, Y. H., Biswas, A. N., & Koh, L. M. (2022). GPS-Derived Slant Water Vapor for Cloud Monitoring in Singapore. Remote Sensing, 14(21), 5459. https://doi.org/10.3390/rs14215459





