Energy-Efficient Controller Placement in Software-Defined Satellite-Terrestrial Integrated Network
Abstract
1. Introduction
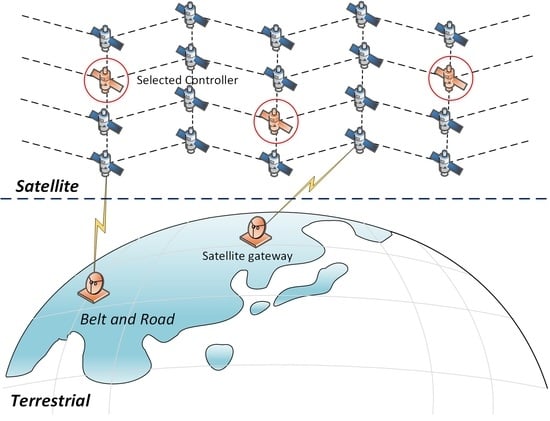
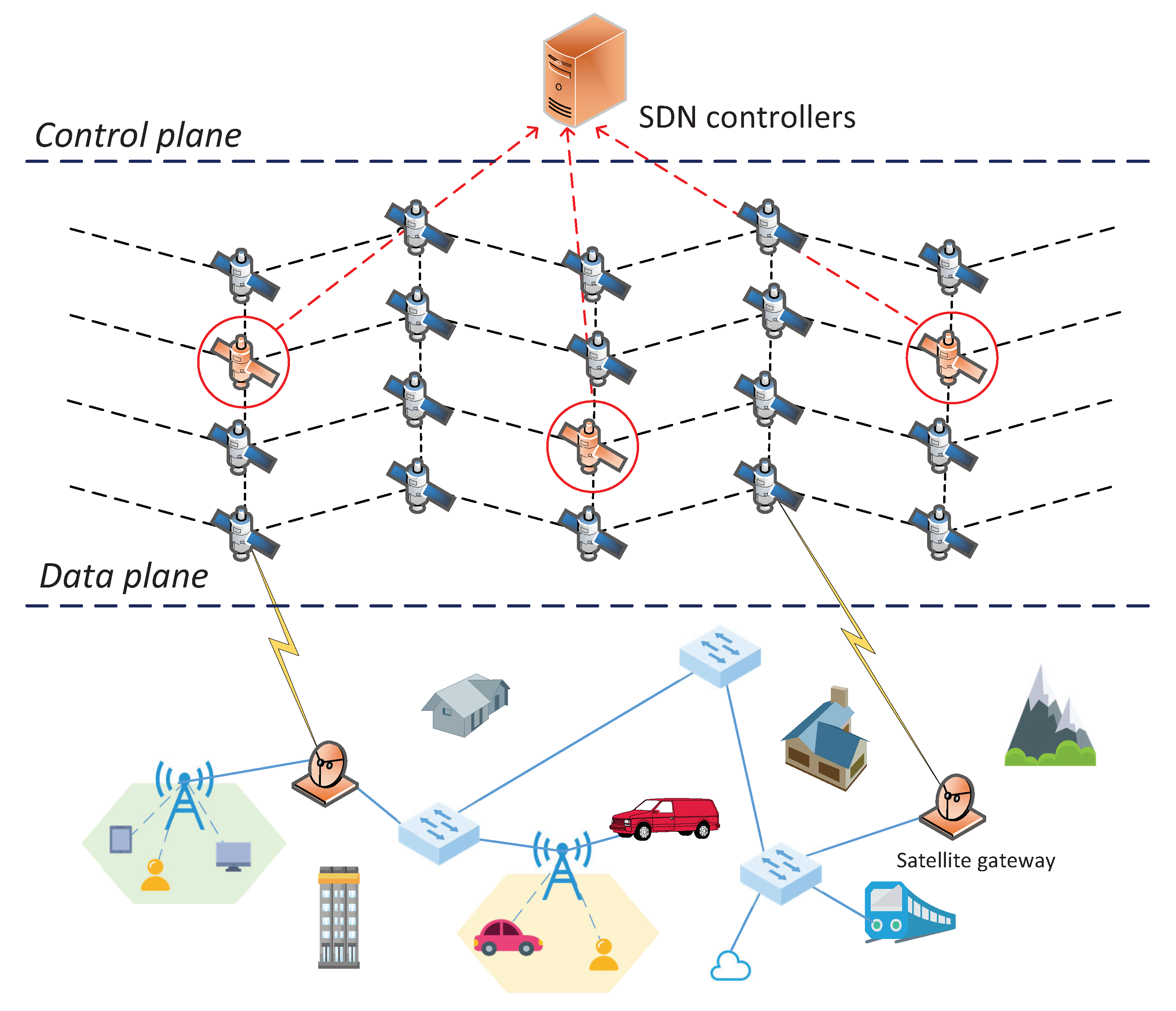
- We consider a software-defined STIN architecture, where controllers are deployed on LEO satellites. Based on the architecture, the EECP problem is defined to establish a relationship between economic concerns and traffic demands. The energy consumption model takes the effect of the real-world traffic demands into account.
- Considering the high complexity of the problem in large-scale networks, we propose a heuristic-based MSAP algorithm to solve the EECP problem. The MSAP algorithm first adopts the greedy way to find the initial set of controllers and then introduces the simulated annealing (SA) algorithm to obtain the optimal placement strategy.
- Extensive simulations are conducted on the simulated STIN with the Iridium constellation and satellite gateways. Simulation results show that the proposed MSAP algorithm outperforms other algorithms in network energy consumption and average latency.
2. Related Work
2.1. Controller Placement in Terrestrial Networks
2.2. Controller Placement in the Software-Defined STIN
3. System Model and Problem Formulation
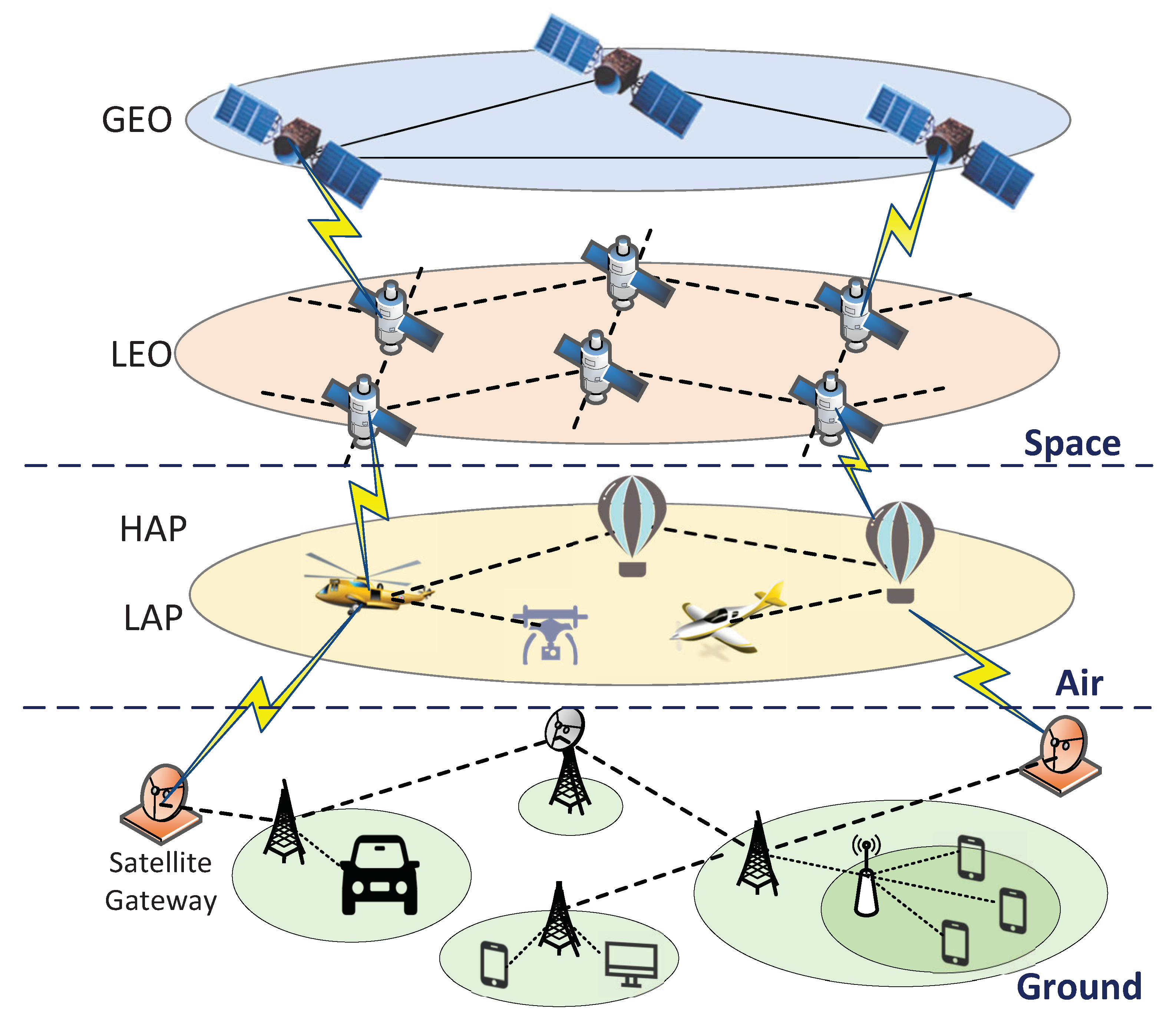
3.1. Software-Defined STIN Architecture
3.2. Energy Consumption Model
4. Heuristic Placement Algorithm
| Algorithm 1 Greedy Initial Algorithm (GI). |
|
| Algorithm 2 Modified Simulated Annealing Placement Algorithm (MSAP). |
|
5. Simulation Results
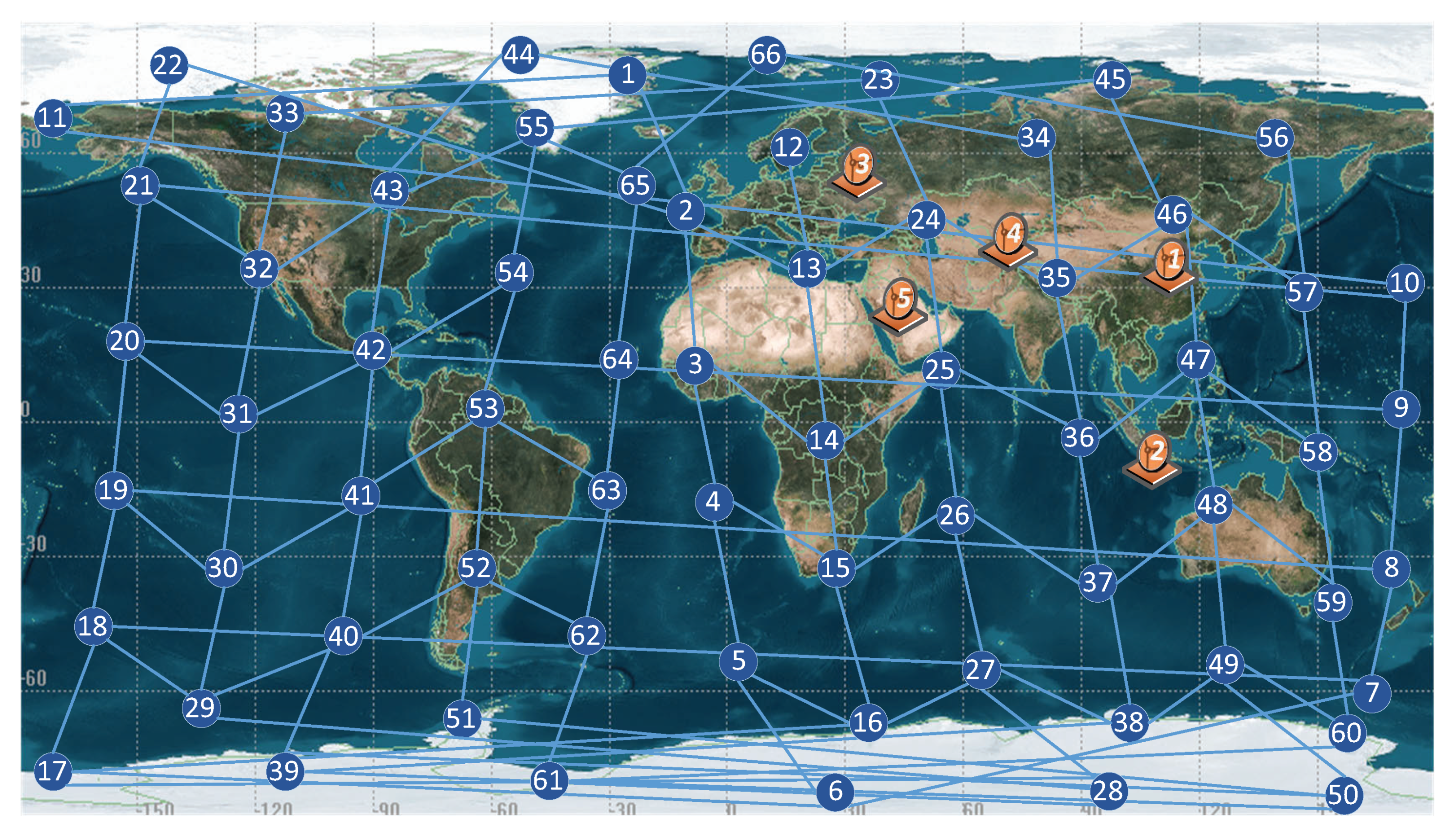
5.1. Simulation Setup
5.2. Analysis of the Architecture
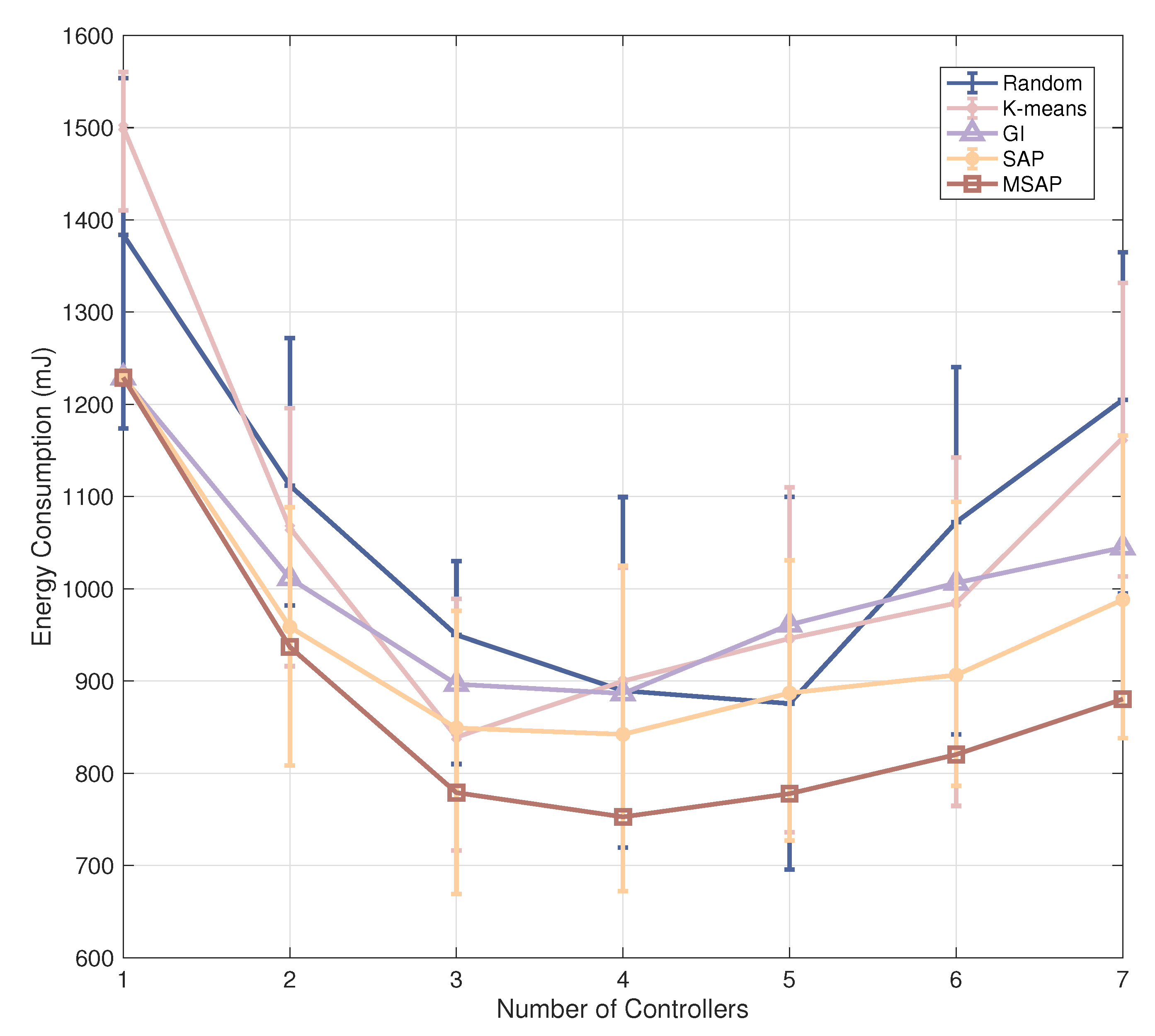
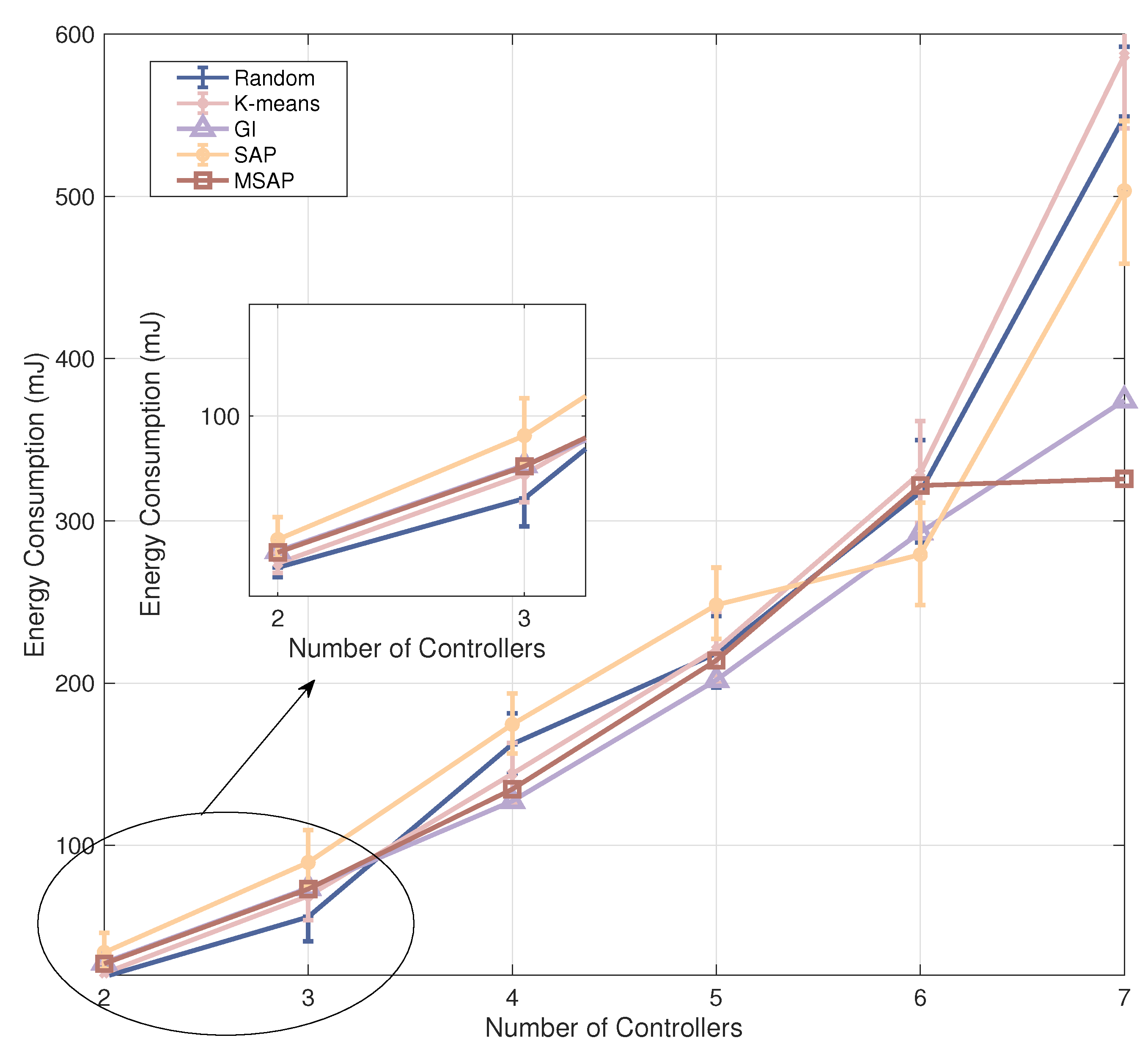
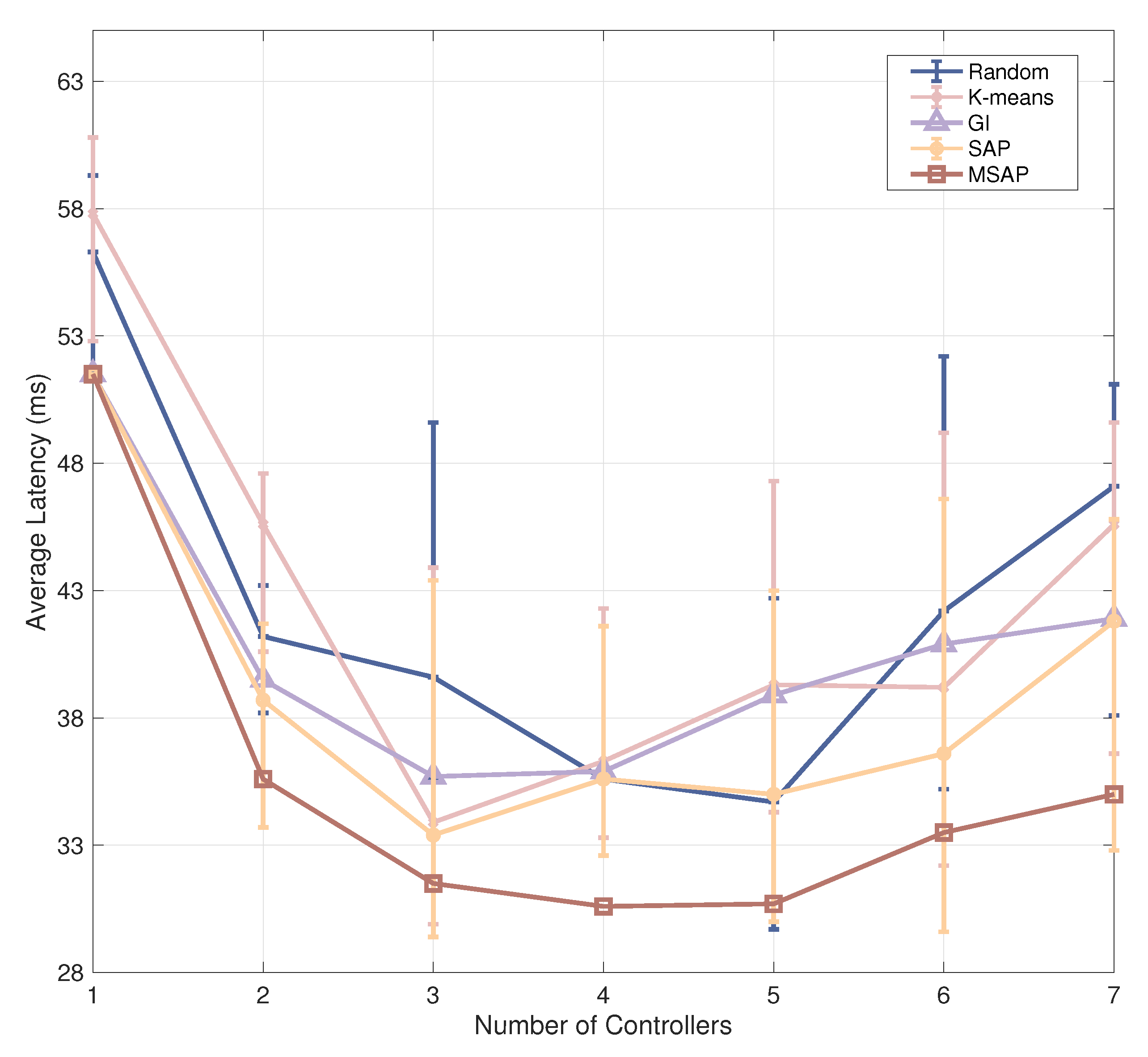
5.3. Comparison with Different Algorithms
- Random algorithm means randomly choosing nodes as controllers. To eliminate the effect of randomness, we run the algorithm 10 times and take the average result as the final output.
- K-means [44] belongs to the clustering algorithm. By calculating the energy consumption between nodes and the selected controllers, the nodes are divided into multiple clusters in STIN.
- Greedy algorithm [19] provides locally optimal results that approximate globally optimal solutions. The controllers are selected one by one, and it assures that the energy consumption of STIN achieves the optimal results at this stage.
- SA algorithm [45] approximates the global optimum solution through a random search technique. The nodes are selected as controllers once the energy consumption of STIN reaches a thermal equilibrium point.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| STIN | Satellite Terrestrial Integrated Network |
| SDN | Software-Defined Networking |
| GEO | Geostationary Earth Orbit |
| MEO | Medium Earth Orbit |
| LEO | Low Earth Orbit |
| HAP | High-Altitude Platforms |
| LAP | Low-Altitude Platforms |
| ISL | Inter-Satellite Links |
| UDL | User Data Links |
| VR | Virtual Reality |
| IoT | Internet of Things |
| CPP | Controller Placement Problem |
| EECP | Energy-Efficient Controller Placement |
| SA | Simulated Annealing |
| SAP | Simulated Annealing Placement |
| MSAP | Modified Simulated Annealing Placement |
| GI | Greedy Initial |
| 6G | 6th Generation Mobile Networks |
| STK | Systems Tool Kit |
| QoS | Quality of Service |
| WAN | Wide-Area Network |
| GA | Genetic Algorithm |
| PSO | Particle Swarm Optimization |
| AA | Approximation Algorithm |
References
- Bacco, M.; Davoli, F.; Giambene, G.; Gotta, A.; Luglio, M.; Marchese, M.; Patrone, F.; Roseti, C. Networking Challenges for Non-Terrestrial Networks Exploitation in 5G. In Proceedings of the 2019 IEEE 2nd 5G World Forum (5GWF), Dresden, Germany, 30 September–2 October 2019; pp. 623–628. [Google Scholar]
- Saad, W.; Bennis, M.; Chen, M. A Vision of 6G Wireless Systems: Applications, Trends, Technologies, and Open Research Problems. IEEE Netw. 2020, 34, 134–142. [Google Scholar] [CrossRef]
- Foust, J. SpaceX’s Space-Internet Woes: Despite Technical Glitches, the Company Plans to Launch the First of Nearly 12,000 Satellites in 2019. IEEE Spectr. 2019, 56, 50–51. [Google Scholar] [CrossRef]
- Radtke, J.; Kebschull, C.; Stoll, E. Interactions of the Space Debris Environment with Mega Constellations—Using the Example of the OneWeb Constellation. Acta Astronaut. 2017, 131, 55–68. [Google Scholar] [CrossRef]
- Liu, J.; Shi, Y.; Fadlullah, Z.M.; Kato, N. Space-Air-Ground Integrated Network: A Survey. IEEE Commun. Surv. Tutor. 2018, 20, 2714–2741. [Google Scholar] [CrossRef]
- Yao, H.; Wang, L.; Wang, X.; Lu, Z.; Liu, Y. The Space-Terrestrial Integrated Network: An Overview. IEEE Commun. Mag. 2018, 56, 178–185. [Google Scholar] [CrossRef]
- Kreutz, D.; Ramos, F.M.V.; Veríssimo, P.E.; Rothenberg, C.E.; Azodolmolky, S.; Uhlig, S. Software-Defined Networking: A Comprehensive Survey. Proc. IEEE 2015, 103, 14–76. [Google Scholar] [CrossRef]
- Yuan, S.; Peng, M.; Sun, Y.; Liu, X. Software Defined Intelligent Satellite-Terrestrial Integrated Networks: Insights and Challenges. Digit. Commun. Netw. 2022. [Google Scholar] [CrossRef]
- Heller, B.; Sherwood, R.; McKeown, N. The Controller Placement Problem. SIGCOMM Comput. Commun. Rev. 2012, 42, 473–478. [Google Scholar] [CrossRef]
- Andrae, A.S.G.; Edler, T. On Global Electricity Usage of Communication Technology: Trends to 2030. Challenges 2015, 6, 117–157. [Google Scholar] [CrossRef]
- Liu, H.; Fang, C.; Miao, Y.; Ma, H.; Zhang, Q.; Zhou, Q. Spatio-Temporal Evolution of Population and Urbanization in the Countries along the Belt and Road 1950–2050. J. Geogr. Sci. 2018, 28, 919–936. [Google Scholar] [CrossRef]
- Isong, B.; Molose, R.R.S.; Abu-Mahfouz, A.M.; Dladlu, N. Comprehensive Review of SDN Controller Placement Strategies. IEEE Access 2020, 8, 170070–170092. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, Z.; Hu, T.; Yi, P.; Lan, J. A Survey of Controller Placement Problem in Software-Defined Networking. IEEE Access 2019, 7, 24290–24307. [Google Scholar] [CrossRef]
- Wang, T.; Liu, F.; Xu, H. An Efficient Online Algorithm for Dynamic SDN Controller Assignment in Data Center Networks. IEEEACM Trans. Netw. 2017, 25, 2788–2801. [Google Scholar] [CrossRef]
- Bera, S.; Misra, S.; Saha, N. Traffic-Aware Dynamic Controller Assignment in SDN. IEEE Trans. Commun. 2020, 68, 4375–4382. [Google Scholar] [CrossRef]
- Singh, A.K.; Maurya, S.; Kumar, N.; Srivastava, S. Heuristic Approaches for the Reliable SDN Controller Placement Problem. Trans. Emerg. Telecommun. Technol. 2020, 31, e3761. [Google Scholar] [CrossRef]
- Liao, C.; Chen, J.; Guo, K.; Liu, S.; Chen, J.; Gao, D. MODECP: A Multi-Objective Based Approach for Solving Distributed Controller Placement Problem in Software Defined Network. Sensors 2022, 22, 5475. [Google Scholar] [CrossRef]
- Liu, J.; Liu, J.; Xie, R. Reliability-based controller placement algorithm in software defined networking. Comput. Sci. Inf. Syst. 2016, 13, 547–560. [Google Scholar] [CrossRef]
- Salam, R.; Bhattacharya, A. Efficient Greedy Heuristic Approach for Fault-Tolerant Distributed Controller Placement in Scalable SDN Architecture. Clust. Comput. 2022, 25, 4543–4572. [Google Scholar] [CrossRef]
- Aravind, P.; Varma, G.P.S.; Reddy, P.V.G.D.P. Simulated Annealing Based Optimal Controller Placement in Software Defined Networks with Capacity Constraint and Failure Awareness. J. King Saud. Univ. Comput. Inf. Sci. 2022, 34, 5721–5733. [Google Scholar] [CrossRef]
- Maity, I.; Dhiman, R.; Misra, S. EnPlace: Energy-Aware Network Partitioning for Controller Placement in SDN. IEEE Trans. Green Commun. Netw. 2022. [Google Scholar] [CrossRef]
- Ruiz-Rivera, A.; Chin, K.-W.; Soh, S. GreCo: An Energy Aware Controller Association Algorithm for Software Defined Networks. IEEE Commun. Lett. 2015, 19, 541–544. [Google Scholar] [CrossRef]
- Hu, Y.; Luo, T.; Beaulieu, N.C.; Deng, C. The Energy-Aware Controller Placement Problem in Software Defined Networks. IEEE Commun. Lett. 2017, 21, 741–744. [Google Scholar] [CrossRef]
- Fernandez-Fernandez, A.; Cervello-Pastor, C.; Ochoa-Aday, L. Achieving Energy Efficiency: An Energy-Aware Approach in SDN. In Proceedings of the 2016 IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–7. [Google Scholar]
- Liu, J.; Shi, Y.; Zhao, L.; Cao, Y.; Sun, W.; Kato, N. Joint Placement of Controllers and Gateways in SDN-Enabled 5G-Satellite Integrated Network. IEEE J. Sel. Areas Commun. 2018, 36, 221–232. [Google Scholar] [CrossRef]
- Bi, Y.; Han, G.; Xu, S.; Wang, X.; Lin, C.; Yu, Z.; Sun, P. Software Defined Space-Terrestrial Integrated Networks: Architecture, Challenges, and Solutions. IEEE Netw. 2019, 33, 22–28. [Google Scholar] [CrossRef]
- Shen, Y.; Chen, W.; Liu, J. Joint Placement of Gateways and Controllers in SDN-Enabled Space-Ground Integration Network. In Proceedings of the 2022 Asia Conference on Electrical, Power and Computer Engineering (EPCE 2022), Shanghai, China, 22 April 2022; ACM: New York, NY, USA, 2022; pp. 1–6. [Google Scholar]
- Bao, J.; Zhao, B.; Yu, W.; Feng, Z.; Wu, C.; Gong, Z. OpenSAN: A Software-Defined Satellite Network Architecture. In Proceedings of the 2014 ACM conference on SIGCOMM, Chicago, IL, USA, 17 August 2014; ACM: New York, NY, USA, 2014; pp. 347–348. [Google Scholar]
- Zhang, Z.; Zhao, B.; Yu, W.; Wu, C. Poster: An Efficient Control Framework for Supporting the Future SDN/NFV-Enabled Satellite Network. In Proceedings of the 23rd Annual International Conference on Mobile Computing and Networking, Snowbird, UT, USA, 16–20 October 2017; Association for Computing Machinery: New York, NY, USA, 2017; pp. 603–605. [Google Scholar]
- Papa, A.; De Cola, T.; Vizarreta, P.; He, M.; Mas Machuca, C.; Kellerer, W. Dynamic SDN Controller Placement in a LEO Constellation Satellite Network. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 206–212. [Google Scholar]
- Chen, C.; Liao, Z.; Ju, Y.; He, C.; Yu, K.; Wan, S. Hierarchical Domain-Based Multi-Controller Deployment Strategy in SDN-Enabled Space-Air-Ground Integrated Network. IEEE Trans. Aerosp. Electron. Syst. 2022. [Google Scholar] [CrossRef]
- Han, Z.; Xu, C.; Xiong, Z.; Zhao, G.; Yu, S. On-Demand Dynamic Controller Placement in Software Defined Satellite-Terrestrial Networking. IEEE Trans. Netw. Serv. Manag. 2021, 18, 2915–2928. [Google Scholar] [CrossRef]
- Wu, S.; Chen, X.; Yang, L.; Fan, C.; Zhao, Y. Dynamic and Static Controller Placement in Software-Defined Satellite Networking. Acta Astronaut. 2018, 152, 49–58. [Google Scholar] [CrossRef]
- Liao, Z.; Chen, C.; Ju, Y.; He, C.; Jiang, J.; Pei, Q. Multi-Controller Deployment in SDN-Enabled 6G Space–Air–Ground Integrated Network. Remote Sens. 2022, 14, 1076. [Google Scholar] [CrossRef]
- Qu, H.; Xu, X.; Zhao, J.; Yue, P. An SDN-Based Space-Air-Ground Integrated Network Architecture and Controller Deployment Strategy. In Proceedings of the 2020 IEEE 3rd International Conference on Computer and Communication Engineering Technology (CCET), Beijing, China, 14–16 August 2020; pp. 138–142. [Google Scholar]
- Radhakrishnan, R.; Edmonson, W.W.; Afghah, F.; Rodriguez-Osorio, R.M.; Pinto, F.; Burleigh, S.C. Survey of Inter-Satellite Communication for Small Satellite Systems: Physical Layer to Network Layer View. IEEE Commun. Surv. Tutor. 2016, 18, 2442–2473. [Google Scholar] [CrossRef]
- Internet Usage Statistics. [Online]. 2015. Available online: http://www.internetworldstats.com/stats.htm (accessed on 31 July 2022).
- Yang, Y.; Xu, M.; Wang, D.; Wang, Y. Towards Energy-Efficient Routing in Satellite Networks. IEEE J. Sel. Areas Commun. 2016, 34, 3869–3886. [Google Scholar] [CrossRef]
- Lombardo, A.; Panarello, C.; Reforgiato, D.; Schembra, G. Measuring and Modeling Energy Consumption to Design a Green NetFPGA Giga-Router. In Proceedings of the 2012 IEEE Global Communications Conference (GLOBECOM), Anaheim, CA, USA, 3–7 December 2012; pp. 3062–3067. [Google Scholar]
- Saha, B.K.; Misra, S.; Pal, S. SeeR: Simulated Annealing-Based Routing in Opportunistic Mobile Networks. IEEE Trans. Mob. Comput. 2017, 16, 2876–2888. [Google Scholar] [CrossRef]
- AGI. Systems Tool Kit (STK). Available online: https://www.agi.com/products/engineering-tools (accessed on 15 December 2021).
- Yao, G.; Bi, J.; Li, Y.; Guo, L. On the Capacitated Controller Placement Problem in Software Defined Networks. IEEE Commun. Lett. 2014, 18, 1339–1342. [Google Scholar] [CrossRef]
- del Portillo, I.; Cameron, B.; Crawley, E. Ground Segment Architectures for Large LEO Constellations with Feeder Links in EHF-Bands. In Proceedings of the 2018 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2018; pp. 1–14. [Google Scholar]
- Wang, G.; Zhao, Y.; Huang, J.; Duan, Q.; Li, J. A K-Means-Based Network Partition Algorithm for Controller Placement in Software Defined Network. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 23–27 May 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Chang, C.; Liu, Y.; Wang, Y. Failure-Based Multi-Controller Placement in Software Defined Satellite Networking. In Proceedings of the 2021 IEEE International Conference on Communications Workshops (ICC Workshops), Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar]



| Ref. | Locations | Algorithms | Metrics | |||
|---|---|---|---|---|---|---|
| Latency | Cost | Reliability | Load | |||
| [35] | Air | K-means | ✓ | |||
| [25] | Ground | SA | ✓ | ✓ | ||
| [30] | Satellites | ILP | ✓ | |||
| [31] | Ground, Satellites | GA | ✓ | ✓ | ||
| [32] | Satellites | AA | ✓ | |||
| [33] | Satellites | PSO | ✓ | ✓ | ✓ | |
| [34] | Satellites | SA | ✓ | |||
| Proposed | Satellites | SA | ✓ | ✓ | ✓ | ✓ |
| Satellite Gateway | Country, City | Longitude | Latitude |
|---|---|---|---|
| SG1 | China, Beijing | 116.4 | 39.9 |
| SG2 | Indonesia, Jakarta | 106.8 | −6.3 |
| SG3 | Russia, Moskva | 37.7 | 55.8 |
| SG4 | Kazakhstan, Almaty | 76.9 | 43.3 |
| SG5 | Saudi Arabia, Al Madinah | 39.7 | 24.4 |
| Parameter | Value |
|---|---|
| (mJ) | 7.639 |
| (mJ) | 1.944 |
| (Byte) | 160 |
| (nJ/B) | 5.634 |
| (nJ/B) | 8.406 |
| R (Mbps) | |
| (Byte) | 280 |
| (C) | 1 |
| (C) | 0.0001 |
| 0.75 |
| Methods | Number of Controllers | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Random | 1 | 0.62 | 0.49 | 0.42 | 0.32 | 0.22 | 0.15 |
| K-means | 1 | 0.70 | 0.60 | 0.39 | 0.32 | 0.25 | 0.15 |
| GI | 1 | 0.61 | 0.46 | 0.38 | 0.26 | 0.20 | 0.16 |
| SAP | 1 | 0.64 | 0.48 | 0.37 | 0.28 | 0.23 | 0.18 |
| MSAP | 1 | 0.66 | 0.53 | 0.41 | 0.32 | 0.25 | 0.20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, L.; Chang, C.; Liu, Y.; Wang, Y. Energy-Efficient Controller Placement in Software-Defined Satellite-Terrestrial Integrated Network. Remote Sens. 2022, 14, 5561. https://doi.org/10.3390/rs14215561
Wei L, Chang C, Liu Y, Wang Y. Energy-Efficient Controller Placement in Software-Defined Satellite-Terrestrial Integrated Network. Remote Sensing. 2022; 14(21):5561. https://doi.org/10.3390/rs14215561
Chicago/Turabian StyleWei, Linhui, Chen Chang, Yu Liu, and Yumei Wang. 2022. "Energy-Efficient Controller Placement in Software-Defined Satellite-Terrestrial Integrated Network" Remote Sensing 14, no. 21: 5561. https://doi.org/10.3390/rs14215561
APA StyleWei, L., Chang, C., Liu, Y., & Wang, Y. (2022). Energy-Efficient Controller Placement in Software-Defined Satellite-Terrestrial Integrated Network. Remote Sensing, 14(21), 5561. https://doi.org/10.3390/rs14215561