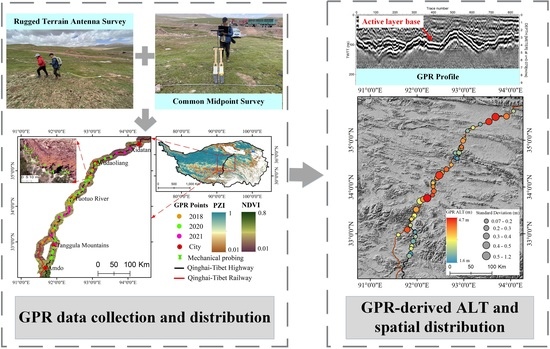
Spatial Variability of Active Layer Thickness along the Qinghai–Tibet Engineering Corridor Resolved Using Ground-Penetrating Radar
Abstract
1. Introduction
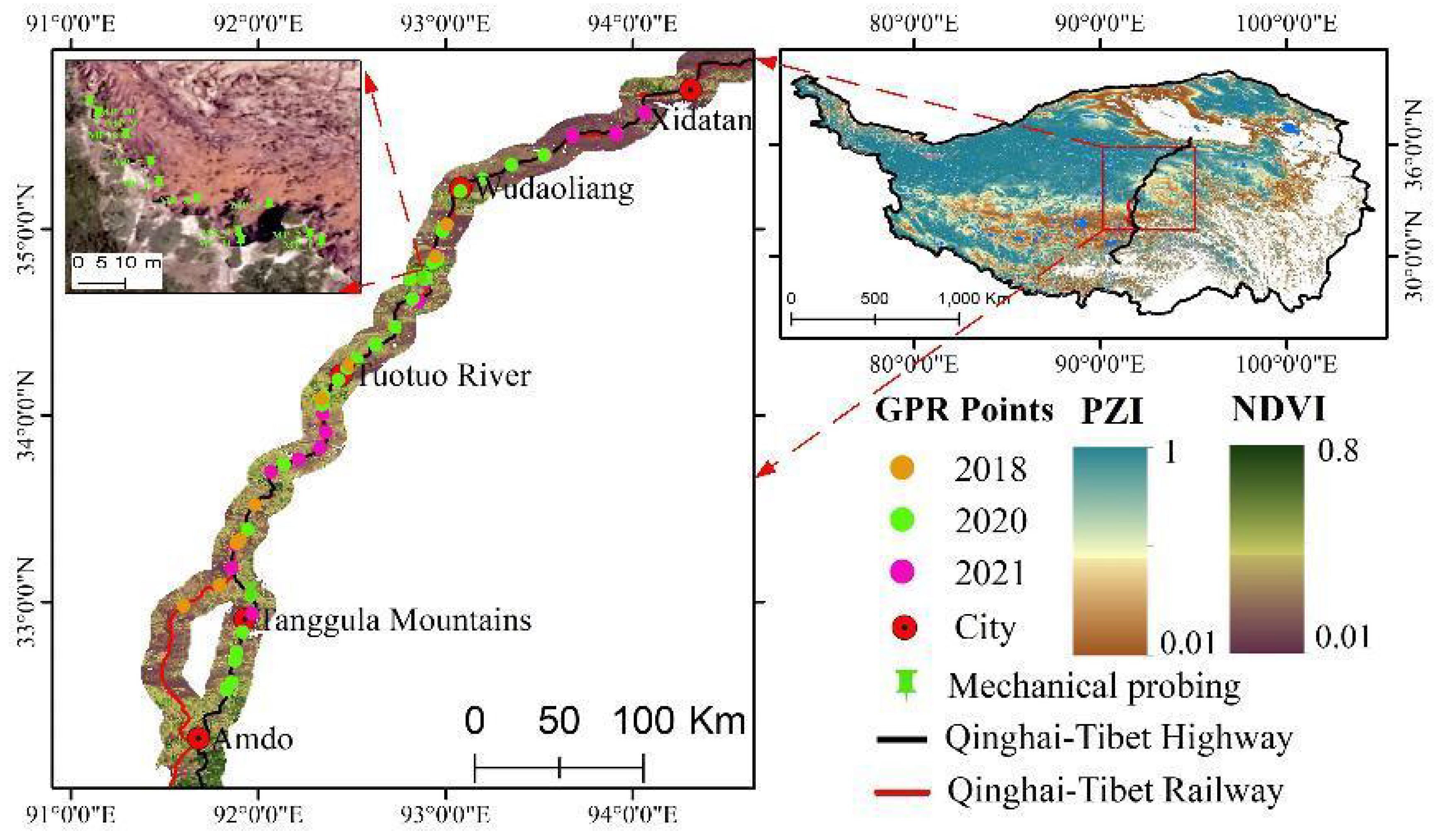
2. Study Area
3. Dataset and Methods
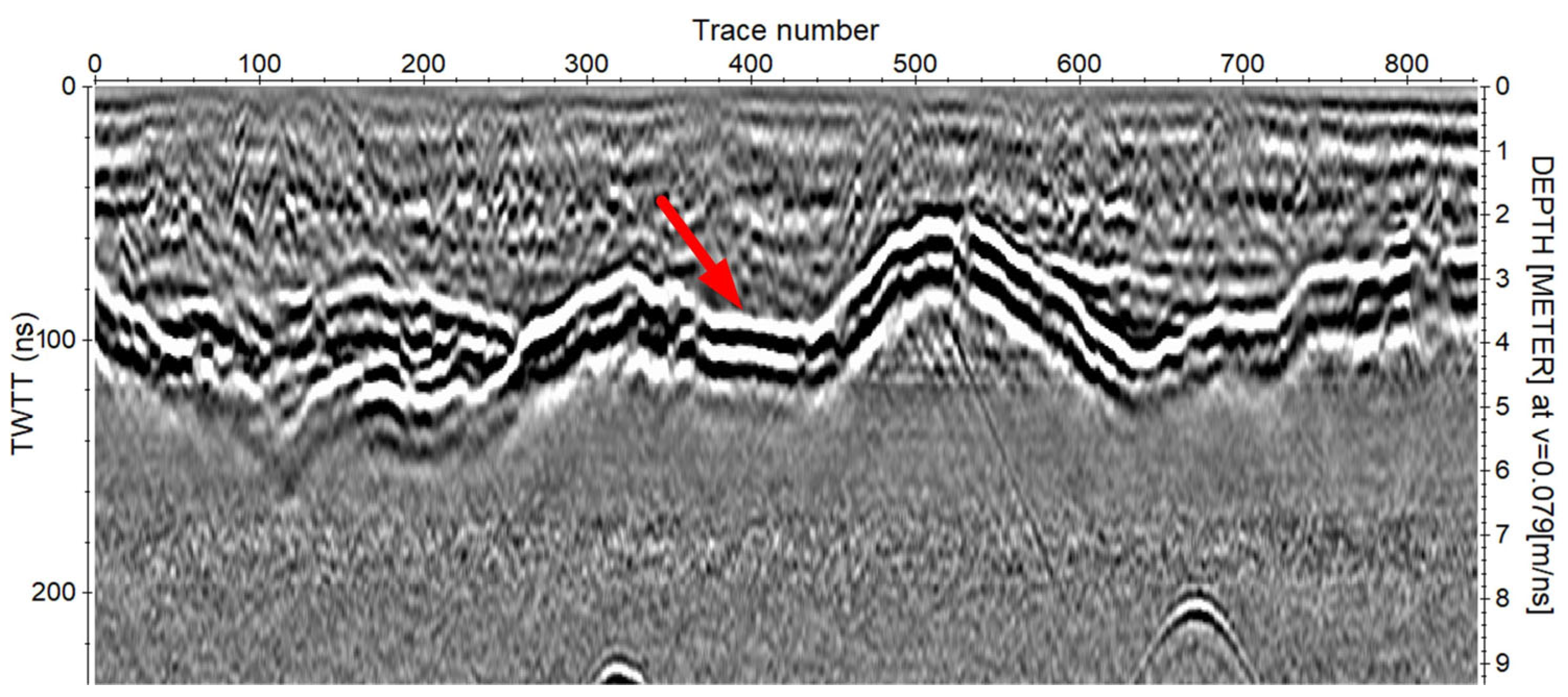
3.1. ALT from GPR Measurements
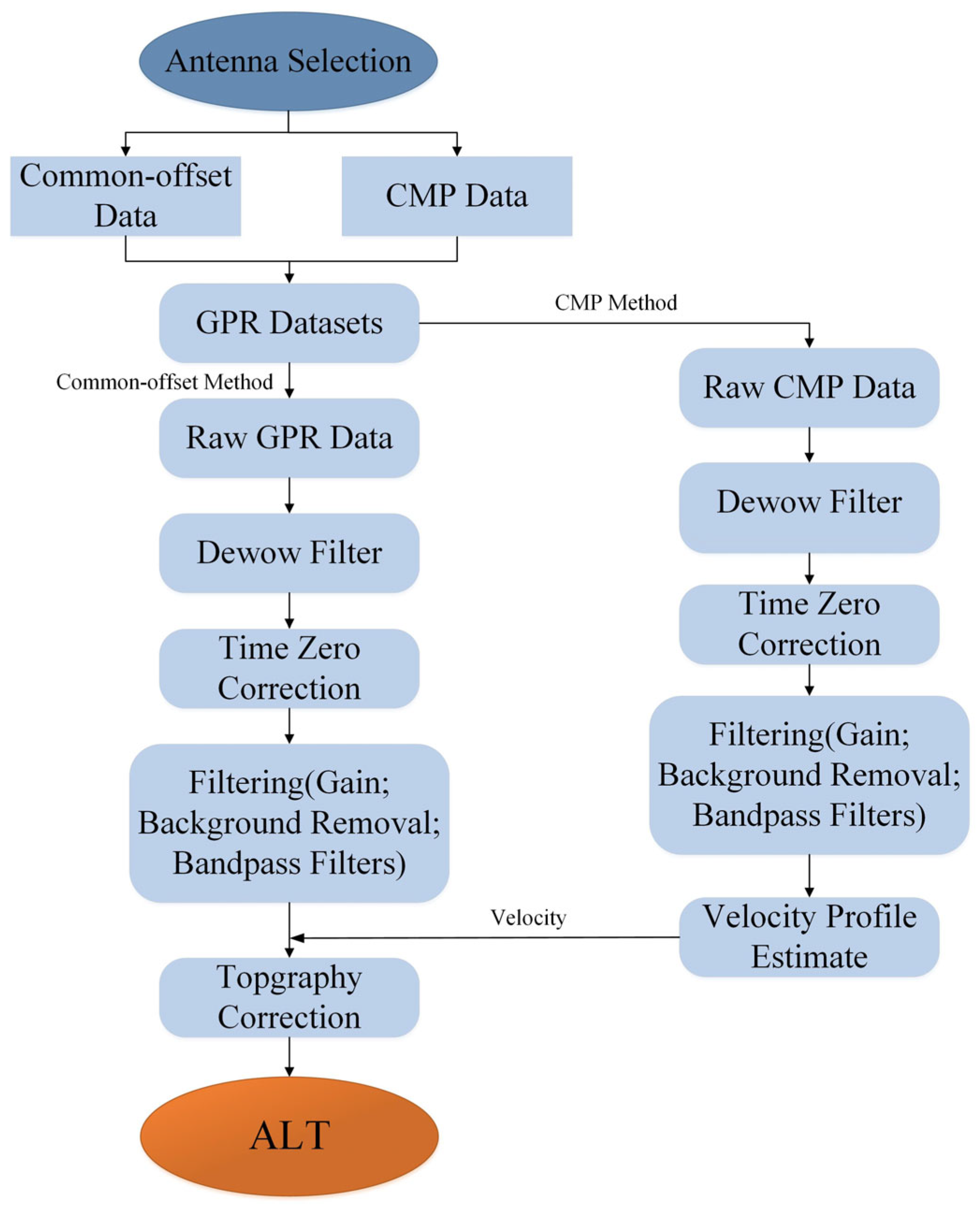
3.1.1. GPR Data Processing
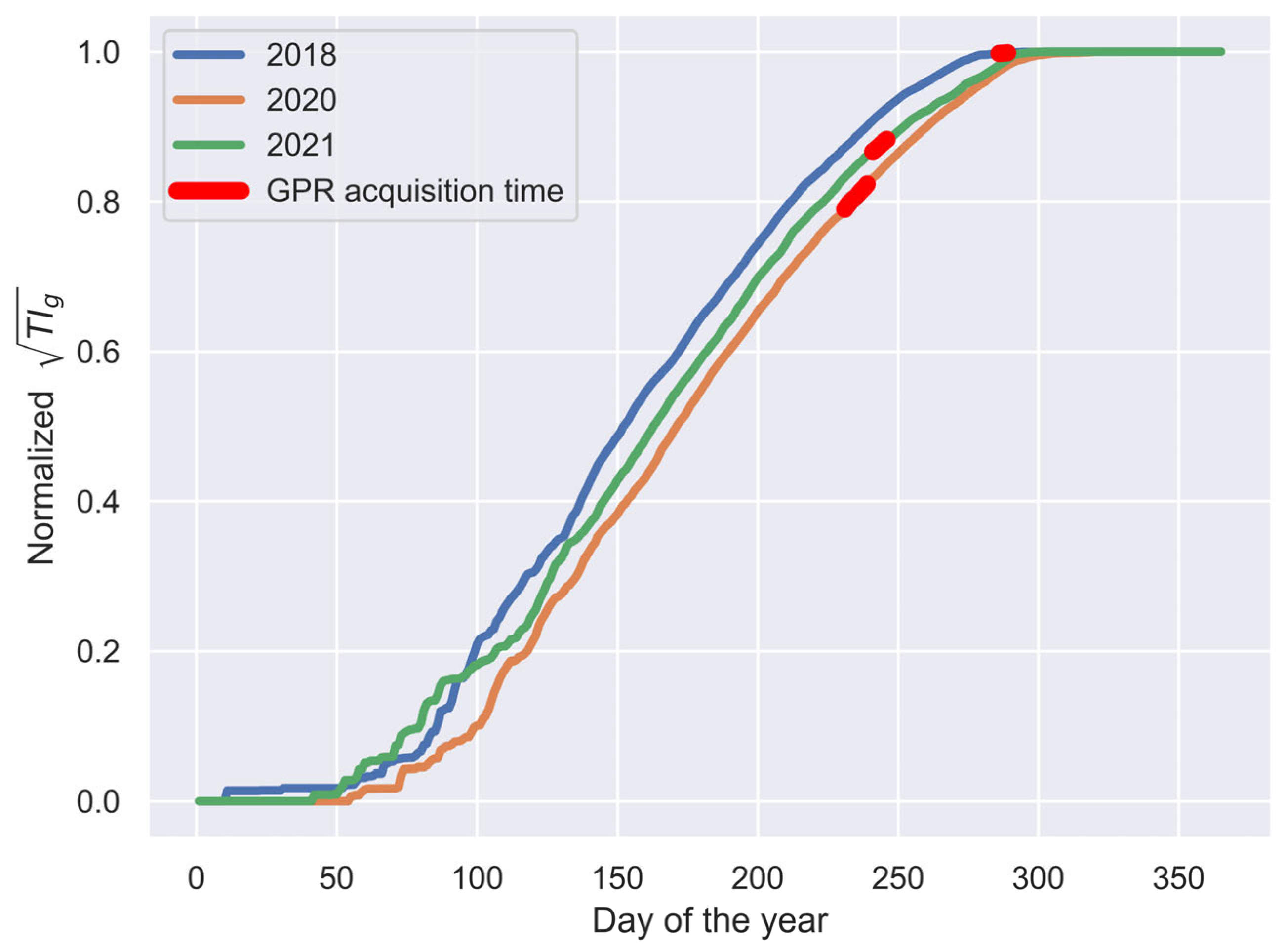
3.1.2. Velocity and ALT
3.2. ALT from In Situ Measurements and Reference Datasets
3.3. Potential Controlling Factors of ALT
3.4. Statistical Model of ALT
4. Results
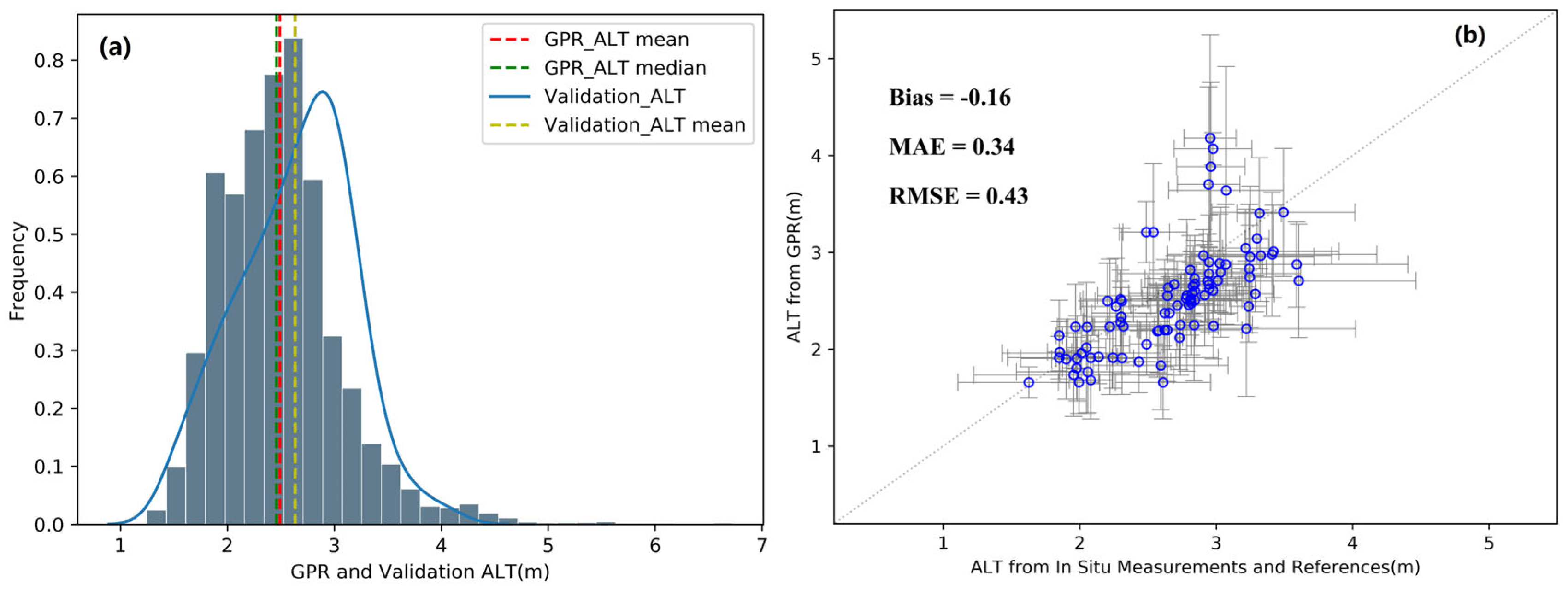
4.1. Evaluation of ALT from GPR
4.2. Spatial Variability of ALT
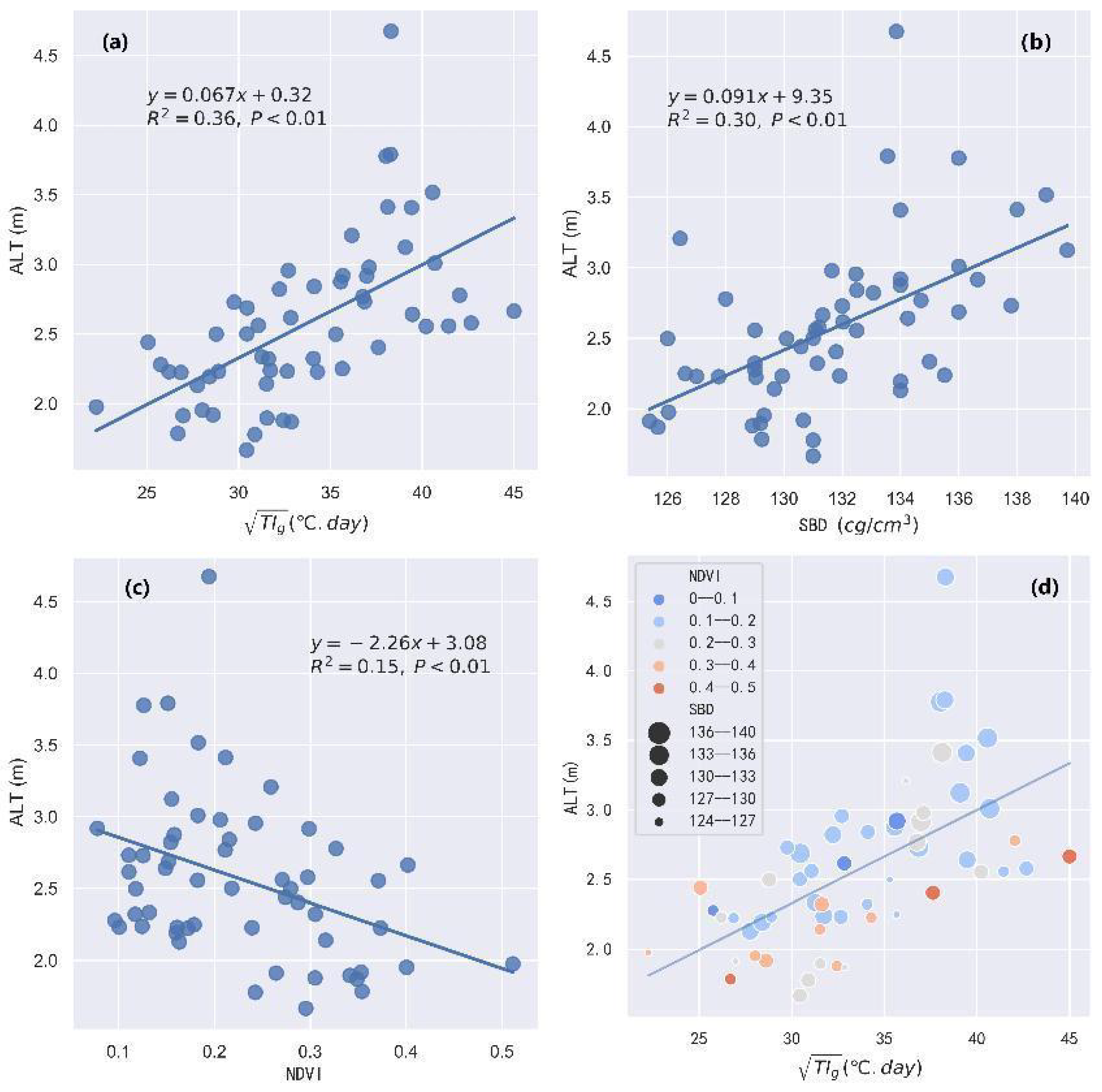
4.3. Influencing Factors of ALT Variation
4.3.1. Effect of Individual Factors on ALT
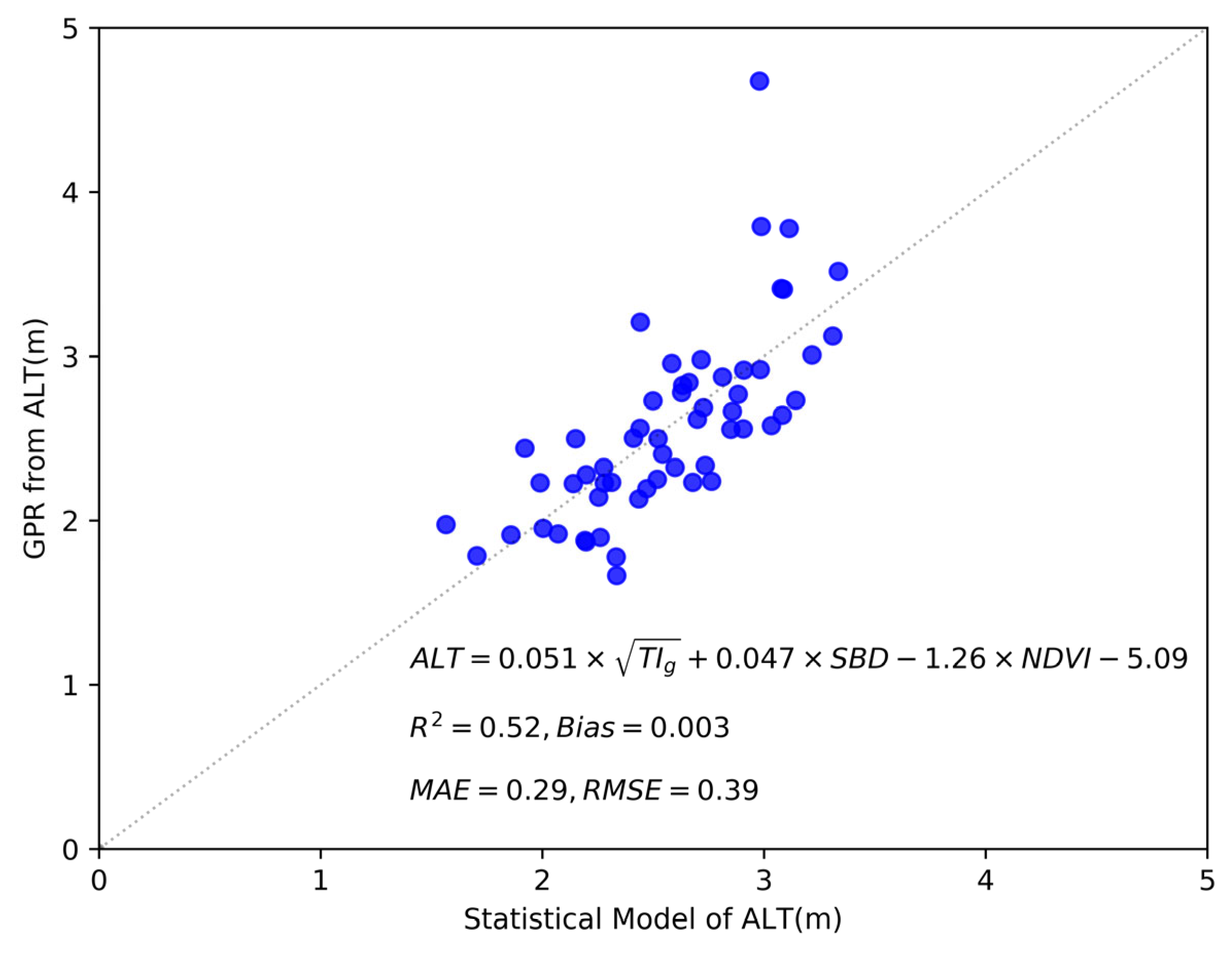
4.3.2. Statistical Model for ALT Estimation
5. Discussion
6. Conclusions
- The value of ALT shows considerable spatial variability along the QTEC, with a range of approximately 1.25–6.70 m and mean of 2.49 ± 0.57 m. Approximately 66% of the estimated ALT values were in the range of 2–3 m, 20% were in the range of 1.25–2.00 m, 12% were in the range of 3–4 m, and the remaining 2% of ALT values were >4 m.
- At the fine scale (i.e., <1 km), ALT shows obvious spatial heterogeneity with standard deviation in the range of 0.07–1.20 m. The variation in ALT was significant in areas where the geomorphic unit and vegetation changed remarkably. The variation in ALT at the fine scale could account for approximately 76.6% of the overall spatial variability at the regional scale, indicating the importance of understanding ALT at the fine scale.
- Observed ALT is mainly controlled by the soil thermal regime, soil properties, and vegetation. The topoclimatic factors of , SBD, and NDVI can be used as suitable predictors for estimating the variation in ALT along the QTEC.
- GPR is a fast yet low-cost method that is suitable for investigation of permafrost in complex terrain. Our results elucidated the spatial distribution of ALT along the QTEC, which could represent a useful benchmark for understanding the change in ALT in a warming climate.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Abbreviation | Full Name | Unit |
|---|---|---|
| ALT | Active layer thickness | m |
| GPR | Ground-penetrating radar | - |
| QTEC | Qinghai–Tibet Engineering Corridor | - |
| QTP | Qinghai–Tibet Plateau | - |
| TIg | Ground thawing index | °C.d |
| PZI | Permafrost zonation index | - |
| RTA | Rugged terrain antenna | - |
| CMP | Common midpoint | - |
| TWTT | Two-way travel time | ns |
| RMSE | Root mean square error | m |
| MAE | Mean absolute error | m |
| LST | Land surface temperature | °C |
| SBD | Soil bulk density | cg/cm3 |
| NDVI | Normalized difference vegetation index | - |
| VIF | Variance inflation factor | - |
| Q1 | Lower quartile of boxplot | - |
| Q3 | Upper quartile of boxplot | - |
References
- Cao, B.; Zhang, T.; Wu, Q.; Sheng, Y.; Zhao, L.; Zou, D. Permafrost zonation index map and statistics over the Qinghai-Tibet Plateau based on field evidence. Permafr. Periglac. Process. 2019, 30, 178–194. [Google Scholar] [CrossRef]
- Cao, B.; Zhang, T.; Peng, X.; Mu, C.; Wang, Q.; Zheng, L.; Wang, K.; Zhong, X. Thermal Characteristics and Recent Changes of Permafrost in the Upper Reaches of the Heihe River Basin, Western China. J. Geophys. Res. Atmos. 2018, 123, 7935–7949. [Google Scholar] [CrossRef]
- Yao, T.; Xue, Y.; Chen, D.; Chen, F.; Thompson, L.; Cui, P.; Koike, T.; Lau, W.K.-M.; Lettenmaier, D.; Mosbrugger, V.; et al. Recent Third Pole’s Rapid Warming Accompanies Cryospheric Melt and Water Cycle Intensification and Interactions between Monsoon and Environment: Multidisciplinary Approach with Observations, Modeling, and Analysis. Bull. Am. Meteorol. Soc. 2019, 100, 423–444. [Google Scholar] [CrossRef]
- Lin, Z.; Luo, J.; Niu, F. Development of a thermokarst lake and its thermal effects on permafrost over nearly 10 yr in the Beiluhe Basin, Qinghai-Tibet Plateau. Geosphere 2016, 12, 632–643. [Google Scholar] [CrossRef]
- Qin, Y.; Wu, T.; Zhao, L.; Wu, X.; Li, R.; Xie, C.; Pang, Q.; Hu, G.; Qiao, Y.; Zhao, G.; et al. Numerical Modeling of the Active Layer Thickness and Permafrost Thermal State Across Qinghai-Tibetan Plateau. J. Geophys. Res. Atmos. 2017, 122, 11,604–11,620. [Google Scholar] [CrossRef]
- Chen, J.; Liu, L.; Zhang, T.; Cao, B.; Lin, H. Using Persistent Scatterer Interferometry to Map and Quantify Permafrost Thaw Subsidence: A Case Study of Eboling Mountain on the Qinghai-Tibet Plateau. J. Geophys. Res. Earth Surf. 2018, 123, 2663–2676. [Google Scholar] [CrossRef]
- Cao, B.; Arduini, G.; Zsoter, E. Brief communication: Improving ERA5-Land soil temperature in permafrost regions using an optimized multi-layer snow scheme. Cryosphere 2022, 16, 2701–2708. [Google Scholar] [CrossRef]
- Koven, C.D.; Lawrence, D.M.; Riley, W.J. Permafrost carbon−climate feedback is sensitive to deep soil carbon decomposability but not deep soil nitrogen dynamics. Proc. Natl. Acad. Sci. USA 2015, 112, 3752–3757. [Google Scholar] [CrossRef]
- Harris, S.A.; French, H.M.; Heginbottom, J.A.; Johnston, G.H.; Ladanyi, B.; Sego, D.C.; van Everdingen, R.O. Glossary of Permafrost and Related Ground-Ice Terms; Technical Memorandum No. 142; National Research Council of Canada, Associate Committee on Geotechnical Research, Permafrost Subcommittee: Ottawa, ON, Canada, 1988; p. 156. [Google Scholar] [CrossRef]
- Ge, S.; McKenzie, J.; Voss, C.; Wu, Q. Exchange of groundwater and surface-water mediated by permafrost response to seasonal and long term air temperature variation. Geophys. Res. Lett. 2011, 38, 1–6. [Google Scholar] [CrossRef]
- Hewitt, R.E.; DeVan, M.R.; Lagutina, I.V.; Genet, H.; McGuire, A.D.; Taylor, D.L.; Mack, M.C. Mycobiont contribution to tundra plant acquisition of permafrost-derived nitrogen. New Phytol. 2020, 226, 126–141. [Google Scholar] [CrossRef]
- Hjort, J.; Karjalainen, O.; Aalto, J.; Westermann, S.; Romanovsky, V.E.; Nelson, F.E.; Etzelmüller, B.; Luoto, M. Degrading permafrost puts Arctic infrastructure at risk by mid-century. Nat. Commun. 2018, 9, 5147. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, T.; Zhong, X. Changes in the timing and duration of the near-surface soil freeze/thaw status from 1956 to 2006 across China. Cryosphere 2015, 9, 1321–1331. [Google Scholar] [CrossRef]
- Peng, X.; Zhang, T.; Frauenfeld, O.W.; Wang, K.; Luo, D.; Cao, B.; Su, H.; Jin, H.; Wu, Q. Spatiotemporal Changes in Active Layer Thickness under Contemporary and Projected Climate in the Northern Hemisphere. J. Clim. 2017, 31, 251–266. [Google Scholar] [CrossRef]
- Zhao, L.; Wu, Q.; Marchenko, S.; Sharkhuu, N. Thermal state of permafrost and active layer in Central Asia during the international polar year. Permafr. Periglac. Process. 2010, 21, 198–207. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, T.; Liu, Y. Permafrost temperatures and thickness on the Qinghai-Tibet Plateau. Glob. Planet. Chang. 2010, 72, 32–38. [Google Scholar] [CrossRef]
- Jia, Y.; Kim, J.-W.; Shum, C.K.; Lu, Z.; Ding, X.; Zhang, L.; Erkan, K.; Kuo, C.-Y.; Shang, K.; Tseng, K.-H.; et al. Characterization of Active Layer Thickening Rate over the Northern Qinghai-Tibetan Plateau Permafrost Region Using ALOS Interferometric Synthetic Aperture Radar Data, 2007–2009. Remote Sens. 2017, 9, 84. [Google Scholar] [CrossRef]
- Liu, L.; Schaefer, K.; Zhang, T.; Wahr, J. Estimating 1992–2000 average active layer thickness on the Alaskan North Slope from remotely sensed surface subsidence. J. Geophys. Res. Earth Surf. 2012, 117, F01005. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Wu, Q.B. Predicting changes of active layer thickness on the Qinghai-Tibet Plateau as climate warming. J. Glaciol. Geocryol. 2012, 34, 505. [Google Scholar]
- Cao, B.; Gruber, S.; Zhang, T.; Li, L.; Peng, X.; Wang, K.; Zheng, L.; Shao, W.; Guo, H. Spatial variability of active layer thickness detected by ground-penetrating radar in the Qilian Mountains, Western China. J. Geophys. Res. Earth Surf. 2017, 122, 574–591. [Google Scholar] [CrossRef]
- Moorman, B.J.; Robinson, S.D.; Burgess, M.M. Imaging periglacial conditions with ground-penetrating radar. Permafr. Periglac. Process. 2003, 14, 319–329. [Google Scholar] [CrossRef]
- Neal, A. Ground-penetrating radar and its use in sedimentology: Principles, problems and progress. Earth-Sci. Rev. 2004, 66, 261–330. [Google Scholar] [CrossRef]
- Wollschläger, U.; Gerhards, H.; Yu, Q.; Roth, K. Multi-channel ground-penetrating radar to explore spatial variations in thaw depth and moisture content in the active layer of a permafrost site. Cryosphere 2010, 4, 269–283. [Google Scholar] [CrossRef]
- Kaverin, D.; Khilko, A.; Pastukhov, A. Application of high-frequency ground penetrating radarto investigations of permafrost-affected soils of peat plateaus (European Northeast of Russia). Earth’s Cryosphere 2018, 22, 86–95. [Google Scholar] [CrossRef]
- Chen, A.; Parsekian, A.D.; Schaefer, K.; Jafarov, E.; Panda, S.; Liu, L.; Zhang, T.; Zebker, H. Ground-penetrating radar-derived measurements of active-layer thickness on the landscape scale with sparse calibration at Toolik and Happy Valley, Alaska. Geophysics 2016, 81, H9–H19. [Google Scholar] [CrossRef]
- Jørgensen, A.S.; Andreasen, F. Mapping of permafrost surface using ground-penetrating radar at Kangerlussuaq Airport, western Greenland. Cold Reg. Sci. Technol. 2007, 48, 64–72. [Google Scholar] [CrossRef]
- Shen, Y.; Zuo, R.; Liu, J.; Tian, Y.; Wang, Q. Characterization and evaluation of permafrost thawing using GPR attributes in the Qinghai-Tibet Plateau. Cold Reg. Sci. Technol. 2018, 151, 302–313. [Google Scholar] [CrossRef]
- You, Y.; Yu, Q.; Pan, X.; Wang, X.; Guo, L. Geophysical Imaging of Permafrost and Talik Configuration Beneath a Thermokarst Lake. Permafr. Periglac. Process. 2017, 28, 470–476. [Google Scholar] [CrossRef]
- Luo, J.; Niu, F.-J.; Lin, Z.-J.; Liu, M.-H.; Yin, G.-A. Variations in the northern permafrost boundary over the last four decades in the Xidatan region, Qinghai–Tibet Plateau. J. Mt. Sci. 2018, 15, 765–778. [Google Scholar] [CrossRef]
- Lu, X.; Song, A.; Qian, R.; Liu, L. Characterization of Subsurface Structure in Different Landforms based on GPR Profiles along the Qinghai-Tibet Highway on Permafrost region. In Proceedings of the 2018 17th International Conference on Ground Penetrating Radar (GPR), Rapperswil, Switzerland, 18–21 June 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Yao, T.; Shilong, P.; Shen, M.; Jing, G.; Wei, Y.; Zhang, G.; Lei, Y.; Yang, G.; Zhu, L.; Xu, B. Chained Impacts on Modern En-vironment of Interaction between Westerlies and Indian Monsoon on Tibetan Plateau. Bull. Chin. Acad. Sci. 2017, 32, 976–984. [Google Scholar] [CrossRef]
- Li, R.; Zhao, L.; Ding, Y.; Wu, T.; Xiao, Y.; Du, E.; Liu, G.; Qiao, Y. Temporal and spatial variations of the active layer along the Qinghai-Tibet Highway in a permafrost region. Chin. Sci. Bull. 2012, 57, 4609–4616. [Google Scholar] [CrossRef]
- Zhao, L.; Zou, D.; Hu, G.; Du, E.; Pang, Q.; Xiao, Y.; Li, R.; Sheng, Y.; Wu, X.; Sun, Z.; et al. Changing climate and the permafrost environment on the Qinghai–Tibet (Xizang) plateau. Permafr. Periglac. Process. 2020, 31, 396–405. [Google Scholar] [CrossRef]
- Wang, Z.-W.; Wang, Q.; Zhao, L.; Wu, X.-D.; Yue, G.-Y.; Zou, D.-F.; Nan, Z.-T.; Liu, G.-Y.; Pang, Q.-Q.; Fang, H.-B.; et al. Mapping the vegetation distribution of the permafrost zone on the Qinghai-Tibet Plateau. J. Mt. Sci. 2016, 13, 1035–1046. [Google Scholar] [CrossRef]
- Jin, H.; Wang, S.; Yu, Q.; Wu, Q.; Wei, Z. Regionalization and assessment of environmental geological conditions of frozen soils along the Qinghai-Tibet Engineering Corridor. Hydrogeol. Eng. Geol. 2006, 33, 66–70. [Google Scholar]
- Chen, X.; Mu, C.; Jia, L.; Li, Z.; Fan, C.; Mu, M.; Peng, X.; Wu, X. High-resolution dataset of thermokarst lakes on the Qing-hai-Tibetan Plateau. Earth Syst. Sci. Data Discuss. 2021, 2021, 1–23. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, T. Changes in active layer thickness over the Qinghai-Tibetan Plateau from 1995 to 2007. J. Geophys. Res. Earth Surf. 2010, 115, D09107. [Google Scholar] [CrossRef]
- Hinkel, K.M.; Doolittle, J.A.; Bockheim, J.G.; Nelson, F.E.; Paetzold, R.; Kimble, J.M.; Travis, R. Detection of subsurface permafrost features with ground-penetrating radar, Barrow, Alaska. Permafr. Periglac. Process. 2001, 12, 179–190. [Google Scholar] [CrossRef]
- Niu, F.; Zheng, H.; Li, A. The study of frost heave mechanism of high-speed railway foundation by field-monitored data and indoor verification experiment. Acta Geotech. 2020, 15, 581–593. [Google Scholar] [CrossRef]
- Ran, Y.; Li, X.; Cheng, G.; Che, J.; Aalto, J.; Karjalainen, O.; Hjort, J.; Luoto, M.; Jin, H.; Obu, J.; et al. New High-Resolution Estimates of the Permafrost Thermal State and Hydrothermal Conditions over the Northern Hemisphere. Earth Syst. Sci. Data Discuss. 2021, 2021, 1–27. [Google Scholar] [CrossRef]
- Mugume, I.; Basalirwa, C.; Waiswa, D.; Reuder, J.; Mesquita, M.D.S.; Tao, S.; Ngailo, T.J. Comparison of Parametric and Nonparametric Methods for Analyzing the Bias of a Numerical Model. Model. Simul. Eng. 2016, 2016, 1–7. [Google Scholar] [CrossRef]
- Cheng, G. Influences of local factors on permafrost occurrence and their implications for Qinghai-Xizang Railway design. Sci. China Ser. D Earth Sci. 2004, 47, 704–709. [Google Scholar] [CrossRef]
- Fisher, J.P.; Estop-Aragonés, C.; Thierry, A.; Charman, D.J.; Wolfe, S.A.; Hartley, I.P.; Murton, J.B.; Williams, M.; Phoenix, G.K. The influence of vegetation and soil characteristics on active-layer thickness of permafrost soils in boreal forest. Glob. Chang. Biol. 2016, 22, 3127–3140. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, Y.; Zhao, L.; Fang, H.; Zhang, G. Construction of an index set for predicting thickness of active layer of per-mafrost in Qinghai-tibet plateau and for mapping. Acta Pedol. Sin. 2015, 52, 499–506. [Google Scholar]
- Shi, Y.; Yang, C.; Che, T. Accuracy verification of the Tibetan Plateau Permafrost Map based on MODIS LST product. J. Glaciol. Geocryol. 2017, 39, 70. [Google Scholar] [CrossRef]
- Li, A.; Xia, C.; Bao, C.; Yin, G. Using MODIS Land Surface Temperatures for Permafrost Thermal Modeling in Beiluhe Basin on the Qinghai-Tibet Plateau. Sensors 2019, 19, 4200. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, J.; Liang, S.; Wang, D. A practical reanalysis data and thermal infrared remote sensing data merging (RTM) method for reconstruction of a 1-km all-weather land surface temperature. Remote Sens. Environ. 2021, 260, 112437. [Google Scholar] [CrossRef]
- Peng, X.; Zhang, T.; Cao, B.; Wang, Q.; Wang, K.; Shao, W.; Guo, H. Changes in Freezing-Thawing Index and Soil Freeze Depth Over the Heihe River Basin, Western China. Arctic, Antarct. Alp. Res. 2016, 48, 161–176. [Google Scholar] [CrossRef]
- Hengl, T.; De Jesus, J.M.; Heuvelink, G.B.M.; Gonzalez, M.R.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef]
- Akinwande, M.O.; Dikko, H.G.; Samson, A. Variance Inflation Factor: As a Condition for the Inclusion of Suppressor Variable(s) in Regression Analysis. Open J. Stat. 2015, 5, 754–767. [Google Scholar] [CrossRef]
- Zhang, B.; Zhou, W. Spatial–Temporal Characteristics of Precipitation and Its Relationship with Land Use/Cover Change on the Qinghai-Tibet Plateau, China. Land 2021, 10, 269. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Y.; Wu, J.; Li, S.; Zhang, B.; Zu, J.; Zhang, H.; Ding, M.; Paudel, B. Increasing sensitivity of alpine grasslands to climate variability along an elevational gradient on the Qinghai-Tibet Plateau. Sci. Total Environ. 2019, 678, 21–29. [Google Scholar] [CrossRef]
- Klotzsche, A.; Jonard, F.; Looms, M.; van der Kruk, J.; Huisman, J. Measuring Soil Water Content with Ground Penetrating Radar: A Decade of Progress. Vadose Zone J. 2018, 17, 180052–180059. [Google Scholar] [CrossRef]
- Westermann, S.; Wollschläger, U.; Boike, J. Monitoring of active layer dynamics at a permafrost site on Svalbard using multi-channel ground-penetrating radar. Cryosphere 2010, 4, 475–487. [Google Scholar] [CrossRef]
- Wu, K.; Rodriguez, G.A.; Zajc, M.; Jacquemin, E.; Clément, M.; De Coster, A.; Lambot, S. A new drone-borne GPR for soil moisture mapping. Remote Sens. Environ. 2019, 235, 111456. [Google Scholar] [CrossRef]
- Parsekian, A.D. Inverse Methods to Improve Accuracy of Water Content Estimates from Multi-offset GPR. J. Environ. Eng. Geophys. 2018, 23, 349–361. [Google Scholar] [CrossRef]
- Jafarov, E.E.; Parsekian, A.D.; Schaefer, K.; Liu, L.; Chen, A.C.; Panda, S.K.; Zhang, T. Estimating active layer thickness and volumetric water content from ground penetrating radar measurements in Barrow, Alaska. Geosci. Data J. 2018, 4, 72–79. [Google Scholar] [CrossRef]
- Bonomo, N.; de la Vega, M.; Martinelli, P.; Osella, A. Pipe-flange detection with GPR. J. Geophys. Eng. 2010, 8, 35–45. [Google Scholar] [CrossRef]
- Prego, F.; Solla, M.; Puente, I.; Arias, P. Efficient GPR data acquisition to detect underground pipes. NDT E Int. 2017, 91, 22–31. [Google Scholar] [CrossRef]
- Iftimie, N.; Savin, A.; Steigmann, R.; Dobrescu, G.S. Underground Pipeline Identification into a Non-Destructive Case Study Based on Ground-Penetrating Radar Imaging. Remote Sens. 2021, 13, 3494. [Google Scholar] [CrossRef]



| Factors | SBD | NDVI | VIF | |
|---|---|---|---|---|
| 1 | - | - | 1.19 | |
| SBD | 0.40 ** | 1 | - | 1.46 |
| NDVI | −0.13 | −0.45 ** | 1 | 1.25 |
| Factors | Model Parameter | Coefficient |
|---|---|---|
| α1 | 0.051 ** | |
| SBD | α2 | 0.047 ** |
| NDVI | α3 | −1.26 * |
| Intercept | β | −5.09 ** |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, S.; Zhang, T.; Hao, J.; Li, C.; Michaelides, R.; Shao, W.; Wei, S.; Wang, K.; Fan, C. Spatial Variability of Active Layer Thickness along the Qinghai–Tibet Engineering Corridor Resolved Using Ground-Penetrating Radar. Remote Sens. 2022, 14, 5606. https://doi.org/10.3390/rs14215606
Jia S, Zhang T, Hao J, Li C, Michaelides R, Shao W, Wei S, Wang K, Fan C. Spatial Variability of Active Layer Thickness along the Qinghai–Tibet Engineering Corridor Resolved Using Ground-Penetrating Radar. Remote Sensing. 2022; 14(21):5606. https://doi.org/10.3390/rs14215606
Chicago/Turabian StyleJia, Shichao, Tingjun Zhang, Jiansheng Hao, Chaoyue Li, Roger Michaelides, Wanwan Shao, Sihao Wei, Kun Wang, and Chengyan Fan. 2022. "Spatial Variability of Active Layer Thickness along the Qinghai–Tibet Engineering Corridor Resolved Using Ground-Penetrating Radar" Remote Sensing 14, no. 21: 5606. https://doi.org/10.3390/rs14215606
APA StyleJia, S., Zhang, T., Hao, J., Li, C., Michaelides, R., Shao, W., Wei, S., Wang, K., & Fan, C. (2022). Spatial Variability of Active Layer Thickness along the Qinghai–Tibet Engineering Corridor Resolved Using Ground-Penetrating Radar. Remote Sensing, 14(21), 5606. https://doi.org/10.3390/rs14215606