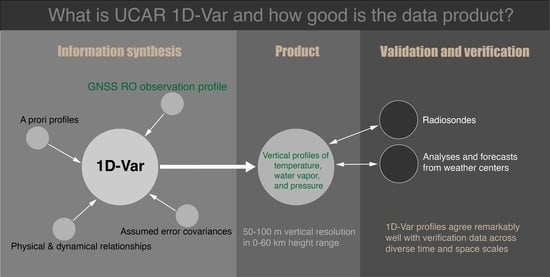
Atmospheric GNSS RO 1D-Var in Use at UCAR: Description and Validation
Abstract
:1. Introduction
2. Materials and Methods
2.1. GNSS RO Overview
2.2. The UCAR 1D-Var
2.2.1. Theoretical Framework
2.2.2. Observation Operators
2.2.3. A Priori Profiles
2.2.4. Error Covariance Matrices
3. Results
3.1. 1D-Var Response to Single-Level Perturbations of the Observation
3.2. Tests Using Synthetic Data
3.3. Validation Using NWP Model Data
3.3.1. Comparison against the Previous 1D-Var Version
3.3.2. Comparison of Observation Operators
3.3.3. Dependence on the Background
3.4. Comparison to High Vertical Resolution Radiosondes
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Melbourne, W.G.; Davis, E.S.; Duncan, C.B.; Hajj, G.A.; Hardy, K.R.; Kursinski, E.R.; Meehan, T.K.; Young, L.E.; Yunck, T.P. The Application of Spaceborne GPS to Atmospheric Limb Sounding and Global Change Monitoring; JPL Publication: Pasadena, CA, USA, 1994. [Google Scholar]
- Kursinski, E.R.; Hajj, G.A.; Schofield, J.T.; Linfield, R.P.; Hardy, K.R. Observing Earth’s atmosphere with radio occultation measurements using the Global Positioning System. J. Geophys. Res. 1997, 102, 23429–23465. [Google Scholar] [CrossRef]
- Hajj, G.A.; Kursinski, E.R.; Romans, L.J.; Bertinger, W.I.; Leroy, S.S. A technical description of atmospheric sounding by GPS occultations. J. Atmos. Sol. Terr. Phys. 2002, 64, 451–469. [Google Scholar] [CrossRef]
- Steiner, A.K.; Ladstädter, F.; Ao, C.O.; Gleisner, H.; Ho, S.-P.; Hunt, D.; Schmidt, T.; Foelsche, U.; Kirchengast, G.; Kuo, Y.-H.; et al. Consistency and structural uncertainty of multi-mission GPS radio occultation records. Atmos. Meas. Tech. 2020, 13, 2547–2575. [Google Scholar] [CrossRef]
- Gleisner, H.; Ringer, M.A.; Healy, S.B. Monitoring global climate change using GNSS radio occultation. npj Clim. Atmos. Sci. 2022, 5, 6. [Google Scholar] [CrossRef]
- Healy, S.B. Forecast impact experiment with a constellation of GPS radio occultation receivers. Atmos. Sci. Lett. 2008, 9, 111–118. [Google Scholar] [CrossRef]
- Buontempo, C.; Jupp, A.; Rennie, M.P. Operational NWP assimilation of GPS radio occultation data. Atmos. Sci. Lett. 2008, 9, 129–133. [Google Scholar] [CrossRef]
- Cucurull, L.; Derber, J.C. Operational implementation of COSMIC observations into NCEP’s global data assimilation system. Wea. Forecast. 2008, 23, 702–711. [Google Scholar] [CrossRef]
- Hajj, G.A.; Romans, L.J. Ionospheric electron density profiles obtained with the Global Positioning System: Results from the GPS/MET experiment. Radio Sci. 1998, 33, 175–190. [Google Scholar] [CrossRef] [Green Version]
- Hajj, G.A.; Lee, L.C.; Pi, X.; Romans, L.J.; Schreiner, W.S.; Straus, P.R.; Wang, C. COSMIC GPS ionospheric sensing and space weather. Terr. Atmos. Ocean. Sci. 2000, 11, 235–272. [Google Scholar] [CrossRef] [Green Version]
- Schreiner, W.S.; Sokolovskiy, S.V.; Rocken, C.; Hunt, D.C. Analysis and validation of GPS/MET radio occultation data in the ionosphere. Radio Sci. 1999, 34, 949–966. [Google Scholar] [CrossRef]
- Yue, X.; Schreiner, W.S.; Lei, J.; Rocken, C.; Kuo, Y.-H.; Wan, W. Climatology of ionospheric upper transition height derived from COSMIC satellites during the solar minimum of 2008. J. Atmos. Solar-Terr. Phys. 2010, 72, 1270–1274. [Google Scholar] [CrossRef]
- Rocken, C.; Anthes, R.A.; Exner, M.; Hunt, D.; Sokolovskiy, S.; Ware, R.; Gorbunov, M.; Schreiner, W.; Feng, D.; Herman, B.; et al. Analysis and validation of GPS/MET data in the neutral atmosphere. J. Geophys. Res. 1997, 102, 29849–29866. [Google Scholar] [CrossRef]
- Kursinski, E.R.; Hajj, G.A.; Hardy, K.R.; Romans, L.J.; Schofield, J.T. Observing tropospheric water vapor by radio occultation using the Global Positioning System. Geophys. Res. Lett. 1995, 22, 2365–2368. [Google Scholar] [CrossRef]
- Kursinski, E.R.; Hajj, G.A. A comparison of water vapor derived from GPS occultations and global weather analyses. J. Geophys. Res. 2001, 106, 1113–1138. [Google Scholar] [CrossRef]
- Feng, D.D.; Herman, B.M. Remotely sensing the Earth’s atmosphere using the Global Positioning System (GPS)—The GPS/MET data analysis. J. Atmos. Ocean. Tech. 1999, 16, 989–1002. [Google Scholar] [CrossRef]
- Anthes, R.; Sjoberg, J.; Feng, X.; Syndergaard, S. Comparison of COSMIC and COSMIC-2 radio occultation refractivity and bending angle uncertainties in August 2006 and 2021. Atmosphere 2022, 13, 790. [Google Scholar] [CrossRef]
- Backus, G.E.; Gilbert, J.F. Numerical Applications of a Formalism for Geophysical Inverse Problems. Geophys. J. Int. 1967, 13, 247–276. [Google Scholar] [CrossRef] [Green Version]
- Lewis, J.M.; Derber, J.C. The use of adjoint equations to solve a variational adjustment problem with advective constraints. Tellus 1985, 37, 309–322. [Google Scholar] [CrossRef]
- Le Dimet, F.X.; Talagrand, O. Variational algorithms for analysis and assimilation of meteorological observations: Theory aspects. Tellus 1986, 38A, 97–110. [Google Scholar] [CrossRef]
- Talagrand, O.; Courtier, P. Variational assimilation of meteorological observations with the adjoint vorticity equation. I: Theory. Quart. J. Roy. Meteor. Soc. 1987, 113, 1311–1328. [Google Scholar] [CrossRef]
- Derber, J.C.; Parrish, D.F.; Lord, S.J. The new global operational analysis system at the National Meteorological Center. Wea. Forecast. 1991, 6, 538–547. [Google Scholar] [CrossRef]
- Parrish, D.F.; Derber, J.C. The National Meteorological Center’s spectral statistical interpolation analysis system. Mon. Wea. Rev. 1992, 120, 1747–1763. [Google Scholar] [CrossRef]
- Eyre, J. Assimilation of Radio Occultation Measurements into a Numerical Weather Prediction System; ECMWF Tech. Memorandum 199: Reading, UK, 1994. [Google Scholar]
- Zou, X.; Kuo, Y.-H.; Guo, Y.-R. Assimilation of atmospheric radio refractivity using a nonhydrostatic adjoint model. Mon. Wea. Rev. 1995, 123, 2229–2249. [Google Scholar] [CrossRef]
- Zou, X.; Wang, B.; Liu, H.; Anthes, R.A.; Matsumura, T.; Zhu, Y.-J. Use of GPS/MET refraction angles in three-dimensional variational analysis. Quart. J. Roy. Meter. Soc. 2000, 126, 3013–3040. [Google Scholar] [CrossRef]
- Ware, R.; Exner, M.; Feng, F.; Gorbunov, M.; Hardy, K.; Herman, B.; Kuo, Y.; Meehan, T.; Melbourne, W.; Rocken, C.; et al. GPS Sounding of the Atmosphere from Low Earth Orbit: Preliminary Results. Bull. Am. Meteorol. Soc. 1996, 77, 19–40. [Google Scholar] [CrossRef]
- Anthes, R.A.; Bernhardt, P.A.; Chen, Y.; Cucurull, L.; Dymond, K.F.; Ector, D.; Healy, S.B.; Ho, S.-P.; Hunt, D.C.; Kuo, Y.-H.; et al. The COSMIC/FORMOSAT-3 Mission: Early Results. Bull. Am. Meteorol. Soc. 2008, 89, 313–334. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Pan, H.-L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The NCEP climate forecast system reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1057. [Google Scholar] [CrossRef] [Green Version]
- Poli, P.; Healy, S.B.; Dee, D.P. Assimilation of Global Positioning System radio occultation data in the ECMWF ERA-Interim reanalysis. Quart. J. Roy. Meteor. Soc. 2010, 136, 1972–1990. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Quart. J. Roy. Meteor. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Healy, S.B.; Eyre, J.R. Retrieving temperature, water vapour and surface pressure information from refractive index profiles derived by radio occultation: A simulation study. Quart. J. Roy. Meteor. Soc. 2000, 126, 1661–1683. [Google Scholar] [CrossRef]
- Poli, P.; Joiner, J.; Kursinski, E.R. 1DVAR analysis of temperature and humidity using GPS radio occultation refractivity data. J. Geophys. Res. 2002, 107, 4448. [Google Scholar] [CrossRef] [Green Version]
- Palmer, P.I.; Barnett, J.J.; Eyre, J.R.; Healy, S.B. A nonlinear optimal estimation inverse method for radio occultation measurements of temperature, humidity, and surface pressure. J. Geophys. Res. 2000, 105, 17513–17526. [Google Scholar] [CrossRef] [Green Version]
- von Engeln, A.; Nedoluha, G.; Kirchengast, G.; Bühler, S. One-dimensional variational (1-D Var) retrieval of temperature, water vapor, and a reference pressure from radio occultation measurements: A sensitivity analysis. J. Geophys. Res. 2003, 108, 4337. [Google Scholar] [CrossRef]
- Palmer, P.I.; Barnett, J.J. Application of an optimal estimation inverse method to GPS/MET bending angle observations. J. Geophys. Res. 2001, 106, 17147–17160. [Google Scholar] [CrossRef] [Green Version]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding–Theory and Practice, Series on Atmospheric Oceanic and Planetary Physics, 2; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2000. [Google Scholar] [CrossRef] [Green Version]
- Wee, T.-K. A variational regularization of Abel transform for GPS radio occultation. Atmos. Meas. Tech. 2018, 11, 1947–1969. [Google Scholar] [CrossRef] [Green Version]
- Fu, E.-J.; Zhang, K.-F.; Marion, K.-Y.; Xu, X.-H.; Marshall, J.; Rea, A.; Weymouth, G.; Kuleshov, Y. Assessing COSMIC GPS radio occultation derived atmospheric parameters using Australian radiosonde network data. Procedia Earth Planet. Sci. 2009, 1, 1054–1059. [Google Scholar] [CrossRef] [Green Version]
- He, W.; Ho, S.-P.; Chen, H.; Zhou, X.; Hunt, D.; Kuo, Y.-H. Assessment of radiosonde temperature measurements in the upper troposphere and lower stratosphere using COSMIC radio occultation data. Geophys. Res. Lett. 2009, 36, L17807. [Google Scholar] [CrossRef] [Green Version]
- Kishore, P.; Namboothiri, S.P.; Jiang, J.H.; Sivakumar, V.; Igarashi, K. Global temperature estimates in the troposphere and stratosphere: A validation study of COSMIC/FORMOSAT-3 measurements. Atmos. Chem. Phys. 2009, 9, 897–908. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Fu, E.; Silcock, D.; Wang, Y.; Kuleshov, Y. An investigation of atmospheric temperature profiles in the Australian region using collocated GPS radio occultation and radiosonde data. Atmos. Meas. Tech. 2011, 4, 2087–2092. [Google Scholar] [CrossRef]
- Chang, L.; Guo, L.; Feng, G.; Wu, X.; Gao, G.; Zhang, Y.; Zhang, Y. Comparison of the Arctic upper-air temperatures from radiosonde and radio occultation observations. Acta Oceanol. Sin. 2018, 37, 30–39. [Google Scholar] [CrossRef]
- Zeng, Z.; Ho, S.-P.; Sokolovskiy, S.; Kuo, Y.-H. Structural evolution of the Madden-Julian Oscillation from COSMIC radio occultation data. J. Geophys. Res. 2012, 117, D22108. [Google Scholar] [CrossRef]
- Sharma, N.; Ali, M.M. An approach to predict cyclogenesis using radio occultation observations. Int. J. Engg. Innov. Technol. 2013, 3, 364–367. [Google Scholar]
- Khaykin, S.M.; Pommereau, J.-P.; Hauchecorne, A. Impact of land convection on temperature diurnal variation in the tropical lower stratosphere inferred from COSMIC GPS radio occultations. Atmos. Chem. Phys. 2013, 13, 6391–6402. [Google Scholar] [CrossRef] [Green Version]
- Sun, B.; Reale, A.; Schroeder, S.; Seidel, D.J.; Ballish, B. Toward improved corrections for radiation-induced biases in radiosonde temperature observations. J. Geophys. Res. Atmos. 2013, 118, 4231–4243. [Google Scholar] [CrossRef]
- Iacovazzi, R.; Lin, L.; Sun, N.; Liu, Q. NOAA operational microwave sounding radiometer data quality monitoring and anomaly assessment using COSMIC GNSS radio-occultation soundings. Remote Sens. 2020, 12, 828. [Google Scholar] [CrossRef] [Green Version]
- Jagadheesha, D.; Simon, B.; Pal, P.; Joshi, P.C.; Maheshwari, A. A new technique for estimation of lower-tropospheric temperature and water vapor profiles from radio occultation refractivity. J. Atmos. Ocean. Tech. 2009, 26, 1075–1089. [Google Scholar] [CrossRef]
- Xia, P.; Ye, S.; Chen, B.; Chen, D.; Xu, K. Improving the weighted mean temperature model: A case study using nine year (2007–2015) radiosonde and COSMIC data in Hong Kong. Meteorol Appl. 2020, 27, e1864. [Google Scholar] [CrossRef] [Green Version]
- Anthes, R.; Sjoberg, J.; Rieckh, T.; Wee, T.-K.; Zeng, Z. COSMIC-2 radio occultation temperature, specific humidity, and precipitable water in Hurricane Dorian (2019). Terr. Atmos. Ocean. Sci. 2021, 32, 925–938. [Google Scholar] [CrossRef]
- Vorob’ev, V.V.; Krasil’nikova, T.G. Estimation of the Doppler shift measurements at frequencies used in the NAVSTAR system. Izv. Acad. Sci. Atmos. Oceanic. Phys. 1994, 29, 602–609. [Google Scholar]
- Jensen, A.S.; Lohmann, M.S.; Benzon, H.-H.; Nielsen, A.S. Full spectrum inversion of radio occultation signals. Radio Sci. 2003, 38, 1040. [Google Scholar] [CrossRef]
- Phinney, R.A.; Anderson, D.L. On the radio occultation method for studying planetary atmospheres. J. Geophys. Res. 1968, 73, 1819–1827. [Google Scholar] [CrossRef] [Green Version]
- Fjeldbo, G.; Kliore, G.A.; Eshleman, V.R. The neutral atmosphere of Venus as studied with the Mariner V radio occultation experiments. Astron. J. 1971, 76, 123–140. [Google Scholar] [CrossRef]
- Smith, E.K.; Weintraub, S. The constants in the equation of atmospheric refractive index at radio frequencies. Proc. IRE 1953, 41, 1035–1037. [Google Scholar] [CrossRef] [Green Version]
- Lorenc, A.C. Analysis methods for numerical weather prediction. Quart. J. Roy. Meteor. Soc. 1986, 112, 1177–1194. [Google Scholar] [CrossRef]
- Courtier, P.; Thépaut, J.-N.; Hollingsworth, A. A strategy for operational implementation of 4D-Var, using an incremental approach. Quart. J. Roy. Meteor. Soc. 1994, 120, 1367–1387. [Google Scholar] [CrossRef]
- Derber, J.C.; Bouttier, F. A reformulation of the background error covariance in the ECMWF global data assimilation system. Tellus 1999, 51A, 195–221. [Google Scholar] [CrossRef]
- Bannister, R.N. A review of forecast error covariance statistics in atmospheric variational data assimilation. II: Modelling the forecast error covariance statistics. Quart. J. Roy. Meteor. Soc. 2008, 134, 1971–1996. [Google Scholar] [CrossRef]
- Trémolet, Y. Incremental 4D-Var convergence study. Tellus 2007, 59A, 706–718. [Google Scholar] [CrossRef] [Green Version]
- Zhu, C.; Byrd, R.H.; Nocedal, J. L-BFGS-B: Algorithm 778: L-BFGS-B, FORTRAN routines for large scale bound constrained optimization. ACM T. Math. Softw. 1997, 23, 550–560. [Google Scholar] [CrossRef]
- Higham, N.J. Accuracy and Stability of Numerical Algorithms, 2nd ed.; SIAM: Philadelphia, PA, USA, 2002; ISBN 978-0-89871-521-7. [Google Scholar] [CrossRef] [Green Version]
- Barker, D.M.; Huang, W.; Guo, Y.-R.; Xiao, Q.N. A Three-Dimensional (3DVAR) data assimilation system for use with MM5: Implementation and initial results. Mon. Wea. Rev. 2004, 132, 897–914. [Google Scholar] [CrossRef]
- Fisher, M. Background Error Covariance Modeling. In Proceedings of the ECMWF Seminar on Recent Developments in Data Assimilation for Atmosphere and Ocean, Reading, UK, 8–12 September 2003; pp. 45–64. [Google Scholar]
- Kuo, Y.-H.; Wee, T.-K.; Sokolovskiy, S.; Rocken, C.; Schreiner, W.; Hunt, D.; Anthes, R.A. Inversion and error estimation of GPS radio occultation data. J. Meteor. Soc. Jpn. 2004, 82, 507–531. [Google Scholar] [CrossRef] [Green Version]
- Schreiner, W.; Sokolovskiy, S.; Hunt, D.; Rocken, C.; Kuo, Y.-H. Analysis of GPS radio occultation data from the FORMOSAT-3/COSMIC and Metop/GRAS missions at CDAAC. Atmos. Meas. Tech. 2011, 4, 2255–2272. [Google Scholar] [CrossRef] [Green Version]
- Hedin, A.E. Extension of the MSIS thermosphere model into the middle and lower atmosphere. J. Geophys. Res. 1991, 96, 1159–1172. [Google Scholar] [CrossRef]
- Wee, T.-K.; Kuo, Y.-H. A noise-aware combination of dual-frequency measurements from GPS radio occultation. J. Geophys. Res. 2013, 118, 12852–12868. [Google Scholar] [CrossRef]
- Karayel, E.T.; Hinson, D.P. Sub-Fresnel-scale vertical resolution in atmospheric profiles from radio occultation. Radio Sci. 1997, 32, 411–423. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Benzon, H.-H.; Jensen, A.S.; Lohmann, M.S.; Nielsen, A.S. Comparative analysis of radio occultation processing approaches based on Fourier integral operators. Radio Sci. 2004, 39, RS6004. [Google Scholar] [CrossRef] [Green Version]
- Hollingsworth, A.; Lönnberg, P. The statistical structure of short-range forecast errors as determined from radiosonde data. Part I: The wind field. Tellus 1986, 38A, 111–136. [Google Scholar] [CrossRef]
- Bouttier, F. Application of Kalman filtering to numerical weather prediction. In Proceedings of the ECMWF Seminar on Data Assimilation, Reading, UK, 2–6 September 1996; pp. 61–90. [Google Scholar]
- Ingleby, N.B. The statistical structure of forecast errors and its representation in the Met Office global three-dimensional variational data assimilation system. Quart. J. Roy. Meteor. Soc. 2001, 127, 209–231. [Google Scholar] [CrossRef]
- Kaiser, H.F. The JK method: A procedure for finding the eigenvectors and eigenvalues of a real symmetric matrix. Comput. J. 1972, 15, 271–273. [Google Scholar] [CrossRef] [Green Version]
- Hyland, R.W.; Wexler, A. Formulations for the thermodynamic properties of the saturated phases of H2O from 173.15 K to 473.15 K. ASHRAE Trans. 1983, 89, 500–519. [Google Scholar]
- Immler, F.J.; Dykema, J.; Gardiner, T.; Whiteman, D.N.; Thorne, P.W.; Vömel, H. Reference Quality Upper-Air Measurements: Guidance for developing GRUAN data products. Atmos. Meas. Tech. 2010, 3, 1217–1231. [Google Scholar] [CrossRef]
- Rieckh, T.; Sjoberg, J.; Anthes, R. 2021: The three-cornered hat method for estimating error variances of three or more atmospheric datasets. Part II: Evaluating recent radio occultation and radiosonde observations, global model forecasts, and reanalyses. J. Atmos. Ocean. Technol. 2021, 35, 1777–1796. [Google Scholar] [CrossRef]
- Berrisford, P.; Kållberg, P.; Kobayashi, S.; Dee, D.; Uppala, S.; Simmons, A.J.; Poli, P.; Sato, H. Atmospheric conservation properties in ERA-Interim. Quart. J. Roy. Meteor. Soc. 2011, 137, 1381–1399. [Google Scholar] [CrossRef]
- Anthes, R.A.; Schreiner, W.S. Six new satellites watch the atmosphere over Earth’s Equator. Eos 2019, 100. [Google Scholar] [CrossRef]
- Schreiner, W.S.; Weiss, J.P.; Anthes, R.A.; Braun, J.; Chu, V.; Fong, J.; Hunt, D.; Kuo, Y.-H.; Meehan, T.; Serafino, W.; et al. COSMIC-2 radio occultation-first results. Geophys. Res. Lett 2020, 47, e2019GL086841. [Google Scholar] [CrossRef]
- Han, J.; Pan, H. Revision of convection and vertical diffusion schemes in the NCEP Global Forecast System. Wea. Forecast. 2011, 26, 520–533. [Google Scholar] [CrossRef]
- Campana, K.; Caplan, P.; Halperin, D.J.; Lapenta, B.; Lilly, S.; Lin, Y.; Penny, A.B.; Saha, S.; Tallapragada, V.; White, G.H.; et al. The Development and Success of NCEP’s Global Forecast System. In Proceedings of the 99th AMS Meeting, Phoenix, AZ, USA, 6–10 January 2019. [Google Scholar]
- Xie, Q.; Huang, K.; Wang, D.; Yang, L.; Chen, J.; Wu, Z.; Li, D.; Liang, Z. An intercomparison of GPS radiosonde soundings during the eastern tropical Indian Ocean experiment. Acta Oceanol. Sin. 2014, 33, 127–134. [Google Scholar] [CrossRef]
- Wee, T.-K.; Kuo, Y.-H. Advanced stratospheric data processing of radio occultation with a variational combination for multifrequency GNSS signals. J. Geophys. Res. 2014, 119, 11011–11039. [Google Scholar] [CrossRef]
- Wee, T.-K.; Kuo, Y.-H.; Lee, D.-K. Development of a curved ray tracing method for modeling of phase paths from GPS radio occultation: A two-dimensional study. J. Geophys. Res. 2010, 115, D24119. [Google Scholar] [CrossRef] [Green Version]
- Wee, T.-K.; Kuo, Y.-H. A perspective on the fundamental quality of GPS radio occultation data. Atmos. Meas. Tech. 2015, 8, 4281–4294. [Google Scholar] [CrossRef]















Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wee, T.-K.; Anthes, R.A.; Hunt, D.C.; Schreiner, W.S.; Kuo, Y.-H. Atmospheric GNSS RO 1D-Var in Use at UCAR: Description and Validation. Remote Sens. 2022, 14, 5614. https://doi.org/10.3390/rs14215614
Wee T-K, Anthes RA, Hunt DC, Schreiner WS, Kuo Y-H. Atmospheric GNSS RO 1D-Var in Use at UCAR: Description and Validation. Remote Sensing. 2022; 14(21):5614. https://doi.org/10.3390/rs14215614
Chicago/Turabian StyleWee, Tae-Kwon, Richard A. Anthes, Douglas C. Hunt, William S. Schreiner, and Ying-Hwa Kuo. 2022. "Atmospheric GNSS RO 1D-Var in Use at UCAR: Description and Validation" Remote Sensing 14, no. 21: 5614. https://doi.org/10.3390/rs14215614
APA StyleWee, T.-K., Anthes, R. A., Hunt, D. C., Schreiner, W. S., & Kuo, Y.-H. (2022). Atmospheric GNSS RO 1D-Var in Use at UCAR: Description and Validation. Remote Sensing, 14(21), 5614. https://doi.org/10.3390/rs14215614