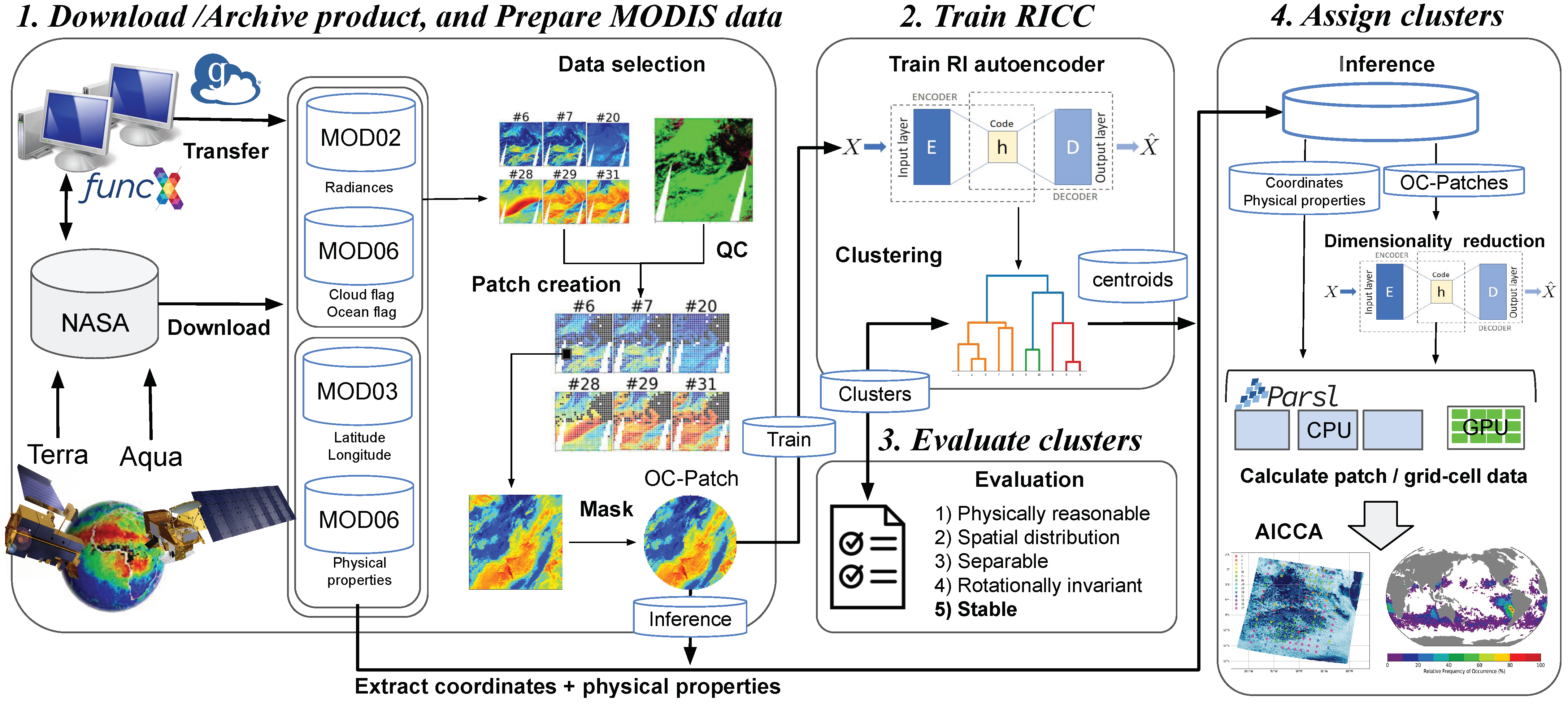
The AICCA production workflow, shown in
Figure 1, consists of four principal stages: (1) download, archive, and prepare MODIS satellite data; (2) train the RICC unsupervised learning algorithm, and cluster cloud patterns and textures; (3) evaluate the reasonableness of the resulting clusters and determine an optimal cluster number; and (4) assign clusters produced by RICC to other MODIS data unseen during RICC training. We describe each stage in turn. The RICC code and Jupyter notebook [
24] used in the analysis are available online [
25], and the trained RI autoencoder used for this study is archived at the Data and Learning Hub for science (DLHub) [
26], a scalable and low-latency model repository to share and publish machine learning models to facilitate reuse and reproduction.
3.1. Stage 1: Download, Archive, and Prepare MODIS Data
Download and archive. As noted in
Section 2.1, we use subsets of three MODIS products in this work, a total of 801 terabytes for 2000–2021. In order to employ high-performance computing resources at Argonne National Laboratory for AI model training and inference, we copied all files to Argonne storage. Transferring the files from NASA archives is rapid for the subset that are accessible on a Globus endpoint at the NASA Center for Climate Simulation, which can be transferred via the automated Globus transfer system [
27]. The remaining files were transferred from NASA LAADS via the more labor-intensive option of wget commands, which we accelerated by using the funcX [
28] distributed function-as-a-service platform to trigger concurrent downloads on multiple machines.
Prepare. The next step involves preparing the
patches used for ML model training and inference. We extract from each swath multiple 128 pixel by 128 pixel (roughly 100 km × 100 km) non-overlapping patches, for a total of ∼331 million patches. We then eliminate those patches that include any non-ocean pixels as indicated by the MOD06 land/water indicator, since, in these cases, radiances depend in part on underlying topography and reflectance. (Note that even ocean-only pixels may involve surface-related artifacts in cases when the ocean is covered in sea ice). We also eliminate those with less than 30% cloud pixels, as indicated by the MOD06 cloud mask. The result is a set of 198,676,800
ocean-cloud patches, which we refer to in the following as
OC-Patches. For each ocean-cloud patch, we take from the MOD02 product six bands (out of 36 total) for use in training and testing the rotation-invariant (RI) autoencoder. We also extract the MOD04 and MOD06 data used for location and cluster evaluation, as described in
Section 2. For an in-depth discussion of data selection, see Kurihana et al. [
18].
We also construct a training set OC-PatchesAE by selecting one million patches at random from the entirety of OC-Patches. Because we do not expect our unsupervised RI autoencoder to be robust to the MODIS data used for training, we collect the 1M patches that they are not overly imbalanced among seasons or locations.
3.2. Stage 2: Train the RICC Autoencoder and Cluster Cloud Patterns
In this stage, we first train the RI autoencoder and then define cloud categories by clustering the compact latent representations produced by the trained autoencoder.
Train RICC. The goal of training is to produce an RI autoencoder capable of generating latent representations (a lower-dimensional embedding as the intermediate layer of the autoencoder) that explicitly capture the variety of input textures among ocean clouds and also map to differences in physical properties. We introduce general principles briefly here; see Kurihana et al. [
18] for further details of the RI autoencoder architecture and training protocol.
An autoencoder [
17,
29] is a widely used unsupervised learning method that leverages dimensionality reduction as a preprocessing tool prior to image processing tasks such as clustering, regression, anomaly detection, and inpainting. An autoencoder comprises an encoder, used to map input images into a compact lower-dimensional latent representation, followed by a decoder, used to map that representation to output images. During training, a loss function minimizes the difference between input and output. The resulting latent representation in the trained autoencoder both (1) retains only relevant features for the target application in input images, and (2) maps images that are similar (from the perspective of the target application) to nearby locations in latent space.
The loss function minimizes the difference between an original and a restored image based on a distance metric during autoencoder training. The most commonly used metric is a simple
distance between the autoencoder’s input and output:
where
S is a set of training inputs;
is the encoder and decoder parameters, for which values are to be set via training; and
x and
are an input in
S and its output (i.e., the restored version of
x), respectively. However, optimizing with Equation (
1) is inadequate for our purposes because it tends to generate different representations for an image
x and the rotated image
, as shown in
Figure 2, with the result that the two images end up in different clusters. Since any particular physically driven cloud pattern can occur in different orientations, we want an autoencoder that assigns cloud types to images consistently, regardless of orientation. Other ML techniques that combine dimensionality reduction with clustering algorithms have not addressed the issue of rotation–invariance within their training process. For example, while non-negative matrix factorization (NMF) [
30] can approximate input data into a low-dimensional matrix—i.e., produce a dimensionally reduced representation similar to an autoencoder—that can be used for clustering, applications of NMF are not invariant to image orientation.
We have addressed this problem in prior work by defining a rotation-invariant loss function [
18] that generates similar latent representations, agnostic to orientation, for similar morphological clouds (
Figure 2b). This RI autoencoder, motivated by the shifted transform invariant autoencoder of Matsuo et al. [
31], uses a loss function
L that combines both a rotation-invariant loss,
, to learn the rotation invariance needed to map different orientations of identical input images into a uniform orientation, and a restoration loss,
, to learn the spatial structure needed to restore structural patterns in inputs with high fidelity. The two loss terms are combined as follows, with values for the scalar weights
and
chosen as described below:
The rotation-invariant loss function
computes, for each image in a minibatch, the difference between the restored original and the 72 images obtained by applying a set
of 72 scalar rotation operators, each of which rotates an input by a different number of degrees in the set {0, 5, ..., 355}:
Thus, minimizing Equation (
3) yields values for
that produce similar latent representations for an image, regardless of its orientation.
The restoration loss,
, learns the spatial substructure in images by computing the sum of minimum differences over the minibatch:
Thus, minimizing Equation (
4) results in values for
that preserve spatial structure in inputs.
Our RI autoencoder training protocol [
18], which sweeps over
values, identifies
as the coefficients for the two loss terms that best balance the transform-invariant and restoration loss terms. We note that the specific values of the two coefficients, not just their relative values, matter. For example, the values
give better results than
.
The neural network architecture is the other factor needed to achieve rotation invariance: Following the heuristic approach of deep convolutional neural networks, we designed an encoder and decoder that stack five blocks of convolutions, each with three convolutional layers activated by leaky ReLU [
32], and with batch normalization [
33] applied at the final convolutional layer in each block before activation. We train our RI autoencoder on our one million training patches for 100 epochs by using stochastic gradient descent with a learning rate of 10
on 32 NVIDIA V100 GPUs in the Argonne National Laboratory ThetaGPU cluster.
Cluster Cloud Patterns. Once we have applied the trained autoencoder to a set of patches to obtain latent representations, we can then cluster those latent representations to identify the centroids that will define our cloud clusters. We use hierarchical agglomerative clustering (HAC) [
16] for this purpose, and select Ward’s method [
34] for the linkage metric, so that HAC minimizes the variance of square distances as it merges clusters from bottom to top. We have shown in previous work [
35] that HAC clustering results outperform those obtained with other common clustering algorithms.
Given
N data points, a naive HAC approach requires
memory to store the distance matrix used when calculating the linkage metric to construct the tree structure [
36]—which would be impractical for the one million patches in
OC-PatchesAE. Thus, we use a smaller set of patches,
OC-PatchesHAC, comprising 74911 ocean-cloud patches from the year 2003 (the first year in which both Terra and Aqua satellites ran for the entire year concurrently) for the clustering phase. We apply our trained encoder to compute latent representations for each patch in
OC-PatchesHAC and then run HAC to group those latent representations into
clusters, in the process identifying
cluster centroids and assigning each patch in
OC-PatchesHAC a cluster label, 1..
. The sequential scikit-learn [
37] implementation of HAC that we use in this work takes around 10 hours to cluster the 74911
OC-PatchesHAC patches on a single core. While we could use a parallelizable HAC algorithm [
38,
39,
40] to increase the quantity of data clustered, this would not address the intrinsic limitation of our clustering process given the 801 terabytes of MODIS data.
3.3. Stage 3: Evaluate Clusters Generated by RICC
A challenge when employing unsupervised learning is to determine how to evaluate results. While a supervised classification problem involves a perfect ground truth against which to output can be compared, an unsupervised learning system produces outputs whose utility must be more creatively evaluated. Therefore, we defined in previous work a series of evaluation protocols to determine whether the cloud classes derived from a set of cloud images are meaningful and useful [
18]. We seek cloud clusters that: (1) are
physically reasonable (i.e., embody scientifically relevant distinctions); (2) capture information on
spatial distributions, such as textures, rather than only mean properties; (3) are
separable (i.e., are cohesive, and separated from other clusters, in latent space); (4) are
rotationally invariant (i.e., insensitive to image orientation); and (5) are
stable (i.e., produce similar or identical clusters when different subsets of the data are used). We summarize in
Table 4 these criteria and the quantitative and qualitative tests that we have developed to validate them.
In our previous work [
18], we showed that an analysis using RICC to separate cloud images into 12 clusters satisfies the first four of these criteria. In this work, we describe how we evaluate the last criterion,
stability. Specifically, we evaluate the extent to which RICC clusters cloud textures and physical properties in a way that is stable against variations in the specific cloud patches considered, and that groups homogeneous textures within each cluster. We describe this process in
Section 4 in the context of how we estimate the
optimal number of clusters for this dataset when maximizing stability and similarity in clustering. For the remaining criteria, the clusters necessarily remain rotationally invariant, and we present in
Section 5 results further validating that the algorithm, when applied to a global dataset, produces clusters that show physically reasonable distinctions, are spatially coherent, and involve distinct textures (i.e., learn spatial information).