1. Introduction
Point clouds contain rich three-dimensional (3D) spatial information and have broad application prospects in areas such as autonomous driving, virtual reality, and power grid inspection [
1,
2]. However, the automatic extraction of interesting information from point clouds, especially in large-scale scenes, remains a huge challenge [
3]. This is because objects in a large scene usually exit a lot of occlusions. Moreover, objects of different classes but with a similar local geometry structure will cause interference for segmentation. Therefore, it is necessary to describe the objects in the large-scale scene from different scales to achieve the effect of efficient extraction [
4].
Deep learning methods based on convolutional neural networks (CNNs) have achieved great success in the field of two-dimensional (2D) image processing. However, directly migrating these image processing networks to 3D point cloud processing tasks is usually infeasible because point clouds are disordered and structurally irregular. Moreover, point clouds contain a large amount of object geometry information, which does not exist in 2D images. In addition, the point cloud collected in the real scene has a large coverage and uneven density of point, but the resolution of the image is fixed. Therefore, how to utilize the geometric features and multi-granularity features of point clouds are two challenges in the field of point cloud interpretation [
5].
The disorder of the point cloud is the problem to be considered primarily in point cloud processing networks based on deep learning. The disordered point clouds can be transformed into a regular form by some strategies, e.g., voxelization [
6] and multi-view projection [
7,
8]. Another idea is to design a symmetric function (such as max-pooling) to counteract the disorder of point clouds. The representative work is PointNet [
9] and its successor, PointNet++ [
10]. PointNet learns the point-wise features using a shared multi-layer perception (MLP) but fails to capture local geometry patterns among neighboring points. PointNet++ tries to learn local contexts by aggregating per-point features in a neighborhood. However, it still deals with each point separately within each neighborhood, and the geometric relations between points are not fully utilized.
In order to obtain more geometric structure information from local neighborhoods, some researchers have proposed some neighborhood-based feature extraction methods. For instance, A-CNN [
11] and KPConv [
12] define convolution kernels within the neighborhood to extract features such as the spatial location of each neighborhood point, and then aggregate the features to the center point. GAPNet [
13] proposes the GAPLayer (namely a multi-head graph attention-based point network layer) which convolves edges to extract the geometric features of a graph. Then, it generates local attention weights and self-attention weights according to local features and assigns attention weights to each edge. The GAPNet has made great contributions to graph attention, but it mainly focuses on point-to-point relationships within neighborhoods and performs poorly on large-scale datasets. We boil it down to three reasons.
Firstly, as shown in
Figure 1, some point clouds may have similar geometries, but they may belong to different categories, as shown by the rectangles ② and ③. As mentioned above, the GAPLayer can only identify the geometric features of a local region but cannot effectively correlate them with the wider contextual information of the region. Therefore, the situation shown in
Figure 1 may be a hindrance when interpreting point clouds.
Secondly, the GAPLayer processes each local region independently, regardless of the correlation between regions, as shown in
Figure 2.
Finally, global features play an important role in classification and part segmentation. Although the GAPLayer does mention global feature extraction, it does not blend well with features at other scales.
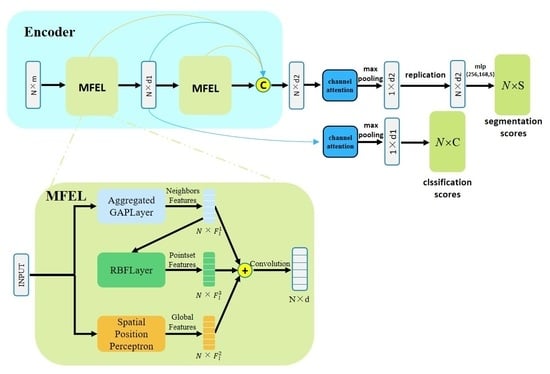
In order to address the above problems and avoid the loss of information caused by down-sampling, we propose the MFEL for the multi-scale feature extraction of point clouds. Further, two end-to-end networks (namely, MFNet and MFNet-S) are proposed for point cloud classification, including object semantic segmentation and part segmentation. The experimental results show that our method achieves significant improvement. Given that our approach builds on previous work, we explicitly point to the contributions of this study:
We propose a new module MEFL that extends the GAPLayer to extract features at three different scales, namely, single point scale, point neighborhood scale, and pointset scale, enabling the network to extract multi-granularity features of point clouds.
We introduce an end-to-end framework named the multi-level feature fusion neural network (MFNet) for the tasks of classification and part segmentation, which effectively fuse features of different scales and levels.
Furthermore, we design a network MFNet-S for semantic segmentation tasks and conduct comparative experiments on large indoor and outdoor datasets.
The remainder of this paper is organized as follows.
Section 2 reviews the related work.
Section 3 gives the details of the proposed methodology.
Section 4 introduces the setting of the experiments, the datasets (including ModelNet40 [
14], ShapeNet [
15], S3DIS [
16], and Sementic3D [
17]), and discusses the experiment results.
Section 5 summarizes our research.
2. Related Work
In this section, we briefly summarize related work on point cloud processing, including deep learning-based frameworks, attention mechanisms, and feature representation methods.
2.1. Deep Learning-Based Methods for Point Cloud Processing
Deep learning-based point cloud processing methods can be classified into two categories according to the input form, namely, regularized input and input that is direct from the original point clouds.
2.1.1. Regularized Representation
Regular data (such as images) can easily extract context features by using a shared convolution kernel. Thus, one approach to process a point cloud by CNN is to transform the point cloud to the regularized form. Voxelization and multi-view projection are two common regularization methods.
Voxelization is to represent the point clouds with regular 3D voxel grids, and each grid represents a spatial unit. For example, VoxNet [
6] uses a supervised 3D CNN-based occupancy grid to extract voxel features. The computational cost of voxel-based models increases dramatically with increasing resolution. To reduce the computational and memory overhead, Wang et al. [
18] used an unbalanced octree to divide the space hierarchically, so that computational resources are concentrated on content-dense regions.
Another method is to project the point cloud onto the planes of multiple views and express 3D point cloud information using 2D images of the multiple planes. The challenge of this approach is how to efficiently aggregate features from multiple views. For example, GVCNN introduces a grouping strategy to consider the content relationship and discrimination between views, and then the group level features are aggregated into the shape descriptor according to their discriminative weights [
7]. Ma et al. used long short-term memory and a sequence voting layer to aggregate view-wise features into a shape descriptor [
8]. The multi-view method only preserves 2D information within a limited number of perspectives and has relatively high computational efficiency [
19]. It is often used for classification or retrieval tasks. However, due to the loss of geometric information in the projection process, the performance of semantic segmentation in large-scale scenes needs to be improved further. To reduce the quantization loss after projecting, ASCNet [
20] employs a module named PSCFE (pillar-wise spatial context features encoding) before projecting, which can capture the context features as vertical-wise within the pillars and the neighborhood geometric information between pillars.
2.1.2. Direct Representation of Original Point Clouds
Point cloud data are unordered and unstructured. Thus, it is not feasible to directly apply CNNs to point clouds. In order to reduce the loss of information and directly process point clouds, some researchers have proposed a series of point-based frameworks, and these works can be roughly divided into point-wise MLP methods and graph-based methods.
(1) Point-wise MLP methods. PointNet [
9] is a pioneering work of applying deep learning directly on point clouds. Specifically, it applies the MLP on each point, and then uses the max-pooling to aggregate features of all points to achieve permutation invariance. PointNet is computationally efficient, but its learning process aims to encode each point individually, regardless of the contextual relationship between points. PointNet++ [
10] is an extension work of the PointNet. It hierarchically samples and groups the input and applies the PointNet pipeline on each group. Then, the features of the local region are aggregated into the centroid as local features. PointNet++ still encodes each local point independently, which makes it hard to utilize the local geometric information. To capture the local patterns better, KPconv [
12] proposes the kernel point convolution. It uses the kernel function to calculate the weight matrix of the points that fall within the range of a sphere, and the matrix is used to transform the features of this point. Aggregating the neighborhood features of points onto a point inspired us to construct local neighborhood graphs and gather the graph features to the central point. To further capture additional local geometric information, PointVGG [
21] defines operations of convolution and pooling, i.e., Pconv and Ppool, respectively. The Pconv could pay attention to the relations between neighbors, and the Ppool makes the network abstract the underlying shape information. LGS-Net [
22] proposes a local geometric structure representation block to model fine-grained geometric structures by fully utilizing relative and global geometric relationships in the neighborhood.
(2) Graph-based methods. This kind of approach attempts to process non-Euclidean structured data (e.g., 3D point clouds or social networks) through deep neural networks [
23,
24]. Relevant works on graph convolution can be divided into spectral-based and non-spectral (or spatial)-based methods [
25].
Spectral-based graph neural networks perform Fourier transformation and eigen decomposition in the Laplace matrix of the graph. The spectral convolution can be defined as the element-wise product of Fourier variations of two signals on the graph [
26]. For example, Yi et al. [
27] parametrized the convolution kernel in the spectral domain and constructed a spectral conversion network to share the network parameters. The disadvantage of spectral-based graph CNN methods is that the entire point cloud needs to be loaded into memory for graph convolution. Since the Laplacian matrix eigen decomposition is time-consuming, the spectral-based CNNs consume a lot of computational resources. To solve this problem, Defferrard et al. [
28] reduced the computational complexity through the Chebyshev polynomials and their approximate calculation scheme. Furthermore, Wang et al. [
29] designed graph convolution on local pointsets and applied recursive clustering and pooling operations to gather spectral information from neighboring nodes to reduce computation. Spectral-based methods can effectively capture the local geometric features. This also means that the feature construction method based on a graph may directly affect the feature extraction.
Spatial-based graph neural networks usually define a neighborhood to perform graph convolution operations on the spatial relationships of nodes within the neighborhood. For instance, Duvenaud et al. [
30] computed local features by summing the weight matrix of adjacent vertices and multiplying by its neighboring nodes, thus sharing the same weights between all edges. DGCNN [
31] applies convolution to each edge where the local neighborhood is connected to the query points and dynamically updates the graph. Wang et al. [
26] introduced a graph attention convolution (GAC) that assigns different attention weights to different neighboring points according to local information. Thus, the kernel of GAC can adjust dynamically to accommodate different objects with different structures.
2.2. Attention Mechanism
In recent years, an attention mechanism has been used to spotlight the important parts of features [
32]. In order to adaptively adjust the weights between channels, SENet [
33] builds feature maps with the help of the inter-channel correlations. The GATs [
34] can assign different weights to different neighboring nodes in graph convolution operations. RandLA-Net [
3] takes a similar strategy to SENet in each neighborhood. That is, neighbor features are fed into a shared MLP followed by
softmax to generate attention scores. Then, the neighbor features are weighted summed according to the score to update the center point features. The difference is that RandLA-Net produces edge weights without dimension compression. SCF-Net [
35] has improved RandLA-Net in the attention mechanism. Specifically, SCF-Net introduces the distance of geometric space and feature space in addition to the neighbor feature itself to generate the attention coefficient. This allows the attention coefficient to contain more information.
A point transformer [
36] introduces the self-attention transformer based on the encoding decoding structure in the NLP (natural language processing) field into the point cloud processing field, and it has achieved remarkable results. However, Zhang et al. [
37] proposed that the calculation cost of existing point transformers is very high because they need to generate a large attention map. Therefore, they proposed Patch attention (PAT) to adaptively learn a much smaller set of bases and calculate attention mapping on this basis.
Inspired by these methods, our model learns the attention weight of each edge in the graph structure through the neighborhood features, to extract local features, so that the model can focus on the edge features in the neighborhood and better facilitate semantic understanding. In addition, SENet is used to filtrate the fused multi-level features to highlight important parts and suppress redundant features.
2.3. Feature Representation Methods
Many feature descriptors are designed based on human experience in point cloud processing. For example, Salti et al. [
38] proposed signatures of histograms of orientations (SHOT), which use local histograms to extract descriptors on the surface of an object. This descriptor is similar to the classic spin image [
39], point feature histograms (PFH) descriptor, and fast point feature histograms (FPFH) descriptor [
40], etc. However, these feature descriptors rely on the stable surface information acquisition of objects, which limits their broad applications. Arandjelov et al. [
41] proposed NetVLAD, which converts non-differentiable functions in VLAD vectors [
42] into differentiable functions in a clever way. It successfully applies BoF-based (bag of feature) [
43] feature descriptors to deep learning networks. Further, PointNetVLAD [
44] combines PointNet with NetVLAD to build an end-to-end model of point cloud retrieval.
In order to make our feature extraction module more robust, similar to the feature descriptor construction process of VLAD, this research uses the radial basis function (RBF) to learn cluster centers to extract pointset level features.
4. Results and Discussion
To verify the effectiveness of the proposed algorithm, we perform a qualitative and quantitative analysis of the proposed algorithm on four indoor and outdoor point cloud datasets. We first conduct ablation study experiments on the ModelNet40 to verify the effectiveness of each part of the MFEL. Then, we implement the MFNet to conduct the part segmentation experiments on the ShapeNet. Finally, the MFNet-S is used to perform semantic segmentation experiments on different point cloud datasets. The comparisons and analysis for the experiments are also provided.
4.1. Datasets
ModelNet40: The ModelNet40 is a synthetic dataset. Compared with the real datasets collected by laser scanning, each object in the ModelNet40 has a complete shape and does not contain noise. The ModelNet40 has 40 common man-made categories, such as cups, hats, and chairs, and contains 12,311 objects in total. We use about 80% (9843) for training and the remaining 20% (2468) for testing.
ShapeNet: The ShapeNet is also a synthetic dataset. The ShapeNet contains 16 categories and 16,881 samples. Each sample contains 2–5 parts, such as an aircraft contains 4 parts, namely, fuselage, wings, engines, and tail. All objects have a total of 50 different parts. As usual, we use 80% of the samples as training data and the remaining 20% as test data.
S3DIS: The S3DIS is a large-scale indoor point cloud dataset developed by Stanford University. The S3DIS is reconstructed from six large indoor areas (Area 1–Area 6) scanned by Matterport camera. The S3DIS is further divided into 271 rooms. Each point in the dataset is semantically labeled by one of the 13 common indoor objects, such as chair, table, and floor. Each point is represented by a 9-dimensional vector, i.e., X, Y, Z, R, G, B, and the normalized X, Y, and Z. Note that the normalized coordinates X, Y, and Z are between 0 and 1.
Semantic3D-8: The Semantic3D is a large-scale outdoor scene dataset scanned by terrestrial laser scanning. The Semantic3D contains different natural and artificial scenarios such as rural areas, sport fields, and urban squares. Each scene contains tens of millions of points, with a total of more than one billion points for the whole dataset. The Semantic3D-8 has 8 categories, such as plant, building, vehicle, etc. Each point contains 3D coordinates, R/G/B color information, and intensity. Compared with the above dataset and indoor dataset, its density distribution is more uneven. The Reduce-8 training set is the same as the Semantic3D-8, but the test set is a uniformly down-sampled sub-dataset with an interval of 0.01 m.
4.2. Evaluation Metrics
On the ModelNet40, we employ overall accuracy (
OA) and mean class accuracy (
mAcc) as our classification task evaluation indicators. If we suppose
l is the number of categories (the number of labels in the semantic segmentation task),
OA is calculated as follows:
where
represents the point predicted to be of class
j but actually of class
i. The
OA reflects the overall classification ability of the network, as it represents the proportion of the number of correctly classified samples to the total number of samples. However, sample balance may affect the
OA value and reduce the generalization of the network.
mAcc calculates the
OA value of the prediction results for each class of objects, and then averages the
OA values of all classes:
For the ShapeNet, S3DIS, and Semantic3D, the evaluation metrics are the same as most of the references to facilitate the comparison of experimental results. Here,
mIoU (mean
IoU) and
mAcc are used on the ShapeNet.
OA and
mIoU are used on the S3DIS and Semantic3D. The
is calculated as follows:
The
mIoU evaluates the semantic segmentation results for all classes, which are calculated by Equation (14):
4.3. Ablation Studies and Parameter Sensitivities Analysis
In this section, we conduct ablation experiments on the MFNet by comparing it with the GAPNet. We also conduct sensitivity experiments on several key hyperparameters. These experiments are conducted on RTX 2080Ti with Tensorflow v1.12.
4.3.1. Ablation Studies
The training parameter settings are the same as the GAPNet: 1024 points as the input, learning rate = 0.001, and training epoch = 250. Data augmentation operations include random rotation and jitter. For optimization, we use Adam to train the model for 250 epochs with batch size = 32. The initial learning rate is set to 0.001. We will sequentially add our proposed modules into the GAPNet. The experimental steps are as follows.
Step 1: The feature extraction module GAPLayer in the GAPNet is replaced by our improved aggregated GAPLayer. The MLP channel numbers in SPP are 8, 16, and 16, respectively. Step 2: The RBFLayer is added to the network after step 1. Here, we choose the number of RBF neurons t = 40. Step 3: The spatial position perceptrons with convolution channels of {32, 64, 64} are added to the network after step 2. Step 4: We embed the SENet channel-attention mechanism into the network. The attention coefficients for all feature channels can be assigned according to the feature map, to highlight significant features and suppress redundant features.
The experimental results of the ablation studies are shown in
Table 1. With the addition of modules, the
OA and
mAcc show an upward trend, indicating that each module has played an active role. When all modules are loaded, the proposed MFNet is formed.
OA and
mAcc reach 93.1% and 91.4%, respectively, which are 0.7% and 1.7% higher than the original GAPNet, respectively. Further comparison can find that the improvement of
mAcc in step 1 is the largest, which is increased by 0.8%, and the improvement of
OA in step 4 is the largest, which is increased by 0.4%. This proves that for small-scale point cloud classification tasks, adding rich geometric features and global features can help the network to distinguish object categories more accurately.
4.3.2. Parameter Sensitivities Analysis
We conduct parameter sensitivity experiments in the classification and segmentation networks of the MFNet, respectively. The training strategy of parameter sensitivity analysis in the classification network is the same as the ablation experiments. In this experiment, we discuss the influence of neighboring point number k and RBF neuron number
t on the classification results. According to
Table 2, when
k = 20 and
t = 40, the MFNet performs best on the ModelNet40. In addition, there is no obvious correlation between the neighboring point number or RBF neurons’ number with classification accuracy because the size of the neighborhood may affect the model’s perception of fine-grained geometric features. According to the experiments, the number of RBF neurons should be approximately equal to the number of categories in the dataset, which will make the RBF neurons describe the characteristics of the pointset best.
For the part segmentation task, each object is sampled with the 2048 point as the input. The initial learning rate is set to 0.005 with the Adam optimizer. The model is trained in 200 epochs with the batch size of 16. Since the part segmentation task is more sensitive to parameters, we further discuss the influence of the head number (
h) and the number of output channels (
C) of each aggregated GAPlayer on the results here. The RBF neurons (
t) are set to 40. The results are shown in
Table 3. By comparing configurations (3), (4), and (6), the three sets of experiments, it can be found that when
k = 30, increasing the number of output channels can improve performance to a certain extent. Increasing the number of channels can compensate to a certain extent for the decrease in accuracy due to the reduction of the head number. On the other hand, reducing the head number will reduce the memory usage to further increase
k to 40; the
mAcc and
mIoU of (2) are 0.1% and 0.6% higher than those in configuration (6), respectively. According to the comparisons of (1), (2), (3), and (4), we find that when the head number drops to 1, the expression capacity of the features cannot be improved even if the number of output channels is greatly increased. Thus, we finally choose the parameter setting of (2).
4.4. Comparison with Other Methods
To further verify the validity of the proposed model, in this section, we will make a detailed comparison of experimental results on four common datasets between our model and other methods.
4.4.1. Classification on ModelNet40
Table 4 shows the comparison results. Referring to the research [
45], we divide the compared methods into three categories, i.e., point-wise MLP methods, convolution-based methods, and graph-based methods. In
Table 4, our method achieves a remarkable performance on both
OA and
mAcc. Compared with graph-based methods such as Grid-GCN [
46], our method achieves the same
OA value, but we improve the
mAcc value by 0.1%. Note that compared to the baseline (GAPNet), we improve 0.7% and 1.7% on
OA and
mAcc, respectively, despite the model size increase of 10 MB. In addition, for convolution-based methods, i.e., methods that focus on efficiently aggregating context within local regions, we also obtain competitive results over them. Compared to the KPconv, we lead by 0.2% in
OA. In comparison with homogeneous methods (namely, the graph-based methods), our method has achieved remarkable results. For example, the PointView-GCN [
47] is a state-of-the-art method, with an
OA of 95.4%. However, the method has only been tested on small-scale datasets. Our method can be applied to semantic segmentation tasks on large-scale datasets as well as achieve remarkable results in the classification tasks on small-scale datasets.
4.4.2. Part Semantic Segmentation on ShapeNet
As shown in
Table 5, we divide the compared methods into four categories: structure-based, voxel-based, point-based MLP, and graph-based. Our method achieves the best
mAcc and
mIoU values among the four types of methods, reaching 83.2% and 85.4%, respectively. Compared with the baseline network, namely GAPNet, we improve
mIoU by 0.7%. Experiments show that the feature extraction layer can extract semantic information very well in the task of part segmentation with a small amount of data. In comparison with homogeneous methods (namely the graph-based methods), our method has achieved the best results. The PatchFormer [
37] achieves the best results on
mIoU with 86.5%, but our method remains ahead on
mAcc. In addition, the PatchFormer has also not been verified on large-scale datasets.
Figure 10 shows the visualization results of ShapeNet semantic segmentation. By comparison, it can be found that our method performs better on both flat and complex structures (such as red rectangles). Thanks to the geometric features extracted from the aggregated GAPLayer and pointset features of the RBFLayer, our network can better distinguish the shapes of various parts of the object, such as the armrest of the chair, the wing of the airplane, and the beam of the earphone. Since the RBFLayer can extract the object features of the pointset, when processing the object parts in
Figure 10c, the connection between the upper and lower beams can be established, and the beams will not be erroneously segmented as with the GAPNet. However, our method incorrectly identifies a part of the line as the earmuffs, possibly because there is a gap in the line. Furthermore, the model mistakenly judges that the two parts separated by a certain distance are the earmuffs, as the distance between the misidentified part and the true earmuff is similar to the distance between the two true earmuffs.
4.4.3. Semantic Segmentation on S3DIS
For the semantic segmentation task on the S3DIS and the Semantic3D, the MFNet-S network is employed. The Adam optimizer with an initial learning rate of 0.01 is used to train our model for 100 epochs. The batch size is set at 6 and 4, respectively, and the number of neighbors is set to 32 and 16, respectively, when training on the S3DIS and Semantic3D, and the decay rate of learning is set to 0.98. These two experiments are conducted on an NVIDIA Quadro RTX 6000 GPU.
Table 6 provides the experimental results. The
OA and
mIoU of our method reach 86.6% and 62.9%, respectively, which are better than most compared methods. Compared with the GAPLayer, the
OA and
mIoU of our method are improved by 0.9% and 3.5%, respectively, and the segmentation results of each category are improved. Since our method integrates multi-scale features and can expand receptive fields, it has obvious advantages to segment large objects such as a column, bookcase, and board.
Compared with the local feature extraction network PointWeb, although the obtained
OA is the same, the
mIoU of our method is 2.5% higher, and it is better than the PointWeb in the segmentation results of most categories. In the graph-based approach (such as TGNet [
61] and Grid-GCN [
46]), our method takes the lead in both
mIoU and
mAcc.
Figure 11 shows the semantic segmentation visualization results of several typical scenes in the S3DIS. Compared with the ground truth and baseline model GAPLayer, our network has a strong recognition ability for large-area connected areas such as doors and window frames on the wall, and also has a good segmentation effect for objects with complex geometric structures (such as indoor furniture). This proves that the RBFLayer in our MFEL can better construct similar features of pointsets and can fully consider the geometric and spatial attributes of adjacent points. However, the boundary prediction of some large-area connection areas is not clear or complete. This is mainly because the limited receptive field limits its ability to learn geometric features to distinguish connected objects.
4.4.4. Semantic Segmentation on Semantic3D
For a fair comparison, we submit our prediction results on the Reduced-8 to the sever and evaluate the
mIoU and
OA.
Table 7 provides a quantitative comparison with several methods. The
mIoU and
OA of our network are 71.9% and 93.7%, respectively, which are significantly better than most existing methods. Compared with the baseline network, the results of our method are improved by 2.6% and 1.3%, respectively. The segmentation of our network in 4 of the 8 categories achieves the highest score in the compared methods. From the prediction results of the visualization in the real large-scale scene shown in
Figure 12, our network can accurately segment small artificial objects such as carts and columns. The segmentation results on flat objects such as a sunshade surface are also complete. However, due to the sparse point cloud and the mixed geometric structure of the high vegetation leaves, the discriminative ability of the network is affected. Thus, our method is obviously inferior to the GAPNet in the recognition of targets such as high vegetation. This is what we will improve in the future.
Figure 11.
Semantic segmentation visualization results on the S3DIS. (a) Ground truth; (b) our method; (c) GAPNet. As shown in the figure, the segmentation result of our method is better than that of GAPNet in the black circle.
Figure 11.
Semantic segmentation visualization results on the S3DIS. (a) Ground truth; (b) our method; (c) GAPNet. As shown in the figure, the segmentation result of our method is better than that of GAPNet in the black circle.
5. Conclusions
In this research, we propose a new multi-scale feature extraction module MFEL for the large-scale point cloud classification. The MFEL first strengthens the local geometric feature extraction capability by adding a multi-layer perceptron channel with pooling layers to the graph convolution. Then, the statistical features of the point clouds at the pointset level are obtained via the RBFLayer. Finally, we combine the spatial location features extracted by the PointNet and design an end-to-end framework for the classification and part segmentation with better results. We also embed the module into a basic framework and perform experiments on large-scale indoor and outdoor point clouds, i.e., S3DIS and Semantic3D, with promising results. By the comparisons on several different types of datasets, our proposed feature extraction module provides greater improvements to the baseline model on large-scale datasets. In large-scale real scenarios, our proposed multi-scale feature extraction is more accurate and a stronger semantic representation for objects with rich geometric shapes.
However, our method is still inadequate in the segmentation of some small objects with complex structures, and inefficient feature fusion may lead to feature redundancy. Therefore, improving the efficiency of feature fusion and enriching the extraction of geometric features will be our future research.