CSCE-Net: Channel-Spatial Contextual Enhancement Network for Robust Point Cloud Registration

Abstract

Seeking reliable correspondences between two scenes is crucial for solving feature-based point cloud registration tasks. In this paper, we propose a novel outlier rejection network, called Channel-Spatial Contextual Enhancement Network (CSCE-Net), to obtain rich contextual information on correspondences, which can effectively remove outliers and improve the accuracy of point cloud registration. To be specific, we design a novel channel-spatial contextual (CSC) block, which is mainly composed of the Channel-Spatial Attention (CSA) layer and the Nonlocal Channel-Spatial Attention (Nonlocal CSA) layer. The CSC block is able to obtain more reliable contextual information, in which the CSA layer can selectively aggregate the mutual information between the channel and spatial dimensions. The Nonlocal CSA layer can compute feature similarity and spatial consistency for each correspondence, and the CSA layer and Nonlocal CSA layer can support each other. In addition, to improve the distinguishing ability between inliers and outliers, we present an advanced seed selection mechanism to select more dependable initial correspondences. Extensive experiments demonstrate that CSCE-Net outperforms state-of-the-art methods for outlier rejection and pose estimation tasks on public datasets with varying 3D local descriptors. In addition, the network parameters of CSCE-Net are reduced from 1.05M to 0.56M compared to the recently learning-based outlier rejection method PointDSC.

1. Introduction

Point cloud registration is widely used in 3D reconstruction [1], object pose estimation [2], simultaneous localization and mapping, [3] and other fields [4,5,6]. The feature-based point cloud registration pipelines commonly start from keypoint detection [7,8,9], feature point description [10,11,12], followed by robust alignment by outlier rejection [13,14,15]. Although feature point detection and 3D local features have developed rapidly, there are still many outliers in the initial correspondences generated by the feature-based matching, especially when the overlap of the two point clouds is very small. In this paper, we mainly design an outlier rejection network, which is a critical step in the robust point cloud registration pipeline, to alleviate the above issue.

Recently, 3D outlier rejection tasks based on deep learning, such as 3DRegNet [13] and DGR [14], formulated the outlier rejection as a classification problem of inlier/outlier. These networks embed deep features of input correspondences and utilize the resulting features to predict the probability that each correspondence is an inlier to remove the outlier. For feature embedding, they solely rely on general descriptors such as pointwise multilayer perceptron (MLP) and sparse convolution to capture contextual feature information of each correspondence. They all ignore the important spatial consistency properties that the inlier should follow in geometric properties in the 3D domain. Instead, PointDSC [15] considers the length of spatial consistency in the feature embedding of each correspondence. The PointDSC combines the length consistency and the spatial feature similarity to capture contextual features about each input correspondence. However, the above networks still cannot focus on essential channels contextual for each correspondence. In addition, they also lack crucial spatial information that would complement the channel features and effectively highlight areas of important spatial feature information extracted along the channel axis. Therefore, each correspondence has poor contextual feature representation in the above networks. In particular, ignoring the channel-spatial global context information would enormously limit the ability of the network to distinguish each correspondence, especially when the point clouds of pairs are less overlapping. As a result, these networks retain more outliers and, thus, reduce the point cloud alignment accuracy. 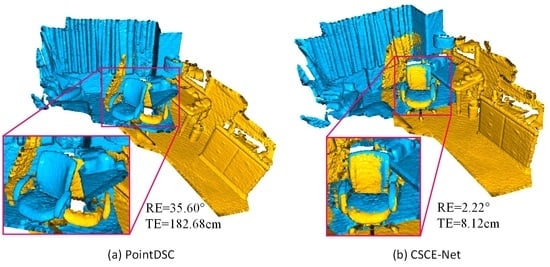Observing Figure 1a, we find that the outlier rejection network PointDSC retains many outliers due to inadequate extraction of contextual features, which results in huge point cloud alignment errors and consequent registration failures.

In this paper, we propose a practical channel-spatial contextual (CSC) block to solve the above issues. CSC block can capture each correspondence’s channel-spatial global context information by computing complementary channel and spatial attention. We also import the spatial consistency and the channel-spatial attention into the nonlocal network to compute the feature similarity for each pair of correspondences in spatial dimension based on the channel and spatial feature fusion. Therefore, the CSC block can separately calculate the channel-spatial features of each correspondence and the correlation between the correspondences, which enables the network to extract sufficient contextual information and process each correspondence distinguishably. Furthermore, we propose an advanced Seed Selection mechanism that more accurately calculates each correspondence’s initial confidence to select the seeds with well-distributed and highly confident, which contributes to the construction of a more reliable consensus set for each seed. Integrating the newly proposed CSC block and advanced Seed Selection mechanism with the Second Order Spatial Compatibility (SC${}^2$) measure [16] and Spectral Matching (SM) [17], we propose a novel outlier rejection network Channel-Spatial Contextual Enhancement Network (CSCE-Net). Specifically, CSCE-Net introduces a CSC block to capture rich global context information and enhance the presentation capability of important channel-spatial map information. In addition, CSCE-Net designs an advanced seeding mechanism to select high-confidence correspondences for the SC${}^2$ measure and SM to improve the inlier/outlier discrimination. In addition, we iteratively used CSCE-Net twice, with the inlier probability obtained from the previous network serving as an additional input to the following network to improve the performance of the final network. Observing Figure 1b, it is not difficult to see that our CSCE-Net is able to retain more inliers in two low-overlap scenes, dramatically reducing alignment errors when performing positional estimation compared to Figure 1a. The quantitative and visual results provide excellent evidence of the effectiveness of our CSCE-Net in seeking reliable correspondence during point cloud registration.

The main contributions of this work are in three aspects:

• We propose a CSC block in which the CSA layer and Nonlocal CSA layer are backbones to capture sufficient contextual information and enhance the representative ability of inliers and important channels and spatial.
• We construct an advanced seed selection mechanism to more accurately calculate seeds with high confidence and well-distributed and facilitate the construction of more reliable consensus sets for each seed.
• Our CSCE-Net outperforms state-of-the-art methods for outlier rejection and pose estimation tasks on two challenging public datasets by combining different 3D local descriptors and better balancing the number of parameters in the network.

The rest of this article is structured as follows: We describe the related literature in Section 2. In Section 3, we introduce the structure information of CSCE-Net, CSC block, and Seed Selection in detail. We exhibit the experimental details and comparative results in Section 4. In the end, we give the relevant conclusions in Section 5.

2. Related Works

In feature-based point cloud registration, firstly, a putative correspondence set has been built by some 3D local features, such as fast point feature histograms (FPFH) [18] and fully convolutional geometric features (FCGF) [10]. Secondly, it is necessary to remove outliers, as the putative correspondence set usually has a large number of incorrect matches. In this section, we briefly introduce some traditional and learning-based outlier rejection methods in Section 2.1 and Section 2.2, respectively.

2.1. Traditional Outlier Rejection

Random Sample Consensus (RANSAC) [19] is still the more popular method of outlier rejection. It iteratively uses the smallest subset obtained by random sampling and employs a least-squares fitting that is not robust to outliers in the model fitting step. Many of its various variants [20,21,22] have introduced new sampling strategies and local optimizations to speed up estimation or improve robustness. LO-RANSAC [20] makes the parametric model calculated for the outlier-free sample consistent with all interior points by applying local optimization to the solution estimated for the random sample. Since most existing registration methods require a set of assumed correspondences obtained by extracting invariant descriptors, SDRSAC [21] presents a new stochastic algorithm for robust point cloud alignment without correspondences. GESAC [22] improves on classical RANSAC by generating a larger subset in the sampling phase and introducing a shape-annealing robust estimate in the model fitting step. However, their main drawback, as with RANSAC, continues to be slow convergence and low accuracy in the case of a relatively large outlier ratio. More recently, Graph-cut RANSAC [23] runs a graph-cutting algorithm in a local optimization step to perform efficient outlier separation. Magsac [24] introduces a $\sigma$-consensus to construct a without inlier-outlier threshold method for RANSAC. As a result, they can improve the efficiency of outliers rejection further.

In addition, spectral matching (SM) [17] is a famous traditional algorithm that relies heavily on 3D spatial consistency to find inlier correspondences. It uses length consistency to construct a compatibility graph and then finds the main clusters of the graph to obtain an inlier set through eigenanalysis. However, as explained in [25], it cannot effectively deal with high outlier ratios, in which case the main internal clusters become less obvious. Moreover, FGR [26] achieves a fast global alignment algorithm for locally overlapping 3D surfaces by manipulating the candidate matches on the covered surface. TEASER [27] reformulates the registration problem using a truncated least squares (TLS) cost and solving the 3D rotation transformation through a general graph-theoretic framework. FGR and TEASER can tolerate outliers using robust loss functions (e.g., GemanMcClure). Quatro [28] utilizes a global alignment method based on degenerate robust decoupling to solve the problem of a large number of anomalous correspondences. Most traditional outlier rejection methods have been summarized in [25,29,30,31,32].

Although widely used in computer vision, traditional outlier rejection methods still suffer from some fundamental drawbacks. For example, as the ratio of outliers in the initial matching set increases dramatically, the above-mentioned traditional algorithms struggle to balance accuracy and efficiency. Hence comes the emergence of deep learning-based outlier rejection.

2.2. Learning-Based Outlier Rejection

In learning-based approaches, some feature learning methods [8,9,10,12] have used convolutional neural networks (CNN) to acquire more reliable keypoints and descriptors. Although these methods have better results than manual methods [18], they do not solve the problem of having a large number of outliers in the initial correspondence set. Therefore, learning-based outlier removal methods are proposed as a post-processing step to solving this problem.

A learning-based outlier rejection approach is introduced for the first time in the 2D image matching area, [33,34,35,36,37,38] where outlier rejection is represented as an inlier/outlier classification problem. CN-Net [33] is the first method to use an end-to-end learning-based approach to label each correspondence as an inlier or outlier value. Meanwhile, the fundamental matrix for recovering the camera pose of two matched images is estimated using a weighted eight-point algorithm. NM-Net [34] redefines neighbors to find reliable correspondence. OANet [35] introduces an order-aware filtering block to cluster correspondences crucial global context. MS2DG-Net [36] uses sparse semantic similarity instead of Euclidean distance to generate dynamic contextual features.

Recent attempts [13,14,15,39,40] have also introduced deep learning networks to perform 3D correspondence pruning. The 3DRegNet [13] redefines the CN-Net [33] into a 3D form and devises a regression module to solve the rigid transformation. DGR [14] recommends the use of a learning-based feature called the full convolutional geometric feature (FCGF) [10] to perform the alignment and employs a 6D convolutional network to predict the likelihood of each correspondence. DetarNet [39] introduces a decoupled solution for translation and rotation, resulting in better performance for both. Using Hough voting in 6D transformed parameter space, DHVR [40] describes a robust and efficient framework for paired registration of realistic 3D scans. However, when performing feature embedding of correspondences and pruning, these networks ignore the important property of spatial consistency that 3D point clouds should follow in the 3D domain. In contrast, the recent PointDSC [15] has developed a non-local module and neural spectrum matching based on the length spatial consistency to accelerate model generation.

However, these networks still do not capture enough contextual information for network learning because their feature embedding networks ignore each correspondence’s channel and spatial features, thus, limiting the feature representation capability. In this paper, our CSCE-Net uses complementary spatial channel attention combined with length spatial consistency to adequately extract the contextual features of each correspondence to improve the performance of outlier rejection and hence the accuracy of the final alignment.

3. Method

In this section, we first introduce the problem formulation in Section 3.1. Then, the network framework is introduced in Section 3.2. Finally, we describe the proposed CSC block and the Seed Selection in Section 3.3 and Section 3.4, respectively.

3.1. Problem Formulation

In this work, we are given two sets of keypoints $\mathbf{U}$∈${\mathbb{R}}^3$ and $\mathbf{V}$∈${\mathbb{R}}^3$ from a pair of partially overlapping 3D point clouds and each keypoint comes with an associated local descriptor. After that, the putative correspondence set $\mathit{S}$ of the network inputs are generated by performing a nearest neighbor search using local descriptors. Each correspondence ${\mathit{s}}_i$∈$\mathit{S}$ is denoted as ${\mathit{s}}_i$ = (${\mathit{u}}_i$,${\mathit{v}}_i$) ∈${\mathbb{R}}^6$, where ${\mathit{u}}_i$∈$\mathbf{U}$, ${\mathit{v}}_i$∈$\mathbf{V}$ are the space coordinates of a pair of 3D keypoints. Our final goal is to find an outlier/inlier label value for ${\mathit{s}}_i$, i.e., ${\mathit{w}}_i$ = 0 or 1, respectively, and then utilize these inliers between two point sets to recover an optimal 3D rigid transformation $\widehat{\mathbf{R}}$, $\widehat{\mathbf{t}}$.

Specifically, we first embed the correspondence of two point sets into the high-dimensional feature. Next, we employ these features to find the high-confidence correspondences as seeds. The corresponding consensus set (i.e., ${\mathit{S}}^{\prime }$) of each seed is obtained by the SC${}^2$ measure. Then we compute the 3D rigid transformation {${\mathbf{R}}^{{}^{\prime }},{\mathbf{t}}^{{}^{\prime }}$} for each seed set by the least-squares fitting [41]:

$${\mathbf{R}}^{{}^{\prime }},{\mathbf{t}}^{{}^{\prime }}=\underset{\mathbf{R},\mathbf{t}}{\mathrm{argmin}}\sum _i^{\mid {\mathit{S}}^{\prime }\mid }{\alpha }_i{\Vert \mathbf{R}{\mathit{u}}_i+\mathbf{t}-{\mathit{v}}_i\Vert }^2,$$

(1)

where $\alpha$ is the weight of inlier probability calculated from the NSM module. Equation (1) is solved by SVD [41].

Further, we find the optimal 3D rigid transformation {$\widehat{\mathbf{R}}$, $\widehat{\mathbf{t}}$} by the number of corresponding relations for each {${\mathbf{R}}^{{}^{\prime }},{\mathbf{t}}^{{}^{\prime }}$} satisfying a given threshold:

$$\widehat{\mathbf{R}},\widehat{\mathbf{t}}=\underset{{\mathbf{R}}^{{}^{\prime }},{\mathbf{t}}^{{}^{\prime }}}{\mathrm{argmax}}\sum _i^{\mid \mathit{S}\mid }[\Vert {\mathbf{R}}^{{}^{\prime }}{\mathit{u}}_i+{\mathbf{t}}^{{}^{\prime }}-{\mathit{v}}_i\Vert <\mu ],$$

(2)

where $\mu$ denotes the inlier threshold and [·] is the Iverson bracket. Finally, the outlier/inlier label $w$∈${\mathbb{R}}^{\mid \mathit{S}\mid }$ is obtained by ${\mathit{w}}_i$ = $[\Vert \widehat{\mathbf{R}}{\mathit{u}}_i+\widehat{\mathbf{t}}-{\mathit{v}}_i\Vert <\mu ]$. We then recompute the final 3D rotation transformation {$\widehat{\mathbf{R}}$, $\widehat{\mathbf{t}}$} by the least squares using all the retained inliers.

Loss Function. Following previous work in PointDSC [15], we optimize the neural network utilizing a hybrid loss function (i.e., a node-wise loss and an edge-wise loss) as follows:

$$\mathit{L}=\beta {\mathit{L}}_{node}+{\mathit{L}}_{edge},$$

(3)

where $\beta$ is a hyper-parameter that balances the two losses.

${\mathit{L}}_{node}$ denotes the node-wise loss that is used to supervise each correspondence individually. We employ binary cross-entropy loss as node-wise supervision to learn the initial confidence:

$${\mathit{L}}_{node}=\mathrm{BCE}(\theta ,\tilde{\mathit{w}}),$$

(4)

where $\theta$ is the initial confidence of the prediction, and $\tilde{\mathit{w}}$ represents the ground-truth outlier/inlier labels constructed by

$${\tilde{\mathit{w}}}_i=[\Vert \tilde{\mathbf{R}}{\mathit{u}}_i+\tilde{\mathbf{t}}-{\mathit{v}}_i\Vert <\mu ],$$

(5)

where $\tilde{\mathbf{R}}$ and $\tilde{\mathbf{t}}$ are the ground truth rotation and translation matrices, and $\mu$ is the inlier threshold.

${\mathit{L}}_{edge}$ is the edge-wise loss, which is applied to supervise the pairwise relationship between correspondences as a complement to node-wise supervision.

$${\mathit{L}}_{edge}=1-{\displaystyle \frac{1}{\mid \mathit{S}{\mid }^2}}\sum _{ij}{({\delta }_{ij}-{\tilde{\delta }}_{ij})}^2,$$

(6)

where ${\delta }_{ij}$ is the relevance value estimated based on feature similarity and ${\tilde{\delta }}_{ij}$=[${\mathit{s}}_i$ and ${\mathit{s}}_j$ are inliers] is the ground-truth relevance value, which is defined as:

$${\delta }_{ij}=[1-{\displaystyle \frac{1}{{ϵ}_f^2}}\parallel {\overline{\mathit{f}}}_i-{\overline{\mathit{f}}}_j{\parallel }^2],$$

(7)

where ${\overline{\mathit{f}}}_i$ and ${\overline{\mathit{f}}}_j$ are the $L_2$-normalized eigenvectors, and ${ϵ}_f$ is a parameter of feature difference sensitivity.

3.2. Network Framework

The framework of our CSCE-Net is shown in Figure 2. The CSCE-Net consists of four main parts: our proposed CSC block, the presented seed selection, the Second Order Spatial Compatibility Measure, and Spectral Matching. Our CSCE-Net starts with $\mathit{N}$ initial correspondences as input and maps the features from 6 to 128 dimensions using a shared perceptron. Next, it adequately extracts the global context information for each correspondence by utilizing 6 CSC blocks. Then, the seed selection mechanism exploits the high-dimensional features obtained from the CSC blocks to calculate the initial confidence of each correspondence and selects these high-confidence and well-distributed correspondences as seeds ($\mathit{Ns}$) using the Non-Maximum Suppression method. Seeds selected for rich contextual information are more likely to be represented as inliers, which contributes to the construction of a more reliable consensus set. In addition, to better distinguish between insertions and outliers, we inserted a second-order spatial compatibility (SC${}^2$) measure proposed by SC${}^2$-PCR [16], which constructs a new global measure of similarity between two correspondences by counting the number of correspondences that are compatible with both correspondences simultaneously. The role of the SC${}^2$ measure is to construct a consensus set for each seed. Finally, CSCE-Net adopts the spectral matching [16,17] to compute the weight vector $\alpha$ of inlier probabilities and the 3D rigid transform {${\mathbf{R}}^{{}^{\prime }},{\mathbf{t}}^{{}^{\prime }}$} for each consensus set by least-squares fitting.

3.3. CSC Block

The CSC block mainly utilizes perceptrons and complementary channel-spatial attention to selectively aggregate information in the channel and spatial dimensions, capture the complex global context of feature maps, and obtain feature maps with solid and expressive capabilities. As shown in Figure 2, the newly proposed CSC block consists of four key parts, i.e., the two identical Context Norm layers, the CSA layer, and the Nonlocal CSA layer. The Context Norm layer contains a Context Normalization layer to get the global context, a Batch Normalization layer with ReLU activation function to speed up network training, and a Multi-Layer Perceptrons layer containing 128 neurons for network learning. We use the Context Norm layer to handle disordered and irregular correspondences.

As shown in Figure 3, the CSA layer reinforces the channel-spatial features by serially concatenating the 2D maps produced by the Channel attention (CA) module and the Spatial attention (SA) module, respectively. The lack of channel-spatial features in feature embeddings greatly limits the ability of the network to reject outliers. Therefore, we construct a novel channel-spatial attention layer to improve the representation ability and emphasize significant characteristics along these two main dimensions: channel and spatial. For aggregating spatial information, the average pooling method is generally used at present [42]. Moreover, Woo et al. [43] believe that max-pooling infers more delicate channel-level and spatial-level attention, combining average pooling and max pooling to retain more feature information. However, max-pooling only preserves important local feature cues. Thus, we apply the global standard deviation pooling operation to channel and spatial attention, which can take global and local feature cues into account, enhance feature representation capabilities, and strengthen the correlation between features of each correspondence. Specifically, to obtain more robust feature maps, we concatenate the 2D attention map ${\mathit{F}}_{\mathbf{c}}\in$$\mathbb{R}$${}^{C\times 1\times 1}$ and ${\mathit{F}}_{\mathbf{s}}\in$$\mathbb{R}$${}^{1\times N\times 1}$, which are output by CA module and SA module, respectively. Our experiments (see Section 4.4) conclude that the optimal connection method of the CA and SA module is sequential connection. Therefore, the CSA layer is summarized as follows:

$$\begin{array}{cc}\hfill {\mathit{F}}^{{}^{\prime }}& \hfill ={\mathit{F}}_{\mathbf{c}}\odot \mathit{F}\hfill \\ \hfill {\mathit{F}}^{{}^{″}}& \hfill ={\mathit{F}}_{\mathbf{s}}\odot {\mathit{F}}^{{}^{\prime }},\hfill \end{array}$$

(8)

where ⊙ represents element-wise multiplication and ${\mathit{F}}^{{}^{″}}$ is the final refinement output of the CSA layer.

CA module: The channel attention module is shown in Figure 4. We first aggregate the spatial information of feature maps by using the standard deviation pooling and average pooling operation to generate two distinct spatial context descriptors: ${\mathit{M}}_{\mathit{std}}^{\mathbf{c}}$ and ${\mathit{M}}_{\mathit{avg}}^{\mathbf{c}}$, which represent std-pooled features and average-pooled features, respectively. Then, the above two features are forwarded to the shared network to generate our channel attention map ${\mathit{F}}_{\mathbf{c}}\in$$\mathbb{R}$${}^{C\times 1\times 1}$, where C is the number of channels. The shared network consists of a multilayer perceptron (MLP) with a hidden layer. The activation size of the hidden layer is set as $\mathbb{R}$${}^{C/\mathit{d}\times 1\times 1}$, where $\mathit{d}$ is the reduction ratio. After applying the shared network to both descriptors, we use element-wise summation to combine the output feature vectors. The channel attention is calculated as follows:

$$\begin{array}{cc}\hfill {\mathit{F}}_{\mathbf{c}}& \hfill =\rho \left(\mathit{MLP}\right(\mathit{StdPool}\left(\mathit{F}\right))+\mathit{MLP}(\mathit{AvgPool}\left(\mathit{F}\right)\left)\right)\hfill \\ \hfill & \hfill =\rho (\mathit{MLP}\left({\mathit{M}}_{\mathit{std}}^{\mathbf{c}}\right)+\mathit{MLP}\left({\mathit{M}}_{\mathit{avg}}^{\mathbf{c}}\right)),\hfill \end{array}$$

(9)

where $\rho$ represents the sigmoid function. MLP stands for the shared network.

SA module: As shown in Figure 5, we first generate two 2D maps ${\mathit{M}}_{\mathit{std}}^{\mathit{s}}\in$$\mathbb{R}$${}^{1\times N\times 1}$ and ${\mathit{M}}_{\mathit{avg}}^{\mathit{s}}\in$$\mathbb{R}$${}^{1\times N\times 1}$ by using two pooling operations to aggregate the channel information of one feature map. Each feature represents the std-pooled and average-pooled features of the entire channel. Then we concatenate the above two features together. After that, we apply a standard convolutional layer to generate a 2D spatial attention map. Finally, the sigmoid function is used to normalize the attention map. The spatial attention is calculated as follows:

$$\begin{array}{cc}\hfill {\mathit{F}}_{\mathit{s}}& \hfill =\rho ({\mathit{O}}^{1\times 1}([\mathit{StdPool}({\mathit{F}}^{{}^{\prime }});\mathit{AvgPool}({\mathit{F}}^{{}^{\prime }})]))\hfill \\ \hfill & \hfill =\rho ({\mathit{O}}^{1\times 1}([{\mathit{M}}_{\mathit{std}}^{\mathit{s}};{\mathit{M}}_{\mathit{avg}}^{\mathit{s}}])),\hfill \end{array}$$

(10)

where ${\mathit{O}}^{1\times 1}$ denotes a convolution operation with a filter size of $1\times 1$ and $\rho$ represents the sigmoid function.

The nonlocal CSA layer is used to update features inspired by PointDSC [15], which mainly introduces a spatial consistency to complement the feature similarity of the nonlocal network [44]. To enhance the channel spatial features, we present the CSA layer to supplement the features of each correspondence after spatial topology and feature similarity computation. Therefore, the nonlocal CSA layer can not only obtain the spatial consistency and feature similarity information of each correspondence but also enhance the representation ability of the channel-spatial.

3.4. Seed Selection

Finding a dominant inlier cluster is difficult in the next SM layer, which cannot clearly distinguish both inlier and outlier. In this instance, utilizing the output of SM via weighted least-squares fitting [41] to transformation estimation may result in a suboptimal solution, since many outliers are still not explicitly eliminated. Therefore, we propose a new seed selection mechanism applied to apply spectral matching locally. In PointDSC [15], the seed selection mechanism is designed by two identical shared perceptrons and ReLu activation functions to compute the initial confidence for each correspondence. However, the random and straightforward structure ignores the global context encoding before calculating the confidence for each correspondence. That causes seed selection to find a suboptimal confidence distribution. Therefore, our new seed selection incorporates two contextual normalizations (shown in Figure 6) that encode each correspondence’s contextual feature maps by means and variances. The new seed selection mechanism can accurately calculate the context of each correspondence before calculating the confidence so that the confidence distribution is optimal. Therefore, it finds well-distributed and more reliable correspondences as seeds and looks for consistent correspondences around them in the feature space. After then, the new seed selection makes each subset have a higher inlier ratio than the set of input correspondences, which contributes SC${}^2$ to construct a more reliable consensus set for each seed.

As shown in Figure 6, we use an MLP to select seeds by calculating the initial confidence for each correspondence, which uses the features learned by the CSC block. Then we utilize Non-Maximum Suppression [45] on these confidences to find well-distributed seeds. These selected seeds will be formed into multiple corresponding consensus sets by SC${}^2$ measure and input into SM.

4. Experiments

In this section, we first present datasets and experimental setup in Section 4.1. Next, we evaluate our CSCE-Net on indoor scenes using different descriptors in Section 4.2. Further, we investigate the generalization ability of CSCE-Net on the outdoor scenes in Section 4.3. Finally, we introduce ablation studies in Section 4.4.

4.1. Datasets and Experimental Setup

Indoor scenes. We follow the same evaluation scheme as 3DMatch [46] to prepare the training and testing data in indoor scenes. For each pair of point clouds, we first down-sample the point clouds using a 5 cm voxel grid. The local feature descriptors were then extracted and matched to form the presumed correspondence. For all 3DMatch scans, we give two non-contiguous scene segments coarsely aligned using Random Sample Consensus (RANSAC). We then remove them from the dataset if RANSAC fails or if the overlap between the two segments is less than 30%. The procedure yielded 2186 pairs of partially overlapping point cloud segments in 8 scenes for training and 1623 for testing. Following [15], to prove the generalizability of CSCE-Net across descriptors, we employed FPFH [18] (handcrafted descriptors) and FCGF [10] (learned descriptors) as feature descriptors, respectively.

Outdoor scenes. We use the KITTI dataset [47] to test its effectiveness for outdoor scenes. KITTI contains a training set of 11 sequences, following [10,14,15] to divide it into train/val/test sets as follows: Sequences 0 to 5 are used for training, sequences 7 to 8 for validation, and sequences 8 to 10 for testing, obtaining 1358 pairs of partially overlapping point clouds for training and 555 pairs for testing. Then we downsample the above point cloud with 30 cm voxels and construct the initial input correspondence by extracting feature descriptors (i.e., FPFH and FCGF).

Evaluation criteria. We evaluate the performance of CSCE-Net on different datasets by the tasks of outlier rejection and scene pose estimation. Firstly, for the outpoint rejection task, we followed [14] to report three evaluation criteria: $\mathit{Inlier}$$\mathit{Precision}$$\left(\mathit{IP}\right)$, $\mathit{Inlier}$$\mathit{Recall}$$\left(\mathit{IR}\right)$, and $\mathit{F}\mathit{1}$$\mathit{score}$$\left(\mathit{F}\mathit{1}\right)$. Secondly, following [15], we also report three evaluation criteria for the scene pose estimation task: $\mathit{Rotation}$$\mathit{Error}$$\left(\mathit{RE}\right)$, $\mathit{Translation}$$\mathit{Error}$$\left(\mathit{TE}\right)$, and $\mathit{Registration}$$\mathit{Recall}$$\left(\mathit{RR}\right)$. The averages $\mathit{RE}$ and $\mathit{TE}$ are calculated only on successfully registered pairs. For RR, an alignment result is deemed successful if $\mathit{RE}$ and $\mathit{TE}$ are less than the given thresholds. The threshold is set to (15${}^{\circ }$, 30 cm) for indoor scenes and (5${}^{\circ }$, 60 cm) for outdoor scenes.

Implementation details. In all experiments, we constructed $\mathit{N}\times \mathit{6}$ initial correspondences by the nearest neighbor search of the feature descriptors FPFH and FCGF. Referring to PointDSC [15], we randomly selected 1000 correspondences for each pair of point clouds during the training process and constructed a batch input of size 16. The inlier threshold $\mathsf{\mu }$ is set to 0.1 cm for indoor scenes and 0.6 cm for outdoor scenes. We set the hyper-parameter $\beta =3$ and make ${ϵ}_f$ learned by the network. Using the ADAM optimizer, we optimized the network at an exponential decay factor of 0.99 and an initial learning rate of 0.0001 and trained the network with 50 epochs. All experiments are performed on PyTorch and RTX2080 graphics cards.

4.2. Evaluation of Indoor Scenes

We first report the results of the 3DMatch dataset in

Table 1. Quantitative results of outlier rejection on the 3DMatch datasets.

	Method	3DMatch
		IP (%↑)	IR (%↑)	F1 (%↑)	Time (s)
FPFH [18]	SM [17]	47.96	70.69	50.70	0.03
	TEASER [27]	73.01	62.63	66.93	0.03
	GC-RANSAC-100 k [23]	48.55	69.38	56.78	0.62
	RANSAC-100k	68.18	67.40	67.47	5.24
	DGR [14]	28.80	12.42	17.35	2.49
	PointDSC [15]	68.63	71.63	69.89	0.08
	CSCE-Net	73.11	77.47	74.75	0.13
FCGF [10]	SM [17]	81.44	38.36	48.21	0.03
	TEASER [27]	82.43	68.08	73.96	0.11
	GC-RANSAC-100 k [23]	64.46	93.39	75.69	0.47
	RANSAC-100 k	78.38	85.30	81.43	5.50
	DGR [14]	67.47	78.94	72.76	1.36
	PointDSC [15]	79.07	86.48	82.31	0.08
	CSCE-Net	79.16	87.02	82.61	0.13

. We compare our method with 6 baselines: $\mathrm{SM}$ [17], $\mathrm{RANSAC}$ [19], $\mathrm{GC}-\mathrm{RANSAC}$ [23] and $\mathrm{TEASER}$ [27], $\mathrm{DGR}$ [14], and $\mathrm{PointDSC}$ [15]. For PointDSC, we use the pre-trained model provided by the method for testing. The results for other baseline methods are from [15].

Combined with FPFH. As shown in Table 1, compared to the learning-based baseline, CSCE-Net outperforms the second-best method PointDSC by more than 4% in $\mathit{F}\mathit{1}$, demonstrating the effectiveness of our outlier rejection method. In addition, the $\mathit{F}\mathit{1}$ of DGR are as low as 17.35%. The reason is precise: each correspondence lacks the channel-spatial contextual features in feature embedding and the indispensable spatial consistency between correspondences in the 3D domain. Furthermore, as shown in

Table 2. Quantitative results of pose estimation on the 3DMatch datasets.

	Method	3DMatch
		RE (°↓)	TE (cm↓)	RR (%↑)	Time (s)
FPFH [18]	SM [17]	2.94	8.15	55.88	0.03
	TEASER [27]	2.48	7.31	75.48	0.03
	GC-RANSAC-100 k [23]	2.33	6.87	67.65	0.62
	RANSAC-100k	3.55	10.04	73.57	5.24
	DGR [14]	3.78	10.80	69.13	2.49
	PointDSC [15]	2.09	6.59	78.56	0.08
	CSCE-Net	2.11	6.73	83.61	0.13
FCGF [10]	SM [17]	2.29	7.07	86.57	0.03
	TEASER [27]	2.73	8.66	85.77	0.11
	GC-RANSAC-100 k [23]	2.33	7.11	92.05	0.47
	RANSAC-100 k	2.49	7.54	91.50	5.50
	DGR [14]	2.40	7.48	91.30	1.36
	PointDSC [15]	2.05	6.54	93.22	0.08
	CSCE-Net	2.06	6.53	93.47	0.13

, thanks to the excellent outlier rejection effect of CSCE-Net, the $\mathit{RR}$ of the two-point clouds also achieves the best results (83.61%) when the two errors of $\mathit{RE}$ and $\mathit{TE}$ are minimized. This result is also 5.05% higher than the second-best PointDSC, demonstrating the competitiveness of CSCE-Net in point cloud registration. In addition, the traditional RANSAC method can achieve competitive results after a sufficient number of iterations. However, our method is about 40 times faster than RANSAC-100k while also achieving higher $\mathit{F}\mathit{1}$ and $\mathit{RR}$. Figure 7 shows the outlier rejection visualization results of our CSCE-Net and the state-of-the-art PointDSC on 3DMatch.

Combined with FCGF. We further evaluate all methods for outlier rejection and pose estimation using the learned descriptor FCGF. As shown in Table 1 and Table 2, our CSCE-Net still outperforms the second-best PointDSC with a $\mathit{F}\mathit{1}$ of 82.61% and $\mathit{RR}$ of 93.47%. We also note that the $\mathit{IP}$ of TEASER and the $\mathit{IR}$ of GC-RANSAC-100k are higher than the respective values for CSCE-Net. At the same time, it is easy to find the $\mathit{IP}$ and $\mathit{IR}$ of CSCE-Net are also higher than those of GC-RANSAC-100k and TEASER, respectively. Therefore, we believe that CSCE-Net is able to balance IP and IR better while achieving higher $\mathit{F}\mathit{1}$. In addition, it is also not difficult to find that most of the methods combined with the more robust descriptor FCGF have better outlier rejection and pose estimation performance than FPFH.

4.3. Evaluation of Outdoor Scenes

To evaluate the generalization of CSCE-Net to unseen domains and new datasets, we re-test the outdoor lidar dataset by using a model trained on 3DMatch and a model retrained on KITTI, respectively. We choose SM [17], RANSAC [19], DGR [14], and PointDSC [15] as baseline methods.

We carefully report two training model results for CSCE-Net under two descriptors: one to test the pre-trained (no extra mark) model obtained on 3DMatch and the other to test the trained model from scratch (marked as “re-trained”) on KITTI. As shown in

Table 3. Quantitative results of outlier rejection and pose estimation on the KITTI datasets.

	Method	KITTI
		F1 (%↑)	RE	TE (cm↓)	RR (%↑)	Time (s)
FPFH [18]	SM [17]	56.37	0.47	12.15	79.64	0.18
	RANSAC-100k	73.13	1.22	25.88	89.37	13.7
	DGR [14]	4.51	1.67	34.74	73.69	0.86
	PointDSC [15]	85.59	0.35	7.17	92.25	0.23
	CSCE-Net	92.84	0.33	7.05	98.74	0.61
	PointDSC re-trained	88.51	0.35	7.16	98.20	0.23
	CSCE-Net re-trained	93.58	0.32	7.03	99.10	0.61
FCGF [10]	SM [17]	22.84	0.50	19.73	96.76	0.10
	RANSAC-100 k	85.42	0.38	22.60	98.38	13.4
	DGR [14]	73.60	0.43	23.28	95.14	0.86
	PointDSC [15]	85.29	0.33	20.99	97.48	0.31
	CSCE-Net	85.81	0.32	20.89	97.84	0.61
	PointDSC re-trained	85.37	0.33	20.94	98.20	0.31
	CSCE-Net re-trained	86.06	0.31	20.89	98.66	0.61

, first, when combined with the FPFH descriptor, the $\mathit{F}\mathit{1}$ of CSCE-Net is approximately 7% higher than that of PointDSC, and the $\mathit{RR}$ is approximately 6.5% higher in the training model of 3DMatch, which fully demonstrates its competitiveness and strong generalization ability to unseen datasets. At the same time, we note that the $\mathit{F}\mathit{1}$ of DGR is only 4.51% because its outlier rejection and pose estimation generalize too weakly on outdoor datasets. When re-trained, the $\mathit{F}\mathit{1}$ and $\mathit{RR}$ of CSCE-Net is as high as 93.58% and 99.10%, respectively, outperforming all baseline methods. In addition, the $\mathit{F}\mathit{1}$ and $\mathit{RR}$ of the CSCE-Net are optimal when combined with the FCGF descriptors. These conclusions also show that our CSCE-Net is equally competitive for outdoor scenes.

4.4. Ablation Studies

In this section, we experimentally demonstrate the effectiveness of our CSCE-Net, our proposed CSC block structure design choice, and the advanced seed selection mechanism. We used the pre-trained model of 3DMatch combined with the FCGF descriptor to test the 3DMatch and KITTI datasets for these ablation studies. We first consider how to combine the channel and spatial attention modules in the CSA layer (

Table 4. Combining methods of the channel and spatial attention. The `+’ indicates a serial connection here and the `&’ indicates a parallel connection. The test results are combined with the FPFH descriptor.

	Description	FPFH
		F1 (%↑)	RR (%↑)
3DMatch	channel & spatial in parallel	72.82	81.78
	spatial + channel	73.76	82.65
	channel + spatial	74.75	83.61
KITTI	channel & spatial in parallel	90.41	96.48
	spatial + channel	91.94	97.84
	channel + spatial	92.84	98.74

). We then test the role of the channel and spatial attention and the position of the CSA layer in the CSC block (

Table 5. Ablation study of CSC blocks on 3DMatch and KITTI datasets. Baseline: PointDSC [15]. CSA1: using the CSA layer. CSA2: using the CSA layer in the Nonlocal CSA layer. CA: using the channel attention module in CSA layers. SA: using the spatial attention module in CSA layers. The test results are combined with the FPFH descriptor.

	Baseline	CSA1	CSA2	CA	SA	FPFH
						F1 (%↑)	RR (%↑)
3DMatch	✓					69.89	78.56
		✓	✓	✓		72.13	80.25
		✓	✓		✓	71.91	80.02
				✓	✓	72.82	80.76
			✓	✓	✓	71.86	79.88
		✓	✓	✓	✓	73.58	81.57
KITTI	✓					85.59	92.25
		✓	✓	✓		88.22	94.32
		✓	✓		✓	87.95	93.86
				✓	✓	88.69	94.79
			✓	✓	✓	87.60	93.56
		✓	✓	✓	✓	89.59	95.88

). Subsequently, to demonstrate the effectiveness of CSCE-Net, we progressively add the proposed and adopted modules to the baseline and report the results (

Table 6. Ablation study of the CSCE-Net blocks on 3DMatch and KITTI datasets. Baseline: PointDSC [15]. CSC: Channel-Spatial Contextual block. Seed: The advanced Seed Selection mechanism. SC${}^2$: Second Order Spatial Compatibility (SC${}^2$) measure. The test results are combined with the FPFH descriptor.

	Baseline	CSC	Seed	SC${}^2$	FPFH
					F1 (%↑)	RR (%↑)
3DMatch	✓				69.89	78.56
		✓			73.58	81.57
		✓	✓		74.02	82.12
		✓	✓	✓	74.75	83.61
KITTI	✓				85.59	92.25
		✓			89.59	95.88
		✓	✓		91.98	97.86
		✓	✓	✓	92.84	98.74

). Finally, the parameter comparison between our CSCE-Net and the recent PointDSC (

Table 7. Compare the network parameters (Param) of PointDSC and our CSCE-Net. PointDSC (6) indicates that the PointDSC feature embedding is reduced from 12 layers to 6 layers. The test results are combined with the 3DMatch dataset.

Method	FPFH	FCGF	Param (M)
	F1/RR	F1/RR
PointDSC [15]	69.89/78.56	82.31/93.22	1.05
PointDSC (6)	67.25/76.96	80.09/92.17	0.53
CSCE-Net	74.75/83.61	82.61/93.47	0.56

). The test results represent the $\mathit{F}\mathit{1}$ and $\mathit{RR}$ obtained by the pre-trained model in 3DMatch combined with the FPFH descriptor in 3DMatch and KITTI.

Arrangement of the channel and spatial attention. In this experiment, we verify the optimal arrangement of the channel and spatial attention of the CSA layer in the CSC block in three orders: channel-spatial, spatial-channel, and channel-spatial parallel. Since the channel and spatial modules have different functions, the order in which they are arranged may affect the entirety of the performance. In short, channel attention is applied globally, while spatial attention works locally. Therefore, the two types of attention can be applied complementary to construct a 3D attention map. From the different arrangements in Table 4, we find that the attention maps generated by channel-spatial attention in sequence are the best. Therefore, the structure of channel-spatial attention in the CSA layer in the ablation experiment below is a sequential arrangement of channel and spatial.

CSC block design. As shown in Table 5, we test the performance of different combinations of outlier rejection and positional estimation tasks within the CSC block on the 3DMatch and KITTI datasets. The first row of the table is PointDSC, which is the most recent state-of-the-art learning-based outlier rejection method. Therefore, we use PointDSC as a baseline for comparison. We can see that all of our iterative combinations perform better than the baseline. Specifically, the channel attention module (CSA1 + CSA2 + CA) achieved RR improvements of 1.69% and 2.07% over baseline in the 3DMatch and KITTI scenes, respectively. The spatial attention module (CSA1 + CSA2 + SA) improved the RR in the 3DMatch and KITTI scenes by 1.46% and 1.61% over baseline, respectively. These two terms indicate that the channel attention module and the spatial attention module are able to capture rich feature map contextual information and, thus, improve the performance of the pose estimation task for the point cloud. For using only CSA layer1 (CSA1 + CA + SA), we obtained a significant improvement over baseline performance, with RR improvements of 2.2% and 2.54% over baseline in the 3DMatch and KITTI scenes, respectively. This demonstrates that this complementary channel-spatial attention we propose outperforms individual channel and spatial attention. For using only CSA layer2 (CSA2 + CA + SA), we also improved 1.32% and 1.31% in RR over baseline on 3DMatch and KITTI. These two terms show that adding CSA layers at different positions of the CSC block is effective. We ended up with a 3.69%/3.01% and 4.0%/3.63% improvement in F1/RR on the 3DMatch and KITTI datasets, respectively, compared to the baseline after inserting CSA layers at different locations in the CSC block.

Final network design. To demonstrate the effect of our CSC block and the advanced improved seed selection mechanism, we conduct ablation experiments to add the CSC block and the enhanced new seed selection mechanism for the baseline. We first add the CSC block as the feature embedding part. By extracting abundant contextual features for each correspondence, the separation of inliers and outliers is facilitated, thus, improving the accuracy of the point cloud registration. As shown in Table 6, the registration recall rate guided by the CSC block was 3.01% higher than PointDSC when combined with FPFH and 3.63% higher when combined with FCGF. We further adopted a new seed selection mechanism for selecting more reliable correspondences as seeds. When a seed acts as an inlier, the consensus set of seeds formed later is more likely to form inlier clusters, thus, improving the accuracy of transformations between point cloud pairs. Finally, to calculate the exact seed consensus set, we inserted the SC${}^2$ measure to optimize the network.

Computational cost. As shown in Table 7, we have considered the network parameters while improving the network performance. The parameters required by our CSCE-Net network (0.56M) are almost half of those required by the current state-of-the-art outlier rejection network PointDSC (1.05M). If we reduce the feature embedding block of PointDSC to use only six layers (i.e., PointDSC(6)), then PointDSC(6) corresponding network parameters are directly reduced to half (0.53M), but then the network performance will also be significantly reduced. Thus, our network achieves a balance between performance and the number of parameters required.

5. Conclusions

In this paper, we propose an efficient CSC block and an advanced Seed Selection mechanism as the backbone of the newly proposed CSCE-Net to find more inliers in the initial correspondence and recover 3D rigid transformation between two point clouds. In particular, our proposed CSC block can collect abundant contextual information for each pair of correspondences and enhance the feature representation through some novel channel-spatial attention operations. The advanced Seed Selection utilizes the features obtained from the CSC block to improve the ratio of inliers. Results of outlier removal and pose estimation tasks in challenging indoor and outdoor scenes to show that our CSCE-Net achieves impressive performance improvements compared to state-of-the-art competing networks by combining different 3D local descriptors. In addition, the network parameters of our proposed CSCE-Net are lower than those of the state-of-the-art outlier rejection network PointDSC.