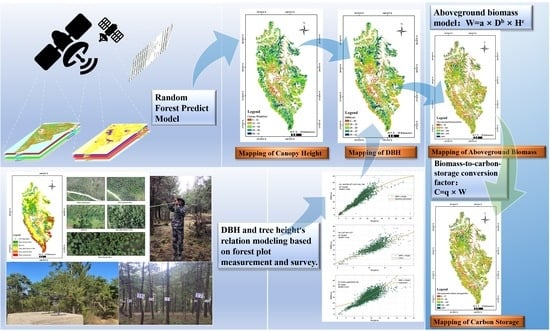
Mapping of Forest Biomass in Shangri-La City Based on LiDAR Technology and Other Remote Sensing Data
Abstract
:1. Introduction
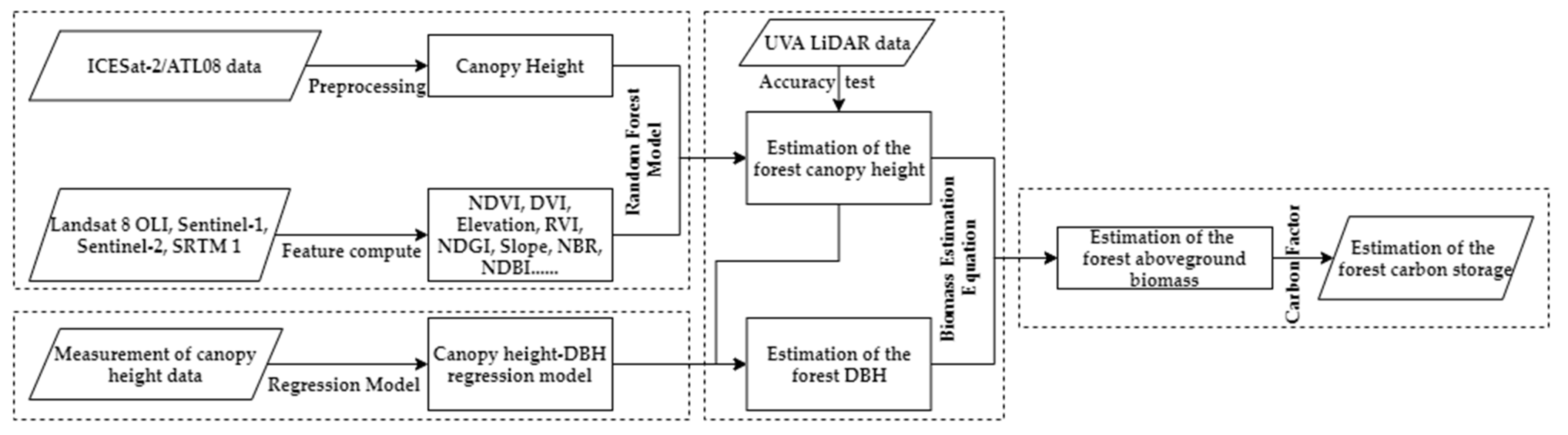
2. Materials and Methods
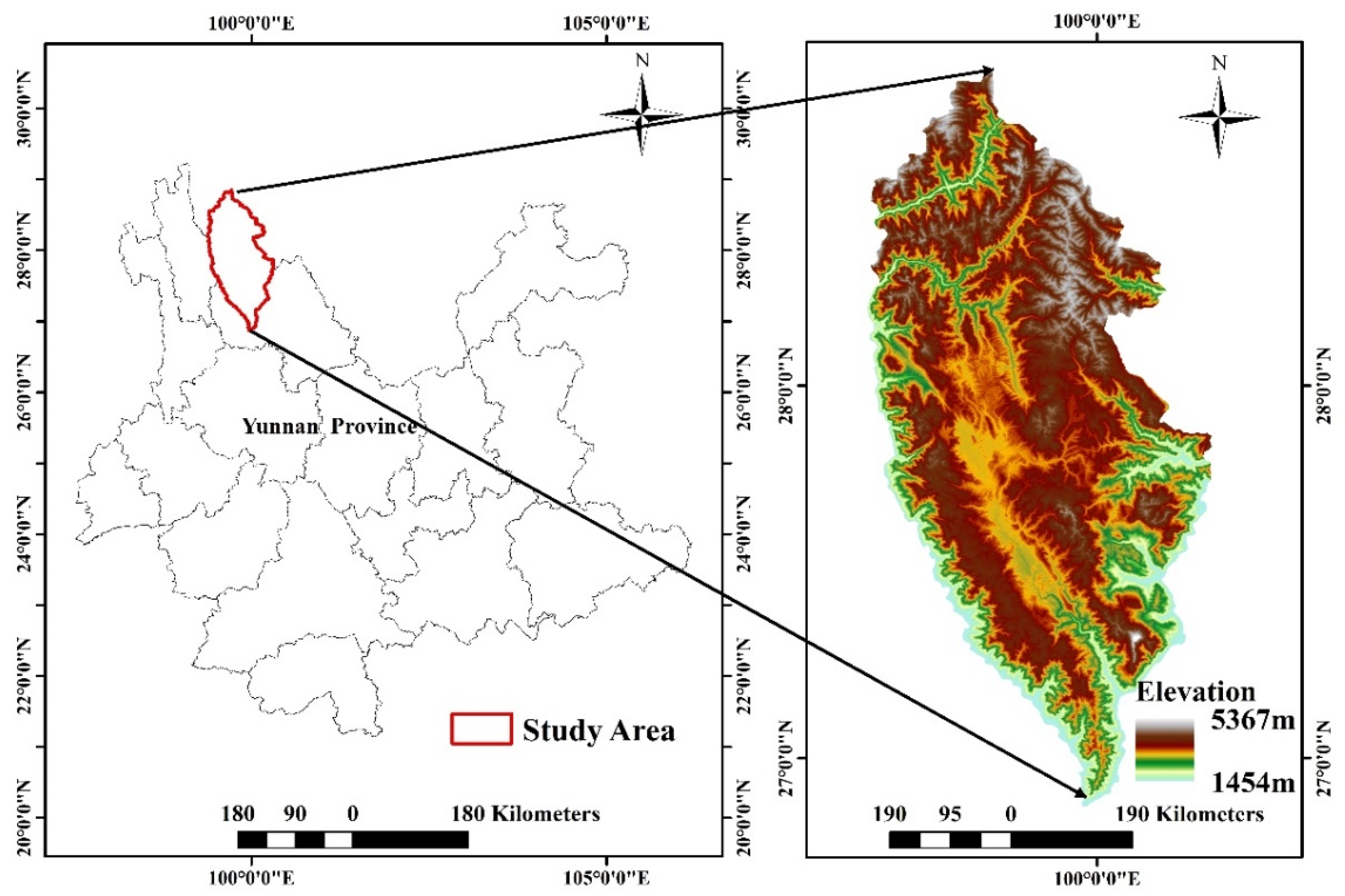
2.1. Study Area
2.2. Data Description and Processing
2.2.1. ICESat-2/ATL08
2.2.2. Optical Remote Sensing and Microwave Remote Sensing Data
2.2.3. SRTM DEM
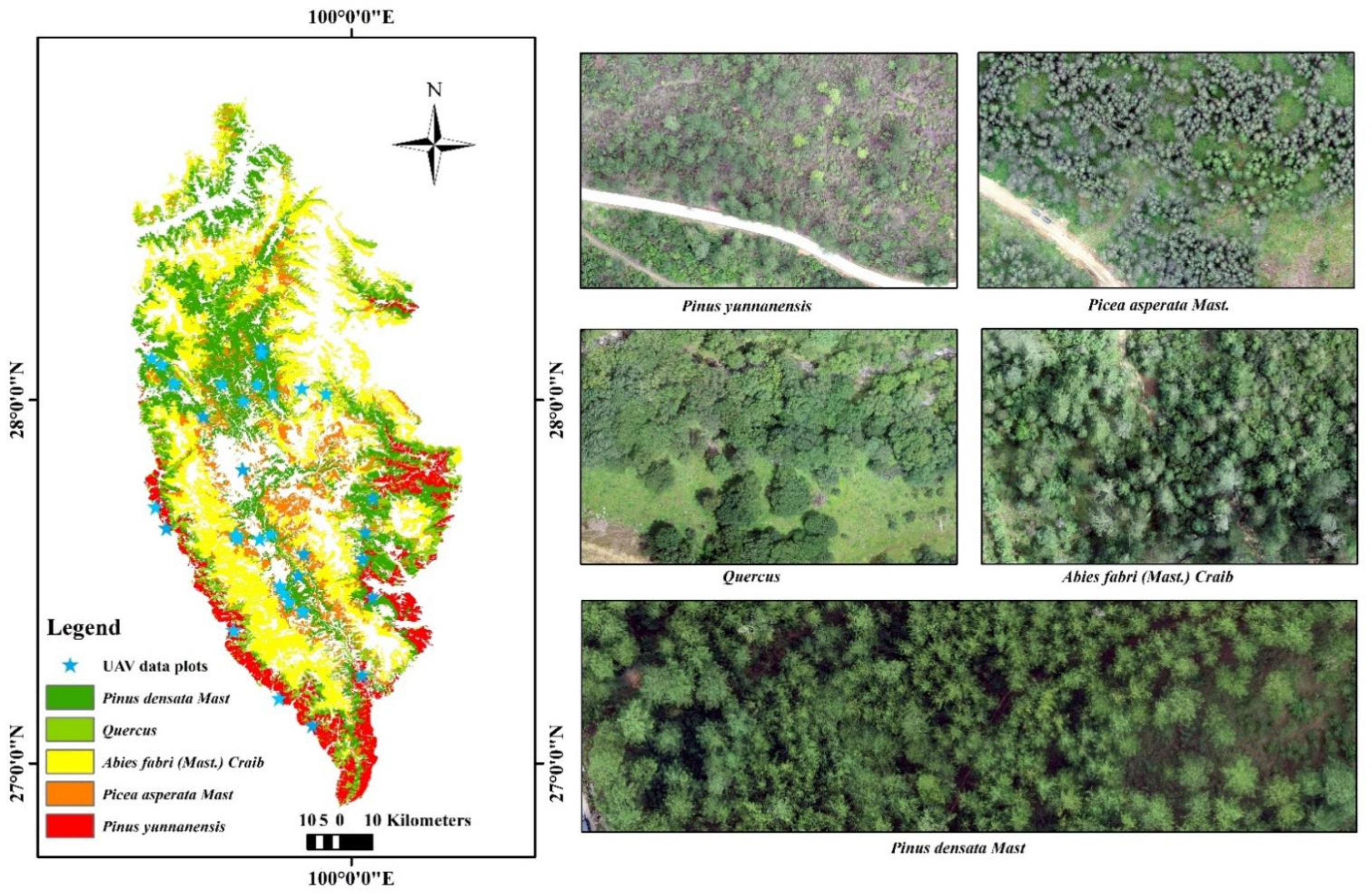
2.2.4. Field, Airborne LiDAR Data Measurements and Forest Survey Data
2.2.5. GlobeLand 30
2.3. Methods
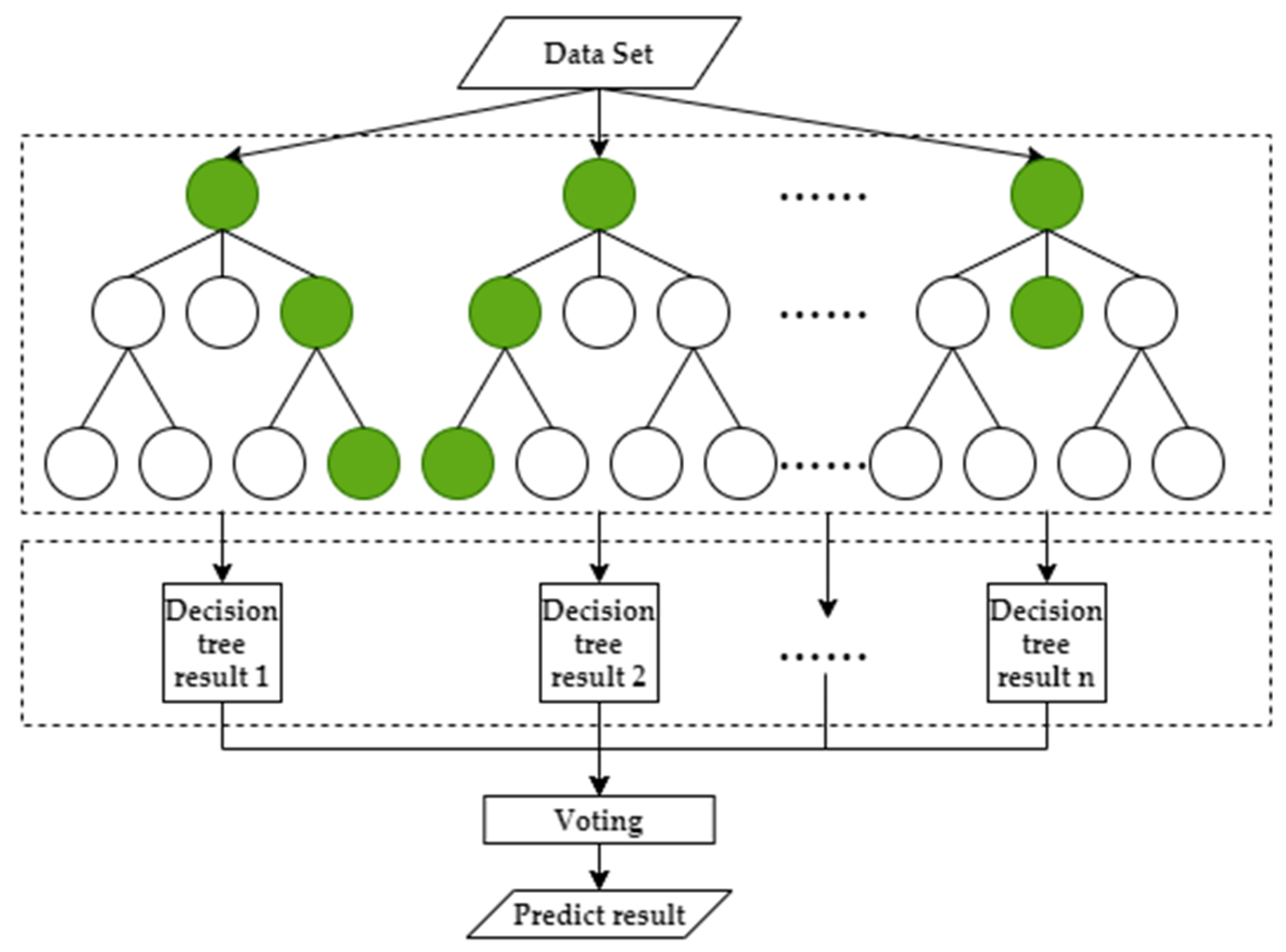
2.3.1. High-Resolution Canopy Height Estimation
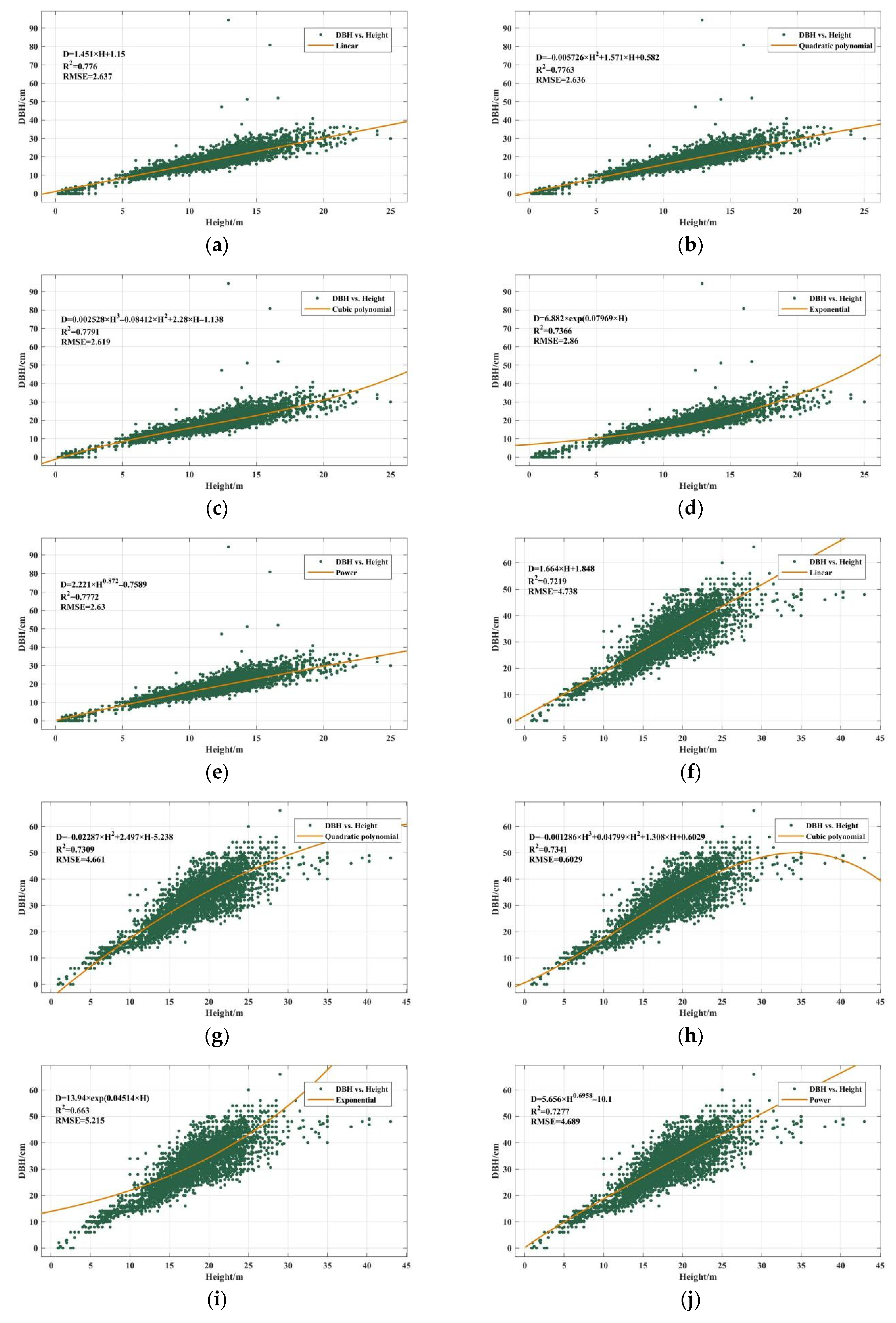
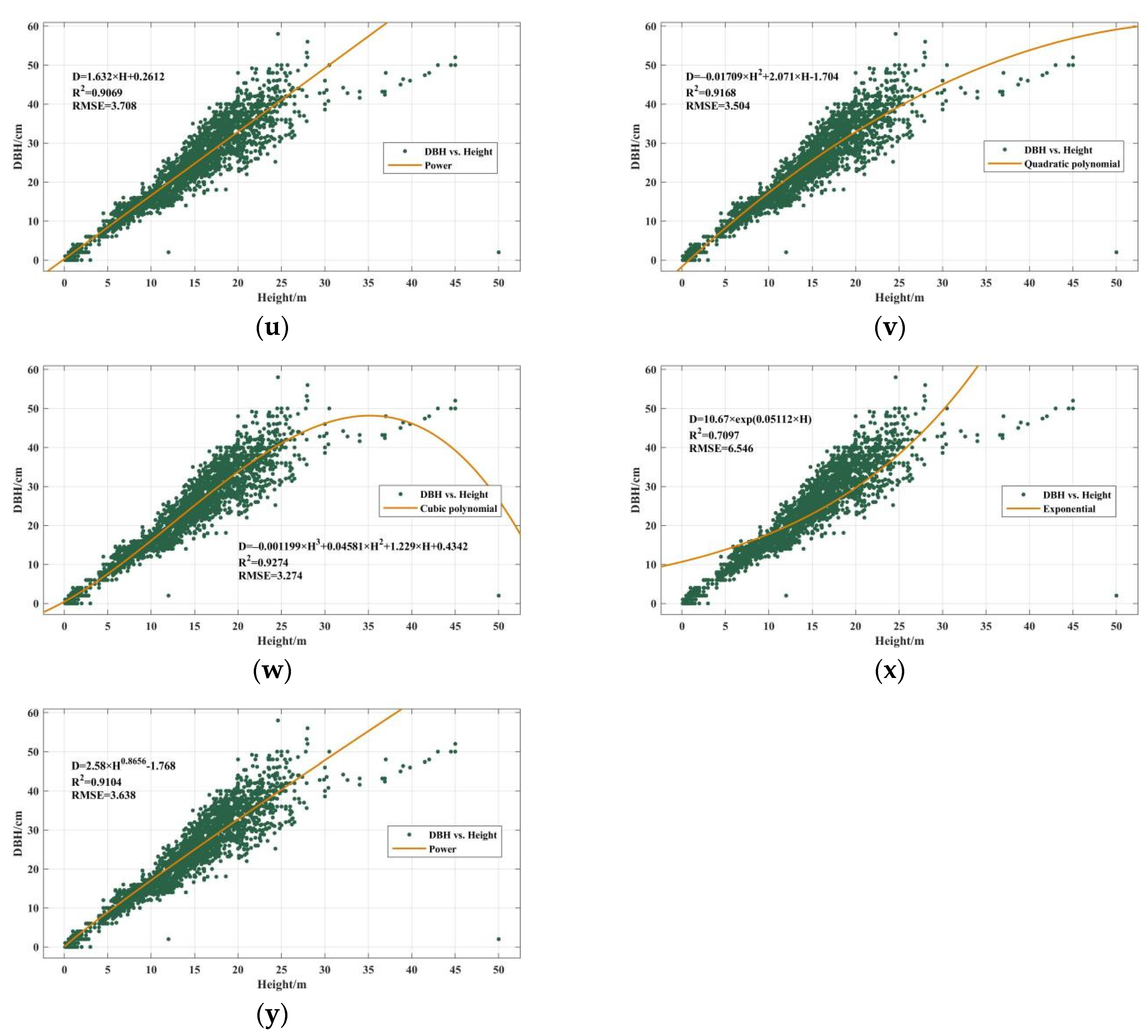
2.3.2. High-Resolution DBH Estimation
2.3.3. Estimation of the Forest Biomass and Carbon Storage
3. Experimental Results
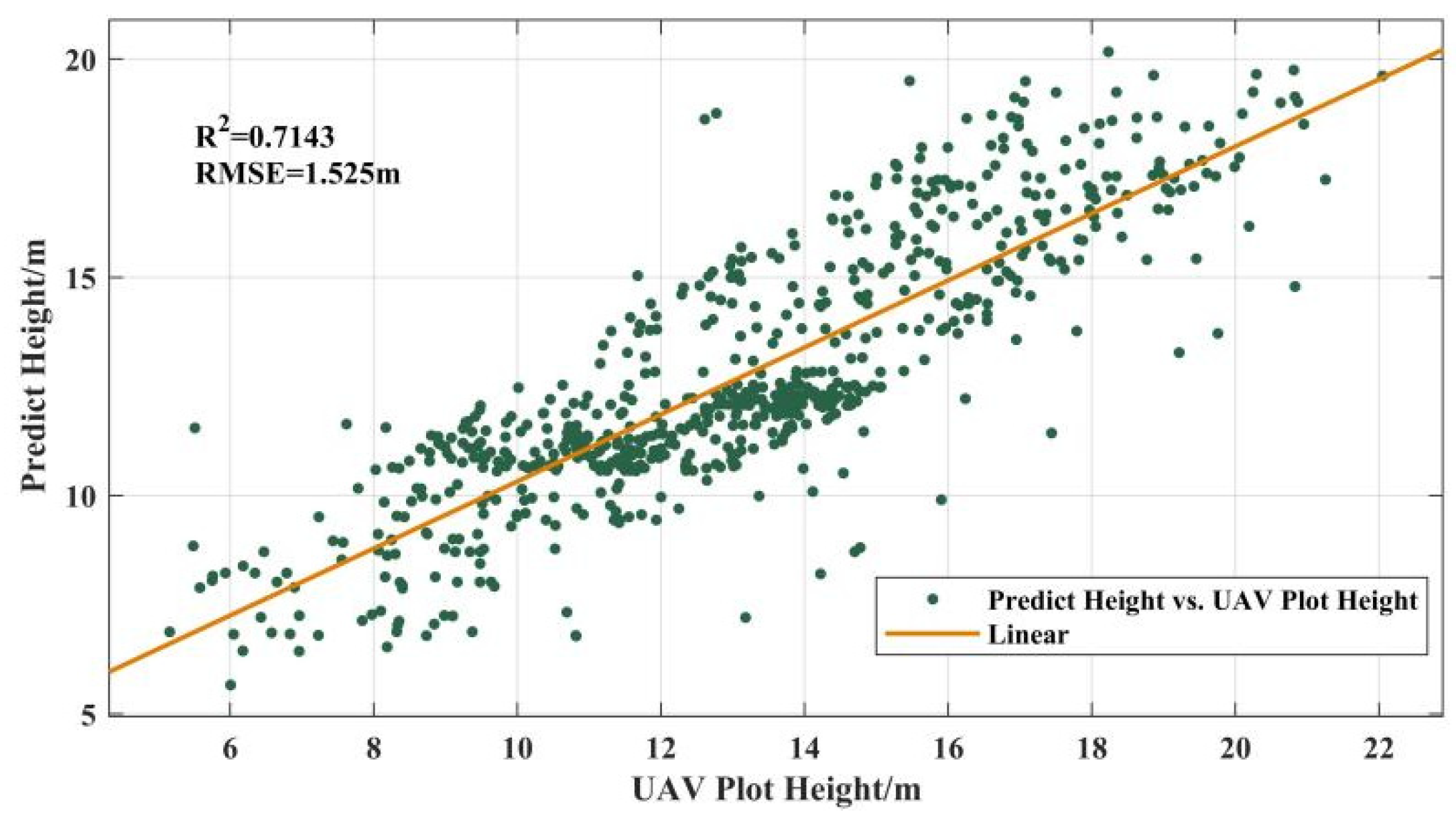
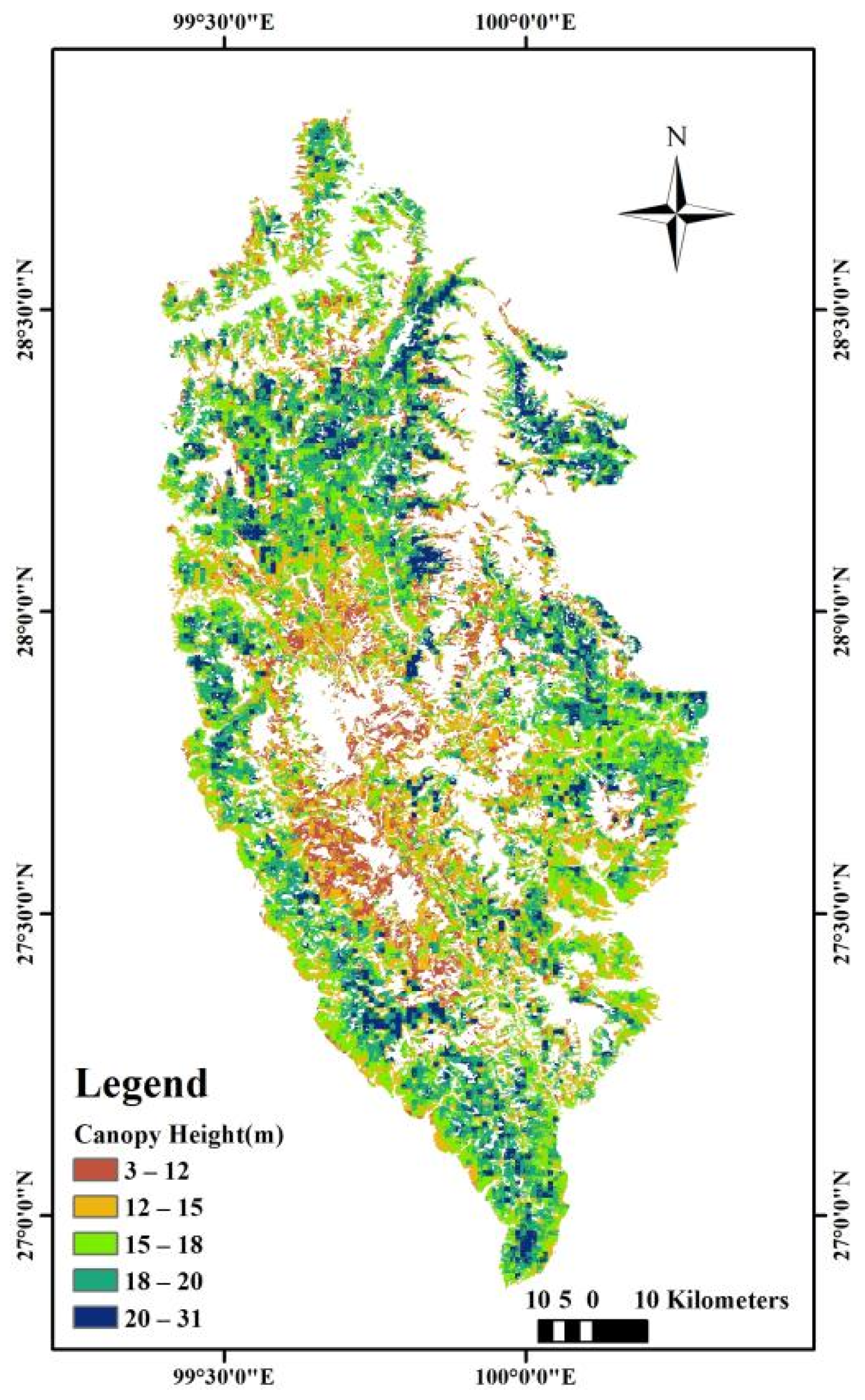
3.1. High-Resolution Canopy Height Mapping
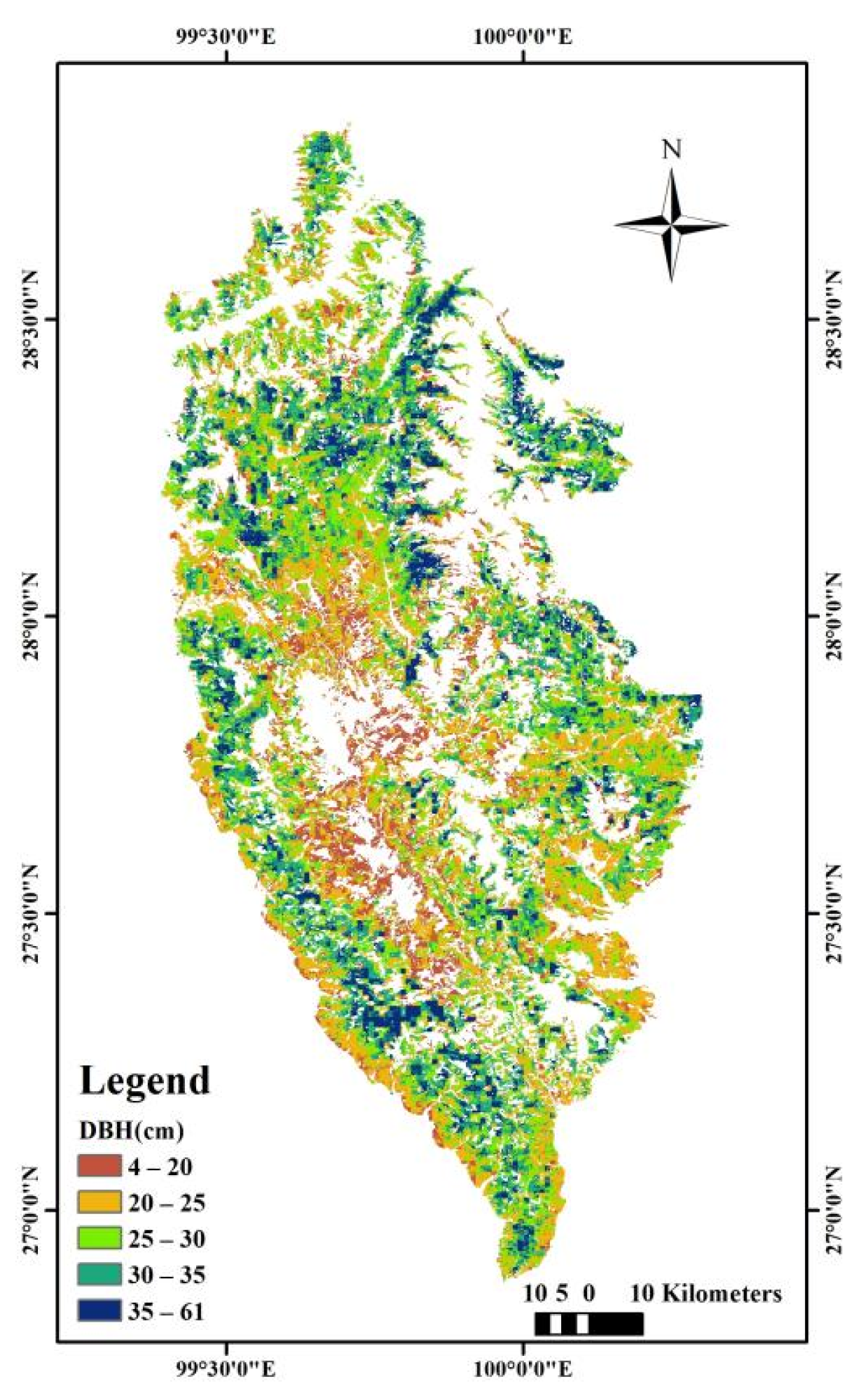
3.2. High-Resolution DBH Mapping
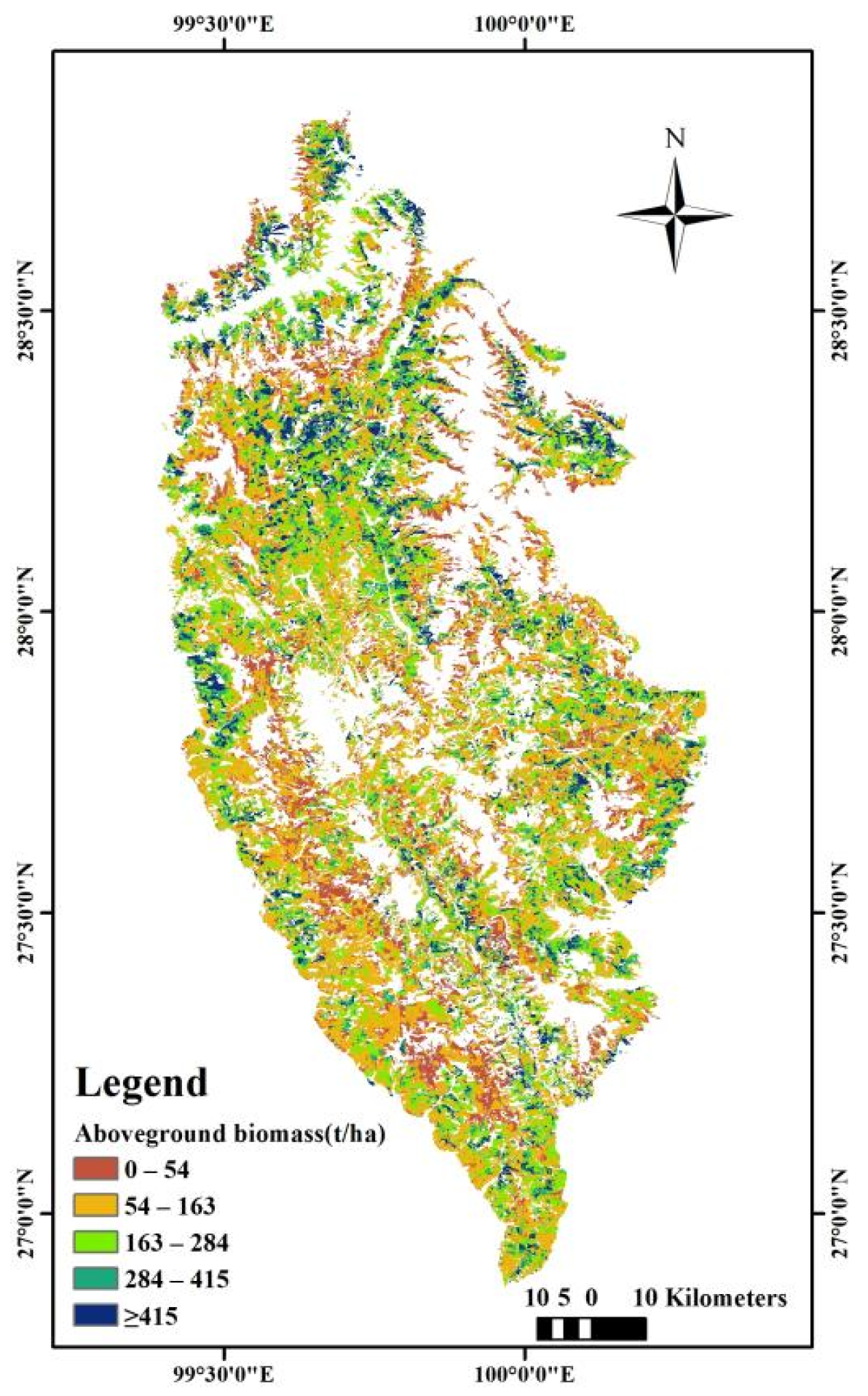
3.3. Mapping of the Forest Biomass and Carbon Storage
4. Discussion
4.1. Importance of Model Variables in Canopy Height Estimation
4.2. Carbon Factor Selection
4.3. Estimation Results for the Forest Aboveground Biomass and Carbon Storage
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, X.; Cao, M.; Li, K. Temporal-Spatial Dynamics of Carbon Storage of Forest Vegetation in China. Prog. Geogr. 2007, 26, 1–10. [Google Scholar]
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A large and Persostent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, S.; Yan, X.; Zhang, L. The relationship between forest ecosystem emergy and forest ecosystem service value in China. Acta Geogr. Sin. 2014, 3, 334–342. [Google Scholar] [CrossRef]
- Meng, X. Tree Surveying, 2nd ed.; China Forestry Publishing House: Beijing, China, 2006; p. 295. [Google Scholar]
- Wang, Y.; Zhao, S. Biomass and net productivity of Picea schrenkiana var tianshanica forest. Chin. J. Appl. Ecol. 1999, 10, 389–391. [Google Scholar]
- Wang, J.; Cheng, P.; Xu, S.; Wang, X.; Cheng, F. Forest biomass estimation in Shangri-La based on the remote sensing. J. Zhejiang A F Univ. 2013, 30, 325–329. [Google Scholar] [CrossRef]
- Li, R.; Liu, J. An Estimation of Wetland Vegetation Biomass in the Poyang Lake Using Landsat ETM Data. Acta Geogr. Sin. 2001, 56, 532–540. [Google Scholar]
- Huang, J.; Ju, W.; Zheng, G.; Kang, T. Estimation of forest aboveground biomass using high spatial resolution remote sensing imagery. Acta Ecol. Sin. 2013, 33, 6497–6508. [Google Scholar] [CrossRef]
- Liu, Q.; Yang, L.; Liu, Q.; Li, J. Review of forest above ground biomass inversion methods based on remote sensing technology. J. Remote Sens. 2015, 19, 62–74. [Google Scholar] [CrossRef]
- Treuhaft, R.N.; Siqueira, P.R. The calculated performance of forest structure and biomass estimate from interferometric Radar. Waves Random Media 2004, 14, 345–358. [Google Scholar] [CrossRef]
- Moghaddam, M.; Dungan, J.L.; Acker, S. Forest variable estimation from fusion of SAR and multispectral optical data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2176–2178. [Google Scholar] [CrossRef]
- Wang, J.; Tang, W. Estimation and analysis of aboveground biomass and carbon storage of arbor forest based on forest resource planning and design survey data: A case study of Shangri-La City. J. Green Sci. Technol. 2021, 23, 14–16. [Google Scholar]
- Zhu, X.; Wang, C.; Nie, S.; Pan, F.; Xi, X.; Hu, Z. Mapping forest height using photon-counting LiDAR data and Landsat 8 OLI data: A case study in Virginia and North Carolina, USA. Ecol. Indic. 2020, 114, 106287. [Google Scholar] [CrossRef]
- Wang, C.; Xi, X.; Luo, S.; Li, G. Spaceborne Ranging LiDAR Data Processing and Application, 1st ed.; Science Press: Beijing, China, 2015. [Google Scholar]
- Lefsky, M.A.; Harding, D.J.; Keller, M.; Cohen, W.B.; Camargo, P.B. Correction to “Estimates of forest canopy height and aboveground biomass using ICESat”. Geophys. Res. Lett. 2006, 33, L05501. [Google Scholar] [CrossRef] [Green Version]
- Naesset, E.; Gobakken, T. Estimation of above-and below-ground biomass across regions of the boreal forest zone using airborne laser. Remote Sens. Environ. 2008, 112, 3079–3090. [Google Scholar] [CrossRef]
- Huang, K.; Pang, Y.; Shu, Q.; Fu, T. Aboveground forest biomass estimation using ICESat GLAS in Yunnan, China. J. Remote Sens. 2013, 17, 165–179. [Google Scholar]
- Han, W.; Wang, J.; Ke, H.; Fu, L. Research on acquiring information of LU/LC by remote sense image based on GIS-A case study of Shangri-La county, the Northwestern Yunnan. Yunnan Geogr. Environ. Res. 2007, 19, 98–102. [Google Scholar]
- Pan, J.; Wang, J.; Gao, F. Research of land use change and ecological security of typical area of alpine canyon in Northwest Yunnan. Ecol. Sci. 2022, 41, 29–40. [Google Scholar] [CrossRef]
- Yang, C.; Wang, J. Dynamic Remote Sensing Monitoring of Soil Erosion in Shangri-La, Northwest Yunnan. J. Kunming Univ. Sci. Technol. (Nat. Sci. Ed.) 2015, 40, 32–39. [Google Scholar] [CrossRef]
- Sun, X.; Yu, Y.; Wang, J.; Liu, W. Analysis of the Spatiotemporal Variation in Habitat Quality Based on the InVEST Model-A Case Study of Shangri-La City, Northwest Yunnan, China. J. Phys. Conf. Ser. 2021, 1961, 012016. [Google Scholar] [CrossRef]
- Wang, C.; Xi, X.; Yang, X.; Nie, S. Introduction to LiDAR Remote Sensing, 1st ed.; Higher Education Press: Beijing, China, 2022; pp. 69–71. [Google Scholar]
- Zhu, X. Forest Height Retrieval of China with a Resolution of 30 m Using ICESat-2 and GEDI Data; University of Chinese Academy of Sciences: Beijing, China, 2021. [Google Scholar]
- Neuenschwander, A.; Pitts, K.; Jelley, B.; Robbins, J.; Klotz, B.; Popescu, S.; Nelson, R.; Harding, D.; Pederson, D.; Sheridan, R. Ice, Cloud, and Land Elevation Satellite 2 (ICESat-2) Algorithm Theoretical Basis Document (ATBD) for Land—Vegetation along-Track Products (ATL08). Available online: https://nsidc.org/sites/nsidc.org/files/technical-references/ICESat2_ATL08_ATBD_r003.pdf (accessed on 6 June 2022).
- Neuenschwander, A.; Pitts, K. The ATL08 land and vegetation product for the ICESat-2 Mission. Remote Sens. Environ. 2019, 221, 247–259. [Google Scholar] [CrossRef]
- Liao, A.; Peng, S.; Wu, H.; Chen, L.; Zhang, W. The Production System of 30 m Global Land Cover Mapping and Its Application. Bull. Surv. Mapp. 2015, 10, 4–8. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the structure and allometry of plant vascular systems. Nature 1999, 400, 664–667. [Google Scholar] [CrossRef]
- Kaitaniemi, P. Testing allometric scaling laws. J. Theor. Biol. 2004, 228, 149–153. [Google Scholar] [CrossRef] [PubMed]
- Ketterings, Q.M.; Coe, R.; Van, N.M.; Ambagau, Y.; Palm, C.A. Reducing uncertainty in the use of allometric biomass equations for predicting above-ground tree biomass in mixed secondary forests. For. Ecol. Manag. 2001, 146, 199–209. [Google Scholar] [CrossRef]
- Ou, G.; Xu, H. A Review on Forest Biomass Models. J. Southwest For. Univ. 2020, 40, 1–10. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X.; Yue, C.; Cheng, F.; Xu, T.; Cheng, P.; Wang, X.; Gao, Y. Carbon content rate in dominant species of four forest types in Shangri-la, northwest Yunnan province. Ecol. Environ. Sci. 2012, 1, 613–619. [Google Scholar] [CrossRef]
- Su, Y.; Guo, Q.; Xue, B.; Hu, T.; Alvarez, O.; Tao, S.; Fang, J. Spatial distribution of forest aboveground biomass in China: Estimation through combination of spaceborne LiDAR, optical imagery, and forest inventory data. Remote Sens. Environ. 2016, 173, 187–199. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.; Xu, X.; Jia, Y.; Wang, D.; Li, Y. Experimental Practice Guidance of Forest Ecology, 1st ed.; China Forestry Publishing House: Beijing, China, 2021; pp. 12–17. [Google Scholar]
- Matasci, G.; Hermosilla, T.; Wulder, M.; White, J.; Coops, N.; Hobart, G.; Zald, H. Large-area mapping of Canadian boreal forest cover, height, biomass and other structural attributes using Landsat composites and LiDAR plots. Remote Sens. Environ. 2018, 209, 90–106. [Google Scholar] [CrossRef]
- Fang, J.; Liu, G.; Xu, S. Carbon Pools of Terrestrial Ecosystems in China, 1st ed.; China Environmental Science Press: Beijing, China, 1996; pp. 109–128. [Google Scholar]
- Yue, C. Forest Biomass Estimation in Shangri-La County Based on Remote Sensing; Beijing Forestry University: Beijing, China, 2011. [Google Scholar]
- Cheng, F. Forest Biomass Estimation of Yunnan Province Using Multi-Source Remote Sensing Data; Yunnan Normal University: Kunming, China, 2011. [Google Scholar]




| Type | Name | Spatial Resolution | Data Source |
|---|---|---|---|
| LiDAR data | ICESat-2/ATLAS | 100 m | NSIDC (https://nsidc.org/data/icesat-2/data-sets (accessed on 6 June 2022)) |
| ULS | - | Rigel-VUX-1 | |
| Optical remote sensing data | Landsat 8 OLI | 30 m | USGS (http://earthexplorer.usgs.gov (accessed on 6 June 2022)) |
| Sentinel-2 | 10 m | USGS (http://earthexplorer.usgs.gov (accessed on 6 June 2022)) | |
| Microwave remote sensing data | Sentinel-1 | 20 m | USGS (http://earthexplorer.usgs.gov (accessed on 6 June 2022)) |
| DEM | SRTM 1 | 30 m | USGS (http://earthexplorer.usgs.gov (accessed on 6 June 2022)) |
| Thematic Data | Globeland 30 | 30 m | www.globallandcover.com (accessed on 6 June 2022) |
| 2016 Forest survey data | Forest government |
| Type | Factors |
|---|---|
| Location | Latitude, Longitude |
| Terrain | Slope, Elevation, |
| Vegetion Index | the normalized difference green index (NDGI), the ratio vegetation index (RVI), the normalized burn ratio (NBR),the enhanced vegetation index (EVI), the difference vegetation index (DVI), the normalized difference vegetation index (NDVI), the normalized difference built-up index (NDBI),the terrestrial chlorophyll index (MTCI),the inverted red-edge chlorophyll index (IRECI), the normalized difference water index (NDWI), modified NDWI (MNDWI), the Pigment-Specific-Simple Ratio (PSSRa) |
| Sentinel-1 | Vertically-polarized (VV), Horizontally-polarized (VH) |
| Landsat8 OLI | The red band(B4_1), the near-infrared band (B5_1), the first short wave infrared band (B6_1), the second short wave infrared band (B7_1) |
| Sentinel-2 | The blue band (B2), the red band (B4), the visible and near-infrared band (B5), the visible and near-infrared band (B6), the visible and near-infrared band (B7), the visible and near-infrared band (B8), the visible and near-infrared band (B8A), the short wave infrared band (B11), the short wave infrared band (B12) |
| ID | Model | Express | Parameters |
|---|---|---|---|
| 1 | Linear | D = a + b × H | a, b |
| 2 | Exponential | D = a × ebH | a, b |
| 3 | Power | D = a × Hb | a, b |
| 4 | Quadratic polynomial | D = a + b × H + c × H2 | a, b, c |
| 5 | Cubic polynomial | D = a + b × H + c × H2 + d × H3 | a, b, c, d |
| Spieces of Trees | Above Ground Biomass Model |
|---|---|
| Abies fabri (Mast.) Craib | W = 0.06127D2.05753H0.50839 |
| Quercus | W = 0.07806D2.06321H0.57393 |
| Pinus densata Mast. | W = 0.0730D2.3560H0.1090 |
| Picea asperata Mast. | W = 0.09152D2.2106H0.25663 |
| Pinus yunnanensis | W = 0.070231D2.10392H0.41120 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Y.; Pan, J.; Wang, J.; Liu, Q.; Zhang, J. Mapping of Forest Biomass in Shangri-La City Based on LiDAR Technology and Other Remote Sensing Data. Remote Sens. 2022, 14, 5816. https://doi.org/10.3390/rs14225816
Deng Y, Pan J, Wang J, Liu Q, Zhang J. Mapping of Forest Biomass in Shangri-La City Based on LiDAR Technology and Other Remote Sensing Data. Remote Sensing. 2022; 14(22):5816. https://doi.org/10.3390/rs14225816
Chicago/Turabian StyleDeng, Yuncheng, Jiya Pan, Jinliang Wang, Qianwei Liu, and Jianpeng Zhang. 2022. "Mapping of Forest Biomass in Shangri-La City Based on LiDAR Technology and Other Remote Sensing Data" Remote Sensing 14, no. 22: 5816. https://doi.org/10.3390/rs14225816
APA StyleDeng, Y., Pan, J., Wang, J., Liu, Q., & Zhang, J. (2022). Mapping of Forest Biomass in Shangri-La City Based on LiDAR Technology and Other Remote Sensing Data. Remote Sensing, 14(22), 5816. https://doi.org/10.3390/rs14225816