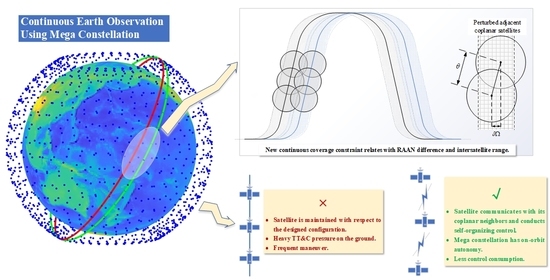
Self-Organizing Control of Mega Constellations for Continuous Earth Observation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Continuous Coverage Constraint of Mega Constellation
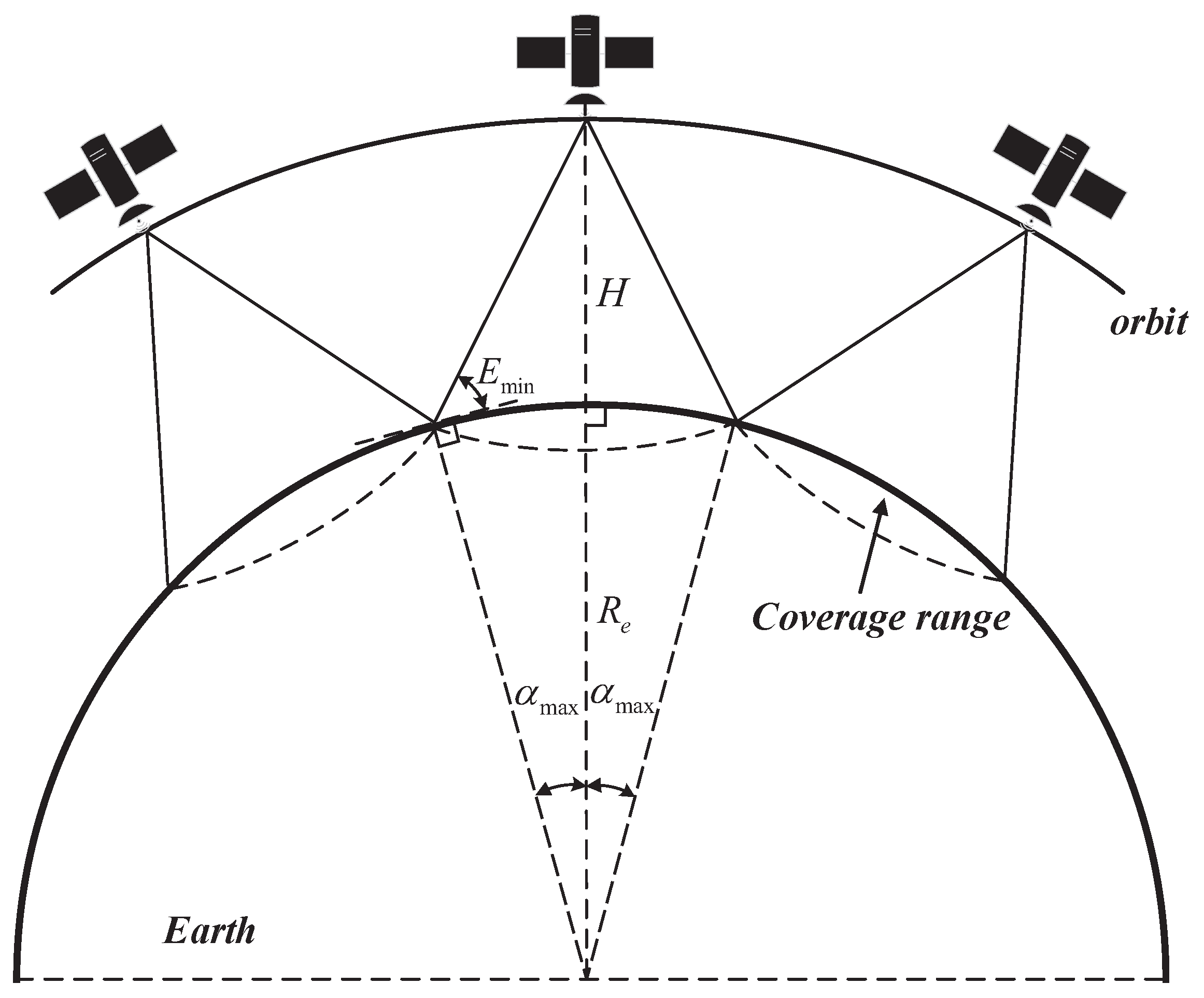
2.1.1. Definition of Continuous Coverage
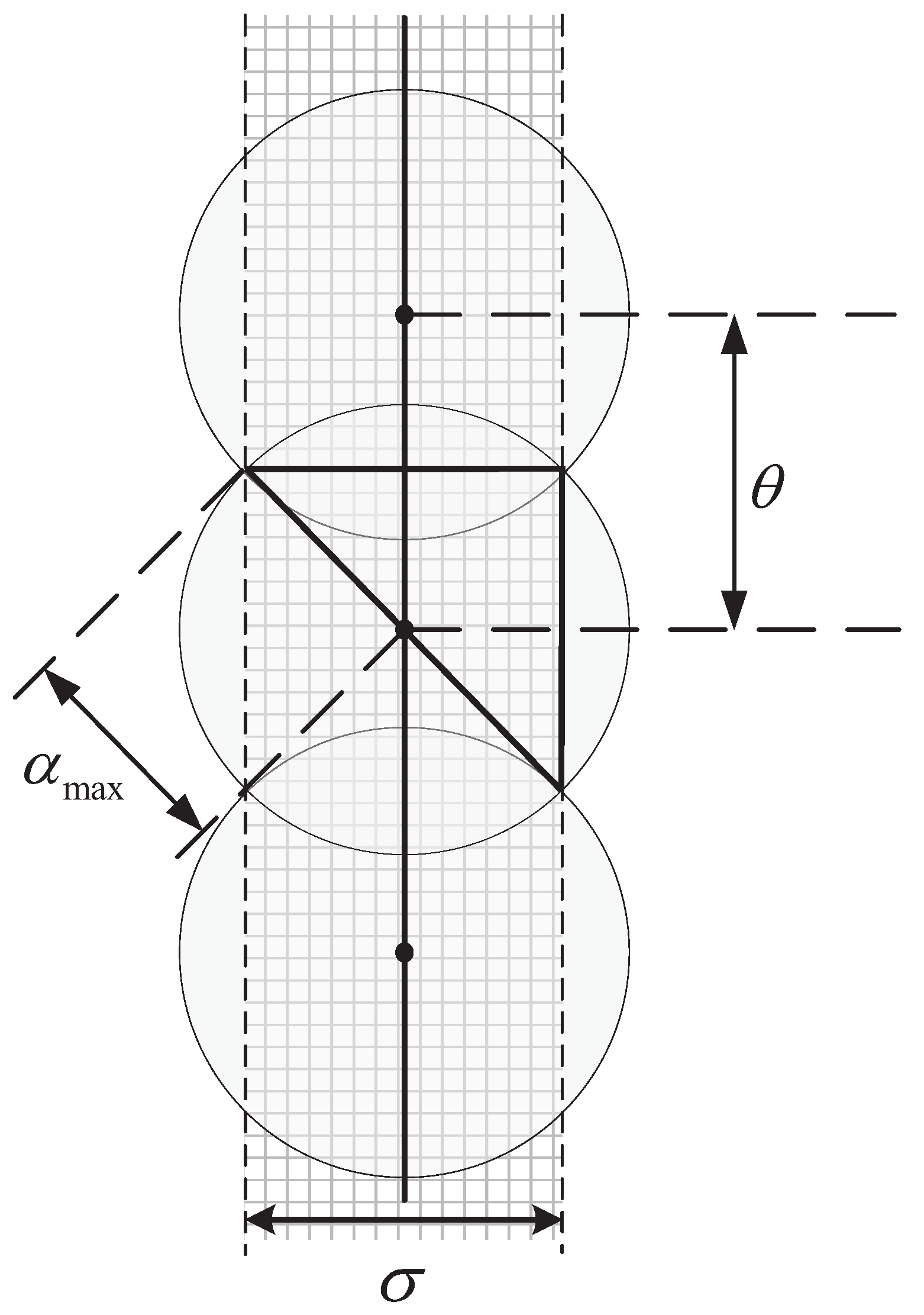
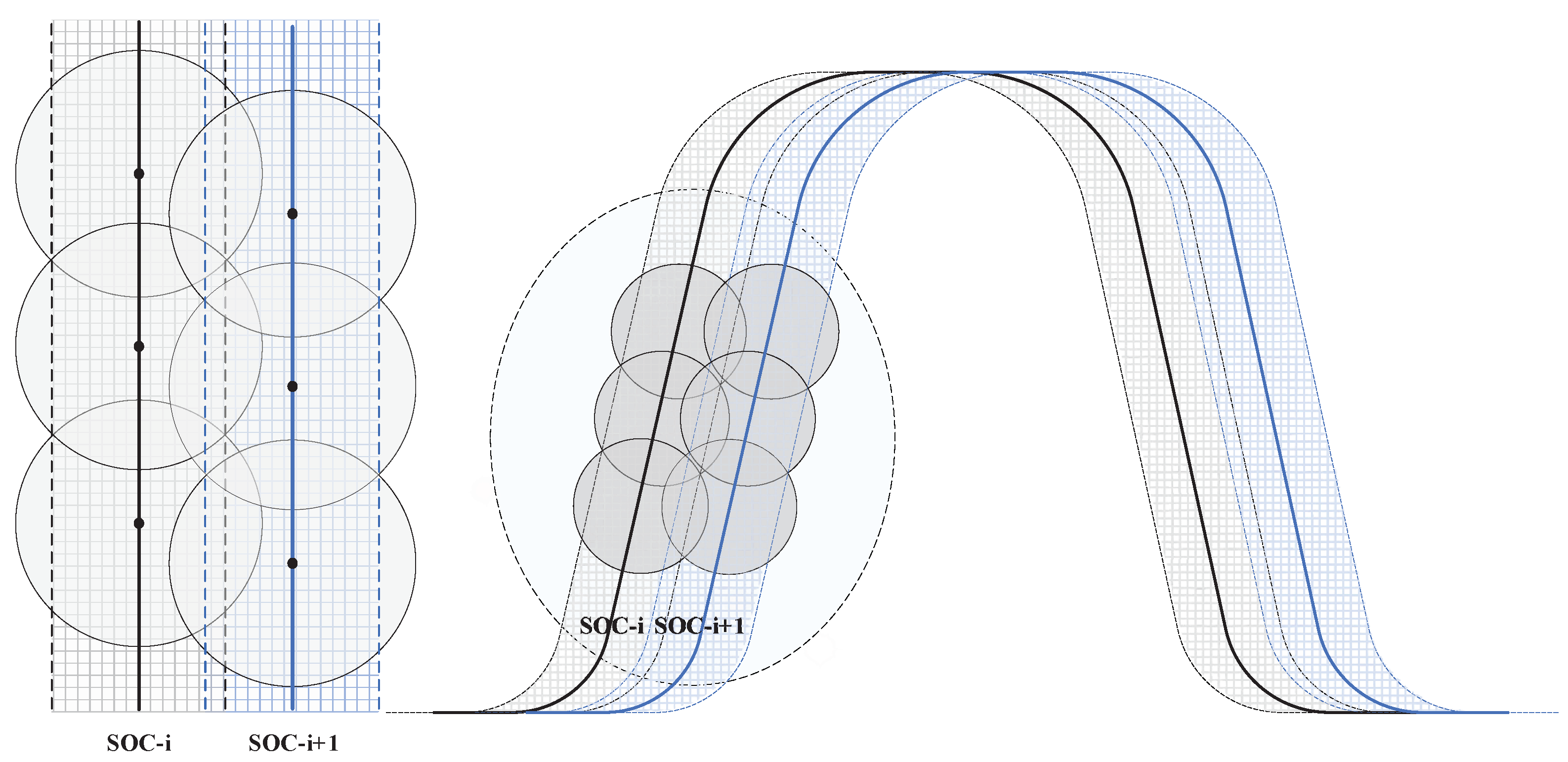
2.1.2. Configuration Requirements for Mega Constellations
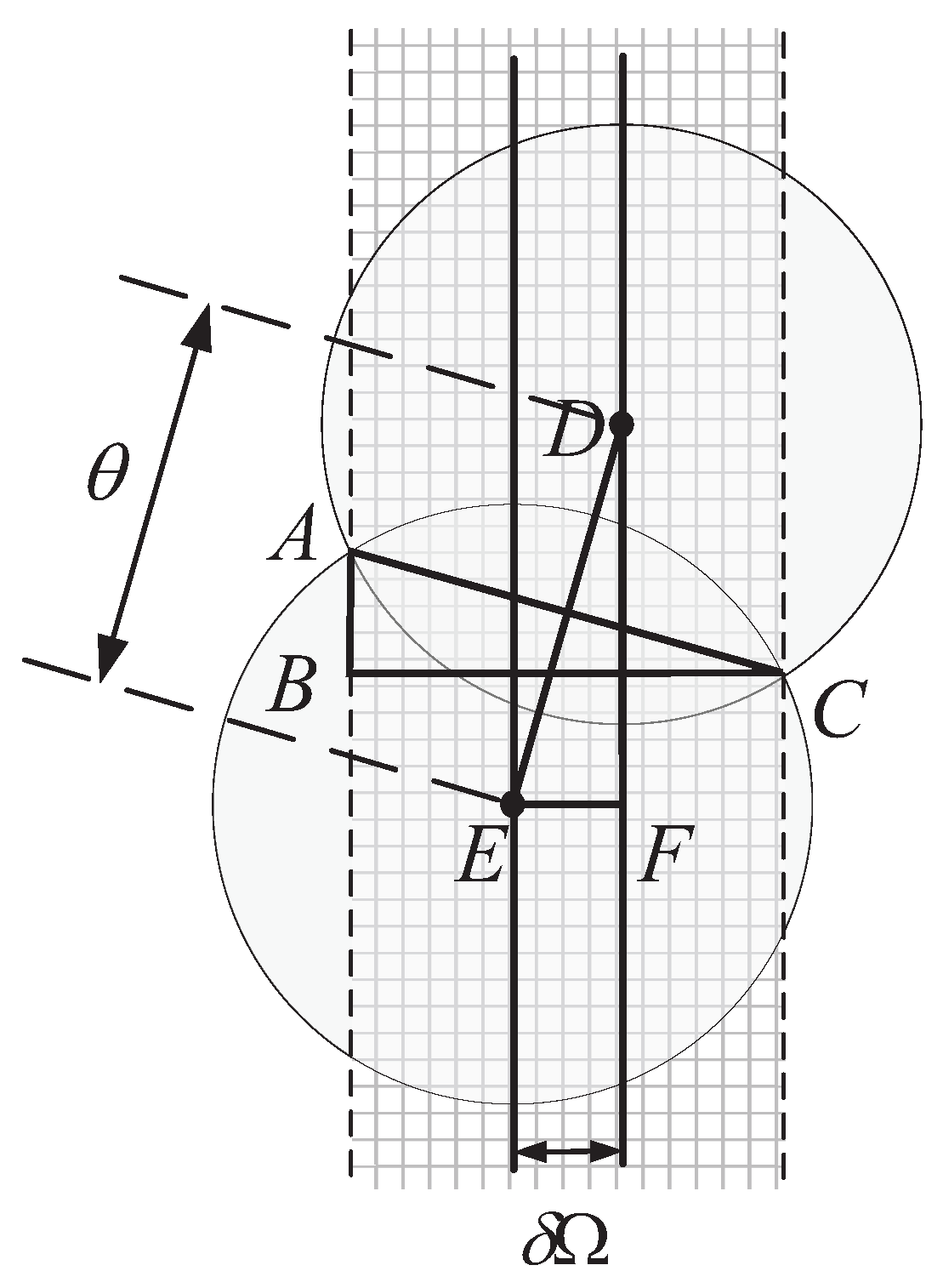
2.1.3. Intersatellite Motion Constraints
2.2. Self-Organizing Control Using Artificial Potential Functions
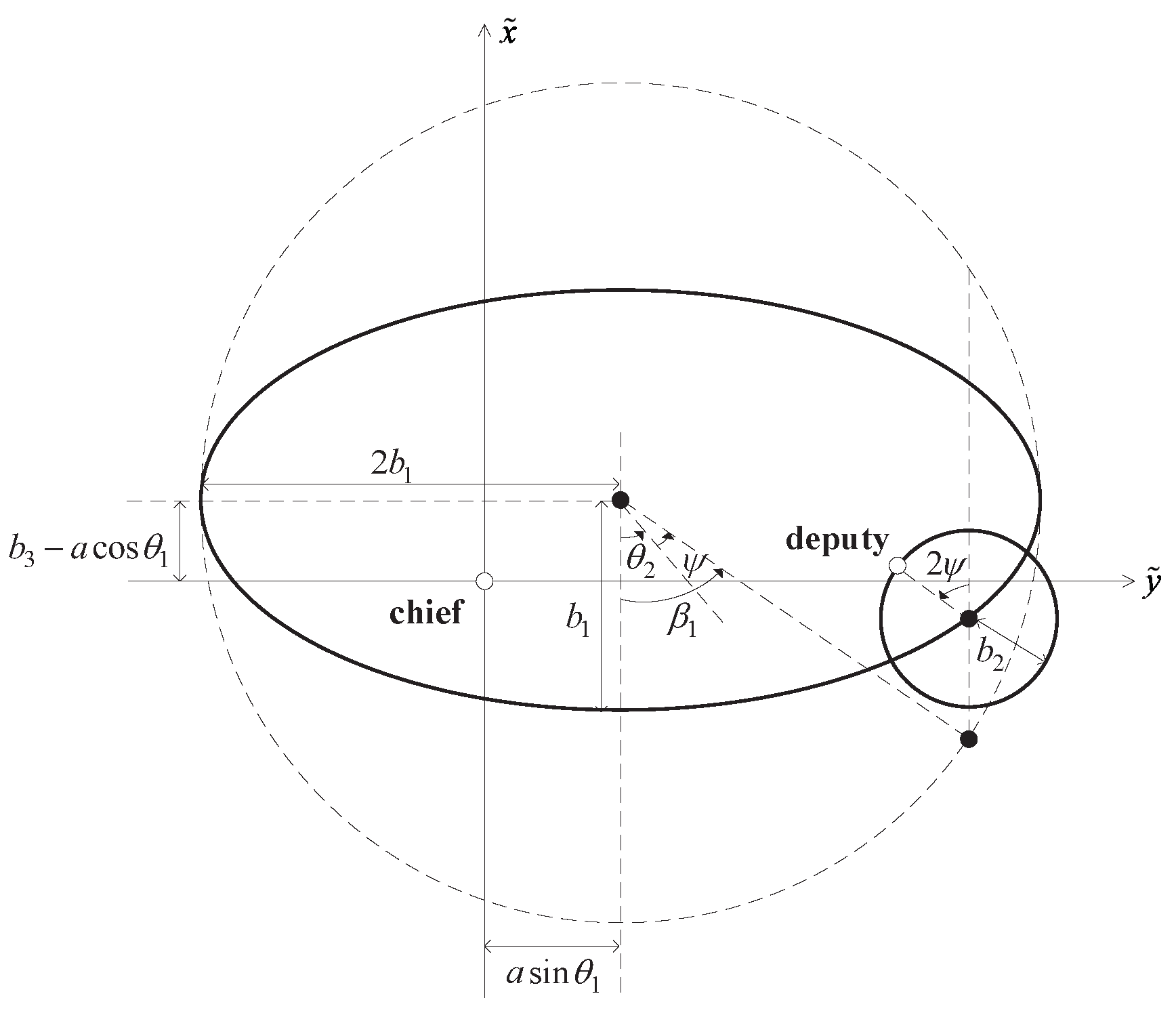
2.2.1. Scale-Independent Relative Orbital Elements and Bound Formulations
2.2.2. Design of Artificial Potential Functions for Single Satellite Control
- (1)
- RAAN Control
- (2)
- Relative Motion-bound Control
- (3)
- Semi-Major Axis Control
2.2.3. Self-Organizing Control Rules for Coplanar Satellites
2.3. Stability Proof of Satellite Control
2.3.1. Stability Proof of RAAN Control and Semi-Major Axis Control
2.3.2. Stability Proof of Relative Motion-Bound Control
2.3.3. Selection Criteria of Quadratic Potential Function Variables
- (1)
- Using and as Control Variables
- (2)
- Using Orbital Elements as Control Variables
- (3)
- Using Relative Orbital Elements as Control Variables
3. Results and Discussion
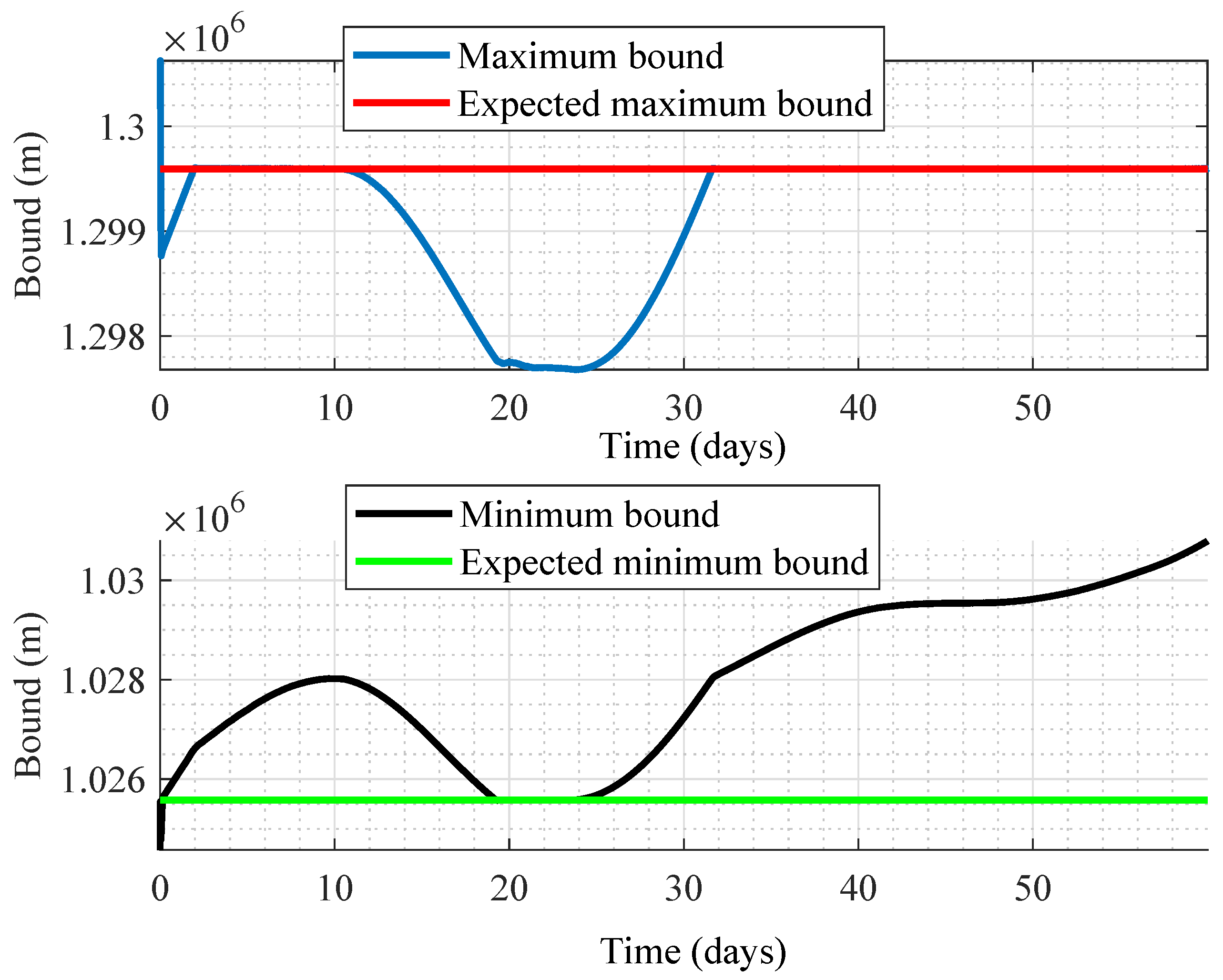
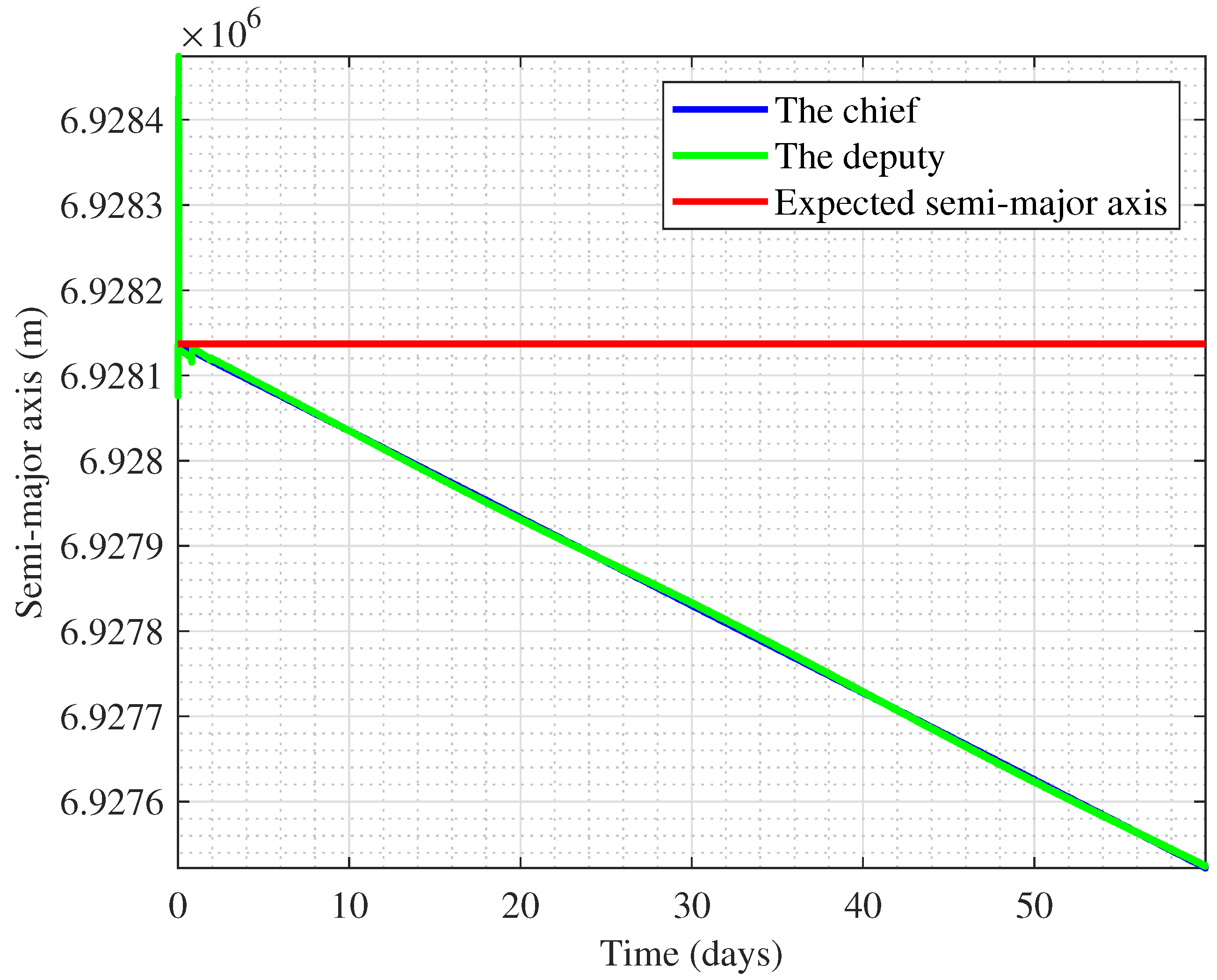
3.1. Self-Organizing Control of Two Satellites
3.2. Self-Organizing Control of Coplanar Satellites
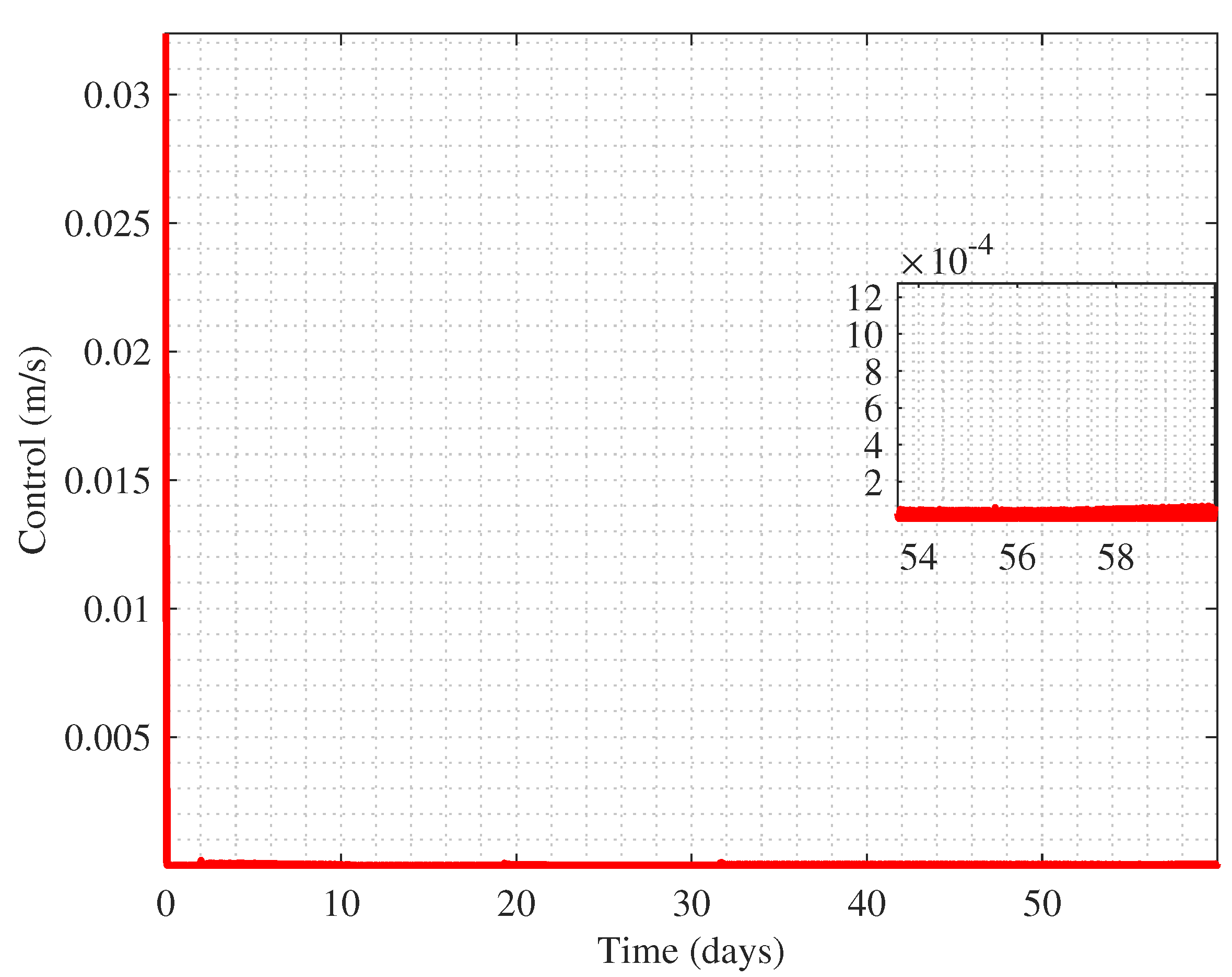
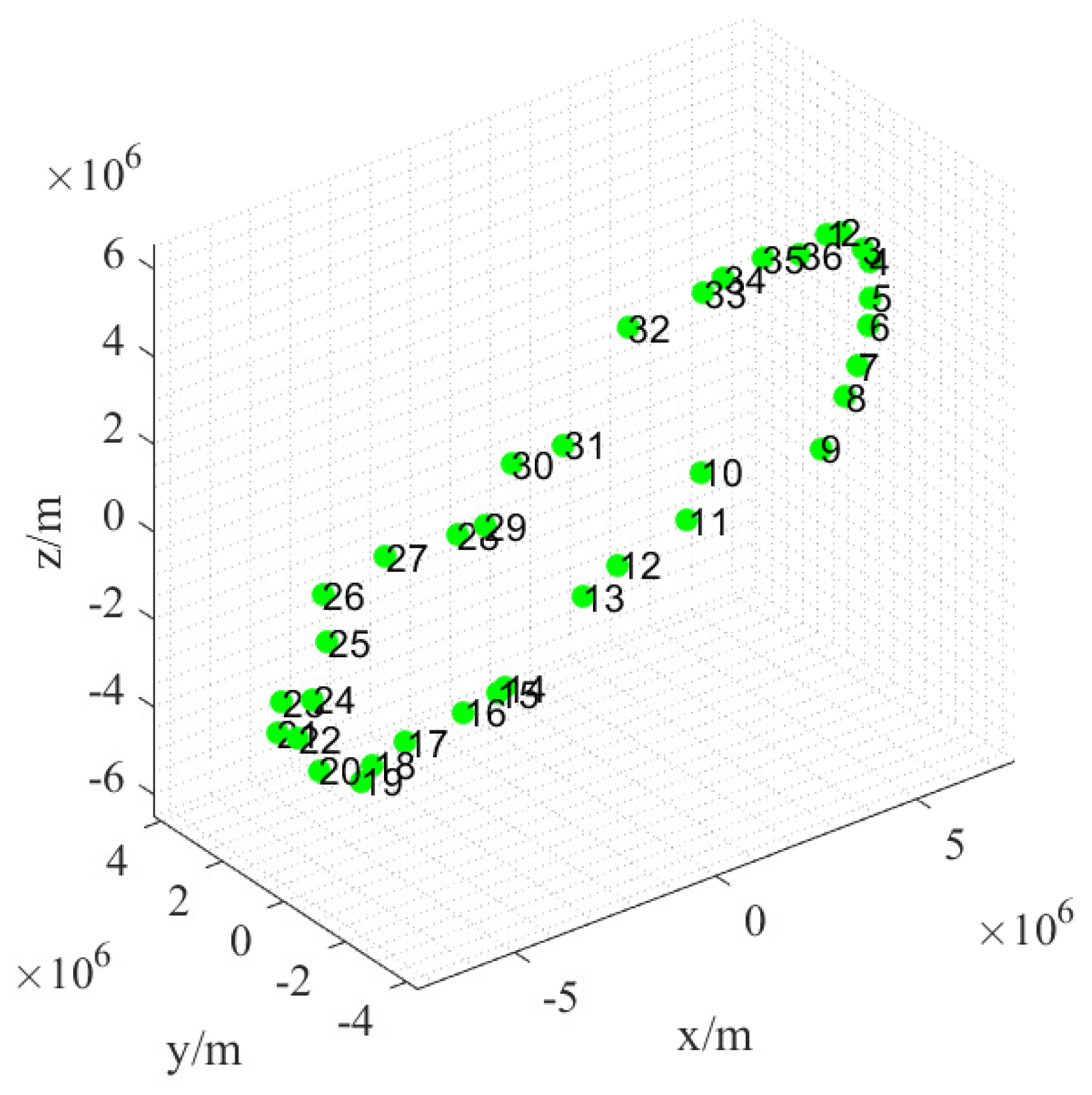
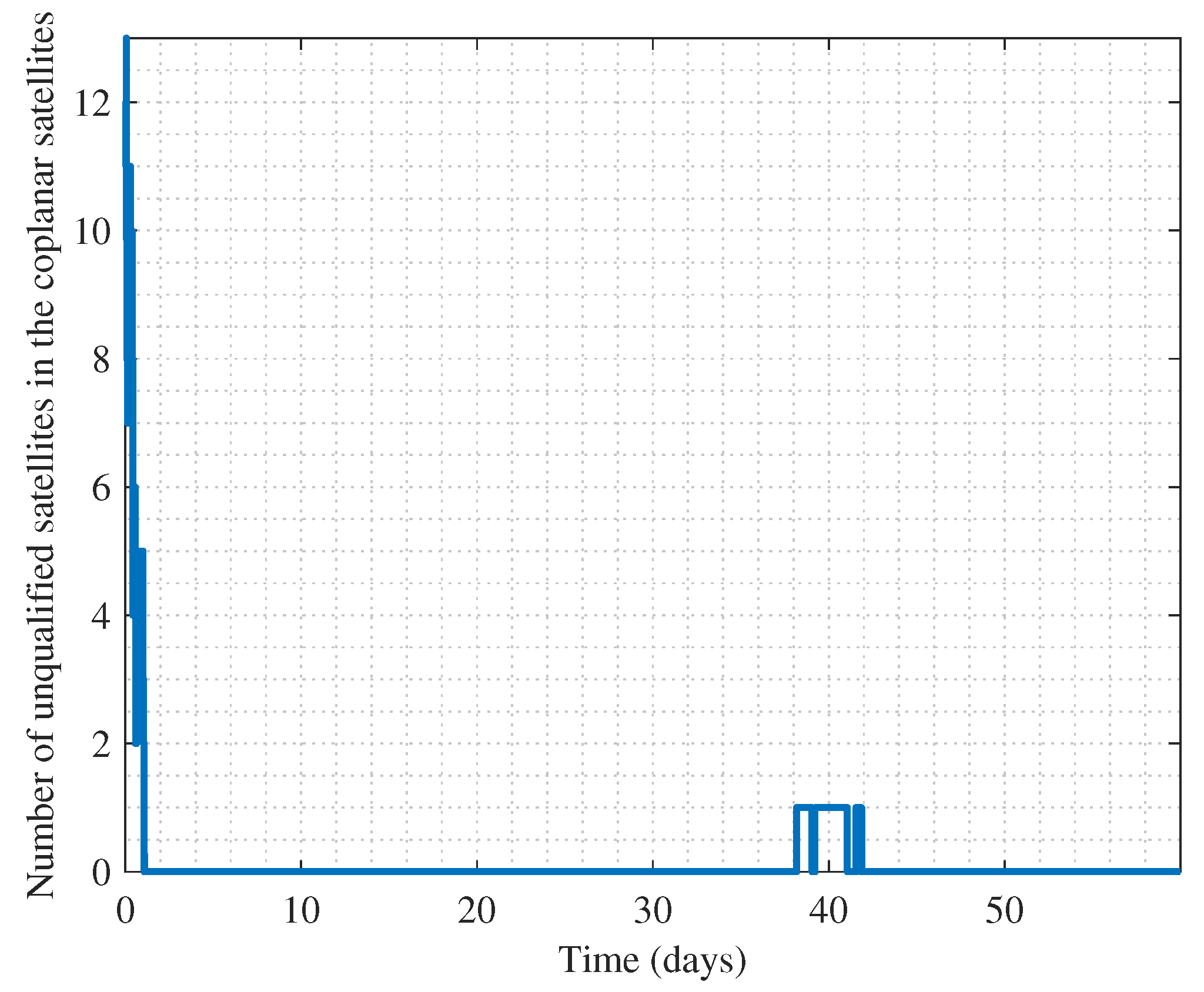
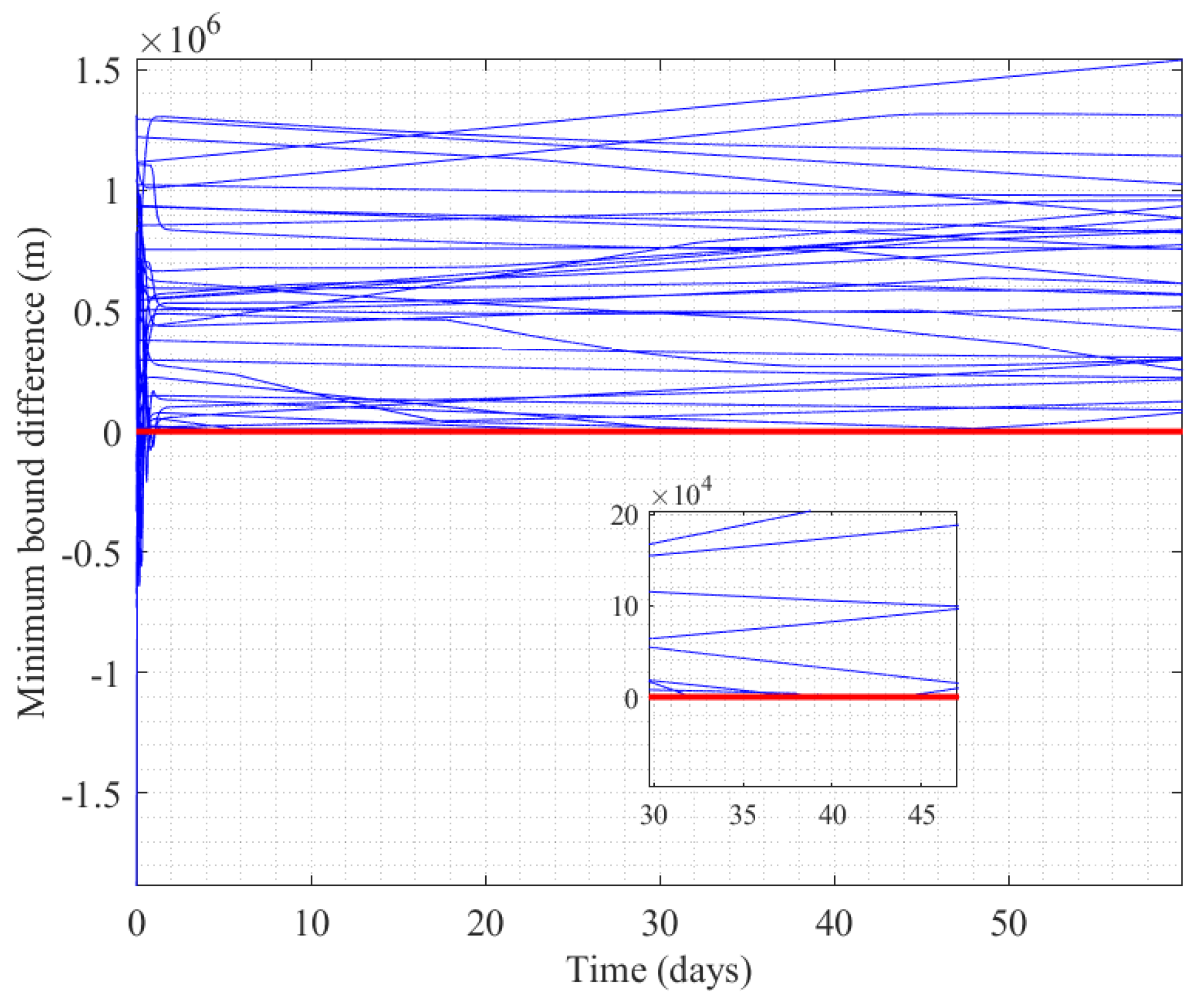
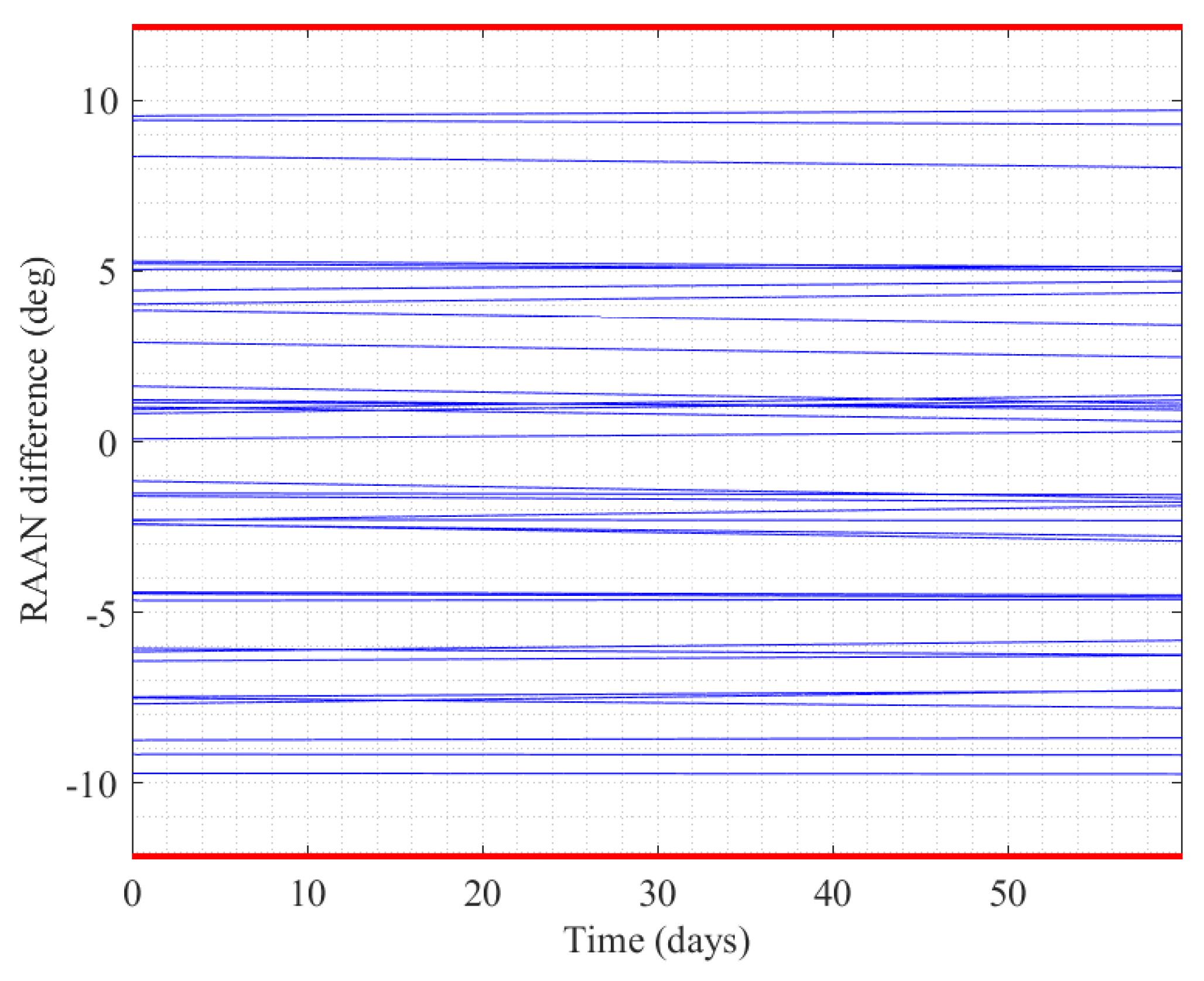
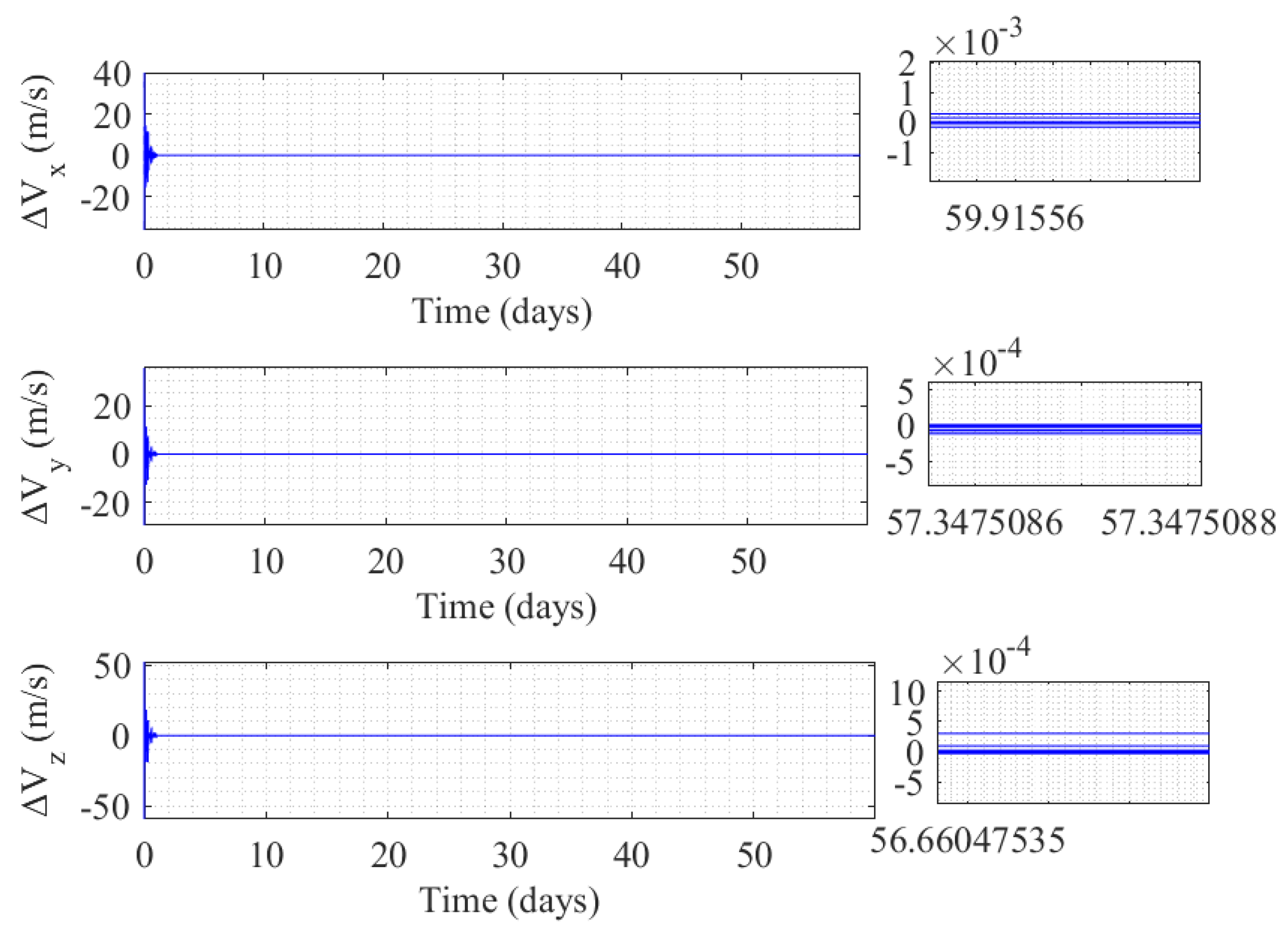
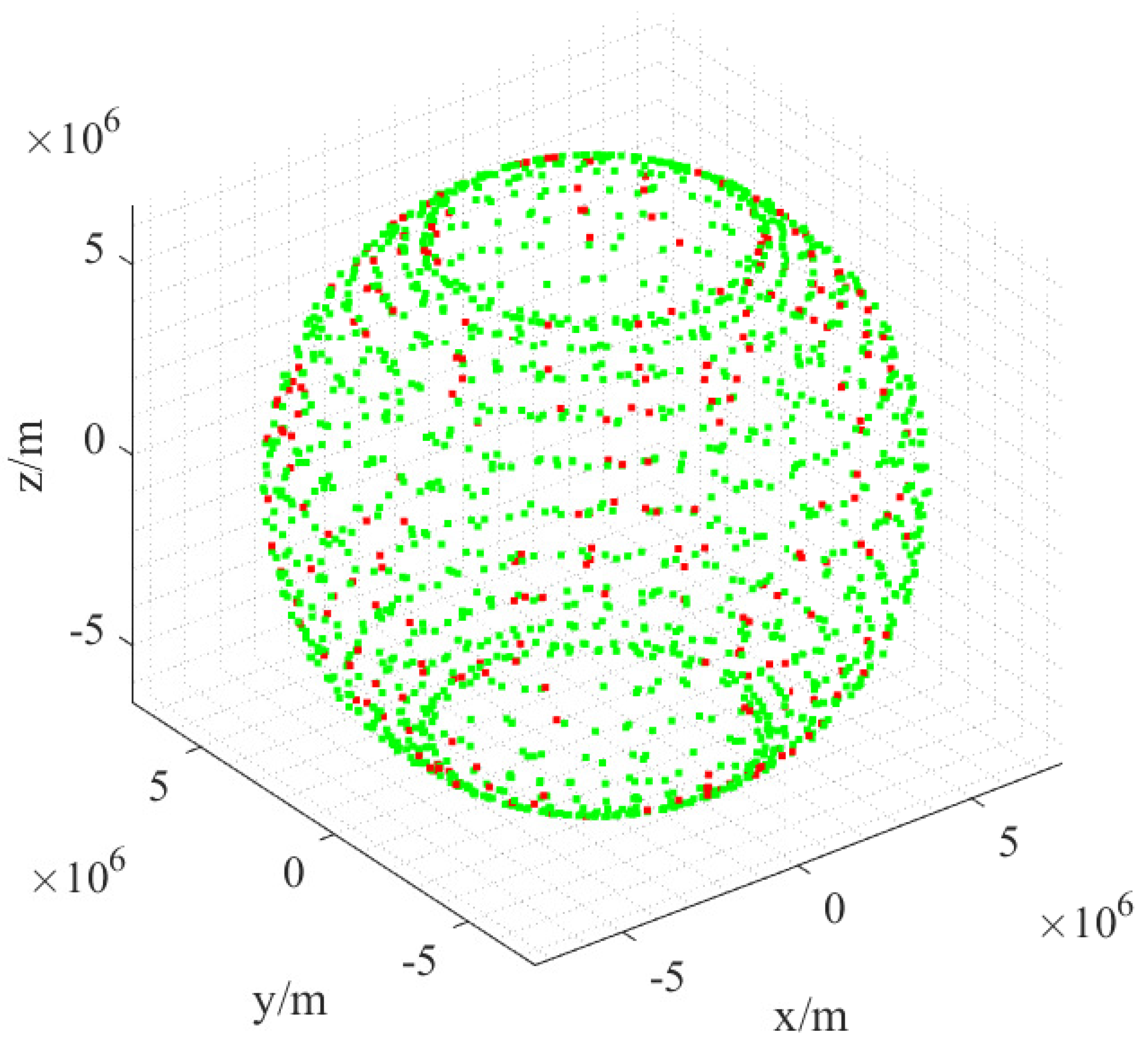
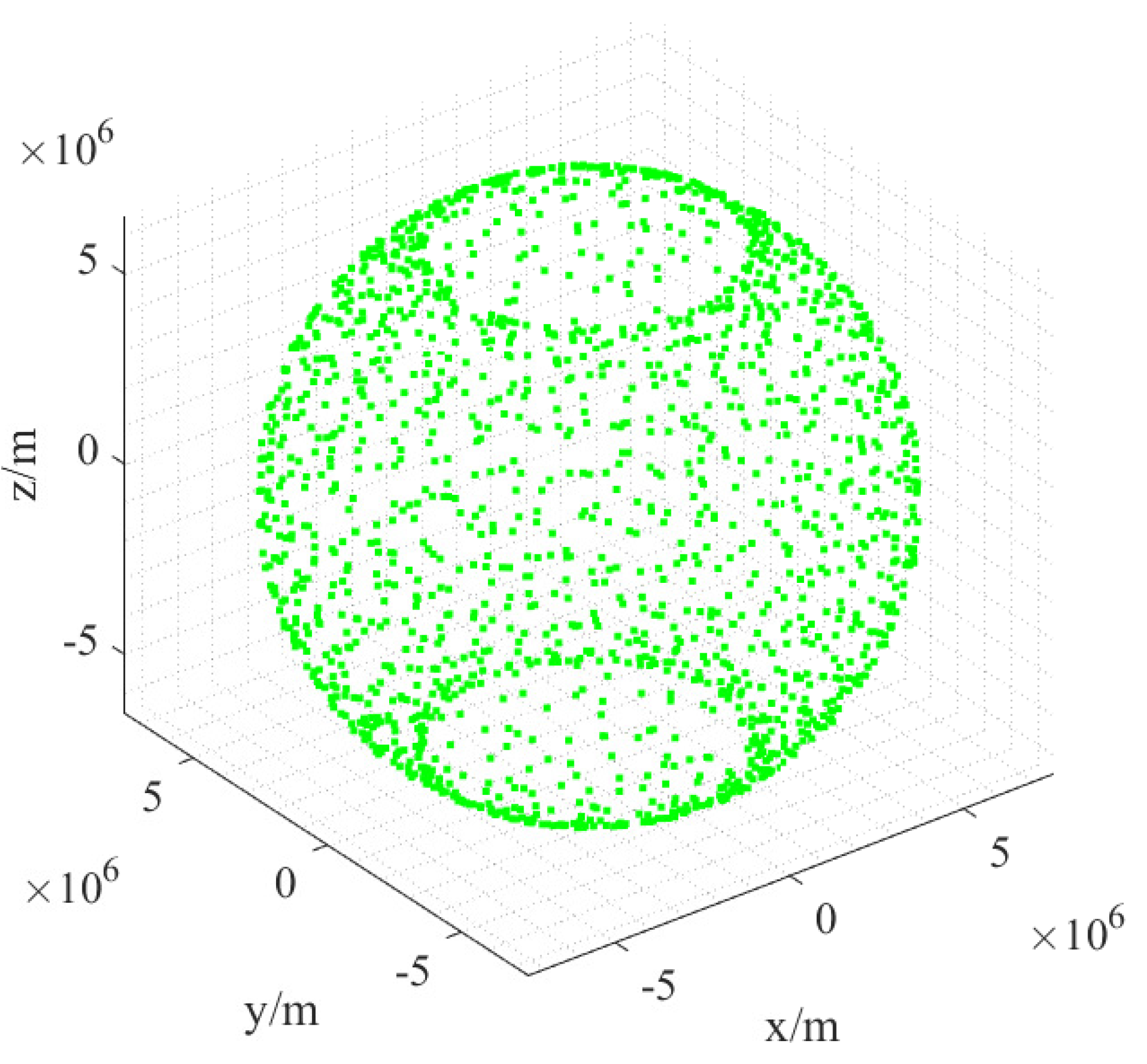
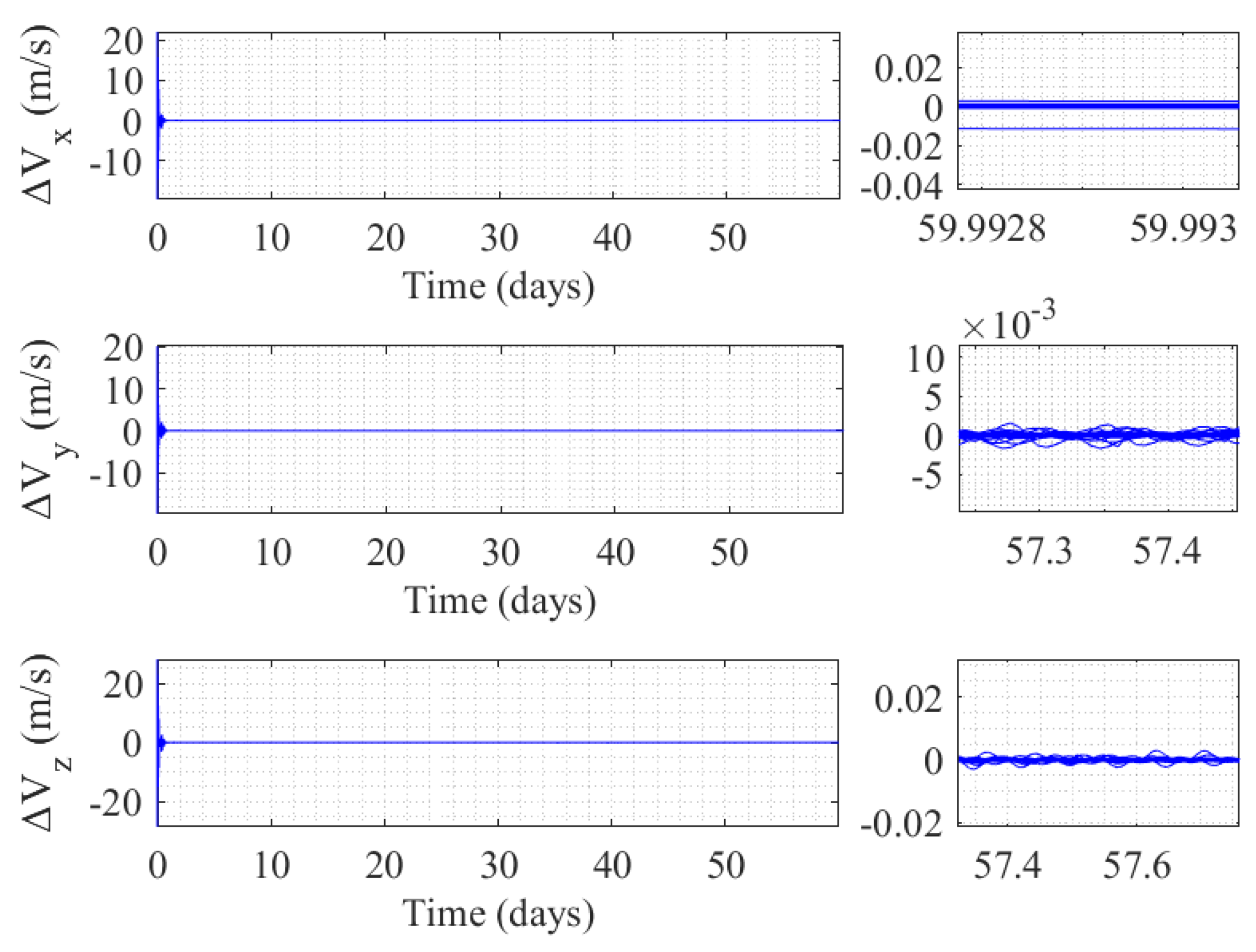
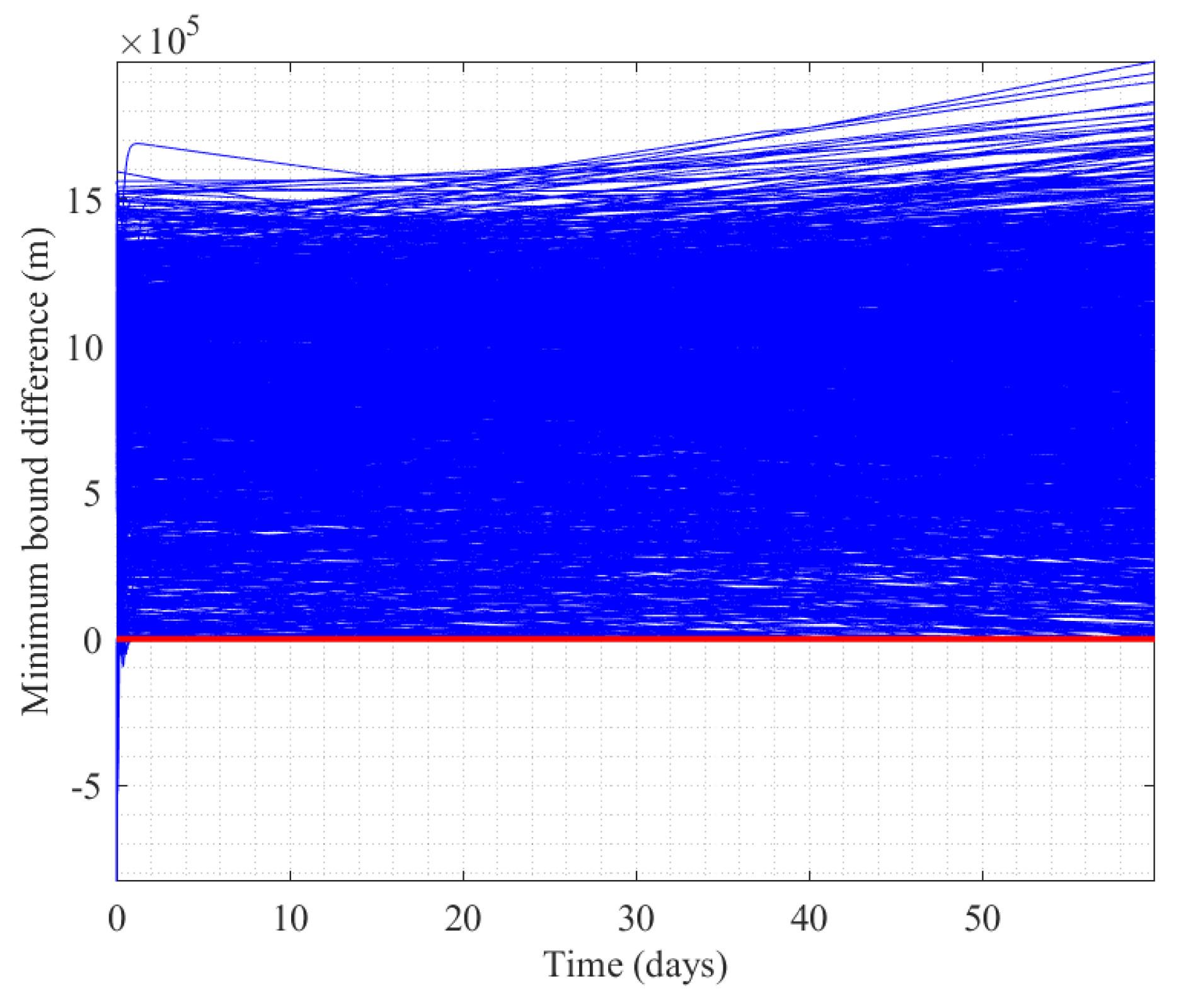
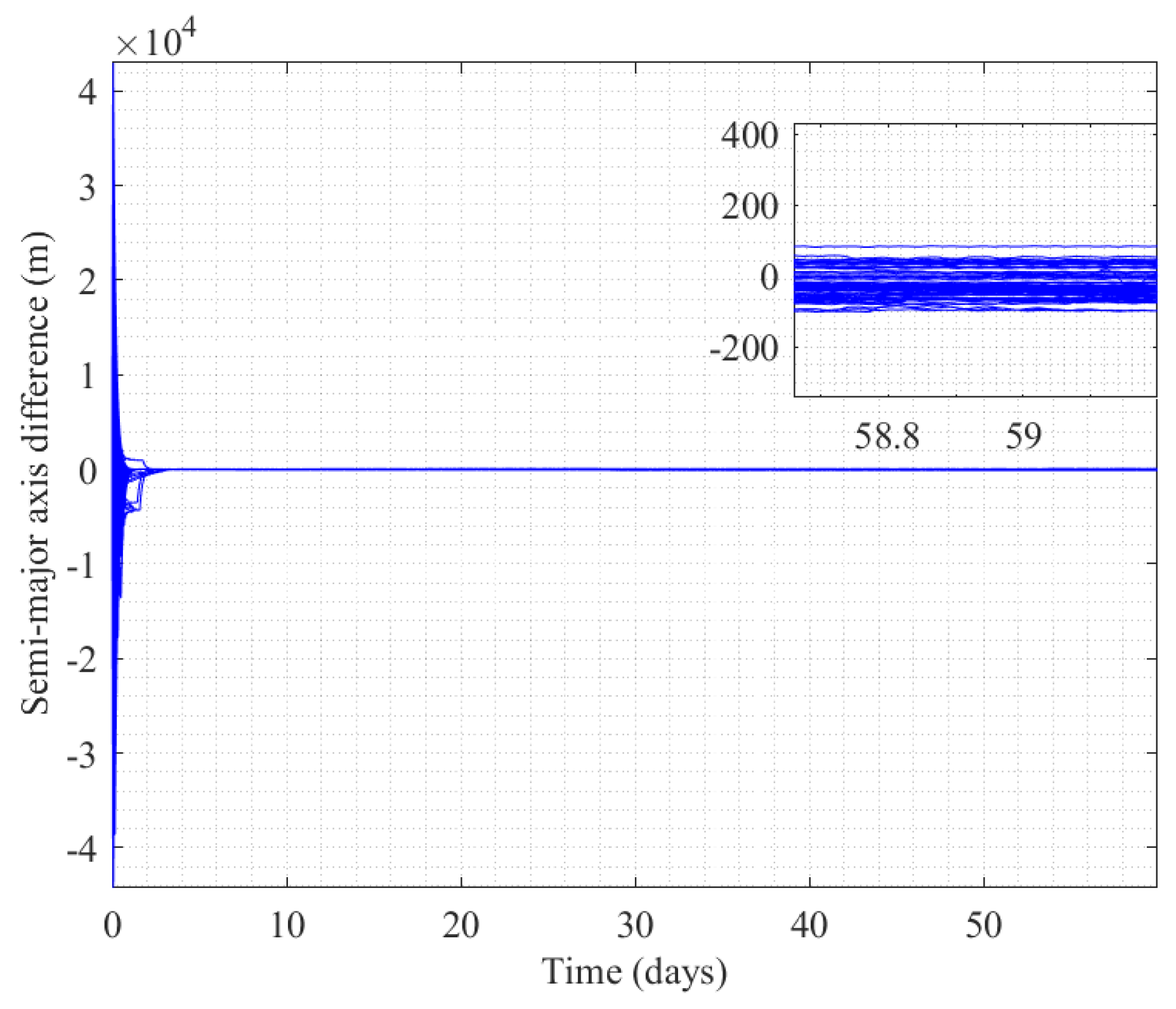
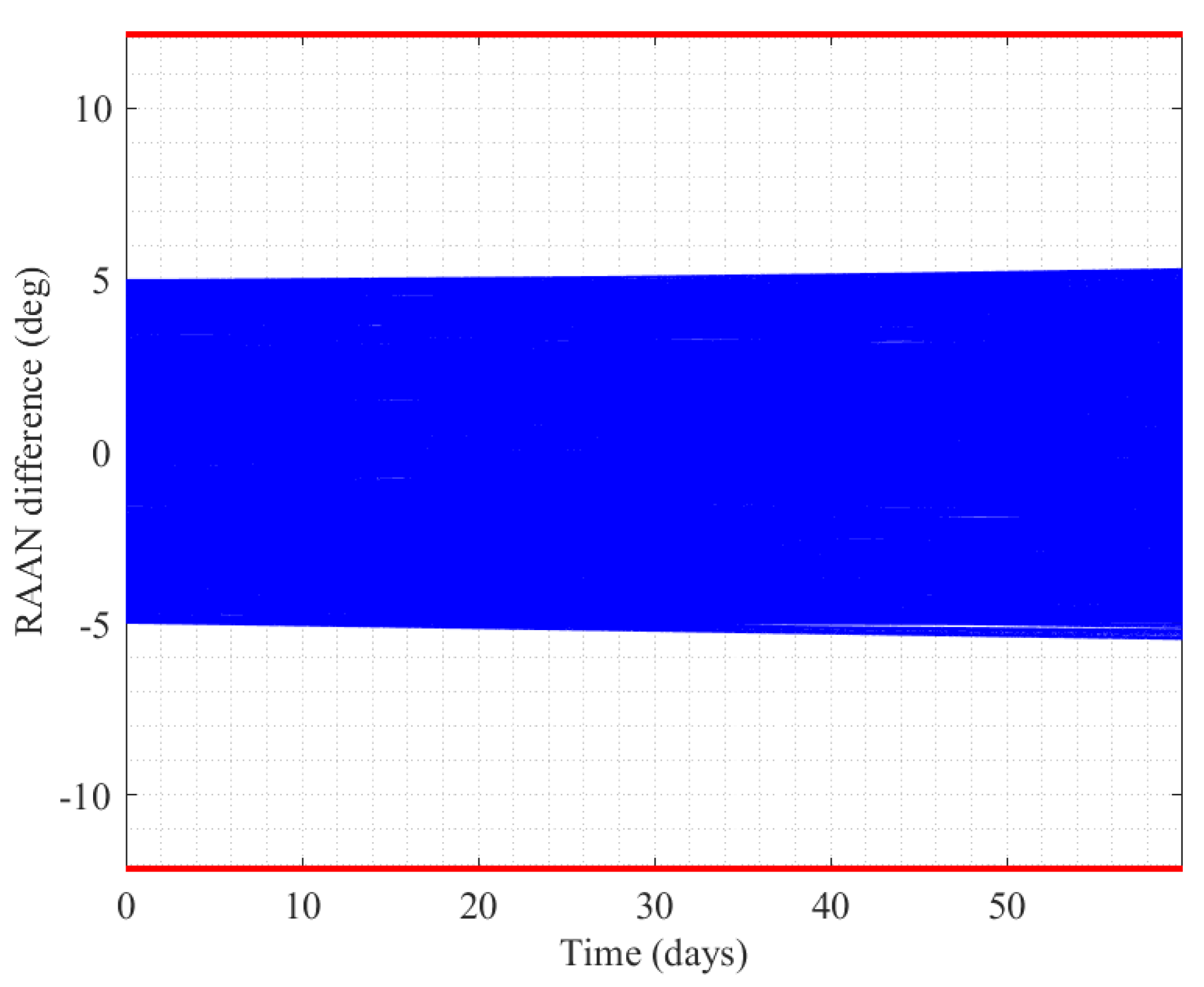
3.3. Self-Organizing Control of Mega Constellation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Del Portillo, I.; Cameron, B.G.; Crawley, E.F. A technical comparison of three low earth orbit satellite constellation systems to provide global broadband. Acta Astronaut. 2019, 159, 123–135. [Google Scholar] [CrossRef]
- Williams, A.; Hainaut, O.; Otarola, A.; Tan, G.H.; Rotola, G. Analysing the impact of satellite constellations and ESO’s role in supporting the astronomy community. arXiv 2021, arXiv:2108.04005. [Google Scholar]
- Boggio, M.; Colangelo, L.; Virdis, M.; Pagone, M.; Novara, C. Earth Gravity In-Orbit Sensing: MPC Formation Control Based on a Novel Constellation Model. Remote Sens. 2022, 14, 2815. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Y.; Wen, G.; Bai, S.; Cai, Y.; Huang, P.; Han, D.; He, Y. Atmospheric Density Model Optimization and Spacecraft Orbit Prediction Improvements Based on Q-Sat Orbit Data. arXiv 2021, arXiv:2112.03113. [Google Scholar]
- Mastro, P.; Masiello, G.; Serio, C.; Pepe, A. Change Detection Techniques with Synthetic Aperture Radar Images: Experiments with Random Forests and Sentinel-1 Observations. Remote Sens. 2022, 14, 3323. [Google Scholar] [CrossRef]
- Lang, T. Low Earth orbit satellite constellations for continuous coverage of the mid-latitudes. In Proceedings of the Astrodynamics Conference, San Diego, CA, USA, 29 July–31 July 1996; p. 3638. [Google Scholar]
- Santos, M.; Shapiro, B. Relating satellite coverage to orbital geometry. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; p. 6609. [Google Scholar]
- Hackett, T.M.; Bilén, S.G.; Bell, D.J.; Lo, M.W. Geometric approach for analytical approximations of satellite coverage statistics. J. Spacecr. Rocket. 2019, 56, 1286–1299. [Google Scholar] [CrossRef]
- Dai, G.; Chen, X.; Wang, M.; Fernández, E.; Nguyen, T.N.; Reinelt, G. Analysis of satellite constellations for the continuous coverage of ground regions. J. Spacecr. Rocket. 2017, 54, 1294–1303. [Google Scholar] [CrossRef] [Green Version]
- Gong, Y.; Zhang, S.; Peng, X. Quick coverage analysis of mega Walker Constellation based on 2D map. Acta Astronaut. 2021, 188, 99–109. [Google Scholar] [CrossRef]
- Huang, S.; Colombo, C.; Bernelli-Zazzera, F. Multi-criteria design of continuous global coverage Walker and Street-of-Coverage constellations through property assessment. Acta Astronaut. 2021, 188, 151–170. [Google Scholar] [CrossRef]
- Arnas, D.; Casanova, D.; Tresaco, E. Relative and absolute station-keeping for two-dimensional–lattice flower constellations. J. Guid. Control. Dyn. 2016, 39, 2602–2604. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, L.; Liu, H.; Li, L.; Liu, J. Analysis of configuration and maintenance strategy of LEO walker constellation. J. Astronaut. 2019, 40, 1296–1303. [Google Scholar]
- Li, J.; Hu, M.; Wang, X.; Li, F.; Xu, J. Analysis of configuration offsetting maintenance method for LEO Walker constellation. Chin. Space Sci. Technol. 2021, 41, 38. [Google Scholar]
- Izzo, D.; Pettazzi, L. Autonomous and distributed motion planning for satellite swarm. J. Guid. Control. Dyn.s 2007, 30, 449–459. [Google Scholar] [CrossRef]
- Nag, S.; Summerer, L. Behaviour based, autonomous and distributed scatter manoeuvres for satellite swarms. Acta Astronaut. 2013, 82, 95–109. [Google Scholar] [CrossRef]
- Hu, Q.; Dong, H.; Zhang, Y.; Ma, G. Tracking control of spacecraft formation flying with collision avoidance. Aerosp. Sci. Technol. 2015, 42, 353–364. [Google Scholar] [CrossRef]
- McInnes, C.R. Autonomous proximity manoeuvring using artificial potential functions. ESA J. 1993, 17, 159–169. [Google Scholar]
- Cao, L.; Qiao, D.; Xu, J. Suboptimal artificial potential function sliding mode control for spacecraft rendezvous with obstacle avoidance. Acta Astronaut. 2018, 143, 133–146. [Google Scholar] [CrossRef]
- Spencer, D.A. Automated trajectory control using artificial potential functions to target relative orbits. J. Guid. Control. Dyn. 2016, 39, 2142–2148. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, Y.; Jiang, C.; Zhang, Y. Self-organizing control for satellite clusters using artificial potential function in terms of relative orbital elements. Aerosp. Sci. Technol. 2019, 84, 799–811. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, Z.; Zhang, Y. Bounded flight and collision avoidance control for satellite clusters using intersatellite flight bounds. Aerosp. Sci. Technol. 2019, 94, 105425. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, Z.; Zhang, Y. Modeling and control of scale-independent relative orbital elements for near-circular orbits. Acta Astronaut. 2022, 198, 642–658. [Google Scholar]
- Jiang, C.; Wang, Z.; Zhang, Y. Decomposition analysis of spacecraft relative motion with different inter-satellite ranges. Acta Astronaut. 2019, 163, 56–68. [Google Scholar]
- An, M.; Wang, Z.; Zhang, Y. Self-organizing control strategy for asteroid intelligent detection swarm based on attraction and repulsion. Acta Astronaut. 2017, 130, 84–96. [Google Scholar] [CrossRef]
- Sun, Y.; Shen, H. The control of mega-constellation at low earth orbit based on TLE. Acta Astronaut. 2020, 42, 156. [Google Scholar]







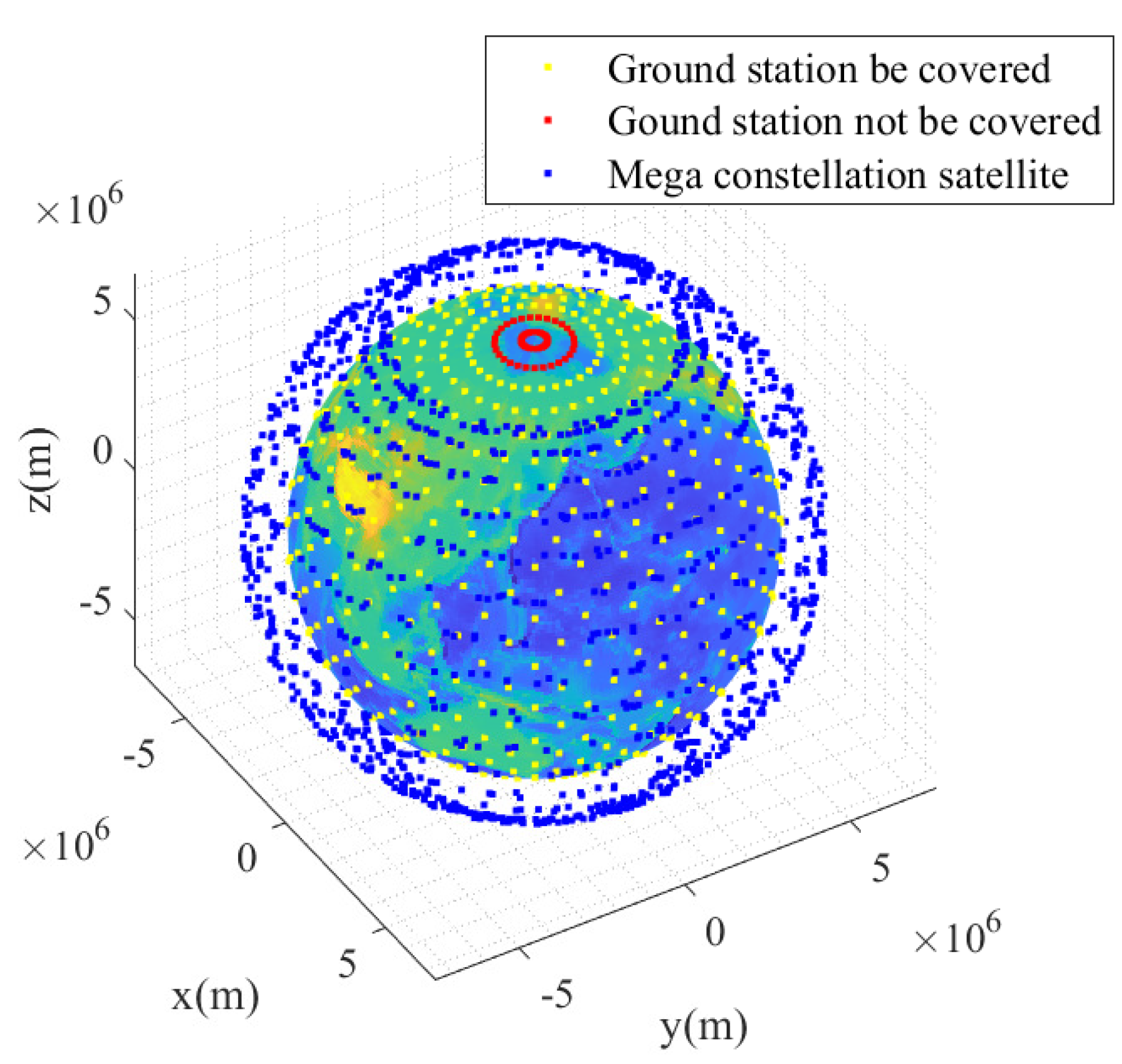
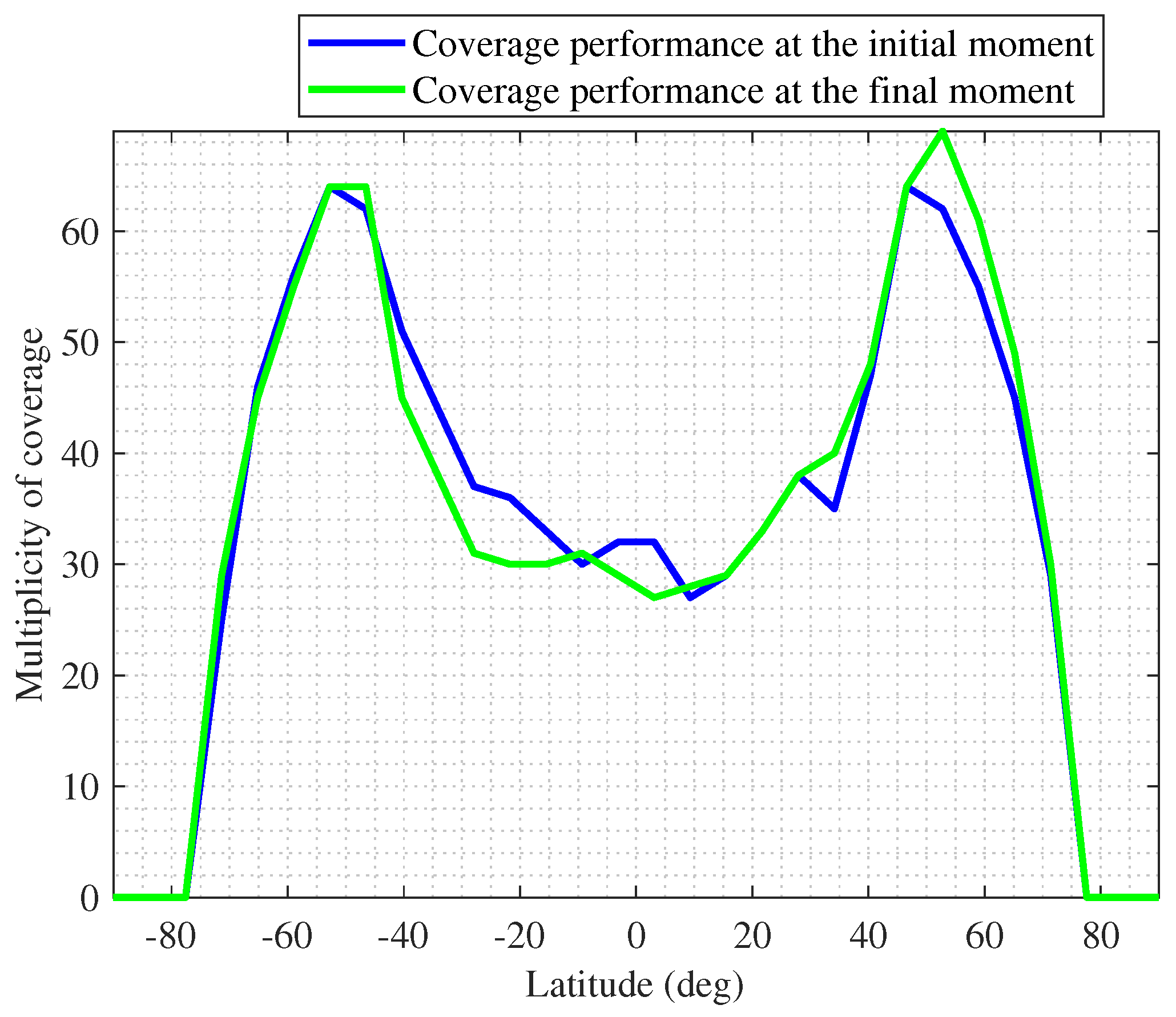
| Constellation | Altitude | Inclination | Planes | Satellites per Plane | Whether Continuous Coverage Constraint Is Satisfied |
|---|---|---|---|---|---|
| Starlink Genaration 1 | 550 km | 53 | 72 | 22 | Yes |
| 540 km | 53.2 | 72 | 22 | Yes | |
| 570 km | 70 | 36 | 20 | Yes | |
| 560 km | 97.6 | 6 | 58 | No | |
| 560 km | 97.6 | 4 | 43 | No | |
| OneWeb | 1120 km | 87.9 | 18 | 40 | Yes |
| 1150 km | 53 | 32 | 50 | Yes | |
| 1110 km | 53.8 | 32 | 50 | Yes | |
| GW-A59 | 590 km | 85 | 16 | 30 | No |
| 600 km | 50 | 40 | 50 | Yes | |
| 508 km | 55 | 60 | 60 | Yes | |
| GW-2 | 1145 km | 30 | 48 | 36 | Yes |
| 1145 km | 40 | 48 | 36 | Yes | |
| 1145 km | 50 | 48 | 36 | Yes | |
| 1145 km | 60 | 48 | 36 | Yes |
| Parameters | Values |
|---|---|
| Simulation Time | 60 days |
| Step Length | 600 s |
| Initial Conditions | |
| Perturbations | , atmospheric drag, lunar gravity, solar gravity |
| Control Coefficients | |
| Ballistic Coefficient | |
| Expected Range |
| Parameters | Values |
|---|---|
| Simulation Time | 60 days |
| Step Length | 600 s |
| Designed Configuration | |
| Initial Orbit Errors | |
| Perturbations | , atmospheric drag, lunar gravity, solar gravity |
| Control Coefficients | |
| Ballistic Coefficient | |
| Minimum Elevation Angle |
| Parameters | Values |
|---|---|
| Simulation Time | 60 days |
| Step Length | 600 s |
| Designed Configuration | |
| Initial Orbit Errors | |
| Perturbations | , atmospheric drag, lunar gravity, solar gravity |
| Control Coefficients | |
| Ballistic Coefficient | |
| Minimum Elevation Angle |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Zhang, Y.; Wang, Z.; He, Y.; Fan, L. Self-Organizing Control of Mega Constellations for Continuous Earth Observation. Remote Sens. 2022, 14, 5896. https://doi.org/10.3390/rs14225896
Xu Y, Zhang Y, Wang Z, He Y, Fan L. Self-Organizing Control of Mega Constellations for Continuous Earth Observation. Remote Sensing. 2022; 14(22):5896. https://doi.org/10.3390/rs14225896
Chicago/Turabian StyleXu, Yun, Yulin Zhang, Zhaokui Wang, Yunhan He, and Li Fan. 2022. "Self-Organizing Control of Mega Constellations for Continuous Earth Observation" Remote Sensing 14, no. 22: 5896. https://doi.org/10.3390/rs14225896
APA StyleXu, Y., Zhang, Y., Wang, Z., He, Y., & Fan, L. (2022). Self-Organizing Control of Mega Constellations for Continuous Earth Observation. Remote Sensing, 14(22), 5896. https://doi.org/10.3390/rs14225896