How Well Can Matching High Spatial Resolution Landsat Data with Flux Tower Footprints Improve Estimates of Vegetation Gross Primary Production
Abstract
:1. Introduction
2. Data and Methods
2.1. The Revised EC-LUE Model and Parameterization
2.2. Satellite Data
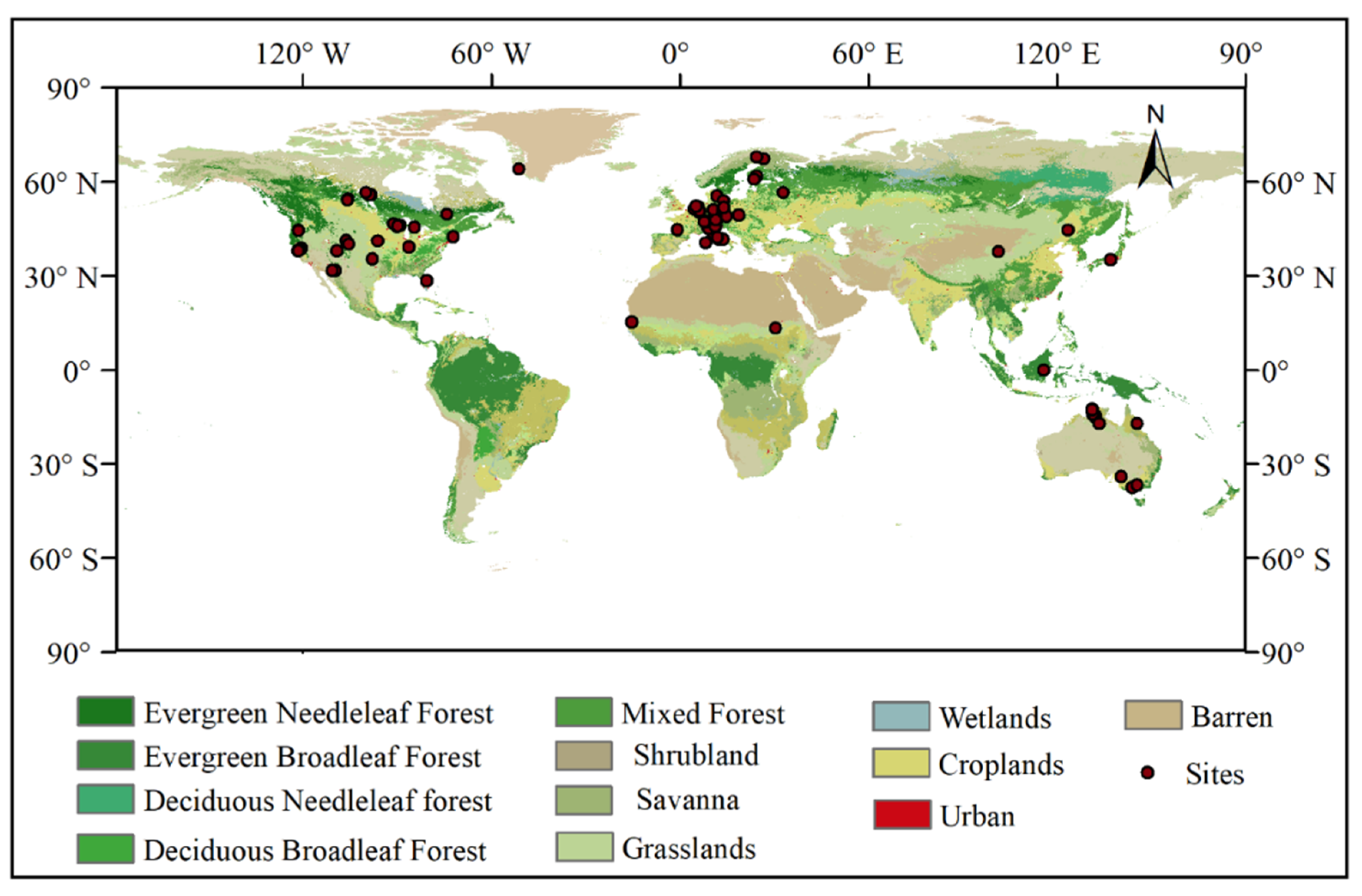
2.3. Eddy Covariance Measurements
2.4. Flux Footprint Modeling
3. Results
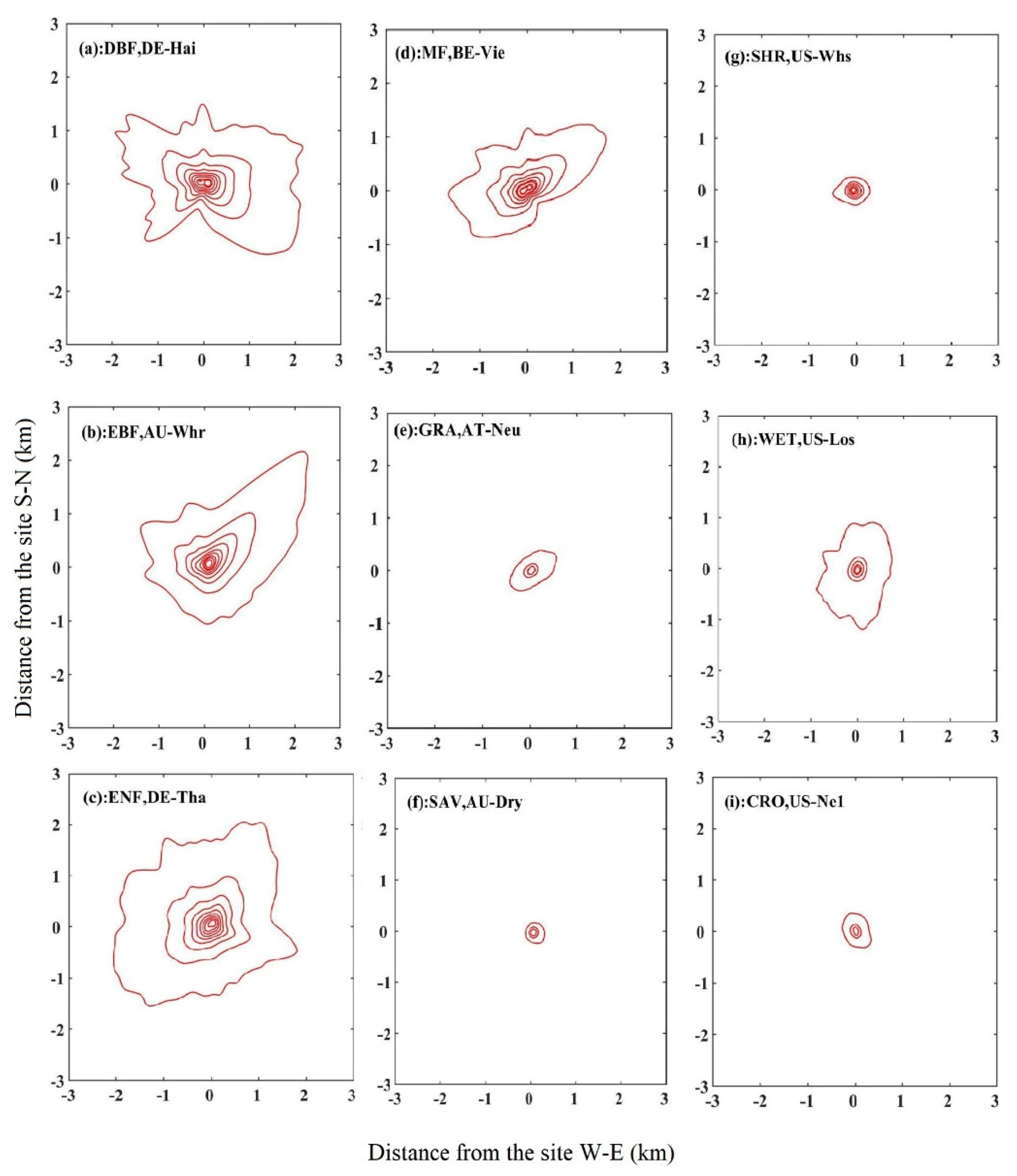
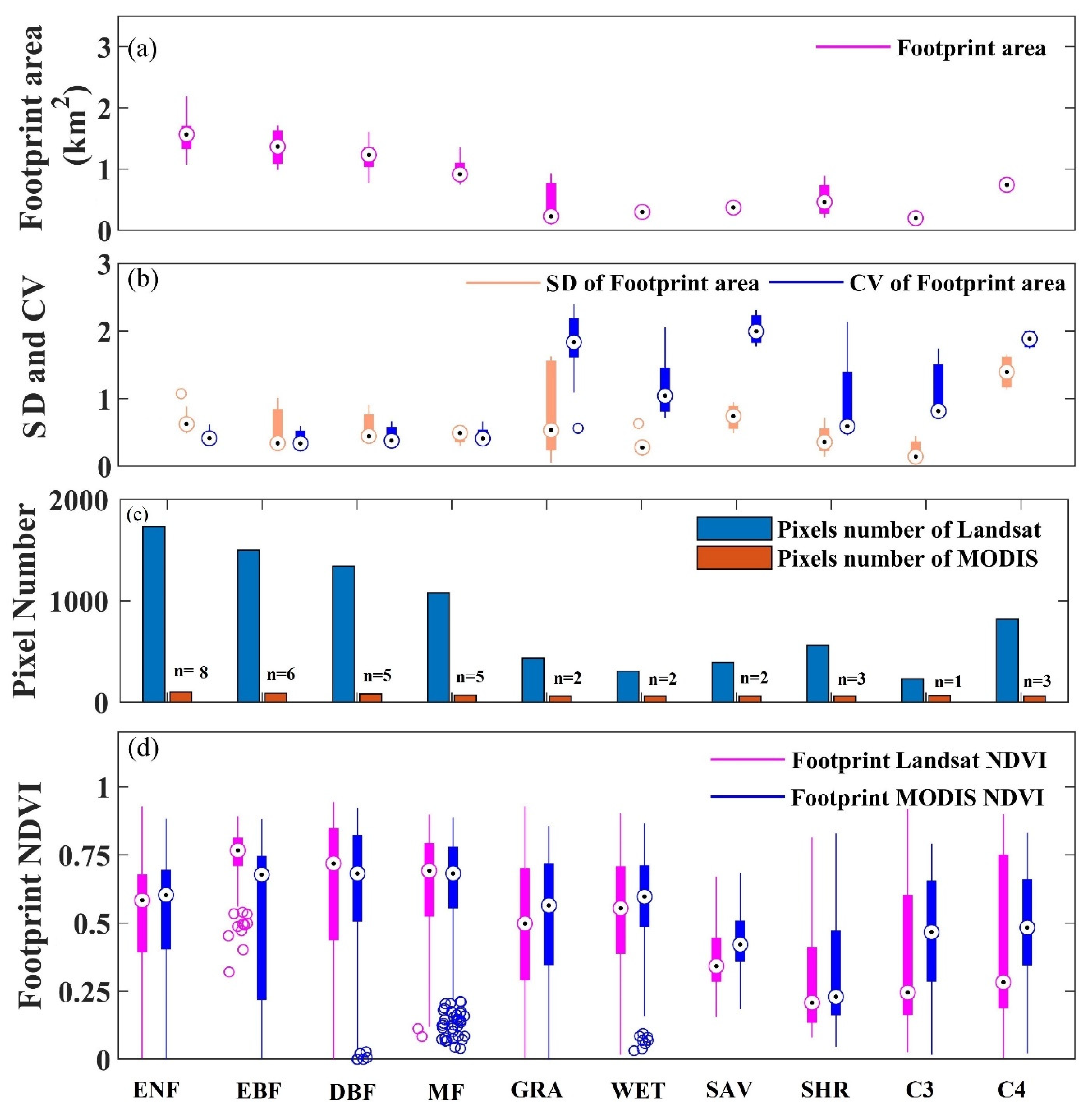
3.1. Heterogeneity of Flux Footprint
3.2. Optimized Parameters
3.3. Model Accuracy Comparison
3.4. The Effect of Landsat Reconstruction on Model Accuracy
4. Discussion
4.1. Impact of Spatial Scale Mismatch on Parameterization
4.2. To What Degree Do Landsat Images Improve GPP Estimation
4.3. Limitations and Perspectives
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiao, J.; Chevallier, F.; Gomez, C.; Guanter, L.; Hicke, J.A.; Huete, A.R.; Ichii, K.; Ni, W.; Pang, Y.; Rahman, A.F.; et al. Remote sensing of the terrestrial carbon cycle: A review of advances over 50 years. Remote Sens. Environ. 2019, 233, 111383. [Google Scholar] [CrossRef]
- Yuan, W.; Piao, S.; Qin, D.; Dong, W.; Xia, J.; Lin, H.; Chen, M. Influence of Vegetation Growth on the Enhanced Seasonality of Atmospheric CO2. Global Biogeochem. Cycles 2018, 32, 32–41. [Google Scholar] [CrossRef]
- Dong, J.; Fu, Y.; Wang, J.; Tian, H.; Fu, S.; Niu, Z.; Han, W.; Zheng, Y.; Huang, J.; Yuan, W. Early-season mapping of winter wheat in China based on Landsat and Sentinel images. Earth Syst. Sci. Data 2020, 12, 3081–3095. [Google Scholar] [CrossRef]
- Huang, X.; Xiao, J.; Ma, M. Evaluating the Performance of Satellite-Derived Vegetation Indices for Estimating Gross Primary Productivity Using FLUXNET Observations across the Globe. Remote Sens. 2019, 11, 1823. [Google Scholar] [CrossRef] [Green Version]
- Xiao, X.M.; Zhang, Q.Y.; Braswell, B.; Urbanski, S.; Boles, S.; Wofsy, S.; Berrien, M.; Ojima, D. Modeling gross primary production of temperate deciduous broadleaf forest using satellite images and climate data. Remote Sens. Environ. 2004, 91, 256–270. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. Bioscience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Yuan, W.P.; Liu, S.; Zhou, G.S.; Zhou, G.Y.; Tieszen, L.L.; Baldocchi, D.; Bernhofer, C.; Gholz, H.; Goldstein, A.H.; Goulden, M.L.; et al. Deriving a light use efficiency model from eddy covariance flux data for predicting daily gross primary production across biomes. Agric. For. Meteorol. 2007, 143, 189–207. [Google Scholar] [CrossRef] [Green Version]
- Yuan, W.; Zheng, Y.; Piao, S.; Ciais, P.; Lombardozzi, D.; Wang, Y.; Ryu, Y.; Chen, G.; Dong, W.; Hu, Z.; et al. Increased atmospheric vapor pressure deficit reduces global vegetation growth. Sci. Adv. 2019, 5, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Farquhar, A.G.D.; Von Caemmerer, S.; Berry, J.A. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 1980, 149, 78–90. [Google Scholar] [CrossRef] [Green Version]
- Friend, A.D.; Arneth, A.; Kiang, N.Y.; Lomas, M.; Ogée, J.; Rödenbeck, C.; Running, S.W.; Santaren, J.D.; Sitch, S.; Viovy, N.; et al. FLUXNET and modelling the global carbon cycle. Glob. Chang. Biol. 2007, 13, 610–633. [Google Scholar] [CrossRef]
- Running, S.W.; Thornton, P.E.; Nemani, R.; Glassy, J.M. Global Terrestrial Gross and Net Primary Productivity from the Earth Observing System. In Methods in Ecosystem Science; Springer: New York, NY, USA, 2000; pp. 44–57. [Google Scholar]
- Zhang, Y.; Xiao, X.; Wu, X.; Zhou, S.; Zhang, G.; Qin, Y.; Dong, J. A global moderate resolution dataset of gross primary production of vegetation for 2000-2016. Sci. Data 2017, 4, 170165. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Y.; Shen, R.; Wang, Y.; Li, X.; Liu, S.; Liang, S.; Chen, J.M.; Ju, W.; Zhang, L.; Yuan, W. Improved estimate of global gross primary production for reproducing its long-Term variation, 1982-2017. Earth Syst. Sci. Data 2020, 12, 2725–2746. [Google Scholar] [CrossRef]
- Huang, X.; Zheng, Y.; Zhang, H.; Lin, S.; Liang, S.; Li, X.; Ma, M.; Yuan, W. High spatial resolution vegetation gross primary production product: Algorithm and validation. Sci. Remote Sens. 2022, 5, 100049. [Google Scholar] [CrossRef]
- Lin, S.; Huang, X.; Zheng, Y.; Zhang, X.; Yuan, W. An Open Data Approach for Estimating Vegetation Gross Primary Production at Fine Spatial Resolution. Remote Sens. 2022, 14. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science 2013 342, 850–853. [CrossRef] [Green Version]
- Parazoo, N.C.; Coleman, R.W.; Yadav, V.; Stavros, E.N.; Hulley, G.; Hutyra, L. Diverse biosphere influence on carbon and heat in mixed urban Mediterranean landscape revealed by high resolution thermal and optical remote sensing. Sci. Total Environ. 2022, 806, 151335. [Google Scholar] [CrossRef]
- Dong, J.; Lu, H.; Wang, Y.; Ye, T.; Yuan, W. Estimating winter wheat yield based on a light use efficiency model and wheat variety data. ISPRS J. Photogramm. Remote Sens. 2020, 160, 18–32. [Google Scholar] [CrossRef]
- Robinson, N.P.; Allred, B.W.; Smith, W.K.; Jones, M.O.; Moreno, A.; Erickson, T.A.; Naugle, D.E.; Running, S.W. Terrestrial primary production for the conterminous United States derived from Landsat 30 m and MODIS 250 m. Remote Sens. Ecol. Conserv. 2018, 4, 264–280. [Google Scholar] [CrossRef]
- Chu, H.; Luo, X.; Ouyang, Z.; Chan, W.S.; Dengel, S.; Biraud, S.C.; Torn, M.S.; Metzger, S.; Kumar, J.; Arain, M.A.; et al. Representativeness of Eddy-Covariance flux footprints for areas surrounding AmeriFlux sites. Agric. For. Meteorol. 2021, 301–302, 108350. [Google Scholar] [CrossRef]
- Chen, B.; Coops, N.C.; Fu, D.; Margolis, H.A.; Amiro, B.D.; Black, T.A.; Arain, M.A.; Barr, A.G.; Bourque, C.P.-A.; Flanagan, L.B.; et al. Characterizing spatial representativeness of flux tower eddy-covariance measurements across the Canadian Carbon Program Network using remote sensing and footprint analysis. Remote Sens. Environ. 2012, 124, 742–755. [Google Scholar] [CrossRef]
- Verma, M.; Friedl, M.A.; Law, B.E.; Bonal, D.; Kiely, G.; Black, T.A.; Wohlfahrt, G.; Moors, E.J.; Montagnani, L.; Marcolla, B.; et al. Improving the performance of remote sensing models for capturing intra- and inter-annual variations in daily GPP: An analysis using global FLUXNET tower data. Agric. For. Meteorol. 2015, 214–215, 416–429. [Google Scholar] [CrossRef] [Green Version]
- Stockli, R.; Rutishauser, T.; Dragoni, D.; O’Keefe, J.; Thornton, P.E.; Jolly, M.; Lu, L.; Denning, A.S. Remote sensing data assimilation for a prognostic phenology model. J. Geophys. Res. 2008, 113, G04021. [Google Scholar] [CrossRef]
- Wagle, P.; Gowda, P.H.; Neel, J.P.S.; Northup, B.K.; Zhou, Y. Integrating eddy fl uxes and remote sensing products in a rotational grazing native tallgrass prairie pasture. Sci. Total Environ. 2020, 712, 136407. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A.A.; Peng, Y.; Masek, J.G.; Rundquist, D.C.; Verma, S.; Suyker, A.; Baker, J.M.; Hatfield, J.L.; Meyers, T. Remote estimation of crop gross primary production with Landsat data. Remote Sens. Environ. 2012, 121, 404–414. [Google Scholar] [CrossRef] [Green Version]
- Knox, S.H.; Dronova, I.; Sturtevant, C.; Oikawa, P.Y.; Matthes, J.H.; Verfaillie, J.; Baldocchi, D. Using digital camera and Landsat imagery with eddy covariance data to model gross primary production in restored wetlands. Agric. For. Meteorol. 2017, 237–238, 233–245. [Google Scholar] [CrossRef] [Green Version]
- Yuan, W.P.; Liu, S.G.; Yu, G.R.; Bonnefond, J.M.; Chen, J.Q.; Davis, K.; Desai, A.R.; Goldstein, A.H.; Gianelle, D.; Rossi, F.; et al. Global estimates of evapotranspiration and gross primary production based on MODIS and global meteorology data. Remote Sens. Environ. 2010, 114, 1416–1431. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.; Xiao, J.; Wang, X.; Ma, M. Improving the global MODIS GPP model by optimizing parameters with FLUXNET data. Agric. For. Meteorol. 2021, 300, 108314. [Google Scholar] [CrossRef]
- Zhang, Y.; Kong, D.; Gan, R.; Chiew, F.H.S.; McVicar, T.R.; Zhang, Q.; Yang, Y. Coupled estimation of 500 m and 8-day resolution global evapotranspiration and gross primary production in 2002–2017. Remote Sens. Environ. 2019, 222, 165–182. [Google Scholar] [CrossRef]
- Eilers, P.H.C. A Perfect Smoother. Anal. Chem. 2003, 75, 3631–3636. [Google Scholar] [CrossRef]
- Atzberger, C.; Eilers, P.H.C. A time series for monitoring vegetation activity and phenology at 10-daily time steps covering large parts of South America. Int. J. Digit. Earth 2011, 4, 365–386. [Google Scholar] [CrossRef]
- Frasso, G.; Eilers, P.H.C. L- and V-curves for optimal smoothing. Stat. Modelling 2015, 15, 91–111. [Google Scholar] [CrossRef]
- Kong, D.; Zhang, Y.; Gu, X.; Wang, D. A robust method for reconstructing global MODIS EVI time series on the Google Earth Engine. ISPRS J. Photogramm. Remote Sens. 2019, 155, 13–24. [Google Scholar] [CrossRef]
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P. A simple two-dimensional parameterisation for Flux Footprint Prediction (FFP). Geosci. Model Dev. 2015, 8, 3695–3713. [Google Scholar] [CrossRef] [Green Version]
- Grimmond, C.S.B.; Cleugh, H.A. A simple method to determine Obukhov lengths for suburban areas. J. Appl. Meteorol. 1994, 33, 435–440. [Google Scholar] [CrossRef]
- Kim, J.; Hwang, T.; Schaaf, C.L.; Kljun, N.; Munger, J.W. Seasonal variation of source contributions to eddy-covariance CO2 measurements in a mixed hardwood-conifer forest. Agric. For. Meteorol. 2018, 253–254, 71–83. [Google Scholar] [CrossRef]
- Pei, Y.; Dong, J.; Zhang, Y.; Yuan, W.; Doughty, R.; Yang, J. Evolution of light use efficiency models: Improvement, uncertainties, and implications. Agric. For. Meteorol. 2022, 317, 108905. [Google Scholar] [CrossRef]
- Zhou, Y.; Xiao, X.; Wagle, P.; Bajgain, R.; Mahan, H.; Basara, J.B.; Dong, J.; Qin, Y.; Zhang, G.; Luo, Y.; et al. Examining the short-term impacts of diverse management practices on plant phenology and carbon fluxes of Old World bluestems pasture. Agric. For. Meteorol. 2017, 237–238, 60–70. [Google Scholar] [CrossRef] [Green Version]
- Gelybó, G.; Barcza, Z.; Kern, A.; Kljun, N. Effect of spatial heterogeneity on the validation of remote sensing based GPP estimations. Agric. For. Meteorol. 2013, 174–175, 43–53. [Google Scholar] [CrossRef]
- Giannico, V.; Chen, J.; Shao, C.; Ouyang, Z.; John, R.; Lafortezza, R. Contributions of landscape heterogeneity within the footprint of eddy-covariance towers to flux measurements. Agric. For. Meteorol. 2018, 260, 144–153. [Google Scholar] [CrossRef]
- Xie, X.; Li, A.; Jin, H.; Yin, G.; Bian, J. Spatial downscaling of gross primary productivity using topographic and vegetation heterogeneity information: A case study in the Gongga Mountain region of China. Remote Sens. 2018, 10, 647. [Google Scholar] [CrossRef]
- Jin, H.; Li, A.; Bian, J.; Nan, X.; Zhao, W.; Zhang, Z.; Yin, G. Intercomparison and validation of MODIS and GLASS leaf area index (LAI) products over mountain areas: A case study in southwestern China. Int. J. Appl. Earth Obs. Geoinf. 2017, 55, 52–67. [Google Scholar] [CrossRef]
- Young, N.E.; Anderson, R.S.; Chignell, S.M.; Vorster, A.G.; Lawrence, R.; Evangelista, P.H. A survival guide to Landsat preprocessing. Ecology 2017, 98, 920–932. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xie, X.; Chen, J.M.; Gong, P.; Li, A. Spatial Scaling of Gross Primary Productivity Over Sixteen Mountainous Watersheds Using Vegetation Heterogeneity and Surface Topography. J. Geophys. Res. Biogeosciences 2021, 126, 1–21. [Google Scholar] [CrossRef]
- Yuan, W.; Cai, W.; Nguy-Robertson, A.L.; Fang, H.; Suyker, A.E.; Chen, Y.; Dong, W.; Liu, S.; Zhang, H. Uncertainty in simulating gross primary production of cropland ecosystem from satellite-based models. Agric. For. Meteorol. 2015, 207, 48–57. [Google Scholar] [CrossRef] [Green Version]
- Beck, H.E.; McVicar, T.R.; van Dijk, A.I.J.M.; Schellekens, J.; de Jeu, R.A.M.; Bruijnzeel, L.A. Global evaluation of four AVHRR–NDVI data sets: Intercomparison and assessment against Landsat imagery. Remote Sens. Environ. 2011, 115, 2547–2563. [Google Scholar] [CrossRef]
- Ju, J.C.; Roy, D.P. The availability of cloud-free Landsat ETM plus data over the conterminous United States and globally. Remote Sens. Environ. 2008, 112, 1196–1211. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, S.; Woodcock, C.E. Improvement and expansion of the Fmask algorithm: Cloud, cloud shadow, and snow detection for Landsats 4-7, 8, and Sentinel 2 images. Remote Sens. Environ. 2015, 159, 269–277. [Google Scholar] [CrossRef]
- Kong, J.; Ryu, Y.; Liu, J.; Dechant, B.; Rey-Sanchez, C.; Shortt, R.; Szutu, D.; Verfaillie, J.; Houborg, R.; Baldocchi, D.D. Matching high resolution satellite data and flux tower footprints improves their agreement in photosynthesis estimates. Agric. For. Meteorol. 2022, 316, 108878. [Google Scholar] [CrossRef]
- Gao, F.; Hilker, T.; Zhu, X.; Anderson, M.; Masek, J.; Wang, P.; Yang, Y. Fusing Landsat and MODIS Data for Vegetation Monitoring. IEEE Geosci. Remote Sens. Mag. 2015, 3, 47–60. [Google Scholar] [CrossRef]
- Emelyanova, I.V.; McVicar, T.R.; Van Niel, T.G.; Li, L.T.; van Dijk, A.I.J.M. Assessing the accuracy of blending Landsat-MODIS surface reflectances in two landscapes with contrasting spatial and temporal dynamics: A framework for algorithm selection. Remote Sens. Environ. 2013, 133, 193–209. [Google Scholar] [CrossRef]
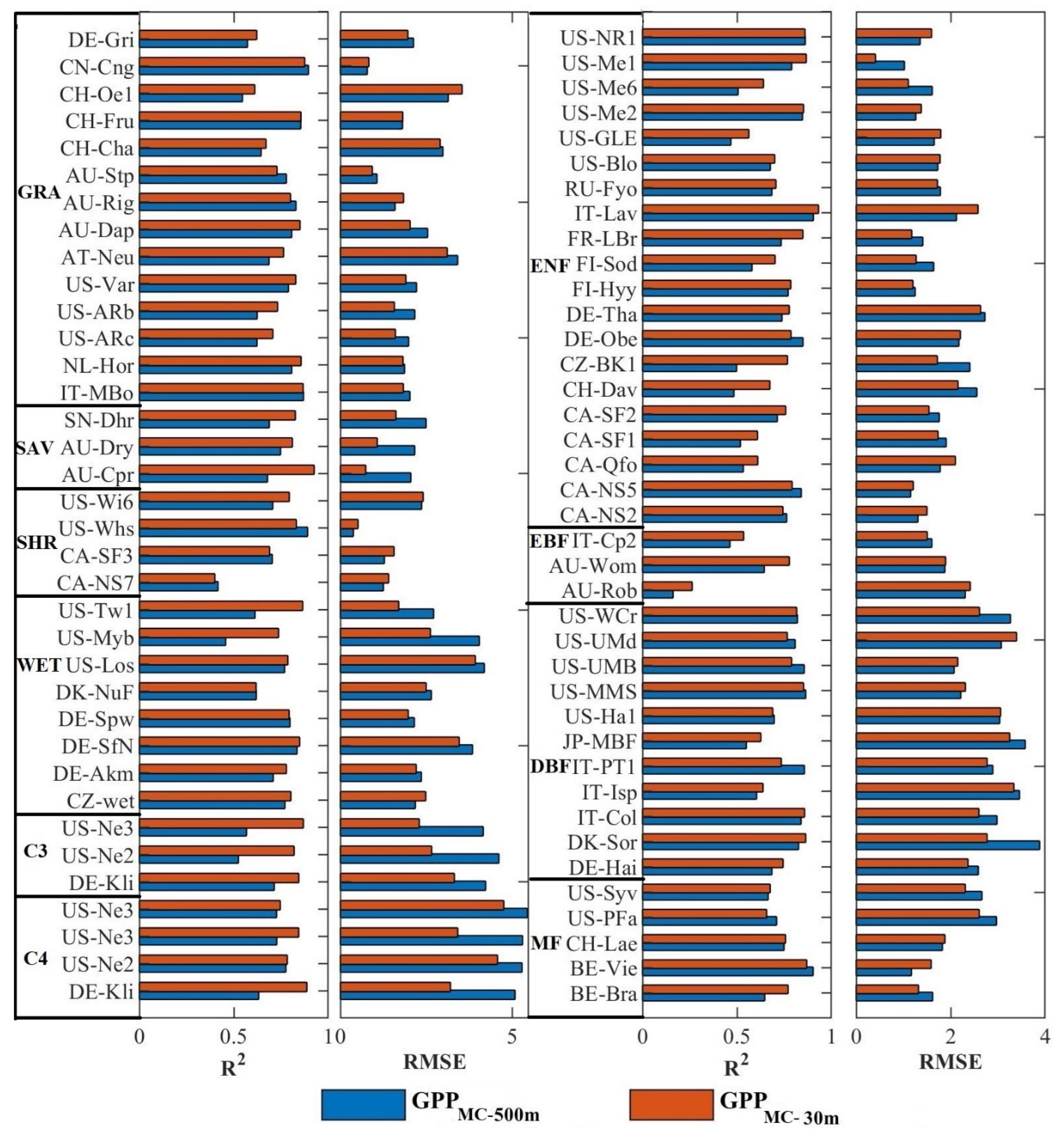
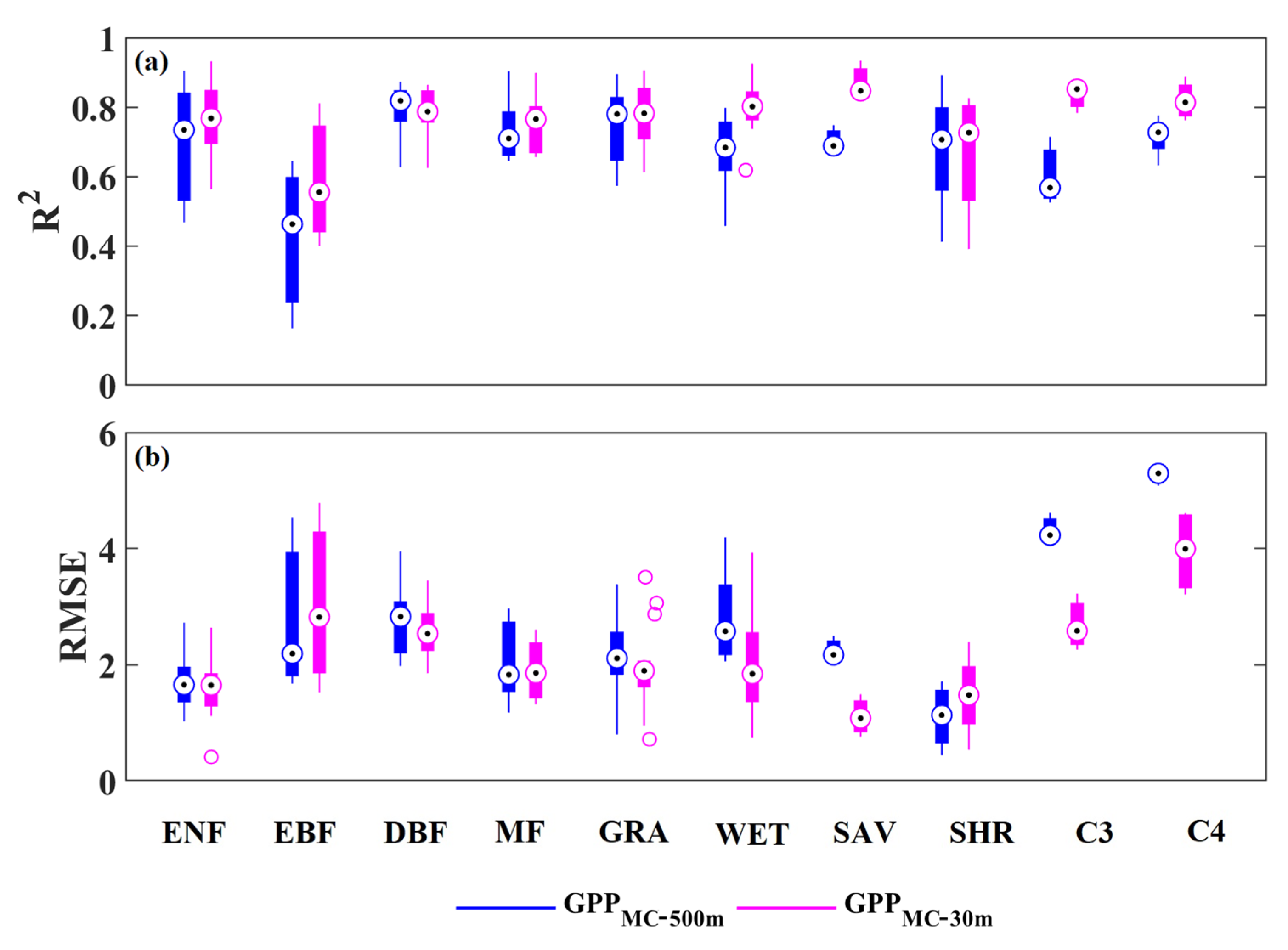
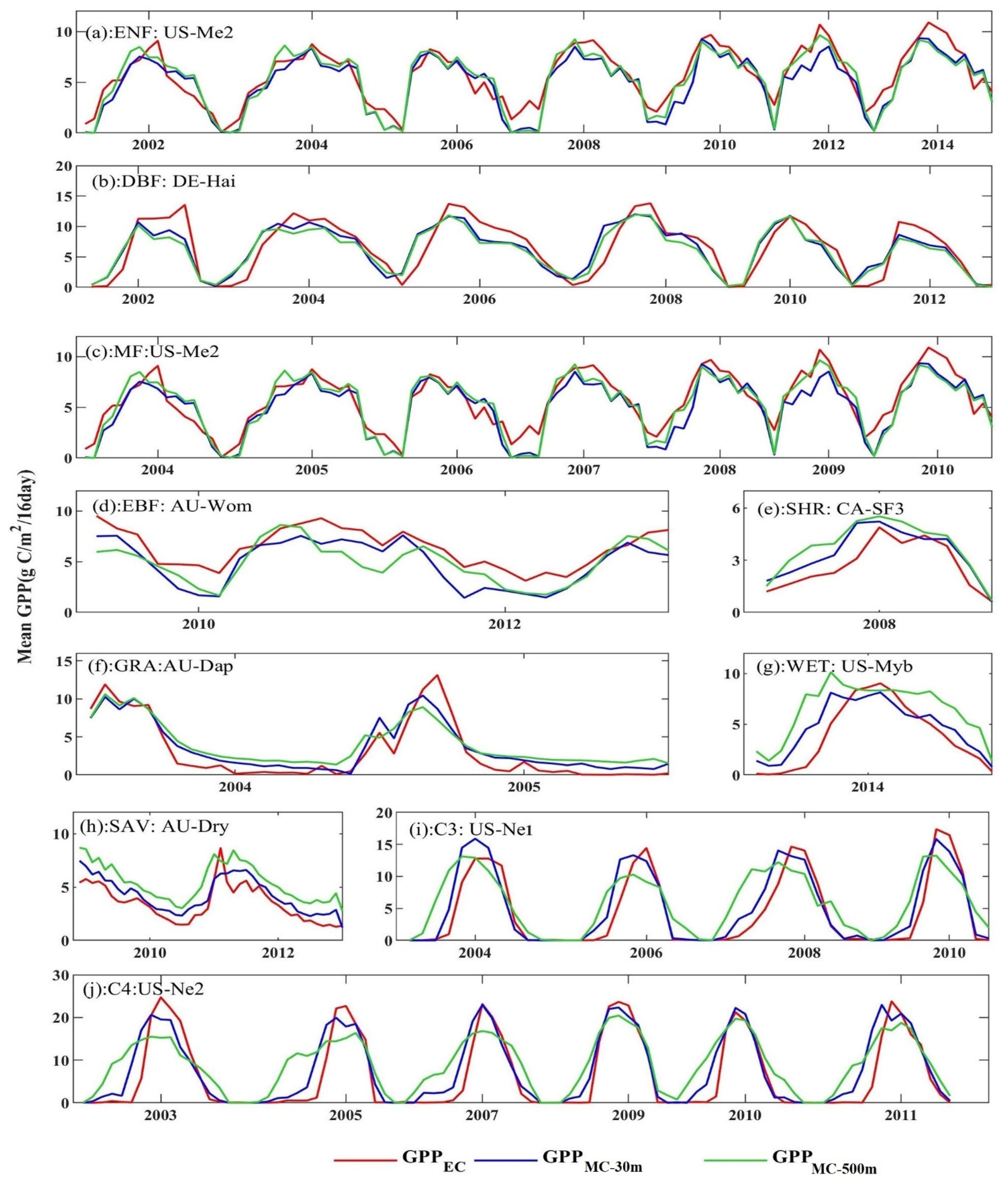
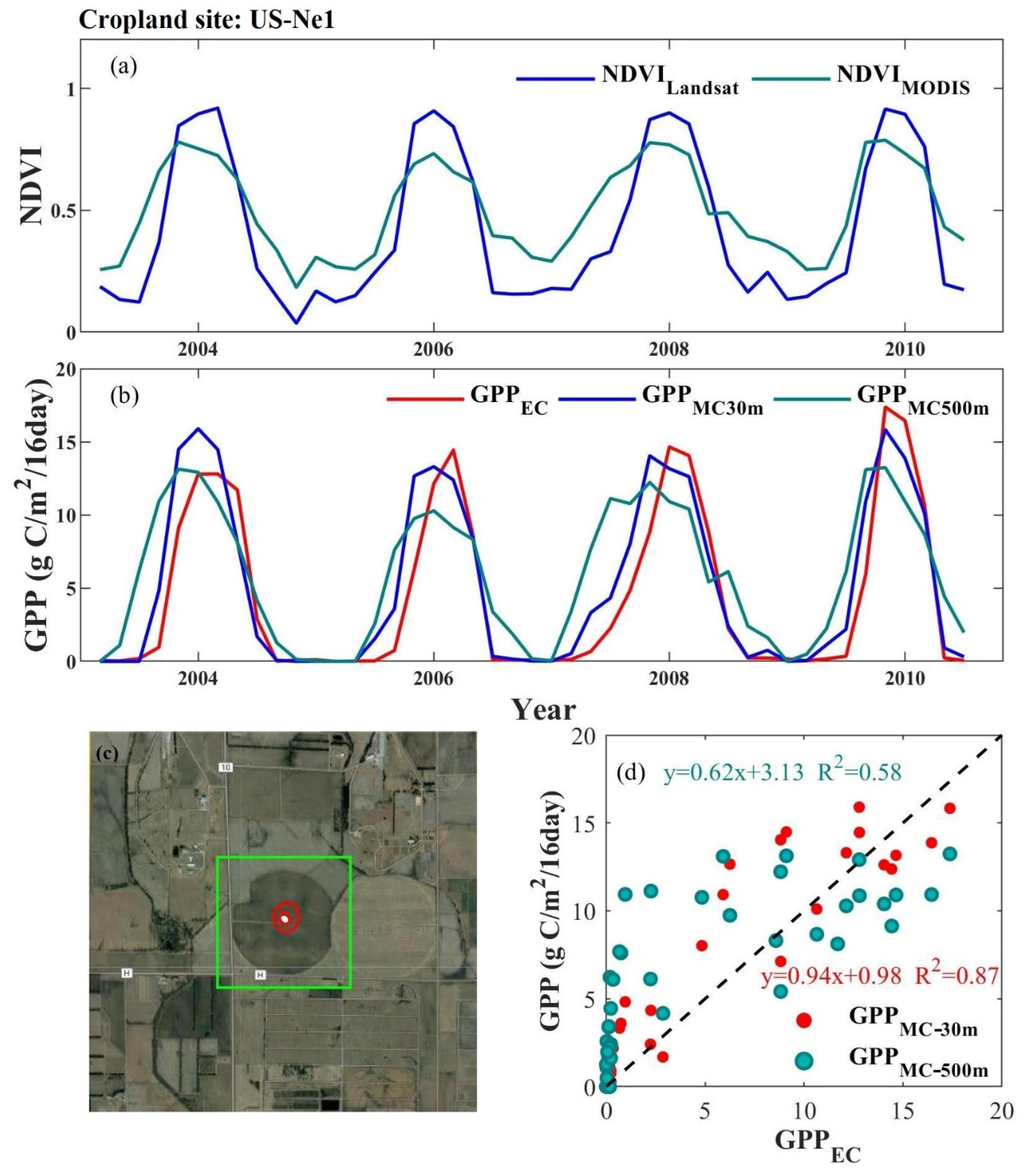
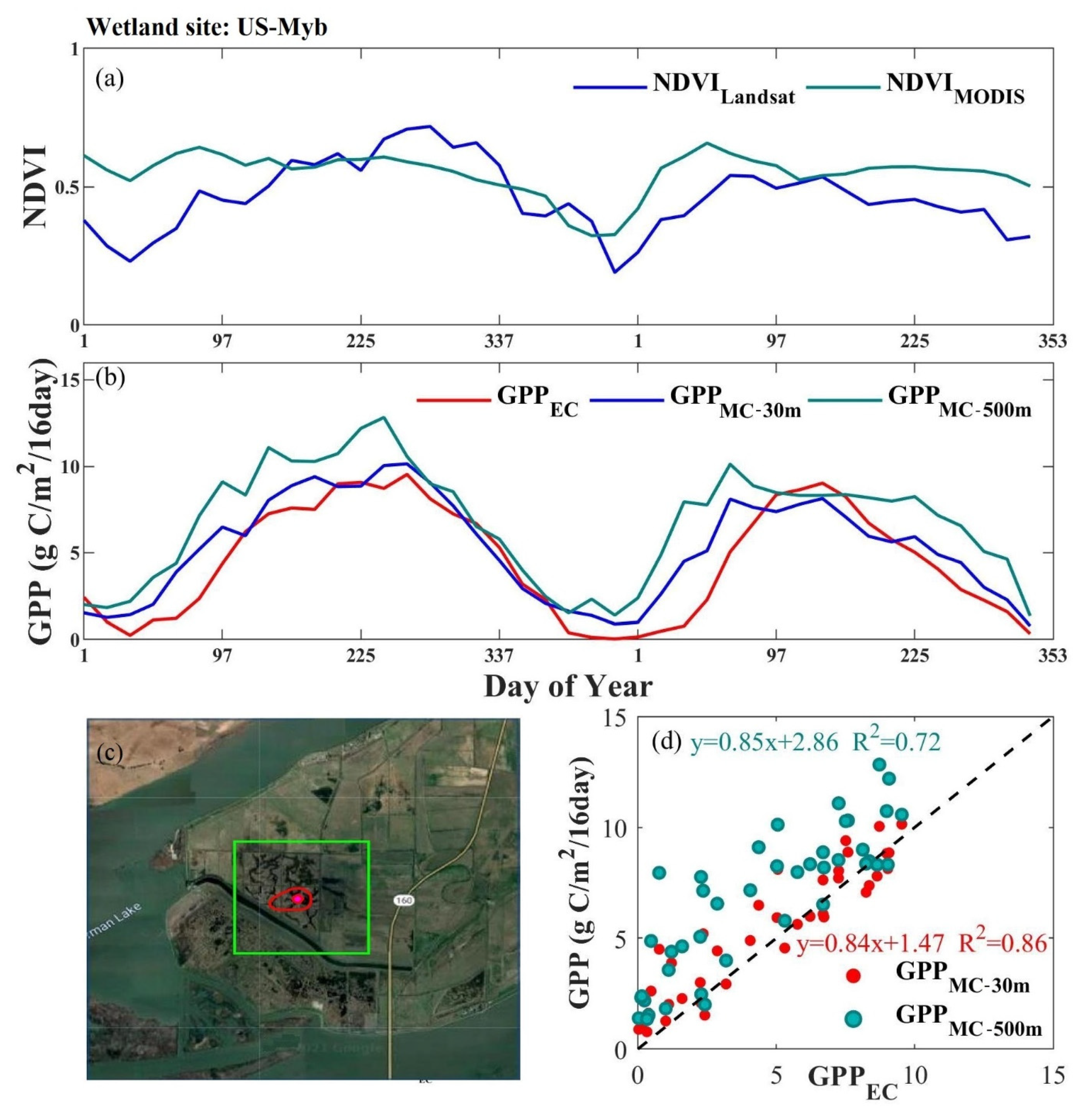
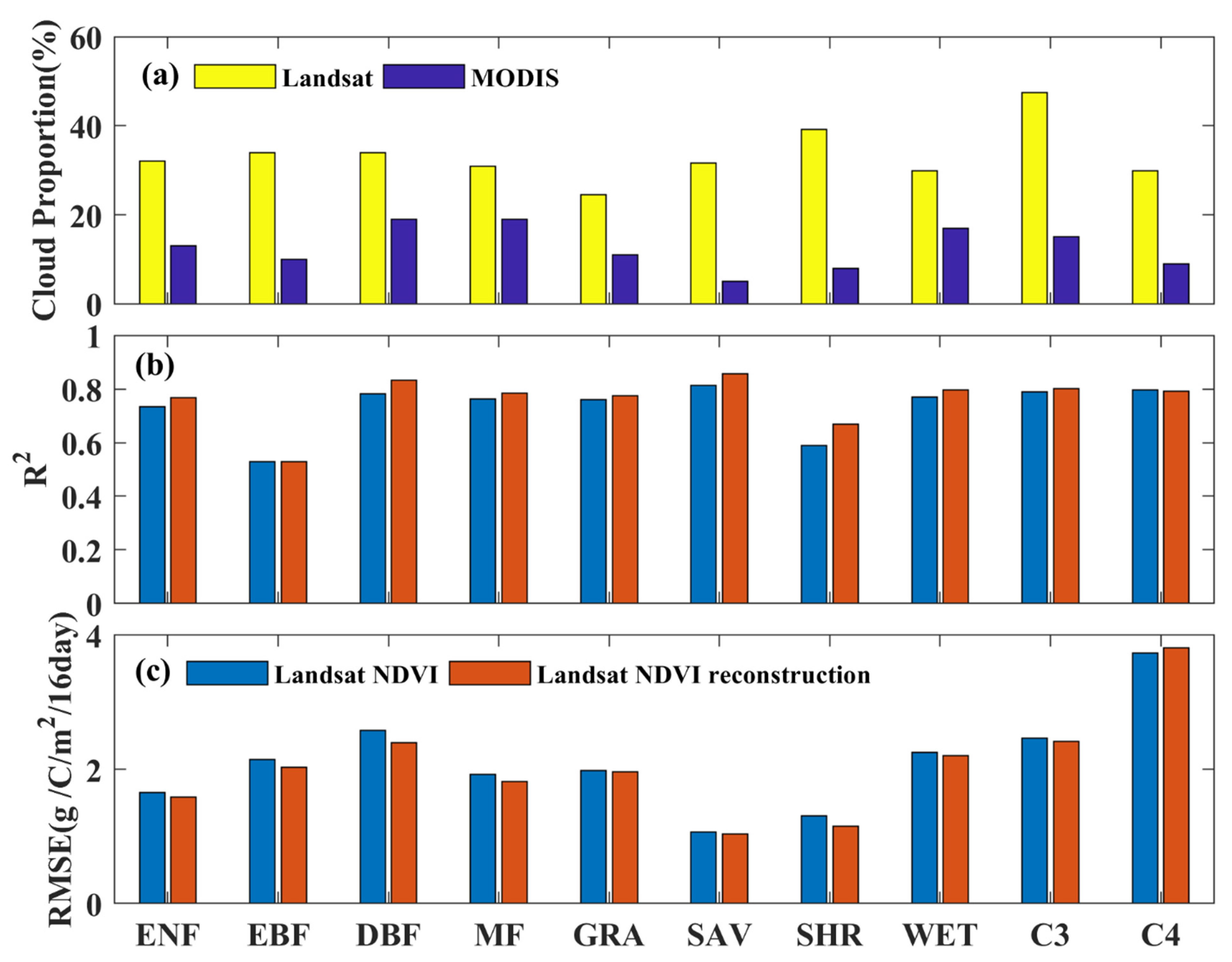
| Vegetation Type | Site Number | 30 m Spatial Resolution | 500 m Spatial Resolution | ||||
|---|---|---|---|---|---|---|---|
| εmax (g C/MJ) | θ (ppm) | VPD0 (k Pa) | εmax (g C/MJ) | θ (ppm) | VPD0 (k Pa) | ||
| EBF | 3 | 3.67 ± 0.59 | 24.25 ± 7.72 | 0.33 ± 0.09 | 3.65 ± 0.59 | 25.27 ± 7.81 | 0.35 ± 0.09 |
| DBF | 12 | 2.97 ± 0.21 | 51.90 ± 6.72 | 1.59 ± 0.09 | 3.04 ± 0.23 | 51.05 ± 7.21 | 1.58 ± 0.09 |
| ENF | 21 | 2.97 ± 0.18 | 35.97 ± 3.26 | 1.08 ± 0.15 | 2.90 ± 0.19 | 31.93 ± 5.23 | 1.30 ± 0.17 |
| MF | 5 | 2.79 ± 0.21 | 43.31 ± 6.07 | 1.34 ± 0.12 | 2.83 ± 0.19 | 43.65 ± 5.45 | 1.34 ± 0.13 |
| GRA | 14 | 4.59 ± 0.06 | 64.72 ± 0.63 | 1.09 ± 0.01 | 4.44 ± 0.08 | 64.72 ± 0.75 | 1.09 ± 0.01 |
| SAV | 3 | 3.19 ± 0.30 | 25.39 ± 5.25 | 1.55 ± 0.15 | 2.60 ± 0.24 | 25.35 ± 5.29 | 1.56 ± 0.14 |
| SHR | 4 | 2.16 ± 0.33 | 57.59 ± 14.18 | 1.26 ± 0.23 | 2.02 ± 0.32 | 58.01 ± 14.23 | 1.24 ± 0.23 |
| WET | 9 | 3.10 ± 0.19 | 59.66 ± 5.15 | 1.40 ± 0.08 | 2.96 ± 0.18 | 59.71 ± 5.17 | 1.41 ± 0.07 |
| C3 Crop | 3 | 3.57 ± 0.29 | 60.55 ± 5.18 | 1.34 ± 0.18 | 3.27 ± 0.19 | 62.63 ± 4.75 | 1.37 ± 0.18 |
| C4 Crop | 4 | 4.81 ± 0.35 | 50.28 ± 5.74 | 1.52 ± 0.14 | 4.47 ± 0.30 | 51.12 ± 5.70 | 1.54 ± 0.15 |
| Sites Name | Long (°) | Lat (°) | Vegetation | Slope (°) | Elevation (m) | GPPMC-30 m | GPPMC-500 m | ||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE (g C/m2/16 Day) | R2 | RMSE (g C/m2/16 Day) | ||||||
| AT-Neu | 47.12 | 11.32 | GRA | 14.83 | 961–1307 | 0.76 | 3.11 | 0.69 | 3.42 |
| CH-Lae | 47.48 | 8.37 | MF | 21.44 | 489–846 | 0.76 | 1.87 | 0.75 | 1.82 |
| JP-MBF | 44.39 | 142.32 | DBF | 14.48 | 478–601 | 0.63 | 3.25 | 0.55 | 3.58 |
| CZ-BK1 | 49.50 | 18.54 | ENF | 13.74 | 761–941 | 0.77 | 1.72 | 0.50 | 2.41 |
| IT-Lav | 45.96 | 11.28 | ENF | 12.10 | 1315–1466 | 0.93 | 2.58 | 0.90 | 2.12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Lin, S.; Li, X.; Ma, M.; Wu, C.; Yuan, W. How Well Can Matching High Spatial Resolution Landsat Data with Flux Tower Footprints Improve Estimates of Vegetation Gross Primary Production. Remote Sens. 2022, 14, 6062. https://doi.org/10.3390/rs14236062
Huang X, Lin S, Li X, Ma M, Wu C, Yuan W. How Well Can Matching High Spatial Resolution Landsat Data with Flux Tower Footprints Improve Estimates of Vegetation Gross Primary Production. Remote Sensing. 2022; 14(23):6062. https://doi.org/10.3390/rs14236062
Chicago/Turabian StyleHuang, Xiaojuan, Shangrong Lin, Xiangqian Li, Mingguo Ma, Chaoyang Wu, and Wenping Yuan. 2022. "How Well Can Matching High Spatial Resolution Landsat Data with Flux Tower Footprints Improve Estimates of Vegetation Gross Primary Production" Remote Sensing 14, no. 23: 6062. https://doi.org/10.3390/rs14236062
APA StyleHuang, X., Lin, S., Li, X., Ma, M., Wu, C., & Yuan, W. (2022). How Well Can Matching High Spatial Resolution Landsat Data with Flux Tower Footprints Improve Estimates of Vegetation Gross Primary Production. Remote Sensing, 14(23), 6062. https://doi.org/10.3390/rs14236062







