Studies and Analysis of Combining BDS-3/GNSS Ultra-Rapid Orbit Products from Different IGS Analysis Centers

Abstract

The third generation of China’s BeiDou Navigation Satellite System (BDS-3) began to provide global service at the end of 2018, and the completion of BDS was announced in July 2020, which includes GEO (Geostationary Earth Orbit), IGSO (Inclined Geosynchronous orbit), and MEO (Medium Earth Orbit) satellites. The resulting BDS orbits vary due to the inconsistent alignment strategies used by different analysis centers. Therefore, it is necessary to study the method of determining the BDS-3 orbit products combined from different analysis centers. In this research, the accuracy of the combined orbits for BDS-3 and other GNSS systems is evaluated and analyzed. To verify the reliability of the orbit combination method proposed in this paper, the GPS orbit is first selected for verification. Compared to the analysis centers, the mean Signal in Space User Ranging Error (SISURE) for GPS combined orbits is significantly reduced, and the mean SISURE of combined orbits for Block IIF, Block IIR, and Block III is 4.15 mm, 5.43 mm, and 5.63 mm, respectively. This demonstrates the effectiveness of the orbit combination method in this research. Besides, the accuracy of the combined orbits is improved by the ERP correction, and the mean RMS of the without Earth rotation Parameters (ERP) correction orbits and with ERP correction orbits is 4.78 mm and 4.53 mm, respectively. This demonstrates that orbit consistency corrections should be considered when performing orbit combinations. Compared to the GFZ orbits, the accuracy of the combined orbits has improved for GPS, GLONASS, GALILEO, and BDS is 8.2%, 9.9%, 9.9%, and 5.5%, respectively. It shows that the orbit combination method improves the orbital accuracy compared to the individual analysis center orbits. The mean RMS of the combined orbits for GPS, GLONASS, GALILEO, BDS MEO, and BDS IGSO is 1.7 cm, 2.61 cm, 2.52 cm, 2.59 cm, and 4.90 cm, respectively. The results demonstrate that the accuracy of the combined orbit for the BDS-3 MEO satellite is already similar to other systems; an orbit combination also available for the BDS-3 satellite.

1. Introduction

With the development of the Global Navigation Satellite System (GNSS), users can adopt Precise Point Positioning (PPP) or Real Time Kinematic (RTK) technology to achieve centimeter or even millimeter-level positioning accuracy. Up to the present, it has been widely used in the fields of deformation monitoring, atmospheric monitoring, unmanned driving, and geodynamics [1,2,3]; reliable satellite orbit and clock products are an important prerequisite for these applications. GNSS high-precision users often use the precise products released by the IGS (International GNSS Service). Currently, the work of the IGS is to combine the satellite orbit and clock products provided by the different analysis centers (ACs) and release more stable and reliable combined products to users. The orbit determination software packages and strategies adopted by each AC are different. For example, both Center for Orbit Determination in Europe (CODE) and Technische Universitaet Muenchen (TUM) use Bernese software, while the other analysis centers use different orbit determination software packages, EPOS by Deutsches GeoForschungsZentrum (GFZ), NAPEOS by European Space Agency (ESA), PANDA by Wuhan University (WHU), POD GINS by Centre National d’Etudes Spatiales (CNES), GAMIT by the Massachusetts Institute of Technology (MIT) and MADOCA by the Japan Aerospace Exploration Agency (JAXA) [4]. Despite that different orbit determination software packages are used, the accuracy of the GPS satellite orbits for each analysis center is better than 3 cm, and the accuracy of the combined orbits released by IGS is better than 2.5 cm [5,6,7]. Many scholars have carried out orbit combination studies using GPS orbits. And the orbit combination method mainly included weighted average combination and orbit dynamic combination. The weighted average combination method converts the AC orbits into a unified reference frame through the Helmert transformation, and the new orbits are combined with the weighted average after removing the systematic errors.

The orbit dynamic method fits the initial orbit parameters according to the orbits of the different ACs. The combined orbits can be obtained by integrating the initial orbit parameters with the weighted average. To eliminate the inconsistency of the different coordinate frames, Beutler et al. [8] used the Earth Rotation Parameters (ERP) to correct the differences between the different coordinate frames. Springer T A [9] and Wei et al. [10] studied the unified coordinate frame by the rotation parameters of station coordinates in the SINEX file. The unified parameter model of the orbit coordinate frame can be corrected using the inconsistency of the different AC’s final products [11]. Yan [12] studied the unification of the reference frames of different ACs using the Helmert rotation parameters. The satellite orbits of the different analysis centers are not uniformly accurate, so it is particularly important to assign reasonable weights to the analysis centers and their satellites in the process of weighted averaging to obtain a combined orbit. Kouba et al. [13] use the absolute deviation between the analysis center orbits and mean orbits to determine the analysis center weights. Weber et al. [14] introduced the GLONASS orbit combination strategy for IGS, which use the root mean square deviation between the analysis center and mean orbits to determine the weights. Xu [15] proposes a weighting method based on the User Range Error (URE), which provides a reference for solving the weighting problem for the combination of multiple types of satellite orbits. Based on the above studies, this paper analyses the influence of different weighting methods on the combined results of the orbits.

The BDS-3 began to provide global services on 27 December 2018, and the completion of BDS was announced in July 2020 [16,17]. At present, BDS-2 consists of fifteen satellites, including three medium earth orbit (MEO) satellites, seven inclined geosynchronous orbiting (IGSO) satellites, and five geostationary earth orbit (GEO) satellites, while BDS-3 has 30 satellites, including 3 GEO satellites, 3 IGSO satellites, and 24 MEO satellites. These BDS-2 satellites transmit signals on three frequencies, i.e., B1I (1561.098 MHz), B2I (1207.14MHz), and B3I (1268.52MHz) [18]. For BDS-3, the satellites are transmitting the original BII and B3I signals, and the new B1C (1575.42 MHz), B2a (1176.45 MHz), B2b (1207.14 MHz), and B2ab (1191.795 MHz) signals. BDS-2 and BDS-3 have overlapping signal frequencies, and BDS-2/BDS-3 joint processing is normally utilized on B1I and B3I, which improves the BDS PNT (positioning, navigation, timing) performance [19]. Currently, the IGS does not provide a combined BDS-3 orbit, and it is unknown whether applying the GPS orbit combination method to BDS-3 is effective. Most of the analysis centers use the same orbit determination strategies for GPS satellites [20], but it is unknown whether the orbit determination is consistent for other GNSS systems. Besides, the BDS constellation includes various orbit types, and hence the effect of the orbit combination for different orbit types may also vary. Based on these assumptions, the products from several analysis centers are selected for orbit combination, and the accuracy of the combined orbits for BDS-3 and other GNSS systems is evaluated and analyzed.

This study starts with models and strategies for orbit determination and orbit combination. The orbit product from the Chinese Academy of Surveying & Mapping (CGS) is first assessed in this study. Then the effectiveness of the orbit combination method and the influence of the ERP correction are analyzed by GPS orbits. After that, the accuracy of the combined ultra-rapid orbits for BDS-3 and other GNSS systems is evaluated and analyzed. Finally, a summary and conclusion are made.

2. Materials and Methods

2.1. Models and Strategies of Orbit Determination

Theoretically, the greater the number of analysis centers involved in the orbit combination, the more reliable the accuracy of the combined orbit. To improve the reliability of the combined orbit, the orbit of the Chinese Academy of Surveying & Mapping (CGS) is determined.

Besides, the ECOM model is used to orbit determination [21,22,23]. The ECOM model can be expressed as follows:

$$\{\begin{array}{l}a=a_0+D(u)\cdot e_D+Y(u)\cdot e_Y+B(u)\cdot e_B\hfill \\ D(u)=D_0+D_{C_u}\cos u+D_{S_u}\sin u\hfill \\ Y(u)=Y_0+Y_{C_u}\cos u+Y_{S_u}\sin u\hfill \\ B(u)=B_0+B_{C_u}\cos u+B_{S_u}\sin u\hfill \end{array}$$

(1)

where $a$ and $a_0$ are the SRP acceleration and priori acceleration, respectively. $u$ is the argument of the ascending node, $D_0$, $D_{C_u}$, $D_{S_u}$, $Y_0$, $Y_{C_u}$, $Y_{S_u}$, $B_0$, $B_{C_u}$, $B_{S_u}$ are estimated in the orbit determination.

2.2. Combined Orbits Process

Different orbit determination strategies of each analysis center can lead to differences in orbit product accuracy. CODE generates long-arc solutions, allowing it, on the one hand, to mitigate the weakness of the estimated ends of the orbital arcs. When generating such a solution based on the normal equation as described in Brockmann [24], none of the observations needs to be processed twice, which speeds up the processing. On the other hand, the resulting length of the long-arc orbit solution is a multiple of the basic processing length of one day, namely 72 h, when adding a normal daily equation before and another after the day of interest. This arc length is significantly longer than that for other analysis centers (e.g., 30 h arcs for JPL; 48 h arcs for CGS). Therefore, it is important to assign a reasonable weight to different analysis centers and different types of satellites during combined orbits. In this paper, the weight is calculated from the Root Mean Square (RMS) of the three-dimensional errors.

(1) Different analysis centers usually choose different observation data, a different number of stations, and different distribution of stations. It will cause the orbit determined by different analysis centers are not in the consistent coordinate framework. To improve the combined orbits’ accuracy, the orbit consistency of different analysis centers needs to be improved by using the ERP, and the reference ERP is provided by IGS. In this paper, the matrix rotation method is used to analyze the center $i$ orbit ${Coor}_{ac}^i\left(X_{ac}^i,Y_{ac}^i,Z_{ac}^i\right)$ to the reference orbit ${Coor}_{ac}^{i\prime }\left(X_{ac}^{i\prime },Y_{ac}^{i\prime },Z_{ac}^{i\prime }\right)$. The matrix rotation method can be described as follows:

$$\{\begin{array}{l}{X}_{ac}^{i_c}=X_{ac}^i+DXp\cdot Z_{ac}^i\hfill \\ Y_{ac}^{i_c}=Y_{ac}^i-DYp\cdot Z_{ac}^i\hfill \\ Z_{ac}^{i_c}=Z_{ac}^i-DXp\cdot X_{ac}^i+DYp\cdot Y_{ac}^i\hfill \end{array}$$

(2)

where $X_{ac}^i$, $Y_{ac}^i$, and $Z_{ac}^i$ are the original orbit coordinates of the analysis center $i$, respectively. $X_{ac}^{i_c}$, $Y_{ac}^{i_c}$, and $Z_{ac}^{i_c}$ are the orbit coordinates corrected by the ERP parameters. $DXp$ and $DYp$ are the difference between the ERP parameters of the analysis center $i$ and the IGS in the X and Y direction, respectively.

(2) After the correction ERP, the orbits of each analysis center are averaged with equal weights, and the averaged orbits are used as reference orbits, which can be expressed as:

$$Coo{r}_{ref}=\frac{{\displaystyle \sum _{ac=1}^{Ncent}Coo{r}_{ac}^{\prime }}}{N\mathrm{cent}}$$

(3)

where $N\mathrm{cent}$ is the number of the analysis center; $Coo{r}_{ref}$ is the reference orbits.

(3) The RMS values of the satellite coordinate three-dimensional errors between each analysis center and reference orbits are calculated as the analysis center’s weight. The weight of the analysis center $P_{ac}$ can be described as follows:

$$P_{ac}=\left(\frac{(3\cdot {\displaystyle \sum _{i=1}^{N_{sat}}Nep{o}_{ac}^i})-7}{{\displaystyle \sum _{i=1}^{N_{sat}}{\displaystyle \sum _{j=1}^{Nep{o}_{ac}^i}RM{S}_{(k,i)}}}}\right)$$

(4)

where $N_{sat}$ is the number of satellites in the analysis center; $Nep{o}_{ac}^i$ is the number of the epoch of satellite $i$ in the analysis center; $RM{S}_{(k,i)}$ denotes the RMS values of the three-dimensional orbit errors of satellite $i$ in epoch $k$.

(4) Next, the combined orbits with equal satellite weights and unequal analysis center weights are calculated as:

$$Coo{r}_w^i=\frac{{\displaystyle \sum _{ac=1}^{Ncent}{P}_{ac}}Coo{r}_{ac}^{\prime }}{{\displaystyle \sum _{ac=1}^{Ncent}{P}_{ac}}}$$

(5)

where $Coo{r}_w^i$ denotes the combined orbits with equal satellite weights.

(5) The corresponding formula is used to calculate the weights of satellites, and the RMS values of the three-dimensional errors between the combined orbits and the analysis center satellites are calculated. The weight of each satellite $P_{sat }$ can be expressed as:

$$P_{sat }=\left(\frac{Ncen{t}^i}{{\displaystyle \sum _{ac}^{Ncen{t}^i}{\displaystyle \sum _k^{Nep{o}_{ac}^i}\frac{RM{S}_{(k,i)}^2}{3 Nep{o}_{ac}^i-7}}}}\right)$$

(6)

(6) The Helmert transformation parameters between $Coo{r}_w^i$ and ${Coor}_{ac}^{i\prime }\left(X_{ac}^{i\prime },Y_{ac}^{i\prime },Z_{ac}^{i\prime }\right)$ with unequal satellite weights are calculated using the least squares method [25,26]. The analysis center orbits ${Coor}_{ac}^{i\prime }\left(X_{ac}^{i\prime },Y_{ac}^{i\prime },Z_{ac}^{i\prime }\right)$ is transformed to ${Coor}_{ac}^{i″}\left(X_{ac}^{i″},Y_{ac}^{i″},Z_{ac}^{i″}\right)$ by Helmert transformation parameters. The final combined orbit $Coo{r}_{comb}^i$ can be expressed as:

$$Coo{r}_{comb}^i=\frac{{\displaystyle \sum _{ac=1}^{Ncent}{P}_{ac}}Coo{r}_{ac}^{i^{″}}}{{\displaystyle \sum _{ac=1}^{Ncent}{P}_{ac}}}$$

(7)

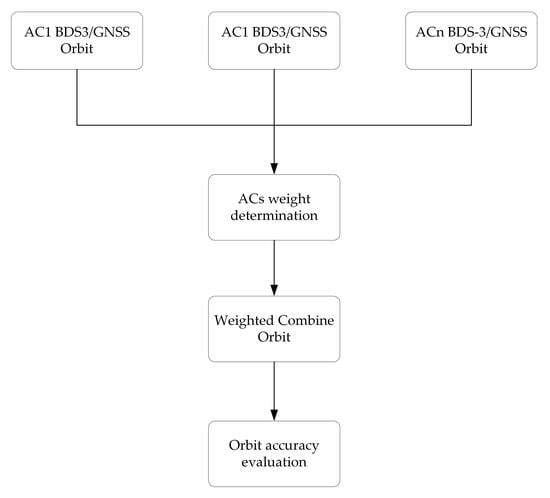
The flow chart of the orbit combination is shown in Figure 1.

3. Results

3.1. Accuracy Assessment of the CGS Orbits

IGS initiated the multi-GNSS experimental (MGEX) in 2011 and built observation networks with multi-GNSS tracking capability. Currently, approximately 250 stations can track multi-GNSS observation signals, including GPS, GLONASS, GALILEO, BDS, and QZSS signals [27]. To ensure the reliability of orbit determination, 140 globally distributed MGEX stations are selected for CGS orbit determination. The distribution of these stations is shown in Figure 2, and data from the DOY 213 to 215 in 2022 are collected in 30 s intervals. These stations are equipped with different receiver types, including Javad, Septentrio, Trimble, and Leica.

Based on the principle of dynamic orbit determination, the observation equation is established by using the dual-frequency pseudo-range and carrier phase observations of the 140 MGEX stations, and the dynamic orbit elements are solved to obtain the CGS orbits. To evaluate the CGS orbit products more comprehensively, the final GBM and final CODE orbits are used as a reference to evaluate the CGS orbits.

The determination of GPS and BDS satellite orbits is performed by using the Figure 2 stations and

Table 1. Summarizes the detailed information on the orbit determination strategies, including the observation and dynamical models.

Item	Method
POD arc length	30 h
Geopotential	EGM 2008 [21,28]
Relativity effect	IERS 2010 [29]
N-body gravitation	JPL DE405 ephemeris [30]
SRP Model	ECOM5 model, ECOM7 model, ECOM9 model [31,32]
Observation	Ionospheric Free (IF) Pseudo-range and carrier phase observations
Cut off ele	7°
Troposphere model	Corrected with Saastamoinen model and global mapping function; residual zenith wet delays estimated with random walk noise [33,34,35]
Perturbation forces	Perturbation of nonspherical figure of the Earth, third body gravity, solid Earth tide, ocean tide, solar radiation [36,37]
EOP parameters	Estimation
PCO and PCV	IGS 2014 atx file [38]

strategy, and the orbit performance is assessed by comparing the 3 days orbit. The results are shown in Figure 3. As can be seen from Figure 3, the RMS values of the GPS satellite’s three-dimensional errors between the CGS and GBM orbits are less than 2 cm, and most are within 1.5 cm. This can demonstrate the reliability of the CGS orbit products estimated in this paper. The mean RMS for the CGS GPS satellites is 1.31 cm in the three-dimensional. For BDS MEO satellites, the RMS values of three-dimensional errors are basically around 5 cm. For BDS IGSO satellites, the RMS values of three-dimensional errors are significantly larger than MEO satellites. The main reason for the larger three-dimensional errors in the BDS satellites is the different orbit determination model and inconsistent PCO values.

Figure 4 displays the RMS values of GPS and BDS orbit errors between the CGS and GBM. Similar to the results the Figure 3, the RMS values of GPS satellites are basically within 1.5 cm, and the mean RMS values between the CGS and CODE GPS orbits is 1.43 cm. The results prove that CGS orbits are consistent with CODE orbits. Besides, the RMS values of the BDS MEO satellite’s three-dimensional errors are around 5 cm. The three-dimensional orbit errors of IGSO satellites are also larger than MEO satellites; among all the satellites, C38 presents worse accuracy than the other satellites.

As shown in Figure 3 and Figure 4, the CGS GPS orbits show the best quality, while the BDS IGSO orbits show the worst quality. As reported by Guo et al. [4], for different analysis centers, the same ECOM model is used to determine the GPS orbits, but the other GNSS satellites use the inconsistent model. The RMS values of the three-dimensional orbit errors agree with the orbit errors of the different analysis centers counted in the Guo et al. [1]. This proves the reliability of the CGS orbit products, and the introduction of CGS orbits in the combination is reasonable.

3.2. Analysis of the Effectiveness of the Orbit Combination Method

In this section, the final GPS orbits from different analysis centers (CGS, CODE, GFZ, ESA, and CNES) are used for orbit combinations to evaluate the effectiveness of the orbit combination method. The final GPS-precise product released by IGS is set as a reference. In this research, we use the Signal in Space User Ranging Error in orbit (SISURE(orb)) for orbit comparison, and it can be calculated as follows [39,40,41]:

$$SISURE(orb)=\sqrt{{(\alpha \cdot R)}^2+\beta (A^2+C^2)}$$

(8)

where $\alpha$ and $\beta$ are weight factors and the values are 0.98 and 1/49 for GPS; for GLONASS, $\alpha =0.98$ and $\beta =1/45$; for Galileo $\alpha =0.98$ and $\beta =1/61$; for BDS GEO/IGSO, $\alpha =0.99$ and $\beta =1/126$, for MEO, $\alpha =0.98$ and $\beta =1/54$; $R$, $A$ and $C$ are orbit error in the radial, along-track, and cross-track directions; $SISURE(orb)$ is the contribution of orbit to SISURE.

As can be seen from Figure 5, the pink bar represents the orbit SISURE between the mean analysis centers and the IGS final products; the blue bar represents the orbit SISURE between the combined orbits and the IGS final products, the subplots in the figure represent the orbit SISURE for different orbit types of GPS satellites. It can be seen that the orbit SISURE of the combined orbits is significantly reduced compared to the mean SISURE for all analysis centers. In addition,

Table 2. Mean SISURE of GPS satellites with different orbit types for mean analysis centers and combined orbits (Unit: mm).

SISURE	Block IIF	Block IIR	Block III
Mean ACs	8.66	10.67	11.28
Comb	4.15	5.43	5.63

shows the mean values of SISURE for different orbit types of GPS satellites. For Block IIF satellites, the mean orbit SISURE and the combined orbit SISURE are 8.66 mm and 4.15 mm, respectively. For Block IIR satellites, the mean orbit SISURE and the combined orbit SISURE are 10.67 mm and 5.43 mm, respectively. For Block III satellites, the mean orbit SISURE and the combined orbit SISURE are 11.28 mm and 5.63 mm, respectively. Based on these statistics, we find that the orbit combination improved orbit accuracy for different types of GPS satellites. This demonstrates the effectiveness of the orbit combination method in this research.

In this section, the influence of the ERP correction on the accuracy of the combined orbits is analyzed and shown in Figure 6. To evaluate the quality of combined orbits, the final precise ERP product of IGS is set as a reference. As seen in the Figure 6 result, the red bar represents the RMS values of the orbit errors between the combined orbits without ERP correction and IGS orbits. The blue bar represents the orbit errors between the combined orbits with ERP correction and IGS orbits. It can be seen from Figure 6 that the accuracy of the combined orbit is improved by the ERP correction. The mean RMS of the without ERP correction orbits and with ERP correction orbits is 4.78 mm and 4.53 mm, respectively.

In addition, the influence of the weighting method on the accuracy of combined orbits is analyzed in this section. As can be seen from Figure 7, the pink bar represents the RMS values of the orbit errors between the IGS orbits and the combined orbits using the URE values to determine the weights; the blue bar represents the orbit errors between the combined orbits using the RMS values to determine the weights and the IGS orbits. The average RMS between the combined orbits obtained by the two weighting methods and the IGS orbits are better than 6 mm, which proves the effectiveness of the two weighting methods. The difference between the orbits combined by the two weighting methods is very small, essentially within 1mm. Therefore, this paper chooses the RMS value to determine the weights for ultra-rapid orbit combinations.

3.3. Analysis Results of MGEX Ultra Rapid Orbit Combination

From the results in Section 3.2, it can be seen that the orbit combination can achieve a significant improvement in GPS satellite orbit accuracy, and it is necessary to analyze whether orbit combination can equally improve the orbital accuracy for BDS satellites. Currently, only the final GPS orbit is provided by IGS, and the inability to select a suitable reference orbit for accurate assessment of the combined BDS-3 orbit. Considering this, we selected the ultra-rapid orbit products of the analysis centers to analyze the influence of orbit combinations on the orbital accuracy of BDS satellites. For comparison, the combined results of the ultra-rapid orbital products of other GNSS systems are also analyzed in this section.

3.3.1. Accuracy Assessment of Combined Orbits

Firstly, the mean value of the Root Mean Square and Standard Variation for all GPS satellites over 30 days is counted, and the statistical results are shown in Figure 8. As can be seen in Figure 8, the cylinders and dashes present the RMS and STD, respectively. It can be seen that the RMS values of the SISURE for the combined orbits are all within 3cm, and most of them are less than 2 cm. The values prove the reliability of the combined GPS ultra-rapid orbits. The SISURE STD for all GPS satellites is also within 3cm over 30 days, further validating the combined orbit accuracy.

Figure 9 shows the RMS and STD statistics results for the GLONASS satellites. As can be seen from Figure 9, apart from the R19 and R20, most of the GLONASS satellites are within 3 cm, which proves the reliability of the combined GLONASS ultra-rapid orbits. Besides, the mean STD for all GLONASS satellites is also within 3cm, similar to the GPS results.

Figure 10 depicts the mean RMS and STD of the SISURE for all GALILEO satellites. The rms and std for all GALILEO satellites shown in the results in Figure 10 are essentially within 3 cm. This proves that the ultra-rapid orbits of GALILEO satellites combined in this paper are equally reliable. The overall RMS statistics for GALILEO satellites are slightly worse than those for GPS systems, mainly because fewer analysis centers are involved in the GALILEO satellite combination.

In addition, the mean RMS and STD of BDS satellites are shown in Figure 11. As seen in Figure 11, the RMS of the combined orbits of the BDS MEO satellites are all within 4 cm, and the RMS of the BDS-3 MEO satellites are all essentially around 2 cm. The RMS values of the integrated orbits of the BDS IGSO satellites are all above 4 cm, significantly larger than those of the MEO satellites, mainly due to the relatively few stations that can observe the IGSO satellites. Besides, the mean STD for all BDS satellites is also within 4 cm, which proves the reliability of the combined BDS ultra-rapid orbits.

In addition,

Table 3. Mean RMS and STD between ultra-rapid and final orbit (unit: cm).

SISURE	GPS	GLONASS	GAL	BDS MEO	BDS IGSO
RMS	1.70	2.61	2.52	2.59	4.90
STD	2.20	2.90	2.50	2.70	2.90

shows the mean RMS and STD of the combined ultra-rapid orbits for all systems. The mean RMS for GPS, GLONASS, GALILEO, BDS MEO, and BDS IGSO is 1.7 cm, 2.61 cm, 2.52 cm, 2.59 cm, and 4.90 cm, respectively. As can be seen from the results, the RMS statistics for the BDS MEO satellite are already similar to other systems. Besides, the mean STD for GPS, GLONASS, GALILEO, BDS MEO, and BDS IGSO is 2.20 cm, 2.90 cm, 2.50 cm, 2.70 cm, and 2.90 cm, respectively. The reliability of the combined ultra-rapid orbit can be demonstrated by the above results.

3.3.2. The Validity of the Orbit Combination

To further verify the validity of the orbit combination, the 10-day combined ultra-rapid orbit is selected for an accuracy comparison with the GFZ ultra-rapid orbit. Figure 12 represents the RMS values for the GPS ultra-rapid orbit and the combined GPS ultra-rapid orbit with the final orbit for GFZ, respectively. As can be seen from Figure 12, compared to the GFZ ultra-rapid orbit, the combined ultra-rapid orbit accuracy significantly improved. Most of the satellites in the GFZ ultra-rapid orbit have error values of 2 cm or more, but the combined ultra-rapid orbit differences are largely within 2 cm. The average RMS of the combined GPS satellites is 1.56 cm, and the average RMS of the GFZ is 1.70 cm; the orbit combination improves the ultra-rapid orbit accuracy of GPS satellites by 8.2%.

Figure 13 depicts the RMS values for the GLONASS ultra-rapid orbit. The results show that the orbit combination is also valid for GLONASS satellites and that the combined GLONASS ultra-rapid orbit is also improved compared to GFZ. The average RMS for the GLONASS satellite combined ultra-rapid orbit and the GFZ ultra-rapid orbit is 2.61 cm and 2.35 cm, respectively. The orbit combination improves the ultra-rapid orbit of GLONASS satellites by 9.9%.

Figure 14 shows the statistical results for the ultra-rapid orbit of the GALILEO satellites. It can be seen that the orbital combination also significantly improves the accuracy of GALILEO satellites. The average RMS for the GALILEO satellite combined orbit and the GFZ orbit is 2.52 cm and 2.30 cm, respectively. The orbit combination improves the ultra-rapid orbit of GLONASS satellites by 9.9%.

Figure 15 shows the statistical results for the ultra-rapid orbit of the BDS satellites. As can be seen in Figure 15, the average RMS for the combined orbit is 3.53 cm, and the average RMS for the GFZ ultra-rapid orbit is 3.30 cm. The statistics from the BDS satellites show that the accuracy of the orbit combination for ultra-rapid orbit has improved for both IGSO and MEO satellites, and the average improvement is 5.5%.

It shows that the orbit combination method improves the orbital accuracy and makes the combined orbit more reliable and stable than the individual analysis center orbits.

4. Discussion

According to the results, the orbit combination method used in this research applies to all GNSS systems. The experimental results of the GNSS ultra-rapid orbits show that the orbital combination of orbit products from several analysis centers can improve the accuracy of the GNSS satellites. The highest combined GPS orbit accuracy due to the most consistent GPS orbit determination strategy used by each analysis center. If the orbit determination strategies of GLONASS, GALILEO, BDS, and other systems of each analysis center are unified, it is believed that the accuracy of the combined orbit products of these systems can be improved. Besides, the combined orbit accuracy of the BDS MEO satellites is now close to that of other systems, with the BDS IGSO satellites having the worst combined orbital accuracy.

Because only the final GPS orbit is provided by IGS, there is an inability to select a suitable reference orbit for accurately assessing the combined other GNSS orbits. Considering this, we selected the ultra-rapid orbit products of the analysis centers to analyze the influence of orbit combinations on orbital accuracy. Afterward, the final products from each analysis center could be selected for orbit combination, and products such as SLR can be used to verify the accuracy of the combined orbit products.

5. Conclusions

Currently, the combined orbit products released by IGS only involve GPS. BDS-3 has been operational for more than a year, but there are still no publicly available combined orbit products for BDS-3. In this research, ultra-rapid orbit products from several analysis centers are selected for orbit combination, and the accuracy of the combined orbits for BDS-3 and other GNSS systems is evaluated and analyzed. The results include the following:

(1) The CGS GPS orbits show the best quality; the mean RMS values of three-dimensional errors between the CGS and GBM GPS orbits is 1.31 cm, and the mean RMS values between the CGS and CODE are 1.43 cm. Due to different orbit determination models and inconsistent PCO values, the BDS orbits of the CGS are relatively different from those of the GBM and CODE but are basically within 5cm. This proves the reliability of the CGS orbit products and the introduction of CGS orbits in the combination is reasonable;

(2) The mean SISURE of combined orbits for Block IIF, Block IIR, and Block III is 4.15 mm, 5.43 mm, and 5.63 mm, respectively. The orbit SISURE of the combined orbits is significantly reduced compared to the mean SISURE for all analysis centers. This demonstrates the effectiveness of the orbit combination method in this research;

(3) The mean RMS of the without ERP correction orbits and with ERP correction orbits is 4.78 mm and 4.53 mm, respectively. This demonstrates that orbit consistency correction can improve the accuracy of the combined orbit;

(4) The orbit SISURE between the combined ultra-rapid orbits and the GFZ final orbits is used to evaluate the accuracy of the combined orbits. The mean RMS for GPS, GLONASS, GALILEO, BDS MEO, and BDS IGSO is 1.7 cm, 2.61 cm, 2.52 cm, 2.59 cm, and 4.90 cm, respectively. And the mean STD for GPS, GLONASS, GALILEO, BDS MEO, and BDS IGSO is 2.20 cm, 2.90 cm, 2.50 cm, 2.70 cm, and 2.90 cm, respectively. Based on the above results, the combined orbits accuracy of BDS-3 MEO satellites is already similar to other systems;

(5) The GFZ ultra-rapid orbits are used to assess the effectiveness of the orbit combination. Compared to the GFZ results, the accuracy of the combined ultra-rapid orbits has improved for GPS, GLONASS, GALILEO, and BDS is 8.2 %, 9.9%, 9.9%, and 5.5 %, respectively. It shows that the orbit combination method improves the orbital accuracy compared to the individual analysis center orbits.