A Multi-Source Data Fusion Method to Improve the Accuracy of Precipitation Products: A Machine Learning Algorithm
Abstract
:1. Introduction
2. Study Area
3. Data and Methods
3.1. Data
3.2. Methods
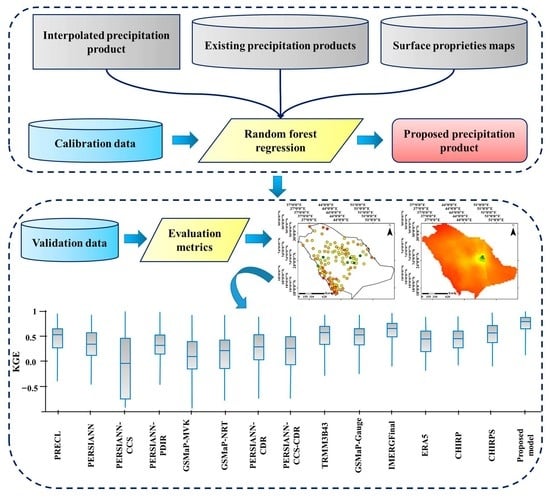
3.2.1. Assessing the Accuracy of Precipitation Products
3.2.2. Proposed Method for Preparing a Precipitation Product
4. Results
4.1. The Importance Degree of Independent Variables
4.2. Evaluate the Accuracy of Precipitation Products Based on a Pixel-to-Pixel Strategy
4.3. Evaluate the Accuracy of Precipitation Products Based on a Point-to-Pixel Strategy
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Salman, S.A.; Shahid, S.; Ismail, T.; Al-Abadi, A.M.; Wang, X.-J.; Chung, E.-S. Selection of gridded precipitation data for Iraq using compromise programming. Measurement 2019, 132, 87–98. [Google Scholar] [CrossRef]
- Seyyedi, H.; Anagnostou, E.N.; Beighley, E.; McCollum, J. Hydrologic evaluation of satellite and reanalysis precipitation datasets over a mid-latitude basin. Atmos. Res. 2015, 164, 37–48. [Google Scholar] [CrossRef]
- Sheffield, J.; Goteti, G.; Wood, E.F. Development of a 50-year high-resolution global dataset of meteorological forcings for land surface modeling. J. Clim. 2006, 19, 3088–3111. [Google Scholar] [CrossRef] [Green Version]
- Sun, W.; Ma, J.; Yang, G.; Li, W. Statistical and hydrological evaluations of multi-satellite precipitation products over Fujiang river basin in humid southeast China. Remote Sens. 2018, 10, 1898. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, K.; Sachindra, D.; Shahid, S.; Iqbal, Z.; Nawaz, N.; Khan, N. Multi-model ensemble predictions of precipitation and temperature using machine learning algorithms. Atmos. Res. 2020, 236, 104806. [Google Scholar] [CrossRef]
- Zhan, Y.; Ren, G.; Yang, S. Change in precipitation over the Asian continent from 1901-2016 based on a new multi-source dataset. Clim. Res. 2018, 76, 41–57. [Google Scholar] [CrossRef]
- Zhou, Y.; Nelson, K.; Mohr, K.I.; Huffman, G.J.; Levy, R.; Grecu, M. A spatial-temporal extreme precipitation database from GPM IMERG. J. Geophys. Res. Atmos. 2019, 124, 10344–10363. [Google Scholar] [CrossRef]
- Guo, B.; Zhang, J.; Xu, T.; Croke, B.; Jakeman, A.; Song, Y.; Yang, Q.; Lei, X.; Liao, W. Applicability assessment and uncertainty analysis of multi-precipitation datasets for the simulation of hydrologic models. Water 2018, 10, 1611. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Xiong, L.; Ma, Q.; Kim, J.-S.; Chen, J.; Xu, C.-Y. Improving daily spatial precipitation estimates by merging gauge observation with multiple satellite-based precipitation products based on the geographically weighted ridge regression method. J. Hydrol. 2020, 589, 125156. [Google Scholar] [CrossRef]
- Qureshi, S.; Koohpayma, J.; Firozjaei, M.K.; Kakroodi, A.A. Evaluation of Seasonal, Drought, and Wet Condition Effects on Performance of Satellite-Based Precipitation Data over Different Climatic Conditions in Iran. Remote Sens. 2021, 14, 76. [Google Scholar] [CrossRef]
- Satgé, F.; Defrance, D.; Sultan, B.; Bonnet, M.-P.; Seyler, F.; Rouche, N.; Pierron, F.; Paturel, J.-E. Evaluation of 23 gridded precipitation datasets across West Africa. J. Hydrol. 2020, 581, 124412. [Google Scholar] [CrossRef] [Green Version]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.L. A review of global precipitation data sets: Data sources, estimation, and intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, P.; Ombadi, M.; Sorooshian, S.; Hsu, K.; AghaKouchak, A.; Braithwaite, D.; Ashouri, H.; Thorstensen, A.R. The PERSIANN family of global satellite precipitation data: A review and evaluation of products. Hydrol. Earth Syst. Sci. 2018, 22, 5801–5816. [Google Scholar] [CrossRef] [Green Version]
- Prakash, S. Performance assessment of CHIRPS, MSWEP, SM2RAIN-CCI, and TMPA precipitation products across India. J. Hydrol. 2019, 571, 50–59. [Google Scholar] [CrossRef]
- Sharifi, E.; Steinacker, R.; Saghafian, B. Assessment of GPM-IMERG and other precipitation products against gauge data under different topographic and climatic conditions in Iran: Preliminary results. Remote Sens. 2016, 8, 135. [Google Scholar] [CrossRef] [Green Version]
- Saemian, P.; Hosseini-Moghari, S.-M.; Fatehi, I.; Shoarinezhad, V.; Modiri, E.; Tourian, M.J.; Tang, Q.; Nowak, W.; Bárdossy, A.; Sneeuw, N. Comprehensive evaluation of precipitation datasets over Iran. J. Hydrol. 2021, 603, 127054. [Google Scholar] [CrossRef]
- Yuan, F.; Zhang, L.; Soe, K.M.W.; Ren, L.; Zhao, C.; Zhu, Y.; Jiang, S.; Liu, Y. Applications of TRMM-and GPM-era multiple-satellite precipitation products for flood simulations at sub-daily scales in a sparsely gauged watershed in Myanmar. Remote Sens. 2019, 11, 140. [Google Scholar] [CrossRef] [Green Version]
- Eini, M.R.; Olyaei, M.A.; Kamyab, T.; Teymoori, J.; Brocca, L.; Piniewski, M. Evaluating three non-gauge-corrected satellite precipitation estimates by a regional gauge interpolated dataset over Iran. J. Hydrol. Reg. Stud. 2021, 38, 100942. [Google Scholar] [CrossRef]
- Beck, H.E.; Pan, M.; Roy, T.; Weedon, G.P.; Pappenberger, F.; Van Dijk, A.I.; Huffman, G.J.; Adler, R.F.; Wood, E.F. Daily evaluation of 26 precipitation datasets using Stage-IV gauge-radar data for the CONUS. Hydrol. Earth Syst. Sci. 2019, 23, 207–224. [Google Scholar] [CrossRef] [Green Version]
- Firozjaei, M.K.; Sedighi, A.; Firozjaei, H.K.; Kiavarz, M.; Homaee, M.; Arsanjani, J.J.; Makki, M.; Naimi, B.; Alavipanah, S.K. A historical and future impact assessment of mining activities on surface biophysical characteristics change: A remote sensing-based approach. Ecol. Indic. 2021, 122, 107264. [Google Scholar] [CrossRef]
- Weng, Q.; Firozjaei, M.K.; Sedighi, A.; Kiavarz, M.; Alavipanah, S.K. Statistical analysis of surface urban heat island intensity variations: A case study of Babol city, Iran. GISci. Remote Sens. 2019, 56, 576–604. [Google Scholar] [CrossRef]
- Valjarević, A.; Morar, C.; Živković, J.; Niemets, L.; Kićović, D.; Golijanin, J.; Gocić, M.; Bursać, N.M.; Stričević, L.; Žiberna, I. Long term monitoring and connection between topography and cloud cover distribution in Serbia. Atmosphere 2021, 12, 964. [Google Scholar] [CrossRef]
- Firozjaei, M.K.; Kiavarz, M.; Alavipanah, S.K.; Lakes, T.; Qureshi, S. Monitoring and forecasting heat island intensity through multi-temporal image analysis and cellular automata-Markov chain modelling: A case of Babol city, Iran. Ecol. Indic. 2018, 91, 155–170. [Google Scholar] [CrossRef]
- Firozjaei, M.K.; Kiavarz, M.; Homaee, M.; Arsanjani, J.J.; Alavipanah, S.K. A novel method to quantify urban surface ecological poorness zone: A case study of several European cities. Sci. Total Environ. 2021, 757, 143755. [Google Scholar] [CrossRef] [PubMed]
- Boloorani, A.D.; Kazemi, Y.; Sadeghi, A.; Shorabeh, S.N.; Argany, M. Identification of dust sources using long term satellite and climatic data: A case study of Tigris and Euphrates basin. Atmos. Environ. 2020, 224, 117299. [Google Scholar] [CrossRef]
- Schmugge, T.J.; Kustas, W.P.; Ritchie, J.C.; Jackson, T.J.; Rango, A. Remote sensing in hydrology. Adv. Water Resour. 2002, 25, 1367–1385. [Google Scholar] [CrossRef]
- Schultz, G.A.; Engman, E.T. Remote Sensing in Hydrology and Water Management; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Liu, J.; Duan, Z.; Jiang, J.; Zhu, A. Evaluation of three satellite precipitation products TRMM 3B42, CMORPH, and PERSIANN over a subtropical watershed in China. Adv. Meteorol. 2015, 2015, 151239. [Google Scholar] [CrossRef] [Green Version]
- Moghaddam, M.H.R.; Sedighi, A.; Fayyazi, M.A. Applying MNDWI index and linear directional mean analysis for morphological changes in the Zarriné-Rūd River. Arab. J. Geosci. 2015, 8, 8419–8428. [Google Scholar] [CrossRef]
- Calera, A.; Campos, I.; Osann, A.; D’Urso, G.; Menenti, M. Remote sensing for crop water management: From ET modelling to services for the end users. Sensors 2017, 17, 1104. [Google Scholar] [CrossRef] [Green Version]
- Fathololoumi, S.; Vaezi, A.R.; Firozjaei, M.K.; Biswas, A. Quantifying the effect of surface heterogeneity on soil moisture across regions and surface characteristic. J. Hydrol. 2021, 596, 126132. [Google Scholar] [CrossRef]
- Fathololoumi, S.; Firozjaei, M.K.; Biswas, A. Improving spatial resolution of satellite soil water index (SWI) maps under clear-sky conditions using a machine learning approach. J. Hydrol. 2022, 615, 128709. [Google Scholar] [CrossRef]
- Firozjaei, M.K.; Daryaei, I.; Sedighi, A.; Weng, Q.; Alavipanah, S.K. Homogeneity Distance Classification Algorithm (HDCA): A Novel Algorithm for Satellite Image Classification. Remote Sens. 2019, 11, 546. [Google Scholar] [CrossRef] [Green Version]
- Fathololoumi, S.; Firozjaei, M.K.; Li, H.; Biswas, A. Surface biophysical features fusion in remote sensing for improving land crop/cover classification accuracy. Sci. Total Environ. 2022, 838, 156520. [Google Scholar] [CrossRef] [PubMed]
- Firozjaei, M.K.; Sedighi, A.; Jelokhani-Niaraki, M. An urban growth simulation model based on integration of local weights and decision risk values. Trans. GIS 2020, 24, 1695–1721. [Google Scholar] [CrossRef]
- Dadras, M.; Shafri, H.Z.; Ahmad, N.; Pradhan, B.; Safarpour, S. Spatio-temporal analysis of urban growth from remote sensing data in Bandar Abbas city, Iran. Egypt. J. Remote Sens. Space Sci. 2015, 18, 35–52. [Google Scholar] [CrossRef] [Green Version]
- Kiavarz, M.; Hosseinbeigi, S.B.; Mijani, N.; Shahsavary, M.S.; Firozjaei, M.K. Predicting spatial and temporal changes in surface urban heat islands using multi-temporal satellite imagery: A case study of Tehran metropolis. Urban Clim. 2022, 45, 101258. [Google Scholar] [CrossRef]
- Coutts, A.M.; Harris, R.J.; Phan, T.; Livesley, S.J.; Williams, N.S.; Tapper, N.J. Thermal infrared remote sensing of urban heat: Hotspots, vegetation, and an assessment of techniques for use in urban planning. Remote Sens Env. 2016, 186, 637–651. [Google Scholar] [CrossRef]
- Mijani, N.; Firozjaei, M.K.; Mijani, M.; Khodabakhshi, A.; Qureshi, S.; Arsanjani, J.J.; Alavipanah, S.K. Exploring the effect of COVID-19 pandemic lockdowns on urban cooling: A tale of three cities. Adv. Space Res. 2022, in press. [Google Scholar] [CrossRef]
- Mijani, N.; Alavipanah, S.K.; Firozjaei, M.K.; Arsanjani, J.J.; Hamzeh, S.; Weng, Q. Modeling outdoor thermal comfort using satellite imagery: A principle component analysis-based approach. Ecol. Indic. 2020, 117, 106555. [Google Scholar] [CrossRef]
- Qureshi, S.; Alavipanah, S.K.; Konyushkova, M.; Mijani, N.; Fathololomi, S.; Firozjaei, M.K.; Homaee, M.; Hamzeh, S.; Kakroodi, A.A. A Remotely Sensed Assessment of Surface Ecological Change over the Gomishan Wetland, Iran. Remote Sens. 2020, 12, 2989. [Google Scholar] [CrossRef]
- Firozjaei, M.K.; Fathololoumi, S.; Kiavarz, M.; Biswas, A.; Homaee, M.; Alavipanah, S.K. Land Surface Ecological Status Composition Index (LSESCI): A novel remote sensing-based technique for modeling land surface ecological status. Ecol. Indic. 2021, 123, 107375. [Google Scholar] [CrossRef]
- Hu, X.; Xu, H. A new remote sensing index for assessing the spatial heterogeneity in urban ecological quality: A case from Fuzhou City, China. Ecol. Indic. 2018, 89, 11–21. [Google Scholar] [CrossRef]
- Firozjaei, M.K.; Alavipanah, S.K.; Liu, H.; Sedighi, A.; Mijani, N.; Kiavarz, M.; Weng, Q. A PCA–OLS Model for Assessing the Impact of Surface Biophysical Parameters on Land Surface Temperature Variations. Remote Sens. 2019, 11, 2094. [Google Scholar] [CrossRef] [Green Version]
- Shorabeh, S.N.; Kakroodi, A.A.; Firozjaei, M.K.; Minaei, F.; Homaee, M. Impact Assessment Modeling of Climatic Conditions on Spatial-temporal Changes in Surface Biophysical Properties Driven by Urban Physical Expansion Using Satellite Images. Sustain. Cities Soc. 2022, 80, 103757. [Google Scholar] [CrossRef]
- Moghaddam, M.H.R.; Sedighi, A.; Fasihi, S.; Firozjaei, M.K. Effect of environmental policies in combating aeolian desertification over Sejzy Plain of Iran. Aeolian Res. 2018, 35, 19–28. [Google Scholar] [CrossRef]
- Trinh-Tuan, L.; Matsumoto, J.; Ngo-Duc, T.; Nodzu, M.I.; Inoue, T. Evaluation of satellite precipitation products over Central Vietnam. Prog. Earth Planet. Sci. 2019, 6, 54. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.; Chen, N.; Moradkhani, H.; Zhang, X.; Hu, C. Improving global monthly and daily precipitation estimation by fusing gauge observations, remote sensing, and reanalysis data sets. Water Resour. Res. 2020, 56, e2019WR026444. [Google Scholar] [CrossRef]
- Ghozat, A.; Sharafati, A.; Hosseini, S.A. Long-term spatiotemporal evaluation of CHIRPS satellite precipitation product over different climatic regions of Iran. Theor. Appl. Climatol. 2021, 143, 211–225. [Google Scholar] [CrossRef]
- Hosseini-Moghari, S.-M.; Tang, Q. Validation of GPM IMERG V05 and V06 precipitation products over Iran. J. Hydrometeorol. 2020, 21, 1011–1037. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.-Y.; Aryastana, P.; Liu, G.-R.; Huang, W.-R. Assessment of satellite precipitation product estimates over Bali Island. Atmos. Res. 2020, 244, 105032. [Google Scholar] [CrossRef]
- Hsu, K.-l.; Gao, X.; Sorooshian, S.; Gupta, H.V. Precipitation estimation from remotely sensed information using artificial neural networks. J. Appl. Meteorol. Climatol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Peng, F.; Zhao, S.; Chen, C.; Cong, D.; Wang, Y.; Ouyang, H. Evaluation and comparison of the precipitation detection ability of multiple satellite products in a typical agriculture area of China. Atmos. Res. 2020, 236, 104814. [Google Scholar] [CrossRef]
- Satgé, F.; Ruelland, D.; Bonnet, M.-P.; Molina, J.; Pillco, R. Consistency of satellite-based precipitation products in space and over time compared with gauge observations and snow-hydrological modelling in the Lake Titicaca region. Hydrol. Earth Syst. Sci. 2019, 23, 595–619. [Google Scholar] [CrossRef] [Green Version]
- Yamamoto, M.K.; Shige, S.; Yu, C.-K.; Cheng, L.-W. Further improvement of the heavy orographic rainfall retrievals in the GSMaP algorithm for microwave radiometers. J. Appl. Meteorol. Climatol. 2017, 56, 2607–2619. [Google Scholar] [CrossRef]
- Taghizadeh, E.; Ahmadi-Givi, F.; Brocca, L.; Sharifi, E. Evaluation of satellite/reanalysis precipitation products over Iran. Int. J. Remote Sens. 2021, 42, 3474–3497. [Google Scholar] [CrossRef]
- Tekeli, A.E.; Fouli, H. Evaluation of TRMM satellite-based precipitation indexes for flood forecasting over Riyadh City, Saudi Arabia. J. Hydrol. 2016, 541, 471–479. [Google Scholar] [CrossRef]
- Ceccherini, G.; Ameztoy, I.; Hernández, C.P.R.; Moreno, C.C. High-resolution precipitation datasets in South America and West Africa based on satellite-derived rainfall, enhanced vegetation index and digital elevation model. Remote Sens. 2015, 7, 6454–6488. [Google Scholar] [CrossRef] [Green Version]
- Basheer, M.; Elagib, N.A. Performance of satellite-based and GPCC 7.0 rainfall products in an extremely data-scarce country in the Nile Basin. Atmos. Res. 2019, 215, 128–140. [Google Scholar] [CrossRef]
- Chen, A.; Chen, D.; Azorin-Molina, C. Assessing reliability of precipitation data over the Mekong River Basin: A comparison of ground-based, satellite, and reanalysis datasets. Int. J. Climatol. 2018, 38, 4314–4334. [Google Scholar] [CrossRef]
- Chen, J.; Wang, Z.; Wu, X.; Chen, X.; Lai, C.; Zeng, Z.; Li, J. Accuracy evaluation of GPM multi-satellite precipitation products in the hydrological application over alpine and gorge regions with sparse rain gauge network. Hydrol. Res. 2019, 50, 1710–1729. [Google Scholar] [CrossRef]
- Li, C.; Tang, G.; Hong, Y. Cross-evaluation of ground-based, multi-satellite and reanalysis precipitation products: Applicability of the Triple Collocation method across Mainland China. J. Hydrol. 2018, 562, 71–83. [Google Scholar] [CrossRef]
- Huang, J.C.; Yu, C.K.; Lee, J.Y.; Cheng, L.W.; Lee, T.Y.; Kao, S.J. Linking typhoon tracks and spatial rainfall patterns for improving flood lead time predictions over a mesoscale mountainous watershed. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Todini, E. A Bayesian technique for conditioning radar precipitation estimates to rain-gauge measurements. Hydrol. Earth Syst. Sci. 2001, 5, 187–199. [Google Scholar] [CrossRef] [Green Version]
- Xiao, S.; Xia, J.; Zou, L. Evaluation of multi-satellite precipitation products and their ability in capturing the characteristics of extreme climate events over the Yangtze River Basin, China. Water 2020, 12, 1179. [Google Scholar] [CrossRef] [Green Version]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Turk, J.T.; Mostovoy, G.V.; Anantharaj, V. The NRL-blend high resolution precipitation product and its application to land surface hydrology. In Satellite Rainfall Applications for Surface Hydrology; Springer: Berlin/Heidelberg, Germany, 2010; pp. 85–104. [Google Scholar]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Xie, P.; Yoo, S.-H. NASA global precipitation measurement (GPM) integrated multi-satellite retrievals for GPM (IMERG). Algorithm Theor. Basis Doc. (ATBD) Version 2015, 4, 26. [Google Scholar]
- Hasanean, H.; Almazroui, M. Rainfall: Features and variations over Saudi Arabia, a review. Climate 2015, 3, 578–626. [Google Scholar] [CrossRef] [Green Version]
- Al-Zahrani, M.; Husain, T. An algorithm for designing a precipitation network in the south-western region of Saudi Arabia. J. Hydrol. 1998, 205, 205–216. [Google Scholar] [CrossRef]
- Hag-elsafi, S.; El-Tayib, M. Spatial and statistical analysis of rainfall in the Kingdom of Saudi Arabia from 1979 to 2008. Weather 2016, 71, 262–266. [Google Scholar] [CrossRef]
- ŞEN, Z.; Al-Suba’i, K. Hydrological considerations for dam siting in arid regions: A Saudi Arabian study. Hydrol. Sci. J. 2002, 47, 173–186. [Google Scholar] [CrossRef]
- Keys, R. Cubic convolution interpolation for digital image processing. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 1153–1160. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Xie, P.; Janowiak, J.E.; Arkin, P.A. Global land precipitation: A 50-yr monthly analysis based on gauge observations. J. Hydrometeorol. 2002, 3, 249–266. [Google Scholar] [CrossRef]
- Sorooshian, S.; Hsu, K.-L.; Gao, X.; Gupta, H.V.; Imam, B.; Braithwaite, D. Evaluation of PERSIANN system satellite-based estimates of tropical rainfall. Bull. Am. Meteorol. Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef]
- Nguyen, P.; Ombadi, M.; Gorooh, V.A.; Shearer, E.J.; Sadeghi, M.; Sorooshian, S.; Hsu, K.; Bolvin, D.; Ralph, M.F. Persiann dynamic infrared–rain rate (PDIR-now): A near-real-time, quasi-global satellite precipitation dataset. J. Hydrometeorol. 2020, 21, 2893–2906. [Google Scholar] [CrossRef]
- Ushio, T.; Sasashige, K.; Kubota, T.; Shige, S.; Okamoto, K.i.; Aonashi, K.; Inoue, T.; Takahashi, N.; Iguchi, T.; Kachi, M. A Kalman filter approach to the Global Satellite Mapping of Precipitation (GSMaP) from combined passive microwave and infrared radiometric data. J. Meteorol. Soc. Japan Ser. II 2009, 87, 137–151. [Google Scholar] [CrossRef] [Green Version]
- Tashima, T.; Kubota, T.; Mega, T.; Ushio, T.; Oki, R. Precipitation extremes monitoring using the near-real-time GSMaP product. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5640–5651. [Google Scholar] [CrossRef]
- Ashouri, H.; Hsu, K.-L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily precipitation climate data record from multisatellite observations for hydrological and climate studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef] [Green Version]
- Sadeghi, M.; Lee, J.; Nguyen, P.; Hsu, K.; Sorooshian, S.; Braithwaite, D. Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks-Cloud Classification System-Climate Data Record (PERSIANN-CCS-CDR). In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 13 December 2019; p. H13P-1964. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [Green Version]
- Xie, P.; Xiong, A.Y. A conceptual model for constructing high-resolution gauge-satellite merged precipitation analyses. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, D.; Li, Z.; Mishra, A.K.; Wang, Y.; Yang, H. Multi-scale evaluation of six high-resolution satellite monthly rainfall estimates over a humid region in China with dense rain gauges. Int. J. Remote Sens. 2014, 35, 1272–1294. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. J. Hydrol. 2000, 228, 113–129. [Google Scholar] [CrossRef]
- Lebrenz, H.; Bárdossy, A. Geostatistical interpolation by quantile kriging. Hydrol. Earth Syst. Sci. 2019, 23, 1633–1648. [Google Scholar] [CrossRef] [Green Version]
- Wackernagel, H. Multivariate Geostatistics: An Introduction with Applications; Springer Science & Business Media: New York, NY, USA, 2003. [Google Scholar]
- Liao, K.; Lai, X.; Liu, Y.; Zhu, Q. Uncertainty analysis in near-surface soil moisture estimation on two typical land-use hillslopes. J. Soils Sediments 2016, 16, 2059–2071. [Google Scholar] [CrossRef]
- Fathololoumi, S.; Vaezi, A.R.; Alavipanah, S.K.; Ghorbani, A.; Biswas, A. Comparison of spectral and spatial-based approaches for mapping the local variation of soil moisture in a semi-arid mountainous area. Sci. Total Environ. 2020, 724, 138319. [Google Scholar] [CrossRef]
- Adhikary, S.K.; Muttil, N.; Yilmaz, A.G. Genetic programming-based ordinary kriging for spatial interpolation of rainfall. J. Hydrol. Eng. 2016, 21, 04015062. [Google Scholar] [CrossRef]
- Xu, R.; Tian, F.; Yang, L.; Hu, H.; Lu, H.; Hou, A. Ground validation of GPM IMERG and TRMM 3B42V7 rainfall products over southern Tibetan Plateau based on a high-density rain gauge network. J. Geophys. Res. Atmos. 2017, 122, 910–924. [Google Scholar] [CrossRef]
- Krakauer, N.Y.; Lakhankar, T.; Dars, G.H. Precipitation trends over the Indus basin. Climate 2019, 7, 116. [Google Scholar] [CrossRef] [Green Version]
- Firozjaei, M.K.; Fathololoumi, S.; Alavipanah, S.K.; Kiavarz, M.; Vaezi, A.R.; Biswas, A. A new approach for modeling near surface temperature lapse rate based on normalized land surface temperature data. Remote Sens. Env. 2020, 242, 111746. [Google Scholar] [CrossRef]
- Bartkowiak, P.; Castelli, M.; Notarnicola, C. Downscaling Land Surface Temperature from MODIS Dataset with Random Forest Approach over Alpine Vegetated Areas. Remote Sens. 2019, 11, 1319. [Google Scholar] [CrossRef]







| Dataset | Data Source | Spatial Resolution | Temporal Resolution | Spatial Coverage | Temporal Coverage | References |
|---|---|---|---|---|---|---|
| PRECL | Gauge-Based Products | 0.5° × 0.5° | 1 mo | Global land | 1948–present | [75] |
| PERSIANN | Satellite-Based Products | 0.25° × 0.25° | 1, 3, 6 h/1 d | 60°S–60°N | 2000–present | [52] |
| PERSIANN-CCS | 0.04° × 0.04° | 1, 3, 6 h/1 d | 60°S–60°N | 2003–present | [76] | |
| PERSIANN-PDIR | 0.04° × 0.04° | 1, 3, 6 h/1 d | 60°S–60°N | 2000–present | [77] | |
| GSMaP-MVK | 0.1° × 0.1° | 1 h/1 d | 60°S–60°N | 2000–present | [78] | |
| GSMaP-NRT | 0.1° × 0.1° | 1 h/1 d | 60°S–60°N | 2000–present | [79] | |
| PERSIANN-CDR | Gauge corrected satellites | 0.25° × 0.25° | 1 d/1 mo | 60°S–60°N | 1983-present | [80] |
| PERSIANN-CCS-CDR | 0.04° × 0.04° | 3, 6 h/1 d | 60°S–60°N | 1983–present | [81] | |
| TRMM3B43 | 0.25° × 0.25° | 3 h/1 d | 50°S–50°N | 1998–present | [67] | |
| GSMaP-Gauge | 0.1° × 0.1° | 1 h/1 d | 60°S–60°N | 2002–present | [78] | |
| IMERGFinal | 0.1° × 0.1° | 30 min | 90°S–90°N | June 2000–present | [16] | |
| ERA5 | Reanalysis Products | 31 km | 1 h/1 mo | 90°S–90°N | 1979–present | [82] |
| CHIRP | 0.05° × 0.05° | 1 d | 50°S–50°N | 1981–present | [83] | |
| CHIRPS | 0.05° × 0.05° | 1d | 50°S–50°N | 1981–present | [83] |
| Statistical Metric | Equation | Perfect Value | Description |
|---|---|---|---|
| Relative Bias (RBias) | 0 | RBias, as a bias indicator, represents the degree of overall underestimation (negative values) or overestimation (positive values) of predictions. | |
| Correlation Coefficient (CC) | 1 | The Pearson correlation coefficient is employed to measure the linear relationship between estimated and measured precipitation. | |
| Root Mean Squared Error (RMSE) | 0 | RMSE represents average the magnitude of the error, which is a negatively oriented score, i.e., lower values show better results. | |
| Random Error (RE) | 1 | Random errors are unpredictable fluctuations in the estimated precipitation concerning the measured precipitation. | |
| Systematic Error (SE) | 0 | Systematic errors are predictable and reproducible inaccuracies that are consistently in the same direction | |
| Kling- Gupta Efficiency (KGE) | ;; | 1 | KGE represents similarity degree between the estimated values from datasets and observations. Multi-component nature of KGE incorporates linear correlation, bias, and variability within a single objective function, providing a more balanced model evaluation. The optimum value of KGE is one. |
| Dataset | KGE | Corr. | Variability Ratio | Rbias | RMSE (mm/mon) | Systematic Error | Random Error |
|---|---|---|---|---|---|---|---|
| PRECL | 0.52 | 0.75 | 0.91 | −0.15 | 11.5 | 0.20 | 0.80 |
| PERSIANN | 0.20 | 0.42 | 1.52 | −0.40 | 16.9 | 0.37 | 0.63 |
| PERSIANN-CCS | −0.03 | 0.18 | 0.65 | 0.71 | 29.6 | 0.20 | 0.80 |
| PERSIANN-PDIR | 0.17 | 0.38 | 0.78 | 0.35 | 17.1 | 0.29 | 0.71 |
| GSMaP-MVK | 0.14 | 0.36 | 1.43 | −0.32 | 20.0 | 0.31 | 0.69 |
| GSMaP-NRT | 0.12 | 0.33 | 1.54 | 0.38 | 21.1 | 0.23 | 0.77 |
| PERSIANN-CDR | 0.15 | 0.38 | 0.75 | 0.41 | 18.5 | 0.15 | 0.85 |
| PERSIANN-CCS-CDR | 0.14 | 0.36 | 0.83 | 0.45 | 19.0 | 0.32 | 0.68 |
| TRMM3B43 | 0.48 | 0.70 | 0.93 | 0.14 | 10.6 | 0.08 | 0.92 |
| GSMaP-Gauge | 0.44 | 0.65 | 1.25 | −0.17 | 12.9 | 0.21 | 0.79 |
| IMERGFinal | 0.56 | 0.80 | 0.91 | 0.10 | 9.7 | 0.10 | 0.90 |
| ERA5 | 0.26 | 0.70 | 1.38 | 0.26 | 16.8 | 0.17 | 0.83 |
| CHIRP | 0.33 | 0.51 | 0.81 | 0.22 | 14.5 | 0.38 | 0.62 |
| CHIRPS | 0.37 | 0.59 | 0.90 | 0.18 | 13.0 | 0.32 | 0.68 |
| Proposed method | 0.75 | 0.92 | 1.04 | 0.04 | 6.6 | 0.07 | 0.93 |
| Dataset | KGE | Corr. | Variability Ratio | Rbias | RMSE (mm/mon) | Systematic Error | Random Error |
|---|---|---|---|---|---|---|---|
| PRECL | 0.36 | 0.25 | 0.71 | −0.19 | 19.5 | 0.50 | 0.50 |
| PERSIANN | 0.15 | 0.19 | 0.60 | −0.32 | 26.5 | 0.67 | 0.33 |
| PERSIANN-CCS | −0.01 | 0.12 | 0.42 | 0.53 | 34.5 | 0.50 | 0.50 |
| PERSIANN-PDIR | 0.19 | 0.22 | 0.65 | 0.35 | 28.5 | 0.59 | 0.41 |
| GSMaP-MVK | 0.17 | 0.20 | 0.63 | 0.41 | 27.1 | 0.61 | 0.59 |
| GSMaP-NRT | 0.14 | 0.23 | 0.60 | 0.45 | 29.7 | 0.43 | 0.57 |
| PERSIANN-CDR | 0.16 | 0.29 | 0.68 | 0.26 | 25.9 | 0.35 | 0.65 |
| PERSIANN-CCS-CDR | 0.13 | 0.20 | 0.59 | 0.32 | 28.4 | 0.52 | 0.48 |
| TRMM3B43 | 0.36 | 0.35 | 0.73 | 0.08 | 18.9 | 0.28 | 0.72 |
| GSMaP-Gauge | 0.31 | 0.32 | 0.83 | −0.06 | 20.6 | 0.41 | 0.59 |
| IMERGFinal | 0.38 | 0.40 | 0.76 | 0.05 | 17.5 | 0.30 | 0.70 |
| ERA5 | 0.27 | 0.46 | 0.53 | 0.30 | 23.5 | 0.37 | 0.63 |
| CHIRP | 0.20 | 0.28 | 0.51 | 0.12 | 22.6 | 0.58 | 0.42 |
| CHIRPS | 0.26 | 0.30 | 0.68 | 0.09 | 21.0 | 0.52 | 0.48 |
| Proposed method | 0.50 | 0.64 | 0.89 | 0.04 | 13.6 | 0.18 | 0.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Assiri, M.E.; Qureshi, S. A Multi-Source Data Fusion Method to Improve the Accuracy of Precipitation Products: A Machine Learning Algorithm. Remote Sens. 2022, 14, 6389. https://doi.org/10.3390/rs14246389
Assiri ME, Qureshi S. A Multi-Source Data Fusion Method to Improve the Accuracy of Precipitation Products: A Machine Learning Algorithm. Remote Sensing. 2022; 14(24):6389. https://doi.org/10.3390/rs14246389
Chicago/Turabian StyleAssiri, Mazen E., and Salman Qureshi. 2022. "A Multi-Source Data Fusion Method to Improve the Accuracy of Precipitation Products: A Machine Learning Algorithm" Remote Sensing 14, no. 24: 6389. https://doi.org/10.3390/rs14246389
APA StyleAssiri, M. E., & Qureshi, S. (2022). A Multi-Source Data Fusion Method to Improve the Accuracy of Precipitation Products: A Machine Learning Algorithm. Remote Sensing, 14(24), 6389. https://doi.org/10.3390/rs14246389