Raindrop Size Distribution Characteristics of the Western Pacific Tropical Cyclones Measured in the Palau Islands

Abstract

Due to the severe threat of tropical cyclones to human life, recent years have witnessed an increase in the investigations on raindrop size distributions of tropical cyclones to improve their quantitative precipitation estimation algorithms and modeling simulations. So far, the raindrop size distributions of tropical cyclones using disdrometer measurements have been conducted at coastal and inland stations, but such studies are still missing for oceanic locations. To the authors’ knowledge, the current study examines—for the first time—the raindrop size distributions of fourteen tropical cyclones observed (during 2003–2007) at an oceanic station, Aimeliik, located in the Palau islands in the Western Pacific. The raindrop size distributions of Western Pacific tropical cyclones measured in the Palau islands showed unlike characteristics between stratiform and convective clusters, with a larger mass-weighted mean diameter and smaller normalized intercept parameter in the convective type. The contribution of the drop diameters to the total number concentration showed a gradual decrease with the increase in drop diameter size. Raindrop size distributions of Western Pacific tropical cyclones measured in the Palau islands differed slightly from Taiwan and Japan. The helpfulness of empirical relations in raindrop size distribution in rainfall estimation algorithms of ground-based (Z–R, μ–Λ, D_m–R, and N_w–R) and remote-sensing (σ_m–D_m, μ_o–D_m, D_m–Z_ku, and D_m–Z_ka) radars are evaluated. Furthermore, the present study also related the rainfall kinetic energy of fourteen tropical cyclones with rainfall rate and mass-weighted mean diameter (KE_time–R, KE_mm–R, and KE_mm–D_m). The raindrop size distribution empirical relations appraised in this study offer a chance to: (1) enhance the rain retrieval algorithms of ground-based, remote sensing radars; and (2) improve rainfall kinetic energy estimations using disdrometers and GPM DPR in rainfall erosivity studies.

1. Introduction

Raindrop size distribution (RSD) is one of the essential parameters of precipitation, offering investigation into cloud and rain microphysics [1]. RSD information can improve cloud modeling parametrization, rain retrieval algorithms of the global precipitation measurement dual-frequency precipitation radar (GPM DPR), and assess rainfall kinetic energy relations [2,3,4,5,6]. RSDs substantially vary with changes in formation and the evolution of precipitation, and show considerable variations with the seasons, different geographical regions, weather conditions, and precipitation types [1,3,7,8,9,10,11,12]. For instance, the RSD measurements in Taiwan showed a greater concentration of large-sized drops in the summer than in the winter seasons [11]. Using an OTT PARSIVEL disdrometer, [13] showed distinctions in the RSDs measured over three oceanic locations (South Western Pacific (SWP), West Western Pacific (WWP), and North Western Pacific (NWP)) during a marine survey from June to July 2014. The typhoon rainfall RSDs measured in Taiwan and Japan exhibited distinct characteristics to that of the non-typhoon rainfall [3,8].

Tropical cyclones (TCs) with gusty winds and torrential rainfall can produce devastating damages, life loss and disruption to daily activities. Henceforth, the socioeconomic threat of TCs demands the use of both ground-based and remote sensing radars’ quantitative precipitation estimation (QPE) algorithms and cloud modeling simulations [6,7,14,15,16,17,18]. So, globally, there has been an increasing interest in understanding the RSDs of TCs [3,7,8,12,19,20,21,22,23,24,25,26].

A relatively high proportion of extreme rainfall and severe damage to livelihood is triggered by TCs from the Western Pacific (WP), over other oceanic regions, suggesting a critical need to understand the cloud and rain microphysics of this region [27]. Hence, the investigations on the WP TCs’ RSDs are predominantly increasing over other oceanic TCs [3,8,16,24,28,29]. For instance, [16] examined the RSDs of WP TCs in Taiwan, and they inferred that the interaction of the WP TCs convective systems with Taiwan’s topography resulted in intermediate RSDs to that of the maritime and continental clusters. For the typhoon Morakot (2009) measured at the southeastern coast of China, [30] noticed distinctions in RSD between the eyewall and rainbands. RSD studies conducted over South Korea, Japan, and Taiwan demonstrated that the D_m (mass-weighted mean diameter) values of WP TCs were smaller than non-typhoon rainfall [3,8,24]. RSDs of seven typhoons measured over China exhibited a higher concentration of smaller drops than the maritime convective clusters [29]. Furthermore, recent studies demonstrated that the RSDs of different rain regions of WP TCs showed distinct characteristics [31,32]. On the other hand, for a given rain segment of a typhoon Mangkhut, [33] observed no spatial variations in RSDs.

The above-mentioned RSD studies for the WP TCs were conducted chiefly from the inland or the coastal stations, and the investigations on TCs’ RSDs over the oceanic site are still lacking in the literature. Though there were reports on the RSDs of seasonal rainfall measured at oceanic locations [13,34,35,36,37], such studies for TCs, especially for WP TCs, are yet to be documented. Henceforth, in the current paper, we investigated the RSD characteristics of fourteen WP TCs measured at an oceanic station located in the Palau islands in the WP. The chief objectives of the present study are: (1) to document the statistical characteristics of WP TCs rainfall by segregating into different rainfall rates and precipitation (stratiform and convective) types; (2) to find out similarities/dissimilarities between the RSDs reported in the present study and the previously reported WP TCs RSDs over the coastal or inland stations; (3) to document the RSDs empirical relations that are useful to improve the ground-based and remote sensing (GPM DPR) radar rain retrieval algorithms; and (4) to report the rainfall kinetic energy relations that are crucial in rainfall erosivity studies. After this brief introduction, the TC’s track information, and the Joss–Waldvogel disdrometer (JWD) measurements are given in Section 2. Section 3 provides the results and discussion followed by a summary and conclusions in Section 4.

2. Data and Methods

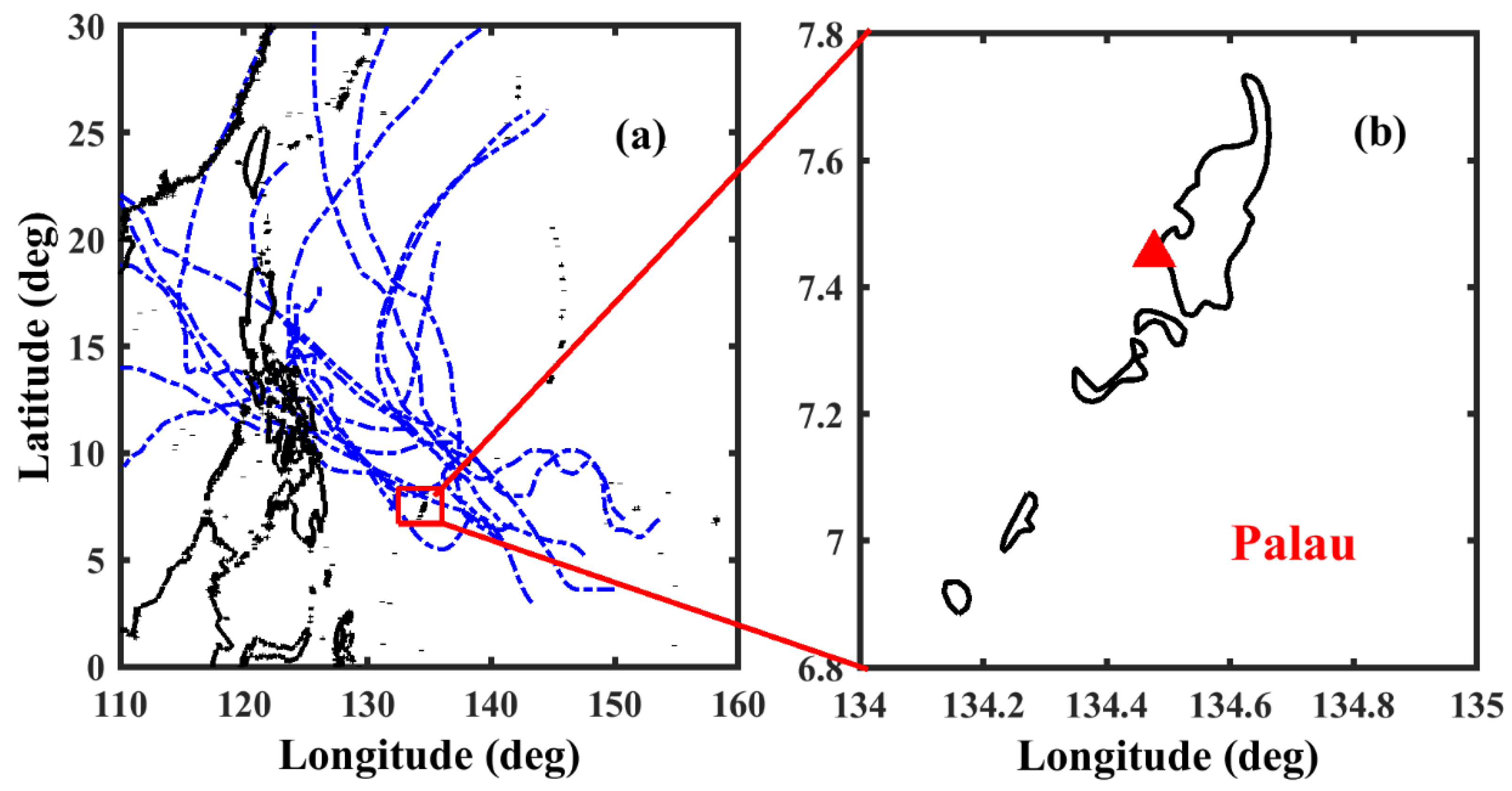
2.1. Observational Site

The Joss–Waldvogel disdrometer (JWD) installed at Aimeliik observational site (7.45222°N E134.47649°E) in the Palau islands measured a total number of fourteen typhoons RSDs during 2003–2007. The track information of these 14 TCs was archived from the joint typhoon warning center (JTWC). In the present study, if there were any TCs around the JWD site within a radial distance of 500 km or less, the corresponding JWD measurements were treated as TC RSDs. Figure 1 shows the tracks of the considered WP TCs and the location of the JWD observational site.

2.2. The Joss–Waldvogel Disdrometer (JWD) Data and Methods

The Joss–Waldvogel disdrometer (JWD) can measure 0.3–5.3 mm diameter raindrops [38]. Once the raindrops hit the JWD, it can infer the size information of the raindrops from the voltage produced by its Styrofoam cone (cross-sectional area 50 cm²), and this information is stored in 20 size intervals. As mentioned in the literature [9], to reduce the sampling errors, the current study also discarded the 1-min RSD samples if the raw drops count was less than ten and the rainfall rate was <0.1 mm h⁻¹. Using the number of raindrops from the JWD, the N(D) and other integral rain parameters, such as R (rainfall rate, mm h⁻¹), Z (radar reflectivity, dBZ), N_t (total number concentration, m⁻³), and LWC (liquid water content, gm⁻³) are estimated:

$$N\left(D\right)\left({\mathrm{m}}^{-3}\mathrm{m}{\mathrm{m}}^{-1}\right)={\displaystyle \sum }_{i=1}^{20}\frac{n_i}{A\times \mathsf{\Delta }t\times V\left(D_i\right)\times \mathsf{\Delta }{D}_i}$$

(1)

where, n_i, A(m²), Δt (s), D_i (mm), ΔD_i (mm)), V(D_i) (m s⁻¹) are the number of raindrops counted in size bin i, sampling area, sampling time, drop diameter for the size bin i, diameter interval for the drop size bin i, and terminal velocity of the raindrops in the ith channel, respectively. The terminal velocity of raindrops at each channel is estimated using the below equation [39].

$$V\left(D_i\right)=9.65-10.3\times \exp \left(-0.6\times D_i\right)$$

(2)

$$Z \left(\mathrm{dB}Z\right)=10\times lo{g}_{10}\left({\displaystyle \sum }_{i=1}^{20}N\left(D_i\right)D_i^6\mathsf{\Delta }{D}_i\right)$$

(3)

$$R ({\mathrm{mm}\mathrm{h}}^{-1})=6\pi \times {10}^{-4}{\displaystyle \sum }_{i=1}^{20}V(D_{i) }N\left(D_i\right) D_i^3\mathsf{\Delta }{D}_i$$

(4)

$$LWC \left({\mathrm{g}\mathrm{m}}^{-3}\right)=\frac{\pi }{6} {10}^{-3}{\rho }_w {\displaystyle \sum }_{i=1}^{20}N\left(D_i\right) D_i^3\mathsf{\Delta }{D}_i$$

(5)

$$N_t \left({\mathrm{m}}^{-3}\right)={\displaystyle \sum }_{i=1}^{20}N\left(D_i\right) \mathsf{\Delta }{D}_i$$

(6)

The nth-order moment (M_n) of raindrop size distribution can be expressed as:

$$M_n={\displaystyle \sum }_{D_{min}}^{D_{max}}{D}_i^{n}N\left(D_i\right) \mathsf{\Delta }{D}_i$$

(7)

The mass-weighted mean diameter, D_m, can be expressed as:

$$D_m \left(\mathrm{mm}\right)=\frac{M_4}{M_3}$$

(8)

The one-min RSD samples are fitted to gamma function as given below [40]:

$$N\left(D\right)=N_0 D^{\mu }\exp \left(-\Lambda D\right).$$

(9)

where D (mm) is the drop diameter, N(D) (m⁻³ mm⁻¹) is the number of drops per unit volume per unit size interval, N₀ (m⁻³ mm⁻¹) is the number concentration parameter, μ (-) is the shape parameter, and Λ (mm⁻¹) is the slope parameter,

$$\Lambda =\frac{\left(\mu +4\right)M_3}{M_4}$$

(10)

$$\mu =\frac{\left(11\times G-8\right)+\sqrt{G\times \left(G+8\right)}}{2\times \left(1-G\right)}$$

(11)

$$G=\frac{M_4^3}{M_6{M}_3^2}$$

(12)

The normalized intercept parameter, N_w, can be expressed as [10]:

$$N_w \left({\mathrm{m}}^{-3}{\mathrm{mm}}^{-1}\right)=\frac{4^4}{\pi {\rho }_w}\left(\frac{{10}^{3}LWC}{D_m^4}\right)$$

(13)

The σ_m (mass spectrum standard deviation, mm) can be estimated using [41,42]:

$${\sigma }_m \left(\mathrm{mm}\right)={\left[\frac{{\sum }_{i=1}^{20} {\left(D_i-D_m\right)}^2 N\left(D_i\right) D_i^3{\mathsf{\Delta }D}_i}{{\sum }_{i=1}^{20}N\left(D_i\right) D_i^3 dD}\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$$

(14)

The JWD measurements of fourteen WP TCs are also used to estimate the rainfall kinetic energy (KE), which can be expressed as KE flux (KE_time, in J m⁻² h⁻¹) and KE content (KE_mm, J m⁻² mm⁻¹), and the formulations for KE_mm and KE_time can be found in [43,44,45].

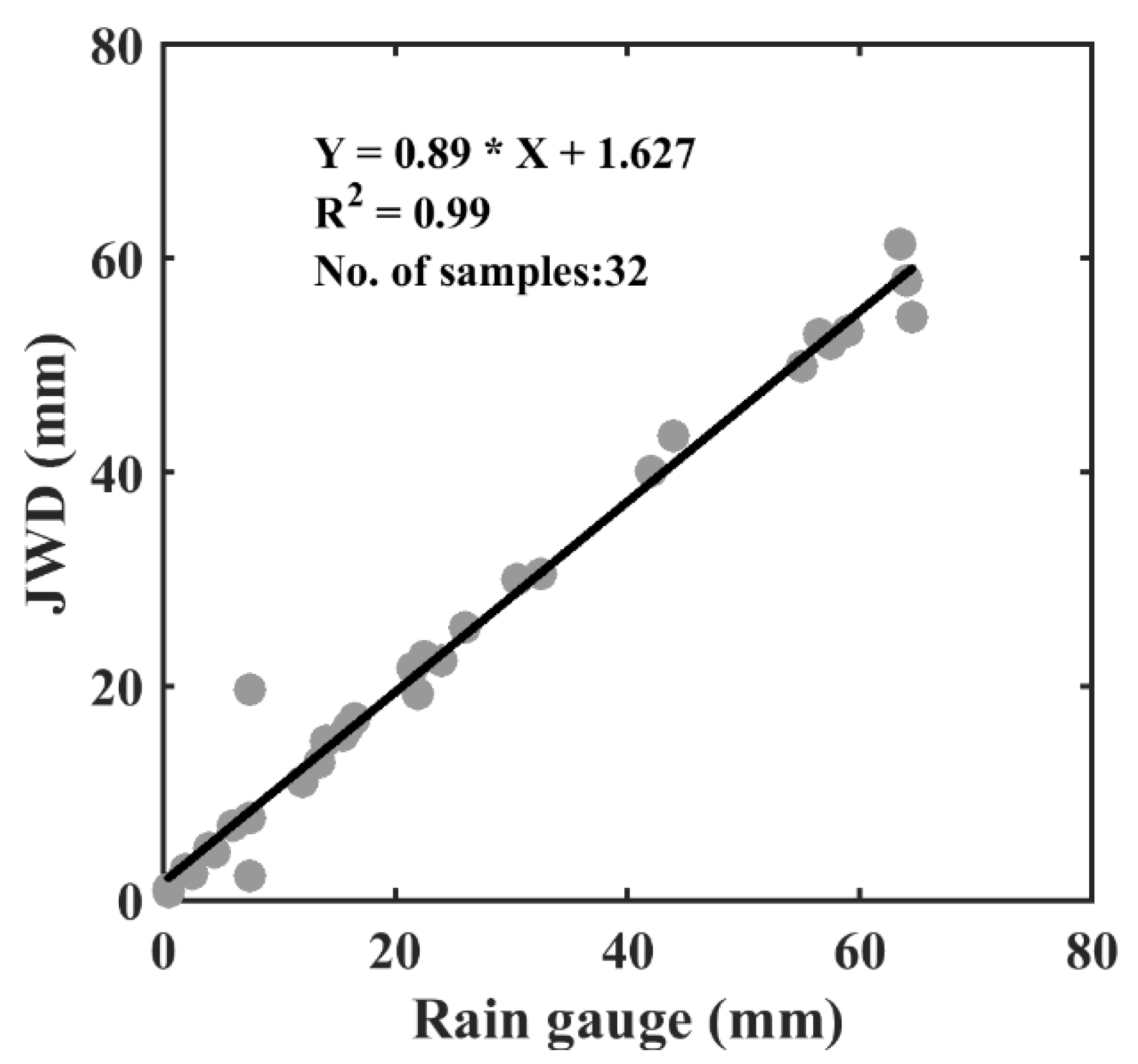
2.3. JWD Data Validation

Before using the RSD information of JWD for further analysis, the daily accumulated rainfall amounts of WP TCs measured with JWD were correlated with the collocated rain gauge, as shown in Figure 2. The comparison clearly shows a good correlation between JWD and the rain gauge measurements, indicating that the JWD measurements are worth enough for further analysis.

3. Results and Discussion

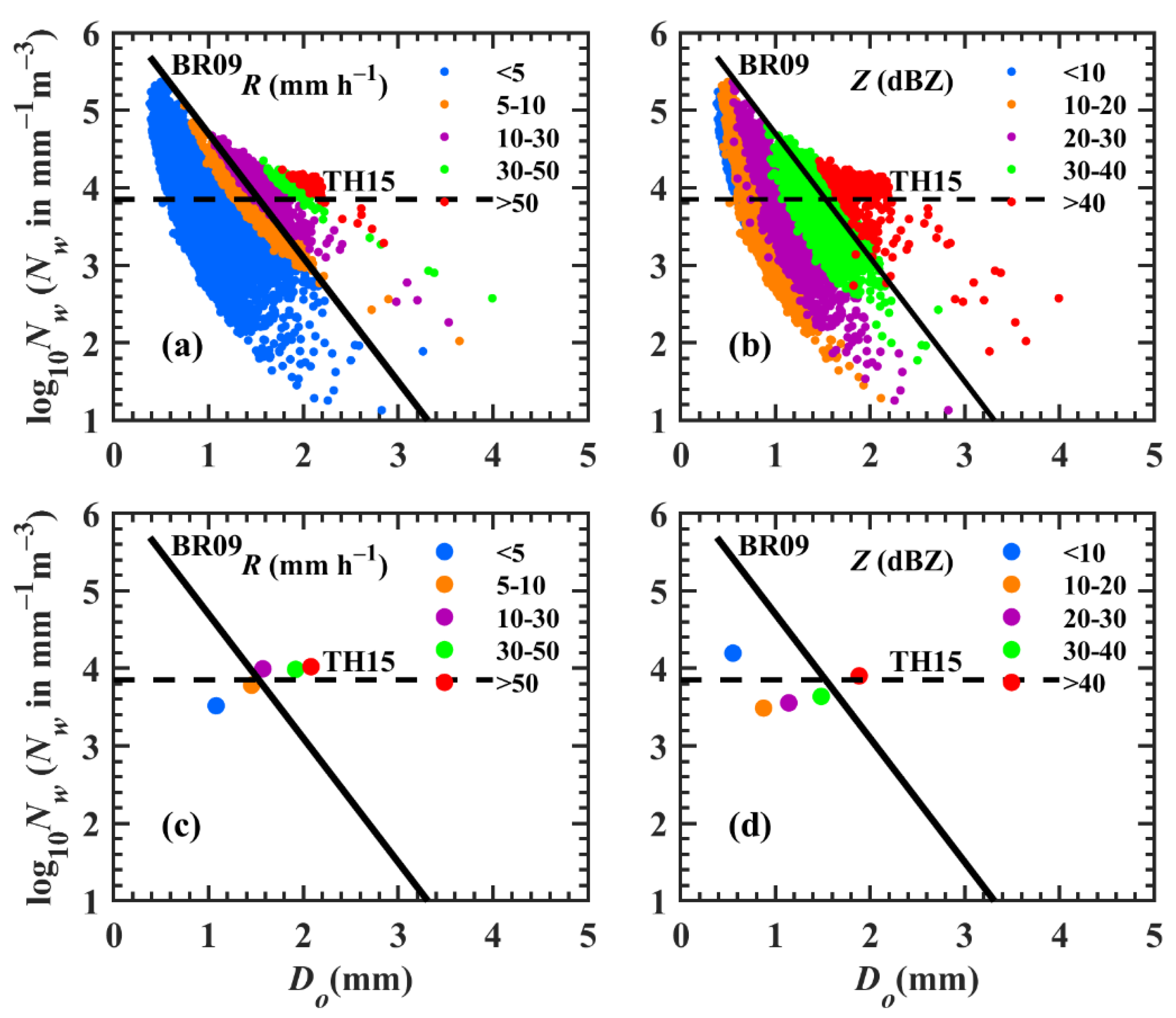
3.1. Distribution of RSD in Different Rainfall Rate and Radar Reflectivity Classes

Figure 3 illustrates the distributions of D_o [D_o = (3.67+ μ)/Λ] and log₁₀N_w in different rainfall rates (<5, 5–10, 10–30, 30–50, and >50 mm h⁻¹) and radar reflectivity (<10, 10–20, 20–30, 30–40, and >40 dBZ) classes for the WP TCs measured in the Palau islands. The stratiform and convective classification lines of [46,47] are denoted with slant solid and horizontal dotted lines.

The distributions of D_o and log₁₀N_w narrowed with the increase in rainfall rates and reflectivity classes. The D_o and log₁₀N_w data points for rainfall rates less (higher) than 10 mm h⁻¹ are distributed in the stratiform (convective) regions of [46], as seen in the precipitation classification line (inclined solid line in Figure 3). Likewise, the D_o and log₁₀N_w data points corresponding to radar reflectivity values higher (less) than 40 dBZ lie above and below the stratiform and convective precipitation line of [46]. The mean values of D_o and log₁₀N_w in different rainfall rates (R, mm h^–1) and radar reflectivity (Z, dBZ) classes are depicted in Figure 3c,d. Mean D_o values are increased with the increase in R and Z classes. Moreover, for higher rainfall rates classes (R > 10 mm h⁻¹), mean D_o, and log₁₀N_w values were distributed in the convective region of [46] (Figure 3). Furthermore, the WP TCs mean log₁₀N_w values were higher than the [47] rainfall classification line for rainfall rates > 10 mm h⁻¹ (Figure 3).

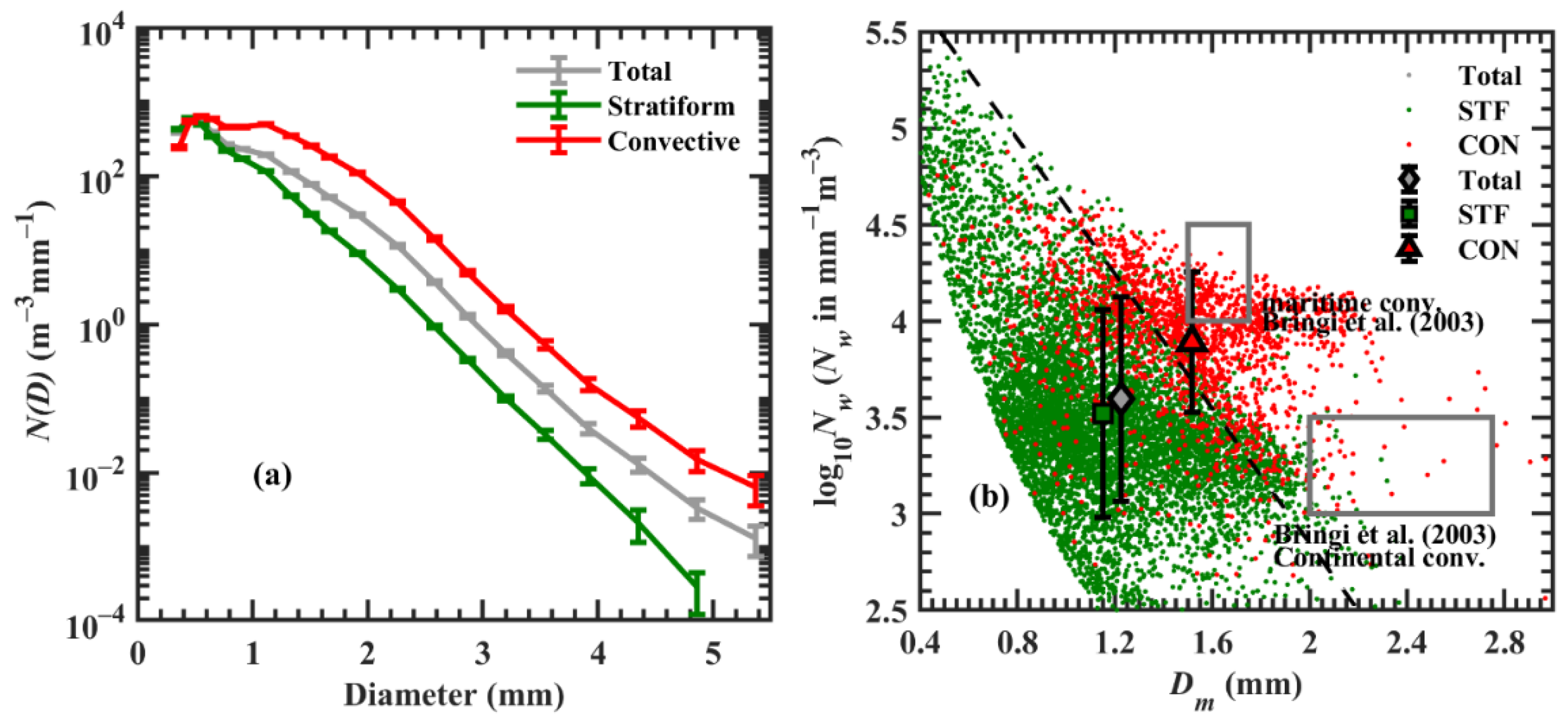
3.2. RSD in Stratiform and Convective Precipitation

The RSDs and their corresponding microphysical properties exhibit profound disparities between stratiform and convective precipitations [9]. Using disdrometer measurements, previous researchers have adopted different methods to segregate the rainfall into two categories (stratiform and convective types) [9,10,14]. The current study separated the WP TCs rainfall measured in the Palau islands into convective and stratiform types using the modified form of [10]. Particularly, if the mean rainfall rate of ten successive 1-min RSD samples was greater than 5 mm h⁻¹ and the standard was greater than 1.5 mm h⁻¹, those samples were considered as convective types, and if this condition was not satisfied, then they were considered as stratiform type. With this classification criteria, around 80% (20%) of RSDs were the stratiform (convective) type, and they contributed to rainfall accumulations of 33% (67%).

The stratiform and convective precipitation mean raindrop size distributions of WP TCs are portrayed in Figure 4a. Except for the first drop size bin, the mean RSDs show a higher concentration in convective than stratiform (Figure 4a). It is apparent from Figure 4a that the stratiform precipitation shows a closely exponential distribution, whereas the convective rainfall exhibited a broader distribution, which could be due to the enhanced collision–breakup processes in the convective compared with the stratiform type [48]. Figure 4b illustrates the scatter plot of D_m and log₁₀N_w values for the stratiform and convective precipitations and the corresponding mean values. From the figure, the WP TCs’ convective and stratiform precipitation mean log₁₀N_w and D_m values align above and below the stratiform–convective segregation line of [10] (inclined black dotted line). The rectangular gray boxes in Figure 4b denote the [10] maritime and continental clusters of RSD measurements from different geographic locations. The comparison of WP TCs’ D_m and log₁₀N_w values shows that the stratiform mean D_m and log₁₀N_w have lower values than the maritime and continental clusters; however, the convective rainfall average D_m is in alignment with maritime convective clusters.

Figure 5 shows the D_m and log₁₀N_w occurrence percentage histograms and their statistical values for the WP TCs. The D_m histogram for total rainfall of WP TCs (Figure 5a) was moderately skewed (skewness, SK = 0.54), whereas the normalized intercept parameter values show a relatively symmetric distribution with a skewness of 0.06. The D_m values show a moderately skewed distribution for both stratiform (SK = 0.54) and convective (SK = 0.56) precipitation (Figure 5b,c). On the other hand, the normalized intercept parameter values exhibited approximately symmetric (SK = 0.35) and highly skewed (SK = −1.02) distribution, in stratiform and convective rainfall, respectively (Figure 5b,c). The D_m and normalized intercept parameters had higher mean values in convective precipitation than the stratiform precipitation.

The WP TCs in the Palau islands showed average D_m values of 1.23 mm, 1.15 mm, 1.52 mm, and average log₁₀N_w values of 3.59, 3.52, and 3.89, for total, stratiform and convective rainfall, respectively. The RSDs of WP TCs measured over Japan (using JWD) indicated that the mean values of mass-weighted mean diameter (D_m = 1.25 mm) and number concentration (log₁₀N_w = 3.74) were larger than the meiyu-baiu front rainfall (D_m = 1.15 mm, log₁₀N_w = 3.59) [8]. On the other hand, summer season rainfall segregated to typhoon and non-typhoon weather conditions in Taiwan showed lower mean D_m (1.25 mm) and higher mean log₁₀N_w (3.63) values in the typhoon than the non-typhoon rainfall (D_m = 1.29 mm, log₁₀N_w = 3.41) [3]. Despite distinctions in the seasonal rainfall RSDs between Palau and Taiwan [35], there was a likeness in the RSDs of WP TCs measured between Palau and the Taiwan islands. Furthermore, the WP TCs measured in Palau also showed nearly identical RSDs to Japan. The WP TCs measurements with a similar type of disdrometer (JWD) interestingly showed nearly identical D_m values among these three islands (mean D_m values in Palau, Taiwan, and Japan are 1.23 mm, 1.25 mm, 1.25, respectively), which signifies that the TCs of WP show no much variation in RSDs with the geographical location.

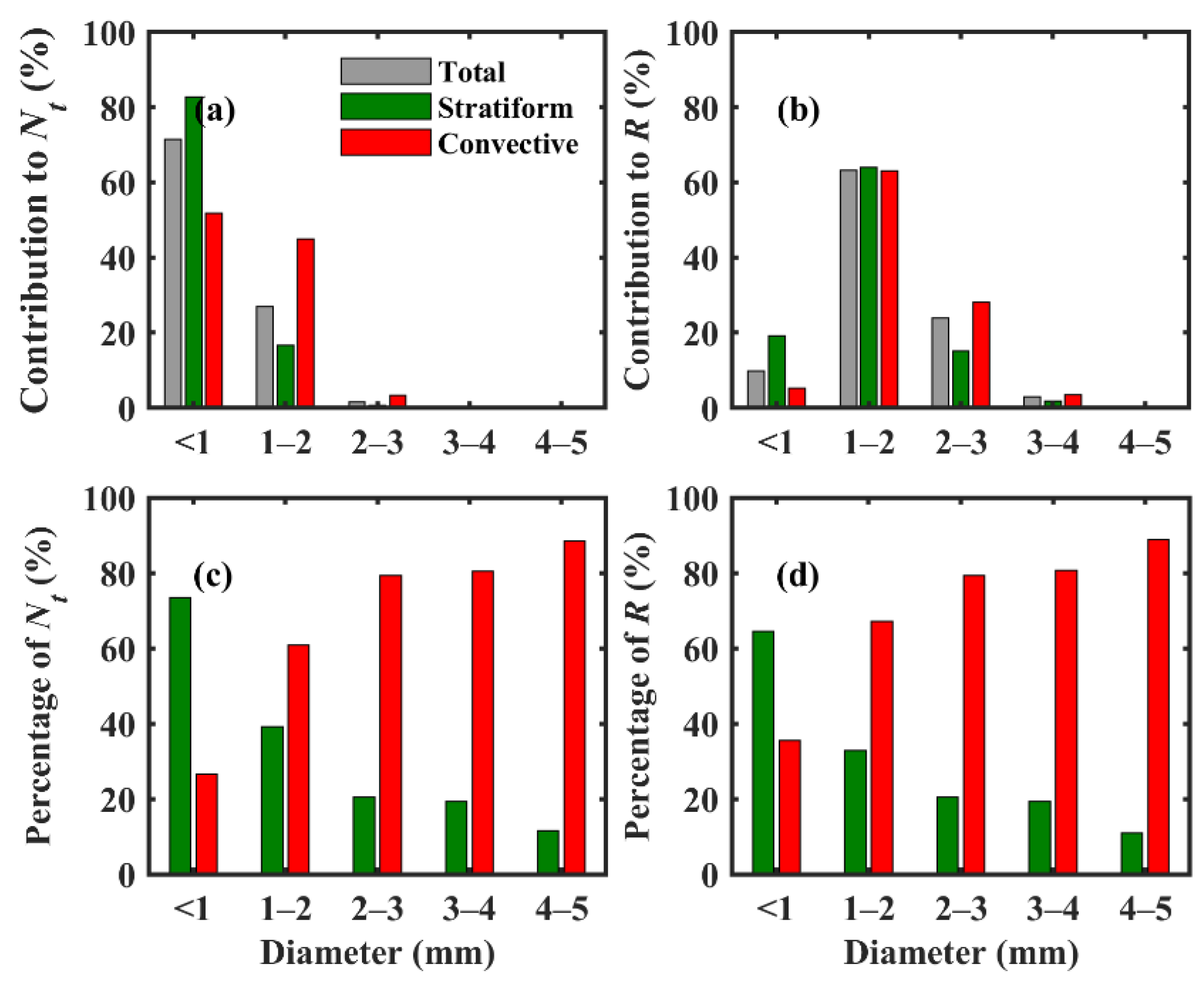
3.3. Raindrops Contribution to N_t and R

Figure 6 elucidates the WP TCs’ raindrops contribution to N_t (total number concentration) and R (rainfall rate). From the figure, we can notice that with the increase in raindrop sizes, the number concentration decreases, and rainfall rates increase and then decrease for total, stratiform and convective rainfall (Figure 6a,b). Similar characteristics were also reported for the WP TCs measured in Japan and Taiwan [3,8].

Small-size drops (<1 mm) largely contributed to N_t for the total, stratiform, and convective rainfall (Figure 6a). The percentage contributions of smaller drops (<1 mm) to the number concentration were predominantly higher in stratiform precipitation than the convective precipitations; conversely, the percentage contribution of raindrops >1 mm diameter were higher in convective than the stratiform rainfall (Figure 6c). Raindrops of diameter 1–2 mm contributed more to the rainfall rate than the raindrops of other diameters (Figure 6b). On the other hand, smaller drops’ (<1 mm) contribution percentage to the rainfall rate was higher in stratiform precipitation than the convective precipitations, and the contribution of raindrops above 1 mm diameter to rainfall rate was predominantly higher in convective than stratiform rainfall (Figure 6d). It is apparent from Figure 6a,b that the raindrops up to 2 mm diameter contribute primarily to the total number concentration and rainfall rate.

3.4. Radar Reflectivity–Rainfall Rate Relations

The empirical relationship between radar reflectivity and rainfall rate (also called Z–R relation), which can be expressed in the form of a power law, i.e., Z = AR^b, with R in mm h⁻¹, Z in mm⁶ m⁻³, can offer the operation radars to estimate the rainfall rate from the observed radar reflectivity. This empirical relationship can be derived by fitting the straight line to logarithmic reflectivity versus logarithmic rainfall rate plot. The radar-derived rainfall information from the Z–R relations has tremendous applications in hydro-meteorological models. These relations showed substantial variations with precipitation types, geographical locations, and intensely rely on RSD features [1,35]. The coefficient (A) and exponent (b) values of Z–R relations (Z = AR^b) can infer the microphysics of given precipitation. The bigger the raindrops, the higher the coefficient A will be. If the exponent is > 1, the size-controlled (collision–coalescence) process is the dominant characteristic of the precipitation. If exponent = 1, then the number-controlled (collision, coalescence, and breakup) processes are related to the given rainfall [49,50,51]. Previous studies have demonstrated that implementing the region and precipitation-specific Z–R relations could reduce the rainfall estimation uncertainties [12,52].

The radar reflectivity and rainfall rate scatter plots for total, stratiform and convective precipitation of WP TCs and the corresponding linear regression lines are depicted in Figure 7, which clearly shows that the Z–R relations differ substantially between stratiform and convective precipitation with a higher coefficient and exponent values in stratiform than the convective. Using a similar kind of disdrometer (JWD), the Z–R relations of WP TCs were documented as Z = 189 R^1.38 in Japan [8] and Z = 217.02 R^1.35 in Taiwan [3]. If we compare the Z–R relationship of the WP TCs evaluated in the present study (Z = 221.51 R^1.35) with the WP TCs measured over Taiwan, both the locations showed identical exponent values (b = 1.35), which can hint that the WP TCs exhibited similar microphysical processes at these two islands.

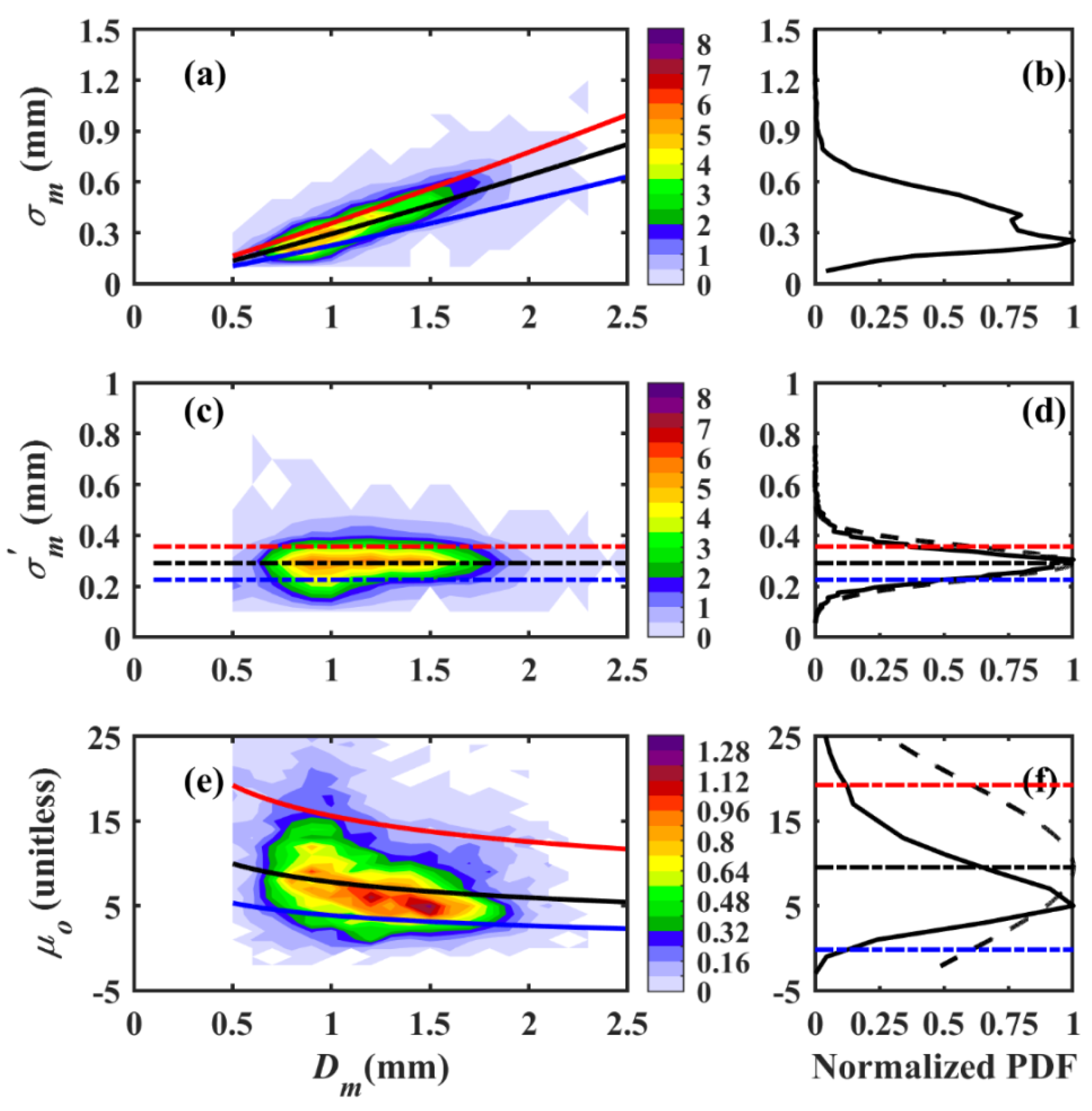
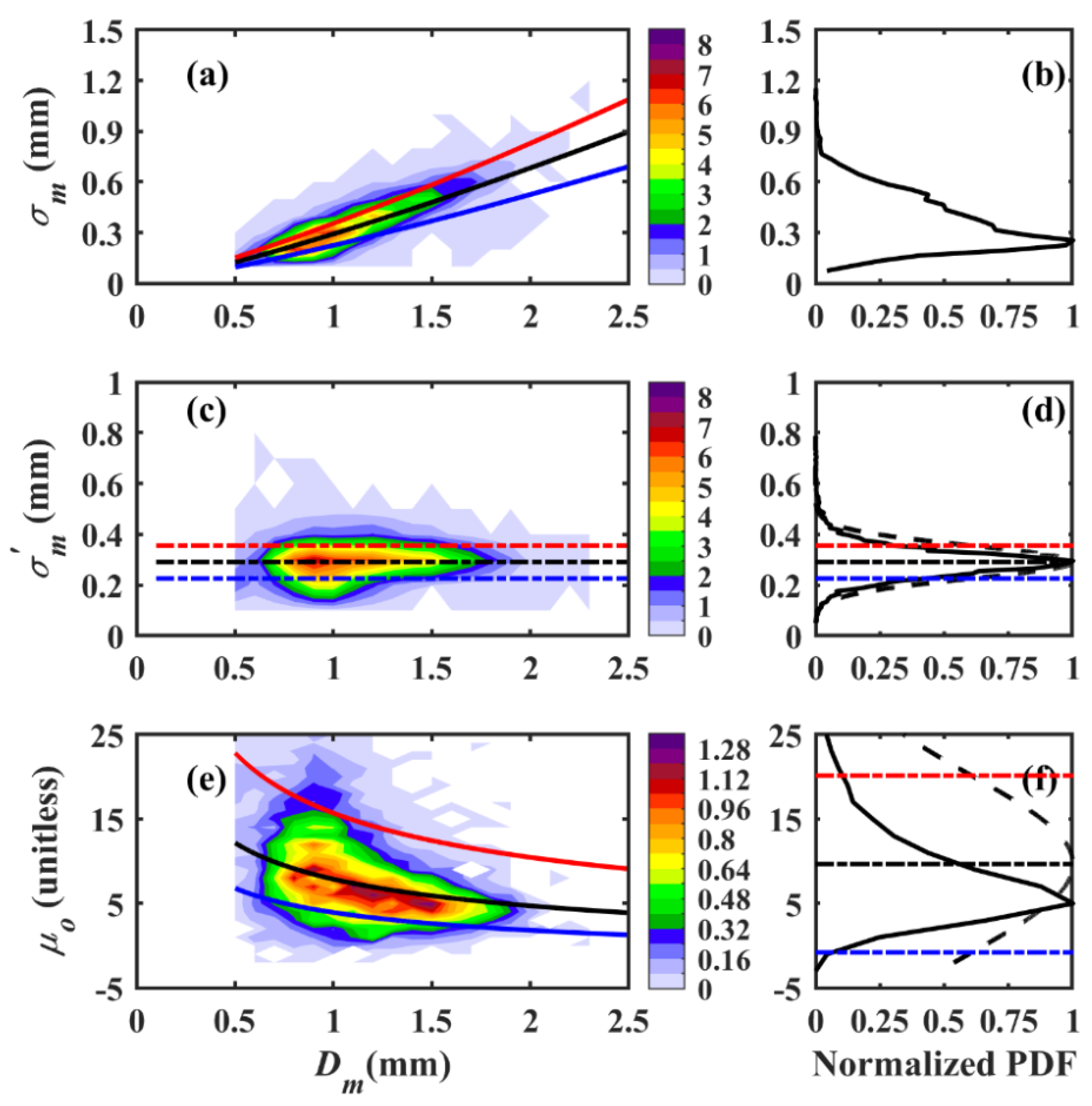
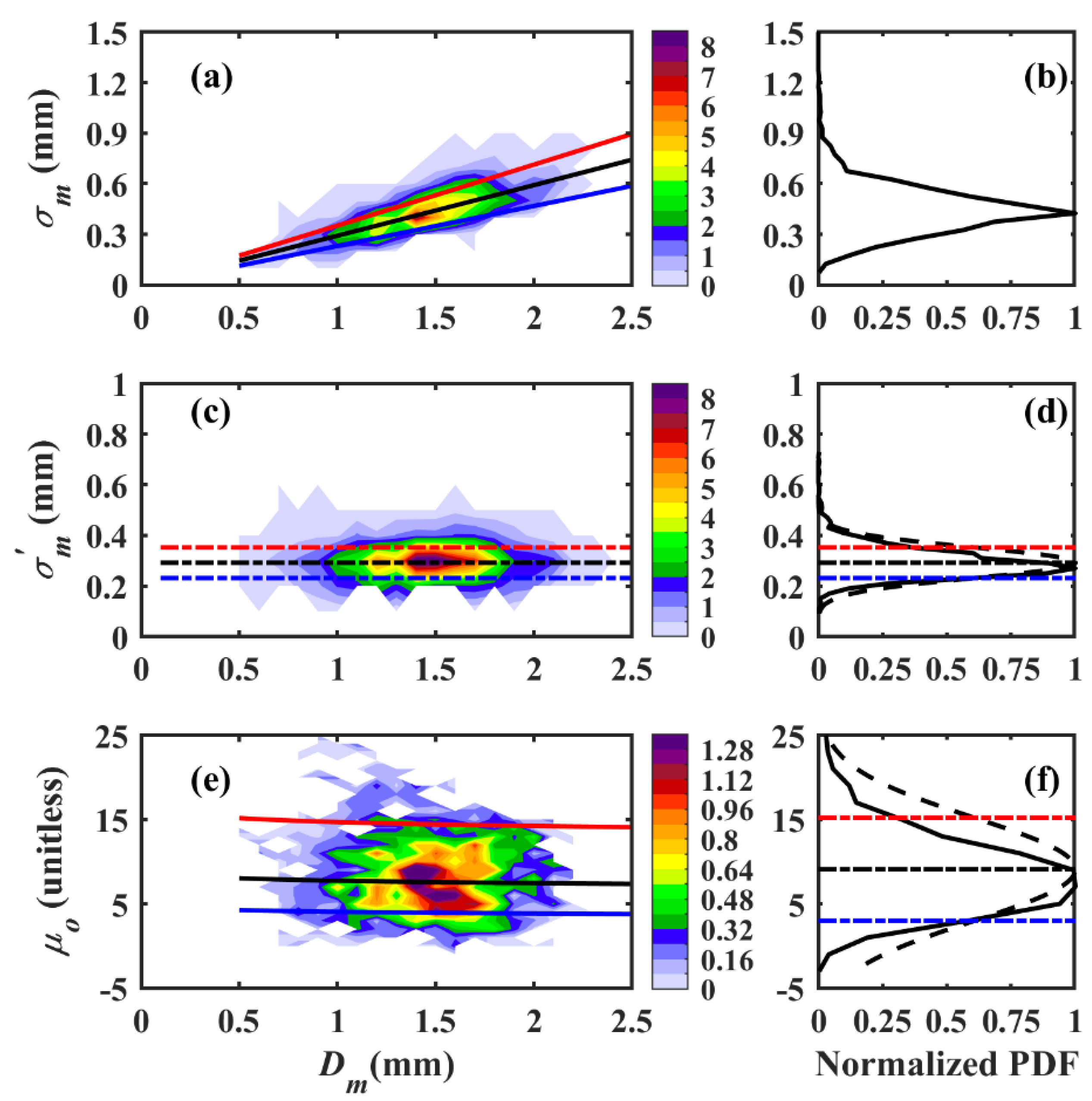
3.5. The Shape–Slope Relationship

The three-parameter Gamma distribution is widely used in bulk microphysics schemes and rain retrieval algorithms of ground-based radars, and it provides better characterization of rain RSDs than two-parameter exponential distribution [40,53,54,55]. Converting three-parameter gamma distribution to two-parameter gamma distribution (also called constrained gamma distribution) using empirical relations between the slope and shape parameters (μ–Λ relations) can reduce the errors in the polarimetric radar rainfall estimators. Initially, [56] argued that, due to the statistical errors in the RSD moment estimation, the empirical relationship between the slope and shape parameters (μ–Λ relations) could not represent the microphysics of precipitation. However, the subsequent study demonstrated that the μ–Λ relationship captured the RSDs’ physical nature, and was least influenced by the errors in the assessment of μ and Λ from the RSD moments [57]. Hence, the μ–Λ relationship is widely used to understand RSD variability, and estimate the rainfall from remote-sensing and ground-based radars [54,57,58,59,60]. It has been demonstrated that μ–Λ relations differ by region and rain type, and it is always essential to customize the region- or precipitation-specific μ–Λ relationship.

The empirical relationships between μ and Λ are derived by adopting the quality control procedure of [60] to the total, stratiform and convective rainfall of WP TCs. As the μ–Λ relations estimated for the light rain/drizzle can lead to statistical errors, the μ and Λ values corresponding to rainfall rate < 5 mm h⁻¹ were removed in the current study [58]. Moreover, values of μ and Λ, higher than 20 and 20 mm⁻¹, respectively, were also discarded [57]. A polynomial least-square fit to the total, stratiform, and convective precipitations of the WP TCs are represented with solid black lines in Figure 8a–c, and their corresponding equations are also depicted in the respective figure panels. The inclined dashed grey lines in Figure 8a–c are computed for different D_m values (D_m = 1, 1.5, 2, and 3 mm) from the relationship ΛD_m = 4 + μ [61]. Along with the present WP TCs’ μ–Λ relations, previously reported TCs’ μ–Λ relations [16,29,30] are also given in Figure 8. We can notice that the WP TCs measured in Taiwan and the coastal location of China showed nearly identical fit lines to that of the WP TCs in the Palau islands. However, there is an apparent disparity between continental convective/WP TCs rainfall fit lines and those of the WP TCs in the Palau islands.

3.6. Relationship of Rainfall Rates with D_m and N_w

The D_m and log₁₀N_w can be used to inspect the microphysics of given precipitation, and these two parameters exhibit profound variations with weather systems and precipitation types [1,19]. To understand the variability of D_m and log₁₀N_w with rainfall rate, Figure 9 displays the distributions of D_m and log₁₀N_w with rainfall rate for the total, stratiform, and convective precipitations of WP TCs. The D_m and log₁₀N_w values show broader distribution at lower rainfall rates, and its spread is reduced with the increase in rainfall rate. The reduction in the spread of D_m values at higher rainfall rates is related to the equilibrium conditions attained by the raindrops through collision–coalescence and breakup process, and further increases in rainfall rate under the equilibrium condition infer further raindrop concentration increases [10,48,62]. On the other hand, for rainfall rates > 25 mm h⁻¹, the spread in D_m values is relatively more in convective precipitation than in the stratiform type. However, the spread in log₁₀N_w values is more in stratiform precipitation than the convective for lower rainfall rates (<10 mm h⁻¹). For a given rainfall rate, comparison of present TCs relationships (D_m =1.143 R^0.145, log₁₀N_w = 3.553 R^0.033) with TCs measured in Taiwan (D_m = 1.133 R^0.153, log₁₀N_w = 3.572 R^0.031) showed a slight difference in D_m/log₁₀N_w values between these two islands [3]. Even though there were reports on the seasonal differences in the RSDs between Taiwan and the Palau islands [35], comparison of TCs’ D_m–R and log₁₀N_w–R relations between these two islands revealed slight variation.

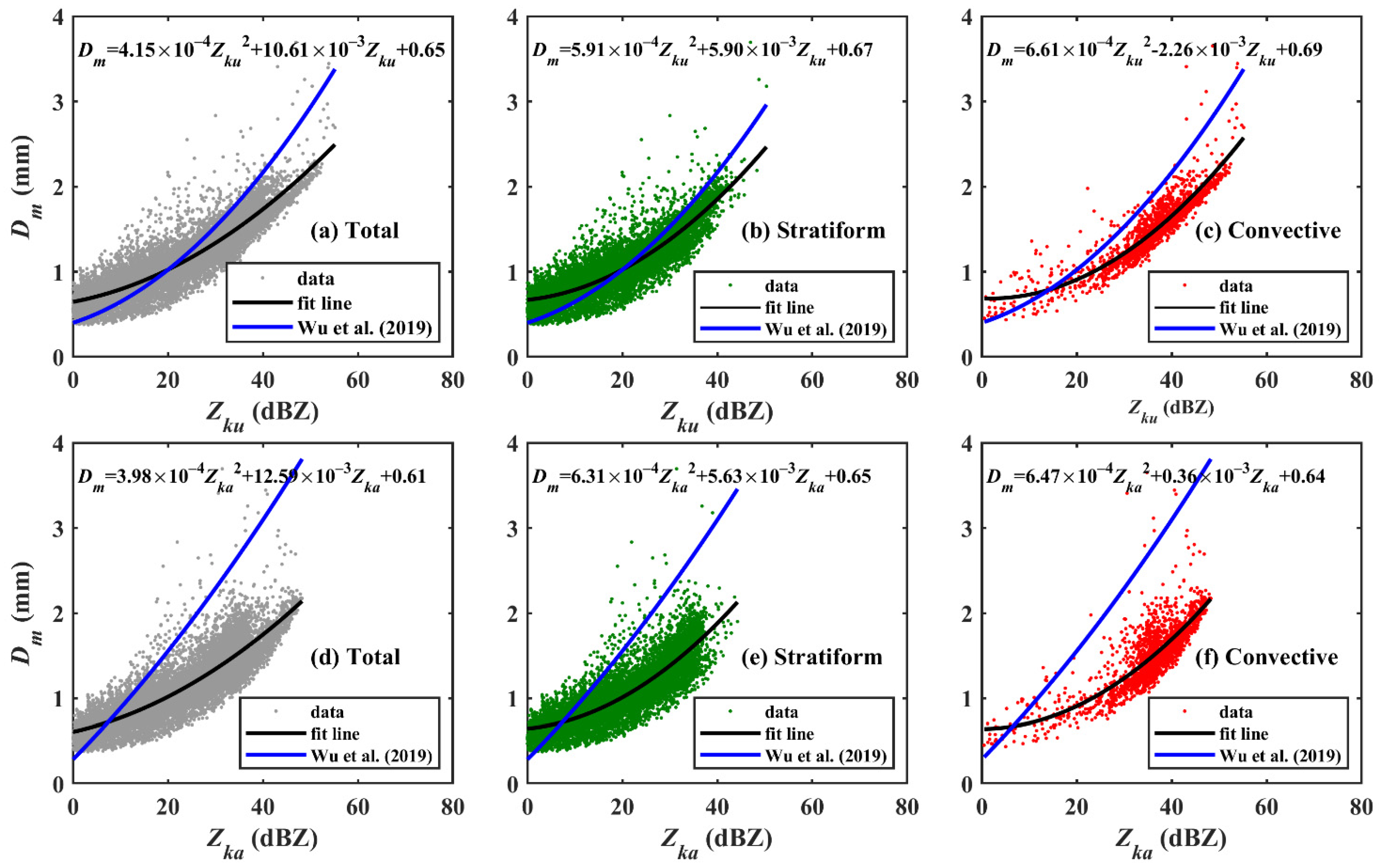
3.7. RSD Implications for Satellite Rainfall Retrievals

The scarcity of statistical individuality among three parameters of the normalized gamma distribution can lead to bias in the GPM satellite rainfall rate retrievals. To reduce this bias, [42] proposed a new framework based on D_m (the mass-weighted mean diameter) and the standard deviation of the mass spectrum (σ_m). They showed that the rainfall rates estimated from D_m–μ constraint relations—using two independent physical attributes (D_m and normalized mass spectrum, σ′_m)—produced smaller biases than assuming a constant μ [63]. Moreover, the D_m–μ constraint relations derived for ice-phase particles also showed an enhanced improvement in retrieving reflectivity than the currently used algorithms in ice-phase precipitation [64]. The σ_m–D_m relations ($D_m=a_m{\sigma }_m^{b_m}$) differ with microphysical mechanisms, and recent studies have demonstrated that these relations vary from geographical location and rain regimes, and also infer rain RSD features [12,41,60,65,66,67,68]. Figure 10 demonstrates the distribution of D_m and σ_m (standard deviation of the mass spectrum) for the total, stratiform, and convective precipitations of WP TCs. The scatter points in Figure 10 are the RSD samples eligible for the quality-controlled method of [42]. The 1-min RSDs should have a minimum number of 50 raindrops for a minimum of three different diameter bins, the Z (radar reflectivity) should be >10 dBZ, and the rainfall rate should be >0.1 mm h⁻¹. Moreover, the σ_m values related to D_m < 0.5 mm are discarded. A total of 8185, 6449, and 1736 1-min RSDs in total, stratiform, and convective precipitations were qualified for the above-mentioned conditions.

The fitting performed for the data points resulted in σ_m–D_m relations as given below:

σ_m = 0.294 D_m^1.122 (total)

(15)

σ_m = 0.293 D_m^1.223 (stratiform)

(16)

σ_m = 0.292 D_m^1.018 (convective)

(17)

Comparable to the findings of previous studies, a higher correlation between σ_m and D_m can be seen for the total, stratiform, and convective precipitations of the WP TCs [42,68]. Using eight years of in-situ shipboard global ocean RSD, ref. [68] evaluated the σ_m–D_m relations for seven latitude bands, and computed σ_m–D_m relation for the Northern Tropics (0°N to 22.5°N) is σ_m = 0.313 D_m^1.438.

Figure 11, Figure 12 and Figure 13 illustrate the mapping of (D_m, μ_o) space from (σ_m, D_m) space for total, stratiform, and convective precipitations of WP TCs, respectively. The occurrence frequency of σ_m with D_m for total, stratiform, and convective precipitations are depicted, in Figure 11a, Figure 12a and Figure 13a, respectively, and the normalized PDF of the mass spectrum (σ_m) are given in Figure 11b, Figure 12b and Figure 13b. The normalized mass spectrum, σ′_m, a statistically independent attribute from D_m [42,67], is computed for total (σ′_m = σ_m/D_m^1.122), stratiform (σ′_m = σ_m/D_m^1.223), and convective (σ′_m = σ_m/D_m^1.018) precipitations, and are plotted in Figure 11c, Figure 12c and Figure 13c with the two-dimensional frequency of occurrence. The normalized mass spectrum mean ($\overline{{\sigma }_m^{\prime }}$) and standard deviation (std(σ′_m)) values were 0.2912 and 0.0653 for the total precipitation of the WP TCs. The mean and standard deviations of the normalized mass spectrum were 0.2902 (0.2918) and 0.0649 (0.0605) for stratiform (convective) precipitation. The solid black line in Figure 11a, Figure 12a and Figure 13a, represents the total, stratiform, and convective σ_m–D_m relations (Equations (15)–(17)), respectively, and the solid red and blue lines denote the upper (Equations (21), (23), and (25)) and lower (Equations (22), (24), and (26)) σ′_m bounds. The σ′_m mean value for total, stratiform, and convective precipitation is represented with a black dash–dotted line, in Figure 11c,d, Figure 12c,d and Figure 13c,d, respectively.

The upper ($\overline{{\sigma }_m^{\prime }}$ + std(σ′_m) = 0.3565, 0.3551, and 0.3523, for total, stratiform, and convective rainfall, respectively) and lower bounds ($\overline{{\sigma }_m^{\prime }}$ − std(σ′_m) = 0.2258, 0.2254, and 0.2313, for total, stratiform, and convective rainfall, respectively) of σ′_m are depicted with red and blue dash–dotted lines in Figure 11c,d, Figure 12c,d and Figure 13c,d, for total, stratiform, and convective rainfall, respectively. These bounds cover 73.19%, 73.87%, and 74.25% of σ′_m data points, for total, stratiform, and convective rainfall, respectively.

The expected value of σ_m for total, stratiform, and convective rainfall are:

$${\sigma }_m^{expected value}=\overline{{\sigma }_m^{\prime }}{D}_m^{b_m}=0.2912D_m^{1.122}\left(\mathrm{total}\right);$$

(18)

$${\sigma }_m^{expected value}=\overline{{\sigma }_m^{\prime }}{D}_m^{b_m}=0.2902D_m^{1.297}\left(\mathrm{stratiform}\right);$$

(19)

$${\sigma }_m^{expected value}=\overline{{\sigma }_m^{\prime }}{D}_m^{b_m}=0.2918D_m^{1.018}\left(\mathrm{convective}\right).$$

(20)

The upper and lower bounds of σ_m for total, stratiform and convective rainfall are:

$${\sigma }_m^{upper\_bound}=[\overline{{\sigma }_m^{\prime }}+\mathrm{std}({{\sigma }^{\prime }}_m)] D_m^{b_m}=0.3565D_m^{1.122}\left(\mathrm{total}\right);$$

(21)

$${\sigma }_m^{lower\_bound}=[\overline{{\sigma }_m^{\prime }}-\mathrm{std}({{\sigma }^{\prime }}_m)] D_m^{b_m}=0.2258D_m^{1.122}\left(\mathrm{total}\right);$$

(22)

$${\sigma }_m^{upper\_bound}=[\overline{{\sigma }_m^{\prime }}+\mathrm{std}({{\sigma }^{\prime }}_m)] D_m^{b_m}=0.3551D_m^{1.297}\left(\mathrm{stratiform}\right);$$

(23)

$${\sigma }_m^{lower\_bound}=[\overline{{\sigma }_m^{\prime }}-\mathrm{std}({{\sigma }^{\prime }}_m)] D_m^{b_m}=0.2254D_m^{1.297}\left(\mathrm{stratiform}\right);$$

(24)

$${\sigma }_m^{upper\_bound}=[\overline{{\sigma }_m^{\prime }}+\mathrm{std}({{\sigma }^{\prime }}_m)] D_m^{b_m}=0.3523D_m^{1.018}\left(\mathrm{convective}\right);$$

(25)

$${\sigma }_m^{lower\_bound}=[\overline{{\sigma }_m^{\prime }}-\mathrm{std}({{\sigma }^{\prime }}_m)] D_m^{b_m}=0.2313D_m^{1.018}\left(\mathrm{convective}\right).$$

(26)

The ${\sigma }_m^{\prime }$and D_m assessments of WP TCs were transformed into μ_o estimates using below-mentioned equations, and are depicted in Figure 11e, Figure 12e and Figure 13e. The μ_o PDF distributions and the normalized Gaussian curve with its mean (black dash–dotted line), mean plus standard deviation (red dash–dotted line), and mean minus standard deviation (blue dash–dotted line) values are illustrated in Figure 11f, Figure 12f and Figure 13f, for total, stratiform and convective rainfall, respectively.

$${\mu }_o=\frac{D_m^{2-2b_m}}{{{\sigma }^{\prime }}_m^2}-4=11.7928 D_m^{-0.244}-4\left(\mathrm{total}\right)$$

(27)

$${\mu }_o=\frac{D_m^{2-2b_m}}{{{\sigma }^{\prime }}_m^2}-4=11.8742 D_m^{-0.594}-4\left(\mathrm{stratiform}\right)$$

(28)

$${\mu }_o=\frac{D_m^{2-2b_m}}{{{\sigma }^{\prime }}_m^2}-4=11.7444 D_m^{-0.036}-4\left(\mathrm{convective}\right)$$

(29)

The expected value of μ_o with the lower and upper bounds for total, stratiform, and convective rainfall was evaluated with the above equation and is shown in Figure 11e, Figure 12e and Figure 13e with black, blue, and red solid lines, respectively.

In the GPM DPR rain-retrieval algorithms, the radar reflectivity at Ka- and Ku-bands (Z_Ka and Z_Ku) and the difference between these two radar reflectivities, known as differential frequency ratio (DFR = 10log₁₀Z_Ku-10log₁₀Z_Ka, in dB), are used to retrieve the RSD parameters (D_m and log₁₀N_w). While estimating D_m values from DFR, previous studies noticed two D_m values for a given negative DFR value, called a dual-value problem, which arises due to the predominance of Rayleigh scattering in light rain at Ku- and Ka-band reflectivities [69,70]. Consistent with the previous studies, we also noticed a double solution problem (figure not shown); hence, rather than relating the D_m values to the DFR, empirical relations between D_m and Z_Ku/Z_Ka are derived. The T-matrix simulations with 25 °C temperature were applied to the disdrometer data to obtain the radar reflectivity at Ku- and Ka-bands for the WP TCs [71].

Figure 14 depicts the scatter plots of D_m versus Z_Ka/Z_Ku for total, stratiform, and convective rainfall of WP TCs. With the increase in reflectivity at Ku/Ka-band frequency, the D_m values increased in WP TC rainfall. The second-degree polynomial fit lines and the corresponding D_m–Z_ku and D_m–Z_ka relations are also depicted in the figure. Along with the present study polynomial fit lines, D_m–Z_ku/Z_ka relations derived for the Southwestern Pacific summer season rainfall from [13] are also depicted in the figure. For a given radar reflectivity, especially for reflectivity values greater than 20 dBZ, WP TCs measured in the present study showed lower D_m values than the oceanic summer season rainfall.

3.8. RSD Implications for Rainfall Kinetic Energy Retrievals

The energy with which the raindrops from the cloud base reach the ground surface is called the kinetic energy (KE) of rain or rainfall KE. The rainfall KE plays a crucial role in estimating the rainfall erosivity factor of the universal soil loss equation, a physical parameter that describes surface erosion caused by rainfall [2,72,73,74]. Due to the expensive experimental setup required for the direct measurement of rainfall KE, indirect measurements such as the utilization of RSD information from the ground-based disdrometers have been adopted globally [2,26,75,76,77,78].

The rainfall KE can be estimated using raindrop size and velocity information. Relating the rainfall KE with the rainfall rate can provide the opportunity to estimate the KE at places with rain gauges and lack of disdrometer measurements. Figure 15 displays the distribution of rainfall KE with the rainfall rate for total, stratiform, and convective rainfall. From the figure, it is apparent that the KE_time increases with the increase in rainfall rate, whereas the KE_mm showed a steep increase for the rainfall rate less than 20 mm h⁻¹, and above 20 mm h⁻¹, a flat increase can be seen. The linear, power, logarithmic, and exponential forms of rainfall KE are provided in Figure 15, and their statistical values are given in

Table 1. Correlation coefficient (R²), root mean square error (RMSE), normalized RMSE values for the rainfall kinetic energy–rainfall rate/mass-weighted mean diameter relations.

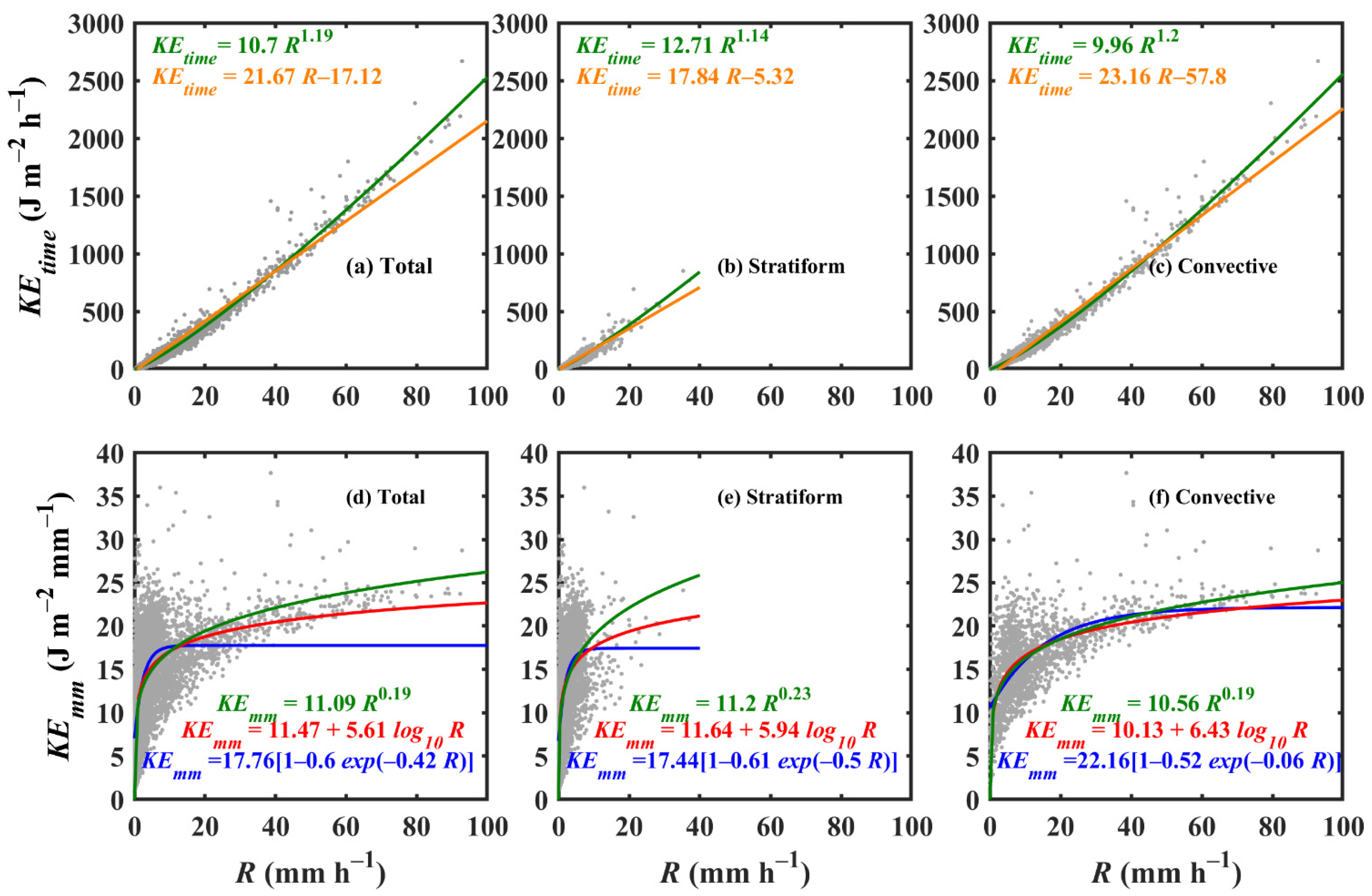
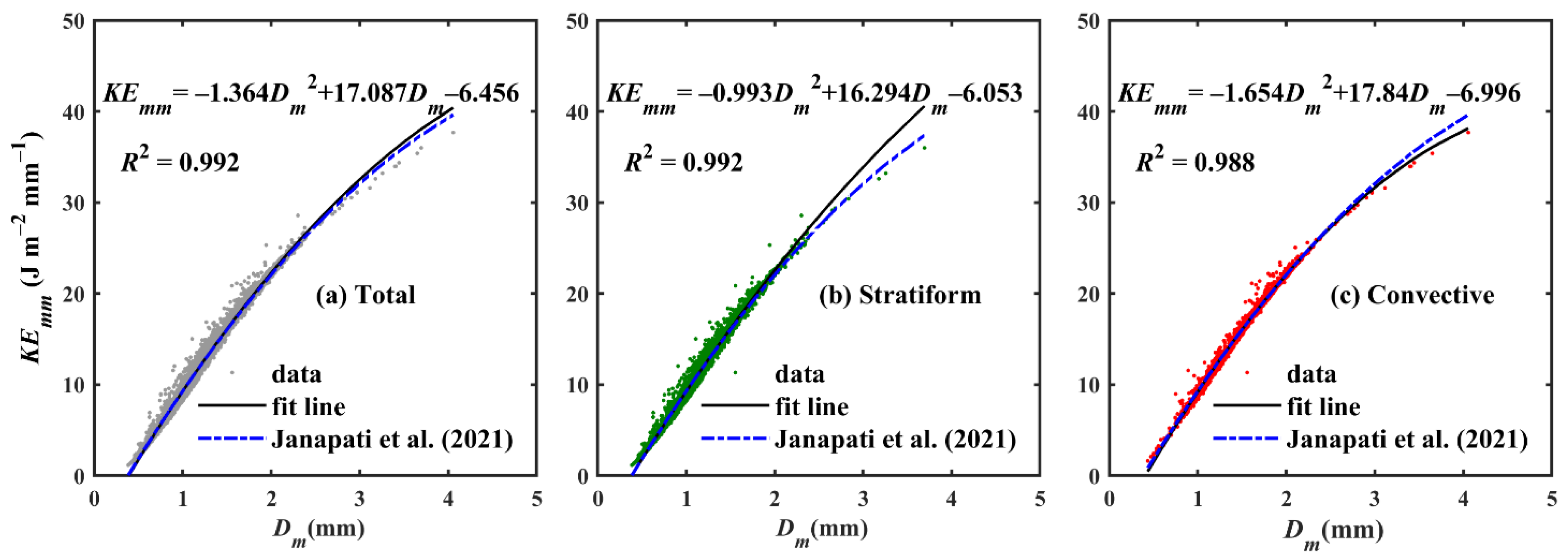
Precipitation Type	Statistical Parameters	KEtime–R		KEmm–R			KEmm–Dm
		Linear	Power	Power	Exp	Log
Total	R2	0.98	0.99	0.7	0.7	0.7	0.99
	RMSE	33.52	25.13	3.78	3.78	3.76	12.04
	NRMSE	0.36	0.27	0.04	0.04	0.04	3.28
Stratiform	R2	0.96	0.96	0.64	0.65	0.64	0.99
	RMSE	12.86	12.34	3.81	3.76	3.83	11.01
	NRMSE	0.35	0.33	0.1	0.1	0.1	3.36
Convective	R2	0.99	0.99	0.7	0.67	0.69	0.99
	RMSE	59.43	49.09	3.35	3.47	3.37	15.13
	NRMSE	0.64	0.53	0.04	0.04	0.04	4.18

.

The GPM DPR offers the RSD parameters (D_m and log₁₀N_w) of given precipitation globally with the dual-polarization capability. The empirical relationship between the rainfall KE and RSD parameters (D_m and log₁₀N_w) can aid in evaluating the rainfall KE using GPM DPR at the places where disdrometers and rain gauges are scarce. Previous researchers reported a reasonable agreement between the rainfall/RSD parameters of GPM DPR and the ground-based disdrometer. For instance, [66] compared the seasonal RSD of PARSIVEL disdrometer with the GPM DPR data products over eastern China, and they reported better agreement for the winter rainfall. A reasonable agreement was reported for the indirect comparison of GPM DPR D_m and log₁₀N_w values with worldwide disdrometer measurements [79].

Recently, a good agreement between RSD parameters (R and D_m) of ground-based disdrometers in Italy and the GPM DPR was reported by [80]. The studies mentioned above have evidently proven the reliability of GPM DPR rain/RSD parameters for hydro-meteorological applications; hence, we can use the D_m values from GPM DPR to estimate the rainfall KE using the empirical relation between D_m and KE. Figure 16 illustrates the distributions of srainfall KE with the mass-weighted mean diameter values for total, stratiform, and convective precipitation.

The figure shows that the KE_mm is highly correlated with the D_m for the WP TCs rainfall with little spread from the respective fit lines. Second-degree polynomial relations computed for KE_mm and D_m are depicted in the respective panels, and their statistical values are given in Table 1. Along with the present TCs fit lines, the KE_mm–D_m relation of WP TCs measured in Taiwan by [3] is portrayed in Figure 16. It is evident that the KE_mm–D_m relations of the WP TCs measured in Palau and Taiwan islands showed minor variations, which can be attributed to no variation in the RSDs of WP TCs measured at these two islands, as pointed out in Section 3.2.

4. Summary and Conclusions

In this study, the raindrop size distribution (RSD) statistical characteristics of fourteen tropical cyclones (TCs) were investigated using Joss–Waldvogel disdrometer (JWD) measurements conducted at an oceanic site in the Palau islands in the Western Pacific (WP). The WP TCs D_o and log₁₀N_w distribution diagram displayed that the mean D_o and log₁₀N_w values were located below (above) the [46] rain classification line for rainfall rates of less than (greater than) 10 mm h⁻¹. The WP TCs RSDs revealed distinct segregation between stratiform and convective types, and the convective RSDs of the considered TCs presented similar features to the maritime convective clusters. The contribution of small-size drops (<1 mm) to number concentration (N_t)/rainfall rate (R) was predominant in the stratiform precipitation than the convective type, and an opposite characteristic is recognized for the raindrops of diameter greater than 1 mm.

For a given type of disdrometer (JWD), average D_m values of WP TCs measured at Palau islands showed minor variations with Japan and Taiwan. Regardless of measurements from different disdrometer types, the WP TCs in Palau inferred nearly identical μ–Λ relations with the WP TCs measured in Taiwan and coastal China; however, these relations were different from the WP TCs measured over inland. In addition, an identical exponent value of the Z–R relations (b = 1.35 in Z = AR^b) observed in Taiwan and the Palau islands inferred that the WP TCs of these two islands were related with identical microphysical processes.

The Z–R, μ–Λ, D_m–R, N_w–R, σ_m–D_m, and μ_o–D_m relations of the WP TCs measured in the Palau islands showed an inequality between stratiform and convective precipitation. The present study offered unique RSD characteristics of WP TCs measured at an oceanic site in the Palau islands, and these results can deliver possible implications for rain retrieval algorithms. For instance, evaluated RSD relations (σ_m –D_m, μ_o–D_m, D_m–Z_ku, and D_m–Z_ka) can aid in optimizing the constraints associated with the global precipitation measurement (GPM) dual-precipitation radar (DPR) rain retrieval algorithms. In addition to the implications of the rain retrieval algorithms, the proposed rainfall kinetic relations (KE_time–R, KE_mm–R, and KE_mm–D_m) can be used to estimate the rainfall kinetic energy of WP TCs using rain gauge and remote sensing (GPM DPR) measurements, and the obtained rainfall KE can offer a better appraisal of rainfall erosivity, an essential parameter used in the soil erosion modeling.