Next Article in Journal
Spectral Retrieval of Eucalypt Leaf Biochemical Traits by Inversion of the Fluspect-Cx Model
Next Article in Special Issue
Sugarcane Yield Estimation Using Satellite Remote Sensing Data in Empirical or Mechanistic Modeling: A Systematic Review
Previous Article in Journal
A First Assessment of Canopy Cover Loss in Germany’s Forests after the 2018–2020 Drought Years
Previous Article in Special Issue
Deriving Aerodynamic Roughness Length at Ultra-High Resolution in Agricultural Areas Using UAV-Borne LiDAR
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 14
Issue 3
10.3390/rs14030565
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Assessment of Drought Indexes on Different Time Scales: A Case in Semiarid Mediterranean Grasslands

by
Andres F. Almeida-Ñauñay
1,2,*,
María Villeta
1,3,
Miguel Quemada
1,4 and
Ana M. Tarquis
1,2
1
Centro de Estudios e Investigación para la Gestión de Riesgos Agrarios y Medioambientales, CEIGRAM, Universidad Politécnica de Madrid, Senda del Rey, 13, 28040 Madrid, Spain
2
Grupo de Sistemas Complejos, Escuela Técnica Superior de Ingeniería Agronómica, Alimentaria y de Biosistemas (ETSIAAB), Universidad Politécnica de Madrid, Avda. Puerta de Hierro, n° 2-4, 28040 Madrid, Spain
3
Departamento de Estadística y Ciencia de los Datos, Facultad de Estudios Estadísticos, Universidad Complutense de Madrid, Avenida Puerta de Hierro s/n, 28040 Madrid, Spain
4
Departamento de Producción Agrícola, ETSIAAB, Universidad Politécnica de Madrid, Avda. Puerta de Hierro, n° 2-4, 28040 Madrid, Spain
*
Author to whom correspondence should be addressed.
Remote Sens. 2022, 14(3), 565; https://doi.org/10.3390/rs14030565
Submission received: 7 December 2021 / Revised: 18 January 2022 / Accepted: 21 January 2022 / Published: 25 January 2022
(This article belongs to the Special Issue Remote Sensing for Agrometeorology)
Browse Figures
Versions Notes

Abstract

:
Drought is a significant challenge to semiarid Mediterranean grasslands, Increasing the accuracy of monitoring allows improving the conservation and management of these vital ecosystems. Meteorological drought is commonly monitored by the Standard Precipitation Index (SPI) or the Standard Precipitation Evapotranspiration Index (SPEI). On the other hand, agriculture drought is estimated by the Vegetation Health Index (VHI). This work aims to optimise the correlation between both drought types using the best transformation of VHI and the most appropriate time scale. Two drought-vulnerable Mediterranean grasslands were selected to evaluate the performance of the drought indexes. The SPI and the SPEI were calculated using data obtained from nearby weather stations. MODIS data were used to calculate the VHI. This index was standardised, naming it as SVHI. Our results revealed that SPEI was better correlated with VHI compared to SPI. In addition, SVHI obtained better results in the critical vegetation phases than VHI. Overall, SPEI and SVHI were the best correlated indexes. The quarterly scale showed stronger relationships than the monthly scale and the most correlated time frame were Mediterranean spring and autumn. This fact suggests that SPEI and SVHI could provide a plus point for increasing the precision of vegetation monitoring during these periods.

Graphical Abstract

1. Introduction

The prairie regions account for about one third of the earth surface [1,2], being the permanent grassland over 7 million hectares of the Iberian Peninsula in 2020 [3]. These ecosystems are particularly important in providing ecological and cultural services, such as biodiversity conservation, landscape preservation and rural population fixation.
Drought is an important driving force in grassland dynamics and is a limiting factor in Mediterranean areas [4]. Climatically, it depends on two main interacting forces, precipitation, and temperature. The amount and timing of precipitation controls grasslands productivity, inducing fluctuations in soil water content throughout the seasons [5]. Temperature can regulate plant growth and reduce water availability in spring and fall in Mediterranean areas [6]. Therefore, it is essential to understand how drought affects grasslands, as these events are expected to increase with climatic change [7].
Drought is perceived as a deficiency in rainfall to normal levels, namely, a meteorological drought [8]. The standardised precipitation index (SPI) is the most widely used indicator of drought episodes. This index can quantify the degree of wetness by comparing the same time frame in an entire time series. Usually, the time frame is defined from 1 up to 24 months. As a result of the statistical techniques applied in SPI estimation, a probabilistic approach uses a z-score transformation to convert the precipitation probability density function as a distribution with mean zero and variance of one [9,10]. SPI has been successfully applied in tracking drought effects on irrigated areas [11], drought monitoring in semiarid regions [12,13] and studying climate change trends through historical rainfall data [14]. The Standardised Precipitation Evapotranspiration Index (SPEI) is presented as an improvement of the SPI index [10] and is another standard index for monitoring drought episodes. To obtain it, potential evapotranspiration (ETP) is calculated and subtracted from precipitation data. Then, the same statistical approach to estimate the SPI is applied to the previously obtained water balance data. In general, SPEI was shown to be a better drought indicator than SPI [15,16] due to the addition of the temperature effect in its calculation.
As it has been reported by several authors, time scale is a critical factor to study the relationships between NDVI and climate, showing differences inter-monthly, inter-seasonal and inter-annual time scales [17,18]. Even more, it has been revealed optimal relationships at different time scales and lagged responses between NDVI and climate [19]. Generally, the SPI and SPEI time frame can be defined from 1 up to 24 months. Depending on the drought monitoring time frame, the most used time scales are the monthly, the quarterly (3-months) and the annual [20,21]. Multiple challenges have been examined through the literature regarding the multi-time-scale approach. Among them, it is the concept of drought in semiarid grasslands. The resilience and stability to drought is dependent [22] on the grassland growth phases. Moreover, multi time scale drought assessment is depending on the vegetation cover, providing different responses vegetation on semiarid and semi humid biomes.
Although drought and aridity are treated in the same way, each reflects two different concepts. Drought is a temporal anomaly; meanwhile, aridity is a constant climatic feature. However, both are defined based on similar climatic variables, such as precipitation and evapotranspiration. The United Nations Environment Programme developed the Aridity Index (AI) in 1992 [23]. AI can be seen as the numerical representation of dryness expressed as the ratio between annual precipitation and evapotranspiration [24]. Artificial intelligence has been used to measure drought episodes [25,26]. Even more, Sanz et al. (2021) [27] related a cumulative AI with cumulative NDVI to characterize the efficient use of water resources in shorter periods than a year.
Thus far, monitoring large surfaces is still a great challenge. Although remote sensing (RS) techniques are appropriate tools to supervise grassland ecosystems in Mediterranean areas [28], because they are statistically reliable, operational robust and economically cost- effective methods. Vegetation indexes are a powerful instrument for characterizing vegetation behaviour. In the study of grasslands, the Normalized Difference Vegetation Index (NDVI) is one of the most used. It has been applied in various research, as an example: in estimating green biomass ratio [29] between green and above-ground total biomass, predicting forage quality [30] and monitoring landscape changes in central US grasslands [31].
Several works have demonstrated the usefulness of NDVI anomalies (NDVIA) in studying the effect of drought on grasslands vegetation. Furthermore, Li et al. (2014) [32] concluded that NDVIA could be considered a more accurate drought monitoring index than NDVI. Later, Nanzad et al. (2019) [33] calculated NDVIA for drought monitoring and correlated it with climatic factors. As a result, NDVIA could be interpreted as an agricultural drought index that combines vegetation and climatic responses. In many works studying the effect of drought on based on the NDVIA index, NDVIAs are calculated by comparing the NDVI value with the standard deviation as a measure of dispersion. Standard deviation implies assuming that NDVI follows a normal distribution [34].
However, in grasslands, the normal distribution is not adequate compared to other types of distributions [6]. This work will apply the same standardisation method used for SPI and SPEI, fitting the vegetation index values to a gamma distribution. As it is commonly used in drought studies [35,36], we will use the Vegetation Health Index (VHI) instead of NDVI due to its great sensitivity to detect drought periods. Furthermore, we standardised the VHI, defined as SVHI, to establish the relationships between the standardised meteorological and agricultural drought indexes.
This study aims to evaluate the performance of several climate droughts (SPI and SPEI) with agricultural drought indexes (VHI and SVHI) in semiarid grasslands at different time scales. Our specific objectives are to determine which standardised drought index performs better and to define which time scale correlates best with the standardised vegetation index.

2. Materials and Methods

2.1. Study Sites and Plot Selection

The study area is in the Mediterranean central area of Spain (Comunidad de Madrid). Two study areas were analysed, ZGU and ZSO (Figure 1), located in Guadalix de la Sierra and Soto del Real, respectively. The area is characterized by scarce precipitation, cold winters, and warm summers. Four pixels of 250 × 250 m2 were selected in each zone contained in an area of approximately 1 km2. First, ZGU is limited between (3°38′00″ W, 3°39′00″ W) and (40°46′00″ N, 40°47′00″ N). Second, ZSO is enclosed between (3°45′00″ W, 3°46′00″ W) and (40°43′00″ N, 40°44′00″ N).
The ZGU area belongs to the Brachypodion phoenicoidis alliance, growing in soils with a heavy texture and an important percentage of clay and silt. The most frequent species in these natural pastures are Dactylis hispanica and Poa angustifolia [38,39].
The ZSO zone is an early Mediterranean grassland abundant in thermophiles and dominated by a vivacious annual vegetation. They are principally acidophilic gramineous of medium size, growing in the Guadarrama Sierra. The predominant species are Festuca Ampla and Agrostis castellana [38].
The altitude is comparable in ZGU and ZSO, 820 and 958 meters above the sea level (m.a.s.l), respectively. However, the slope of ZGU is fairly higher than ZSO (Table 1). Each soil trench presents differences in their physical and chemical soil properties [40]. The ZGU soil is a caloric regosol [41] with a topsoil between (0–5 cm) and an AB horizon (5–25 cm). Both horizons present the same colour and show a clay loam texture, with a great content of clay and a pH of 7.2. The ZSO soil is classified as a dystric cambisol presenting an Au topsoil (3 cm) and an Au2 horizon (20 cm) with a distinct colour in each of them, both present a sandy loam texture, with a grand content of sand (around 75% with both types of sand) and a pH ranging from 5.4 to 5.8. The topsoil and the beneath horizon water holding capacity (WHC) is estimated from the pedotransfer function suggested by [42]. For more information about the soil properties, see [37].

2.2. Satellite Data and Vegetation Index Calculations

MODIS (Terra and Aqua) and Landsat are the most employed imagery in long-term vegetation research [1], being successfully applied in the study of semiarid grassland cover and playing an important role in the pasture insurance policy in Spain [43]. The MOD09Q1 product offers imagery at 250 m resolution of the RED (620–670 nm) and NIR (841–876 nm) surface reflectance. Observations from the same orbit are composited by observational coverage and the highest coverage observations are stored in an 8-days period. Each orbit’s observation is rated based on multiple criteria: clouds, cloud shadow, aerosol quantity, and view angle. [44]. Atmospheric correction is computed using an LPDAAC algorithm specialized in curing MODIS imagery data [45,46]. The reflectance of the study plot was monitored from 2001 to 2020. Each year, 46 images were acquired, giving a total of 920 images during the study period. Vegetation indexes (Table 2) were calculated from the reflectance bands of these images.
The normalized difference vegetation index (NDVI) is an adequate estimator of the photosynthetic activity and vegetation growth. Dense and healthy vegetation show high values (>0.5), whereas sparse or stressed vegetation present low values, due to adverse conditions, mainly climate and soil. NDVI series was calculated in each pixel, and their average value was employed in the analysis.
According to scientific literature, the vegetation health index (VHI) is shown to be an improved version of NDVI, allowing to detect drought and non-drought periods [48]. Two components define it mathematically. The first represents the vegetation component, named as vegetation condition index (VCI), and the second component corresponds to the land surface temperature and is defined as temperature condition index (TCI). TCI is considered a thermal stress indicator to quantify temperature-related drought periods. This index is sensitive to vegetation drought stress based on soil moisture variations during wet and drought periods. Land surface temperature (LST) was obtained from MOD11A2 product, which provided the temperature average 8-day per-pixel with a spatial resolution of 1 Km [49].

2.3. Climatic Data

Daily meteorological data were obtained from two different AEMET stations (Agencia Estatal de Meteorologia). ZGU station is established at Venturada (40°47′53.79″ N, 3°37′30.49″ W) and ZSO meteorological station is situated between Soto del Real and Colmenar Viejo (40°41′46.008″ N, 3°45′54.019″ W). Both are nearby to the selected zones (see Figure 1) [37].
Daily series of average temperature and precipitation from 2001 to 2020 were extracted. Annual average precipitation and temperature were obtained from a 20-year time series (Table 1) at each location. The average precipitation of Guadalix de la Sierra (576 mm) was higher than Soto del Real, whereas the temperature (12.6 °C) was lower than Soto del Real (560 mm), respectively.
Precipitation and temperature series were resampled to an eight-day frequency to be analysed on the same time scale as the VHI time series. Precipitation (PCP) is the accumulated precipitation every eight days, and the temperature (TEMP) is the average temperature in the same period. Both series were analysed using descriptive statistics to characterize the climate conditions of the study. Then the Hargreaves-Samani expression [50] was used to calculate the reference evapotranspiration (ET0; mm d−1) based on Equation (1).
E T 0 = 0.0135 ∗ k R S ∗ 0.408 ∗ H 0 ∗ T m + 17.8   ∗   T x − T n 0.5
where kRS is the Hargreaves empirical coefficient; H0 is extraterrestrial radiation (MJ m−2 d−1); and Tm, Tx and Tn are the daily averages, maximum and minimum air temperature (°C), respectively. Daily extraterrestrial radiation (H0) is calculated based on the day of the year and the geographical position of each plot [51]. The value of kRS was set at 0.16 as recommended for arid and semiarid interior regions [52].

2.4. Standardised Indexes

As mentioned above, standardised indexes are calculated on various time scales. In our case, we have used monthly (1 month) and quarterly (3 months) the scales in this work, as these are the most usual time scales found in the literature [20,21,53] and the most suitable to be studied. Annual scale was not considered in this work because quarterly trends and tendencies of VHI could be vanished. On the quarterly scale, each trimester presented a constant time length and a VHI trend, representing the semi-arid grasslands studied in Spain. The first one goes from January to March, and the last one from October to December.

2.4.1. Standardised Precipitation Index

The SPI is computed by fitting a given precipitation series’ gamma probability density function (PDF). This adjustment is performed separately for each temporal basis on which the precipitation is built. Then, the data is transformed to a normal distribution where the mean SPI for the station and the needed period is zero.
Positive SPI values show excess rainfall, while negative SPI values correspond to a precipitation deficit. Further details on the SPI method could be found in the [54,55] works.

2.4.2. Standardised Precipitation Evapotranspiration Index

To obtain the SPEI, we calculated the daily water balance, which is the difference between the daily precipitation and the daily potential evapotranspiration. We then aggregated the values at the time scales of interest to acquire the starting data [56]. Later, the same standardisation method of SPI is applied to the water balance time series. The method used to calculate SPEI is fully described in [10] work.

2.4.3. Standardised Vegetation Index

The approach to calculating the standardised vegetation health index (SVHI) is primarily based on the standardisation method used in SPI calculation applied to VHI values. Standardisation is applied to the VHI values of the month’s last date when working on a monthly scale. In the case of the quarterly scale, it is applied at VHI values of the trimester’s last date.
A scientific review revealed that it is recommended to use a variable depending on the study area [57,58]. Therefore, we maximized the correlation between SVHI, SPI, and SPEI to obtain the optimal α in each zone and time scale. From now on, the subsequent analyses were applied to the optimal SVHI. The optimal VHI was estimated using the same α values obtained in the optimization of SVHI.

2.5. Correlation Analysis

We used Pearson’s correlation analysis to examine the standardised indexes relations in each zone. In the first step, we calculated the correlation values along with the whole time series. Equation (2) is used to compute Pearson’s correlation values.
ρ = c o v S V I i , y i , l σ S V I i ∗ σ y i , l
where SVIi is the SVHI or VHI values at i time scale, and the yi,l is the l indexes (SPI or SPEI) values at the i time scale. We calculated the correlation for each unit scale: month and quarterly to determine the best correlated time frame in the series.

2.6. Classification and Quantification of Drought Episodes

Based on a bibliography review in the field of meteorological and agricultural drought indexes [59,60,61], we classified SPI, SPEI, VHI, and SVHI to define four different drought classes. Values were classified as follows in Table 3:

3. Results

3.1. Descriptive Statistics

We estimated the VHI time series to reveal the drought epochs in the vegetation. VHI was composed of two elements. VCI, which characterized the vegetation behaviour (Figure 2a) and TCI, which represented the land surface temperature (Figure 2b). It was important to notice that the higher the value of TCI and VCI was, the better the vegetation condition was. In one hand, we observed that VCI is higher in ZGU during Q2 and Q3, during the most drought vulnerable seasons in the year (spring and the summer). On the other hand, the TCI of ZGU is higher in the entire year, showing that vegetation is in a better state than ZGU. Overall, we could expect a minor number of drought events in ZGU compared to ZSO.
The dispersion and evolution of the VHI through the different quarters showed a similar pattern for the two zones under study (Figure 3). The summer presented the lowest values, which began to increase in Q3 and reached a peak in Q4. The variation in VHI data throughout the year ranged from 10 to 82, with the highest dispersion at Q2 and Q4. Generally, the VHI values at ZGU were higher than those of ZSO in the Q2 and Q3 quarters. This difference is probably because of the difference in temperature in both sites (Table 1). However, during the middle Q4 and Q1, the VHI values in ZSO were higher than in ZGU.
A similar quarterly pattern appeared in the VHI and the precipitation dispersion (Figure 3 and Figure 4a). Both zones shared similar behaviour in the volume and dispersion of precipitation. Although precipitation appeared to be erratic, presenting a great dispersion in Q4 and Q2. Meanwhile, the lowest data dispersion was observed in Q3. The highest temperature dispersion was found in spring (Figure 4b). Temperature variation at both sites was around 1 °C. Differences were more noticeable during Q3 (mainly summer) and at the beginning of Q4 (October).
Summarising the annual cycle in both zones, precipitation and temperature patterns were quite similar. The lack of precipitation was noticeable during summer; autumn rain events were synchronised with the increase in VHI. A similar result is obtained at the beginning of spring when precipitation and VHI increased simultaneously in both zones.

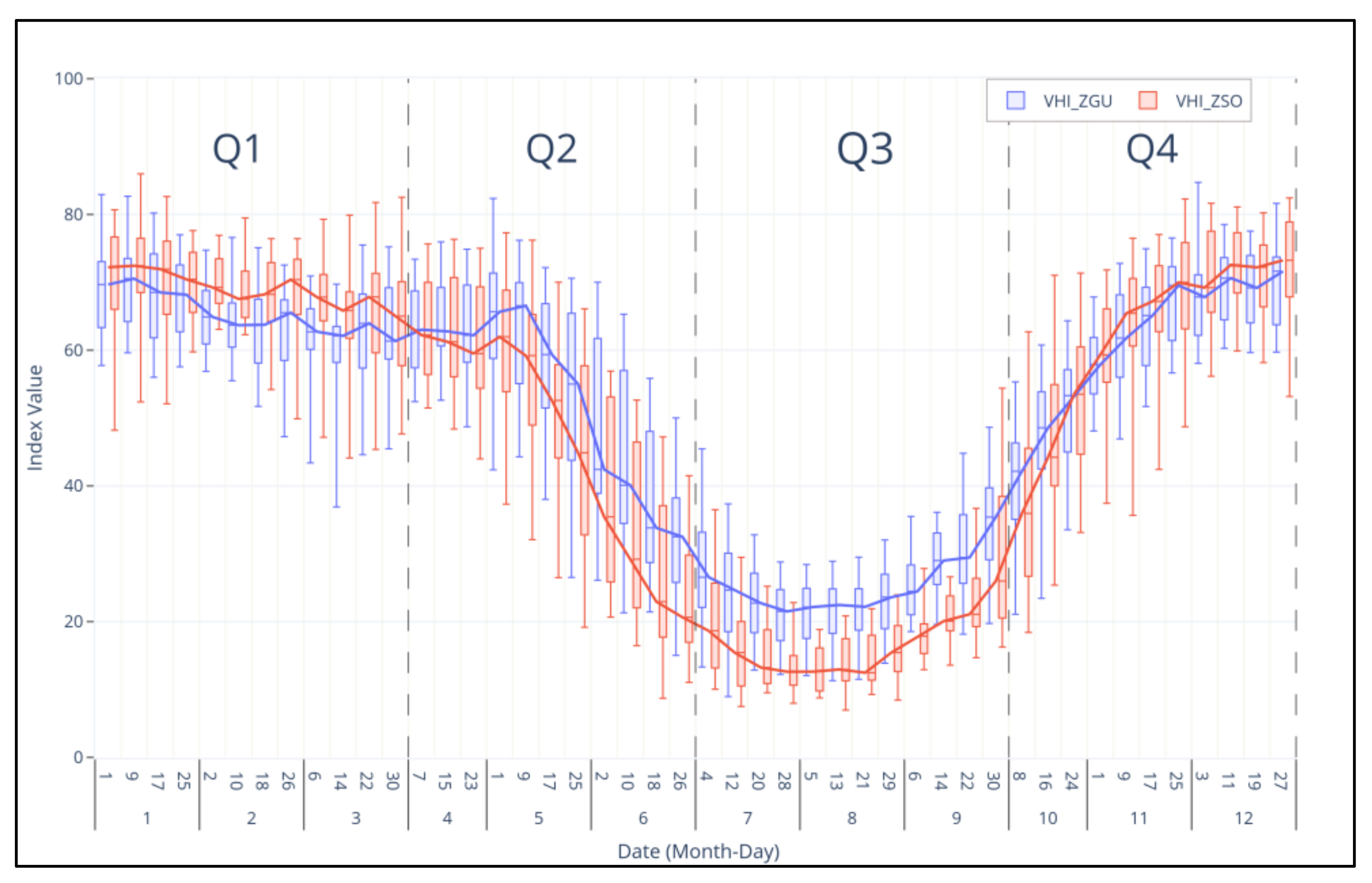
3.2. Standardised Indexes Time Series

The SVHI pattern showed a better similarity with the meteorological drought indexes in the quarterly division than on the monthly time scale (Figure 5 and Figure 6). There is no easily perceived remarkable difference between SPI and SPEI. We could also note that the ZSO time series might be better correlated than the ZGU time series. Especially at the end of the time series, we could detect that SPI and SPEI are better overlapped with SVHI in ZSO than ZGU.
We could observe in Figure 7 the effects of standardisation and the use of a variable alpha in the correlation between SVHI and drought indexes. We recognised a parabolic trend on the monthly scale and a logarithm shape on the quarterly time scale in both zones. We could detect that both time scales presented a remarkable maximum, being (α = 0.2) in the monthly’s monthly scale and (α = 0.6) in the quarterly case.

3.3. Correlation Analysis

A considerable difference in the correlation values between the entire time series of the VHI, SVHI, and drought indexes (SPI, SPEI) at different time scales was observed (Table 4). The correlation increased when standardisation was applied to the VHI in both zones. At the same time, we confirm the supposition exposed in the time series plots, where the quarterly division seemed to be the most suitable time scale to analyse drought indexes.
The correlation between SVHI and SPI revealed that the most correlated months were March and May in both zones (Table 5). This fact is repeated in SPEI, in exception of ZGU, which showed the higher correlation in May and September. The most correlated seasons were spring (April–June) and winter (October–December) in both zones on the quarterly scale, achieving values greater than 0.68 in all cases. Nevertheless, we could still observe differences between zones. Generally, ZGU obtained values smaller than ZSO. However, it is interesting to note that the trend reversed in (Q3) mainly summer months when ZGU obtained higher values than ZSO in both indexes.
Overall, the previous time series plots and correlation analysis support the idea that the quarterly time scale is the most suitable for analysing the studied semiarid Mediterranean grasslands.

3.4. Drought Classification

The drought classification suggested that ZGU suffered a minor number of drought events compared to ZSO (Table 6). As we could observe, the SPI did not show a notable difference between zones, neither on the monthly nor quarterly time scales. SPEI and SVHI showed better results, especially on the quarterly time scale, where moderate drought increased compared to SPI. However, the VHI was the best approach to distinguish between both zones. The VHI showed a remarkable difference in the case number of extreme drought cases between both zones monthly.
Meanwhile, on the quarterly scale, the critical point was the number of severe drought cases. In general, we speculate that LST influenced the TCI and VHI values. Therefore, VHI was able to better distinguish between both zones. However, it is important to note that SVHI was better correlated with SPI and SPEI at meteorological drought epochs.

4. Discussion

Vegetation indexes are an effective indicator of grassland cover. Their response is highly interrelated with climate and agricultural conditions [62,63]. In fact, multiple authors [64,65] have reported a clear relationship between grasslands vegetation and water availability. In this line, the amount, variability, and timing of precipitation and temperature are determining factors of grassland production [6,66].
Regarding VIs, when precipitation rise, generally, the VI value increases [67,68] with a potential delay between both of them [69]. Our results reach the same conclusion, VCI and VHI showed greater values during the autumn and spring transition phases and achieved low stable values during winter and summer, when temperature and precipitation are limiting. Similar trends for MODIS NDVI were reported by [27,70], suggesting that NDVI is restricted, as well as grassland vegetation, during the summer and winter seasons.
The precipitation amount and dispersion increased during autumn (Figure 4a); as a result, VIs spread simultaneously in the same time frame [71,72]. This fact could be explained because of the rainfall patterns that define the temporal variability of soil moisture and, in turn, vegetation activity in soils [73]. At both zones, the precipitation pattern is similar. However, the ZSO VIs were higher than in the ZGU, suggesting that the temperature difference could explain the decrease in VIs due to cold stress induced in grassland vegetation during winter and drought stress during summer [74].
Analysing the effect of temperature on the VIs, during autumn, the VIs (VCI and VHI) in ZSO indicate a higher increase with similar precipitation, most likely due to a higher temperature in ZSO. At the start of spring, the VIs in ZGU show a remarkable increase whereas, in ZSO the VIs remained constant. This fact is reflecting the growth of biomass as the temperature increases, producing the Mediterranean spring herbage flush [75]. In the second part of the spring, the VIs decreased more quickly in ZSO than in ZGU. At the end of spring, both zones achieved similar VIs. However, the value of ZSO was slightly lower during the summer. The results of the WHC (water holding capacity) indicate that the ZGU soil is able to retain more water compared to the ZSO soil. Thus, the soil mixed interactions between moisture and lower temperatures in ZGU might explain the difference with ZSO during spring and summer. In general, soil moisture is defined as a connection element between vegetation growth and precipitation, regulating rainfall storage and availability, therefore determining vegetation dynamics [76,77,78,79].
The Results section shows that the SVI series pattern was more distinctive on the quarterly time scale than in the monthly scale. These results are in line with those obtained by [80]. We speculate that the main reason is the time scale increment (from 1 month to 3 months). This increase allows changing the number of drought events as the time series becomes smoother with fewer abrupt changes. As the reference period rises, the aggregate rainfall value changes from one month to three months; hence, the variations are minor and less significant [81].
It has been thoroughly discussed the optimal time scale to be used in the SPI and SPEI studies. At monthly scale [53], vegetation appears to show a more obvious response to hydrothermal conditions. Whereas quarterly time scale seems to reveal seasonal trends and patterns (3-months) between drought and vegetation response. In our case, we could observe that the highest values were obtained in the quarterly time scale. This in line with [82] research, revealing that grassland cover showed the highest correlation with SPEI-3. Although, other works suggest that monthly and annual time scales might be more explanatory [16,64]. Thus, it is essential to consider the influence of the local conditions in the vegetation response to drought.
Our results suggest that spring and autumn, and particularly May and September, are the most correlated time frames throughout the year. Similar conclusions were drawn from the work [13] that obtained higher correlations in the crop growth period. In our case, spring, and autumn are the seasons when the NDVI reaches its peak.
All standardised indexes showed significant indicators of SVI status in the critical phases, spring, and autumn. SPEI stands out over SPI; this probably results from the addition of evapotranspiration to the analysis. This result aligns with research [12], where SPEI showed better results than SPI. Therefore, we should consider the growth period of grassland vegetation in these zones, and this reaffirms the utility of standardised indexes in the critical growth phases.

5. Conclusions

Remote sensing imagery, particularly MODIS time-series data, have great potential to assess grassland dynamics. However, it is difficult to choose a suitable drought index to monitor these ecosystems in arid and semiarid conditions. Therefore, in this work, two standardised indexes (SPI and SPEI) were selected to examine their performance in semiarid grasslands.
Our statistical analysis showed that a previous VIs standardisation improved the correlation with climate variables. Therefore, it is recommended to consider the possibility of including a data pre-treatment to obtain the most accurate relationships between drought and aridity indexes (SPI and SPEI) with vegetation indexes (VHI and SVHI). It is also notable that optimisation of the α coefficient further improves the correlation values.
These results emphasise the importance of the time scale as a determinant factor in monitoring semiarid grasslands. The three months scale proved to be the most appropriate for estimating these standardised indexes in semiarid grasslands.
We have obtained satisfactory results, showing that SPI and SPEI are suitable vegetation and water status indicators. Therefore, our approach has the potential to improve the monitoring and management of semiarid grasslands. Future research should consider the estimation of these indexes in grasslands under different climates and the implementation of computing methods involving vegetation and drought indexes complementary.

Author Contributions

Conceptualization, A.F.A.-Ñ., M.V., M.Q. and A.M.T.; methodology, M.V. and A.M.T.; formal analysis, A.F.A.-Ñ., M.V., M.Q. and A.M.T.; writing—original draft preparation A.F.A.-Ñ.; writing—review and editing, A.F.A.-Ñ., M.V., M.Q. and A.M.T.; supervision, A.M.T.; funding acquisition, M.V., M.Q. and A.M.T. All authors have read and agreed to the published version of the manuscript.

Funding

The authors acknowledge the support from Project No. PGC2018-093854-B-I00 of the Spanish Ministerio de Ciencia Innovación y Universidades of Spain, the funding from the Comunidad de Madrid (Spain), the Structural Funds 2014-2020 512 (ERDF and ESF), through project AGRISOST-CM S2018/BAA-4330 and the support of the grant from Agencia Estatal de Investigación (PID2019-106433GB-I00/AEI/10.13039/501100011033) of Spain, are highly appreciated.

Data Availability Statement

Data are available on request from the authors.

Acknowledgments

The authors sincerely thank the support from CEIGRAM’s personal, and the funding provided by the Comunidad de Madrid and Agencia Estatal de Investigación.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Reinermann, S.; Asam, S.; Kuenzer, C. Remote Sensing of Grassland Production and Management—A Review. Remote Sens. 2020, 12, 1949. [Google Scholar] [CrossRef]
  2. White, R.P.; Murray, S.; Rohweder, M. Pilot Analysis of Global Ecosystems---Grassland Ecosystems; World Resources Institute: Washington, DC, USA, 2000; ISBN 1569734615. [Google Scholar]
  3. Eurostat Utilised Agricultural Area by Categories-Permanent Grasslands. 2021. Available online: https://ec.europa.eu/eurostat/databrowser/view/tag00025/default/table?lang=en (accessed on 4 December 2021).
  4. Vicente-Serrano, S.; Azorin-Molina, C.; Peña-Gallardo, M.; Tomas-Burguera, M.; Domínguez-Castro, F.; Martin-Hernández, N.; Beguería, S.; El Kenawy, A.; Noguera, I.; García, M. A High-Resolution Spatial Assessment of the Impacts of Drought Variability on Vegetation Activity in Spain from 1981 to 2015. Nat. Hazards Earth Syst. Sci. 2019, 19, 1189–1213. [Google Scholar] [CrossRef] [Green Version]
  5. Scheuring, I.; Riedi, R.H. Application of Multifractals to the Analysis of Vegetation Pattern. J. Veg. Sci. 1994, 5, 489–496. [Google Scholar] [CrossRef]
  6. Martín-Sotoca, J.J.; Saa-Requejo, A.; Moratiel, R.; Dalezios, N.; Faraslis, I.; Tarquis, A.M. Statistical Analysis for Satellite-Index-Based Insurance to Define Damaged Pasture Thresholds. Nat. Hazards Earth Syst. Sci. 2019, 19, 1685–1702. [Google Scholar] [CrossRef] [Green Version]
  7. Gao, Q.; Zhu, W.; Schwartz, M.W.; Ganjurjav, H.; Wan, Y.; Qin, X.; Ma, X.; Williamson, M.A.; Li, Y. Climatic Change Controls Productivity Variation in Global Grasslands. Sci. Rep. 2016, 6, 26958. [Google Scholar] [CrossRef]
  8. Mishra, A.K.; Singh, V.P. A Review of Drought Concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
  9. Loukas, A.; Vasiliades, L.; Dalezios, N.R. Intercomparison of Meteorological Drought Indices for Drought Assessment and Monitoring in Greece. In Proceedings of the 8th International Conference on Environmental Science and Technology, Lemnos Island, Greece, 8–10 September 2003; Volume B, pp. 484–491. [Google Scholar]
  10. Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef] [Green Version]
  11. Khan, S.; Gabriel, H.F.; Rana, T. Standard Precipitation Index to Track Drought and Assess Impact of Rainfall on Watertables in Irrigation Areas. Irrig. Drain. Syst. 2008, 22, 159–177. [Google Scholar] [CrossRef]
  12. Zarei, A.R.; Shabani, A.; Moghimi, M.M. Accuracy Assessment of the SPEI, RDI and SPI Drought Indices in Regions of Iran with Different Climate Conditions. Pure Appl. Geophys. 2021, 178, 1387–1403. [Google Scholar] [CrossRef]
  13. Hadri, A.; Saidi, M.E.M.; Boudhar, A. Multiscale Drought Monitoring and Comparison Using Remote Sensing in a Mediterranean arid Region: A Case Study from West-Central Morocco. Arab. J. Geosci. 2021, 14, 118. [Google Scholar] [CrossRef]
  14. Li, W.; Fu, R.; Juárez, R.I.N.; Fernandes, K. Observed Change of the Standardized Precipitation Index, Its Potential Cause and Implications to Future Climate Change in the Amazon Region. Philos. Trans. R. Soc. B Biol. Sci. 2008, 363, 1767–1772. [Google Scholar] [CrossRef] [PubMed]
  15. Tan, C.; Yang, J.; Li, M. Temporal-Spatial Variation of Drought Indicated by SPI and SPEI in Ningxia Hui Autonomous Region, China. Atmosphere 2015, 6, 1399–1421. [Google Scholar] [CrossRef] [Green Version]
  16. Pei, Z.; Fang, S.; Wang, L.; Yang, W. Comparative Analysis of Drought Indicated by the SPI and SPEI at Various Timescales in Inner Mongolia, China. Water 2020, 12, 1925. [Google Scholar] [CrossRef]
  17. Li, C.; Leal Filho, W.; Yin, J.; Hu, R.; Wang, J.; Yang, C.; Yin, S.; Bao, Y.; Ayal, D.Y. Assessing Vegetation Response to Multi-Time-Scale Drought across Inner Mongolia Plateau. J. Clean. Prod. 2018, 179, 210–216. [Google Scholar] [CrossRef]
  18. Zhang, Y.; Wang, X.; Li, C.; Cai, Y.; Yang, Z.; Yi, Y. NDVI Dynamics under Changing Meteorological Factors in a Shallow Lake in Future Metropolitan, Semiarid Area in North China. Sci. Rep. 2018, 8, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  19. Mu, S.; Yang, H.; Li, J.; Chen, Y.; Gang, C.; Zhou, W.; Ju, W. Spatio-Temporal Dynamics of Vegetation Coverage and Its Relationship with Climate Factors in Inner Mongolia, China. J. Geogr. Sci. 2013, 23, 231–246. [Google Scholar] [CrossRef]
  20. Kang, W.; Wang, T.; Liu, S. The Response of Vegetation Phenology and Productivity to Drought in Semi-Arid Regions of Northern China. Remote Sens. 2018, 10, 727. [Google Scholar] [CrossRef] [Green Version]
  21. An, Q.; He, H.; Nie, Q.; Cui, Y.; Gao, J.; Wei, C.; Xie, X.; You, J. Spatial and Temporal Variations of Drought in Inner Mongolia, China. Water 2020, 12, 1715. [Google Scholar] [CrossRef]
  22. Zhang, Q.; Kong, D.; Singh, V.P.; Shi, P. Response of Vegetation to Different Time-Scales Drought across China: Spatiotemporal Patterns, Causes and Implications. Glob. Planet. Chang. 2017, 152, 1–11. [Google Scholar] [CrossRef] [Green Version]
  23. Middleton, N.; Thomas, D. World Atlas of Desertification; Arnold, E., Ed.; Wiley: London, UK, 1992; ISBN 0340555122. [Google Scholar]
  24. Livada, I.; Assimakopoulos, V.D. Spatial and Temporal Analysis of Drought in Greece Using the Standardized Precipitation Index (SPI). Theor. Appl. Climatol. 2007, 89, 143–153. [Google Scholar] [CrossRef]
  25. Dong, J.; Liu, J.; Zhang, G.; Basara, J.B.; Greene, S.; Xiao, X. Climate Change Affecting Temperature and Aridity Zones: A Case Study in Eastern Inner Mongolia, China from 1960–2008. Theor. Appl. Climatol. 2013, 113, 561–572. [Google Scholar] [CrossRef]
  26. Bannayan, M.; Sanjani, S.; Alizadeh, A.; Lotfabadi, S.S.; Mohamadian, A. Association between Climate Indices, Aridity Index, and Rainfed Crop Yield in Northeast of Iran. F. Crop. Res. 2010, 118, 105–114. [Google Scholar] [CrossRef]
  27. Sanz, E.; Saa-Requejo, A.; Díaz-Ambrona, C.H.; Ruiz-Ramos, M.; Rodríguez, A.; Iglesias, E.; Esteve, P.; Soriano, B.; Tarquis, A.M. Normalized Difference Vegetation Index Temporal Responses to Temperature and Precipitation in Arid Rangelands. Remote Sens. 2021, 13, 840. [Google Scholar] [CrossRef]
  28. Ali, I.; Cawkwell, F.; Dwyer, E.; Barrett, B.; Green, S. Satellite Remote Sensing of Grasslands: From Observation to Management. J. Plant Ecol. 2016, 9, 649–671. [Google Scholar] [CrossRef] [Green Version]
  29. Ren, H.; Zhou, G. Estimating Green Biomass Ratio with Remote Sensing in Arid Grasslands. Ecol. Indic. 2019, 98, 568–574. [Google Scholar] [CrossRef]
  30. Wijesingha, J.; Astor, T.; Schulze-Brüninghoff, D.; Wengert, M.; Wachendorf, M. Predicting Forage Quality of Grasslands Using UAV-Borne Imaging Spectroscopy. Remote Sens. 2020, 12, 126. [Google Scholar] [CrossRef] [Green Version]
  31. Zhou, Q.; Rover, J.; Brown, J.; Worstell, B.; Howard, D.; Wu, Z.; Gallant, A.L.; Rundquist, B.; Burke, M. Monitoring Landscape Dynamics in Central U.S. Grasslands with Harmonized Landsat-8 and Sentinel-2 Time Series Data. Remote Sens. 2019, 11, 328. [Google Scholar] [CrossRef] [Green Version]
  32. Li, R.; Tsunekawa, A.; Tsubo, M. Index-Based Assessment of Agricultural Drought in a Semi-Arid Region of Inner Mongolia, China. J. Arid Land 2014, 6, 3–15. [Google Scholar] [CrossRef]
  33. Nanzad, L.; Zhang, J.; Tuvdendorj, B.; Nabil, M.; Zhang, S.; Bai, Y. NDVI Anomaly for Drought Monitoring and Its Correlation with Climate Factors over Mongolia from 2000 to 2016. J. Arid Environ. 2019, 164, 69–77. [Google Scholar] [CrossRef]
  34. Meroni, M.; Fasbender, D.; Rembold, F.; Atzberger, C.; Klisch, A. Near Real-Time Vegetation Anomaly Detection with MODIS NDVI: Timeliness vs. Accuracy and Effect of Anomaly Computation Options. Remote Sens. Environ. 2019, 221, 508–521. [Google Scholar] [CrossRef]
  35. Gidey, E.; Dikinya, O.; Sebego, R.; Segosebe, E.; Zenebe, A. Analysis of the Long-Term Agricultural Drought Onset, Cessation, Duration, Frequency, Severity and Spatial Extent Using Vegetation Health Index (VHI) in Raya and Its Environs, Northern Ethiopia. Environ. Syst. Res. 2018, 7, 13. [Google Scholar] [CrossRef] [Green Version]
  36. Kogan, F.N. Application of Vegetation Index and Brightness Temperature for Drought Detection. Adv. Sp. Res. 1995, 15, 91–100. [Google Scholar] [CrossRef]
  37. Almeida-Ñauñay, A.F.; Benito, R.M.; Quemada, M.; Losada, J.C.; Tarquis, A.M. Recurrence Plots for Quantifying the Vegetation Indices Dynamics in a Semi-Arid Grassland. Geoderma 2022, 406, 115488. [Google Scholar] [CrossRef]
  38. Peco, B.; Sánchez, A.M.; Azcárate, F.M. Abandonment in Grazing Systems: Consequences for Vegetation and Soil. Agric. Ecosyst. Environ. 2006, 113, 284–294. [Google Scholar] [CrossRef]
  39. San Miguel-Ayanz, A.; Barbeito Sanchez, I.; Roig Gomez, S.; Rodríguez Rojo, M.P. Los Pastos en la Comunidad de Madrid. Tipología, Cartografía y Evaluación; Dirección General de Medio Ambiente. Conserjería de Medio Ambiente, Vivienda y Ordenación del Territorio: Madrid, Spain, 2009. [Google Scholar]
  40. Schmid, T.; Millán, R.; Lago, C.; Trueba, C. Caracterización Edafológica e Índices de Vulnerabilidad de la Comunidad Autónoma de Madrid. Escala 1:200.000; Editorial CIEMAT: Madrid, Spain, 2000. [Google Scholar]
  41. WBRS. World Reference Base for Soil Resources 2014. International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; IUSS Working Group WRB, Ed.; FAO: Rome, Italy, 2014; ISBN 9789251083697. [Google Scholar]
  42. Saxton, K.E.; Rawls, W.J. Soil Water Characteristic Estimates by Texture and Organic Matter for Hydrologic Solutions. Soil Sci. Soc. Am. J. 2006, 70, 1569–1578. [Google Scholar] [CrossRef] [Green Version]
  43. Sanz, E.; Saa-requejo, A.; Díaz-ambrona, C.H.; Ruiz-ramos, M.; Rodríguez, A.; Iglesias, E.; Esteve, P.; Soriano, B.; Tarquis, A.M. Generalized Structure Functions and Multifractal Detrended Fluctuation Analysis Applied to Vegetation Index Time Series: An Arid Rangeland Study. Entropy 2021, 23, 576. [Google Scholar] [CrossRef]
  44. Vermote, E.F. MOD09A1 MODIS/Terra Surface Reflectance 8-Day L3 Global 500m SIN Grid V006 2015. Available online: https://doi.org/10.5067/MODIS/MOD09A1.006 (accessed on 29 April 2021). [CrossRef]
  45. Vermote, E.F.; El Saleous, N.Z.; Justice, C.O. Atmospheric Correction of MODIS Data in the Visible to Middle Infrared: First Results. Remote Sens. Environ. 2002, 83, 97–111. [Google Scholar] [CrossRef]
  46. Vermote, E.F.; Saleous, N. Operational Atmospheric Correction of MODIS Visible to Middle Infrared Land Surface Data in the Case of an Infinite Lambertian Target. In Earth Science Satellite Remote Sensing: Science and Instruments; Qu, J.J., Gao, W., Kafatos, M., Murphy, R.E., Salomonson, V.V., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; Volume 1, pp. 123–153. ISBN 978-3-540-37293-6. [Google Scholar]
  47. Rouse, J.W., Jr.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with ERTS. In NASA Special Publication; NASA/GSFC: Greenbelt, MD, USA, 1974; Volume 351, p. 309. [Google Scholar]
  48. Kogan, F.N. Global Drought Watch from Space. Bull. Am. Meteorol. Soc. 1997, 78, 621–636. [Google Scholar] [CrossRef]
  49. Wan, Z.; Hook, S.; Hulley, G. MOD11A2 MODIS/Terra Land Surface Temperature/Emissivity 8-Day L3 Global 1km SIN Grid V006. Available online: https://doi.org/10.5067/MODIS/MOD11A2.006 (accessed on 12 May 2021). [CrossRef]
  50. Hargreaves, G.H.; Samani, Z.A. Reference Crop Evapotranspiration from Temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
  51. Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 4th ed.; Wiley: New York, NY, USA, 2013; ISBN 978-1-118-41541-2. [Google Scholar]
  52. Hargreaves, G.H. Simplified Coefficients for Estimating Monthly Solar Radiation in North America and Europe.; Department of Biological and Irrigation Engineering, Utah State University: Logan, UT, USA, 1994. [Google Scholar]
  53. Pei, Z.; Fang, S.; Yang, W.; Wang, L.; Wu, M.; Zhang, Q.; Han, W.; Khoi, D.N. The Relationship between NDVI and Climate Factors at Different Monthly Time Scales: A Case Study of Grasslands in Inner Mongolia, China (1982–2015). Sustainability 2019, 11, 7243. [Google Scholar] [CrossRef] [Green Version]
  54. Asadi Zarch, M.A.; Sivakumar, B.; Sharma, A. Droughts in a Warming Climate: A Global Assessment of Standardized Precipitation Index (SPI) and Reconnaissance Drought Index (RDI). J. Hydrol. 2015, 526, 183–195. [Google Scholar] [CrossRef]
  55. Malik, A.; Kumar, A. Application of Standardized Precipitation Index for Monitoring Meteorological Drought and Wet Conditions in Garhwal Region (Uttarakhand). Arab. J. Geosci. 2021, 14, 800. [Google Scholar] [CrossRef]
  56. Jiang, W.; Wang, L.; Feng, L.; Zhang, M.; Yao, R. Drought Characteristics and Its Impact on Changes in Surface Vegetation from 1981 to 2015 in the Yangtze River Basin, China. Int. J. Climatol. 2020, 40, 3380–3397. [Google Scholar] [CrossRef]
  57. Bento, V.A.; Trigo, I.F.; Gouveia, C.M.; DaCamara, C.C. Contribution of Land Surface Temperature (TCI) to Vegetation Health Index: A Comparative Study Using Clear Sky and All-Weather Climate Data Records. Remote Sens. 2018, 10, 1324. [Google Scholar] [CrossRef] [Green Version]
  58. Bento, V.A.; Gouveia, C.M.; DaCamara, C.C.; Trigo, I.F. A Climatological Assessment of Drought Impact on Vegetation Health Index. Agric. For. Meteorol. 2018, 259, 286–295. [Google Scholar] [CrossRef]
  59. Ali, Z.; Hussain, I.; Faisal, M.; Nazir, H.M.; el Moemen, M.A.; Hussain, T.; Shamsuddin, S. A Novel Multi-Scalar Drought Index for Monitoring Drought: The Standardized Precipitation Temperature Index. Water Resour. Manag. 2017, 31, 4957–4969. [Google Scholar] [CrossRef]
  60. Gidey, E.; Dikinya, O.; Sebego, R.; Segosebe, E.; Zenebe, A. Using Drought Indices to Model the Statistical Relationships between Meteorological and Agricultural Drought in Raya and Its Environs, Northern Ethiopia. Earth Syst. Environ. 2018, 2, 265–279. [Google Scholar] [CrossRef]
  61. Ye, X.C.; Li, Y.L.; Li, X.H.; Xu, C.Y.; Zhang, Q. Investigation of the Variability and Implications of Meteorological Dry/Wet Conditions in the Poyang Lake Catchment, China, during the Period 1960–2010. Adv. Meteorol. 2015, 1–11, 1–11. [Google Scholar] [CrossRef] [Green Version]
  62. Yang, L.; Wylie, B.K.; Tieszen, L.L.; Reed, B.C. An Analysis of Relationships among Climate Forcing and Time-Integrated NDVI of Grasslands over the U.S. Northern and Central Great Plains. Remote Sens. Environ. 1998, 65, 25–37. [Google Scholar] [CrossRef]
  63. Almeida-Ñauñay, A.F.; Benito, R.M.; Quemada, M.; Losada, J.C.; Tarquis, A.M. The Vegetation–Climate System Complexity through Recurrence Analysis. Entropy 2021, 23, 559. [Google Scholar] [CrossRef] [PubMed]
  64. Liu, S.; Zhang, Y.; Cheng, F.; Hou, X.; Zhao, S. Response of Grassland Degradation to Drought at Different Time-Scales in Qinghai Province: Spatio-Temporal Characteristics, Correlation, and Implications. Remote Sens. 2017, 9, 1329. [Google Scholar] [CrossRef] [Green Version]
  65. Wu, T.; Feng, F.; Lin, Q.; Bai, H. Advanced Method to Capture the Time-Lag Effects between Annual NDVI and Precipitation Variation Using RNN in the Arid and Semi-Arid Grasslands. Water 2019, 11, 1789. [Google Scholar] [CrossRef] [Green Version]
  66. Grime, J.P.; Fridley, J.D.; Askew, A.P.; Thompson, K.; Hodgson, J.G.; Bennett, C.R. Long-Term Resistance to Simulated Climate Change in an Infertile Grassland. Proc. Natl. Acad. Sci. USA 2008, 105, 10028–10032. [Google Scholar] [CrossRef] [Green Version]
  67. Wang, J.; Rich, P.M.; Price, K.P. Temporal Responses of NDVI to Precipitation and Temperature in the Central Great Plains, USA. Int. J. Remote Sens. 2003, 24, 2345–2364. [Google Scholar] [CrossRef]
  68. Chen, F.; Weber, K.T. Assessing the Impact of Seasonal Precipitation and Temperature on Vegetation in a Grass-Dominated Rangeland. Rangel. J. 2014, 36, 185. [Google Scholar] [CrossRef]
  69. Fabricante, I.; Oesterheld, M.; Paruelo, J.M. Annual and Seasonal Variation of NDVI Explained by Current and Previous Precipitation across Northern Patagonia. J. Arid Environ. 2009, 73, 745–753. [Google Scholar] [CrossRef]
  70. Wang, X.; Ge, L.; Li, X. Pasture Monitoring Using SAR with COSMO-SkyMed, ENVISAT ASAR, and ALOS PALSAR in Otway, Australia. Remote Sens. 2013, 5, 3611–3636. [Google Scholar] [CrossRef] [Green Version]
  71. Chandrasekar, K.; Sesha Sai, M.V.R.; Roy, P.S.; Dwevedi, R.S. Land Surface Water Index (LSWI) Response to Rainfall and NDVI Using the MODIS Vegetation Index product. Int. J. Remote Sens. 2010, 31, 3987–4005. [Google Scholar] [CrossRef]
  72. Iglesias, A. Climate Changes in the Mediterranean Region: Physical Aspects and Effects on Agriculture. In Mediterranean Climate; Bolle, H.-J., Ed.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 107–111. ISBN 978-3-642-62862-7. [Google Scholar]
  73. Harper, C.W.; Blair, J.M.; Fay, P.A.; Knapp, A.K.; Carlisle, J.D. Increased Rainfall Variability and Reduced Rainfall amount Decreases Soil CO2 Flux in a Grassland Ecosystem. Glob. Chang. Biol. 2005, 11, 322–334. [Google Scholar] [CrossRef]
  74. Bonan, G. Ecological Climatology; Cambridge University Press: Cambridge, UK, 2016; ISBN 9781107339200. [Google Scholar]
  75. Bugalho, M.N.; Abreu, J.M.F. The multifunctional role of grasslands. In Sustainable Mediterranean Grasslands and their Multi-Functions; Options Méditerranéennes: Série A. Séminaires Méditerranéens; Porqueddu, C., Tavares de Sousa, M.M., Eds.; CIHEAM: Zaragoza, Spain; FAO: Zaragoza, Spain; ENMP: Zaragoza, Spain; SPPF: Zaragoza, Spain, 2008; Volume 79, pp. 25–30. [Google Scholar]
  76. Laio, F.; Porporato, A.; Fernandez-Illescas, C.; Rodriguez-Iturbe, I. Plants in Water-Controlled Ecosystems: Active Role in Hydrologic Processes and Response to Water Stress. Adv. Water Resour. 2001, 24, 745–762. [Google Scholar] [CrossRef]
  77. Scanlon, T.M.; Caylor, K.K.; Manfreda, S.; Levin, S.A.; Rodriguez-Iturbe, I. Dynamic Response of Grass Cover to Rainfall Variability: Implications for the Function and Persistence of Savanna Ecosystems. Adv. Water Resour. 2005, 28, 291–302. [Google Scholar] [CrossRef]
  78. Rodriguez-Iturbe, I. Ecohydrology: A Hydrologic Perspective of Climate-Soil-Vegetation Dynamies. Water Resour. Res. 2000, 36, 3–9. [Google Scholar] [CrossRef] [Green Version]
  79. Quemada, M. Predicting Crop Residue Decomposition Using Moisture Adjusted Time Scales. Nutr. Cycl. Agroecosyst. 2005, 70, 283–291. [Google Scholar] [CrossRef]
  80. Marini, G.; Fontana, N.; Mishra, A.K. Investigating Drought in Apulia Region, Italy Using SPI and RDI. Theor. Appl. Climatol. 2019, 137, 383–397. [Google Scholar] [CrossRef]
  81. Mishra, A.K.; Singh, V.P.; Desai, V.R. Drought Characterization: A Probabilistic Approach. Stoch. Environ. Res. Risk Assess. 2009, 23, 41–55. [Google Scholar] [CrossRef]
  82. Zhao, A.; Zhang, A.; Cao, S.; Liu, X.; Liu, J.; Cheng, D. Responses of Vegetation Productivity to Multi-Scale Drought in Loess Plateau, China. Catena 2018, 163, 165–171. [Google Scholar] [CrossRef]
Remotesensing 14 00565 g001 550
Figure 1. Site and climate station’s location, ZSO is on the left and ZGU is on the right. Images were obtained from the Mosaic of current orthophotos corresponding to sheet 0509 of the MTN50 in Spain during the years 2017, 2018. Pixel plot size: 250 × 250 m2, Pixel orthophotographs size: 0.05 × 0.05 m2. RGB composition. Blue crosses are the locations of the climate station locations and red pinpoints are the soil trench locations. Adapted from: [37].
Figure 1. Site and climate station’s location, ZSO is on the left and ZGU is on the right. Images were obtained from the Mosaic of current orthophotos corresponding to sheet 0509 of the MTN50 in Spain during the years 2017, 2018. Pixel plot size: 250 × 250 m2, Pixel orthophotographs size: 0.05 × 0.05 m2. RGB composition. Blue crosses are the locations of the climate station locations and red pinpoints are the soil trench locations. Adapted from: [37].
Remotesensing 14 00565 g001
Remotesensing 14 00565 g002 550
Figure 2. Vegetation Condition Index (VCI) (a) and Temperature Condition Index (TCI) (b) statistics from 2001 to 2020, along the year in each zone: ZGU = Guadalix de la Sierra, ZSO = Soto del Real. The Y-axis shows a box and whisker plot of VCI and TCI on each date. The error bars indicate the maximum and minimum values; horizontal lines indicate the median value, and the box indicates the 25% and 75% percentiles. Q1, Q2, Q3 and Q4 are the quarters of the year.
Figure 2. Vegetation Condition Index (VCI) (a) and Temperature Condition Index (TCI) (b) statistics from 2001 to 2020, along the year in each zone: ZGU = Guadalix de la Sierra, ZSO = Soto del Real. The Y-axis shows a box and whisker plot of VCI and TCI on each date. The error bars indicate the maximum and minimum values; horizontal lines indicate the median value, and the box indicates the 25% and 75% percentiles. Q1, Q2, Q3 and Q4 are the quarters of the year.
Remotesensing 14 00565 g002
Remotesensing 14 00565 g003 550
Figure 3. VHI vegetation index statistics, from 2001 to 2020, throughout the year in each zone: ZGU = Guadalix de la Sierra, ZSO = Soto del Real. The Y-axis shows a box-and-whisker plot of VHI (Vegetation Health Index) on each date. The error bars indicate the maximum and minimum values; horizontal lines indicate the median values, and the box indicates the 25% and 75% percentiles. Q1, Q2, Q3 and Q4 are the quarters of the year.
Figure 3. VHI vegetation index statistics, from 2001 to 2020, throughout the year in each zone: ZGU = Guadalix de la Sierra, ZSO = Soto del Real. The Y-axis shows a box-and-whisker plot of VHI (Vegetation Health Index) on each date. The error bars indicate the maximum and minimum values; horizontal lines indicate the median values, and the box indicates the 25% and 75% percentiles. Q1, Q2, Q3 and Q4 are the quarters of the year.
Remotesensing 14 00565 g003
Remotesensing 14 00565 g004 550
Figure 4. Accumulated 8-day precipitation (PCP) (a) and temperature (TEMP) (b) statistics throughout the year, including from 2001 to 2020, in each zone: ZGU = Guadalix de la Sierra, ZSO = Soto del Real. The Y-axis shows a box and whisker plot of (a) PCP_ZGU, PCP_ZSO, and (b) TEMP_ZGU and TEMP_ZSO on each date. The error bars indicate the maximum and minimum values, the horizontal lines indicate the median values, and the box indicates the 25% and 75% percentiles. Q1, Q2, Q3 and Q4 are the quarters of the year.
Figure 4. Accumulated 8-day precipitation (PCP) (a) and temperature (TEMP) (b) statistics throughout the year, including from 2001 to 2020, in each zone: ZGU = Guadalix de la Sierra, ZSO = Soto del Real. The Y-axis shows a box and whisker plot of (a) PCP_ZGU, PCP_ZSO, and (b) TEMP_ZGU and TEMP_ZSO on each date. The error bars indicate the maximum and minimum values, the horizontal lines indicate the median values, and the box indicates the 25% and 75% percentiles. Q1, Q2, Q3 and Q4 are the quarters of the year.
Remotesensing 14 00565 g004
Remotesensing 14 00565 g005 550
Figure 5. SVHI (Standardised Vegetation Index), SPI (Standardised Precipitation Index), and SPEI (Standardised Precipitation Evapotranspiration Index) time series at different time scales in ZGU (Guadalix de la Sierra). The red dotted lines mark ±1 values.
Figure 5. SVHI (Standardised Vegetation Index), SPI (Standardised Precipitation Index), and SPEI (Standardised Precipitation Evapotranspiration Index) time series at different time scales in ZGU (Guadalix de la Sierra). The red dotted lines mark ±1 values.
Remotesensing 14 00565 g005
Remotesensing 14 00565 g006 550
Figure 6. SVHI (Standardised Vegetation Index), SPI (Standardised Precipitation Index), and SPEI (Standardised Precipitation Evapotranspiration Index) time series at different time scales in ZSO (Soto del Real). The red dotted lines mark ±1 values.
Figure 6. SVHI (Standardised Vegetation Index), SPI (Standardised Precipitation Index), and SPEI (Standardised Precipitation Evapotranspiration Index) time series at different time scales in ZSO (Soto del Real). The red dotted lines mark ±1 values.
Remotesensing 14 00565 g006
Remotesensing 14 00565 g007 550
Figure 7. Correlation between meteorological drought indexes (SPI and SPEI) and standardised vegetation index (SVHI) at different time scales (M: Monthly, Q: Quarterly) in ZGU (Guadalix de la Sierra) and ZSO (Soto del Real). The alpha corresponds to the α value in the VHI equation in Table 2.
Figure 7. Correlation between meteorological drought indexes (SPI and SPEI) and standardised vegetation index (SVHI) at different time scales (M: Monthly, Q: Quarterly) in ZGU (Guadalix de la Sierra) and ZSO (Soto del Real). The alpha corresponds to the α value in the VHI equation in Table 2.
Remotesensing 14 00565 g007
Table
Table 1. Soil horizons and zone characteristics of both study areas. ZGU = Guadalix de la Sierra, ZSO = Soto del Real. Adapted from: [37,40].
Table 1. Soil horizons and zone characteristics of both study areas. ZGU = Guadalix de la Sierra, ZSO = Soto del Real. Adapted from: [37,40].
ZGUZSO
AThickness (cm)5AuThickness (cm)3
Colour10YR3/4Colour10YR3/2
Silt (%)29Silt (%)19
Coarse Sand (%)12Coarse Sand (%)37
Fine Sand (%)25Fine Sand (%)38
Clay (%)34Clay (%)6
Bulk Density (g/cm3)1.2Bulk Density (g/cm3)1.5
Water Holding Capacity (%)13.3Water Holding Capacity (%)11.7
ABThickness (cm)20Au2Thickness (cm)12
Colour10YR3/4Colour10YR4/4
Silt (%)22Silt (%)18
Coarse Sand (%)24Coarse Sand (%)30
Fine Sand (%)13Fine Sand (%)47
Clay (%)41Clay (%)5
Bulk Density (g/cm3)1.2Bulk Density (g/cm3)1.7
Water Holding Capacity (%)12.6Water Holding Capacity (%)11.1
Zone
attributes		Slope (%)11.7Zone
attributes		Slope (%)4.7
Height (m)820Height (m)958
Precipitation (mm)576Precipitation (mm)550
Temperature (°C)12.6Temperature (°C)13.6
Table
Table 2. Selected vegetation-drought indices used in this study and their reference.
Table 2. Selected vegetation-drought indices used in this study and their reference.
IndexEquationReference
Normalized difference vegetation index (NDVI) 1 N D V I = NIR   860   nm − R E D 660   nm NIR   860   nm + R E D 660   nm   [47]
Vegetation condition index (VCI) V C I = 100   ∗   N D V I i − N D V I m i n N D V I m a x − N D V I m i n [48]
Temperature condition index (TCI) 2 T C I = 100   ∗   L S T m a x − L S T i L S T m a x − L S T m i n [48]
Vegetation health index (VHI) 3 V H I = α   ∗   V C I + 1 − α   ∗   T C I [48]
1 NIR is the near-infrared reflectance (860 nm), and RED is the red reflectance (660 nm). 2 L S T i is the LST value in each date. 3 α is a coefficient that depends on the dry conditions of the area.
Table
Table 3. Classification of meteorological and agricultural drought indicators using the index value (IV). The threshold values of IV are adapted from [59,60,61].
Table 3. Classification of meteorological and agricultural drought indicators using the index value (IV). The threshold values of IV are adapted from [59,60,61].
SPI, SPEI and SVHIVHI
Extremely droughtIV < −2IV < 10
Severe drought−2 < IV < −1.510 < IV < 20
Moderate drought−1.5 < IV < −120 < IV < 35
No droughtIV > −1IV > 35
Table
Table 4. Pearson series correlation values between VHI (Standardised Vegetation Index) and SVHI with SPI (Standardised Precipitation Index) and SPEI (Standardised Precipitation-Evapotranspiration Index) at different time scales. M is the monthly time scale; Q is the quarterly time scale.
Table 4. Pearson series correlation values between VHI (Standardised Vegetation Index) and SVHI with SPI (Standardised Precipitation Index) and SPEI (Standardised Precipitation-Evapotranspiration Index) at different time scales. M is the monthly time scale; Q is the quarterly time scale.
ZoneScaleVHI-SPIVHI-SPEISVHI-SPISVHI-SPEI
ZGUM0.140.130.400.42
Q0.300.300.640.65
ZSOM0.130.140.410.43
Q0.280.300.690.71
Table
Table 5. Correlation values between SVHI (Standardised Vegetation Health Index), SPI (Standardised Precipitation Index), and SPEI (Standardised Precipitation Evapotranspiration at different time frames in both zones: ZGU (Guadalix de la Sierra) and ZSO (Soto del Real). M is the monthly scale; Q is the quarterly scale.
Table 5. Correlation values between SVHI (Standardised Vegetation Health Index), SPI (Standardised Precipitation Index), and SPEI (Standardised Precipitation Evapotranspiration at different time frames in both zones: ZGU (Guadalix de la Sierra) and ZSO (Soto del Real). M is the monthly scale; Q is the quarterly scale.
SVHI-SPI
JanuaryFebruaryMarchAprilMayJuneJulyAugustSeptemberOctoberNovemberDecember
ZGUM0.190.330.630.140.630.340.370.500.590.070.280.66
Q0.510.690.660.72
ZSOM0.180.350.720.300.690.470.050.540.640.320.360.27
Q0.720.800.560.69
SVHI-SPEI
JanuaryFebruaryMarchAprilMayJuneJulyAugustSeptemberOctoberNovemberDecember
ZGUM0.210.210.640.170.690.430.470.450.670.120.290.66
Q0.480.700.690.73
ZSOM0.180.260.730.320.780.570.240.500.660.300.400.28
Q0.680.830.610.74
Table
Table 6. Drought classified data frequency of drought index (SPI, SPEI), non-standardised vegetation health index (VHI), and standardised vegetation health index (SVHI) in both zones, Guadalix de la Sierra (ZGU) and Soto del Real (ZSO). M is the monthly scale. Q is the quarterly scale.
Table 6. Drought classified data frequency of drought index (SPI, SPEI), non-standardised vegetation health index (VHI), and standardised vegetation health index (SVHI) in both zones, Guadalix de la Sierra (ZGU) and Soto del Real (ZSO). M is the monthly scale. Q is the quarterly scale.
ZoneScaleClass DroughtSPISPEIVHISVHI
ZGUMNo drought202201171205
Moderate drought17304819
Severe drought129209
Extremely drought9017
TOTAL240240240240
QNo drought71685768
Moderate drought69217
Severe drought2222
Extremely drought1103
TOTAL80808080
ZSOMNo drought203193162205
Moderate drought17363622
Severe drought1311317
Extremely drought70116
TOTAL240240240240
QNo drought73654966
Moderate drought4121510
Severe drought22161
Extremely drought1103
TOTAL80808080
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Almeida-Ñauñay, A.F.; Villeta, M.; Quemada, M.; Tarquis, A.M. Assessment of Drought Indexes on Different Time Scales: A Case in Semiarid Mediterranean Grasslands. Remote Sens. 2022, 14, 565. https://doi.org/10.3390/rs14030565

AMA Style

Almeida-Ñauñay AF, Villeta M, Quemada M, Tarquis AM. Assessment of Drought Indexes on Different Time Scales: A Case in Semiarid Mediterranean Grasslands. Remote Sensing. 2022; 14(3):565. https://doi.org/10.3390/rs14030565

Chicago/Turabian Style

Almeida-Ñauñay, Andres F., María Villeta, Miguel Quemada, and Ana M. Tarquis. 2022. "Assessment of Drought Indexes on Different Time Scales: A Case in Semiarid Mediterranean Grasslands" Remote Sensing 14, no. 3: 565. https://doi.org/10.3390/rs14030565

APA Style

Almeida-Ñauñay, A. F., Villeta, M., Quemada, M., & Tarquis, A. M. (2022). Assessment of Drought Indexes on Different Time Scales: A Case in Semiarid Mediterranean Grasslands. Remote Sensing, 14(3), 565. https://doi.org/10.3390/rs14030565

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop