Estimating the Near-Ground PM2.5 Concentration over China Based on the CapsNet Model during 2018–2020
Abstract
:1. Introduction
- (1)
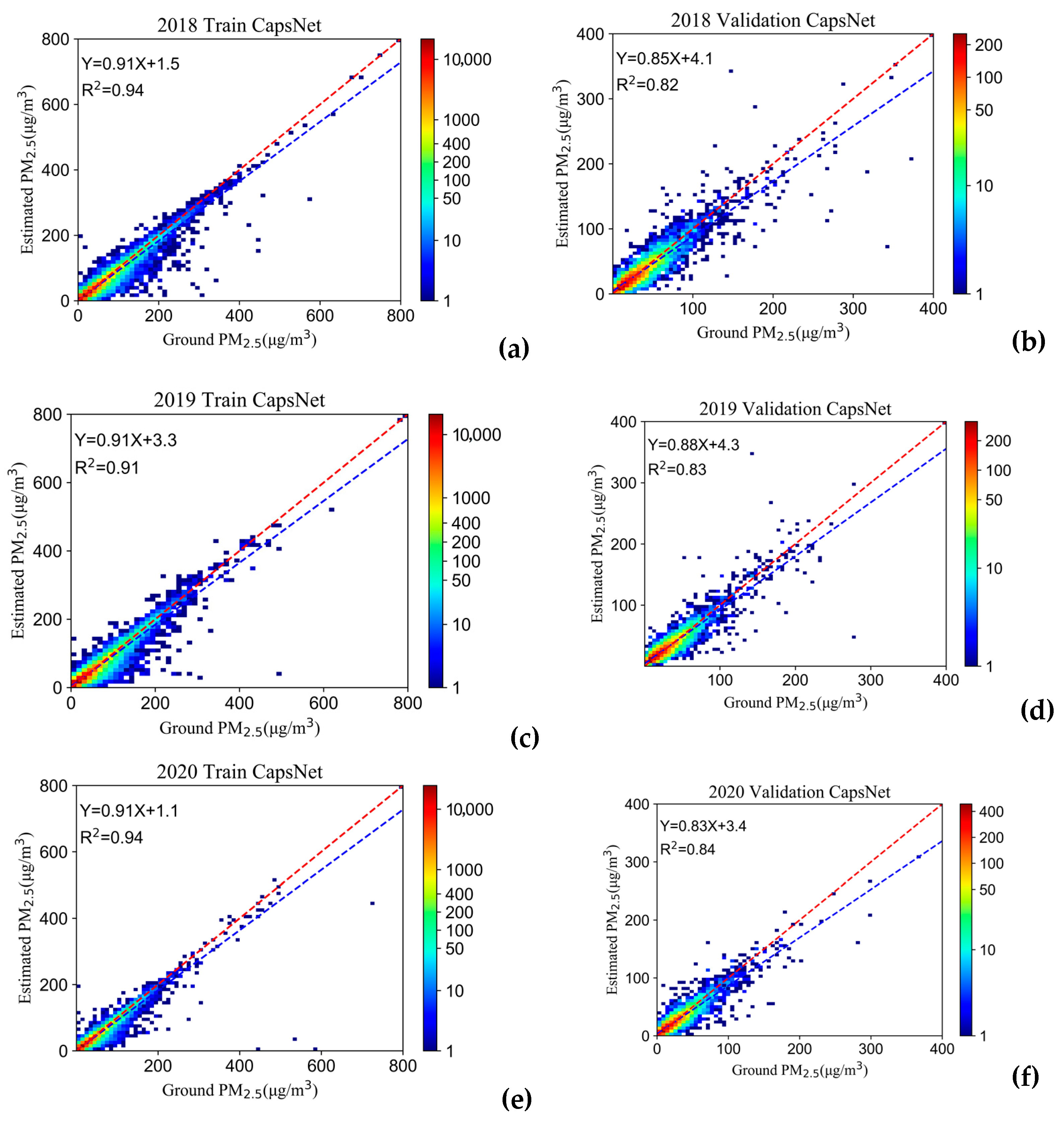
- We proposed a CapsNet model that introduced the capsule structure and dynamic routing algorithm to estimate daily PM2.5 concentrations over China. The longitude (LON) and latitude (LAT) of pixels were used as input parameters to verify whether it is helpful to improve the accuracy of the model. The coefficient of determination (R2), root mean square error (RMSE), mean relative error (MRE), and mean absolute error (MAE) are used as the evaluation metrics.
- (2)
- To evaluate the CapsNet proposed by us effectively, the DNN model was executed, and the LON and LAT were also included in the DNN model. We discussed the accuracy of CaspNet and DNN in both the cold season and warm season, and the results indicate that CaspNet performs better. Therefore, we used CaspNet to estimate daily PM2.5 concentrations and analyzed the characteristics of PM2.5 concentration variations.
- (3)
- We examined the different advanced capsule layers in CaspNet, which influence the accuracy of PM2.5 estimation. Multiple capsules and a single weight are better when considering the accuracy and operating efficiency. Moreover, we verified the accuracy of the CaspNet model in different regions.
2. Methodology
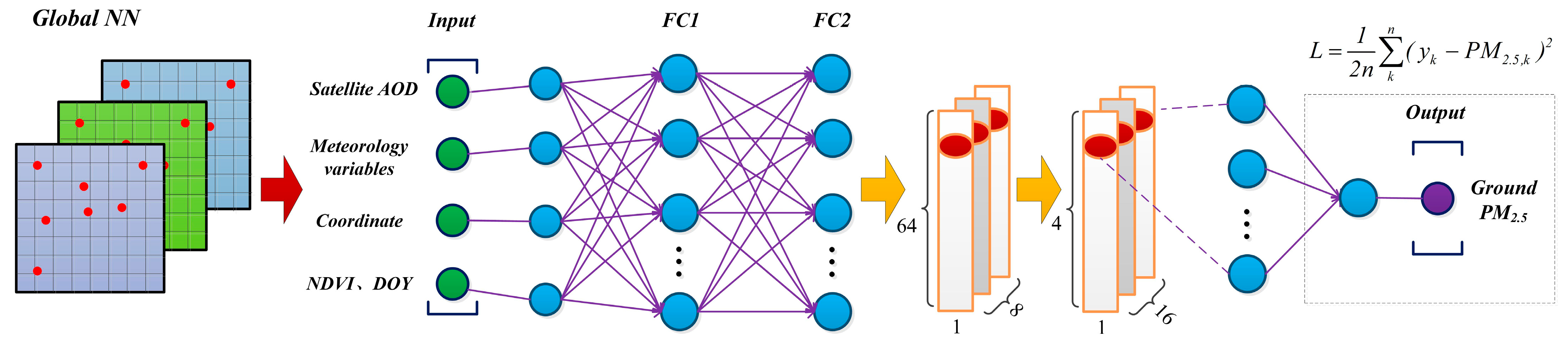
2.1. CapsNet Structure
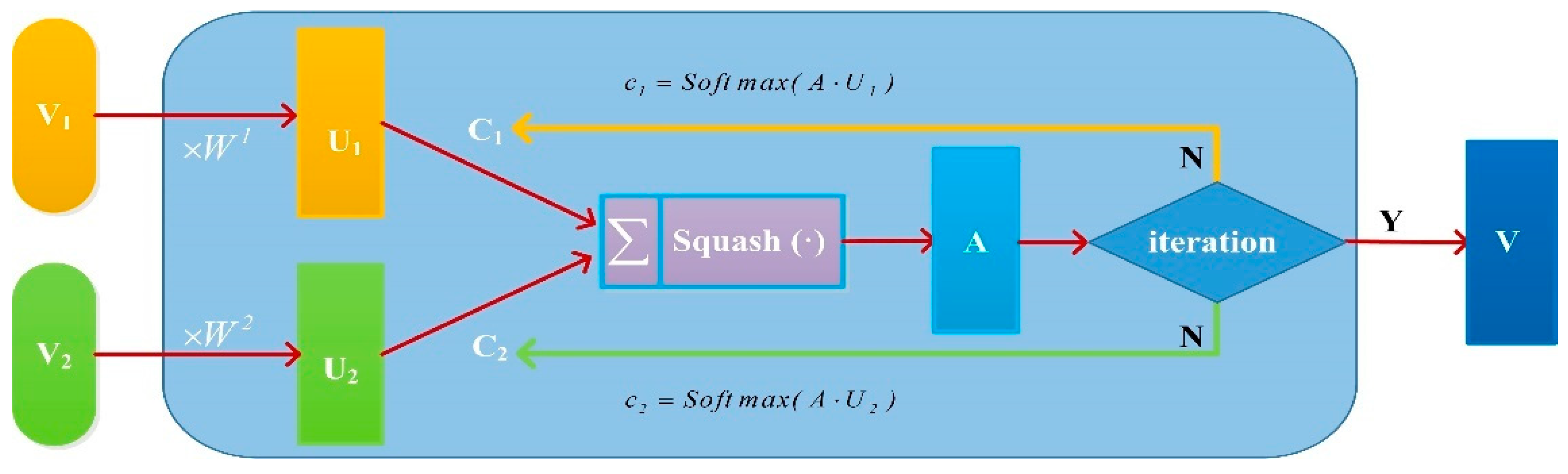
2.2. The Dynamic Routing Algorithm
2.3. Parameters Setting
2.4. Evaluation Metric
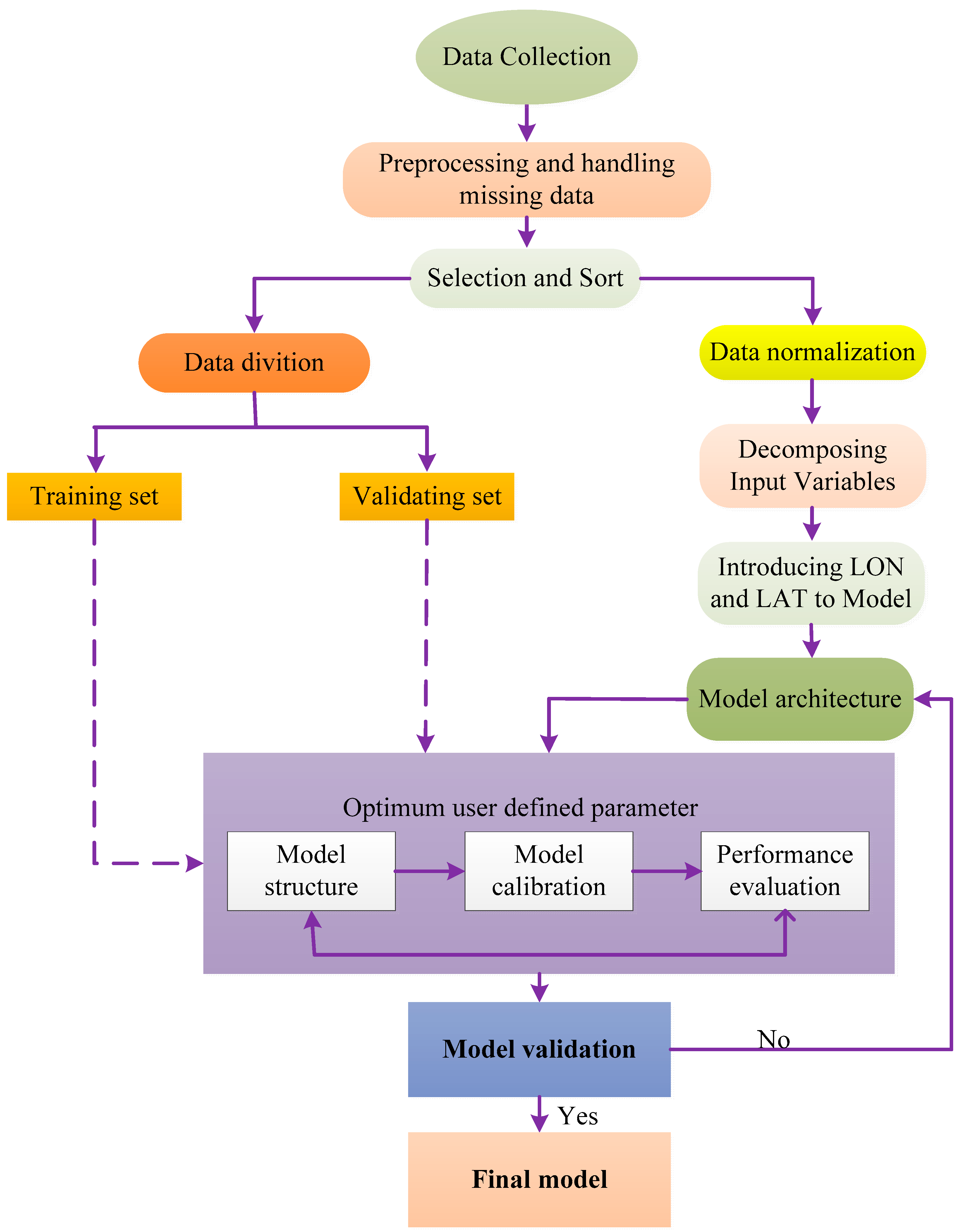
3. Data and Preprocessing
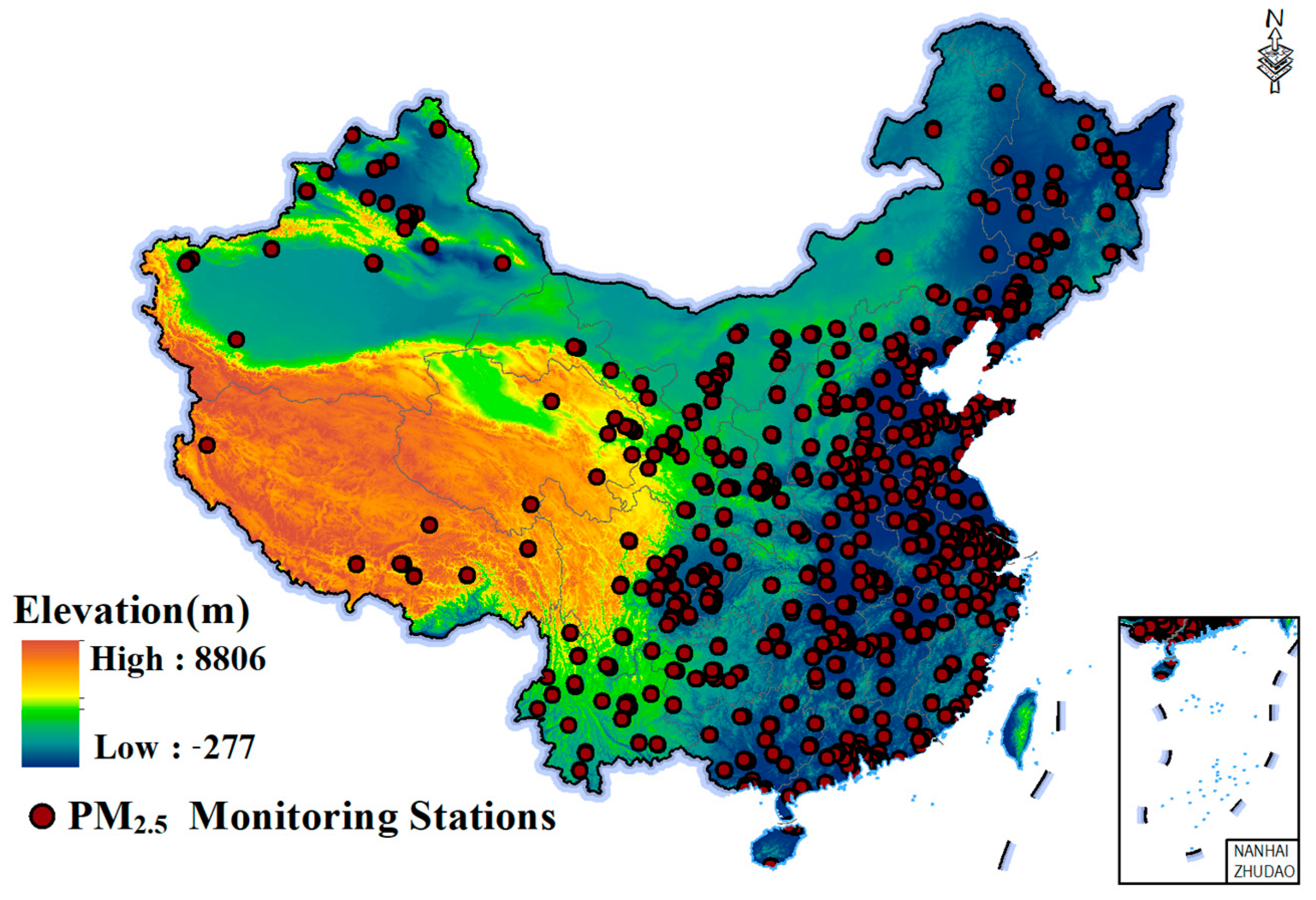
3.1. The Ground-Based PM2.5
3.2. AOD Products
3.3. European Centre for Medium-Range Weather Forecasts Data and Other Auxiliary Data
3.4. Data Preprocessing
4. Experiment Analysis
4.1. Experimental Results
4.1.1. Normalization Methods
4.1.2. Parameter Validation
4.1.3. Accuracy Validation
4.2. Model Comparison
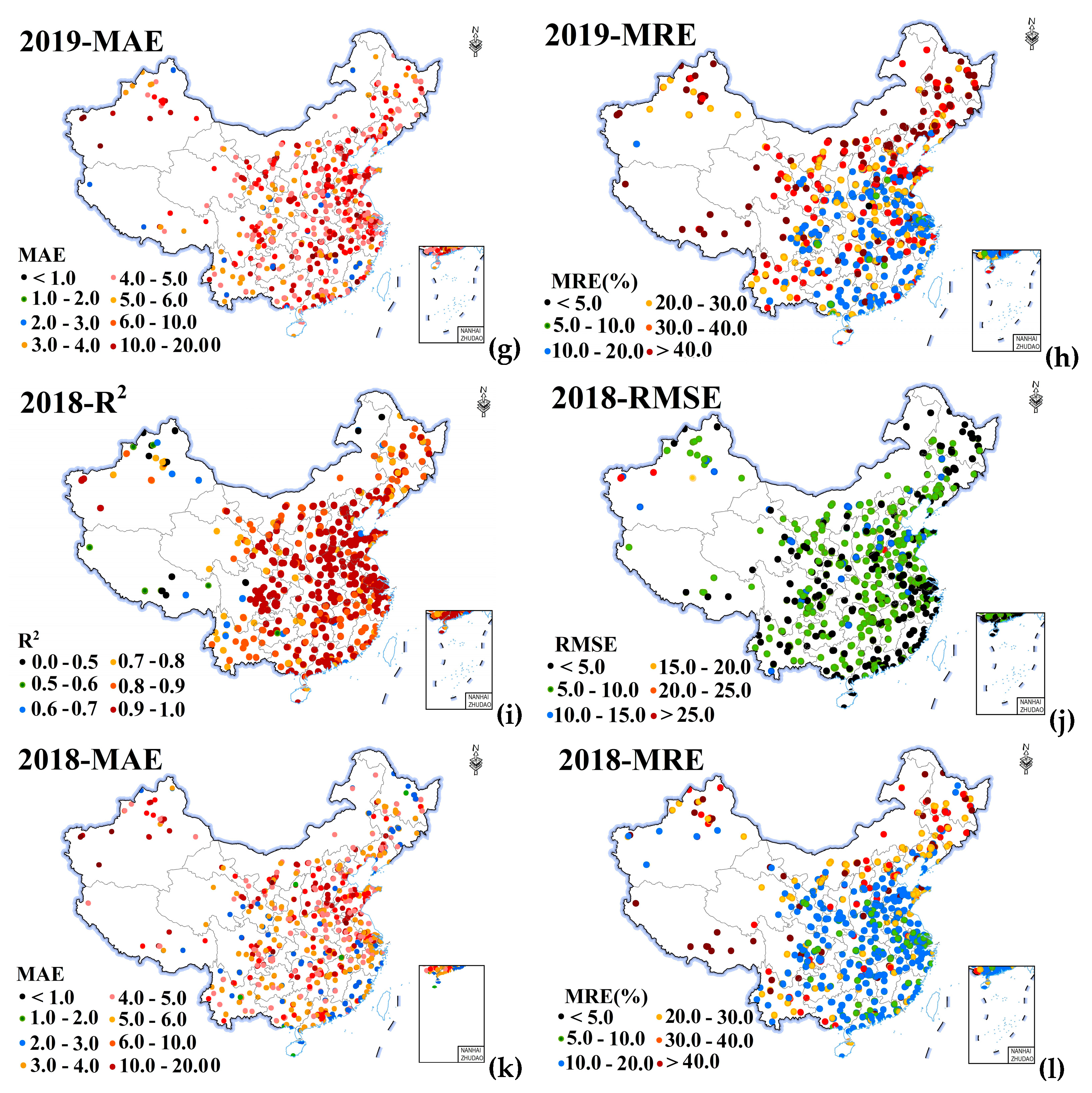
4.3. Spatiotemporal Patterns of PM2.5
4.3.1. Seasonal Distribution
4.3.2. Annual Distribution
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Crouse, D.L.; Peters, P.A.; Donkelaar, A.V.; Goldberg, M.S.; Villeneuve, P.J.; Brion, O.; Khan, S.; Atari, D.O.; Jerrett, M.; Pope, C.A.; et al. Risk of Nonaccidental and Cardiovascular Mortality in Relation to Long-term Exposure to Low Concentrations of Fine Particulate Matter: A Canadian National-Level Cohort Study. Environ. Health Perspect. 2012, 120, 708–714. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.P.; Yin, J.H.; Zang, L.; Zhao, M.D. Stacking machine learning model for estimating hourly PM2.5 in China based on Himawari 8 aerosol optical depth data. Sci. Total Environ. 2019, 697, 134021. [Google Scholar] [CrossRef]
- Wei, J.; Huang, W.; Li, Z.P.; Xue, Y.P.; Peng, Y.R.; Sun, L.; Cribb, M. Estimating 1-km-resolution PM2.5 concentrations across China using the space-time random forest approach. Remote Sens. Environ. 2019, 231, 111221. [Google Scholar] [CrossRef]
- Guo, B.; Zhang, D.M.; Pei, L.; Su, Y.; Wang, X.X.; Bian, Y.; Zhang, D.H.; Yao, W.Q.; Zhou, Z.X.; Guo, L.Y. Estimating PM2.5 concentrations via random forest method using satellite, auxiliary, and ground-level station dataset at multiple temporal scales across China in 2017. Sci. Total Environ. 2021, 778, 146228. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.Y.; Zhang, S.J.; Wu, X.; Guo, X.; Han, L.; Liu, H.; Wu, Y.; Hao, J.M. Air quality and health impacts from using ethanol blended gasoline fuels in China. Atoms. Environ. 2020, 228, 117396. [Google Scholar] [CrossRef]
- Zhang, T.H.; Zhu, Z.M.; Gong, W.; Zhu, Z.R.; Sun, K.; Wang, L.C.; Huang, L.C.; Mao, X.F.; Shen, H.F.; Li, Z.W.; et al. Estimation of ultrahigh resolution PM2.5 concentrations in urban areas using 160m Gaofen-1 AOD retrievals. Remote Sens. Environ. 2018, 216, 91–104. [Google Scholar] [CrossRef]
- Hutchison, K.D.; Smith, S.; Faruqui, S.J. Correlating MODIS aerosol optical thickness data with ground-based PM2.5 observations across Texas for use in a real-time air quality prediction system. Atoms. Environ. 2005, 39, 7190–7203. [Google Scholar] [CrossRef]
- Yao, F.; Si, M.; Li, W.; Wu, J. A multidimensional comparison between MODIS and VIIRS AOD in estimating ground-level PM2.5 concentrations over a heavily polluted region in China. Sci. Total Environ. 2018, 618, 819–828. [Google Scholar] [CrossRef]
- Sreekanth, V.; Mahesh, B.; Niranjan, K. Satellite Remote Sensing of Fine Particulate air pollutants over Indian Mega Cities. Adv. Space Res. 2017, 60, 2268–2276. [Google Scholar] [CrossRef]
- Ma, Z.; Hu, X.; Sayer, A.M.; Levy, R.; Zhang, Q.; Xue, Y.; Tong, S.; Bi, J.; Huang, L.; Liu, Y. Satellite-Based Spatiotemporal Trends in PM2.5 Concentrations: China, 2004–2013. Environ. Health Perspect. 2016, 124, 184–192. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Li, Z. Remote sensing of atmospheric fine particulate matter (PM2.5) mass concentration near the ground from satellite observation. Remote Sens. Environ. 2015, 160, 252–262. [Google Scholar] [CrossRef]
- Lee, H.J.; Liu, Y.; Coull, B.A.; Schwartz, J.; Koutrakis, P. A novel calibration approach of MODIS AOD data to predict PM2.5 concentrations. Atmos. Chem. Phys. 2011, 11, 9769–9795. [Google Scholar] [CrossRef] [Green Version]
- You, W.; Zang, Z.; Pan, X.; Zhang, L.; Chen, D. Estimating PM2.5 in Xi’an, China using aerosol optical depth: A comparison between the MODIS and MISR retrieval models. Sci. Total Environ. 2015, 505, 1156–1165. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Franklin, M.; Kahn, R.; Koutrakis, P. Using aerosol optical thickness to predict ground-level PM2.5 concentrations in the St. Louis area: A comparison between MISR and MODIS. Remote Sens. Environ. 2007, 107, 33–44. [Google Scholar] [CrossRef]
- Liu, Y.; Paciorek, C.J.; Koutrakis, P. Estimating regional spatial and temporal variability of PM2.5 concentrations using satellite data, meteorology, and land use information. Environ. Health Perspect. 2009, 117, 886. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Hu, H. Improving Satellite-Driven PM2.5 Models with VIIRS Nighttime Light Data in the Beijing–Tianjin–Hebei Region, China. Remote Sens. 2017, 9, 908. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Aegerter, C.; Xu, X.; Szykman, J.J. Potential application of VIIRS Day/Night Band for monitoring nighttime surface PM2.5 air quality from space. Atmos. Environ. 2016, 124, 55–63. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Mao, F.; Du, L.; Pan, Z.; Gong, W.; Fang, S. Deriving Hourly PM2.5 Concentrations from Himawari-8 AODs over Beijing–Tianjin–Hebei in China. Remote Sens. 2017, 9, 858. [Google Scholar] [CrossRef] [Green Version]
- Mao, F.Y.; Hong, J.; Min, Q.L.; Gong, W.; Zang, L.; Yin, J.H. Estimation hourly full-coverage PM2.5 over China base on TOA reflectance data from the Fengyun-4A satellite. Environ. Pollut. 2021, 270, 116119. [Google Scholar] [CrossRef]
- Liu, Y.; Park, R.J.; Jacob, D.J.; Qinbin Li, Q.B.; Vasu Kilaru, K.; Sarnat, J. Mapping annual mean ground-level PM2.5 concentrations using Multiangle Imaging Spectroradiometer aerosol optical thickness over the contiguous United States. J. Geophys. Res. Atmos. 2004, 109, D22206. [Google Scholar]
- Donkelaar, A.V.; Martin, R.V.; Park, R.J. Estimating ground-level PM2.5 using aerosol optical depth determined from satellite remote sensing. J. Geophys. Res. Atmos. 2006, 111, 5049–5066. [Google Scholar]
- Wang, Z.F.; Chen, L.F.; Tao, J.H.; Zhang, Y.; Su, L. Satellite-based estimation of regional particulate matter (PM) in Beijing using vertical-and-RH correcting method. Remote Sens. Environ. 2010, 114, 50–63. [Google Scholar] [CrossRef]
- Guo, J.P.; Zhang, X.Y.; Che, H.Z.; Gong, S.L.; An, X.Q.; Cao, C.X.; Guang, J.; Zhang, H.; Wang, Y.Q.; Zhang, X.C.; et al. Correlation between concentrations and aerosol optical depth in eastern China. Atmos. Environ. 2009, 43, 5876–5886. [Google Scholar] [CrossRef]
- Hu, X.; Waller, L.A.; Al-Hamdan, M.Z.; Crosson, W.L.; Estesjr, M.G.; Estes, S.M.; Quattrochi, D.A.; Sarnat, J.A.; Liu, Y. Estimating ground-level PM2.5 concentrations in the southeastern U.S. using geographically weighted regression. Environ. Res. 2013, 121, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.X.; Tang, Q.H.; Gong, D.Y.; Zhang, Z.Y. Estimating ground-level PM2.5 concentrations in Beijing using a satellite-based geographically and temporally weighted regression model. Remote Sens. Environ. 2017, 198, 140–149. [Google Scholar] [CrossRef]
- Liu, Y.; Sarnat, J.A.; Kilaru, V.; Jacob, D.J.; Koutrakis, P. Estimating ground-level PM2.5 in the eastern United States using satellite remote sensing. Environ. Sci. Technol. 2005, 39, 3269. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koelemeijer, R.; Homan, C.D.; Matthijsen, J. Comparison of spatial and temporal variations of aerosol optical thickness and particulate matter over Europe. Atoms. Environ. 2006, 40, 5304–5315. [Google Scholar] [CrossRef]
- Chu, D.A.; Tsai, T.C.; Chen, J.P.; Cheng, S.C.; Jeng, Y.J.; Chiang, W.L.; Lin, N.H. Interpreting aerosol lidar profiles to better estimate surface PM2.5 for columnar AOD measurements. Atoms. Environ. 2013, 79, 172–187. [Google Scholar] [CrossRef]
- Lin, C.Q.; Li, Y.; Yuan, Z.B.; Lau, A.K.H.; Li, C.C.; Fung, J.C.H. Using satellite remote sensing data to estimate the high-resolution distribution of ground-level PM2.5. Remote Sens. Environ. 2015, 156, 117–128. [Google Scholar] [CrossRef]
- Sun, Y.B.; Zeng, Q.L.; Geng, B.; Lin, X.W.; Sude, B.; Chenl, L.F. Deep learning architecture for estimating hourly ground-level PM2.5 using satellite remote sensing. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1343–1347. [Google Scholar] [CrossRef]
- Li, L.F.; Franklin, M.; Girguis, M.; Lurmann, F.; Wu, J.; Pavlovic, N.; Breton, C.; Gilliland, F.; Habre, R. Spatiotemporal Imputation of MAIAC AOD Using Deep Learning with Downscaling. Remote Sens. Environ. 2020, 237, 111584. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.F.; Li, T.W.; Yuan, Q.Q.; Zhang, L.P. Estimating Regional Ground-Level PM2.5 Directly from Satellite Top-Of-Atmosphere Reflectance Using Deep Belief Networks. J. Geophys. Res. Atmos. 2018, 123, 13875–13886. [Google Scholar] [CrossRef] [Green Version]
- Hong, D.F.; Gao, L.R.; Yao, J.; Zhang, B.; Plaza, A.; Chanussot, J. Graph Convolutional Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5966–5978. [Google Scholar] [CrossRef]
- Hong, D.F.; Gao, L.R.; Yokoya, N.; Yao, J.; Chanussot, J.; Du, Q.; Zhang, B. More Diverse Means Better: Multimodal Deep Learning Meeets Remote-Sensing Imagery Classificaion. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4340–4354. [Google Scholar] [CrossRef]
- Sabour., S.; Frosst, N.; Hinton, G. Dynamic routing between capsules. In Proceedings of the Neural Information Processing Systems (NIPS Proceeding), Long Beach, CA, USA, 4–9 December 2017; pp. 3856–3866. [Google Scholar]
- Afshar, P.; Mohammadi, A.; Plataniotis, K.N. Brain tumor type classification via capsule networks. In Proceedings of the 25th IEEE International Conference on Image Processing, Athens, Greece, 7–10 October 2018; pp. 3129–3133. [Google Scholar]
- Levy, R.C.; Mattoo, S.; Munchak, L.A.; Remer, L.A.; Sayer, A.M.; Patadia, F.; Hsu, N.C. The Collection 6 MODIS aerosol products over land and ocean. Atmos. Meas. Tech. 2013, 6, 2989–3034. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.Y.; Wang, Y.X.; Zhang, K.; Dong, W.H.; Lv, B.; Bai, Y.Q. Daily estimation of ground-level PM2.5 concentrations over Beijing using 3 km resolution MODIS AOD. Environ. Sci. Technol. 2015, 49, 12280–12288. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, N.; Zou, B.; Feng, H.H.; Wang, W.; Tang, Y.Q.; Liang, Y. Evaluation and comparison of multiangle implementation of the atmospheric correction algorithm, Dark Target, and Deep Blue aerosol products over China. Atmos. Chem. Phys. 2019, 19, 8243–8268. [Google Scholar] [CrossRef] [Green Version]
- Lyapustin, A.; Wang, Y.; Laszlo, I.; Kahn, R.; Korkin, S.; Remer, L.; Levy, R.; Reid, J.S. Multiangle implementation of atmospheric correction (MAIAC): 2. Aerosol algorithm. J. Geophys. Res. Atmos. 2011, 116, 1–15. [Google Scholar] [CrossRef]
- Tao, M.H.; Wang, J.; Li, R.; Wang, L.L.; Wang, L.C.; Wang, Z.F.; Tao, J.H.; Chen, H.Z.; Chen, L.F. Performance of MODIS high-resolution MAIAC aerosol algorithm in China: Characterization and limitation. Atmos. Environ. 2019, 213, 159–169. [Google Scholar] [CrossRef]
- Zhi, X.; Xu, H.M. Comparative analysis of free atmospheric temperature between three reanalysis datasets and radiosonde dataset in China: Annual mean characteristic. Trans. Atmos. Sci. 2013, 36, 77–87. [Google Scholar]
- Song, Z.G.; Bai, Y.; Wang, D.F.; Li, T.; He, X.Q. Satellite Retrieval of Air Pollution Changes in Central and Eastern China during COVID-19 Lockdown Based on a Machine Learning Model. Remote Sens. 2021, 13, 2525. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, J.; Du, R.G.; Teng, X.M.; Hu, R.; Yuan, Q.; Tang, S.S.; Ren, C.H.; Huang, X.; Xu, L.; et al. Chemistry of atmospheric fine particles during the COVID-19 pandemic in a megacity of Eastern China. Geophys. Res. Lett. 2021, 48, 2020GL091611. [Google Scholar] [CrossRef] [PubMed]


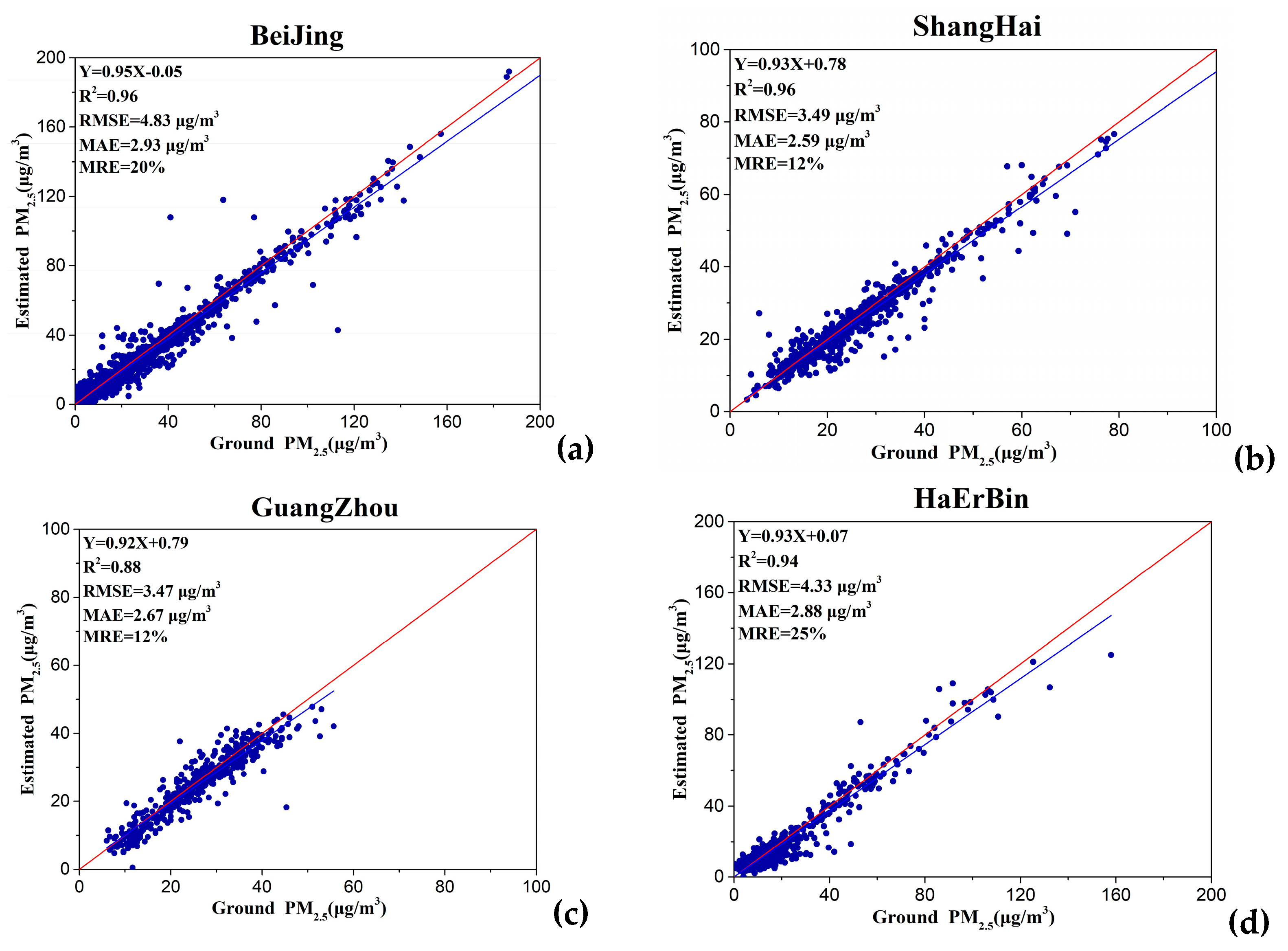
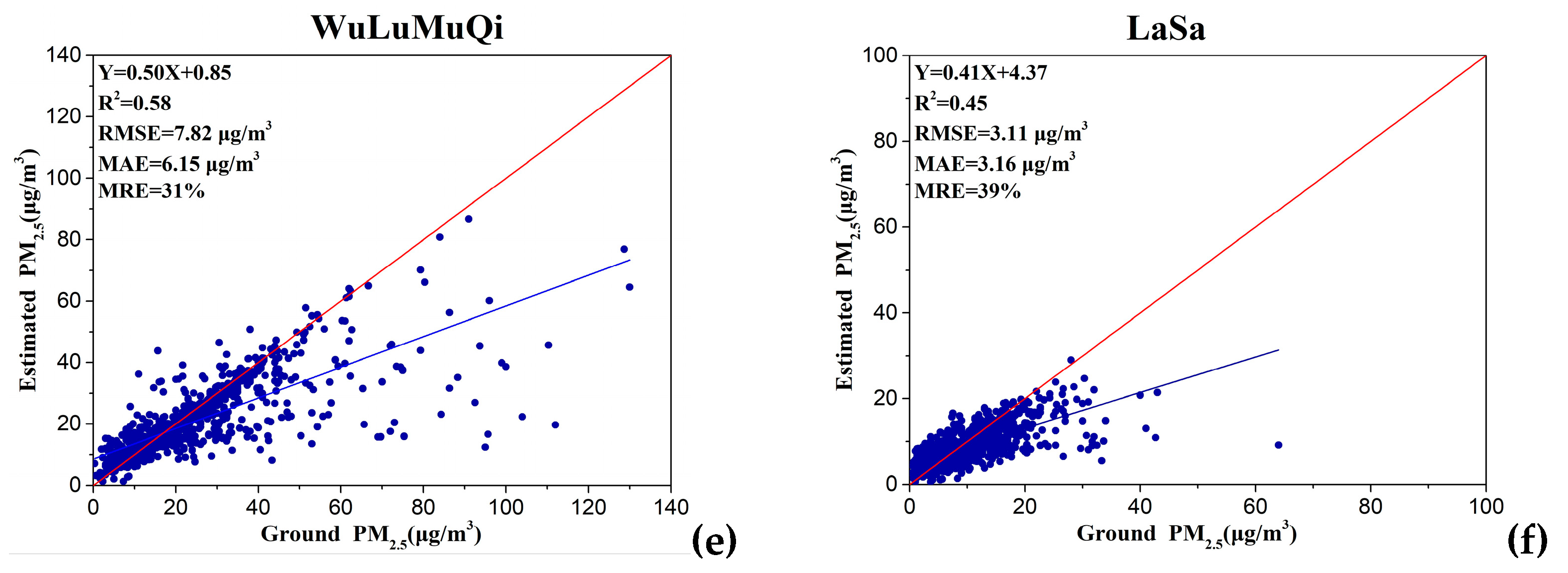
| Methods | Dataset | R2 | RMSE | MRE | MAE |
|---|---|---|---|---|---|
| minimum–maximum | Train | 0.89 | 9.84 | 30% | 6.06 |
| Validation | 0.79 | 13.30 | 40% | 8.06 | |
| Z-score | Train | 0.96 | 6.39 | 18% | 3.23 |
| Validation | 0.81 | 12.75 | 41% | 7.93 |
| Year | Factors | Train (Validation) | |||
|---|---|---|---|---|---|
| R2 | RMSE | MRE | MAE | ||
| 2018 | - | 0.92 (0.75) | 9.92 (16.60) | 26% (45%) | 4.84 (10.01) |
| LON, LAT | 0.94 (0.82) | 7.99 (13.30) | 21% (35%) | 4.58 (8.66) | |
| 2019 | - | 0.90 (0.78) | 8.96 (13.46) | 18% (44%) | 3.55 (8.58) |
| LON, LAT | 0.91 (0.83) | 8.45 (11.03) | 24% (36%) | 5.11 (7.21) | |
| 2020 | - | 0.92 (0.80) | 8.75 (12.31) | 24% (42%) | 4.77 (8.11) |
| LON, LAT | 0.94 (0.84) | 5.34 (10.98) | 24% (37%) | 3.25 (6.59) | |
| Year | Factors | Train (Validation) | |||
|---|---|---|---|---|---|
| R2 | RMSE | MRE | MAE | ||
| 2018 | - | 0.92 (0.74) | 9.43 (17.10) | 25% (47%) | 5.06 (10.36) |
| LON, LAT | 0.94 (0.79) | 7.89 (15.14) | 22% (40%) | 4.52 (9.14) | |
| 2019 | - | 0.90 (0.77) | 8.96 (13.83) | 18% (42%) | 3.55 (8.65) |
| LON, LAT | 0.94 (0.81) | 7.14 (12.43) | 21% (37%) | 3.87 (7.83) | |
| 2020 | - | 0.94 (0.73) | 5.57 (13.27) | 23% (45%) | 3.46 (7.90) |
| LON, LAT | 0.94 (0.78) | 5.63 (12.00) | 29% (42%) | 3.64 (7.07) | |
| Time | Method | Train or Validation | R2 | RMSE | MRE | MAE |
|---|---|---|---|---|---|---|
| 2018cold | DNN | Train | 0.95 | 6.65 | 18% | 3.67 |
| Validation | 0.83 | 14.16 | 39% | 8.76 | ||
| CapsNet | Train | 0.95 | 7.09 | 18% | 3.75 | |
| Validation | 0.83 | 13.93 | 36% | 8.46 | ||
| 2018warm | DNN | Train | 0.94 | 8.47 | 18% | 4.27 |
| Validation | 0.72 | 19.39 | 38% | 10.17 | ||
| CapsNet | Train | 0.95 | 6.29 | 15% | 2.73 | |
| Validation | 0.75 | 18.23 | 37% | 9.82 | ||
| 2019cold | DNN | Train | 0.95 | 7.44 | 17% | 3.68 |
| Validation | 0.82 | 13.33 | 36% | 8.40 | ||
| CapsNet | Train | 0.93 | 8.86 | 23% | 4.67 | |
| Validation | 0.84 | 12.52 | 36% | 7.87 | ||
| 2019warm | DNN | Train | 0.94 | 6.22 | 22% | 3.19 |
| Validation | 0.75 | 12.59 | 47% | 7.47 | ||
| CapsNet | Train | 0.88 | 8.63 | 26% | 4.52 | |
| Validation | 0.77 | 12.20 | 42% | 7.03 | ||
| 2020cold | DNN | Train | 0.95 | 6.18 | 19% | 2.98 |
| Validation | 0.81 | 11.52 | 33% | 7.36 | ||
| CapsNet | Train | 0.95 | 6.29 | 15% | 2.73 | |
| Validation | 0.82 | 11.50 | 31% | 7.34 | ||
| 2020warm | DNN | Train | 0.94 | 5.13 | 19% | 2.53 |
| Validation | 0.67 | 11.15 | 43% | 6.76 | ||
| CapsNet | Train | 0.94 | 5.25 | 14% | 2.35 | |
| Validation | 0.72 | 10.14 | 43% | 6.64 |
| Structures | R2 | RMSE | MRE | MAE |
|---|---|---|---|---|
| single capsule | 0.92 | 8.79 | 0.37 | 5.87 |
| Multiple capsules and single weight | 0.93 | 8.02 | 0.22 | 4.14 |
| Multi-capsule and multi-weight | 0.93 | 7.85 | 0.28 | 4.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Q.; Xie, T.; Zhu, S.; Fan, M.; Chen, L.; Tian, Y. Estimating the Near-Ground PM2.5 Concentration over China Based on the CapsNet Model during 2018–2020. Remote Sens. 2022, 14, 623. https://doi.org/10.3390/rs14030623
Zeng Q, Xie T, Zhu S, Fan M, Chen L, Tian Y. Estimating the Near-Ground PM2.5 Concentration over China Based on the CapsNet Model during 2018–2020. Remote Sensing. 2022; 14(3):623. https://doi.org/10.3390/rs14030623
Chicago/Turabian StyleZeng, Qiaolin, Tianshou Xie, Songyan Zhu, Meng Fan, Liangfu Chen, and Yu Tian. 2022. "Estimating the Near-Ground PM2.5 Concentration over China Based on the CapsNet Model during 2018–2020" Remote Sensing 14, no. 3: 623. https://doi.org/10.3390/rs14030623
APA StyleZeng, Q., Xie, T., Zhu, S., Fan, M., Chen, L., & Tian, Y. (2022). Estimating the Near-Ground PM2.5 Concentration over China Based on the CapsNet Model during 2018–2020. Remote Sensing, 14(3), 623. https://doi.org/10.3390/rs14030623





