Evaluating the Potential of Different Evapotranspiration Datasets for Distributed Hydrological Model Calibration
Abstract
:1. Introduction
2. Study Area and Datasets
2.1. Study Area
2.2. Datasets
2.2.1. Meteorological Data
2.2.2. Observed Streamflow and Soil Moisture Data
2.2.3. Gridded Evapotranspiration (ET) Datasets
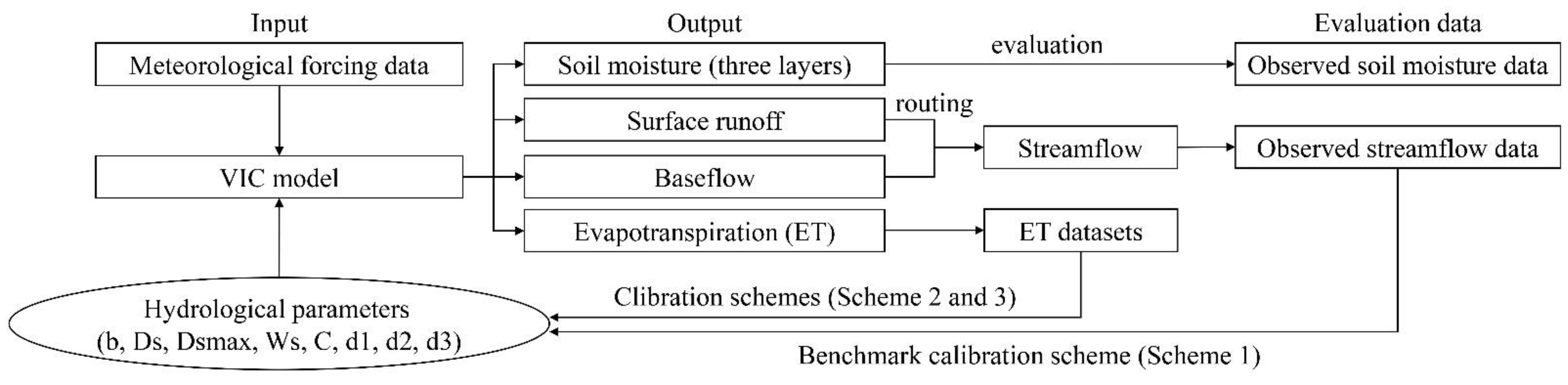
3. Methodology
3.1. Hydrological Model
3.2. Model Calibration and Evaluation
3.2.1. Calibration on Streamflow Data—Benchmark Scheme
3.2.2. Calibration on ET Dataset
3.2.3. Model Evaluation Metrics
3.3. Evaluation Method of ET Datasets
4. Results
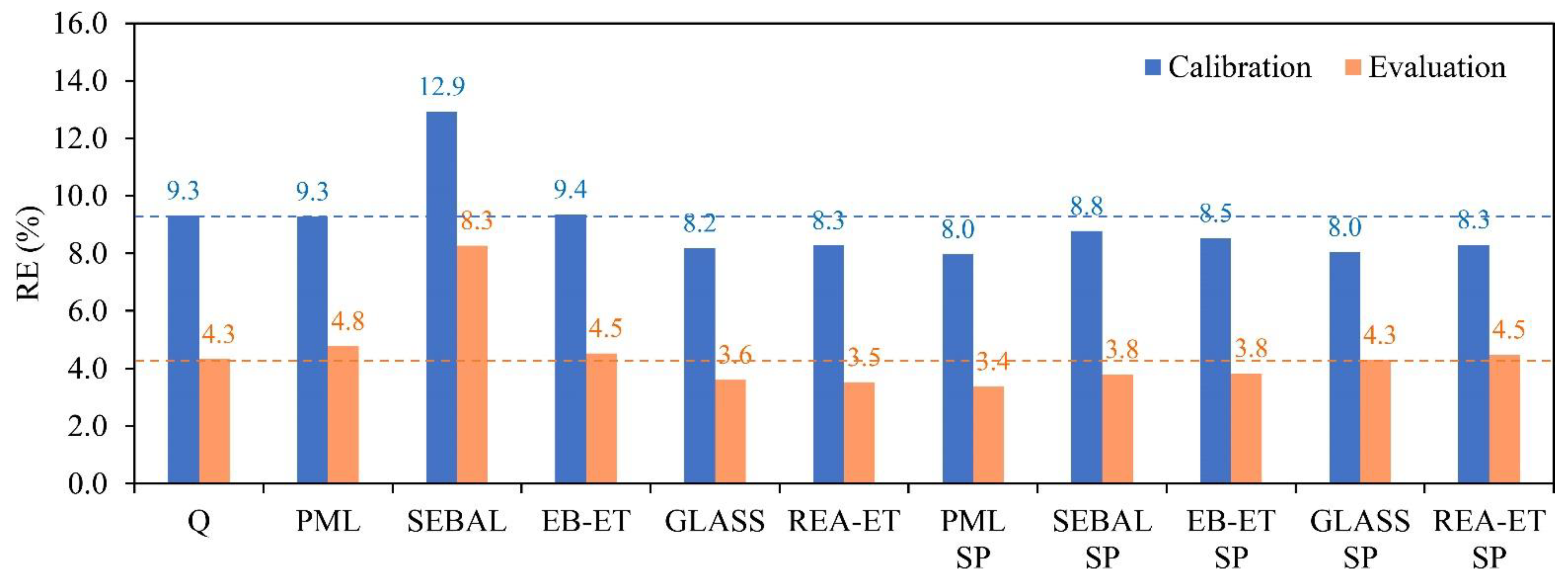
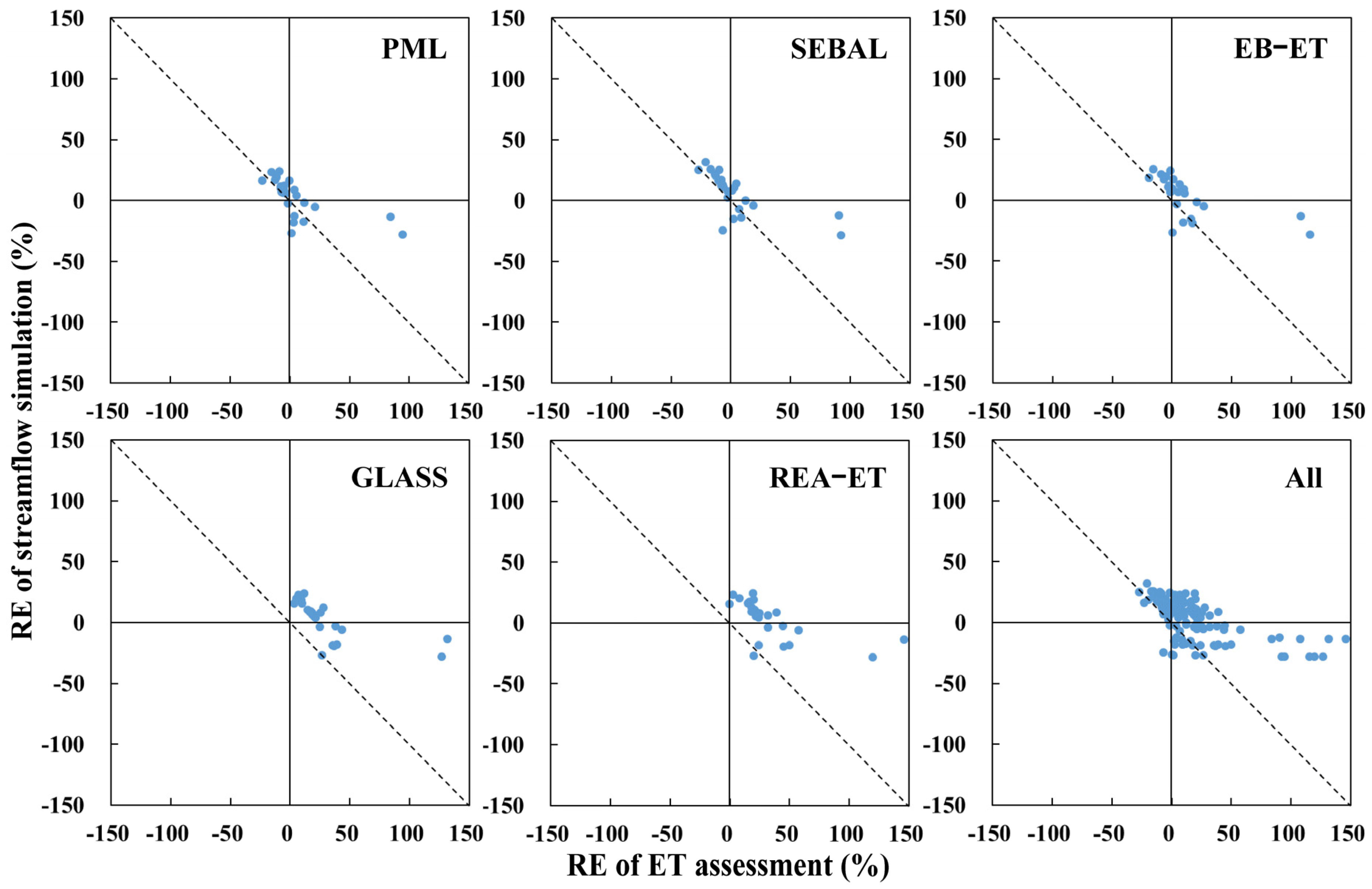
4.1. Assessment of ET Datasets
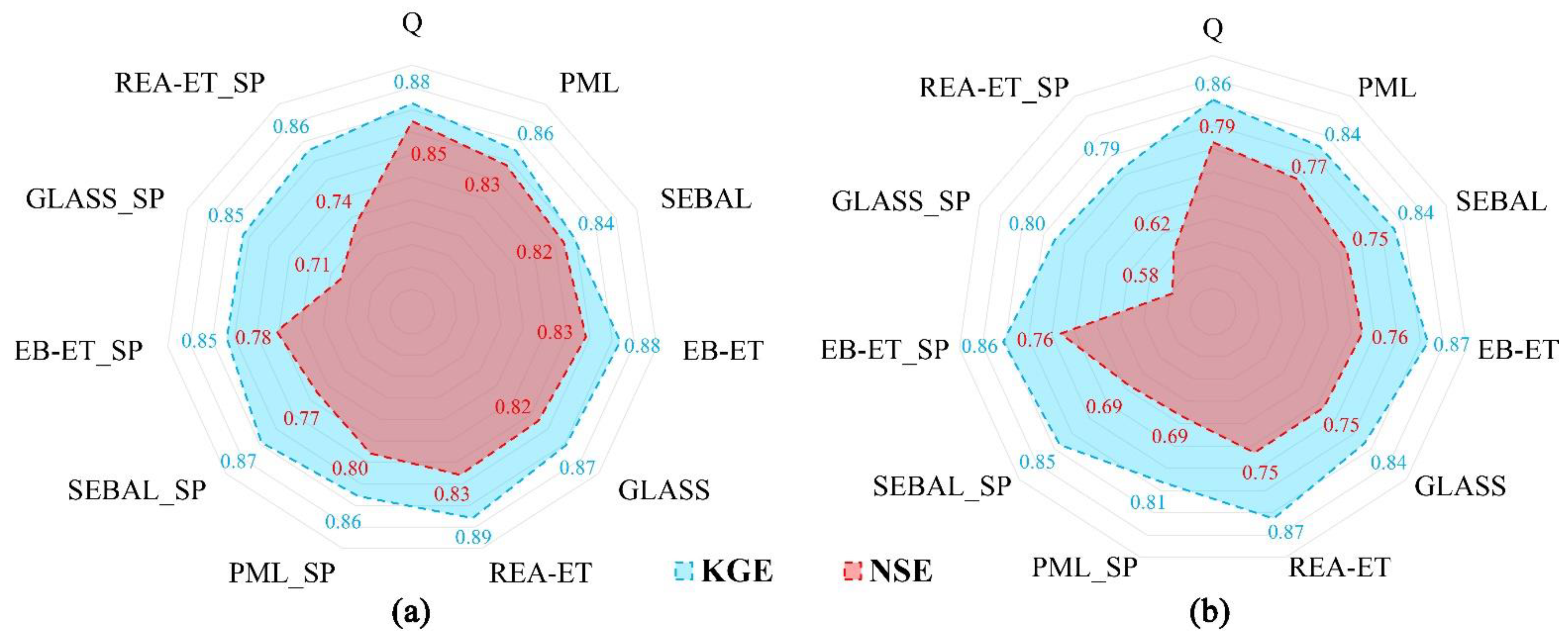
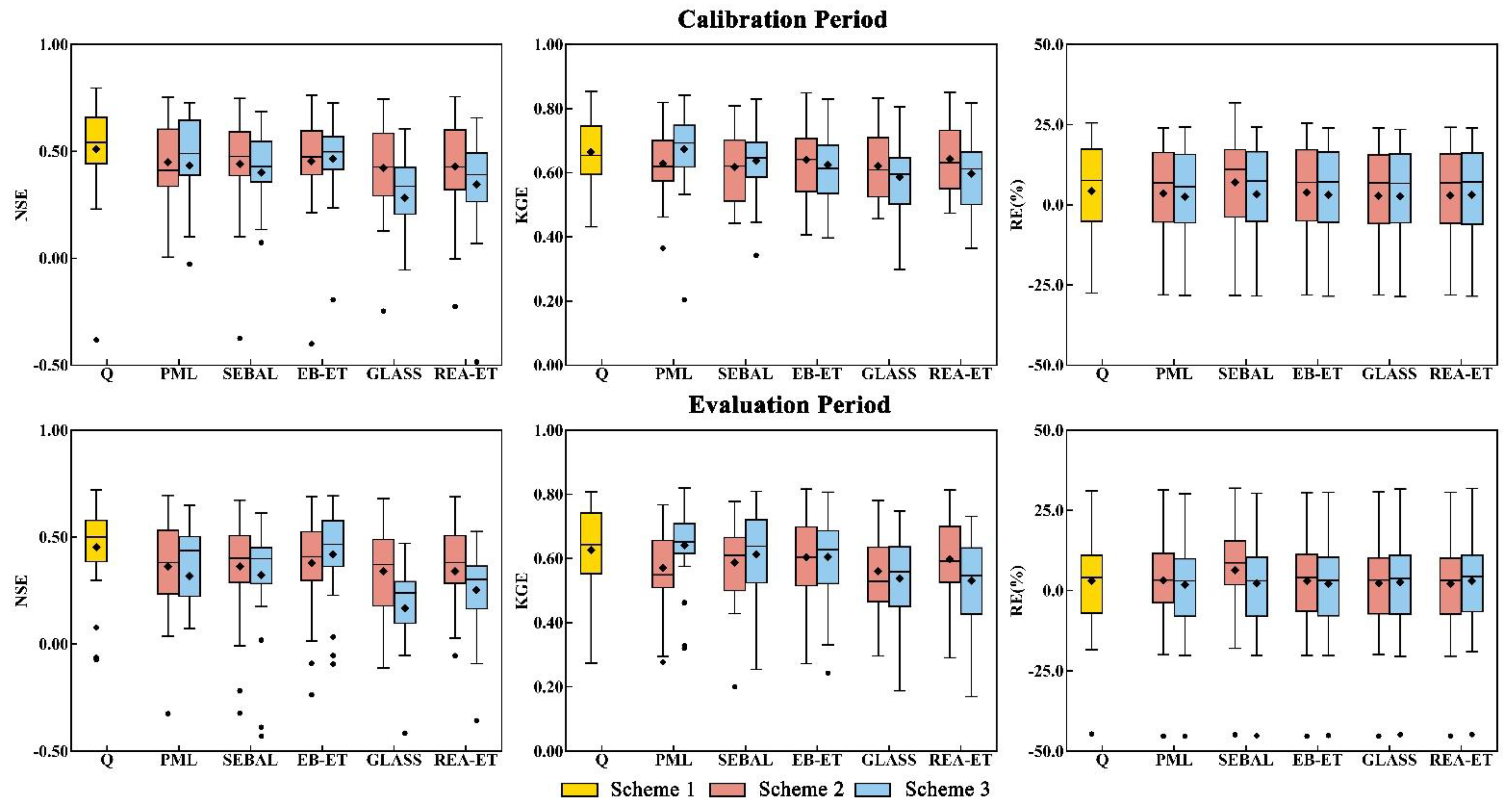
4.2. Model Performance for Streamflow at the Outlet of the Ganjiang River Basin (GRB)
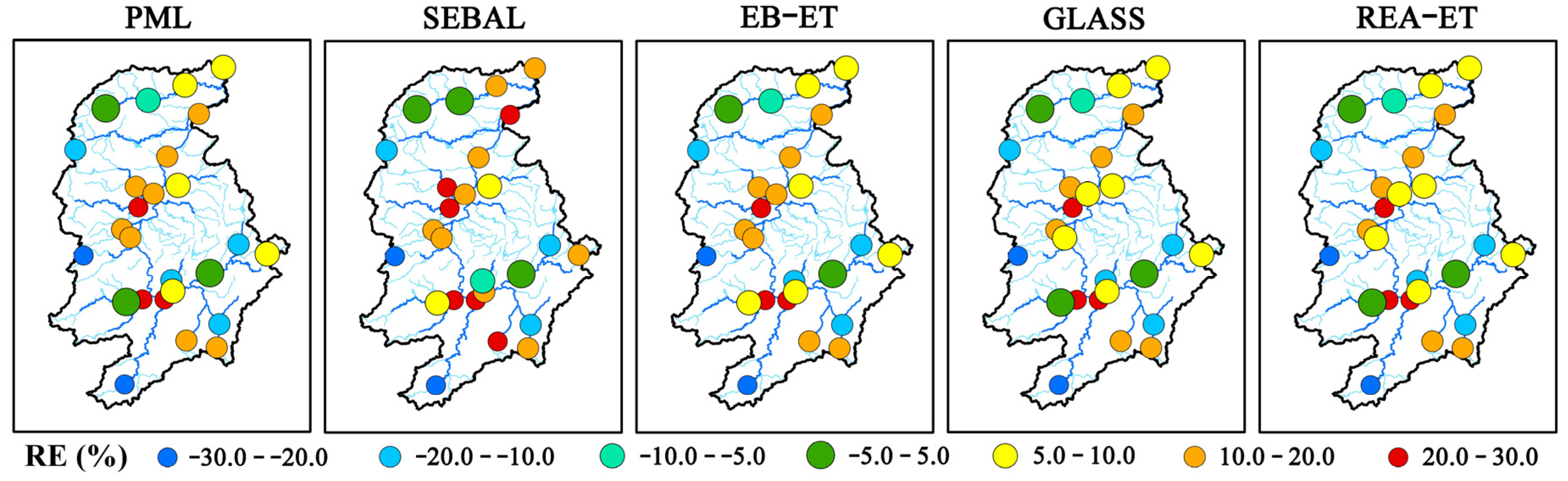
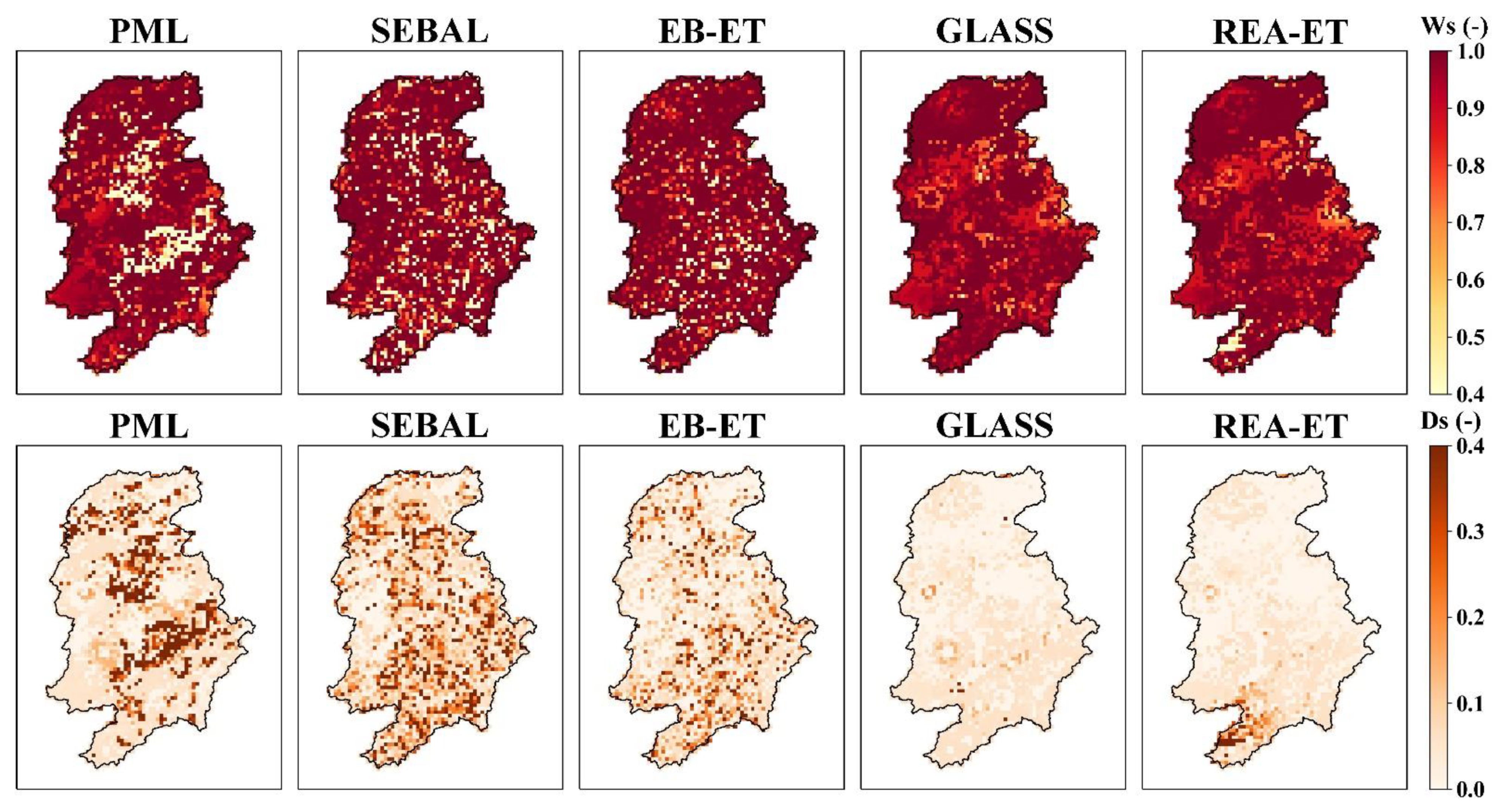
4.3. Model Performance for Streamflow in Sub-Basins
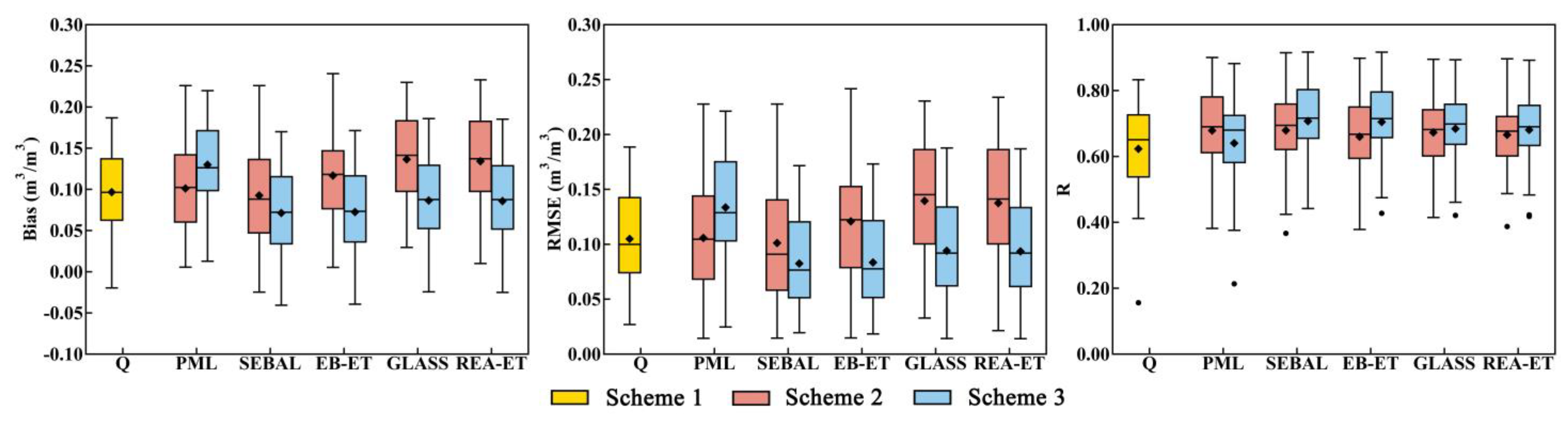
4.4. Model Performance for Soil Moisture
5. Discussion
6. Conclusions
- There is great potential for using different ET datasets to calibrate hydrological model parameters. Directly using optimized parameters for streamflow and soil moisture simulations can obtain satisfactory results.
- Compared to the benchmark Scheme 1 calibrated by observed streamflow only, most simulation performances of streamflow at the outlet and in sub-basins decreased, but some were as good as Scheme 1 when the ET datasets were used to calibrate parameters. A better soil moisture simulation was obtained by calibration schemes for different ET datasets.
- The accuracy of ET datasets has an important impact on model performance. The performance of streamflow simulations was consistent with the results of ET assessment performed using the water balance method.
- Overall, the model calibration cases with EB-ET and PML datasets produced the best performance on streamflow simulations, and the calibration case with the SEBAL dataset provided the highest contribution in improving soil moisture simulation. These three datasets also performed well in the evaluation of dataset accuracy using the water balance method.
Author Contributions
Funding
Conflicts of Interest
References
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef] [Green Version]
- Refsgaard, J.C. Parameterisation, calibration and validation of distributed hydrological models. J. Hydrol. 1997, 198, 69–97. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, P.; Zhao, X.; Gao, X.; Shi, Y. Assessing the spatial and temporal variation of the rainwater harvesting potential (1971–2010) on the Chinese Loess Plateau using the VIC model. Hydrol. Process. 2012, 28, 534–544. [Google Scholar] [CrossRef]
- Kittel, C.M.; Arildsen, A.L.; Dybkjær, S.; Hansen, E.R.; Linde, I.; Slott, E.; Tøttrup, C.; Bauer-Gottwein, P. Informing hydrological models of poorly gauged river catchments–A parameter regionalization and calibration approach. J. Hydrol. 2020, 587, 124999. [Google Scholar] [CrossRef]
- Bloschl, G.; Sivapalan, M. Scale issues in hydrological modelling: A review. Hydrol. Process. 1995, 9, 251–290. [Google Scholar] [CrossRef]
- Clark, M.P.; Rupp, D.E.; Woods, R.A.; Zheng, X.; Ibbitt, R.P.; Slater, A.G.; Schmidt, J.; Uddstrom, M.J. Hydrological Data Assimilation with the Ensemble Kalman Filter: Use of Streamflow Observations to Update States in a Distributed Hydrological Model. Adv. Water Resour. 2008, 31, 1309–1324. [Google Scholar] [CrossRef]
- Garavaglia, F.; Le Lay, M.; Gottardi, F.; Garçon, R.; Gailhard, J.; Paquet, E.; Mathevet, T. Impact of model structure on flow simulation and hydrological realism: From a lumped to a semi-distributed approach. Hydrol. Earth Syst. Sci. 2017, 21, 3937–3952. [Google Scholar] [CrossRef] [Green Version]
- Hrachowitz, M.; Fovet, O.; Ruiz, L.; Euser, T.; Gharari, S.; Nijzink, R.; Freer, J.; Savenije, H.H.G.; Gascuel-Odoux, C. Process Consistency in Models: The Importance of System Signatures, Expert Knowledge, and Process Complexity. Water Resour. Res. 2014, 50, 7445–7469. [Google Scholar] [CrossRef] [Green Version]
- Adhikary, P.P.; Sena, D.R.; Dash, C.J.; Mandal, U.; Nanda, S.; Madhu, M.; Sahoo, D.C.; Mishra, P.K. Effect of Calibration and Validation Decisions on Streamflow Modeling for a Heterogeneous and Low Runoff–Producing River Basin in India. J. Hydrol. Eng. 2019, 24, 05019015. [Google Scholar] [CrossRef]
- Lettenmaier, D.P.; Alsdorf, D.; Dozier, J.; Huffman, G.J.; Pan, M.; Wood, E.F. Inroads of remote sensing into hydrologic science during the WRR era. Water Resour. Res. 2015, 51, 7309–7342. [Google Scholar] [CrossRef]
- McCabe, M.F.; Rodell, M.; Alsdorf, D.E.; Miralles, D.G.; Uijlenhoet, R.; Wagner, W.; Lucieer, A.; Houborg, R.; Verhoest, N.E.C.; Franz, T.E.; et al. The future of Earth observation in hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 3879–3914. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, X.; Li, J.; Tolson, B.A. Progress in integrating remote sensing data and hydrologic modeling. Prog. Phys. Geogr. Earth Environ. 2014, 38, 464–498. [Google Scholar] [CrossRef] [Green Version]
- Corbari, C.; Mancini, M. Calibration and Validation of a Distributed Energy–Water Balance Model Using Satellite Data of Land Surface Temperature and Ground Discharge Measurements. J. Hydrometeorol. 2014, 15, 376–392. [Google Scholar] [CrossRef]
- Wu, H.; Robert, F.; Adler Yudong, T.; Huffman, G.J.; Li, H.; Wang, J. Real-Time Global Flood Estimation Using Satellite-Based Precipitation and a Coupled Land Surface and Routing Model. Water Resour. Res. 2014, 50, 2693–2717. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Wu, Z.; Crow, W.T.; Dong, J.; He, H. Improving Spatial Patterns Prior to Land Surface Data Assimilation via Model Calibration Using SMAP Surface Soil Moisture Data. Water Resour. Res. 2020, 56, e2020WR027770. [Google Scholar] [CrossRef]
- Berezowski, T.; Nossent, J.; Chormański, J.; Batelaan, O. Spatial sensitivity analysis of snow cover data in a distributed rainfall-runoff model. Hydrol. Earth Syst. Sci. 2015, 19, 1887–1904. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.; Shi, L.; Lin, G.; Lin, L. Comparison of physical-based, data-driven and hybrid modeling approaches for evapotranspiration estimation. J. Hydrol. 2021, 601, 126592. [Google Scholar] [CrossRef]
- Oki, T.; Kanae, S. Global Hydrological Cycles and World Water Resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Chiew, F.H.S.; Liu, C.; Tang, C.; Xia, J.; Tian, J.; Kong, D.; Li, C. Can Remotely Sensed Actual Evapotranspiration Facilitate Hydrological Prediction in Ungauged Regions without Runoff Calibration? Water Resour. Res. 2020, 56, e2019WR026236. [Google Scholar] [CrossRef]
- Elnashar, A.; Wang, L.; Wu, B.; Zhu, W.; Zeng, H. Synthesis of global actual evapotranspiration from 1982 to Earth Syst. Sci. Data 2021, 13, 447–480. [Google Scholar] [CrossRef]
- Lu, J.; Wang, G.; Chen, T.; Li, S.; Hagan, D.F.T.; Kattel, G.; Peng, J.; Jiang, T.; Su, B. A Harmonized Global Land Evaporation Dataset from Reanalysis Products Covering 1980–2017. Earth Syst. Sci. Data Discuss. 2021, 13, 5879–5898. [Google Scholar] [CrossRef]
- Dembélé, M.; Hrachowitz, M.; Savenije, H.H.G.; Mariéthoz, G.; Schaefli, B. Improving the Predictive Skill of a Distributed Hydrological Model by Calibration on Spatial Patterns With Multiple Satellite Data Sets. Water Resour. Res. 2020, 56, e2019WR026085. [Google Scholar] [CrossRef]
- Immerzeel, W.; Droogers, P. Calibration of a distributed hydrological model based on satellite evapotranspiration. J. Hydrol. 2008, 349, 411–424. [Google Scholar] [CrossRef]
- Jiang, L.; Wu, H.; Tao, J.; Kimball, J.S.; Alfieri, L.; Chen, X. Satellite-Based Evapotranspiration in Hydrological Model Calibration. Remote Sens. 2020, 12, 428. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Brunner, P.; Kinzelbach, W.; Li, W.; Dong, X. Calibration of a groundwater model using pattern information from remote sensing data. J. Hydrol. 2009, 377, 120–130. [Google Scholar] [CrossRef]
- Demirel, M.C.; Mai, J.; Mendiguren, G.; Koch, J.; Samaniego, L.; Stisen, S. Combining satellite data and appropriate objective functions for improved spatial pattern performance of a distributed hydrologic model. Hydrol. Earth Syst. Sci. 2018, 22, 1299–1315. [Google Scholar] [CrossRef] [Green Version]
- Dembélé, M.; Ceperley, N.; Zwart, S.; Salvadore, E.; Mariethoz, G.; Schaefli, B. Potential of satellite and reanalysis evaporation datasets for hydrological modelling under various model calibration strategies. Adv. Water Resour. 2020, 143, 103667. [Google Scholar] [CrossRef]
- Herman, M.R.; Hernandez-Suarez, J.S.; Nejadhashemi, A.P.; Kropp, I.; Sadeghi, A.M. Evaluation of Multi- and Many-Objective Optimization Techniques to Improve the Performance of a Hydrologic Model Using Evapotranspiration Remote-Sensing Data. J. Hydrol. Eng. 2020, 25, 04020006. [Google Scholar] [CrossRef]
- Nesru, M.; Shetty, A.; Nagaraj, M.K. Multi-variable calibration of hydrological model in the upper Omo-Gibe basin, Ethiopia. Acta Geophys. 2020, 68, 537–551. [Google Scholar] [CrossRef]
- Sirisena, T.; Maskey, S.; Ranasinghe, R. Hydrological Model Calibration with Streamflow and Remote Sensing Based Evapotranspiration Data in a Data Poor Basin. Remote. Sens. 2020, 12, 3768. [Google Scholar] [CrossRef]
- Shahrban, M.; Walker, J.P.; Wang, Q.J.; Robertson, D.E. On the Importance of Soil Moisture in Calibration of Rainfall-Runoff Models: Two Case Studies. Hydrol. Sci. J. 2018, 63, 1292–1312. [Google Scholar] [CrossRef] [Green Version]
- Xiong, L.; Zeng, L. Impacts of Introducing Remote Sensing Soil Moisture in Calibrating a Distributed Hydrological Model for Streamflow Simulation. Water 2019, 11, 666. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Wang, L.; Zhou, J.; Li, Y.; Sun, F.; Fu, G.; Li, X.; Sang, Y.-F. A worldwide evaluation of basin-scale evapotranspiration estimates against the water balance method. J. Hydrol. 2016, 538, 82–95. [Google Scholar] [CrossRef] [Green Version]
- Jiang, S.; Zhang, Z.; Huang, Y.; Chen, X.; Chen, S. Evaluating the TRMM Multisatellite Precipitation Analysis for Extreme Precipitation and Streamflow in Ganjiang River Basin, China. Adv. Meteorol. 2017, 2017, 1–11. [Google Scholar] [CrossRef]
- Reynolds, C.A.; Jackson, T.J.; Rawls, W.J. Estimating soil water-holding capacities by linking the Food and Agriculture Organization Soil map of the world with global pedon databases and continuous pedotransfer functions. Water Resour. Res. 2000, 36, 3653–3662. [Google Scholar] [CrossRef]
- Zhang, Y.; Kong, D.; Gan, R.; Chiew, F.H.S.; McVicar, T.R.; Zhang, Q.; Yang, Y. Coupled estimation of 500 m and 8-day resolution global evapotranspiration and gross primary production in 2002–2017. Remote Sens. Environ. 2019, 222, 165–182. [Google Scholar] [CrossRef]
- Cheng, M.; Jiao, X.; Li, B.; Yu, X.; Shao, M.; Jin, X. Long time series of daily evapotranspiration in China based on the SEBAL model and multisource images and validation. Earth Syst. Sci. Data 2021, 13, 3995–4017. [Google Scholar] [CrossRef]
- Chen, X.; Su, Z.; Ma, Y.; Trigo, I.; Gentine, P. Remote Sensing of Global Daily Evapotranspiration based on a Surface Energy Balance Method and Reanalysis Data. J. Geophys. Res. Atmos. 2021, 126, e2020JD032873. [Google Scholar] [CrossRef]
- Liang, S.; Zhao, X.; Liu, S.; Yuan, W.; Cheng, X.; Xiao, Z.; Zhang, X.; Liu, Q.; Cheng, J.; Tang, H.; et al. A long-term Global LAnd Surface Satellite (GLASS) data-set for environmental studies. Int. J. Digit. Earth 2013, 6, 5–33. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, N.; Peubey, C.; Radu, R.; Schepers, D.; et al. The Era5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (Merra-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef] [PubMed]
- Sheffield, J.; Wood, E.F. Characteristics of Global and Regional Drought, 1950–2000: Analysis of Soil Moisture Data from Off-Line Simulation of the Terrestrial Hydrologic Cycle. J. Geophys. Res. Atmos. 2007, 112, D17115. [Google Scholar] [CrossRef] [Green Version]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.B. A Simple Hydrologically Based Model of Land Surface Water and Energy Fluxes for General Circulation Models. J. Geophys. Res. Atmos. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Liang, X.; Wood, E.E.; Lettenmaier, D.P. Surface Soil Moisture Parameterization of the Vic-2l Model: Evaluation and Modification. Glob. Planet. Chang. 1996, 13, 195–206. [Google Scholar] [CrossRef]
- Fangni, L.; Crow, W.T.; Holmes, T.R.H.; Hain, C.; Anderson, M.C. Global Investigation of Soil Moisture and Latent Heat Flux Coupling Strength. Water Resour. Res. 2018, 54, 8196–8215. [Google Scholar] [CrossRef]
- Xie, Z.; Yuan, F.; Duan, Q.; Zheng, J.; Liang, M.; Chen, F. Regional Parameter Estimation of the VIC Land Surface Model: Methodology and Application to River Basins in China. J. Hydrometeorol. 2007, 8, 447–468. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Wu, Z.; Singh, V.P.; He, H.; He, J.; Yin, H.; Zhang, Y. Coupled hydrology-crop growth model incorporating an improved evapotranspiration module. Agric. Water Manag. 2020, 246, 106691. [Google Scholar] [CrossRef]
- Rosenbrock, H.H. An Automatic Method for Finding the Greatest or Least Value of a Function. Comput. J. 1960, 3, 175–184. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Lu, G.; Wen, L.; Lin, C.A.; Zhang, J.; Yang, Y. Thirty-Five Year (1971–2005) Simulation of Daily Soil Moisture Using the Variable Infiltration Capacity Model over China. Atmos. Ocean. 2007, 45, 37–45. [Google Scholar] [CrossRef]
- Lu, G.; Liu, J.; Wu, Z.; He, H.; Xu, H.; Lin, Q. Development of a Large-Scale Routing Model with Scale Independent by Considering the Damping Effect of Sub-Basins. Water Resour. Manag. 2015, 29, 5237–5253. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. Am. Soc. Agric. Biol. Eng. 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424–425, 264–277. [Google Scholar] [CrossRef]
- Penna, D.; Borga, M.; Norbiato, D.; Fontana, G.D. Hillslope scale soil moisture variability in a steep alpine terrain. J. Hydrol. 2009, 364, 311–327. [Google Scholar] [CrossRef]
- Wu, Z.; Zhou, J.; He, H.; Lin, Q.; Wu, X.; Xu, Z. An advanced error correction methodology for merging in-situ observed and model-based soil moisture. J. Hydrol. 2018, 566, 150–163. [Google Scholar] [CrossRef]
- Dong, J.; Crow, W.T.; Tobin, K.J.; Cosh, M.H.; Bosch, D.D.; Starks, P.J.; Seyfried, M.; Collins, C.H. Comparison of Microwave Remote Sensing and Land Surface Modeling for Surface Soil Moisture Climatology Estimation. Remote. Sens. Environ. 2020, 242, 111756. [Google Scholar] [CrossRef]
- Prudhomme, C.; Jakob, D.; Svensson, C. Uncertainty and climate change impact on the flood regime of small UK catchments. J. Hydrol. 2003, 277, 1–23. [Google Scholar] [CrossRef]
- Shah, S.; Duan, Z.; Song, X.; Li, R.; Mao, H.; Liu, J.; Ma, T.; Wang, M. Evaluating the added value of multi-variable calibration of SWAT with remotely sensed evapotranspiration data for improving hydrological modeling. J. Hydrol. 2021, 603, 127046. [Google Scholar] [CrossRef]
- Hulsman, P.; Savenije, H.H.G.; Hrachowitz, M. Learning from satellite observations: Increased understanding of catchment processes through stepwise model improvement. Hydrol. Earth Syst. Sci. 2021, 25, 957–982. [Google Scholar] [CrossRef]
- Poméon, T.; Diekkrüger, B.; Springer, A.; Kusche, J.; Eicker, A. Multi-Objective Validation of SWAT for Sparsely-Gauged West African River Basins—A Remote Sensing Approach. Water 2018, 10, 451. [Google Scholar] [CrossRef] [Green Version]
- Beck, H.E.; Pan, M.; Lin, P.; Seibert, J.; van Dijk, A.I.J.M.; Wood, E.F. Global Fully Distributed Parameter Regionalization Based on Observed Streamflow from 4,229 Headwater Catchments. J. Geophys. Res. Atmos. 2020, 125, e2019JD031485. [Google Scholar] [CrossRef]
- Huang, Q.; Qin, G.; Zhang, Y.; Tang, Q.; Liu, C.; Xia, J.; Chiew, F.H.S.; Post, D. Using Remote Sensing Data-Based Hydrological Model Calibrations for Predicting Runoff in Ungauged or Poorly Gauged Catchments. Water Resour. Res. 2020, 56, e2020WR028205. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Y. Regionalising rainfall-runoff modelling for predicting daily runoff: Comparing gridded spatial proximity and gridded integrated similarity approaches against their lumped counterparts. J. Hydrol. 2017, 550, 279–293. [Google Scholar] [CrossRef]
- Bai, P.; Liu, X. Intercomparison and evaluation of three global high-resolution evapotranspiration products across China. J. Hydrol. 2018, 566, 743–755. [Google Scholar] [CrossRef]
- Sorensson, A.A.; Ruscica, R.C. Intercomparison and Uncertainty Assessment of Nine Evapotranspiration Estimates over South America. Water Resour. Res. 2018, 54, 2891–2908. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Grimaldi, S.; Pauwels, V.R.N.; Walker, J.P. Hydrologic Model Calibration Using Remotely Sensed Soil Moisture and Discharge Measurements: The Impact on Predictions at Gauged and Ungauged Locations. J. Hydrol. 2018, 557, 897–909. [Google Scholar] [CrossRef]
- Cayrol, P.; Kergoat, L.; Moulin, S.; Dedieu, G.; Chehbouni, A. Calibrating a Coupled SVAT–Vegetation Growth Model with Remotely Sensed Reflectance and Surface Temperature—A Case Study for the HAPEX-Sahel Grassland Sites. J. Appl. Meteorol. 2000, 39, 2452–2472. [Google Scholar] [CrossRef]
- Wanders, N.; Bierkens, M.F.P.; de Jong, S.M.; de Roo, A.; Karssenberg, D. The benefits of using remotely sensed soil moisture in parameter identification of large-scale hydrological models. Water Resour. Res. 2014, 50, 6874–6891. [Google Scholar] [CrossRef] [Green Version]

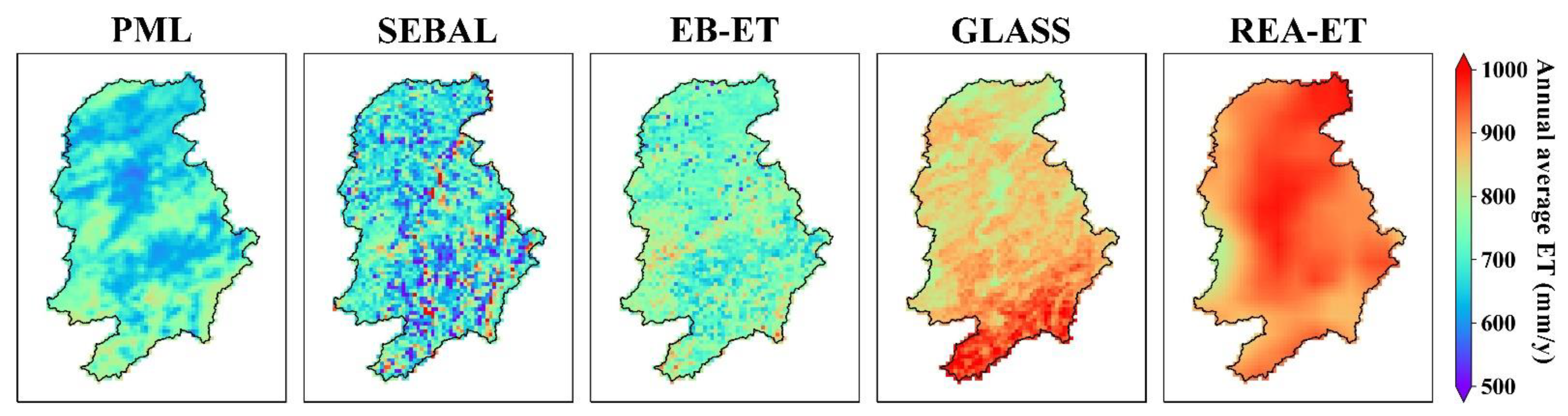
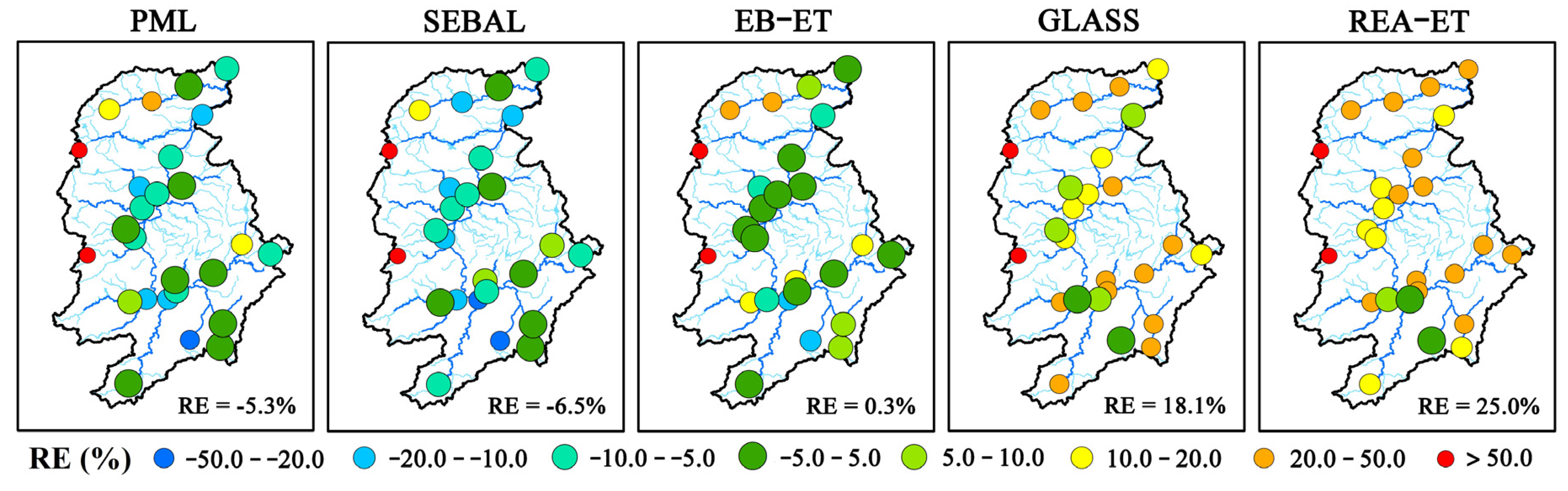


| ID | Name | Lat (°) | Lon (°) | Drainage Area (km2) | Timespan |
|---|---|---|---|---|---|
| 1 | Waizhou | 28.63 | 115.83 | 80,860 | 1980–2014 |
| 2 | Zhangshu | 28.07 | 115.53 | 71,190 | 1998–2014 |
| 3 | Xiajiang | 27.55 | 115.15 | 62,690 | 1980–2014 |
| 4 | Ji’an | 27.10 | 114.98 | 56,180 | 1980–2014 |
| 5 | Dongbei | 26.57 | 114.70 | 40,190 | 1980–2014 |
| 6 | Xiashan | 25.92 | 115.22 | 15,940 | 1980–2014 |
| 7 | Julongtan | 25.82 | 115.12 | 7742 | 1980–2014 |
| 8 | Bashang | 25.82 | 114.85 | 7457 | 1980–2014 |
| 9 | Fenkeng | 26.13 | 115.67 | 6358 | 1980–2014 |
| 10 | Gan’an | 28.42 | 115.37 | 6062 | 1991–2014 |
| 11 | Shangshalan | 26.93 | 114.80 | 5258 | 1980–2014 |
| 12 | Shanggao | 28.23 | 114.92 | 3706 | 1986–2014 |
| 13 | Xintian | 27.20 | 115.28 | 3546 | 1980–2014 |
| 14 | Tiantou | 25.78 | 114.65 | 3196 | 1980–2014 |
| 15 | Saikuang | 27.18 | 114.77 | 3071 | 1980–2014 |
| 16 | Hanlinqiao | 26.05 | 115.20 | 2659 | 1980–2014 |
| 17 | Ningdu | 26.48 | 116.02 | 2286 | 1980–2014 |
| 18 | Mazhou | 25.52 | 115.78 | 1742 | 1980–2014 |
| 19 | Linkeng | 26.67 | 114.60 | 993 | 1980–2014 |
| 20 | Weifang | 28.13 | 114.40 | 975 | 1980–2014 |
| 21 | Shicheng | 26.37 | 116.37 | 659 | 1980–2014 |
| 22 | Yangxinjiang | 25.32 | 115.38 | 561 | 1980–2014 |
| 23 | Junmenling | 25.23 | 115.75 | 455 | 1984–2014 |
| 24 | Dutou | 24.78 | 114.63 | 434 | 1980–2014 |
| 25 | Luxi | 27.63 | 114.03 | 330 | 1980–2014 |
| 26 | Chuzhou | 26.35 | 114.13 | 287 | 1980–2014 |
| ID | Name | Lat (°N) | Lon (°E) | Land Use | Soil Texture of the First Layer | Soil Texture of the Second Layer | Timespan |
|---|---|---|---|---|---|---|---|
| 1 | 57992 | 25.68 | 114.78 | Wooded grassland | Clay loam | Clay loam | 2013–2014 |
| 2 | 623A1600 | 27.83 | 115.03 | Cropland | Clay | Clay | 2011–2014 |
| 3 | 623A1700 | 25.73 | 114.73 | Wooded grassland | Clay loam | Clay loam | 2011–2014 |
| 4 | 623A1800 | 25.28 | 114.93 | Wooded grassland | Clay loam | Clay | 2011–2014 |
| 5 | 623A1900 | 25.83 | 115.13 | Wooded grassland | Clay loam | Clay loam | 2011–2012 |
| 6 | 623A2100 | 26.58 | 115.38 | Woodland | Clay loam | Clay | 2011–2012 |
| 7 | 623A2200 | 24.78 | 114.48 | Woodland | Clay loam | Clay | 2011–2012 |
| 8 | 623A2500 | 26.13 | 116.18 | Woodland | Clay loam | Clay | 2011–2012 |
| 9 | 623A2600 | 26.08 | 115.58 | Grassland | Clay loam | Clay loam | 2011–2012 |
| 10 | 623A2700 | 25.53 | 115.78 | Cropland | Clay loam | Clay loam | 2011–2014 |
| 11 | 623A2800 | 27.33 | 115.13 | Grassland | Clay | Clay | 2011–2013 |
| 12 | 623A2900 | 26.58 | 114.73 | Woodland | Clay | Clay | 2011–2012 |
| 13 | 623A3100 | 26.38 | 114.58 | Cropland | Clay | Clay | 2012–2013 |
| 14 | 623A3200 | 27.08 | 115.63 | Wooded grassland | Clay loam | Clay | 2011–2014 |
| 15 | 623A3300 | 26.68 | 114.68 | Cropland | Clay | Clay | 2012–2014 |
| 16 | 623A3500 | 27.38 | 114.58 | Woodland | Clay | Clay | 2011–2013 |
| 17 | 623A3600 | 27.03 | 114.33 | Wooded grassland | Clay loam | Clay | 2011–2013 |
| 18 | 623A3900 | 27.13 | 114.93 | Cropland | Clay | Clay | 2011–2012 |
| 19 | 623A4000 | 28.13 | 114.48 | Wooded grassland | Clay loam | Clay | 2011–2014 |
| 20 | 623A4300 | 27.33 | 114.48 | Woodland | Clay loam | Clay | 2011–2012 |
| 21 | 623A5100 | 28.18 | 115.63 | Cropland | Clay | Clay | 2011–2012 |
| 22 | 623A5300 | 28.38 | 115.43 | Cropland | Clay | Clay | 2011–2014 |
| 23 | 623A5700 | 28.08 | 115.33 | Cropland | Clay loam | Clay | 2012–2014 |
| 24 | 623A5900 | 27.88 | 114.78 | Wooded grassland | Clay | Clay | 2012–2013 |
| 25 | 623A6100 | 27.33 | 115.73 | Grassland | Clay loam | Clay | 2011–2014 |
| 26 | J7258 | 27.13 | 113.98 | Woodland | Clay loam | Clay | 2013–2014 |
| 27 | J8248 | 26.83 | 114.93 | Wooded grassland | Clay | Clay | 2013–2014 |
| 28 | J9901 | 26.43 | 115.98 | Wooded grassland | Clay loam | Clay loam | 2013–2014 |
| Dataset | Method | Resolution | Reference/Data Portal | Timespan | Spatial Coverage | |
|---|---|---|---|---|---|---|
| Spatial | Temporal | |||||
| PML | PML | 0.05° | 8d | Zhang, et al. [36] https://data.tpdc.ac.cn/en/data/48c16a8d-d307-4973-abab-972e9449627c/, accessed on 25 October 2021. | 2002–2019 | Global |
| SEBAL | SEBAL | 1km | daily | Cheng, et al. [37] https://zenodo.org/record/4243988, accessed on 25 October 2021. | 2001–2018 | China |
| EB-ET | SEBS | 5km | daily | Chen, et al. [38] https://data.tpdc.ac.cn/en/data/df4005fb-9449-4760-8e8a-09727df9fe36, accessed on 25 October 2021. | 2000–2017 | Global |
| GLASS | MOD16, RRS-PM, P-T, MS-PT, UMD-SEMI | 1km | 8d | Liang, et al. [39] http://www.glass.umd.edu/, accessed on 25 October 2021. | 2000–present | Global |
| REA-ET | Merged dataset (ERA5, MERRA2, GLDAS) | 0.25° | daily | Lu, Wang, Chen, Li, Hagan, Kattel, Peng, Jiang and Su [21] https://zenodo.org/record/4595941, accessed on 25 October 2021. | 1980–2017 | Global |
| Parameter | Unit | Description | Feasible Range | |
|---|---|---|---|---|
| Minimum | Maximum | |||
| b | - | variable infiltration curve parameter | 0.0001 | 0.35 |
| Ds | - | fraction of Dsmax where non-linear baseflow begins | 0.0001 | 0.4 |
| Dsmax | mm | maximum velocity of baseflow | 0.0 | 40.0 |
| Ws | - | fraction of maximum soil moisture where non-linear baseflow occurs | 0.4 | 1.0 |
| C | - | exponent of the nonlinear part of the baseflow curve | 2.0 | 2.0 |
| d1 | m | thickness of first soil moisture layer | 0.1 | 0.1 |
| d2 | m | thickness of second soil moisture layer | 0.1 | 1.5 |
| d3 | m | thickness of third soil moisture layer | 0.1 | 1.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, X.; Wu, Z.; He, H.; Xu, Z. Evaluating the Potential of Different Evapotranspiration Datasets for Distributed Hydrological Model Calibration. Remote Sens. 2022, 14, 629. https://doi.org/10.3390/rs14030629
Guo X, Wu Z, He H, Xu Z. Evaluating the Potential of Different Evapotranspiration Datasets for Distributed Hydrological Model Calibration. Remote Sensing. 2022; 14(3):629. https://doi.org/10.3390/rs14030629
Chicago/Turabian StyleGuo, Xiao, Zhiyong Wu, Hai He, and Zhengguang Xu. 2022. "Evaluating the Potential of Different Evapotranspiration Datasets for Distributed Hydrological Model Calibration" Remote Sensing 14, no. 3: 629. https://doi.org/10.3390/rs14030629
APA StyleGuo, X., Wu, Z., He, H., & Xu, Z. (2022). Evaluating the Potential of Different Evapotranspiration Datasets for Distributed Hydrological Model Calibration. Remote Sensing, 14(3), 629. https://doi.org/10.3390/rs14030629





